28. Последовательное соединение r, l, c. Резонанс напряжения.

№27. Параллельное соединение R, L, C. Резонанс токов.

Резонанс токов, или параллельный резонанс, получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор включен вне контура (рис.1 а). Сам же колебательный контур, рассматриваемый отвлеченно от генератора, надо по-прежнему представлять себе как последовательную цепь из L и С. Не следует считать, что в схеме резонанса токов генератор и контур соединены между собой параллельно. Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор/

Условия получения резонанса токов такие же, как и для резонанса напряжений: f =fo или xL = хC. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным.

Полное (эквивалентное) сопротивление контура для генератора при резонансе токов Rэ можно подсчитать по любой из следующих формул

где L и С — в генри и фарадах, а Rэ, р и r — в омах. Сопротивление Rэ, называемое резонансным сопротивлением, является чисто активным и поэтому при резонансе токов нет сдвига фаз между напряжением генератора и его током. На (рис.1 б смотри выше, где рис. 1а)) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f. В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости IL и IС можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи IL, и IC в действительности имеют сдвиг фаз несколько меньше 180° и ток IL немного( меньше Iс.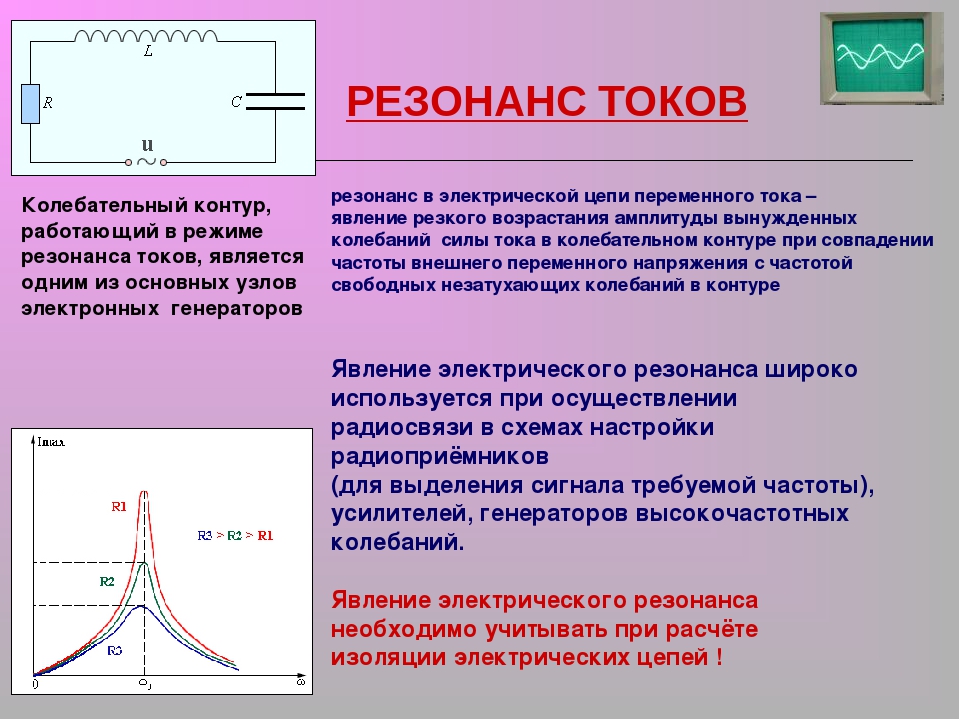

Поэтому по первому закону Кирхгофа для точки разветвления можно написать

Чем меньше активное сопротивление в контуре, тем меньше разница между IC и IL, тем меньше ток генератора и тем больше сопротивление контура. Это вполне понятно. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний. Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности. Активная мощность, расходуемая генератором, может быть подсчитана как

или как мощность потерь в активном сопротивлении контура

где I к — ток в контуре, равный IL или IC. Для резонанса токов так же, как и для резонанса напряжений, характерно возникновение в контуре мощных колебаний при незначительной затрате мощности генератора.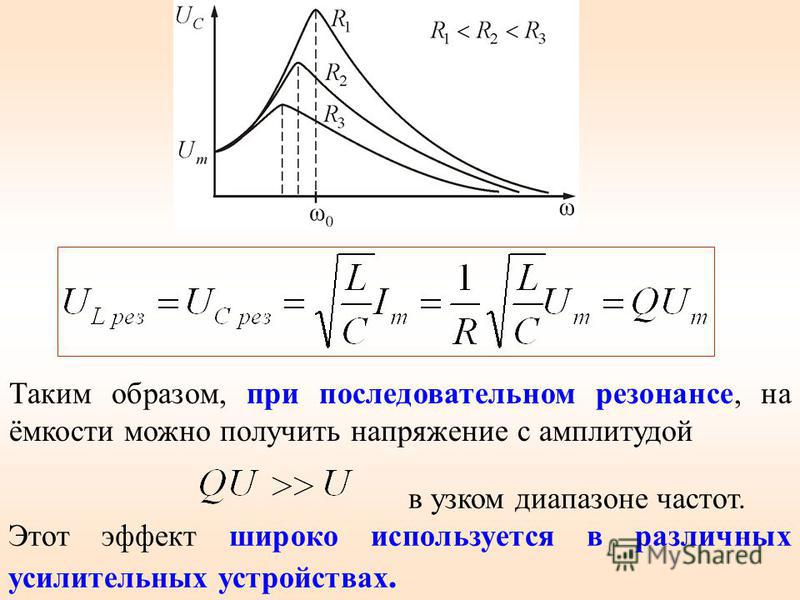 На явление резонанса в параллельном контуре большое влияние оказывает внутреннее сопротивление Ri питающего генератора. Если это сопротивление мало, то напряжение на зажимах генератора, а следовательно, и на контуре незначительно отличается от эдс генератора и остается почти постоянным по амплитуде, несмотря на изменения тока при изменении частоты. Действительно, U = Е — IRi, но так как Ri величина малая, то потеря напряжения внутри генератора IRi также незначительна и U = Е. Полное сопротивление цепи в этом случае приближенно равно только сопротивлению контура. При резонансе последнее сильно возрастает и ток генератора резко уменьшается. Кривая изменения тока на (рис.1 б) соответствует именно такому случаю. Постоянство амплитуды напряжения на контуре также объясняет формула U = I * z. Для случая резонанса z велико, но I — величина малая, а если резонанса нет, то z уменьшается, но зато I увеличивается и произведение I*z остается примерно прежним. Как видно, при малом Ri генератора параллельный контур не обладает резонансными свойствами в отношении напряжения: при резонансе напряжение на контуре почти не возрастает.

Не будут заметно увеличиваться и токи IL И IС. Следовательно, при малом Ri генератора контур не имеет резонансных свойств и по отношению к токам в катушке и конденсаторе. В радиотехнических схемах параллелыный контур обычно питается от генератора с большим внутренним сопротивлением, роль которого выполняет электронная лампа или полупроводниковый прибор. Если внутреннее сопротивление генератора значительно больше, чем сопротивление контура r, то параллельный контур приобретает резко выраженные резонансные свойства. В этом случае полное сопротивление цепи приближенно равно одному Ri и почти неизменно при изменении частоты. Ток I, питающий контур, также почти постоянен по амплитуде:

Но тогда напряжение на контуре U = I * z при изменении частоты будет следовать за изменениями сопротивления контура z, т.е. при резонансе U резко увеличится. Соответственно возрастут токи IL и IC. Таким образом, при большом Ri генератора кривая изменения z (рис.1 б) будет в других масштабах приближенно показывать также изменение напряжения на контуре U и изменения токов IL и IC На (рис.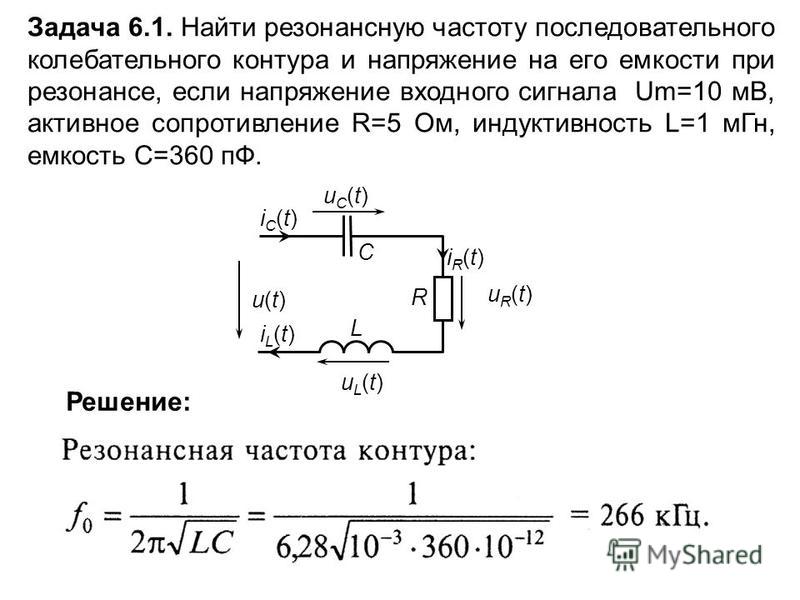 2) изображена подобная кривая вместе с графиком тока генератора, который в данном случае почти не меняется.

Рис.2 — Резонансные кривые параллельного контура при большом внутреннем сопротивлении генератора

Основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты.

Имеются два случая резонанса в колебательных контурах: резонанс напряжений и резонанс токов. Резонанс напряжений, или последовательный резонанс, наблюдается в случае, когда генератор переменной эдс нагружен

Рис.1 — Схема и резонансные кривые для резонанса напряжений

на соединенные последовательно L и С контура (рис.1 а), т.е. включен внутри контура. В такой цепи имеется активное сопротивление г и общее реактивное сопротивление х, равное

Разность хL, и xC берется потому, что индуктивное и емкостное сопротивления оказывают противоположные влияния на ток. Первое вызывает отставание по фазе тока от напряжения, а второе, наоборот, создает отставание напряжения от тока. Для собственных колебаний xL и хс равны друг другу. Если частота генератора равна частоте контура, то для тока, создаваемого генератором, xL и хC также одинаковы. Тогда общее реактивное сопротивление х станет равным нулю и полное сопротивление цепи для генератора равно только одному активному сопротивлению, которое в контурах имеет сравнительно небольшую величину. Благодаря этому ток значительно возрастает и устраняется сдвиг фаз между напряжением генератора и током. Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным. Условием резонанса напряжений является равенство частот генератора и контура f = fo, или равенство индуктивного и емкостного сопротивлений для тока генератора: xL = хC. Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера.

Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера. В любом из этих случаев при отклонении от резонанса полное сопротивление контура возрастает по сравнению а его величиной при резонансе. На (рис.1 б) показаны графики изменения полного сопротивления контура z и тока I при изменении частоты генератора f. Для расчета сопротивления контура и тока при резонансе напряжений служат простые формулы:

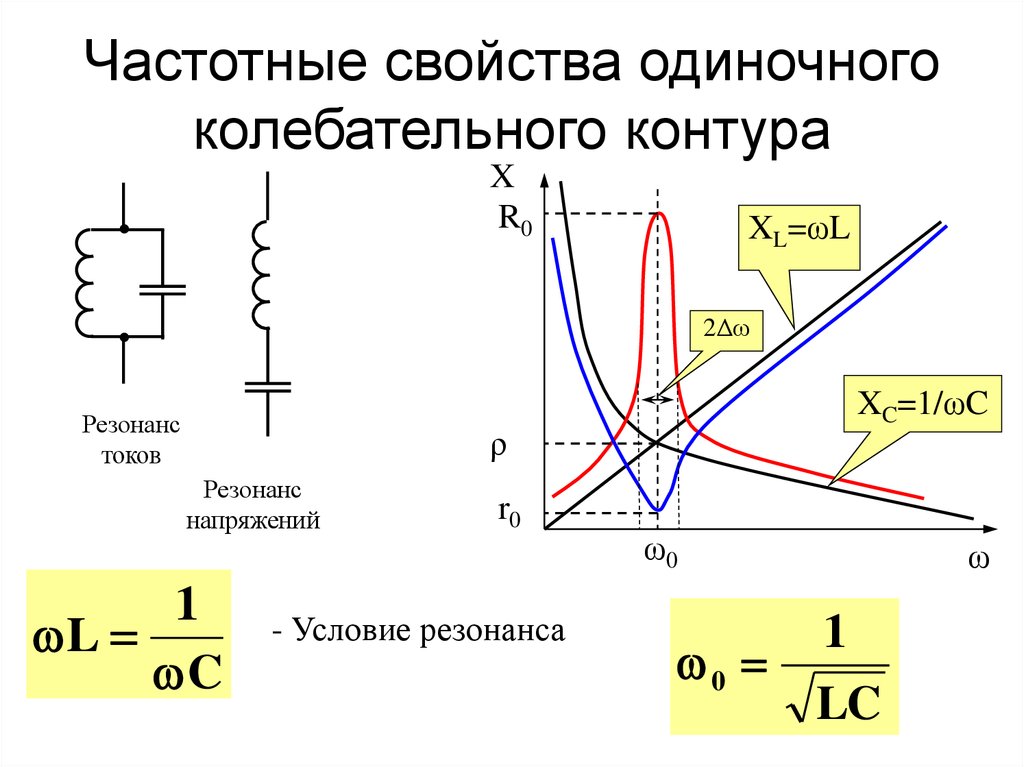
Таким образом, напряжение генератора U равно падению напряжения на активном сопротивлении (г). Большой ток в контуре при резонансе создает на индуктивном и емкостном сопротивлениях напряжения, значительно превышающие напряжение генератора. Они равны:

Так как хL = хC = р, то эти напряжения равны, но они противоположны по фазе и взаимно компенсируют друг друга. Действительно, напряжение на катушке опережает ток на 90°, а напряжение на конденсаторе отстает от тока на 90°.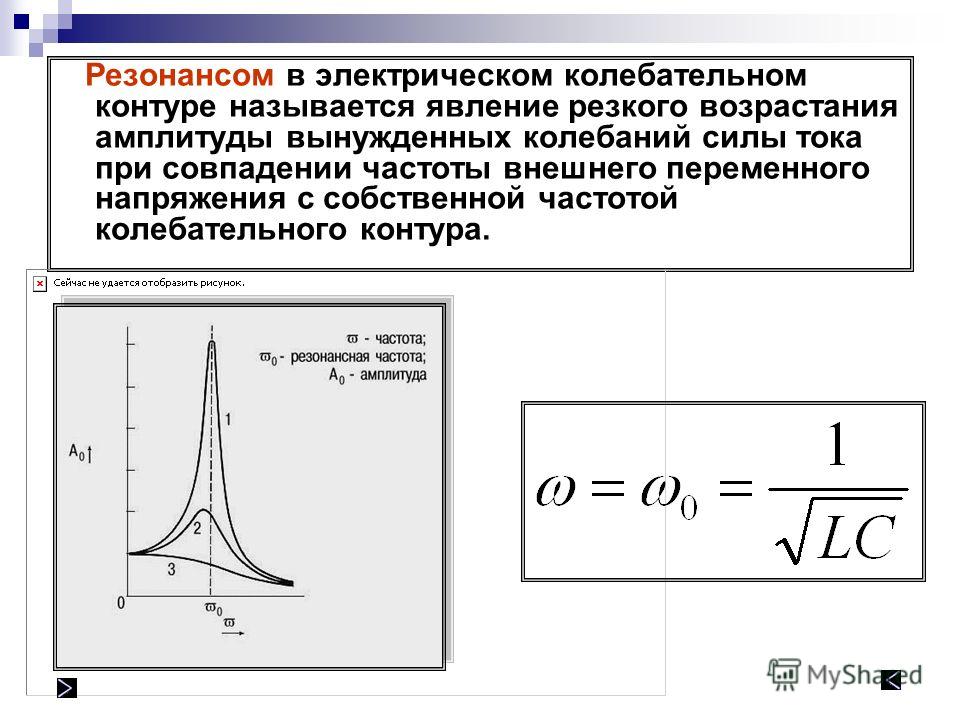 Ясно, что между этими напряжениями сдвиг фаз равен 180°. Кривая резонанса для тока, приведенная на (рис.1 6), при небольшом Изменении частоты показывает также изменение напряжения UL и Uс (только в ином масштабе). Это следует из того, что при изменении частоты вблизи резонанса ток меняется сильно, а сопротивления xL и хC — сравнительно мало. Например, если fpeз — 1000 кгц и частота изменяется на 20 кгц, т.е. на 2%, то сопротивления xL и хС изменяются каждое также только на 2%. В результате напряжения UL = IxL и Uc = IxС изменяются почти точно пропорционально току. При резонансе напряжение на катушке или на конденсаторе в Q раз больше, чем напряжение генератора, равное U — Ir. Напряжение на L или С равно UL = Uc = р. Поэтому

Чем выше добротность контура Q, тем больше увеличение напряжения при резонансе. Повышение напряжения на катушке и на конденсаторе характерно для резонанса напряжений, само название которого подчеркивает увеличение напряжения в момент резонанса. Большие напряжения на катушке и конденсаторе получаются за счет постепенного накопления энергии в контуре в процессе возникновения в нем колебаний. Эдс генератора возбуждает в контуре колебания, амплитуда которых нарастает до тех пор, пока энергия, даваемая генератором, не станет равна потерям энергии в активном сопротивлении контура. После этого в контуре происходят мощные колебания, характеризующиеся большой величиной тока и большими напряжениями, а генератор расходует небольшую мощность только для компенсации потерь энергии. Подобно этому можно, раскачивая тяжелый маятник легкими движениями руки с частотой, равной его собственной частоте, постепенно довести амплитуду колебаний маятника до значительной величины, во много раз превышающей амплитуду колебаний руки, играющей роль генератора. Резонанс напряжений применяется в радиотехнике для получения максимального тока и напряжения в контуре. Например, антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей. Входной контур приемника также настраивают на резонанс напряжений для того, чтобы получить усиление напряжения сигналов той радиостанции, на частоту которой настроен контур. Напряжения сигналов других радиостанций, частоты которых отличаются от резонансной частоты приемного контура, усиливаются незначительно. При резонансе напряжений в величину активного сопротивления контура входит внутреннее сопротивление генератора. Если оно велико, то качество контура может стать низким и резонансные свойства его будут выражены слабо. Поэтому для резонанса напряжений генератор, питающий контур, должен иметь малое внутреннее сопротивление.

Последовательный колебательный контур. Резонанс напряжений. Внутреннее сопротивление источника ЭДС

Другие предметы \ Основы радиоэлектроники

Страницы работы

2 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

1.39) Последовательный колебательный контур. Резонанс напряжений

Последовательным колебательным контуром называют такую цепь, в которой катушка и конденсатор соединены последовательно относительно входных зажимов (рисунок 30).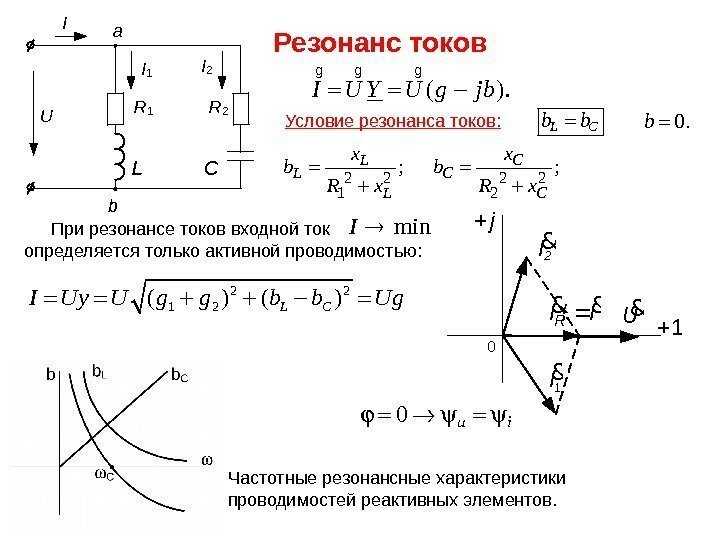 В такой цепи можно наблюдать резонанс напряжений. При резонансе напряжений индуктивное и емкостное сопротивления взаимно компенсируются и в результате этого реактивные сопротивление и мощность цепи равны нулю.

При резонансе напряжений, возникающем в цепи с последовательным соединением индуктивных и емкостных элементов, ток и напряжение цепи совпадают по фазе. В этом случае угол сдвига фаз между током и напряжением равен нулю (φ = 0) и полное сопротивление цепи равно ее активному сопротивлению. Если  то угол φ=0 при Х=0. Следовательно, при резонансе  и  или , откуда угловая частота при резонансе  и резонансная частота .

исунок 30

Таким образом, условием возникновения резонанса напряжения в цепи является равенство реактивных сопротивлений Х_L= Х_С, так как в этом случае частота колебательного контура ω₀ равна частоте сети, питающей данную цепь.

Мгновенные значения  энергии магнитного и электрического поля соответственно запишутся

Т.е. в электрической цепи происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарное значение которой постоянно. Вся энергия поступающая от источника в момент резонанса расходуется в сопротивлении R.

Отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи при резонансе, называют добротностью контура или коэффициентом резонанса.

где  - характеристическое (волновое) сопротивление контура.

Относительной расстройкой частоты по отношению к резонансной частоте контура называют величину: .

Величину обратную добротности называют коэффициентом затухания контура:                                                            .

Полное сопротивление цепи минимально при резонансе напряжений, при этом ток в цепи достигает максимального значения.

Полосу частот вблизи резонанса (рисунок 31), на границах которой ток снижается до максимального значения I₀ принято называть полосой пропускания резонансного контура ,_,  гдеf₁ ,  f₂ – нижняя и верхняя граничная частота.        

Величина добротности Q характеризует остроту резонансной кривой (рисунок 32).

Рисунок 31                                          Рисунок 32

Внутреннее сопротивление источника ЭДС R_iвлияет на добротность и полосу пропускания колебательного контура. Чем больше R_i тем ниже добротность и шире полоса пропускания.

В условиях близких к резонансу, U_L и U_C могут быть велики.

Векторная диаграмма тока и напряжения при резонансе напряжений представлена на рисунке 33.                                      

Зависимость напряжений на емкости и индуктивности от частоты при резонансе напряжений показана на рисунке 34, где U₀ – напряжение при резонансе.

Рисунок 33                     Рисунок 34

2.40) Параллельный колебательный контур. Резонанс токов

Рассмотрим параллельный колебательный контур, простейшим  видом которого является параллельное соединение индуктивной катушки и конденсатора (рисунок 35).

Рисунок 35

Резонансом токов называют такой режим параллельного колебательного контура, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением (φ=0), а мощность, потребляемая из сети, равна активной мощности контура. Реактивная мощность при резонансе из сети не потребляется. 

При резонансе токов . При резонансе токов возможны ситуации, когда реактивные токи  и  намного превышают суммарный ток суммарный ток в цепи, в следствие чего резонанс при параллельном соединении называют резонансом токов. Это возможно при условии g< b_L  или g< b_C.

Определим резонансную частоту контура:

.

После преобразования получаем                              

, откуда  , где ; .

Как видно из выражения для резонансной частоты w_r, резонанс токов возможен при одновременном выполнении условий r>R₁, r>R₂ или r<R₁ и r<R ₂. Если эти условия не выполняются, то w_r - линейное число. В случае, когда R₁ = R₂  w_r =  w_о при R₁ = R₂ = r; w_r = 0/0, т.е. резонанс токов наступает при любой частоте источника.

Следовательно, ток  в неразветвленной части цепи не зависит от частоты. Если R_{1и R2 - сопротивления, учитывающие потери реальных конденсаторов и индуктивной катушки (R1 = RС ; R2 = RL), то как правило, r>>R1, r>>R2 при этом  wr wо.}

В контуре без потерь (R₁ = R₂ = 0), , токи I_{Lи IC равны по величине}

Похожие материалы

Информация о работе

Скачать файл

Резонансный контур серии

, онлайн калькулятор

Калькулятор и формулы для последовательной цепи, состоящей из катушки, конденсатора и резистора

• Геометрия
• Финансы
• Электрика

Схемный калькулятор серии RCL

Этот калькулятор возвращает наиболее важные значения последовательного резонансного контура, состоящего из резистора, катушки и конденсатора.

Активное сопротивление R представляет собой внешний демпфирующий резистор или сопротивление потерь в катушке.

Вычислитель резонансных цепей серии

Формулы для резонансного контура серии RLC

Последовательный колебательный контур представляет собой ситовую или фильтрующую схему. Пропускаются частоты, близкие к резонансной частоте.

Ток одинаков во всех точках измерения.

• Ток и напряжение совпадают по фазе на омическом сопротивлении.

• При индуктивном сопротивлении катушки напряжение опережает ток на +90°.

• При емкостном реактивном сопротивлении конденсатора напряжение отстает от тока на -90°.

• Поэтому U _L и U _C сдвинуты по фазе на 180°, т.е. не в фазе

Общее сопротивление резонансного контура называется импедансом Z. Закон Ома распространяется на всю цепь. Импеданс Z наименьший на резонансной частоте, когда X _L = X _C .

92} \)

В резонансе X _L = X _C . Фаза напряжения противоположна; два значения компенсируют друг друга, и применяется следующее:

\(\ Displaystyle Z=R \)

Ток и напряжение

Ток наибольший в резонансе

\(\displaystyle I_0=\frac{U}{Z_0}=\frac{U}{R} \)

Если есть резонанс, есть рост напряжения. Напряжение на L и C может быть больше, чем приложенное напряжение

Качество Q и демпфирование d

Качество Q указывает на увеличение напряжения

\(\displaystyle Q=\frac{U_L}{U}=\frac{U_C}{U}=\frac{X_L}{R}=\frac{X_C}{R} \)

Демпфирование:   \(\displaystyle d=\frac{1}{Q} \)

Полоса пропускания

Полоса пропускания определяет частотный диапазон между верхней и нижней частотой среза. Чем выше добротность Q, тем уже резонансный контур.

\(\displaystyle b=\frac{f_0}{Q}=f_0 ·d =\frac{f_0 · R}{X_L} =\frac{f_0 · U}{U_L} \)

Частоты среза

Верхняя частота среза:   \(\displaystyle f_{go}=f_0+\frac{b}{2} \)

Нижняя частота среза:   \(\displaystyle f_{go}=f_0-\frac{b}{2} \)

Для частоты среза применяется следующее:

\(\displaystyle f=f_{go}\) или \(\displaystyle f=f_{gu}\)

\(\displaystyle φ=45°\)

\(\displaystyle I_g=\frac{I_0}{\sqrt{2}} \)

\(\displaystyle U_R=\frac{U}{\sqrt{2}} \)

\(\displaystyle Z_g=\sqrt{2}·Z_0 \)

Полезна ли эта страница? Спасибо за отзыв! Извините за это Как мы можем улучшить его?

---

8.

2: Серия Resonance — Engineering LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25287

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

Начнем с простейшей схемы RLC; один, состоящий из одного источника напряжения, последовательно соединенного с одним резистором, катушкой индуктивности и конденсатором, как показано на рисунке \(\PageIndex{1}\). Особый интерес представляет то, как общий импеданс изменяется в частотном спектре и какое влияние это оказывает на ток и напряжения трех компонентов.

Рисунок \(\PageIndex{1}\): Последовательная цепь RLC.

Импеданс, видимый источником, представляет собой просто сумму трех составляющих, или

\[Z = R+ jX_L − j X_C \номер\]

Можно расширить до

\[Z = = R+ j 2\pi f L −j \frac{1}{2\pi f C} \nonumber \]

Здесь интересно то, что первый член не является функцией частоты, второй член прямо пропорционален частоте, а третий обратно пропорционален частоте. Кроме того, учитывая, что положительное и отрицательное реактивное сопротивление ведут себя противоположно, кажется, что на некоторой частоте они могут компенсироваться, оставляя только сопротивление.

Чтобы уточнить это, мы ожидаем, что на низких частотах конденсатор будет доминировать в импедансе. Другими словами, \(X_C\) будет наибольшим из трех омических значений. Это означает, что общий импеданс будет иметь тенденцию имитировать как величину, так и фазу емкостного реактивного сопротивления. С другой стороны, на очень высоких частотах индуктор будет доминировать над импедансом. \(X_L\) будет наибольшим из трех значений. В этой области суммарный импеданс будет отражать импеданс индуктора. Короче говоря, на низких частотах величина импеданса будет большой, и цепь будет казаться емкостной, в то время как на высоких частотах величина импеданса будет большой, и цепь будет казаться индуктивной. В середине все становится интереснее.

График сопротивления или реактивного сопротивления трех элементов показан на рисунке \(\PageIndex{2}\). Сумма трех также показана (красный). Ось частот использует логарифмическую шкалу, чтобы показать симметричный характер комбинированной кривой импеданса.

Рисунок \(\PageIndex{2}\): Серийное изменение импеданса в зависимости от частоты.

Провал в центре соответствует импедансу, равному \(R\). На этой частоте емкостное и индуктивное сопротивления равны по величине и эффективно компенсируют друг друга. Остается только резистивная составляющая \(R\). Эта частота известна как резонансная частота и обозначается \(f_0\).

\[\text{Последовательная резонансная частота, } f_0, \text{ — частота, при которой величины индуктивного и емкостного сопротивлений равны.} \label{8.1} \]

Это означает, что коэффициент мощности равен единице при резонансе. Кроме того, в реальной схеме \(R\) представляет собой комбинацию последовательного сопротивления плюс любое сопротивление катушки индуктивности. Мы можем вывести формулу для \(f_0\) следующим образом. Определение заявляет, что величина \(X_L\) должна равняться величине \(X_C\). Следовательно, мы можем установить формулы емкостного и индуктивного реактивного сопротивления равными друг другу, а затем найти результирующую частоту. 9{\circ}\)). Этот коэффициент формы описывается параметром \(Q\). Чем круче или уже кривая, тем выше \(Q\).

При наличии источника постоянного напряжения неудивительно, что график результирующего тока будет представлять собой инверсию кривой импеданса. Это показано на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Серийный ток в зависимости от частоты.

Если масштабировать кривые таким образом, чтобы они обе имели нормированный пик единицы, разницу в формах было бы немного легче увидеть. Это показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Нормализованный последовательный ток в зависимости от частоты.

Теперь мы можем более точно определить \(Q\). В частности, «резкость» кривой связана с частотами половинной мощности или «-3 дБ», \(f_1\) и \(f_2\). ¹ Это частоты, при которых ток (при условии, что источник напряжения) падает до 0,707 от максимального значения при резонансе.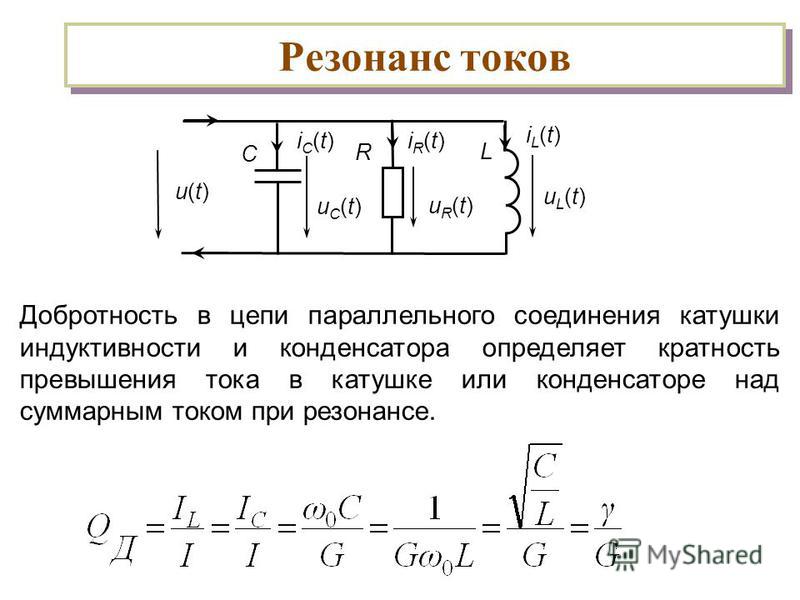 Следовательно, они представляют собой частоты, на которых мощность упадет до половины максимального значения, наблюдаемого при резонансе (напомним, что мощность зависит от квадрата тока, и что 0,707 в квадрате примерно равно 0,5). \(f_1\) находится ниже \(f_0\), а \(f_2\) находится выше. Разница между этими двумя частотами называется полосой пропускания, BW.

\[BW = f_2 − f_1 \метка{8.3} \]

\[Q_{схема} = \frac{f_0}{BW} \label{8.4} \]

Связь между этими переменными показана на рисунке \(\PageIndex{5}\). Вертикальная ось показана в процентах от максимума. Для последовательного резонансного контура, управляемого источником напряжения, эта ось является токовой; однако, как мы увидим, это может быть напряжение в случае параллельного резонансного контура. Если этот график сравнить с кривыми на рисунке \(\PageIndex{4}\), должно быть очевидно, что для более низких цепей \(Q\) \(f_1\) и \(f_2\) расходятся, удаляясь от резонансной частоты \(f_0\). Таким образом, для любого заданного \(f_0\) меньшее значение \(Q\) означает более широкую (большую) полосу пропускания.

Рисунок \(\PageIndex{5}\): расположение \(f_1\) и \(f_2\) и определение пропускной способности (BW).

Резонансная частота, \(f_0\), в общем случае расположена неравномерно между \(f_1\) и \(f_2\). На самом деле он расположен в их среднем геометрическом. Другими словами,

\[f_0 = \sqrt{f_1 f_2} \label{8.5} \]

Из уравнения \ref{8.5} мы можем получить:

\[\frac{f_0}{f_1} = \frac{f_2}{f_0} \label{8.6} \]

Чтобы найти точные значения для \(f_1\) и \(f_2\), мы можем определить коэффициент \(k_0\). Вывод \(k_0\) находится в Приложении C. 92} +1} \метка{8.7} \]

\[f_1 = \frac{f_0}{k_0} \label{8.8} \]

\[f_2 = f_0\times k_0 \метка{8.9} \]

Для более высоких \(Q\) цепей (\(Q_{схема} \geq 10\)), мы можем аппроксимировать симметрию, и, таким образом,

\[f_1 \приблизительно f_0 − \frac{BW}{2} \label{8.10} \]

\[f_2 \приблизительно f_0+ \frac{BW}{2} \label{8.11} \]

Как упоминалось ранее, \(Q\) может быть функцией отношения \(R\) или \(L/C\).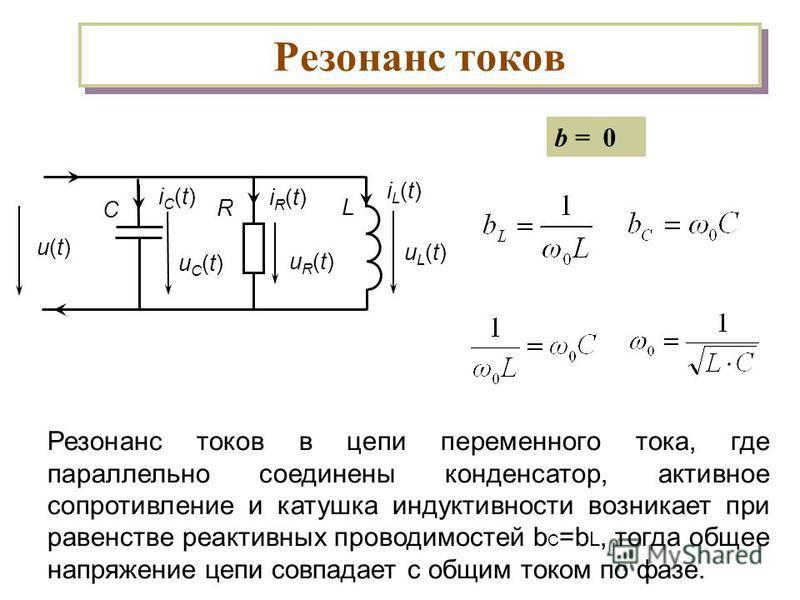 На рисунках \(\PageIndex{6}\) и \(\PageIndex{7}\) представлены кривые импеданса для двух случаев. Ось частот нормирована на \(f_0\) (т.е. \(f_0\) равно единице). На рисунке \(\PageIndex{6}\) мы изменяем значение сопротивления, чтобы увидеть, как оно влияет как на величину, так и на фазу импеданса по частоте. Рисунок \(\PageIndex{7}\) аналогичен, за исключением того, что мы изменили соотношение индуктор/конденсатор.

Рисунок \(\PageIndex{6}\): Величина и фаза импеданса для изменения сопротивления.

Глядя сначала на фазу (синяя, левая ось), мы видим, что в обоих случаях схемы с высокой добротностью демонстрируют быстрый переход от отрицательного (емкостного) фазового угла к положительному (индуктивному) фазовому углу. Мы также замечаем, что фазовый сдвиг достигает нуля при \(f_0\), что подразумевает единичный коэффициент мощности.

Графики величины импеданса показывают немного другую картину. Хотя верно то, что графики с более высоким \(Q\) более четкие, они получают это с помощью других механизмов. В случае резистора более низкая \(Q\) достигается за счет большего сопротивления. Это приводит к затуплению вершины кривой и снижению тока при \(f_0\) по сравнению со случаем с высоким значением \(Q\) (как показано на рисунке \(\PageIndex{3}\)). Напротив, уменьшение \(Q\) за счет уменьшения соотношения индуктор/конденсатор уширяет всю кривую. Величина импеданса на провале не меняется, и, следовательно, ток на \(f_0\) не меняется. С практической точки зрения, \(Q\) для последовательной цепи, \(Q_{серия}\), также может быть определено отношением реактивного сопротивления цепи к общему последовательному сопротивлению при резонансе.

\[Q_{серия} = \frac{X_0}{R_T} \label{8.12} \]

Где

\(Q_{серия}\) — это \(Q\) последовательного резонансного контура (т.е. \(Q_{контур}\) для последовательного),

\(R_T\) — полное последовательное сопротивление (\(R_{серия} + R_{катушка}\)),

\(X_0\) — реактивное сопротивление (либо \(X_L\), либо \(X_C\)) при \(f_0\).

Рисунок \(\PageIndex{7}\): Величина и фаза импеданса для изменения соотношения катушка индуктивности/конденсатор.

Из уравнения \ref{8.12} мы можем вывести выражение для \(Q_{серии}\) через \(R\), \(L\) и \(C\) следующим образом: 92}}{R_T} \номер\]

В резонансе \(X_L\) и \(X_C\) имеют одинаковую величину, поэтому мы также можем сказать:

\[Q_{серия} = \frac{\sqrt{X_L X_C}}{R_T} \nonnumber \]

\[Q_{серия} = \frac{1}{R_T} \sqrt{X_L X_C} \nonumber \]

\[Q_{серия} = \frac{1}{R_T} \sqrt{ \frac{2 \pi f L}{2\pi f C}} \nonumber \]

Что упрощает до:

\[Q_{серия} = \frac{1}{R_T} \sqrt{\frac{L}{C}} \label{8.13} \]

Влияние добротности на напряжения компонентов

\(Q\) создаст умножающий эффект на напряжения катушки индуктивности и конденсатора при резонансе. В точке \(f_0\) ток в цепи будет равен напряжению источника, деленному на \(R\), потому что \(X_C\) и \(X_L\) компенсируются. Этот ток также протекает через конденсатор и катушку индуктивности. Уравнение \ref{8.12} показывает, что их реактивные сопротивления в \(Q\) раз выше, чем \(R\), и поэтому их напряжения будут в \(Q\) раз выше, чем напряжение источника. КВЛ не нарушается, так как напряжения на \(L\) и \(C\) сдвинуты по фазе на 180 градусов и компенсируют друг друга. По мере увеличения цепи \(Q\) эффект увеличения напряжения становится более выраженным. В экстремальных случаях можно создавать напряжения на катушках индуктивности и конденсаторах, которые более чем в 100 раз превышают напряжение источника. По мере удаления от резонансной частоты эффект умножения уменьшается. На частотах намного ниже, чем \(f_0\), почти все напряжение источника будет появляться на конденсаторе, а на резисторе и катушке индуктивности будет немного. На гораздо более высоких частотах почти весь потенциал источника появляется на катушке индуктивности, а на конденсаторе или резисторе ничего не видно. Это видно на рисунке \(\PageIndex{8}\), где напряжение источника равно единице.

При уменьшении \(Q\) не только уменьшаются напряжения на конденсаторе и катушке индуктивности, но и проявляется другой эффект. При относительно высоких значениях \(Q\), скажем, 10 и более, максимальные напряжения конденсатора и катушки индуктивности возникают примерно при \(f_0\). При более низких значениях \(Q\) пики имеют тенденцию расходиться, при этом пик конденсатора ниже \(f_0\), а индуктора выше \(f_0\). Это показано на рисунке \(\PageIndex{9}\) (опять же, источник — это unity).

Рисунок \(\PageIndex{8}\): Последовательный резонанс: напряжения компонентов для высоких \(Q\).Рисунок \(\PageIndex{9}\): Последовательный резонанс: напряжения компонентов для низких \(Q\).

Пример \(\PageIndex{1}\)

Рассмотрим последовательную цепь на рисунке \(\PageIndex{10}\) со следующими параметрами: источник 10 вольт пик, \(L\) = 1 мГн, \ (С\) = 1 нФ и \(R = 50 \Омега\). Найдите резонансную частоту, систему \(Q\) и полосу пропускания, а также частоты половинной мощности \(f_1\) и \(f_2\).

Рисунок \(\PageIndex{10}\): Схема для примера \(\PageIndex{1}\).

Начнем с определения резонансной частоты.

\[f_0 = \frac{1}{2\pi \sqrt{LC}} \nonumber \]

\[f_0 = \frac{1}{2\pi \sqrt{1e-3\cdot 1e- 9}} \nonumber \]

\[f_0 = 159 кГц \nonumber \]

Теперь мы найдем величину индуктивного сопротивления и, исходя из этого, систему \(Q_{серии}\) с помощью уравнения \ref{ 8. 12}.

\[X_L = 2\pi f_0 L \без номера \]

\[X_L = 2\pi 159 кГц 1 мГн \без номера \]

\[X_L = 1000\Omega \без номера \]

\[Q_{ серия} = \frac{X_L}{R_T} \nonumber \]

\[Q_{серия} = \frac{1000\Omega}{50\Omega} \nonnumber \]

\[Q_{серия} = 20 \nonnumber \]

Зная \(Q\), полоса пропускания и угловые частоты могут быть найдены с помощью уравнений \ref{8.4}, \ref{8.10} и \ref{8.11}.

\[BW = \frac{f_0}{Q} \nonumber \]

\[BW = \frac{159 кГц}{20} \nonumber \]

\[BW = 7,95 кГц \nonumber \]

\[f_1 = f_0 − \frac{BW}{2} \nonumber \]

\[f_1 = 159 кГц − \frac{7,95kHz}{2} \nonumber \]

\[f_1 \приблизительно 155 кГц \номер \]

\[f_2 = f_0 + \frac{BW}{2} \номер \]

\[f_2 = 159 кГц + \frac{7,95 кГц}{2 } \nonumber \]

\[f_2 \приблизительно 163 кГц \nonumber \]

При пиковом напряжении источника 10 вольт напряжения на конденсаторе и катушке индуктивности при резонансной частоте 159 кГц будут в \(Q\) раз больше или 200 вольт. На более высоких или более низких частотах повышенный импеданс снижает ток, а также снижает напряжение на компонентах. На низких частотах большая часть источника будет проходить через конденсатор, в то время как на высоких частотах напряжение дросселя будет приближаться к напряжению источника.

Серия рафинирования Q

Как отмечалось в главе 2, все катушки индуктивности имеют определенное последовательное сопротивление, обычно называемое \(R_{катушка}\). Это сопротивление необходимо включить как часть общего сопротивления цепи, добавляя к любому другому существующему последовательному сопротивлению. Хотя можно измерить сопротивление катушки постоянному току с помощью цифрового мультиметра, это не обязательно даст точное значение на высоких частотах. Таким образом, предпочтительный метод состоит в том, чтобы определить \(Q_{катушка}\) на желаемой частоте из спецификации катушки индуктивности и, используя рассчитанное реактивное сопротивление на этой частоте, определить значение \(R_{катушка}\).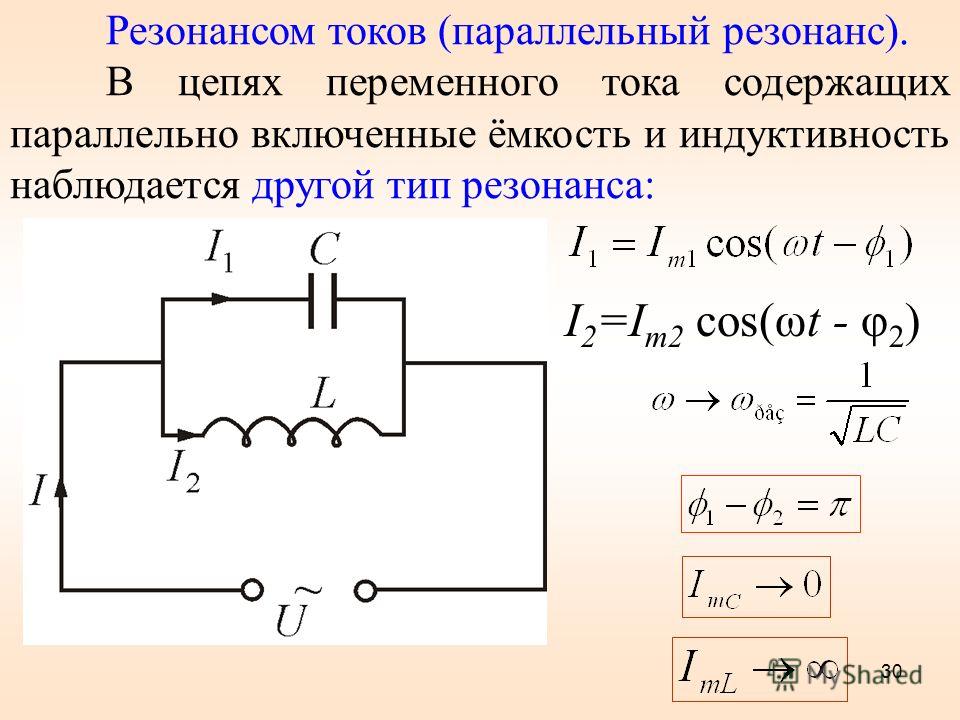 Пример такой кривой показан на рисунке \(\PageIndex{11}\).

Рисунок \(\PageIndex{11}\): График индуктора \(Q\).

Например, используя кривую A, \(Q_{катушка}\) на частоте 100 кГц составляет приблизительно 90. Если \(X_L\) равно 450 \(\Omega \) на этой частоте, то \(R_{катушка}\) будет 450 \(\Omega /90\) или 5 \(\Omega \).

По сути, \(Q_{coil}\) устанавливает потолок для \(Q\) последовательного резонансного контура, \(Q_{series}\). То есть система \(Q\) никогда не может быть выше катушки \(Q\). Для этого в контуре потребуется меньшее сопротивление, чем \(R_{катушка}\), что практически невозможно. Также стоит отметить, что \(R_{катушка}\) создаст отклонение напряжения катушки индуктивности по сравнению с идеальным случаем. Это связано с тем, что \(v_L\) покрывает комбинацию индуктивного сопротивления последовательно с \(R_{катушка}\), поэтому величина будет несколько больше, чем ожидалось, а угол будет меньше 90 градусов. Эти отклонения, как правило, довольно малы, если только \(Q\) индуктора не является достаточно низким, а оставшееся сопротивление цепи не намного больше, чем \(R_{катушка}\).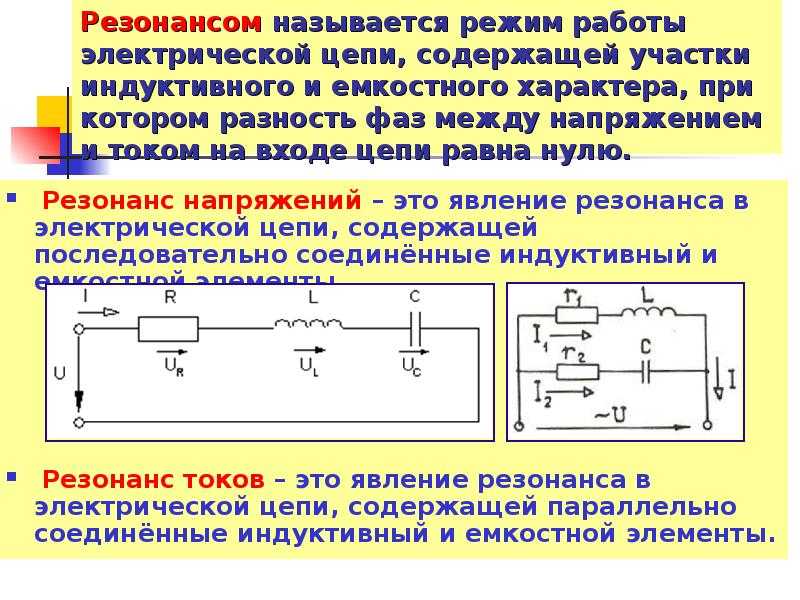

Пример \(\PageIndex{2}\)

Для схемы на рисунке \(\PageIndex{11}\) определите резонансную частоту, систему \(Q\), полосу пропускания и идеальное максимальное напряжение по каждому из трех компонентов. Используйте кривую A на рисунке \(\PageIndex{11}\) для катушки индуктивности.

Рисунок \(\PageIndex{12}\): Схема для примера \(\PageIndex{2}\).

Первым важным пунктом является определение резонансной частоты.

\[f_0 = \frac{1}{2 \pi \sqrt{LC}} \nonumber \]

\[f_0 = \frac{1}{2\pi \sqrt{22e-3 H50e-9F} } \nonumber \]

\[f_0 = 4,8 кГц \nonumber \]

Индуктивное сопротивление:

\[X_L = 2\pi f_0 L \nonumber \]

\[X_L = 2\pi 4,8kHz 22 мГн \номер \]

\[X_L = 663,3\Омега \неномер \]

Из графика \(Q_{катушка}\) приблизительно равно 95, что означает \(R_{катушка}\):

\[R_{coil} = \frac{X_L}{Q_{coil}} \nonumber \]

\[R_{coil} = \frac{663.3 \Omega}{95} \nonumber \]

\ [R_{coil} = 7\Omega \nonnumber \]

В сочетании с резистором 140 \(\Omega \) у нас остается 147 \(\Omega \), что примерно на 5% больше, чем если бы мы его игнорировали.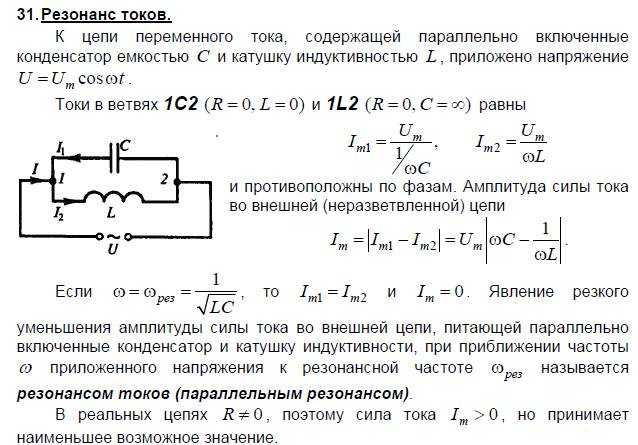 Система \(Q\):

\[Q_{серии} = \frac{X_L}{R_T} \nonumber \]

\[Q_{серии} = \frac{663.3\Omega}{147\Omega } \номер \]

\[Q_{серия} = 4,51 \неномер \]

\(Q\) находится на низком уровне, но не слишком сильно. Теперь о пропускной способности:

\[BW = \frac{f_0}{Q} \nonumber \]

\[BW = \frac{4,8 кГц}{4,51} \nonumber \]

\[BW = 1,06 кГц \nonumber \]

В идеале при \(f_0\) мы ожидаем, что \(v_R\) будет равно источнику пикового напряжения в 1 вольт, а напряжения на катушке индуктивности и конденсаторе будут в \(Q\) раз больше, или примерно в 4,5 пик вольт. На самом деле \(R_{катушка}\) создаст делитель напряжения, уменьшив падение на резисторе 140 \(\Омега\) примерно до 0,9.{\circ} \Омега \). Система \(Q\) относительно низкая (\(<10\)), поэтому пики \(v_C\) и \(v_L\) немного сместятся от \(f_0\), при этом \(v_C\) с пиком на немного более низкой частоте и \(v_L\) немного выше.

Компьютерное моделирование

Особый интерес в предыдущем примере представляет точная форма откликов компонентов в зависимости от частоты.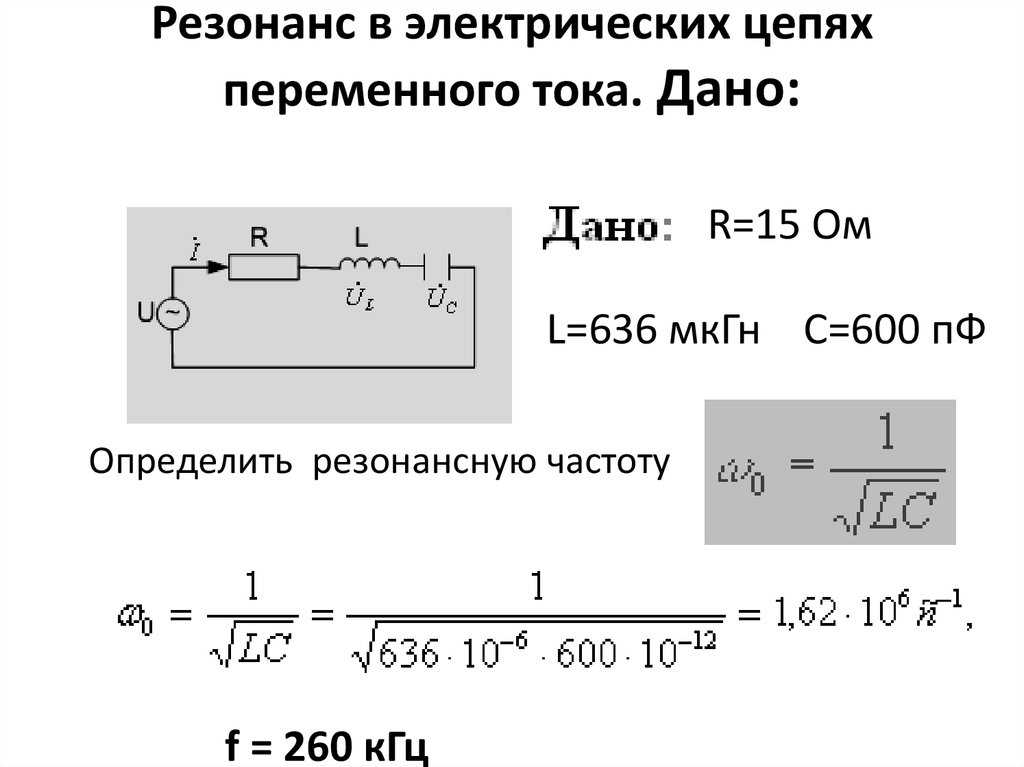 Это может быть получено с помощью моделирования переменного тока или частотной области. Схема на рисунке \(\PageIndex{12}\) захвачена в симуляторе, как показано на рисунке \(\PageIndex{13}\), и изменена путем добавления сопротивления катушки индуктивности ниже катушки индуктивности.

Представляющие интерес элементы: чистое напряжение резистора, которое появляется между узлами 1 и 2, напряжение конденсатора между узлами 2 и 3, и напряжение катушки индуктивности, которое появляется между узлом 3 и землей. Анализ выполняется в диапазоне от 500 Гц до 50 кГц, что дает нам 10-кратный коэффициент частоты по обе стороны от \(f_0\), как показано на рисунке \(\PageIndex{14}\). Во-первых, пики чуть ниже 5 кГц, как и ожидалось. Напряжение резистора (синее) составляет около 0,95 вольт, а напряжение катушки индуктивности (красный) и конденсатора (зеленый) составляет около 4,5 вольт, как рассчитано.

Рисунок \(\PageIndex{13}\): Схема примера \(\PageIndex{2}\) в симуляторе.

Также обратите внимание на небольшой разброс между пиками напряжения конденсатора и катушки индуктивности: \(v_C\) чуть ниже \(f_0\), а \(v_L\) чуть выше, опять же, как и ожидалось. На самых низких частотах весь источник появляется на конденсаторе, а на самых высоких частотах весь источник появляется на катушке индуктивности. Обратите внимание на сходство между этими кривыми и кривыми на рисунках \(\PageIndex{8}\) и \(\PageIndex{9).}\)

Рисунок \(\PageIndex{14}\): Напряжение в зависимости от частоты для каждого из трех компонентов схемы на рисунке \(\PageIndex{13}\).

А теперь для смены темпа; проблема дизайна.

Пример \(\PageIndex{3}\)

Разработайте последовательный резонансный контур с резонансной частотой 100 кГц и полосой пропускания 2 кГц с использованием катушки индуктивности 10 мГн. Предполагается, что индуктор следует кривой B на рисунке \(\PageIndex{14}\).

Мы можем найти значение емкости, изменив уравнение резонансной частоты: 92 10 мГн} \номер \]

\[C = 253,3 пФ \номер \]

Зная ширину полосы и резонансную частоту, находим систему \(Q\):

\[Q_{серия} = \frac {f_0}{BW} \nonumber \]

\[Q_{серия} = \frac{100 кГц}{2 кГц} \nonumber \]

\[Q_{серия} = 50 \nonumber \]

At резонанса, индуктивное сопротивление будет:

\[X_L = 2\pi f_0 L \номер \]

\[X_L = 2\pi 100 кГц 10 мГн \неномер \]

\[X_L = 6283\Омега \ не число \]

Предыдущее говорит нам, что общее последовательное сопротивление должно быть:

\[R_{серия} = \frac{X_L}{Q_{серия}} \nonumber \]

\[R_{серия} = \frac{ 6283\Omega}{50} \nonnumber \]

\[R_{серия} = 125,7\Omega \nonnumber \]

Кривая B показывает, что \(Q_{катушка}\) приблизительно равно 115 при 100 кГц. Таким образом, \(R_{coil}\) равно:

\[R_{coil} = \frac{X_L}{Q_{coil}} \nonumber \]

\[R_{coil} = \frac{6283\ Omega}{115} \nonumber \]

\[R_{coil} = 54.6\Omega \nonumber \]

Следовательно, мы должны добавить \(125,7 \Омега — 54,6 \Омега\) или \(71,1 \Омега \) к последовательной сети, чтобы получить желаемую систему \(Q\). Невыполнение этого требования приведет к гораздо более высокому \(Q\), чем указано, что приведет к значительному снижению пропускной способности. Завершенный дизайн показан на рисунке \(\PageIndex{15}\).

Рисунок \(\PageIndex{15}\): Завершенный проект схемы для примера \(\PageIndex{3}\).

Каталожные номера

¹ Децибелы подробно описаны в главе 10.

---

Эта страница под названием 8.2: Series Resonance распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts.