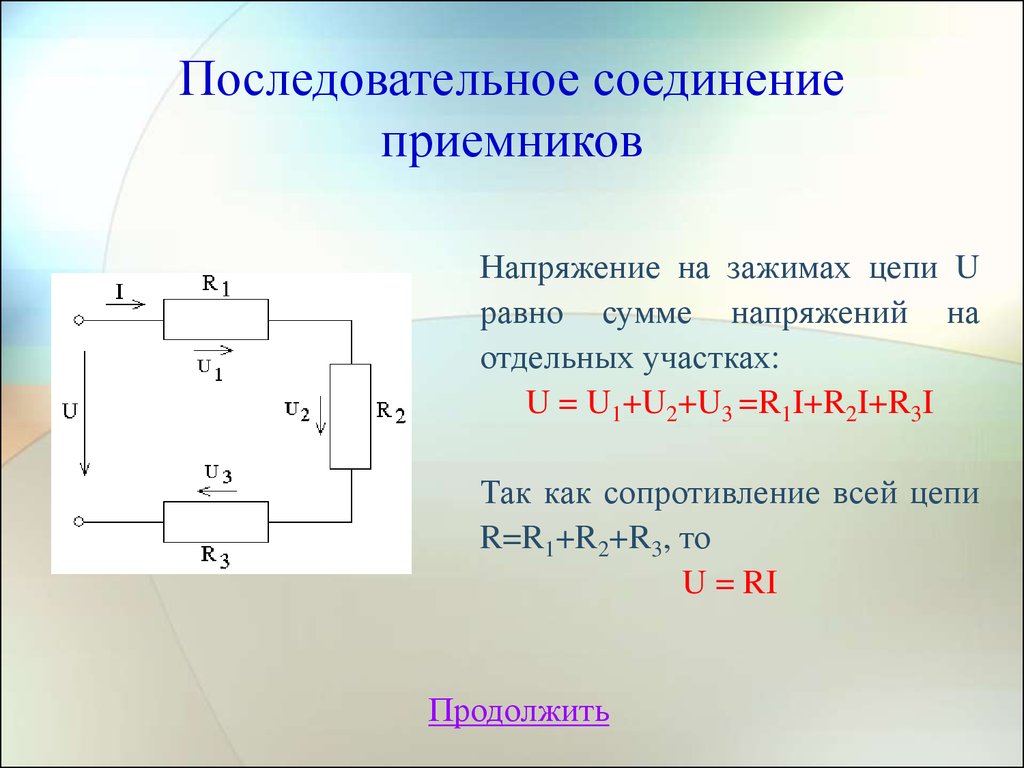
Последовательное соединение проводников – законы, определение, схема с формулами

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

Электрические схемы (цепи) разрабатывают для преобразования электрической энергии от аккумулятора постоянного (или переменного тока) в напряжение нужной величины, формы или частоты. Для этого используются различные электронные компоненты (резисторы, конденсаторы, индуктивности, трансформаторы и т.д.). Все эти элементы имеют различные сопротивления. Чаще всего встречаются параллельное или последовательное соединения. Далее будем говорить о последовательном соединении проводников.

Сопротивление или резистор

На электрических схемах все элементы имеют свои символические обозначения. Элемент, который используется в схемах для ограничения электрической мощности с помощью регулирования силы тока называется сопротивлением или резистором (англ. слово resistor — сопротивление) и изображается в виде прямоугольника (в России и Европе), либо “кусочка пилы” (в США). Величина рабочих резисторов зависит от их сопротивления, которое измеряется в омах — единицах, получивших свое название в честь немецкого естествоиспытателя Георга Симона Ома.

Рис. 1. Графическое обозначение сопротивлений и резисторов в Европе и США

Для проектирования и расчета электрических цепей применяется формула закона Ома:

$$R={U \over I}$$

где:

R — сопротивление, Ом;

U — напряжение, В;

I — сила тока в амперах, А.

Напряжение и ток измеряются с помощью приборов — вольтметра и амперметра. Прибор, которым измеряют значения сопротивлений резисторов, называется омметром.

Что такое последовательное соединение

Если взять два резистора R

1 и R₂ и соединить их друг за другом, то это и будет последовательное соединение.

Рис. 2. Схема последовательного соединения двух резисторов

Резисторы соединяют между собой проводами, сопротивление которых очень мало (обычно это медные провода), и им можно пренебречь.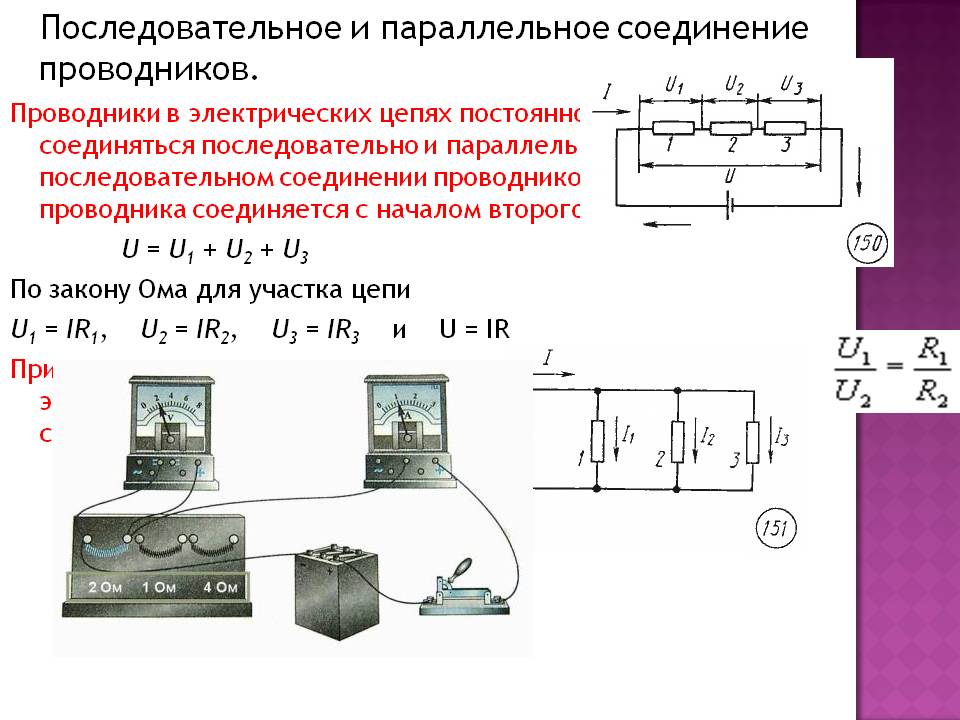 Когда требуются более тщательные расчеты для схем повышенной точности, то необходимо учитывать вклад этих сопротивлений.

Определение общего сопротивления цепи из двух резисторов

Если подключить напряжение U к левому концу R₁ и правому концу R₂, то в этой замкнутой цепи потечет ток I, величина которого одинакова для обоих резисторов. Падение напряжений U

1 и U₂ на сопротивлениях согласно закону Ома будут равны:

$U_1={I * R_1}$ (1)

$ U_2={I * R_2}$ (2)

Полное напряжение U равно сумме этих напряжений:

$U={U_1 + U_2}$ (3)

Применяя закон Ома для всей цепи, можно записать:

$ U={I * R_{общ}}$ (4)

где R_общ — общее сопротивление всей цепи. Из формул 1, 2, 3 и 4 следует, что:

$U={I * R_{общ}}={I * R_1}+{I * R_2}$ (5)

Сокращая обе части уравнения на I, получим:

$R_{общ} =R_1+R_2$

Последовательное соединение большого числа резисторов

Если последовательно соединить N резисторов — R_1,R_2…

R_N, то, пользуясь вышеприведенными соображениями и формулами (1) – (5), можно получить выражение для величины общего сопротивления такой цепи R_N:

$R_N = R_1+ R_2 +…+ R_N$ (6)

Таким образом, можно сформулировать общее правило: при последовательном соединении нескольких резисторов величина общего сопротивления цепи равна сумме сопротивлений включенных резисторов.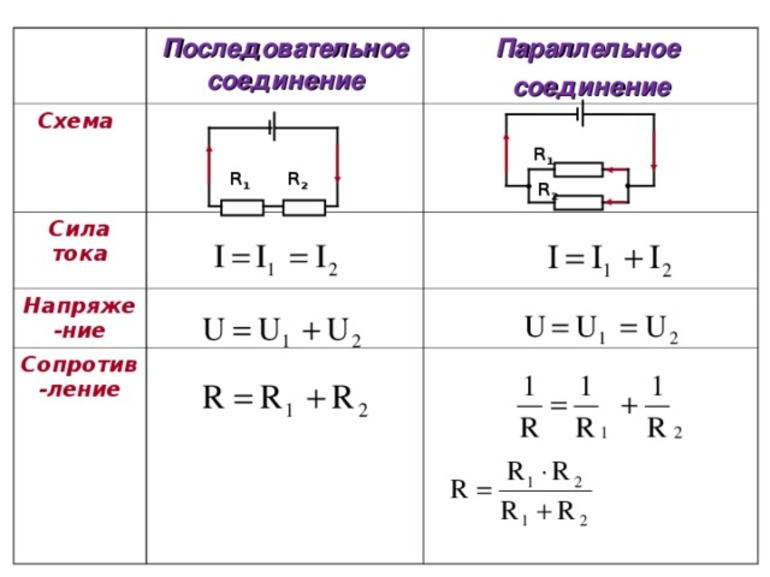

Если последовательно соединить N одинаковых резисторов величиной R то, пользуясь последней формулой (6), получим общее сопротивление цепи:

$R_N =N*R $

Рис. 3. Схема последовательного соединения нескольких резисторов R _1,R_2… R_N

Смешанное соединение проводников

Обычно электрические схемы представляют собой комбинацию из отдельных участков либо с параллельно соединенными проводниками, либо с последовательно соединенными. Такое соединение называют смешанным. Для расчета сопротивлений таких схем производится разбивка цепи на простые, составные части, которые рассчитываются отдельно, а потом складываются друг с другом.

Что мы узнали?

Итак, мы узнали законы последовательного соединения проводников (сопротивлений) в электрических цепях. Нами был получены формулы для расчетов сопротивления цепи, состоящей из двух и более резисторов.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 72.

---

А какая ваша оценка?

Последовательное соединение проводников | 8 класс

Содержание

Вы уже знаете, что есть два типа соединения элементов электрической цепи: последовательный и параллельный. Последовательно мы подключали в цепь амперметр, а параллельно — вольтметр.

На данном уроке мы более подробно рассмотрим последовательное соединение. Мы будем использовать сразу несколько потребителей электроэнергии и узнаем, каким закономерностям подчиняются уже известные нам величины (сила тока, сопротивление и напряжение) при таком соединении элементов в цепи.  

Последовательное включение элементов в электрическую цепь

Соберем электрическую цепь. Последовательно соединим две электролампы, два источника тока и ключа (рисунок 1).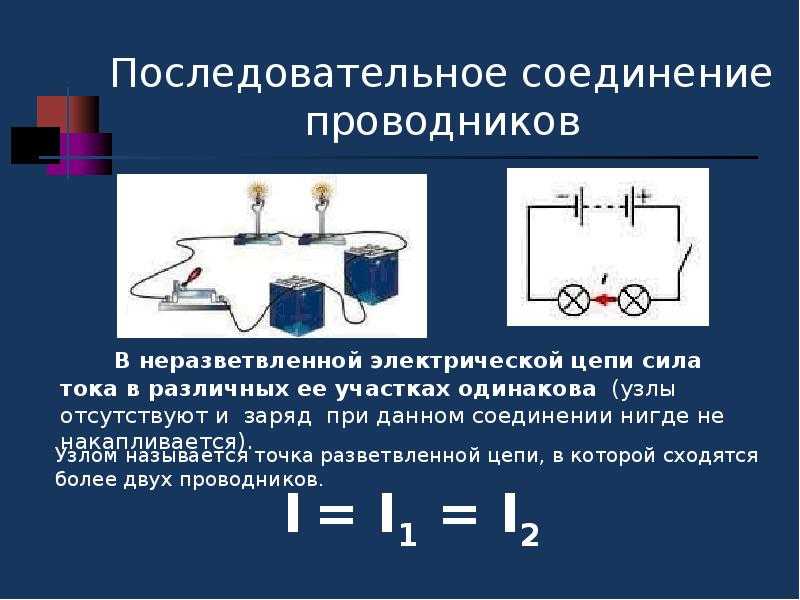

Обратите внимание, что при таком подключении аккумуляторов соблюдается определенная полярность подключения: провод, идущий от положительного полюса одного аккумулятора необходимо соединить с отрицательным полюсом другого аккумулятора. И, наоборот, провод идущий от отрицательного полюса одного аккумулятора соединяется с положительным полюсом другого.

Рисунок 1. Электрическая цепь с последовательным подключением электроламп

Если в такой цепи попытаться выключить только одну лампу, то погаснет и вторая.

Схема этой электрической цепи показана на рисунке 2.

Рисунок 2. Схема электрической цепи с последовательным подключением электроламп

В такую цепь мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества последовательно подключенных в цепь проводников.

{"questions":[{"content":"При последовательном соединении двух аккумуляторов необходимо провод, идущий от положительного полюса одного аккумулятора, подсоединить к  [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["отрицательному полюсу другого аккумулятора","положительному полюсу другого аккумулятора","нельзя соединять аккумуляторы друг с другом"],"answer":[0]}}}]}

Сила тока в цепи при последовательном соединении проводников

При изучении силы тока мы измеряли ее на различных участках электрической цепи (рисунок 3). Полученные с помощью амперметра значения силы тока были одинаковы.

Рисунок 3. Измерение силы тока на различных участках электрической цепи при последовательном соединении ее элементов

При этом все элементы у нас были соединены последовательно. Сделаем вывод.

При последовательном соединении сила тока в любых частях цепи одна и та же:
$I = I_1 = I_2 = … = I_n$.

{"questions":[{"content":"При последовательном соединении элементов электрической цепи сила тока[[choice-5]]","widgets":{"choice-5":{"type":"choice","options":["различна на разных участках цепи","одинакова на всех участках цепи","одинакова только на тех участках цепи, которые содержат одинаковые проводники"],"answer":[1]}}}]}

Сопротивление в цепи при последовательном соединении проводников

Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?

Давайте порассуждаем. В цепи был один проводник с определенным сопротивлением.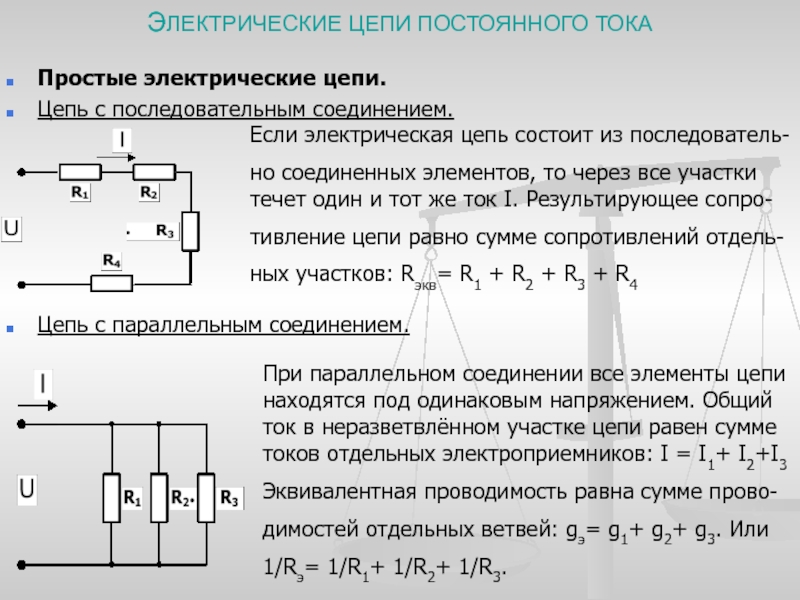 Мы последовательно подключаем второй. Представим эти два проводника в виде одного элемента цепи. Тогда получается, что, подсоединив второй проводник, мы увеличили длину первого.

Сопротивление же зависит от длины проводника. Поэтому суммарное сопротивление цепи будет точно больше сопротивления одного проводника.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
$R = R_1 + R_2 + … + R_n$.

На схемах электрических цепей последовательное соединение нескольких проводников изображается так, как показано на рисунке 4.

Рисунок 4. Последовательное соединение проводников на схеме электрической цепи

{"questions":[{"content":"При последовательном соединении проводников общее сопротивление в цепи будет равно[[choice-10]]","widgets":{"choice-10":{"type":"choice","options":["сумме сопротивлений всех проводников в цепи","сопротивлению самого мощного потребителя электроэнергии в цепи","произведению сопротивлений всех проводников в цепи"],"answer":[0]}}}]}

Напряжение в цепи при последовательном соединении проводников

Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков:
$U_1 = IR_1$,
$U_2 = IR_2$,
…
$U_n = IR_n$.

Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.

Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
$U = U_1 + U_2 + … + U_n$.

{"questions":[{"content":"Напряжение на полюсах источника тока равно[[choice-14]]","widgets":{"choice-14":{"type":"choice","options":["полному напряжению в цепи","напряжению на участке цепи с самым мощным потребителем электроэнергии","напряжению на концах замкнутого ключа"],"answer":[0]}}}]}

Полное напряжение в цепи и закон сохранения энергии

Давайте вспомним, что напряжение определяется работой электрического тока. Эта работа совершается при прохождении по участку цепи электрического заряда, равного $1 \space Кл$:
$U = \frac{A}{q}$.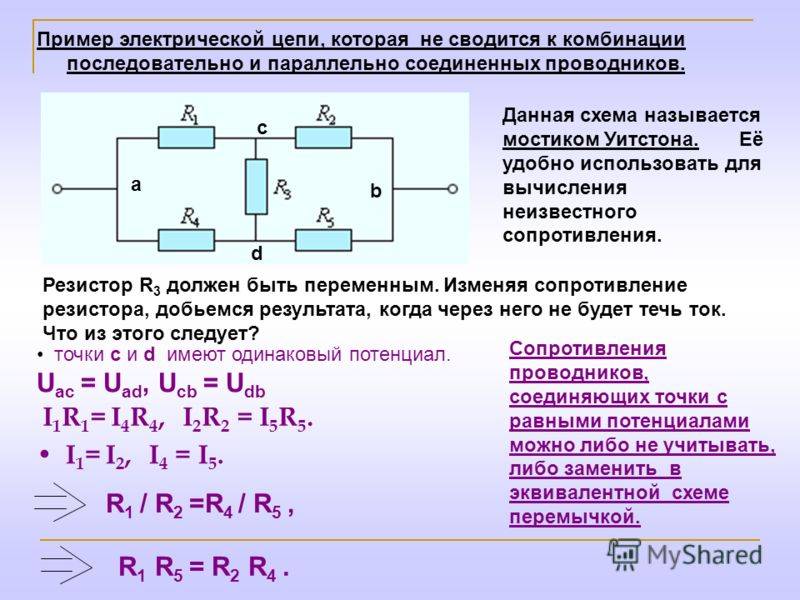

За счет чего совершается эта работа? Мы уже говорили, что электрическое поле обладает некоторой энергией. Именно за счет нее и идет совершение работы.

Такая работа совершается на каждом участке цепи, которую мы рассматриваем. Пользуясь законом сохранения энергии, мы можем сделать следующий вывод.

Энергия, израсходованная на всей цепи, равна сумме энергий, которые расходуются на отдельных ее участках (проводниках).

{"questions":[{"content":"Работа электрического тока в цепи совершается за счет[[choice-17]]","widgets":{"choice-17":{"type":"choice","options":["энергии электрического поля","напряжения","электрического заряда","силы тока"],"answer":[0]}}}]}

Пример задачи

Два проводника сопротивлением $R_1 = 2 \space Ом$ и $R_2 = 3 \space Ом$ соединены последовательно. Сила тока в цепи равна $1 \space А$. Определите сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Так как проводники соединены последовательно, мы будем использовать формулы, полученные на данном уроке.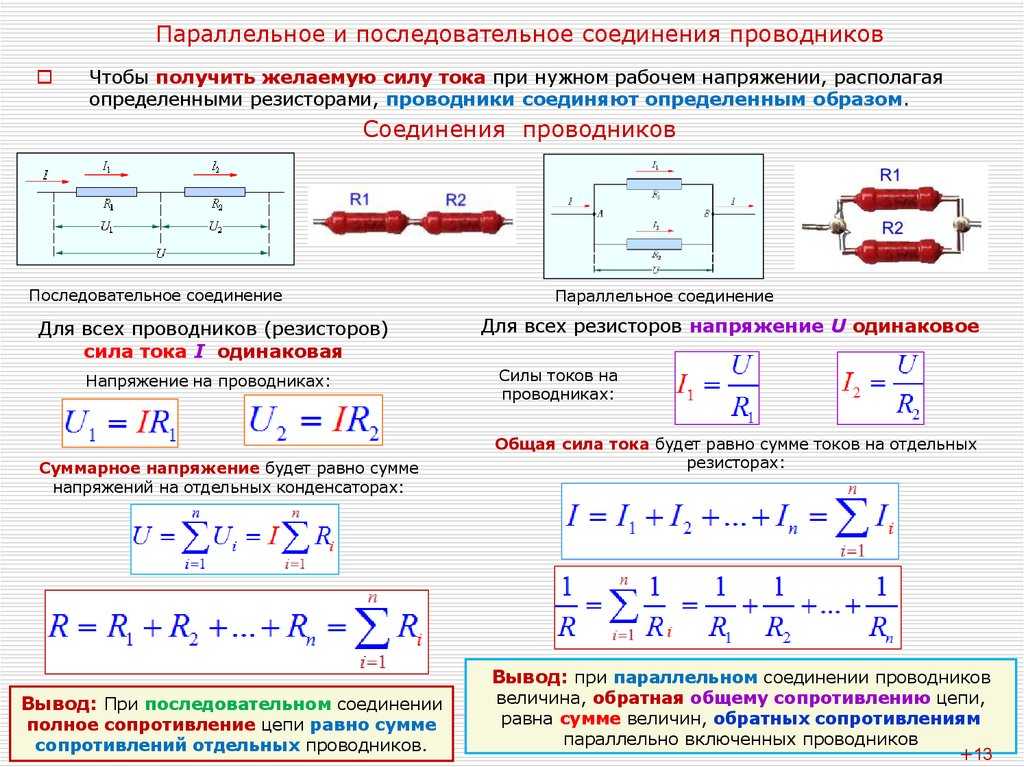

Дано:
$R_1 = 2 \space Ом$
$R_2 = 3 \space Ом$
$I = 1 \space А$

$R — ?$
$U_1 — ?$
$U_2 — ?$
$U — ?$

Решение:

Общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников:
$R = R_1 + R_2$.

Рассчитаем его:
$R = 2 \space Ом + 3 \space Ом = 5 \space Ом$.

Сила тока на всех участках цепи будет одинакова и равна $1 \space А$.

Запишем закон Ома для участка цепи с первым проводником и выразим из него напряжение на концах первого проводника:
$I = \frac{U_1}{R_1}$,
$U_1 = IR_1$.

Рассчитаем его:
$U_1 = 1 \space А \cdot 2 \space Ом = 2 \space В$.

Так же рассчитаем напряжение на концах второго проводника:
$I = \frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 1 \space А \cdot 3 \space Ом = 3 \space В$.

При последовательном соединении проводников полное напряжение в цепи мы можем рассчитать двумя способами.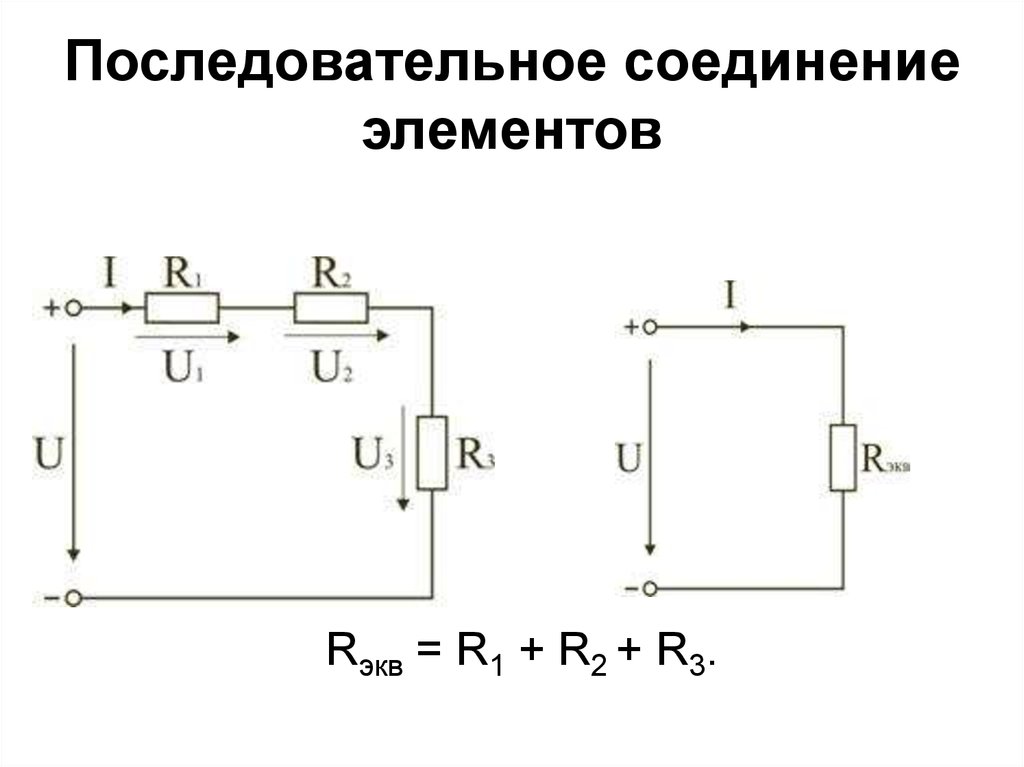

Способ №1
Напряжение на всей цепи равно сумме напряжений на концах проводников в этой цепи:
$U = U_1 + U_2$,
$U = 2 \space В + 3 \space В = 5 \space В$.

Способ №2
Мы уже знаем общее сопротивление двух проводников. Получается, что эти два проводника мы можем представить как один целый. Используем закон Ома для участка цепи:
$I = \frac{U}{R}$,
$U = IR$,
$U = 1 \space А \cdot 5 \space Ом = 5 \space В$.

Ответ: $R = 5 \space Ом$, $U_1 = 2 \space В$, $U_2 = 3 \space В$, $U = 5 \space В$.

Упражнения

Упражнение №1

Цепь состоит из двух последовательно соединённых проводников, сопротивление которых $4 \space Ом$ и $6 \space Ом$. Сила тока в цепи равна $0.2 \space А$. Найдите напряжение на каждом из проводников и общее напряжение.

Дано:
$R_1 = 4 \space Ом$
$R_2 = 6 \space Ом$

$I = 0.2 \space А$

$U_1 — ?$
$U_2 — ?$
$U — ?$

Показать решение и ответ

Скрыть

Решение:

Используя закон Ома для участка цепи,  мы рассчитаем значения напряжения на концах первого и второго проводников. Сила тока на всех участках цепи одинакова.

Напряжение на концах первого проводника:
$I = \frac{U_1}{R_1}$,
$U_1 = IR_1$,
$U_1 = 0.2 \space А \cdot 4 \space Ом = 0.8 \space В$.

Напряжение на концах второго проводника:
$I = \frac{U_2}{R_2}$,
$U_2 = IR_2$,
$U_2 = 0.2 \space А \cdot 6 \space Ом = 1.2 \space В$.

Общее напряжение будет равно сумме напряжений на концах каждого проводника:
$U = U_1 + U_2$,
$U = 0.8 \space В + 1.2 \space В = 2 \space В$.

Ответ: $U_1 = 0.8 \space В$, $U_2 = 1.2 \space В$, $U = 2 \space В$.

Упражнение №2

Для электропоездов применяют напряжение, равное $3000 \space В$. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение $50 \space В$ каждая?

Такие лампы можно соединить последовательно в одну цепь. Главное, чтобы их суммарное напряжение не превышало общее. Рассчитаем количество таких ламп, которое мы можем включить в цепь.

Дано:
$U = 3000 \space В$
$U_1 = 50 \space В$

$n — ?$

Показать решение и ответ

Скрыть

Решение:

Все лампы будут иметь одинаковое напряжение в $50 \space В$.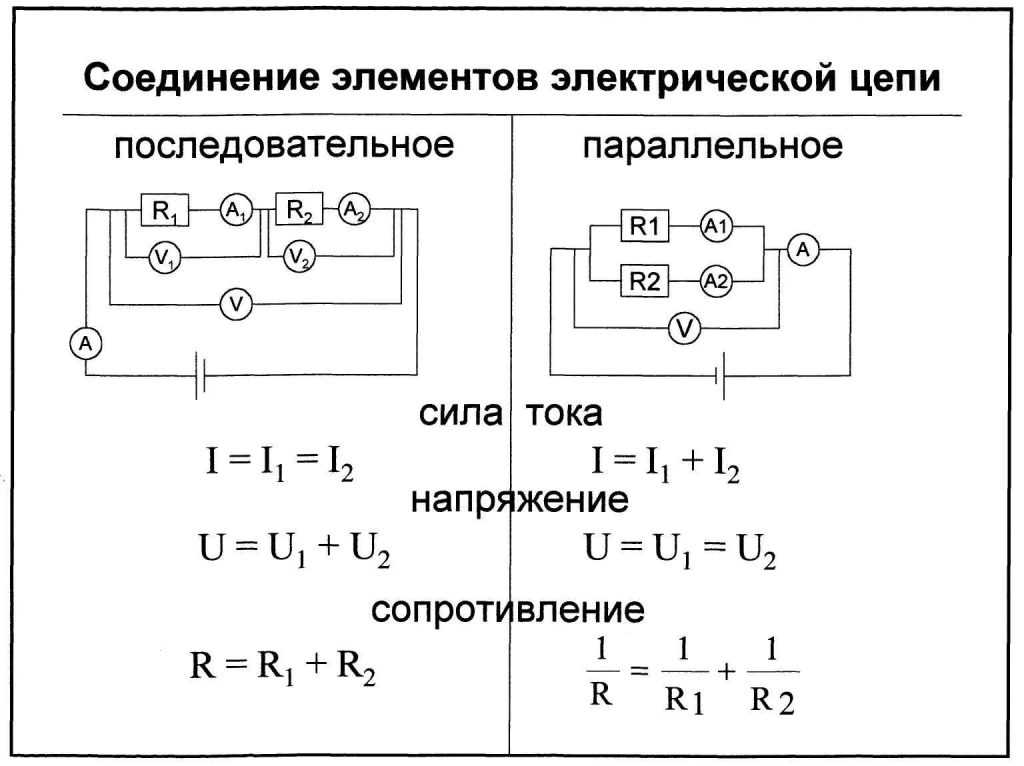 Напряжение на всей цепи равно сумме напряжений на каждой лампе. Тогда:
$n = \frac{U}{U_1}$,
$n = \frac{3000 \space В}{50 \space} = 60$.

Получается, что в таком электропоезде мы можем разместить 60 ламп для освещения вагонов, соединив их последовательно.

Ответ: при последовательном соединении мы можем использовать $n = 60$ ламп.

Упражнение №3

Две одинаковые лампы, рассчитанные на $220 \space В$ каждая, соединены последовательно и включены в сеть с напряжением $220 \space В$. Под каким напряжением будет находиться каждая лампа?

Дано:

$U = 220 \space В$

$U_1 — ?$
$U_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Лампы соединены последовательно. Значит, $U = U_1 + U_2$.

Если лампы одинаковые, то они имеют одинаковые сопротивления $R$. Сила тока тоже одинакова в каждой лампе. Из этого мы можем сделать вывод, что напряжение на лампах будет одинаковым:
$U_1 = IR$, $U_2 = IR$, $U_1 = U_2$.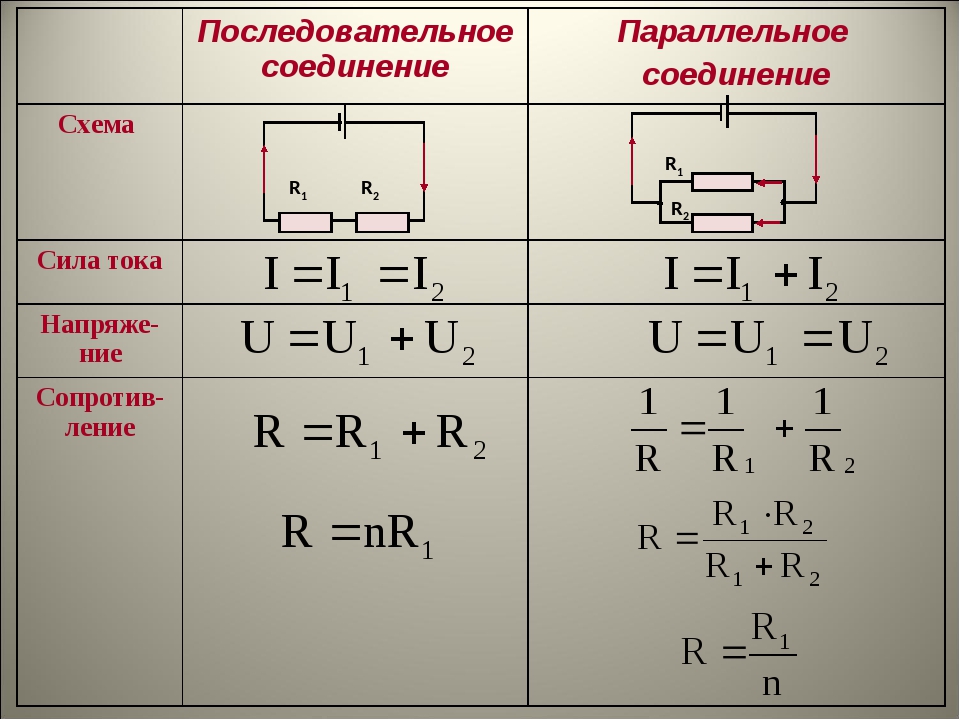

Тогда мы можем записать следующее:
$U = U_1 + U_2 = 2U_1$.

Рассчитаем напряжение на одной лампе:
$U_1 = U_2 =  \frac{U}{2}$,

$U_1 = U_2  = \frac{220 \space В}{2} = 110 \space В$.

Ответ: $U_1 = U_2 = 110 \space В$.

Упражнение №4

Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение, равное $6 \space В$, лампочки от карманного фонаря с сопротивлением в $13.5 \space Ом$, двух спиралей c сопротивлением $3 \space Ом$ и $2 \space Ом$, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.

Схема такой цепи изображена на рисунке 5.

Рисунок 5. Схема электрической цепи к упражнению №4

Дано:
$U = 6 \space В$
$R_1 = 13.5 \space Ом$
$R_2 = 3 \space Ом$
$R_3 = 2 \space Ом$

$I — ?$
$U_1 — ?$
$U_2 — ?$
$U_3 — ?$

Показать решение и ответ

Скрыть

Решение:

Сначала рассчитаем общее сопротивление на всей цепи:
$R = R_1 + R_2 + R_3$,
$R = 13.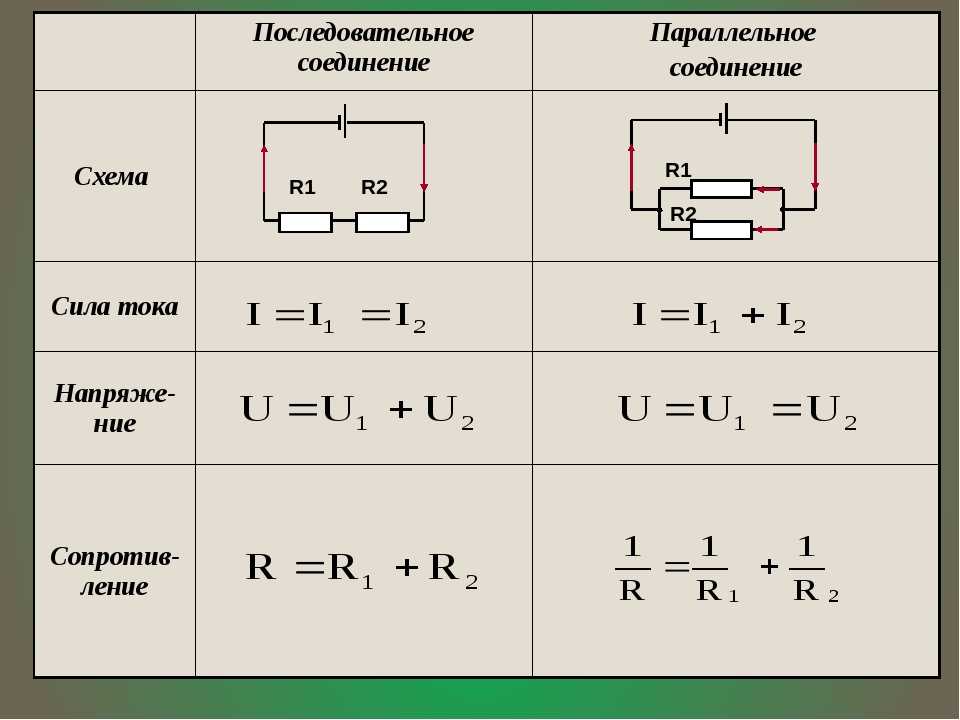 5 \space Ом + 3 \space Ом + 2 \space Ом = 18.5 \space Ом$.

Теперь используем закон Ома для того, чтобы рассчитать силу тока в цепи:
$I = \frac{U}{R}$,
$I = \frac{6 \space В}{18.5 \space Ом} \approx 0.32 \space А$.

Сила тока на каждом участке цепи при последовательном соединении элементов будет одинакова. Теперь мы будем использовать закон Ома отдельно для каждого проводника.

Рассчитаем напряжение на лампочке от карманного фонаря:
$U_1 = IR_1$,
$U_1 = 0.32 \space А \cdot 13.5 \space Ом \approx 4.3 \space В$.

Рассчитаем напряжение на первой спирали:
$U_2 = IR_2$,
$U_2 = 0.32 \space А \cdot 3 \space Ом \approx 1 \space В$.

Рассчитаем напряжение на второй спирали:
$U_3 = IR_3$,
$U_3 = 0.32 \space А \cdot 2 \space Ом \approx 0.6 \space В$.

Ответ: $I \approx 0.32 \space А$, $U_1 \approx 4.3 \space В$, $U_2 \approx 1 \space В$, $U_3 \approx 0.6 \space В$.

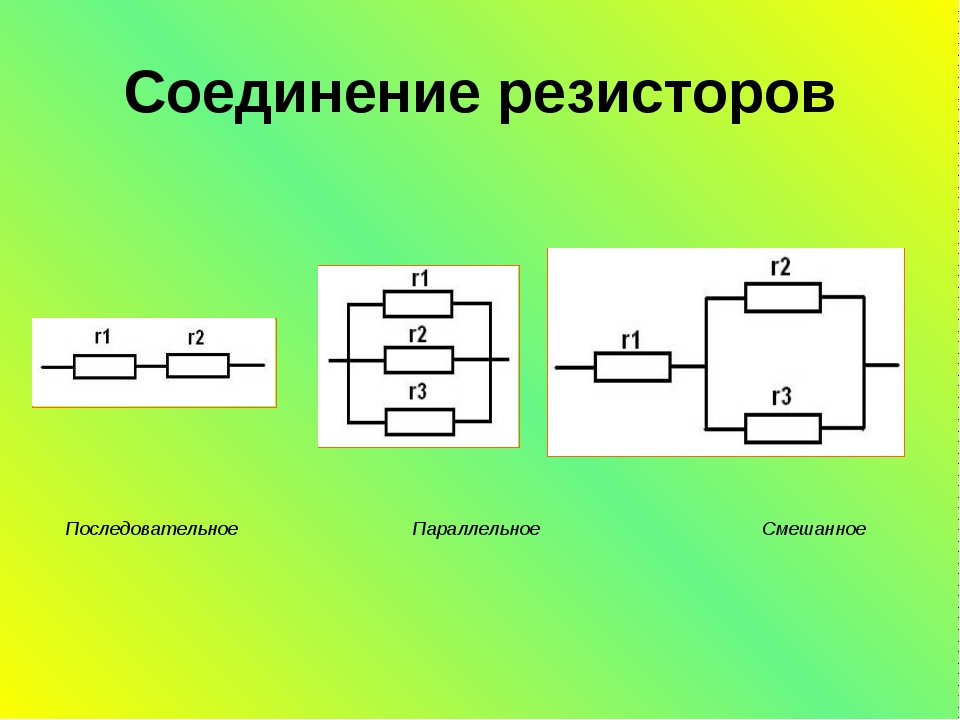
В чем разница между параллельным и последовательным соединением

Ключевое различие между параллельным и последовательным соединением заключается в том, что при параллельном соединении компоненты соединяются друг с другом, образуя ровно два набора электрически общих точек, тогда как последовательное соединение имеет все компоненты, соединенные встык, образуя единый путь для протекания тока.

Нам нужны разные схемы подключения, когда два или более электрических устройства подключены в цепь с источником энергии. Параллельные паттерны и паттерны серий — два таких основных паттерна. В параллельном соединении все компоненты имеют два общих узла. При последовательном соединении все компоненты соединены таким образом, что два компонента используют один и тот же узел.

СОДЕРЖАНИЕ

1. Обзор и основные отличия
2. Что такое параллельное соединение
3. Что такое последовательное соединение
4. Параллельное и последовательное соединение в табличной форме
5. Резюме — параллельное и последовательное соединение

Что такое параллельное подключение?

В параллельном соединении все компоненты имеют два общих узла. В этом типе комбинации электронные устройства подключаются параллельно друг другу; поэтому все устройства используют одни и те же два узла. Более того, входное напряжение всегда равно напряжению на каждом устройстве, а электрический ток, проходящий через устройства, распределяется между подключенными устройствами.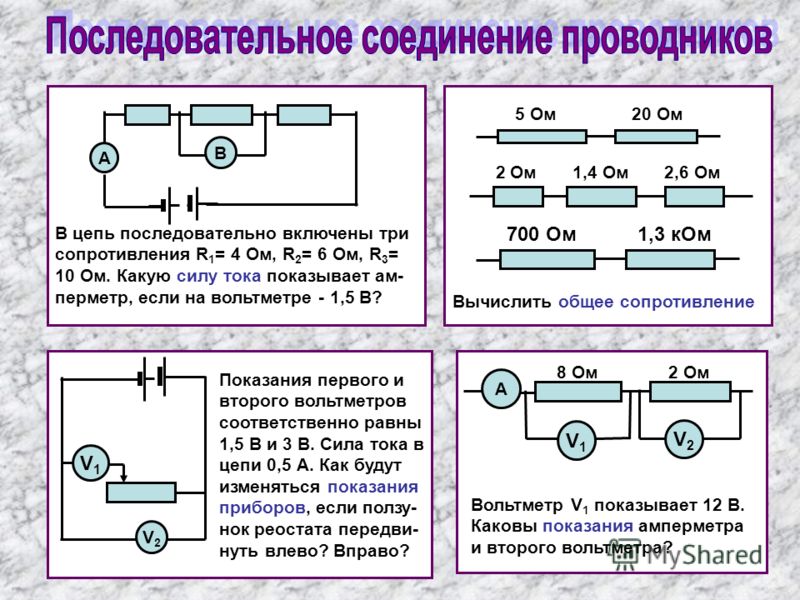

Более того, для получения эквивалентного сопротивления этой системы требуется конкретная формула.

Рисунок 01: Параллельное соединение (слева) и последовательное соединение (справа)

Подробную информацию о напряжении, токе и сопротивлении параллельного соединения можно суммировать следующим образом:

1. Напряжение: одинаковое для всех компоненты в параллельной цепи

E _общий = E1 = E2 = E3 = ………

2. Ток: общий ток цепи равен сумме токов в отдельной ветви

я _всего

= I1 + I2 + I3 + ……….
3. Сопротивление: полное сопротивление уменьшается при добавлении дополнительных компонентов/устройств

1/R _всего = 1/R1 + 1/R2 + 1/R3 + ……

Что такое последовательное соединение?

При последовательном соединении все компоненты соединены таким образом, что два компонента используют один и тот же узел. В этом типе комбинации электронные устройства соединяются друг с другом последовательно по схеме сквозного соединения.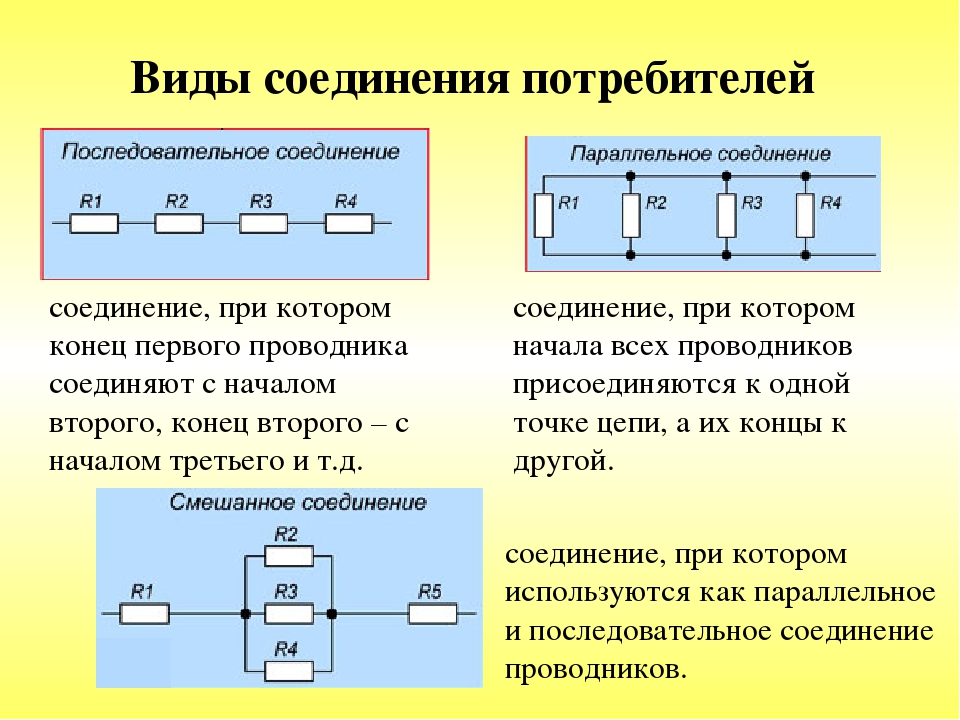 Поэтому два устройства всегда используют один и тот же узел, но не все устройства используют одни и те же два узла, как при параллельном соединении.

Более того, входное напряжение разделено на последовательные составляющие, поэтому входное напряжение не равно выходному, которое поступает от конкретного устройства в данном соединении. Кроме того, мы можем просто сложить значения резисторов, чтобы получить эквивалентное сопротивление системы. Электрический ток, проходящий через каждое устройство, не влияет на проходящий электрический ток, поэтому он остается постоянным.

Рисунок 02: Последовательное соединение

Мы можем обобщить информацию о напряжении, токе и сопротивлении последовательного соединения следующим образом:

1. Напряжение: равно сумме отдельных падений напряжения

E _всего = E1 + E2 + E3 + ……….

2. Ток: одинаковый на каждом резисторе

I _общее = I1 = I2 = I3 = ………

3. Сопротивление: общее сопротивление равно сумме отдельных сопротивлений

R _всего = R1 + R2 + R3 + ……. .

В чем разница между параллельным и последовательным соединением?

В параллельном соединении все компоненты имеют два общих узла, а в последовательном соединении все компоненты соединены таким образом, что два компонента используют один и тот же узел. Основное различие между параллельным и последовательным соединением заключается в том, что при параллельном соединении компоненты соединяются друг с другом, образуя ровно два набора электрически общих точек, тогда как при последовательном соединении все компоненты соединяются встык, образуя единый путь для текущего потока.

Более того, при параллельном соединении входное напряжение всегда равно напряжению на каждом устройстве; однако при последовательном соединении входное напряжение не равно напряжению на каждом устройстве, поскольку входное напряжение делится на последовательные составляющие.

Приведенная ниже инфографика представляет различия между параллельным и последовательным соединением в табличной форме для параллельного сравнения.

Резюме — параллельное и последовательное соединение

Существует два основных типа комбинаций компонентов при соединении электрических устройств. Это параллельные соединения и последовательные соединения. Основное различие между параллельным и последовательным соединением заключается в том, что при параллельном соединении компоненты соединяются друг с другом, образуя ровно два набора электрически общих точек, тогда как при последовательном соединении все компоненты соединяются встык, образуя единый путь для текущего потока.

Ссылка:

1. Тиле, Тимоти. «Обзор электрических соединений в вашем доме и вокруг него». The Spruce , The Spruce, 11 ноября 2019 г.

Изображение предоставлено:

электрическая цепь» (CC0) через Pixabay

Серия

и параллельные цепи в источниках питания

Пожалуйста, включите Javascript в вашем браузере для лучшего взаимодействия с пользователем.

Фотогальванические модули и батареи являются строительными блоками системы. Хотя каждый модуль или батарея имеют номинальное напряжение или силу тока, их также можно соединить вместе, чтобы получить желаемое системное напряжение.

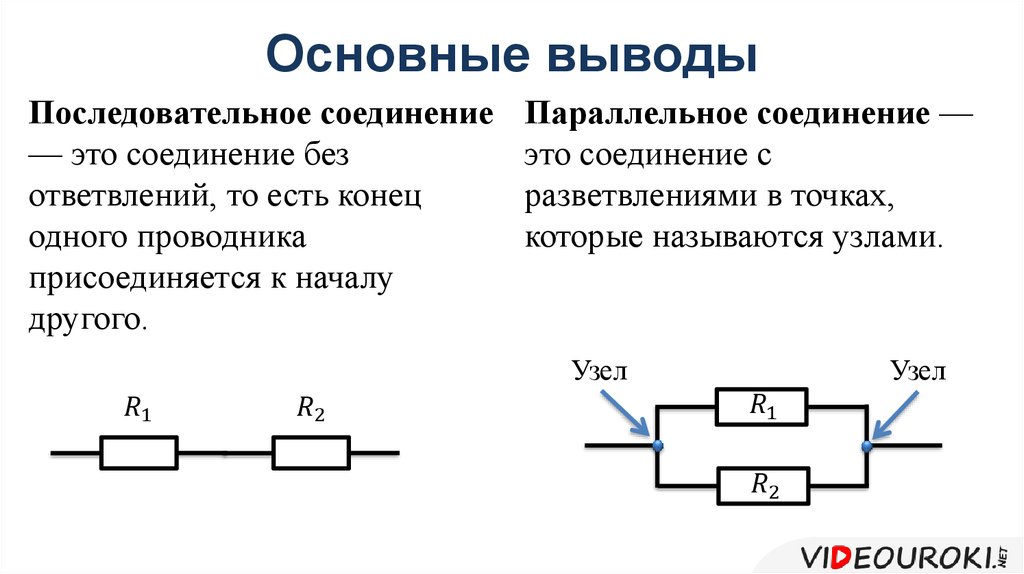
1. Последовательные цепи

Последовательные соединения проводки выполняются от положительного (+) конца одного модуля к отрицательному (-) концу другого модуля. Когда нагрузки или источники питания соединены последовательно, напряжение увеличивается. Последовательное подключение не увеличивает производимую силу тока. На изображении справа показаны два последовательно соединенных модуля, что дает 24 В и 3 А. 9Схемы серии 0005

также можно проиллюстрировать с помощью батареек для фонарей. Аккумуляторы фонарика часто соединяют последовательно для увеличения напряжения и питания лампы с более высоким напряжением, чем одна батарея может питать в одиночку.

Вопрос: Когда четыре батареи постоянного тока 1,5 В соединены последовательно, каково итоговое напряжение?

Ответ: 6 вольт

2.

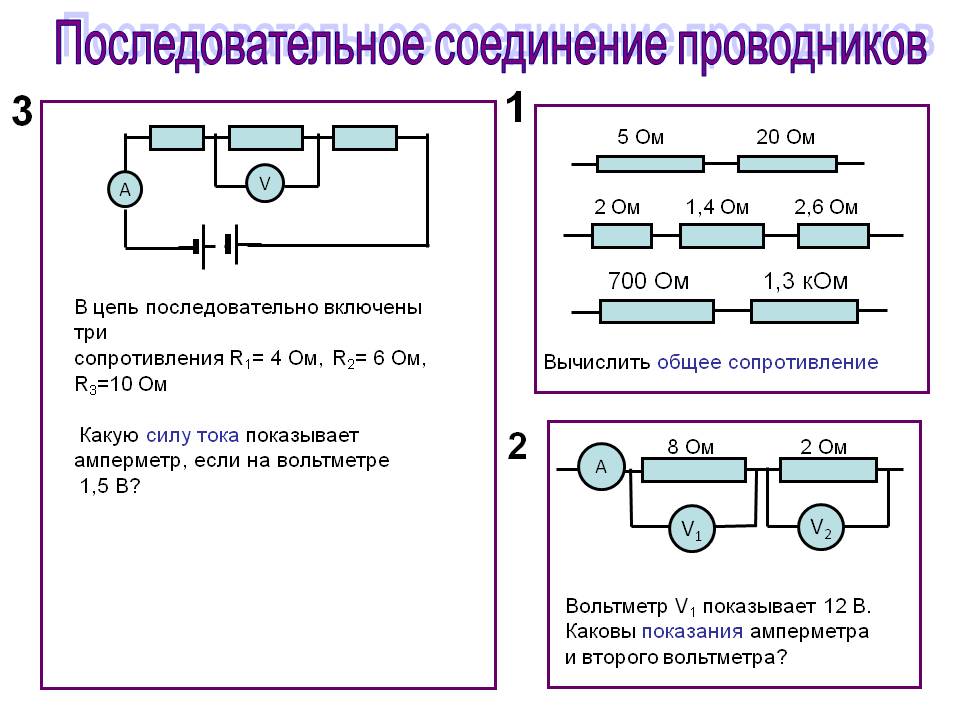
Параллельные цепи

Параллельные соединения выполняются от положительной (+) к положительной (+) клемме и отрицательной (-) к отрицательной (-) клеммам между модулями. Когда нагрузки или источники подключены параллельно, токи складываются, а напряжение одинаково во всех частях цепи. Чтобы увеличить силу тока системы, источники напряжения должны быть подключены параллельно. На изображении справа показаны фотоэлектрические модули, соединенные параллельно, чтобы получить систему на 12 В и 6 ампер. Обратите внимание, что параллельное соединение увеличивает производимый ток, но не увеличивает напряжение.

Батареи также часто подключаются параллельно для увеличения общего количества ампер-часов, что увеличивает емкость аккумулятора и продлевает время работы.s

3. Последовательные и параллельные цепи получить необходимые напряжения и силы тока. На изображении справа показаны четыре модуля на 3 А и 12 В постоянного тока, соединенные последовательно и параллельно. Строки из двух модулей соединены последовательно, увеличивая напряжение до 24В.

Каждая из этих цепочек подключена параллельно цепи, увеличивая силу тока до 6 ампер. В результате получается 6-амперная система с напряжением 24 В постоянного тока.

4. Батареи в последовательном и параллельном соединении

Преимущества параллельной схемы можно проиллюстрировать, наблюдая, как долго будет работать фонарь, прежде чем батареи полностью разрядятся. Чтобы фонарик работал в два раза дольше, необходимо удвоить емкость аккумулятора.

На рисунке слева ряд из четырех батарей добавлен параллельно другому ряду из четырех батарей для увеличения емкости (ампер-часы). Новая цепочка батарей подключается параллельно, что увеличивает доступный ампер-час, тем самым добавляя дополнительную емкость и увеличивая время использования. Вторую цепочку нельзя было добавить последовательно, потому что общее напряжение было бы 12 вольт, что несовместимо с 6-вольтовой лампой.

5. Высоковольтные фотоэлектрические батареи

До сих пор в этой главе мы обсуждали только входные напряжения до номинального значения 24 В.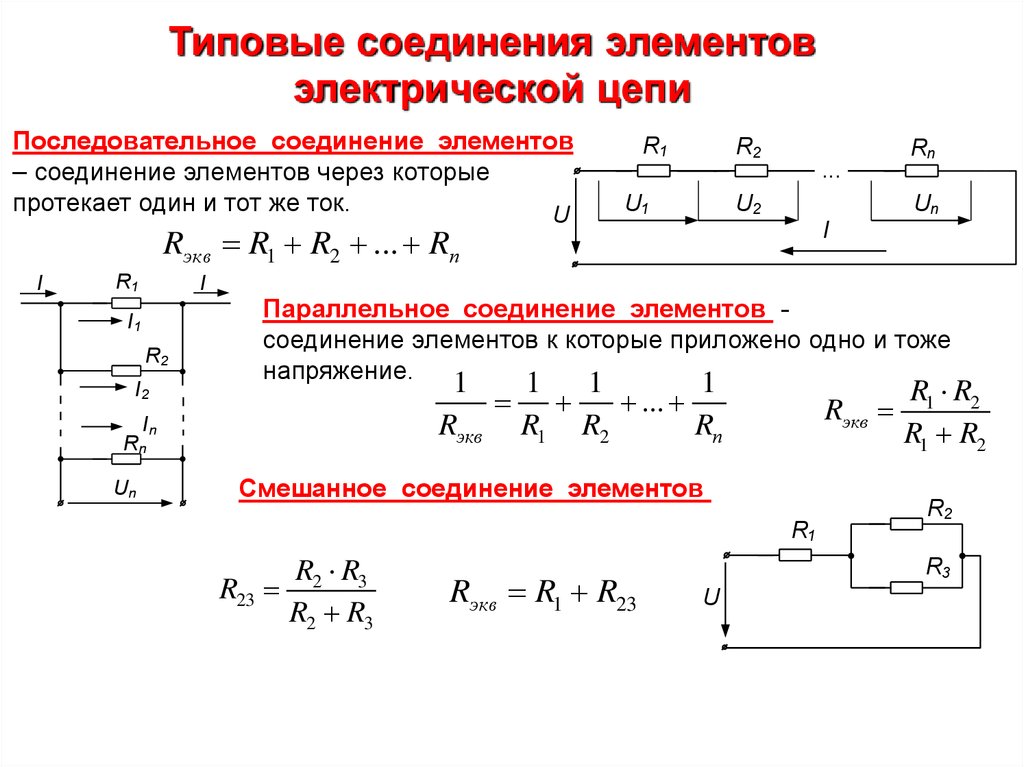 Сегодня большинство безбатарейных сетевых инверторов, представленных на рынке, требуют высокого напряжения на входе постоянного тока. Это входное окно обычно находится в диапазоне от 350 до 550 В постоянного тока. Из-за требований инвертора к высокому входному напряжению фотоэлектрические модули должны быть соединены последовательно, чтобы достаточно увеличить напряжение.

6. Примеры последовательного и параллельного подключения и инструкции

1. Соедините фотогальванические модули (массив) последовательно или параллельно, чтобы получить необходимое системное напряжение.

2. Рассчитать общий выход модуля для вольт и ампер.

3. Подключите массив к контроллеру заряда.

4. Соедините аккумуляторы последовательно или параллельно, чтобы получить требуемое системное напряжение.

5. Рассчитайте общее напряжение батареи и емкость в ампер-часах.

6. Подключите аккумуляторную батарею к контроллеру заряда.

Источник : «ФОТОЭЛЕКТРОЭНЕРГЕТИКА — Руководство по проектированию и установке» компании Solar Energy International.

Сертификационное обучение солнечной энергии от профессиональных специалистов по установке солнечной энергии

С 18 сертифицированными IREC-ISPQ инструкторами по солнечной фотоэлектрической энергии и 24 сертифицированными NABCEP установщиками солнечной фотоэлектрической энергии — больше, чем в любой другой организации по обучению солнечной энергии — опытная команда Solar Energy International находится в авангарде образования в области возобновляемых источников энергии. Если вы ищете онлайн-обучение по солнечной энергии или личное лабораторное обучение для экзамена начального уровня NABCEP или сертификации установщика NABCEP, почему бы не получить образование у команды самых опытных специалистов по установке солнечной энергии в отрасли? Многие инструкторы SEI участвовали в самых известных солнечных установках в своих сообществах в США и в развивающихся странах.