Импеданс параллельного и последовательного соединения резисторов и конденсаторов

Автор Aluarius На чтение 5 мин. Просмотров 11k. Опубликовано 28.05.2020

Для чего предназначены резисторы и конденсаторы

Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.

Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.

Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд. Величина, которую способно накопить устройство, называют «ёмкость».

Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.

После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.

Особенности соединения резистора и конденсатора в цепи

Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.

Параллельное соединение резистора и конденсатора

Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.

При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.

Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.

Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.

Последовательное соединение

Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.

Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/С_общ = 1/С₁ + 1/С₂ + … + 1/С_n.

Как рассчитать импеданс в цепи

Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс — векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.

Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.

К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.

Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.

Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.

Практические расчеты импеданса чаще всего выполняются по следующей формуле:

Z = Um/Im.

Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.

Энергия будет храниться и выделяться в двух типах:

• Магнитного поля. Реактивная часть является индуктивной.
• Электрического поля.

Как рассчитать время разряда и заряда конденсатора через резистор

Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.

Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.

Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.

Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток.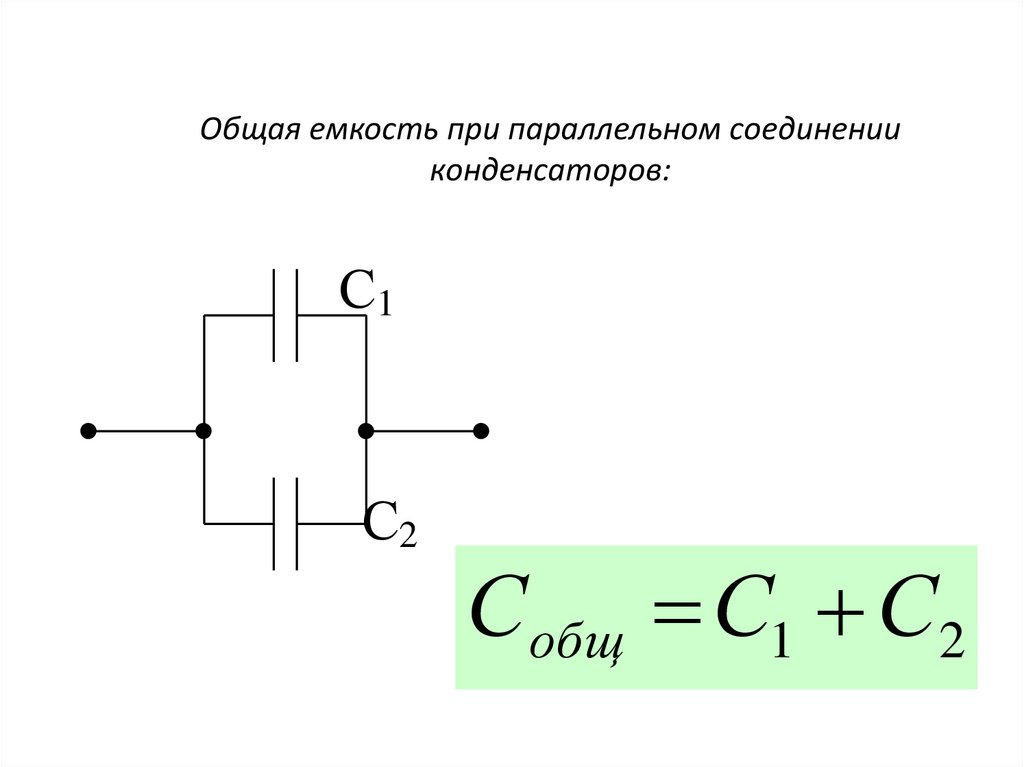 Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.

По мере того как конденсатор станет заряжаться, величина R на нём будет падать.

Время процесса зарядки будет зависеть от следующих величин:

1. Внутреннее сопротивление электрического генератора.
2. Способность конденсатора принять количество тока.

Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.

Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.

В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.

Продолжительность разряда устройства имеет зависимость от:

• Отношению заряда к разности потенциалов;
• Удельному электрическому сопротивлению.

Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.

Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.

Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.

Последовательное соединение резистора, конденсатора и катушки индуктивности

Пользуясь полученными выше результатами, можно найти соотношения между колебаниями тока и напряжения в любой цепи. Рассмотрим последовательное соединение резистора, конденсатора и катушки индуктивности (рис. 8.).

Рис.8. Последовательное соединение резистора, конденсатора и катушки индуктивности

Рис. 9. Векторная диаграмма

Положим по-прежнему, что ток в цепи изменяется по закону

,

и вычислим напряжение между концами цепи u. Так как при последовательном соединении проводников складываются напряжения, то искомое напряжение u есть сумма трех напряжений: на сопротивлении , на емкости и на индуктивности , причем каждое из этих напряжений, как мы видели, изменяется со временем по закону косинуса:

, (5)

, (6)

. (7)

Для сложения этих трех колебаний воспользуемся векторной диаграммой напряжений. Колебания напряжения на сопротивлении изображаются на ней вектором , направленным вдоль оси токов и имеющим длину, колебания же напряжений на емкости и индуктивности — векторамии, перпендикулярными к оси токов, с длинами (I_m/C) и (I_mL) (рис.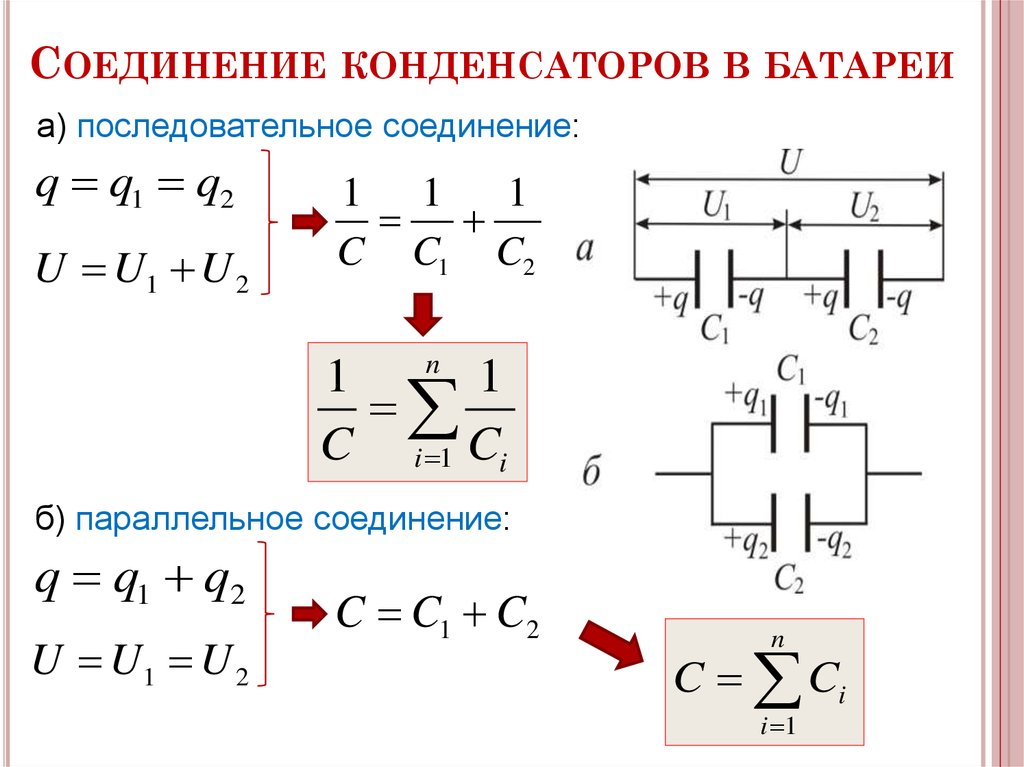 9.). Представим себе, что эти векторы вращаются против часовой стрелки вокруг общего начала с угловой скоростью . Тогда проекции на ось токов векторов ,и, будут описываться соответственно формулами (5)-(7). Очевидно, что проекция на ось токов суммарного вектора

равна сумме , то есть равна общему напряжению на участке цепи. Максимальное значение этого напряжения равно модулю вектора . Эта величина легко определяется геометрически. Сначала целесообразно найти модуль вектора:

,

а затем по теореме Пифагора:

. (8)

Из рисунка также видно, что

. (9)

Для напряжения на участке цепи можно записать

,

где амплитуда напряжения и фазовый сдвиг между током и напряжением определяются формулами (8), (9). Если , то напряжение по фазе опережает ток, в противном случае — напряжение отстает по фазе.

Формула (8) имеет сходство с законом Ома в том смысле, что амплитуда напряжения пропорциональна амплитуде тока. Поэтому ее иногда называют законом Ома для переменного тока. Однако нужно помнить, что эта формула относится только к амплитудам, но не к мгновенным значениям и. Величину

называют сопротивлением цепи для переменного тока, величину

называют реактивным сопротивлением цепи, а величину

R — активным сопротивлением.

Полученные формулы справедливы и для замкнутой цепи, включающей в себя генератор переменного напряжения, если под R, C и L понимать их значения для всей цепи (например R представляет собой суммарное активное сопротивление цепи, включая и внутреннее сопротивление генератора). В этом случае во всех формулах следует заменить u на ЭДС генератора. Действительно, для всех наших рассуждений было безразлично, в каком именно месте сосредоточены емкость, индуктивность и сопротивление, поэтому в замкнутой цепи (рис. 8) мы можем считать, что представляет собой суммарное активное сопротивление цепи, включая и внутреннее сопротивление генератора, аи- емкость и индуктивность цепи, и заменить реальный генератор воображаемым, у которого внутреннее сопротивление равно нулю. При этом напряжение

u между точками a и b будет равно ЭДС генератора . Отсюда следует, что формулы (8), (9) справедливы и для замкнутой цепи переменного тока, если под,, ипонимать их значения для всей цепи и заменить во всех формулахu на ЭДС генератора .

RC-цепь — объяснение, зарядка, примеры решений

Резисторно-конденсаторная цепь (RC-цепь) — это электрическая цепь, состоящая из пассивных компонентов, таких как резисторы и конденсаторы, приводимая в действие источником тока или источником напряжения.

Конденсатор накапливает энергию, а резистор, подключенный к цепи, управляет скоростью зарядки или разрядки.

Зарядка и разрядка конденсатора не является мгновенным процессом, а занимает некоторое время. Если резистор и конденсатор соединены последовательно, конденсатор постепенно заряжается через резистор, пока напряжение на резисторе не сравняется с напряжением питания.

Зарядка конденсатора

Предположим, что к цепи подключен полностью разряженный конденсатор и выключатель разомкнут. Начальное состояние цепи: время (t) = 0, заряд (q) = 0 и ток (i) = 0. Когда переключатель замкнут, время начнется с t = 0, и ток начнет течь через конденсатор и резистор. Первоначально незаряженный конденсатор можно считать соединительным проводом сразу после замыкания цепи.

В момент времени t = 0 разность потенциалов на конденсаторе равна нулю и продолжает быть равной нулю сразу после момента времени t = 0.

Ток, протекающий в это время, называется зарядным током и рассчитывается по закону Ома. Значение тока

i = i ₀ = ε/R.

Здесь ε – ЭДС ячейки.

Ом — сопротивление резистора.

С течением времени конденсатор заряжается, и на конденсаторе возникает разность потенциалов. Рассмотрим в любой момент времени «t», заряд конденсатора равен «q», а ток в цепи равен «i». Разность потенциалов на конденсаторе равна q/C, а разность потенциалов на резисторе равна iR. 9{\ гидроразрыва {-t} {RC}} \ конец {массив} \)

Ток называется переходным током и зависит от времени.

Постоянная времени

Постоянная времени (τ) при зарядке конденсатора – это время, необходимое для увеличения заряда конденсатора на 37% от его окончательного заряда. Это мера того, насколько быстро конденсатор может быть заряжен.

постоянная времени (τ) = RC

Решенные примеры

Вопрос 1: Конденсатор емкостью 1000 мкФ соединен последовательно с резистором сопротивлением 150 кОм и батареей напряжением 1,5 В. Найдите максимальный ток, протекающий через резистор при зарядке.

Ответ:

I = Ɛ/R = 1,5 В/150 кОм = 0,01 мА

Вопрос 2: В сеть серии RC подается напряжение 50 В переменного тока. {2}}\end{массив} \) 9{2}}\конец{массив} \)

\(\begin{array}{l}\Rightarrow V_{c}= 30 V\end{array} \)

Вопрос 3: Полное сопротивление RC-цепи равно Z ₁ для частоты f и Z ₂ для частоты 2f. Тогда Z ₁ / Z ₂ равно

.

а) между 1 и 2

б) 2

в) Между ½ и 1

г) ½

Ответ: а) между 1 и 2

Решение:

Для частоты f 9{2}}}}\конец{массив} \)

Z ₁ /Z ₂ лежит между 1 и 2.

Вопрос 4: Незаряженный конденсатор и резистор соединены последовательно, как показано на рисунке ниже. ЭДС батареи ε = 12 В, C = 8 мкФ, R = 500 кОм

После замыкания переключателя найти

(а) Постоянная времени RC-цепи.

(b) Максимальный заряд конденсатора.

(в) Заряд конденсатора через 6 с после замыкания ключа.

Решение:

(a) Постоянная времени RC-цепи, τ = (500 x 10 ^-3 Ом) (8 x 10 ^-6 ) = 4S

(б) Q = Q _f (1 – e ^-t/RC )

Q _f = CƐ — последний заряд

Максимальный заряд конденсатора, Ом _max = CƐ

= (8 х 10 ^-6 ) (12) = 96 мкКл

(c) Заряд конденсатора через 6 с после замыкания ключа равен

Q = Q _f (1 – e ^-t/τ )

= 96 (1 – е ^-6/4 )

= 74,5 мкКл

Видеоурок – RC-схема

Часто задаваемые вопросы о RC-цепи

Что обязательно подразумевает последовательная RC-цепь?

Последовательная RC-цепь состоит из резистора и конденсатора, последовательно соединенных с источником переменного тока.

Где вы видите RC-цепи в повседневной жизни?

В цепи конденсаторы и резисторы часто встречаются вместе. В реальной жизни такие RC-цепи встречаются часто. Они используются во вспышках фотоаппаратов, кардиостимуляторах, для управления скоростью работы дворников ветрового стекла автомобиля, синхронизацией сигналов светофора и разнообразным другим электрическим оборудованием.

Как работает RC-цепь?

Конденсатор накапливает энергию, а скорость зарядки или разрядки контролируется резистором, подключенным к цепи.

Конденсаторы последовательно и параллельно — Конденсаторы

Конденсаторы

Конденсаторы могут быть соединены последовательно или параллельно, чтобы получить результирующее значение, которое может быть либо сумма отдельных значений (параллельно) или значение меньше, чем у наименьшей емкости (последовательно).

Конденсаторы серии

Цепь, состоящая из нескольких последовательно соединенных конденсаторов, в некоторых отношениях похожа на одну.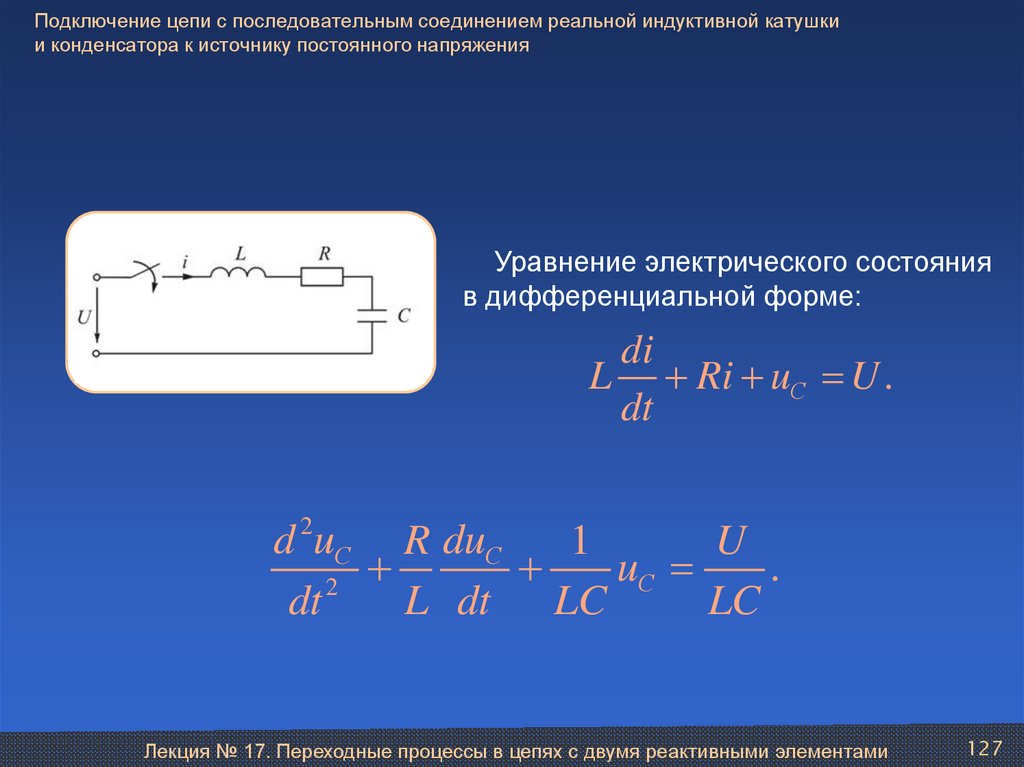 несколько последовательно соединенных резисторов. В последовательной емкостной цепи один и тот же ток смещения протекает через каждую часть цепи, и приложенное напряжение будет делиться на отдельные конденсаторы. На рисунке ниже показана схема, содержащая источник и три последовательных конденсатора.

Конденсаторы последовательно.

Сумма напряжений на конденсаторе должна равняться напряжению источника (закон напряжения Кирхгофа).

Заряды на всех конденсаторах должны быть одинаковыми, так как конденсаторы соединены последовательно и любые движение заряда в одной части цепи должно происходить во всех частях последовательной цепи. Решение уравнения C = Q / V для напряжения через емкость и заряд ( V = Q / C ), для каждого из рядов получены следующие результаты конденсаторов и суммарной емкости ( C _т )

Подставив эти результаты в приведенное выше уравнение закона Кирхгофа для напряжения

Разделив обе части приведенного выше уравнения на общий множитель Q

Взяв обратную величину обеих сторон и предполагая любое количество конденсаторов

Это уравнение является общим уравнением, используемым для расчета общей емкости конденсаторов. соединены последовательно. Обратите внимание на сходство между этим уравнением и тем, которое использовалось для нахождения эквивалента. сопротивление параллельных резисторов. Если в цепи всего два конденсатора, произведение превышает можно использовать формулу суммы

Из приведенных выше формул должно быть видно, что суммарная емкость конденсаторов при последовательном соединении меньше емкости любого из отдельных конденсаторов.

Пример:
Определите общую емкость последовательной цепи, содержащей три конденсатора, номиналы которых составляют 10 нФ, 0,25 мкФ и 50 нФ соответственно.

Решение:

Общая емкость 8 нФ немного меньше самого маленького конденсатора (10 нФ).

Параллельные конденсаторы

При параллельном соединении конденсаторов (см. рисунок ниже) одна пластина каждого конденсатора подключается напрямую. к одной клемме источника, а другая пластина каждого конденсатора подключена к другой терминал источника.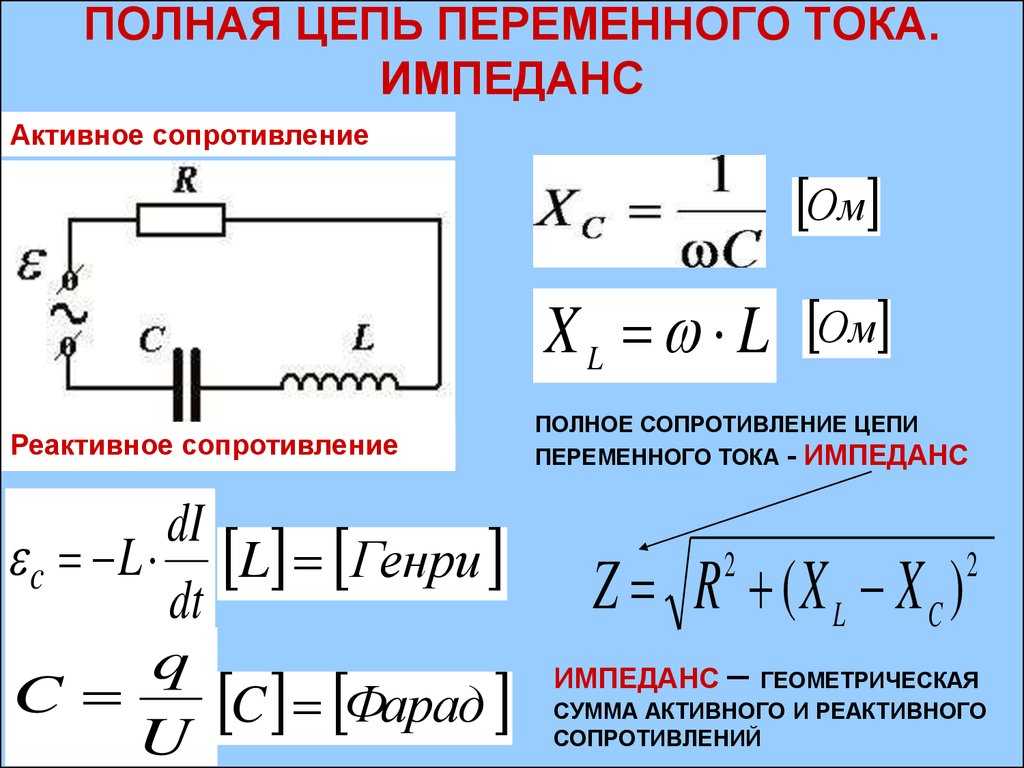 На рисунке ниже все отрицательные пластины конденсаторов соединены вместе, и все положительные пластины соединены вместе. Суммарная (эквивалентная) емкость Кл _t , следовательно, выступает как емкость с пластиной площадь равна сумме площадей всех отдельных пластин. Как упоминалось ранее, емкость напрямую зависит от площади пластины. Эффективное параллельное соединение конденсаторов увеличивает площадь пластины и тем самым увеличивает общую емкость.

Параллельные конденсаторы.

Полную емкость можно рассчитать математически. Применяя уравнение C = Q / V на каждый конденсатор и на общую емкость

Общий заряд Q _t есть сумма зарядов на каждом конденсаторе

Из уравнения C = Q / V следует, что Q = C V , а если заряд записывается в этой форме и подставляется в приведенное выше уравнение, это уравнение приводит к

Разделив обе части приведенного выше уравнения на общий множитель В и приняв любое количество конденсаторов

Это уравнение математически утверждает, что общая емкость ряда конденсаторов параллельно сумма отдельных емкостей.