Последовательная RC-цепь

Рассмотрим последовательную RC-цепь, состоящую из последовательно соединенных резистора и конденсатора.

Напряжение на зажимах цепи

По второму закону Кирхгофа это же напряжение можно определить как сумму падений напряжений на резисторе и конденсаторе

где

Тогда первое выражение можно переписать в следующем виде

Ток в цепи равен

Подставив в выражение выше, и выполнив интегрирование, получим

Напряжение на резисторе равно

Напряжение на конденсаторе

Как видно из последнего выражения напряжение на конденсаторе отстает от тока на угол π/2.

Реактивное (емкостное) сопротивление конденсатора равно

С уменьшением частоты емкостное сопротивление конденсатора увеличивается. При постоянном токе оно равно бесконечности, так как частота равна нулю.

Сдвиг фаз в последовательной RC – цепи можно определить по формуле

Полное сопротивление RC-цепи

Амплитудное значение тока

Рассмотрим пример решения задачи с RC-цепью

Полное сопротивление последовательной RC— цепи равно 24 Ом. Напряжение на резисторе равно 10 В, а его сопротивление 20 Ом. Найдите С, Uc, U, I, сдвиг фаз φ. Постройте векторную диаграмму.

Найдем ток, протекающий через резистор. Так как соединение последовательное, то этот ток будет общим для всей цепи.

Зная ток и сопротивление цепи, найдем напряжение

Емкостное сопротивление конденсатора

Зная сопротивление, найдем напряжение и емкость

Сдвиг фаз

Построим векторную диаграмму RC – цепи, при этом учитываем, что напряжение на конденсаторе отстает от тока (это видно по знаку сдвига фаз).

Сначала откладывается вектор тока в цепи, затем напряжение на резисторе и напряжение на конденсаторе. Затем строится вектор общего напряжения как сумма векторов напряжений на конденсаторе и на резисторе.

Читайте также — Последовательная RL-цепь

Просмотров: 13303

Последовательное соединение: резисторы и конденсаторы

Физика > Резисторы и конденсаторы в последовательной связи

 

Изучите последовательное соединение резистора и конденсатора: формула напряжения в электрической цепи, движение постоянного тока, зарядка и разрядка, уравнения.

Схема RC располагает резистором и конденсатором, где последний при подключении к постоянному току заряжается экспоненциально во времени.

Задача обучения

• Охарактеризовать составляющие и функции циркуляции RC.

Основные пункты

• Ток снижается от исходного значения I₀ = ЭДС/R к нулю, потому что напряжение на конденсаторе достигает того же показателя, что и ЭДС.
• Напряжение на конденсаторе с самого начала равняется нулю и быстро растет, потому что начальный ток выступает максимальным: 
• Постоянная времени (τ) в схеме определяется как RC. Определена в секундах и показывает стремительность заряда и разряда.

Термины

• Дифференциальное уравнение – уравнение с производными функциями.
• Прямой ток – однонаправленный поток электрического заряда.
• Конденсатор – электронная составляющая, способная сберегать электрический заряд.

Схема RC включает резистор (R) и конденсатор (С). Последний отображает электрическую составляющую, сберегающую электрический заряд.

Зарядка

На нижнем рисунке зафиксирована простая схема электрической сети для резисторов и конденсатора, где используется источник постоянного напряжения. Изначально конденсатор лишен подзарядки. Как только выключатель замыкается, ток переходит к нему и из него. С ростом заряда на пластинах создается сопротивление потоку заряда и подобные отталкиваются.

(а) – Схема RC с изначально незаряженным конденсатором. Ток проходит в конкретном направлении, как только замыкается выключатель. Отталкивание между подобными зарядами постепенно тормозит поток при зарядке конденсатора и останавливает его при полном заряде, где Q = C

⋅ ЭДС. (b) – График напряжения на конденсаторе зависит от времени при закрытии выключателя в момент t = 0

Напряжение конденсатора: V_c = Q/C (Q – количество заряда, хранящегося на каждой пластине, а C – емкость). Оно вступит в сопротивление с батареей, увеличиваясь с 0 к максимальной ЭДС. В итоге, ток сократится с изначального I₀ = ЭДС/R к 0, потому что напряжение на конденсаторе приравняется к ЭДС.

Первоначальное напряжение на конденсаторе приравнивается к 0 и быстро растет, потому что начальный ток – максимальный. На рисунке отображен график напряжения конденсатора, основываясь на времени, и начинается с закрытия выключателя при t = 0. Напряжение приближается к ЭДС асимптотически. Формула решения:

где V (t) – напряжение на конденсаторе, а ЭДС равно ЭДС источника постоянного напряжения. Можно определить постоянную времени при τ = RC (показывает стремительность зарядки или разрядки).

Разрядка

Вывод конденсатора через резистор осуществляется также, как отмечено на рисунке. Изначально ток (I₀ = V₀/R) контролировался начальным напряжением V₀ на конденсаторе. С падением напряжения скорость разряда также уменьшилась. Если используем вычисление напряжения на конденсаторе, разряжаемое резистором, то выходим на:

---

Постоянный электрический ток — §4. Последовательное и параллельное соединения — ЗФТШ, МФТИ

Для расчёта цепей особое значение имеют два типа соединений элементов: последовательное и параллельное. В ходе их анализа достаточно изобразить на схеме лишь рассматриваемый участок (а не всю цепь), поэтому возможные подключения других элементов цепи мы будем отмечать на схеме многоточиями  .

Два элемента, имеющих по два вывода у каждого, называются соединёнными последовательно, если есть точка соединения одного вывода первого элемента с одним выводом второго элемента и к этой точке больше ничего не подключено

, либо если есть третий элемент, который соединён последовательно с каждым из двух рассматриваемых.

Два  элемента, имеющих по два вывода у каждого, называются соединёнными параллельно, если есть точка соединения одного вывода первого элемента с одним выводом второго элемента, а также есть точка соединения другого вывода первого элемента с другим выводом второго элемента.

4.1 Основные свойства и примеры соединений

Последовательно соединённые резисторы можно видеть на рис. 4.1 и 4.2, а конденсаторы – на рис. 4.3 и 4.4. Последовательно можно соединить любое количество элементов, причём они могут быть разных типов (рис. 4.5).

 

Вне зависимости от количества (пусть их будет `n` штук) и типа последовательно соединённых элементов справедливы следующие утверждения:

1. Общая сила тока через последовательно соединённые элементы равна силе тока через любой из них:

 `I=I_1=I_2=…=I_n`.                                                                           (4.1)

2. Общее напряжение на последовательно соединённых элементах равно сумме напряжений на каждом из них:

`U=U_1+U_2+…+U_n`.                                                                       (4.2)

 Параллельно соединённые резисторы можно видеть на рис. 4.6 и 4.7, а конденсаторы – на рис. 4.8 и 4.9. Параллельно можно соединить любое количество элементов, причём они могут быть разных типов (рис. 4.10).

Вне зависимости от количества (пусть их будет `n` штук) и типа параллельно соединённых элементов справедливы следующие утверждения:

1. Общая сила тока через параллельно соединённые элементы равна сумме сил токов через каждый из них:

 `I=I_1+I_2+…+I_n`.                                                                             (4.3)

2. Общее напряжение на параллельно соединённых элементах равно напряжению на любом из них:

`U=U_1=U_2=…=U_n`.                                                                        (4.4)

При использовании формул (4.2) и (4.3) очень важно помнить, что сумма в них подразумевается алгебраическая (с учётом знака). Если полярность некоторого элемента не соответствует полярности последовательного соединения в целом, то в (4.2) перед напряжением на этом элементе следует ставить минус. Если ток через некоторый элемент направлен против тока через параллельное соединение в целом, то в (4.3) перед силой тока через этот элемент следует ставить минус.

Существует множество схем, элементы которых соединены не последовательно, но и не параллельно. Приведём в качестве примера пару таких схем, которые даже получили собственные названия: «треугольник» (рис. 4.11) и «звезда» (рис. 4.12). Одним из методов упрощения схем является преобразование «треугольника» в «звезду».

Как (последовательно или параллельно) соединены батарейка, лапочка и ключ в карманном фонарике?

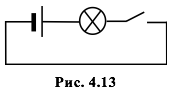
Рассмотрим оба соединения: последовательное (рис. 4.13) и параллельное (рис. 4.14). В первой схеме: когда ключ замкнут, лампочка горит; а когда разомкнут, – не  горит.  Во второй схеме: когда ключ разомкнут, лампочка горит; а когда  замкнут, существенная часть создаваемого батарейкой тока пойдёт через ключ (а не через лампочку). Про лампочку в этом случае мы пока (до следующего параграфа) ничего сказать не можем, однако ясно, что во второй схеме ток через батарейку идёт при любом положении ключа, то есть она разряжается всё время (даже при выключенном фонарике). Следовательно, вторая схема нерациональна и на практике не используется. Таким образом, ответ получен – элементы соединены последовательно.

 .               

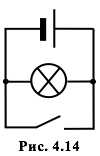
Как (последовательно или параллельно) соединены несколько лампочек в обычной люстре?

Без сомнения всем случалось наблюдать люстру, в которой горят не все лампочки (остальные перегорели или выкручены). У перегоревшей лампочки разрывается спираль и она больше не пропускает ток. Если бы лампочки были соединены последовательно, то в силу (4.1) сила тока через все лампочки была бы равна нулю, то есть ни одна лампочка не горела бы. Это противоречит экспериментальным наблюдениям, следовательно, лампочки в люстре соединены параллельно.

Как (последовательно или параллельно) соединены между собой телевизор и холодильник, включённый в сеть в одной комнате?

Напряжение сети (`220` В) одинаково для каждого бытового электроприбора вне зависимости от того, что включено в соседнюю розетку. Это полностью соответствует свойству (4.4). Кроме того, можно непосредственно проследить путь проводов, и тогда от любого прибора мы придём к счётчику электроэнергии. Таким образом, все приборы в одной квартир соединены параллельно. Утверждать то же самое для приборов в разных квартирах нельзя, так как счётчик у них не общий.

4.2. Резисторы

Рассмотрим последовательное (рис. 4.15) и параллельное (рис. 4.16) соединения двух резисторов сопротивлениями `R_1` и `R_2`.  В обоих случаях напряжения `U_1` и `U_2` на каждом из резисторов и силы токов `I_1` и `I_2` через них связаны законом Ома, который мы запишем в двух видах:

`U_1=R_1I_1`, `U_2=R_2I_2`,                                                    (4.5)

или

     `I_1=(U_1)/(R_1)`,   `I_2=(U_2)/(R_2)`.                                                     (4.6)

А вот общее напряжение `U` на обоих резисторах и общая сила тока `I` через них  будут зависеть от способа подключения.

  

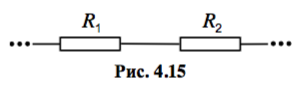
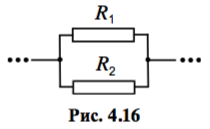
В случае последовательного соединения `U=U_1+U_2`, `I=I_1=I_2`. Используя эти свойства и соотношения (4.5), выразим общее сопротивление участка цепи, состоящего из двух резисторов:

`R=U/I=(U_1+U_2)/I=(R_1I_1+R_2I_2)/I=(R_1I+R_2I)/I=R_1+R_2`.

Это означает, что два последовательно соединённых резистора сопротивлениями `R_1` и `R_2` эквивалентны одному резистору сопротивлением  `R=R_1+R_2`.

Аналогичным образом можно доказать более общее утверждение: последовательно соединённые резисторы сопротивлениями `R_1,R_2,…R_n`  эквивалентны одному резистору сопротивлением

`R=R_1+R_2+…+R_n`.                                                         (4.7)

В  случае  параллельного  соединения `U=U_1=U_2`, `I=I_1+I_2`. 

 Используя эти свойства и соотношения (4.6), выразим общее сопротивление участка цепи, состоящего из двух резисторов:

`R=U/I=U/(I_1+I_2)=U/(U_1/R_1+U_2/R_2)=U/(U/R_1+U/R_2)=1/(1/R_1+1/R_2)=(R_1R_2)/(R_1+R_2)`.

Это означает, что два параллельно соединённых резистора сопротивлениями `R_1` и `R_2` эквивалентны одному резистору сопротивлением

`R=(R_1R_2)/(R_1+R_2)`.                                                          (4.8)

Аналогичным образом можно доказать более общее утверждение: параллельно соединённые резисторы сопротивлениями `R_1,R_2,…,R_n` эквивалентны одному резистору сопротивлением

`R=1/(1/R_1+1/R_2+…+1/R_n)`.                                                   (4.9)

Отметим, что выражение (4.8) получено после алгебраического преобразования, пригодного только для случая двух резисторов, поэтому его формальное обобщение приводит к неправильному (даже по размерности!) результату:

R=R1R2·…·RnR1+R2+…+Rn.\xcancel{R=\dfrac{R_1R_2\cdot…\cdot R_n}{R_1+R_2+…+R_n}.}

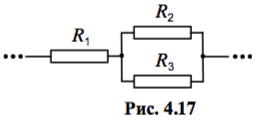
Найдите сопротивление  `R` изображённого на рис. 4.17 участка цепи. Значения отмеченных на рисунке параметров элементов известны.

Резисторы `R_2` и `R_3` соединены параллельно, поэтому их можно заменить одним резистором сопротивлением `R_(23)=R_2R_3//(R_2+R_3)`. После замены резисторы `R_1` и `R_(23)` оказываются соединены последовательно, значит, их можно заменить одним резистором сопротивлением `R_(123)=R_1+R_(23)`. После второй замены остаётся один резистор, следовательно, искомое сопротивление

`R=R_(123)=R_1+R_(23)=R_1+(R_2R_3)/(R_2+R_3)`.

  

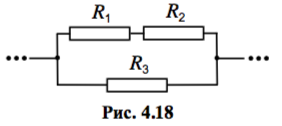
Найдите сопротивление `R` изображённого на рис. 4.18 участка цепи. Значения отмеченных на рисунке параметров элементов известны.

Резисторы `R_1` и `R_2` соединены последовательно, поэтому их можно заменить одним резистором сопротивлением `R_(12)=R_1+R_2`. После замены резисторы `R_(12)` и `R_3` оказываются соединены параллельно, значит, их можно заменить одним резистором сопротивлением `R_(123)=R_(12)R_3//(R_(12)+R_3)`. После второй замены остаётся один резистор, следовательно, искомое сопротивление

`R=R_(123)=(R_(12)R_3)/(R_(12)+R_3)=((R_1+R_2)R_3)/((R_1+R_2)+R_3)`.

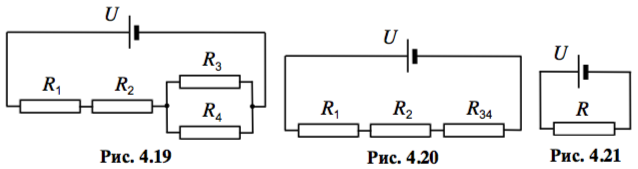
Найдите отношение напряжений `U_1` и `U_2` на резисторах `R_1` и `R_2`, а также отношение сил токов `I_3` и `I_4` через резисторы `R_3` и `R_4` (4.19). Значения отмеченных на рисунке параметров элементов известны.

1. В силу свойств последовательного соединения силы токов через резисторы `R_1` и `R_2` одинаковы: `I_1=I_2`. По закону Ома `U_1=R_1I_1` и `U_2=R_2I_2`.

Отсюда искомое отношение `U_1//U_2=R_1//R_2`.

2. В силу свойств параллельного соединения напряжения на резисторах `R_3` и `R_4` одинаковы: `U_3=U_4`. По закону Ома  `I_3=U_3//R_3` и `I_4=U_4//R_4`. Отсюда искомое отношение  `I_3//I_4=R_4//R_3`.

Обратите внимание, что каждый из ответов не зависит от остальной части схемы. Таким образом, напряжения на последовательно соединённых резисторах пропорциональны их сопротивлениям, а силы тока через параллельно соединённые резисторы обратно пропорциональны их сопротивлениям.

Найдите силу тока `I` через источник постоянного тока, напряжение на котором постоянно и равно `U` (4.19). Значения отмеченных на рисунке параметров элементов известны.

Резисторы `R_3` и `R_4` соединены параллельно, поэтому их можно заменить на один резистор сопротивлением `R_(34)=R_3R_4//(R_3+R_4)`. После замены резисторы `R_1`, `R_2` и `R_(34)` оказываются соединены последовательно (4.20), значит, их можно заменить одним резистором сопротивлением

`R=R_1+R_2+R_(34)=R_1+R_2+(R_3R_4)/(R_3+R_4)`.

В результате в схеме остаются только источник и один резистор (4.21). Их можно рассматривать как соединённые и последовательно, и параллельно. В силу первого сила тока через резистор равна искомой, а в силу второго напряжение на резисторе равно `U`. Тогда по закону Ома

`I=U/R=U/(R_1+R_2+(R_3R_4)/(R_3+R_4))`.

4.3. Конденсаторы

Прежде чем перейти к расчётам цепей с конденсаторами, вспомним их основные свойства, которые были подробно изучены в рамках электростатики.

Конденсатор – это система из двух изолированных друг от друга проводников (называемых обкладками), к которым подведены контакты.

В обычном режиме работы конденсатора заряды обкладок противоположны (равны по модулю и имеют разные знаки). Это условие может быть нарушено, если на одной из обкладок изначально был ненулевой заряд, что можно осуществить только при «изготовлении» конденсатора (но не за счёт каких-либо подключений его к цепи, так как заряд притёкший по проводу на одну обкладку, заставляет такой же по величине заряд покинуть другую обкладку по второму проводу конденсатора). Далее всюду будем предполагать обычный режим, если иное не оговорено особо.

Заряд на конденсаторе – это заряд одной  из обкладок, выбор которой является такой же условностью, как и выбор положительного направления тока в определении силы тока.

Следует чётко отличать приведённое выше понятие заряда на конденсаторе, применяемое при расчётах цепей, от полного заряда конденсатора как тела (суммы зарядов всех его частиц), который в обычном режиме равен нулю. Наличие зарядов на обкладках приводит к появлению между ними разности потенциалов, которая называется напряжением на конденсаторе.

Ёмкость конденсатора `C` — это величина, равная отношению заряда `q` на конденсаторе к напряжению `U` на нём: `C=q//U`.  Ёмкость измеряется в фарадах (Ф), причём Ф`=`Кл/В. 

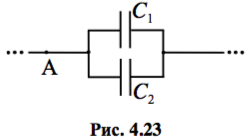
Рассмотрим последовательное  (рис. 4.22) и параллельное (рис.4.23) соединения двух конденсаторов ёмкостями `C_1` и `C_2`. В обоих случаях напряжения `U_1` и `U_2` на каждом из конденсаторов и заряды `q_1` и `q_2` на них можно связать через ёмкости:

`U_1=(q_1)/(C_1)`,     `U_2=(q_2)/(C_2)`,                                           (4.10)

или                                                                           

      `q_1=C_1U_1`,     `q_2=C_2U_2`.                                                  (4.11)

А вот общее напряжение `U` на обоих конденсаторах и общий заряд `q` на конденсаторах в целом (заряд, протёкший через точку `A` в процессе зарядки) будут зависеть от способа подключения.   

  

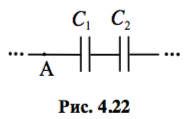
В случае последовательного соединения `U=U_1+U_2`, а заряд `q`, протёкший через точку `A`, окажется на каждом из конденсаторов, то есть `q=q_1=q_2`. Используя эти свойства и соотношения (4.10), выразим общую ёмкость участка цепи, состоящего из двух конденсаторов:

`C=q/U=q/(U_1+U_2)=q/(q_1/C_1+q_2/C_2)=q/(q/C_1+q/C_2)=1/(1/C_1+1/C_2)=(C_1C_2)/(C_1+C_2)`.

Это означает, что два последовательно соединённых конденсатора ёмкостями `C_1` и `C_2`, заряженных соответственно до напряжений `U_1` и `U_2`,  эквивалентны одному конденсатору ёмкостью

`C=(C_1C_2)/(C_1+C_2)`,                                                          (4.12)

заряженному до напряжения  `U=U_1+U_2` и несущему заряд  `q=CU`.

Аналогичным образом можно доказать более общее утверждение: последовательно соединённые конденсаторы ёмкостями `C_1,C_2,…C_n`, заряженные соответственно до напряжений `U_1,U_2,…,U_n`, эквивалентны одному конденсатору ёмкостью `C`, заряженному до напряжения `U` (соответствующего заряду  `q=CU`):

            `C=1/(1/C_1+1/C_2+…+1/C_n)`,         `U=U_1+U_2+…+U_n`.                                (4.13)

Отметим, что выражение (4.12) получено после алгебраического преобразования, пригодного для случая двух конденсаторов, поэтому его формальное обобщение приводит к неправильному (даже по размеренности!) результату:

C=C1C2·…·CnC1+C2+…+Cn.\xcancel{C=\dfrac{C_1C_2\cdot…\cdot C_n}{C_1+C_2+…+C_n}}.

В случае параллельного соединения `U=U_1=U_2`, а заряд `q`, протёкший через точку `A`, разделится между конденсаторами, то есть `q=q_1+q_2`. Используя эти свойства и соотношения (4.11), выразим общую ёмкость участка цепи, состоящего из двух конденсаторов:

`C=q/U=(q_1+q_2)/U=(C_1U_1+C_2U_2)/U=(C_1U+C_2U)/U=C_1+C_2`.

Это означает, что два параллельно соединённых конденсатора ёмкостями `C_1` и `C_2`, несущие соответственно заряды `q_1` и `q_2`, эквивалентны одному конденсатору ёмкостью `C=C_1+C_2`, несущему заряд `q=q_1+q_2` и заряженному до напряжения `U=q//C`. 

Аналогичным образом можно доказать более общее утверждение: параллельно соединённые конденсаторы ёмкостями `C_1,C_2,…,C_n`, несущие соответственно заряды `q_1,q_2,…,q_n`, эквивалентны одному конденсатору ёмкостью `C`, несущему заряд  `q` (соответствующий напряжению  `U=q//C`):

`C=C_1+C_2+…+C_n`,      `q=q_1+q_2+…+q_n`.                                          (4.14)

Суммы напряжений в (4.13) и зарядов в (4.14) подразумеваются алгебраические (с учётом полярности заряженных конденсаторов). А вот в выражениях для общей ёмкости минусов никогда не бывает. Формулы (4.13) и (4.14) справедливы при любых напряжениях на конденсаторах (даже не только для обычного режима), в частности, когда некоторые конденсаторы заряжены, а некоторые – нет. Из понятия эквивалентности следует, что если к системе конденсаторов подключить вольтметр, то он покажет напряжение на эквивалентном конденсаторе, а если систему конденсаторов замкнуть проводом, то по нему протечёт заряд эквивалентного конденсатора.

Три конденсатора ёмкостями `C_1=20` мкФ, `C_2=40` мкФ и `C_3=40` мкФ соединили последовательно с ключом (рис. 4.24). Конденсатор `C_1` изначально был не заряжен, а напряжения на конденсаторах `C_2` и `C_3` были соответственно `U_2=2` B и `U_3=3` B. Найдите заряд  `q`, который протечёт через ключ после замыкания цепи.

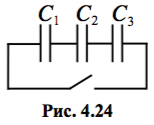
Искомая величина – это заряд эквивалентного конденсатора. В соответствии с (4.13) сначала найдём его ёмкость

`C=1/(1/C_1+1/C_2+1/C_3)=10` мкФ,

а потом выразим напряжение `U=0+-U_2+-U_3`. 

Знаки `+-` означают, что нам неизвестно, в какой полярности конденсаторы соединены друг с другом. В зависимости от выбора знаков мы получим четыре значения для `U:` `5`B,  `1`B, `-1`B, `-5`B. Поскольку в итоге нам нужно найти `|q|=C|U|`, то последние два значения `U` дадут тот же результат, что и первые два, поэтому их можно отбросить. Из оставшихся двух выбрать какое-то одно невозможно (не хватает данных). Поэтому задача имеет два ответа:  `q_1=50` мкКл и `q_2=10` мкКл.

Цепь собрана из бесконечного числа звеньев, состоящих из двух конденсаторов ёмкостями `C_1` и `C_2` (рис. 4.25). Многоточия на этой схеме обозначают остальные звенья цепи, а не произвольные элементы. Чему эквивалентен участок цепи между точками  `A` и `B`?

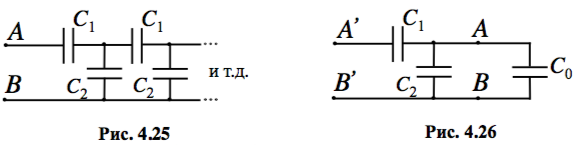
Любая схема, состоящая только из конденсаторов и имеющая два вывода, эквивалентна одному конденсатору. Нужно лишь найти его ёмкость `C_0`. Заменим исходную цепь на эквивалентный ей конденсатор `C_0` и добавим к схеме ещё одно звено (рис. 4.26). Пользуясь свойствами последовательного и параллельного соединений, рассчитаем ёмкость `C_0^’` участка цепи между точками `A^’` и `B^’`. Конденсаторы `C_2` и`C_0` соединены параллельно, поэтому их можно заменить на один конденсатор ёмкостью `C_(20)=C_2+C_0`. Конденсаторы `C_1` и `C_(20)` соединены последовательно, значит, их общая ёмкость

`C_0^’=(C_1C_(20))/(C_1+C_(20))=(C_1(C_2+C_0))/(C_1+(C_2+C_0))`.                            (4.15)

Теперь сравним исходную и полученную цепи. Добавление одного звена не меняет факта бесконечности цепи. Поскольку все звенья одинаковы, то цепь с дополнительным звеном эквивалентна исходной, а их ёмкости равны: `C_0^’=C_0`, откуда после подстановки (4.15) получаем `C_0^2+C_2C_0-C_1C_2=0`. Решая полученное квадратное уравнение относительно `C_0` и отбрасывая отрицательный корень, не имеющий физического смысла, находим

`C_0=1/2(sqrt(C_2^2+4C_1C_2)-C_2)`.

Рассмотренная задача является типичным примером целого класса задач – на бесконечные цепочки. В качестве элементов цепочки могут быть также  резисторы, источники и т. д. Кроме того, звенья цепи могут быть не одинаковы, например, сопротивление резисторов в каждом следующем звене в два раза больше, чем в предыдущем. Вообще, звенья могут состоять из разнотипных элементов, например, в схеме на 4.25 заменим мысленно все конденсаторы ёмкостью `C_1` на резисторы. В этом случае цепь будет эквивалентна не одному элементу, а участку из нескольких разнотипных элементов.

1) заменяем исходную бесконечную цепочку не эквивалентный ей элемент `X` и добавляем к нему ещё одно звено исходной цепочки;

2) рассчитываем параметры цепи с дополнительным звеном, полагая известными параметры элемента `X`; 

3) сравниваем полученную цепь с исходной и определяем соотношение их параметров; 4) поставляем в это соотношение выражение из пункта №2 и решаем уравнение.

Последовательное соединение резистора и конденсатора (конденсатор с потерями). Временная и векторная диаграммы. Закон Ома для действующих и амплитудных значений тока и напряжения.

⇐ ПредыдущаяСтр 6 из 10Следующая ⇒

Последовательное соединение резистора и конденсатора (конденсатор с потерями).
Конденсатор (ёмкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:

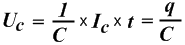
Величина ёмкости измеряется в фарадах (Ф). 1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.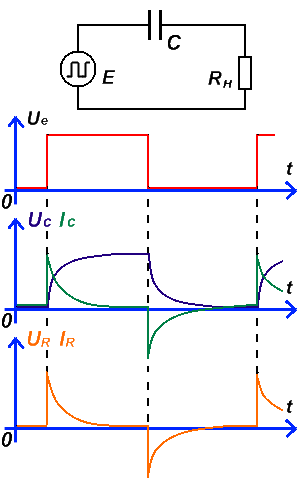
1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10^-12; нанофарад – 10^-9; микрофарад – 10^-6.

Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.
Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.

Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.
Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.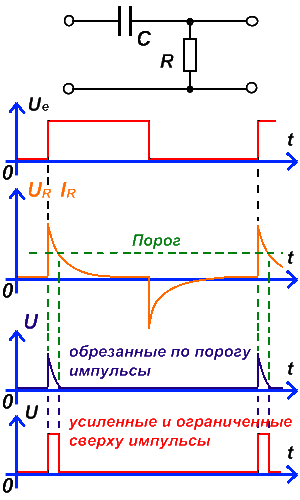
Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.

Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xcили Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:

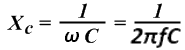
Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.
Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.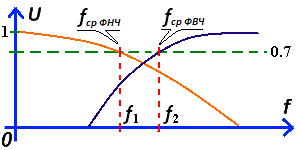
То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.
Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.

Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.

Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.

Рекомендуемые страницы:

1.2.1.3 Последовательное соединение резистора (r) и конденсатора (с)

На рис. 1.2.5 показана схема замещения последовательной RC — цепи.

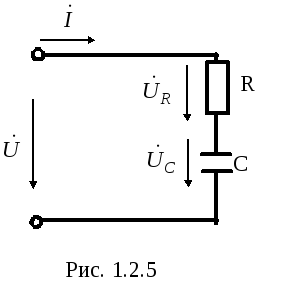
В емкостном элементе начальная фаза напряжения U_C отстает от начальной фазы тока 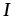на угол =90⁰ из-за того, что конденсатор обладает возможностью накапливать энергию электрического поля

,

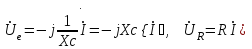где Хс=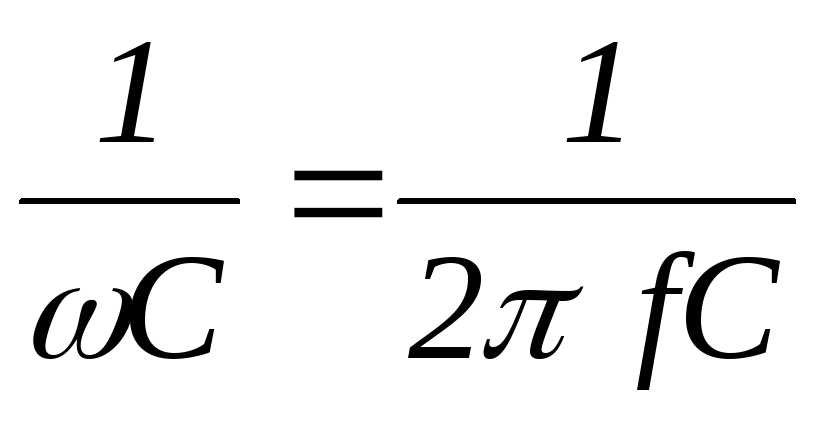— емкостное сопротивление ,Ом.

Реактивная (емкостная) мощность характеризует скорость поступления энергии в электрическое поле конденсатора и возврат ее, источнику

.

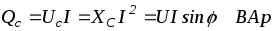Полное комплексное сопротивление цепи

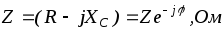
где 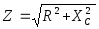— полное сопротивление, Ом;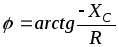— угол сдвига фаз между током и напряжением, <0 .

На рис. 1.2.6 представлена векторная диаграмма цепи, а также полученные из нее треугольники сопротивлений и мощностей.

Коэффициентом мощности электрической цепи называется отношение активной мощности Р к полной мощности S

.

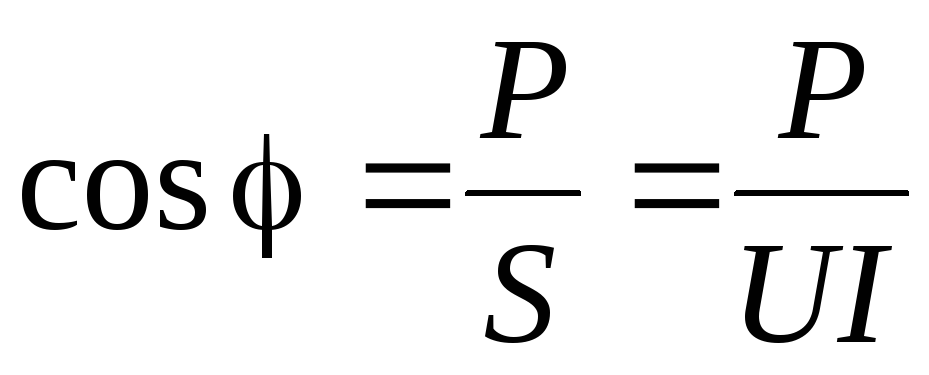-jQ_C=-jX_CI²

Рис. 1.2.6

Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды и, в частности, используется на выполнение полезной работы, поэтому является важным технико-экономическим показателем работы цепи.

1.2.1.4 Последовательное соединение активного, индуктивного и емкостного сопротивления

При расчете неразветвленной электрической цепи переменного тока с последовательно соединенными R, L и С элементами( рис. 1.2.7) воспользуемся уравнениями, записанными на основе второго закона Кирхгофа. В комплексной форме это уравнение имеет вид

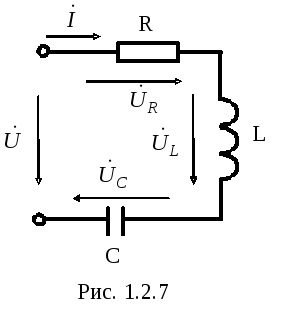
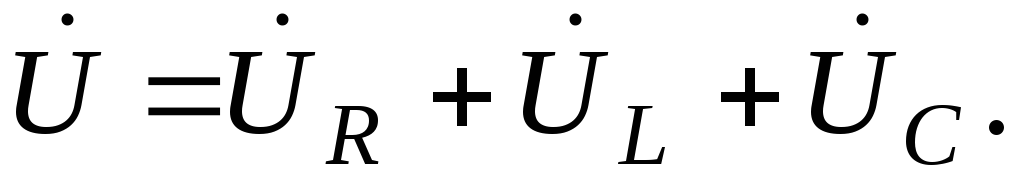(1.2.1)

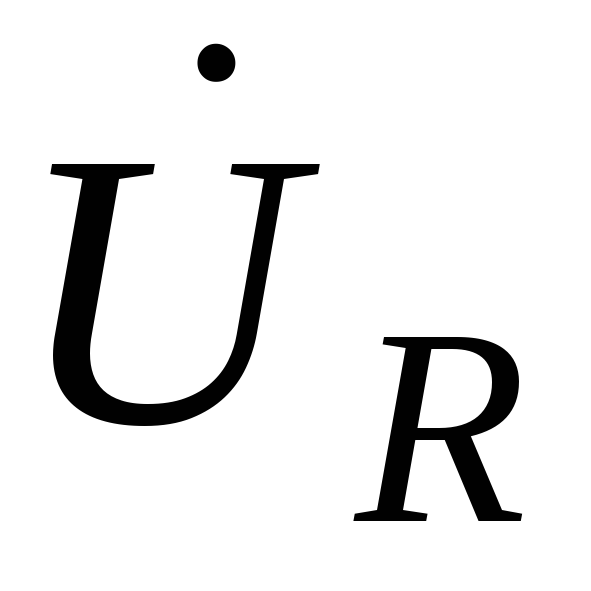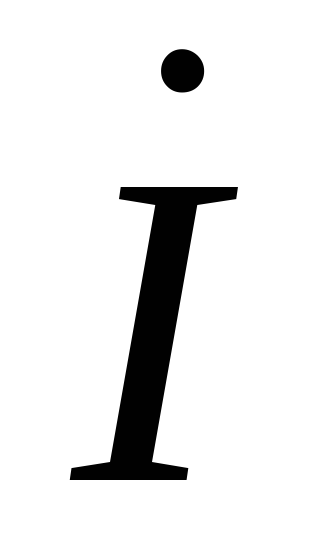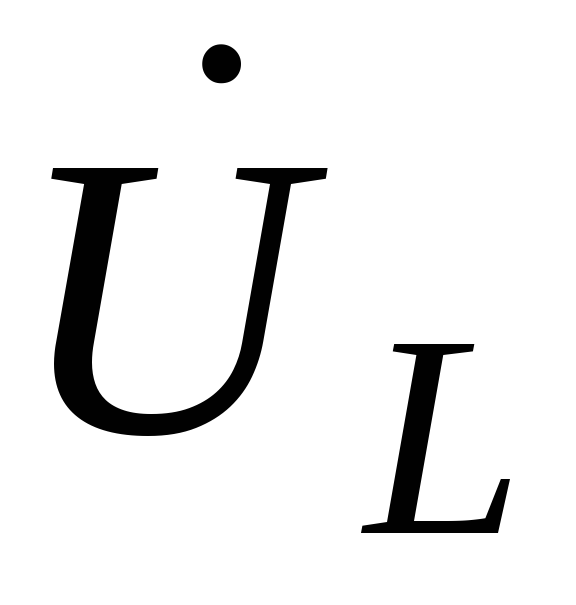Учитывая, что напряжение на сопротивлении совпадает по фазе с током, напряжениена индуктивном элементе опережает, а напряжение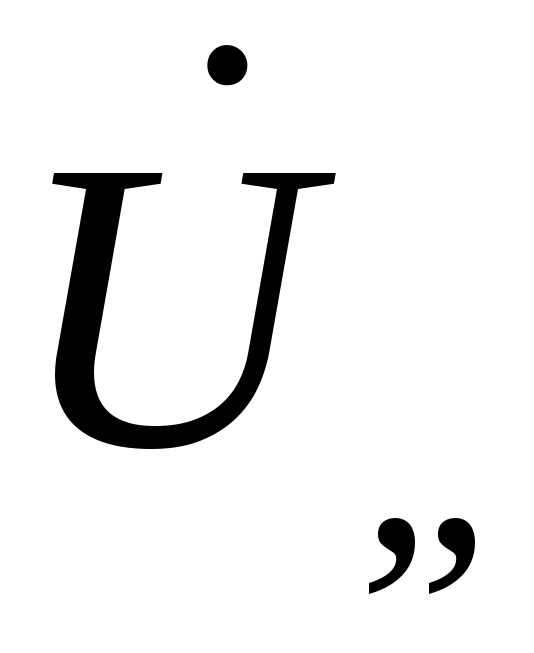на емкостном элементе отстает от токаI на 2, получаем

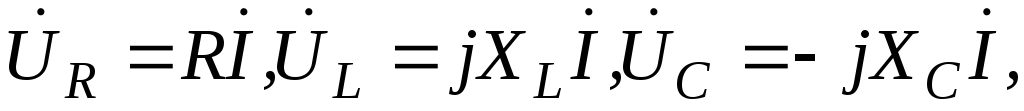(1.2.2)

где X_L= L , X_C= -1/C,  = 2f.

Тогда комплексное напряжение на зажимах неразветвленной цепи переменного тока примет вид

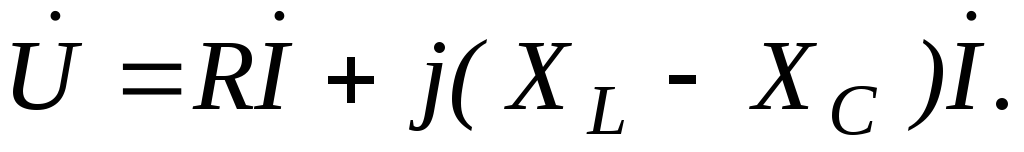(1.2.3)

Обозначив разность X_L — X_C = X, окончательно получим

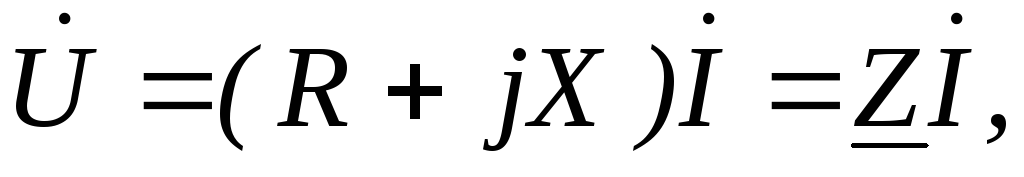(1.2.4)

где Х -реактивное сопротивление цепи, а

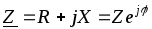(1.2.5)

представляет собой комплексное сопротивление цепи, причем

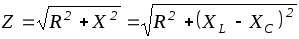(1.2.6)

-модуль комплексного числа ,а

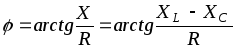(1.2.7)

-аргумент комплексного числа, определяющий угол сдвига фаз между напряжением и током.

Векторные диаграммы напряжений и тока в неразветвленной цепи синусоидального тока строят на комплексной плоскости в соответствии с уравнением второго закона Кирхгофа (1.2.1) с учетом фазовых сдвигов напряжений 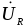,,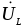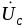и тока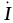во времени (рис. 5.2 , 5.3).





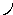
+j

+j

+1

+1







 

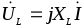
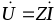
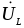
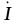
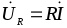
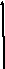
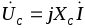
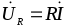
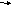
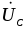
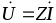
Рис. 1.2.9

Рис. 1.2.8

Первая диаграмма относится к случаю, когда реактивное сопротивление X>0, т.е. в цепи преобладает индуктивная нагрузка, ток 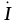отстает от напряжения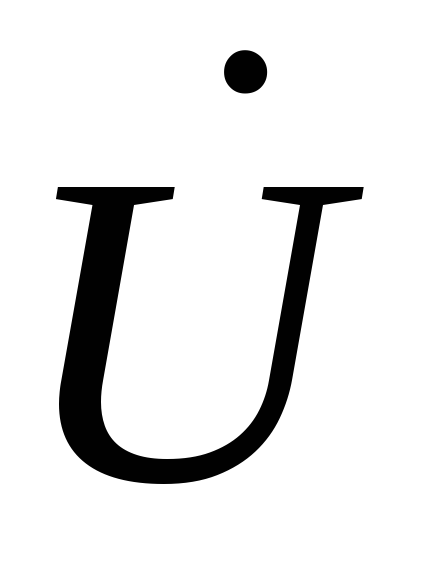и угол сдвига фаз положительный. Вторая диаграмма соответствует случаю, когда X<0, т.е. в цепи преобладает емкостная нагрузка, ток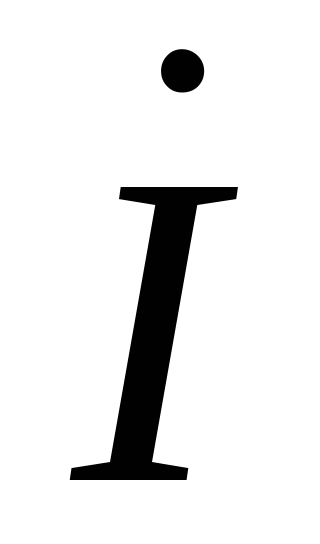опережает напряжение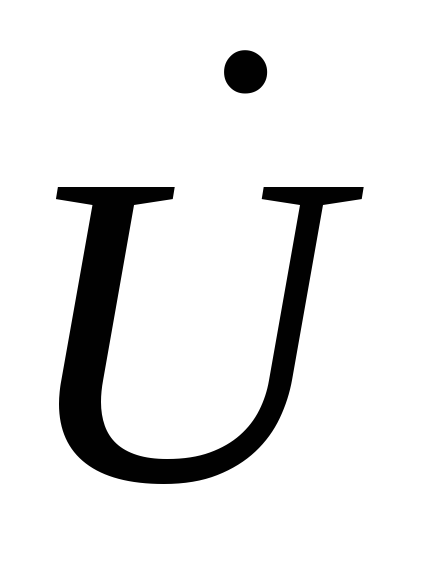, а угол сдвига фаз отрицательный.

Угол сдвига фаз  между током 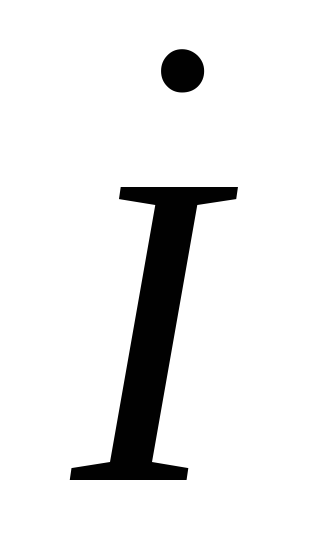и приложенным напряжением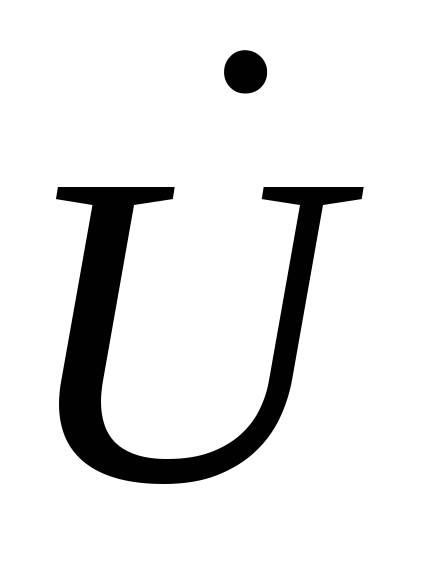принимается положительным, если он направлен от тока к напряжению в направлении против движения часовой стрелки, в противном случае — угол принимается отрицательным (рисунки 5.2 , 5.3).

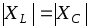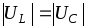В цепи с последовательно соединенными R, L, C — элементами возможен режим, когда реактивное сопротивление X=0 и =0 , что имеет место при равенстве абсолютных значений и индуктивного и емкостного сопротивлений, т.е. при . При этом выполняется условиеи =0, причем действующие значения этих напряжений могут превышать напряжение U на зажимах цепи. Это явление называется резонансом напряжений. Векторная диаграмма для этого случая показана на рисунке 5.4

+j

+1

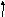
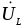
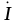
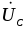
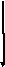
U_L=U_C,

=0

Рис. 1.2.10

1.2.1.3 Последовательное соединение резистора (r) и конденсатора (с)

На рис. 1.2.5 показана схема замещения последовательнойRC — цепи.

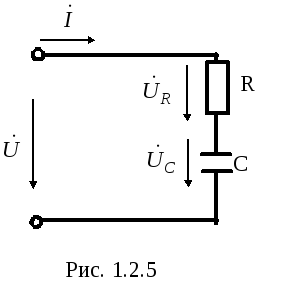
В емкостном элементе начальная фаза напряженияU_C отстает от начальной фазы тока 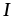на угол=90⁰из-за того, что конденсатор обладает возможностью накапливать энергию электрического поля

,

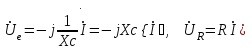где Хс=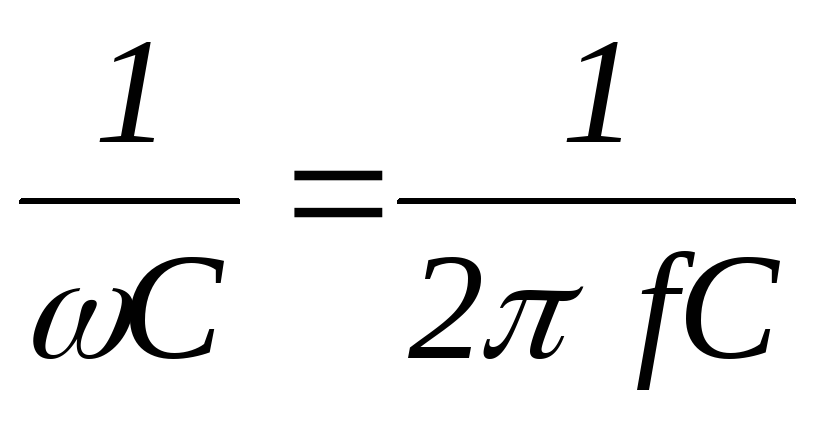— емкостное сопротивление ,Ом.

Реактивная (емкостная) мощность характеризует скорость поступления энергии в электрическое поле конденсатора и возврат ее, источнику

.

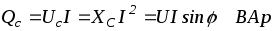Полное комплексное сопротивление цепи

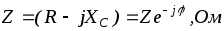
где 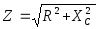— полное сопротивление, Ом;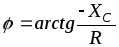— угол сдвига фаз между током и напряжением, <0 .

На рис. 1.2.6 представлена векторная диаграмма цепи, а также полученные из нее треугольники сопротивлений и мощностей.

Коэффициентом мощности электрической цепи называется отношение активной мощностиРк полной мощностиS

.

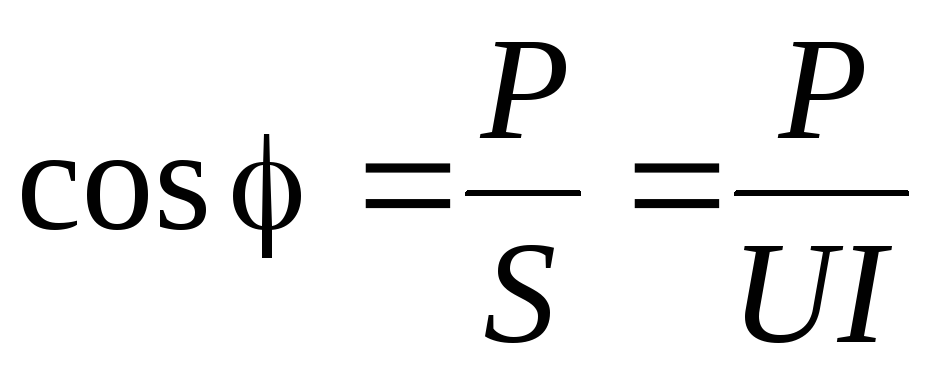-jQ_C=-jX_CI²

Рис. 1.2.6

Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды и, в частности, используется на выполнение полезной работы, поэтому является важным технико-экономическим показателем работы цепи.

1.2.1.4Последовательное соединение активного, индуктивного и емкостного сопротивления

При расчете неразветвленной электрической цепи переменного тока с последовательно соединеннымиR, LиСэлементами( рис. 1.2.7) воспользуемся уравнениями, записанными на основе второго закона Кирхгофа. В комплексной форме это уравнение имеет вид

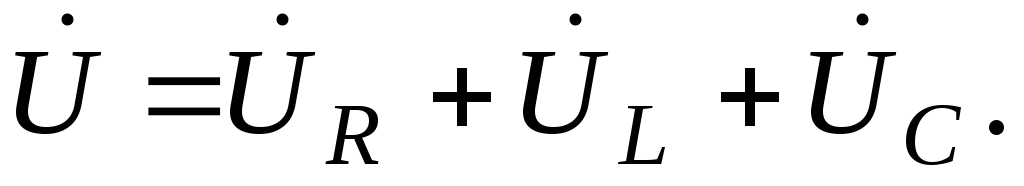(1.2.1)

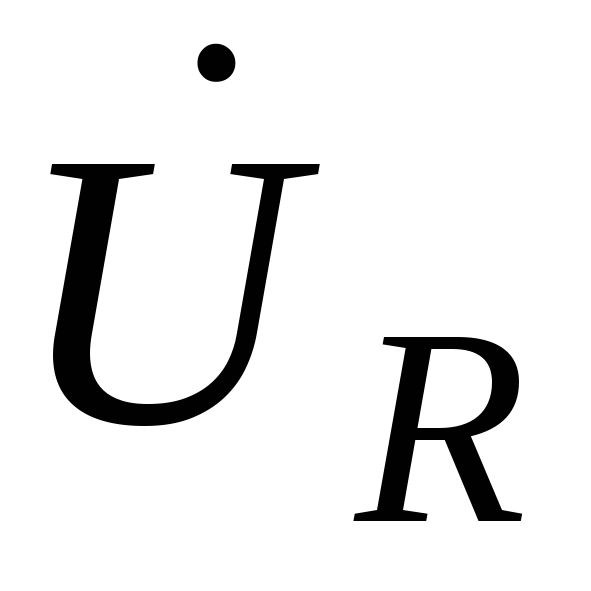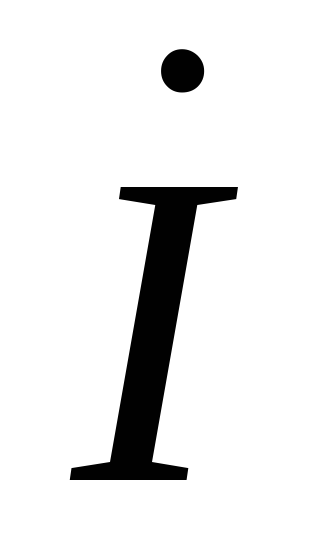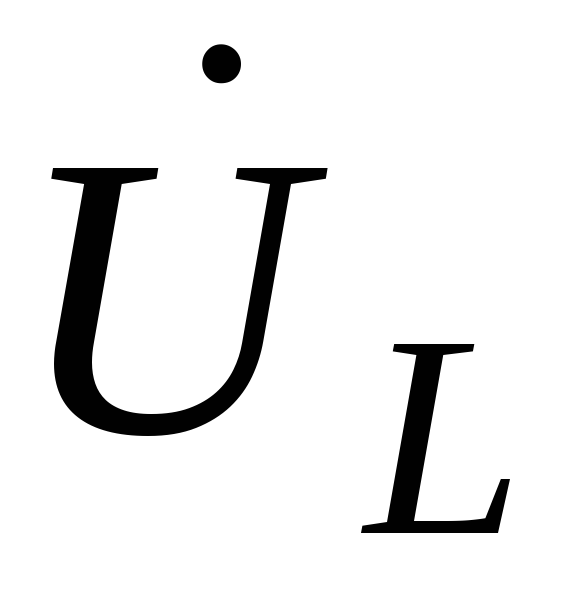Учитывая, что напряжение на сопротивлении совпадает по фазе с током, напряжениена индуктивном элементе опережает, а напряжение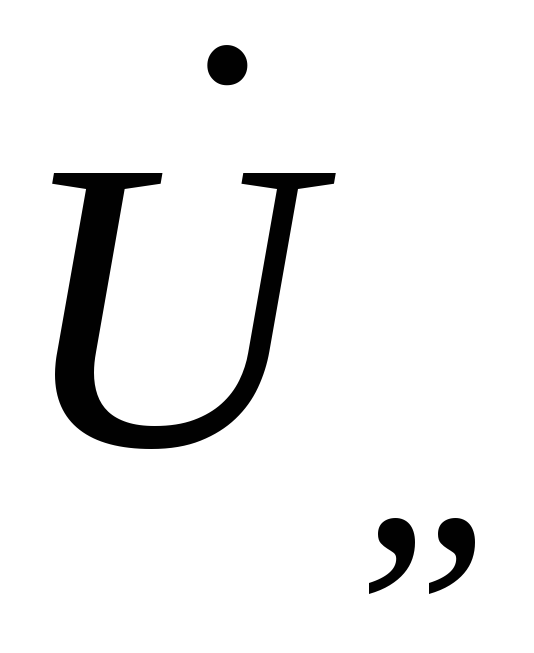на емкостном элементе отстает от токаIна2, получаем

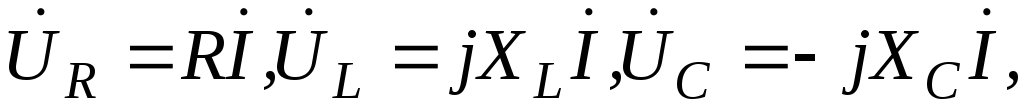(1.2.2)

где X_L= L , X_C= -1/C,  = 2f.

Тогда комплексное напряжение на зажимах неразветвленной цепи переменного тока примет вид

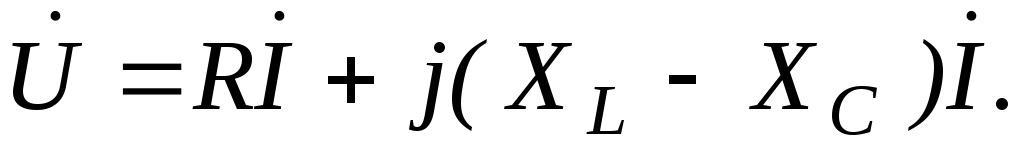(1.2.3)

Обозначив разность X_L — X_C = X, окончательно получим

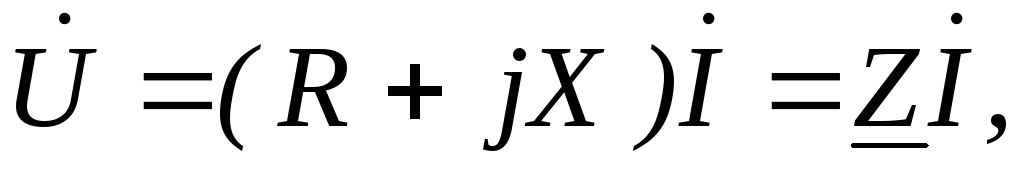(1.2.4)

где Х-реактивное сопротивление цепи, а

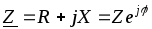(1.2.5)

представляет собой комплексное сопротивление цепи, причем

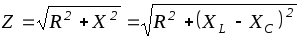(1.2.6)

-модуль комплексного числа ,а

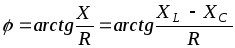(1.2.7)

-аргумент комплексного числа, определяющий угол сдвига фаз между напряжением и током.

Векторные диаграммы напряжений и тока в неразветвленной цепи синусоидального тока строят на комплексной плоскости в соответствии с уравнением второго закона Кирхгофа (1.2.1) с учетом фазовых сдвигов напряжений 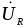,,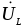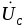и тока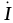во времени (рис. 5.2 , 5.3).





+j

+j

+1

+1







 

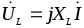
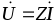
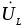
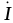
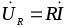
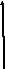
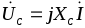
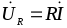
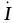
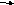
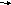
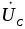
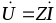
Рис. 1.2.9

Рис. 1.2.8

Первая диаграмма относится к случаю, когда реактивное сопротивление X>0, т.е. в цепи преобладает индуктивная нагрузка, ток отстает от напряжения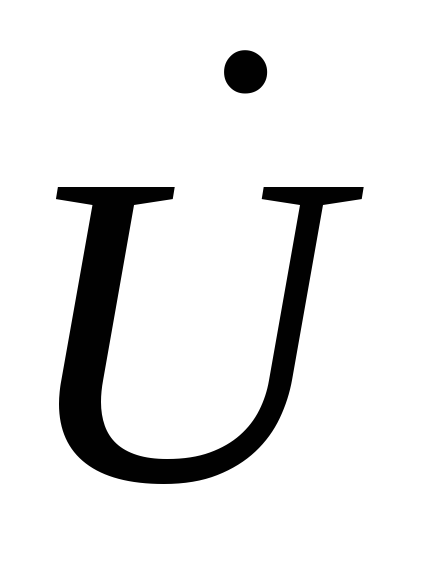и угол сдвига фаз положительный. Вторая диаграмма соответствует случаю, когда X<0, т.е. в цепи преобладает емкостная нагрузка, ток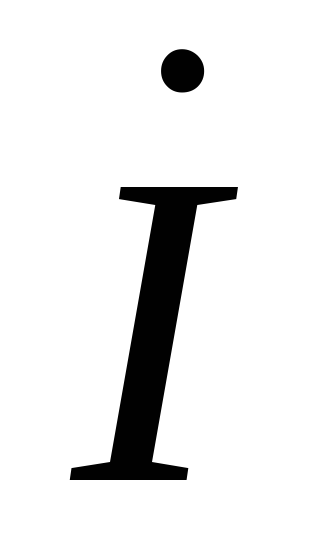опережает напряжение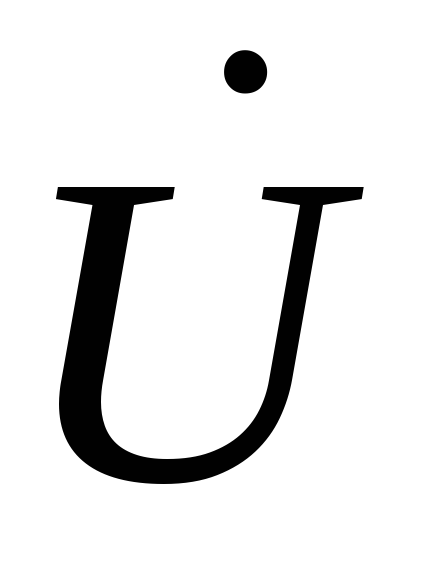, а угол сдвига фазотрицательный.

Угол сдвига фаз  между током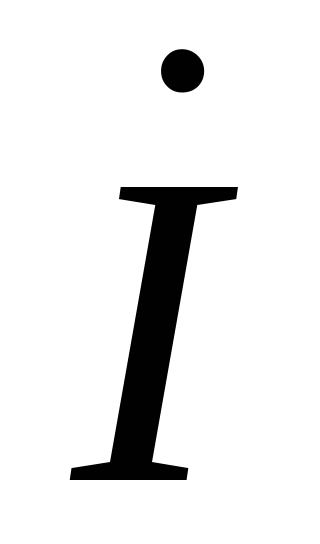и приложенным напряжением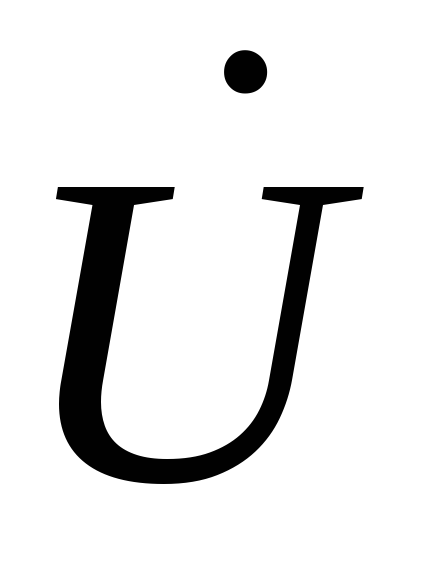принимается положительным, если он направлен от тока к напряжению в направлении против движения часовой стрелки, в противном случае — угол принимается отрицательным (рисунки 5.2 , 5.3).

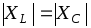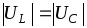В цепи с последовательно соединенными R, L, C— элементами возможен режим, когда реактивное сопротивлениеX=0и =0 , что имеет место при равенстве абсолютных значений и индуктивного и емкостного сопротивлений, т.е. при. При этом выполняется условиеи =0, причем действующие значения этих напряжений могут превышать напряжениеUна зажимах цепи. Это явление называетсярезонансом напряжений. Векторная диаграмма для этого случая показана на рисунке 5.4

+j

+1

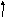
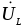
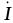
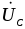
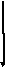
U_L=U_C,

=0

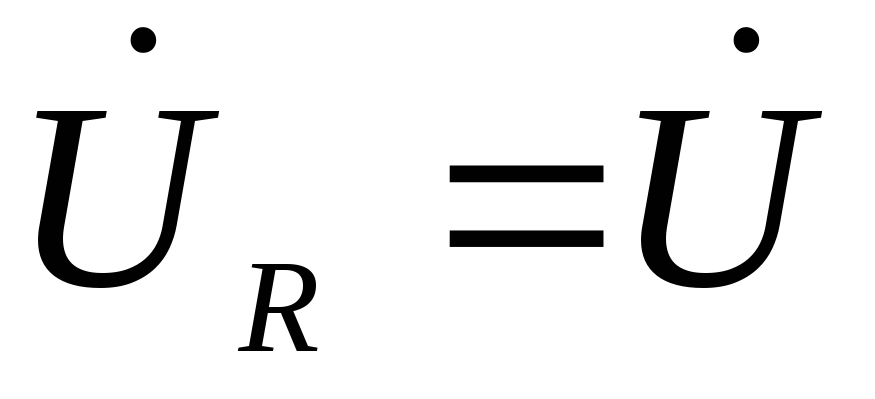
Рис. 1.2.10

6.2. Последовательное соединение резистора и конденсатора, резистора и катушки

индуктивности

6.2.1. Общие сведения

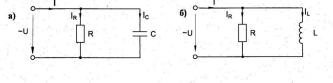
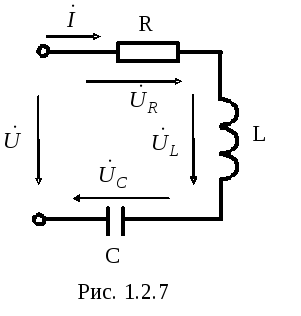
Когда к цепи (рис. 6.2.1) с последовательным соединением резистора и конденсатора (а) или резистора и катушки индуктивности (б) подается переменное синусоидальное напряжение, один и

тот же синусоидальный ток имеет место в обоих компонентах цепи, а напряжение на входе цепи равно сумме напряжений на двух компонентах. Поскольку эти два напряжения сдвинуты

относительно друг друга по фазе, непосредственное сложение их действующих значений или амплитуд невозможно. Необходимо либо складывать мгновенные значения этих напряжений, либо

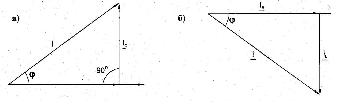
векторы, соответствующие этим напряжениям, как показано на рис. 6.2.2а и б.

Рис. 6.2.2

Вектор напряжения на конденсаторе U отстаёт от вектора тока I на 900, а вектор напряжения на индуктивности UL опережает ток на 90°. Из векторных диаграмм следует, что в цепи с

конденсатором

U = √(UR + UC ), = -arctg(UC /UR).

Поскольку UR = R · I , a UC = XC·I, получаем

U = I»/(R + ХC ) = I·Z и =-arctg(XC/R),

где Z = √(R + ХC ) — полное сопротивление цепи, и <0, т.е. ток опережает напряжение.

Аналогично, в цепи с индуктивностью:

U = √(UR + UL ) = l√(R + XL ) = I · Z, где Z = √(R + XL ),

=

•

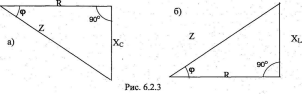
и

φ = arctg (XL/ R)>0, т.е. ток отстаёт от напряжения.

Если каждую сторону треугольника напряжений разделить на ток, то получим тре-

угольник сопротивлений, подобный треугольнику напряжений. (рис.6.2.3а и б). Из треугольников

сопротивлений следует, что

R = Z · cos φ, ХC = Z · sin φ и XL Z · sin φ.

6.2.2. Экспериментальная часть

Задание

Для цепи с последовательным соединением резистора и конденсатора, а также резистора и индуктивности измерьте потребляемую активную мощность, действующие значения напряжений

на резисторе UR и реактивном элементе UC, UL и ток I. Рассчитайте угол сдвига фаз , полное сопротивление цепи Z, реактивное сопротивление X и активное сопротивление R, постройте

векторную диаграмму.

Порядок выполнения работы

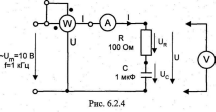
Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник

синусоидального

напряжения

установите

максимальную

амплитуду

синусоидального

напряжения с частотой f = 1 кГц.

•

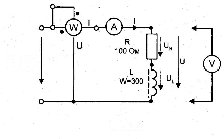
В/дел Цепь с катушкой ти=…

Выполните измерения активной мощности, действующих значений тока и напряжений,

Вычислите: фазовый угол = arctg (Р/UI), полное сопротивление цепи Z = U/I,

Замените в схеме конденсатор на катушку индуктивности с малым активным сопро-

В

В

В

I,

φ,

R,

X,

Z,

	Р, Вт	U,	UR,	U C , U L ,	мА	град	Ом	Ом	Ом
Цепь с конденсатором
Цепь с катушкой

•

5

~и

т

^200

Гц

•

указанных в табл. 6.2.1. При измерениях напряжений подключайте мультиметр к различным зажимам цепи.

Таблица 6.2.1.

•

сопротивление цепи R = Z·cos и ёмкостное сопротивление ХC = Z·sin .

активное

Выберите масштаб и постройте векторную диаграмму напряжений (рис. 6.2.5).

Цепь с конденсатором тц=…

В/дел

Рис.6.2.

•

тивлением (рис.6.2.6). В качестве такой катушки используйте обмотку 300 витков

=10 в

Рис.6.2.6

разборного трансформатора. Чтобы создать немагнитный зазор в магнитопроводе, вставьте между двумя частями сердечника квадратики обычной писчей бумаги в один или два слоя.

Убавьте частоту до 200 Гц и повторите измерения, расчёт и построение векторной диаграммы.

2

2

2

2

2

2

—

—

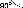
V.

90°

^

*

• *

—

•

*

*

•

•

•

—