Последовательное соединение индуктивно связанных элементов
Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно (рис. 30.1).
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 30.1, а). Токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу. При встречном включении катушек конец второй присоединяется к концу первой (рис. 30.1, б).
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений:
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений:
где Z1 и Z2 – комплексные сопротивления катушек, а ZM – комплексное сопротивление взаимной индукции:
Из формулы выше вытекают формулы, определяющие общую индуктивность цепи и суммарное индуктивное сопротивление:
причем
т.е.
Можно определить результирующее индуктивное сопротивление каждой катушки. У первой оно равно X1+-XM. И здесь при согласном включении оно больше чем при встречном. Физически это объясняется тем, что в первом случае магнитный поток, охватывающий каждую катушку, больше чем во втором; например, для первой катушки ФIсогл=Ф1+Ф21, а ФIвстр=Ф1-Ф21. Вследствие этого ЭДС электромагнитной индукции, оказывающая току индуктивное сопротивление, при согласном включении больше, чем при встречном.
На рис. 30.1 изображены векторные диаграммы, построенные по уравнениям (30.1) и (30.2).
При встречном включении возможен так называемый «емкостный» эффект, когда у одной из катушек напряжение на зажимах отстает по фазе от тока (напряжение на рис. 30.1, б). Это имеет место, когда индуктивность катушки меньше величины взаимной индуктивности. В этом случае результирующая индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна: L2-M < 0. Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
3.2. Последовательное соединение индуктивно связанных элементов
Пусть
две катушки, обладающие сопротивлениями  и
и 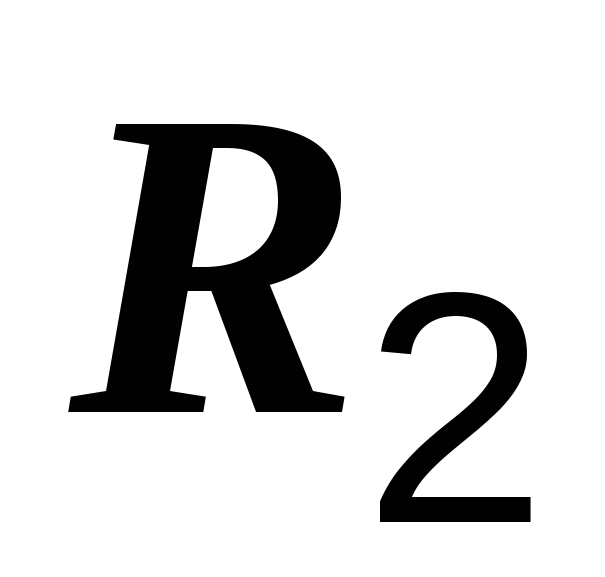
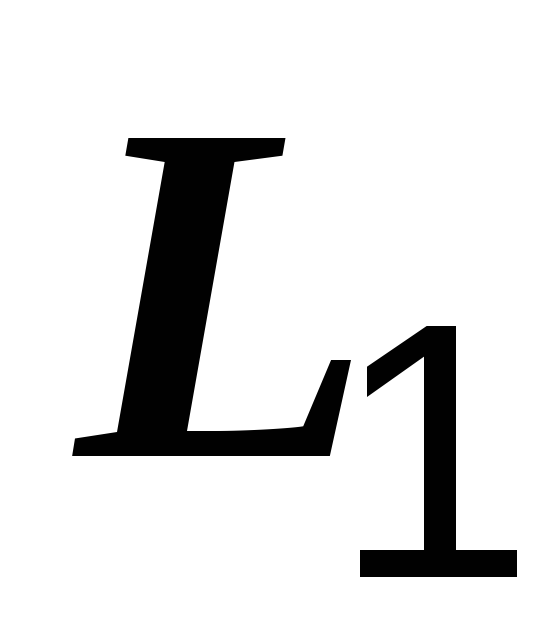 и
и 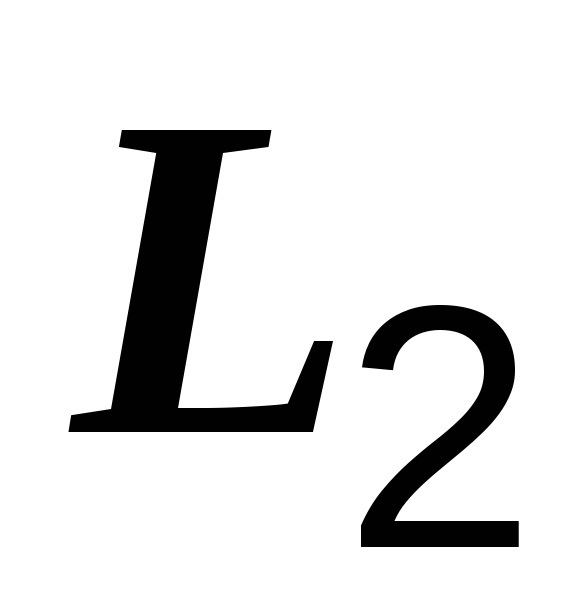 и взаимной индуктивностью
и взаимной индуктивностью 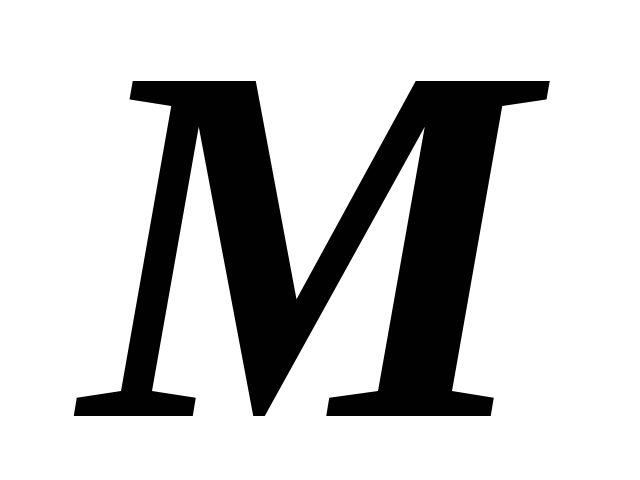 ,
соединены последовательно (рис. 3.3).
,
соединены последовательно (рис. 3.3). 
Рис. 3.3. Последовательное соединение индуктивно связанных элементов
Возможны два вида их соединения – согласное и встречное. Если считать, что звездочками отмечены начала обмоток, то при согласном включении начало второй подключается к концу первой (рис. 3.3,
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
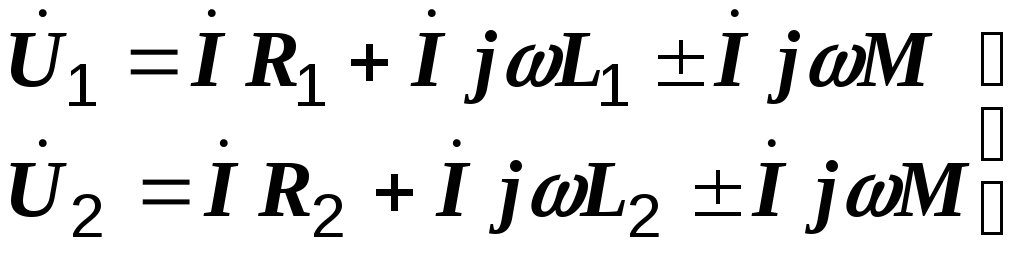 (3.1)
(3.1)
Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений
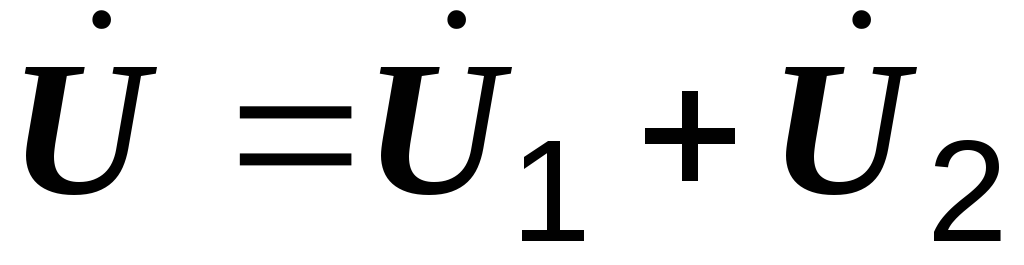 .
(3.2)
.
(3.2)
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений
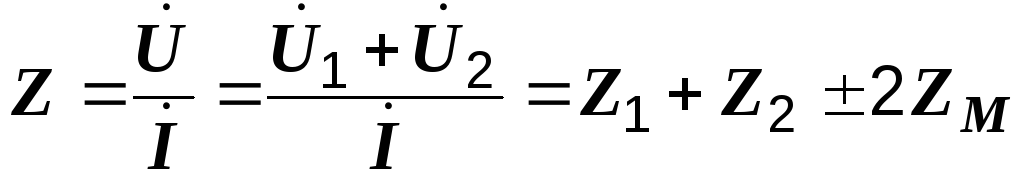 ,
(3.3)
,
(3.3)
где 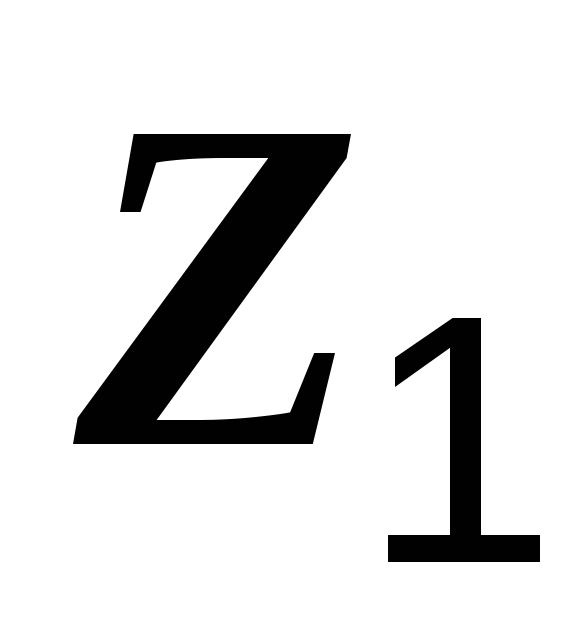 и
и 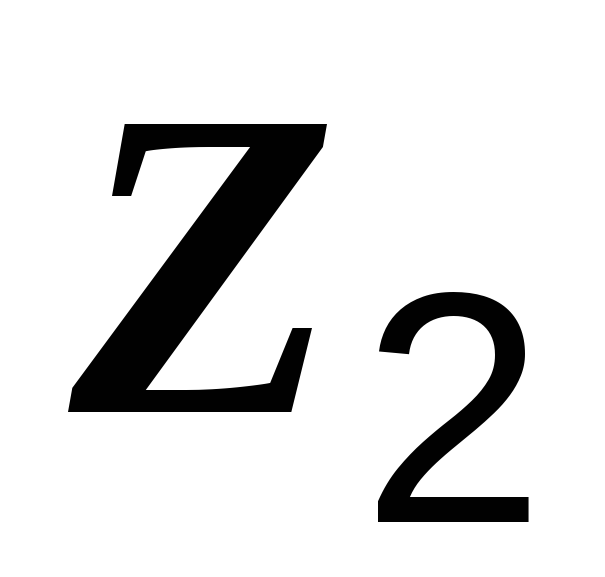 – комплексные сопротивления катушек,
а
– комплексные сопротивления катушек,
а 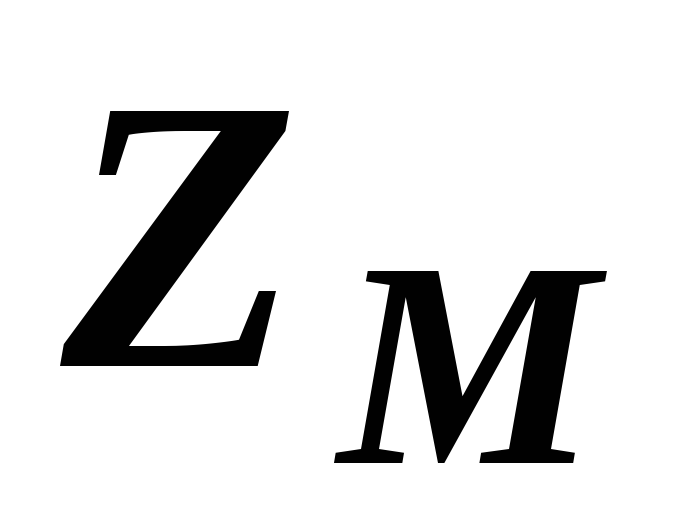
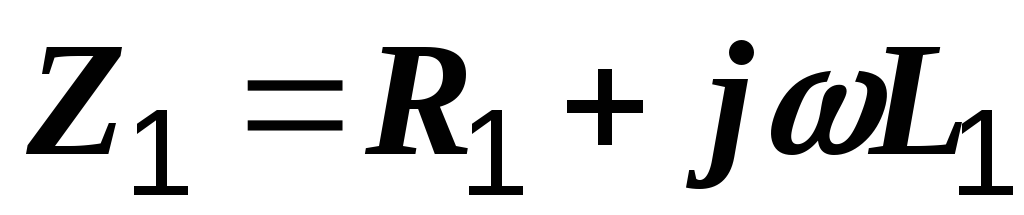 ,
, 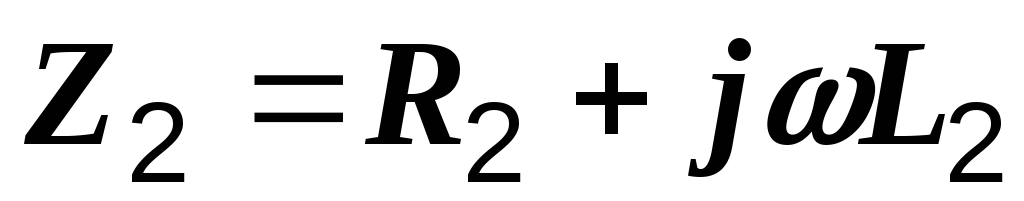 ,
, 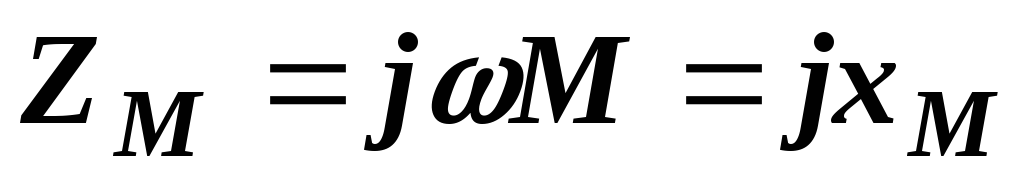 .
.
Из (3.3) вытекают формулы, определяющие общую индуктивность цепи и суммарное индуктивное сопротивление:
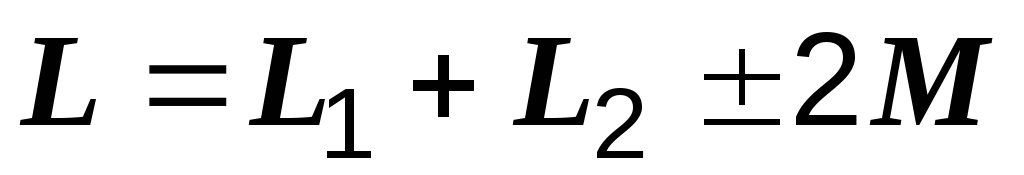 ,
, 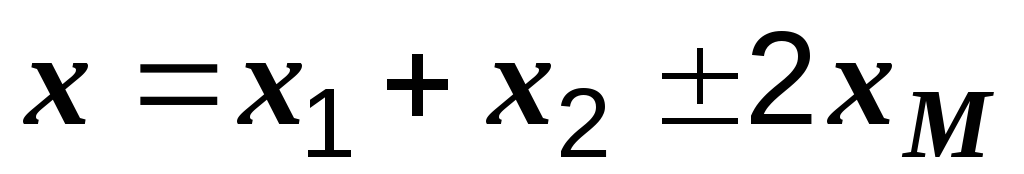
причем 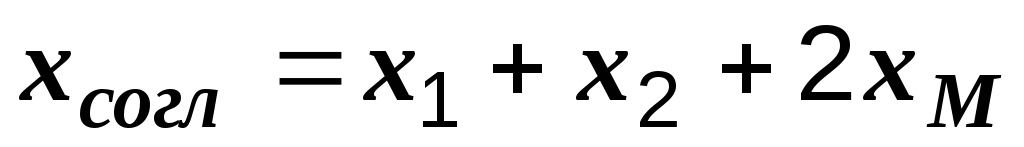 ,
, 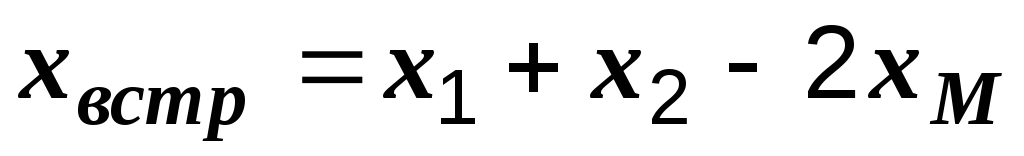 ,
,
т.е.  .
.
Можно
определить результирующее индуктивное
сопротивление каждой катушки. У первой
оно равно 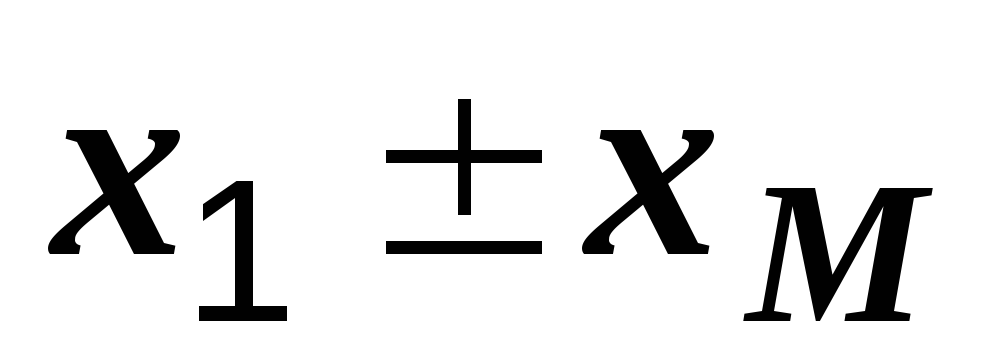 .
И здесь при согласном включении оно
больше чем при встречном. Физически это
объясняется тем, что в первом случае
магнитный поток, охватывающий каждую
катушку, больше чем во втором; например,
для первой катушки
.
И здесь при согласном включении оно
больше чем при встречном. Физически это
объясняется тем, что в первом случае
магнитный поток, охватывающий каждую
катушку, больше чем во втором; например,
для первой катушки 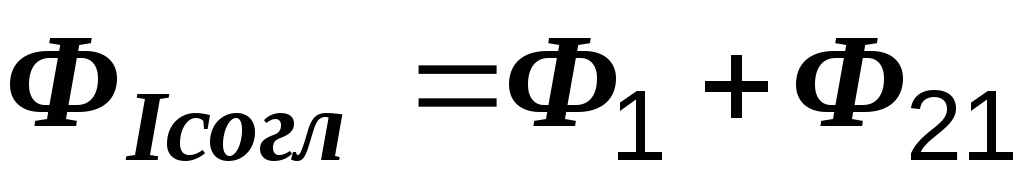
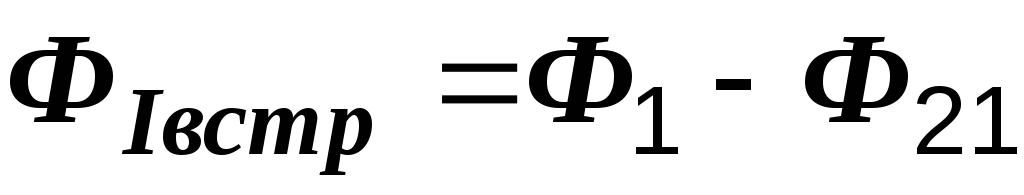 .
Вследствие этого ЭДС электромагнитной
индукции, оказывающая току индуктивное
сопротивление, при согласном включении
больше, чем при встречном.
.
Вследствие этого ЭДС электромагнитной
индукции, оказывающая току индуктивное
сопротивление, при согласном включении
больше, чем при встречном.На рис. 3.4 изображены векторные диаграммы, построенные по уравнениям (3.1) и (3.2).
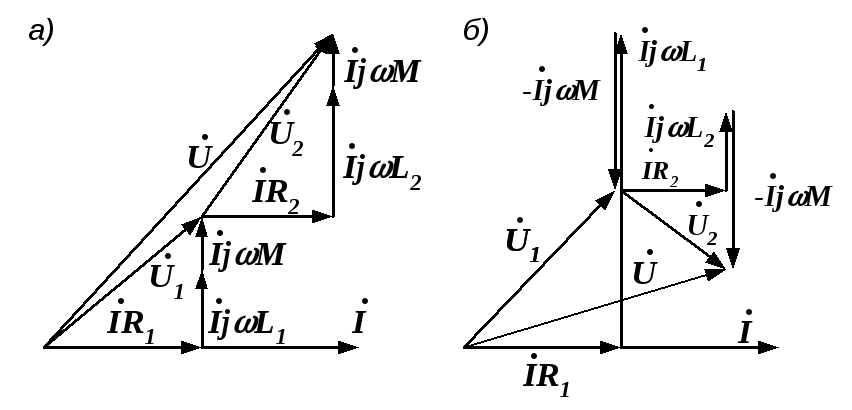
Рис. 3.4. Векторные диаграммы последовательной цепи при согласном (а) и встречном (б) включениях
При
встречном включении возможен так
называемый «емкостный» эффект,
когда у одной из катушек напряжение на
зажимах отстает по фазе от тока (напряжение на рис. 3.4, б).
Это имеет место, когда индуктивность
катушки меньше величины взаимной
индуктивности. В этом случае результирующая
индуктивность рассматриваемой катушки (с учетом взаимной индукции) отрицательна: 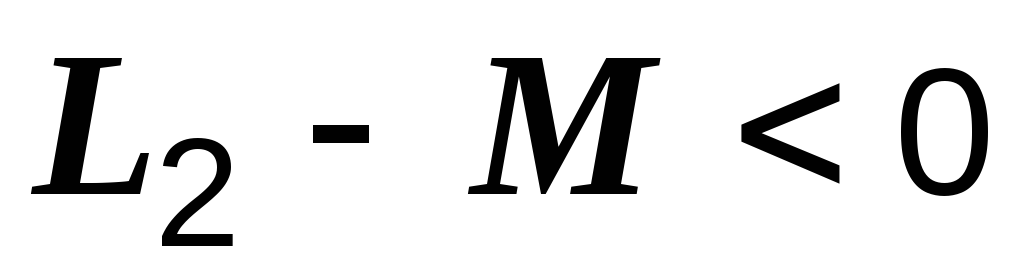 .
Для всей цепи такой эффект невозможен.
Ее индуктивность всегда положительна,
и цепь носит активно-индуктивный
характер.
.
Для всей цепи такой эффект невозможен.
Ее индуктивность всегда положительна,
и цепь носит активно-индуктивный
характер.
Пример
3.2. В схемах рис. 3.3 производились измерения
напряжения, тока и активной мощности
на входе цепи. При согласном (с) и встречном
(в) включениях приборы дали следующие
показания: 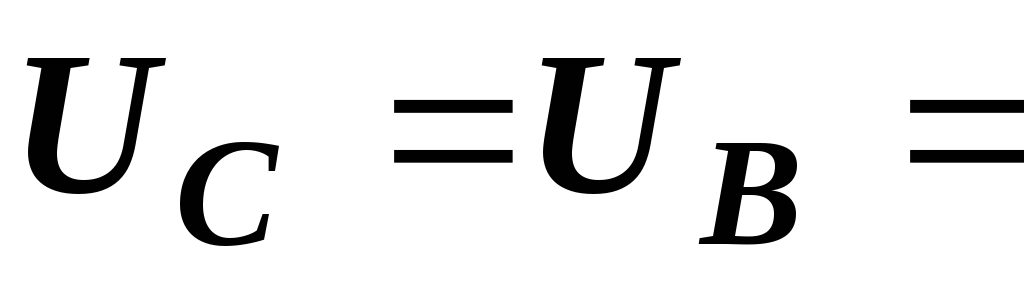 220 В,
220 В, 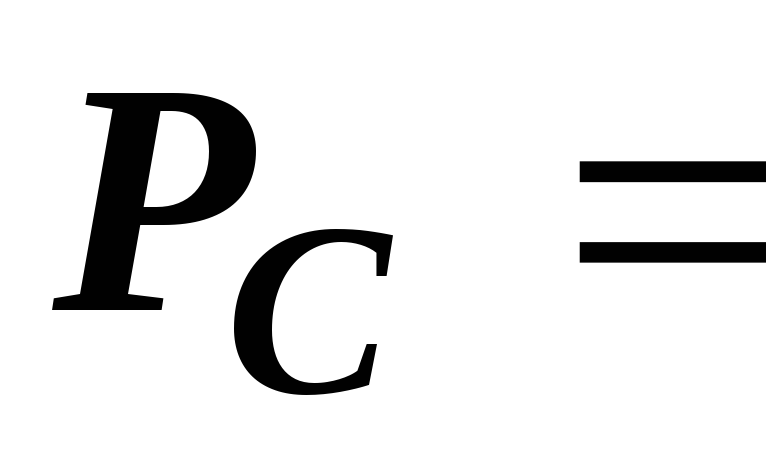 150 Вт,
150 Вт, 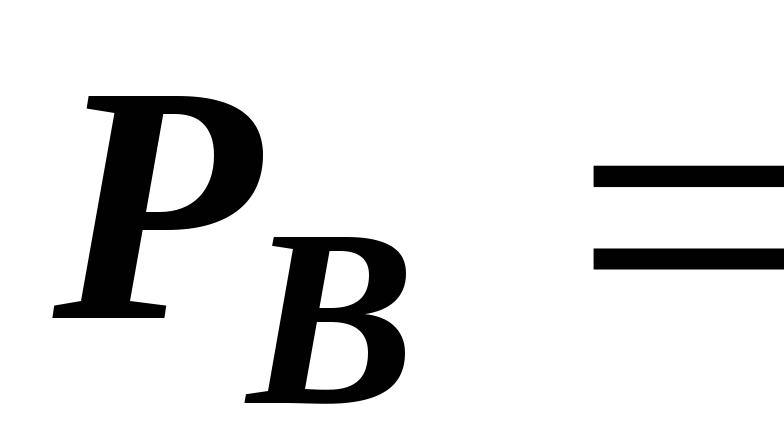 234,5
Вт,
234,5
Вт, 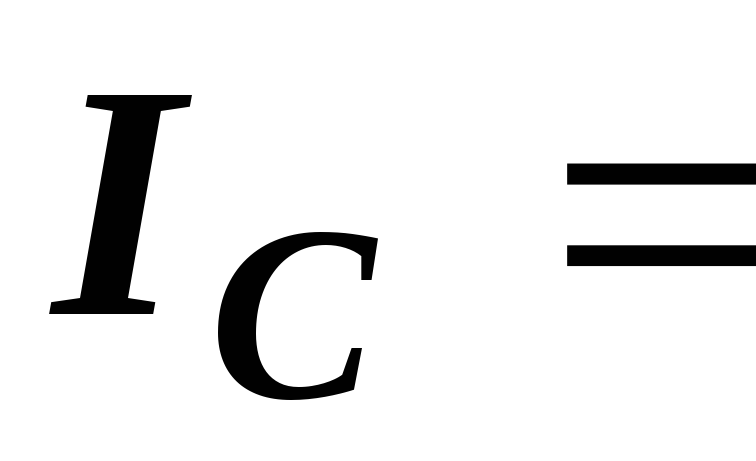 1
А,
1
А,  1,25
А.
Чему равна взаимная индуктивность
катушек, если частота питающего напряжения
1,25
А.
Чему равна взаимная индуктивность
катушек, если частота питающего напряжения 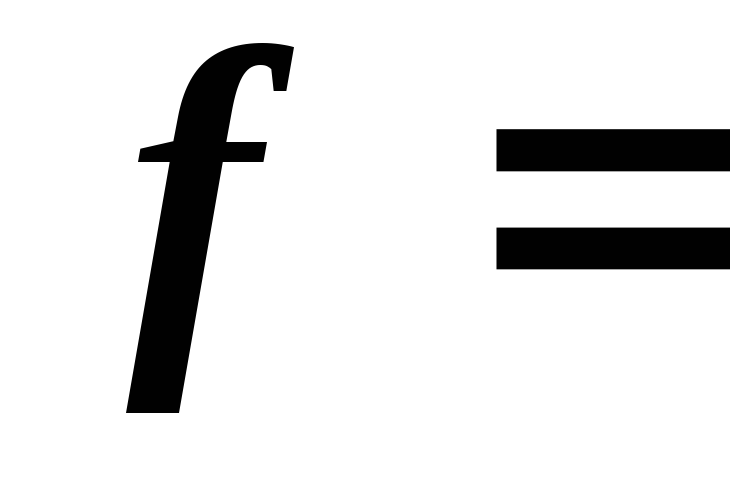
Р е ш е н и е. Определим полные, активные и реактивные сопротивления обеих схем
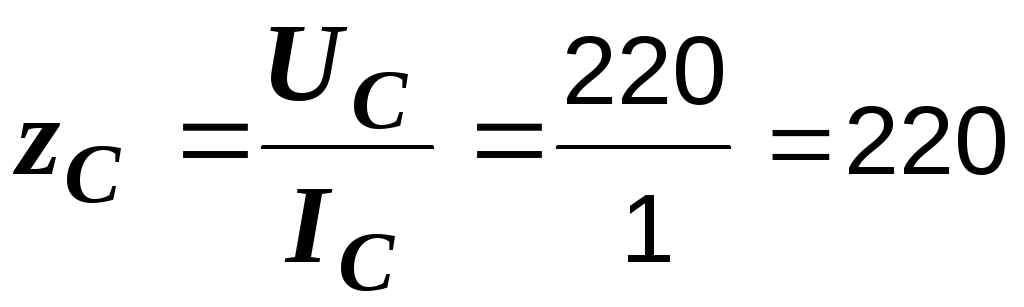 Ом,
Ом, 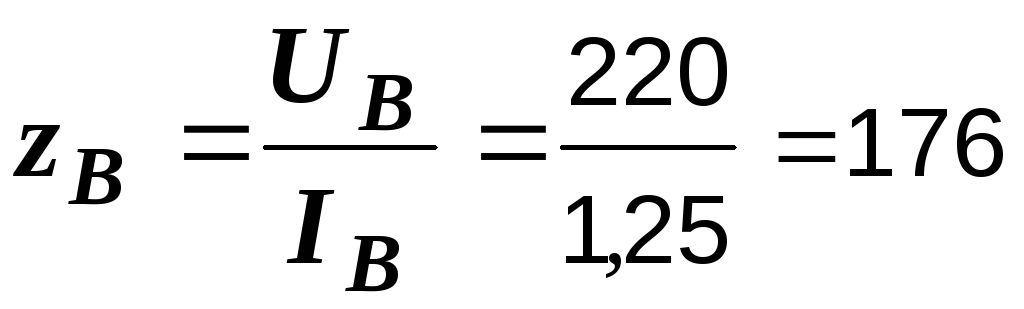 Ом,
Ом,
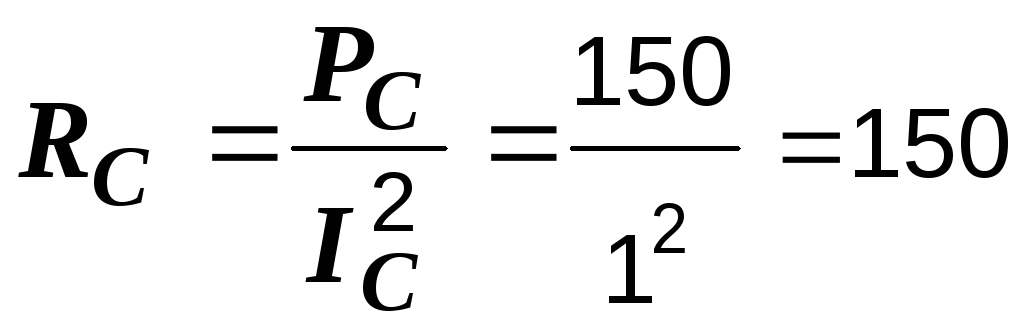 Ом,
Ом, 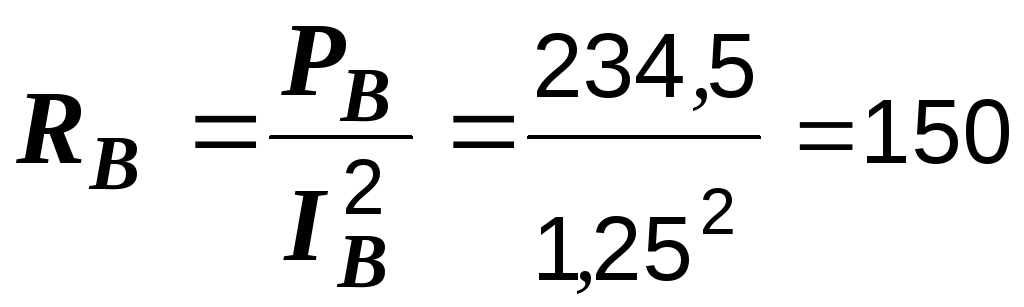 Ом.
Ом.
При переключении катушек с согласного соединения на встречное общее активное сопротивление цепи не меняется. Оно остается равным сумме их активных сопротивлений.
2.6.3. Последовательное соединение двух индуктивно связанных катушек
Рассмотрим две катушки, соединенные
последовательно и имеющие активные
сопротивления 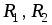 ,
индуктивности
,
индуктивности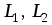 и взаимную индуктивность
и взаимную индуктивность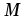 .
Возможны два вида их включения –
согласное (рис. 2.21 а) и встречное (рис.
2.21 б). При согласном включении ток в
обеих катушках направлен одинаково
относительно одноименных зажимов,
поэтому падение напряжения на взаимной
индуктивности в уравнениях Кирхгофа
для мгновенных значений запишем со
знаком «плюс»
.
Возможны два вида их включения –
согласное (рис. 2.21 а) и встречное (рис.
2.21 б). При согласном включении ток в
обеих катушках направлен одинаково
относительно одноименных зажимов,
поэтому падение напряжения на взаимной
индуктивности в уравнениях Кирхгофа
для мгновенных значений запишем со
знаком «плюс»
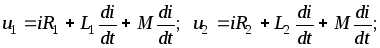
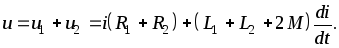
Эти же уравнения в комплексной форме
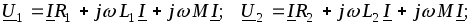
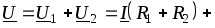
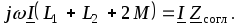 (2.52)
(2.52)
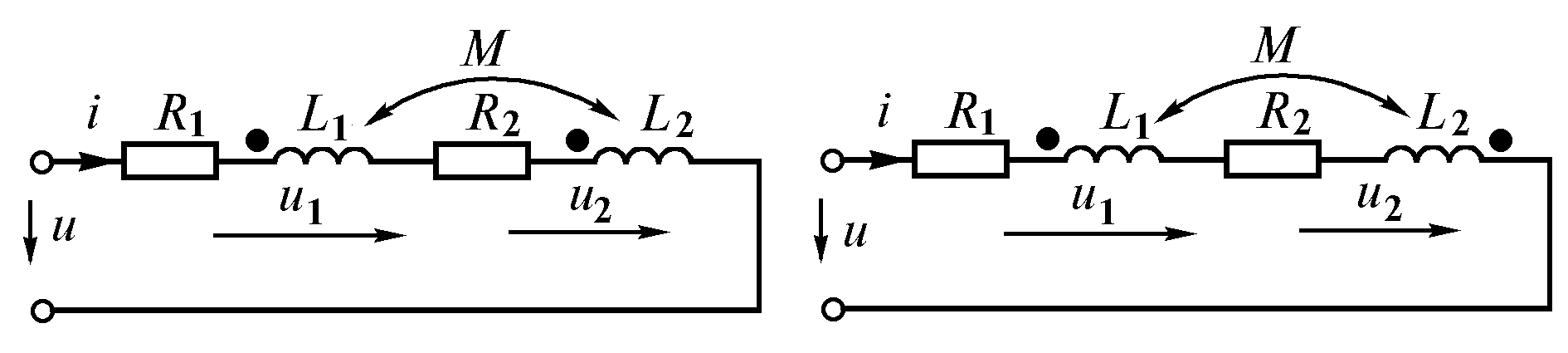
а) б)
Рис. 2.21
Полное сопротивление цепи при согласном включении
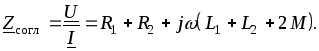
При встречном включении (рис. 2.21 б) ток в катушках направлен противоположно относительно одноименных зажимов, поэтому напряжения на взаимной индуктивности записывают со знаком «минус». В этом случае уравнения Кирхгофа в комплексной форме имеют вид
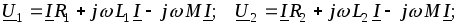
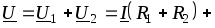
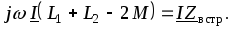 (2.53)
(2.53)
Полное сопротивление цепи при встречном включении
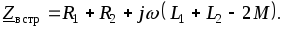
Полное сопротивление цепи при согласном включении больше, чем при встречном. Этим можно пользоваться для определения опытным путем одноименных зажимов индуктивно связанных катушек.
На рис. 2.22 построены векторные диаграммы
для согласного и встречного включения
катушек. Начальная фаза вектора тока,
являющегося общим для всех элементов
цепи, принята равной нулю. По вектору
тока сориентированы в порядке записи
все слагаемые напряжений 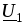 и
и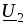 (2.52, 2.53). Упрощает выбор направления
векторов правило о том, что умножение
комплекса на
(2.52, 2.53). Упрощает выбор направления
векторов правило о том, что умножение
комплекса на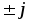 соответствует его повороту на90°. Многоугольники векторов
соответствует его повороту на90°. Многоугольники векторов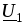 ,
,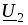 ,
,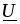 ,
построенные на диаграмме соответственно
с законом Кирхгофа, для наглядности
заштрихованы.
,
построенные на диаграмме соответственно
с законом Кирхгофа, для наглядности
заштрихованы.
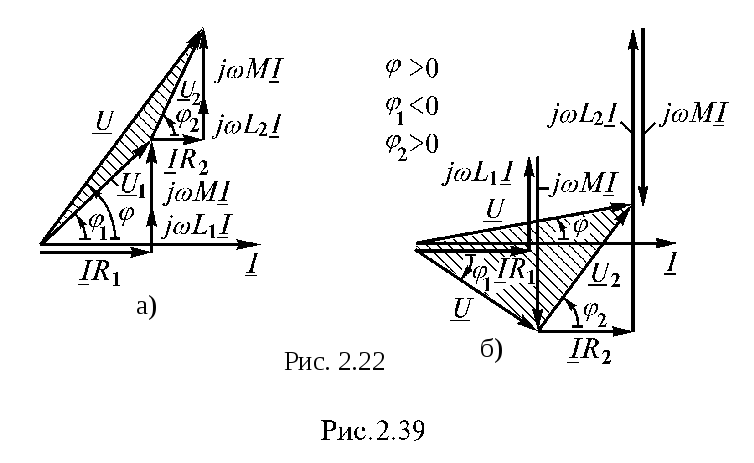
Векторная диаграмма (рис. 2.22 б) при
встречном включении катушек построена
в предположении, что 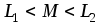 .
При таком соотношении параметров в
первой катушке наблюдается емкостный
эффект, т.к. напряжение
.
При таком соотношении параметров в
первой катушке наблюдается емкостный
эффект, т.к. напряжение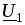 отстает от тока
отстает от тока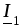 .
В цепи нет конденсаторов, но индуктивность
первой катушки
.
В цепи нет конденсаторов, но индуктивность
первой катушки получается отрицательной, что равноценно
включению конденсатора. Однако в
целом цепь всегда имеет индуктивный
характер, т.к. вектор тока отстает от
вектора напряжения на входе в виду того,
что
получается отрицательной, что равноценно
включению конденсатора. Однако в
целом цепь всегда имеет индуктивный
характер, т.к. вектор тока отстает от
вектора напряжения на входе в виду того,
что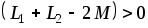 .
.
При согласном включении катушек емкостный эффект невозможен.
59
2.12. Последовательное соединение активного сопротивления, индуктивности и емкости
В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 2.23), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах
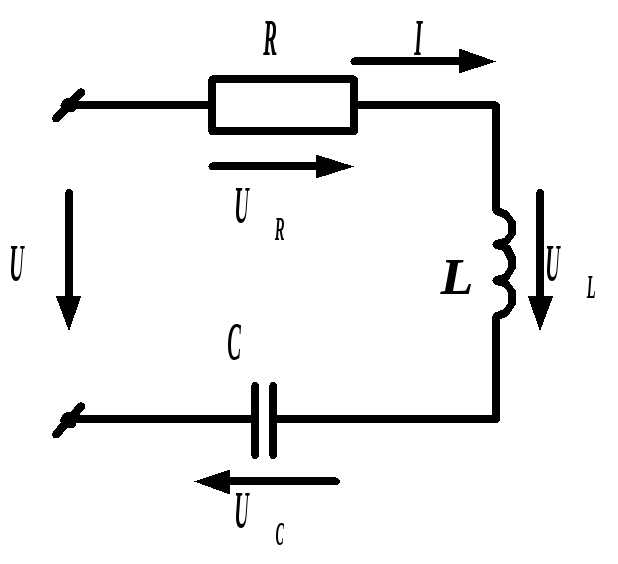
Рис. 2.23. Последовательная цепь переменного тока
При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы. В
последовательной цепи общим для всех
элементов является протекающий по ним
ток, поэтому именно с него начинаем
построение векторной диаграммы. Проводим
его изображение горизонтально (рис.
2.24). Вообще, направление первого вектора
при построении диаграмм произвольно.
Оно диктуется соображениями удобства.
Дальше мы должны показать векторы
напряжений на всех элементах и в
соответствии со вторым законом Кирхгофа
в векторной форме 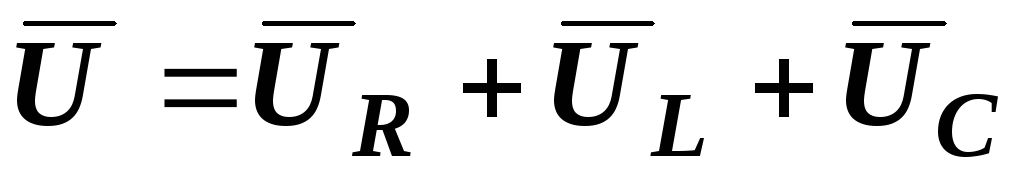 получить вектор входного напряжения.
Сложение векторов можно выполнять по
правилу параллелограмма, однако удобнее
применять правило многоугольника, когда
каждый последующий вектор пристраивается
к концу предыдущего.
получить вектор входного напряжения.
Сложение векторов можно выполнять по
правилу параллелограмма, однако удобнее
применять правило многоугольника, когда
каждый последующий вектор пристраивается
к концу предыдущего.
Рис. 2.24. Векторная диаграмма последовательной цепи
Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор UR мы направляем по вектору I. К его концу пристраиваем вектор UL и направляем его вверх, так как напряжение на индуктивности опережает ток на 90. Напряжение UС находится в противофазе с UL, т.е. отстает от тока на тот же угол 90, поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма UR, UL и UС дает вектор приложеного напряжения U.
Величины напряжений на отдельных элементах цепи нам известны:
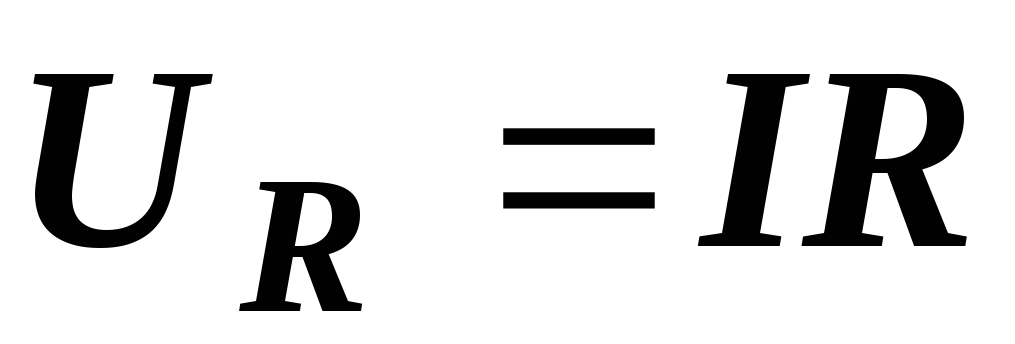 ,
, 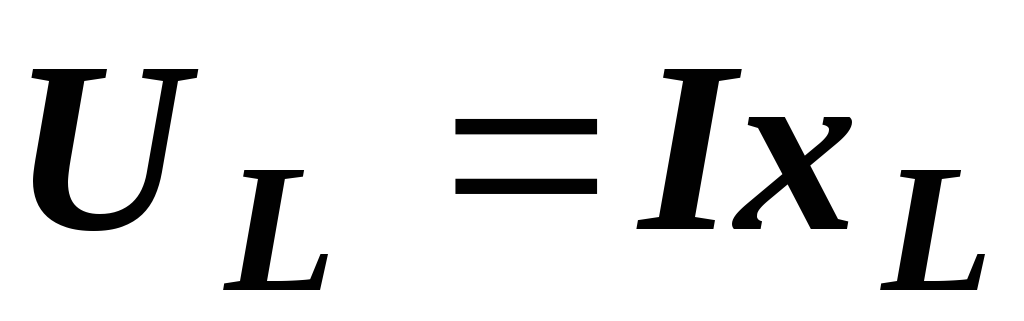 ,
, 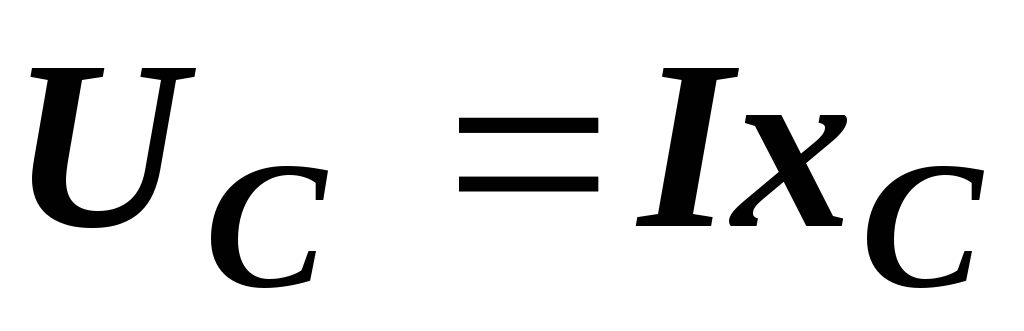 .
(2.23)
.
(2.23)
Из
треугольника 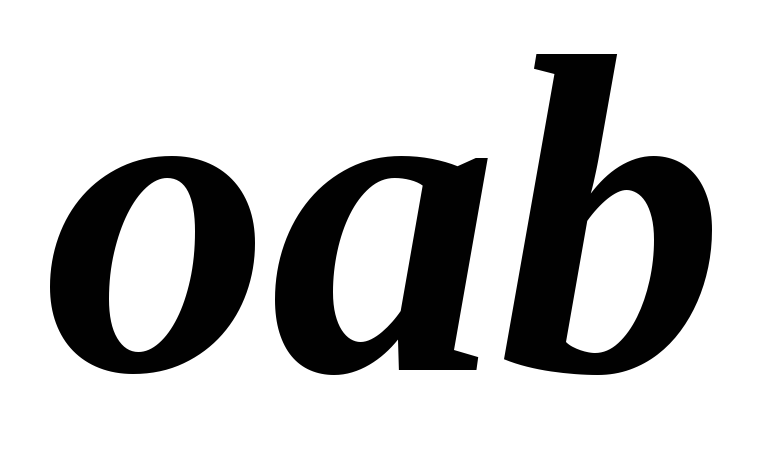 (рис. 2.24) по теореме Пифагора находим
(рис. 2.24) по теореме Пифагора находим
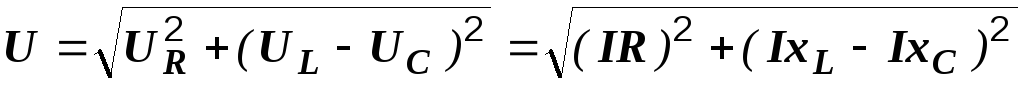 .
.
Вынося 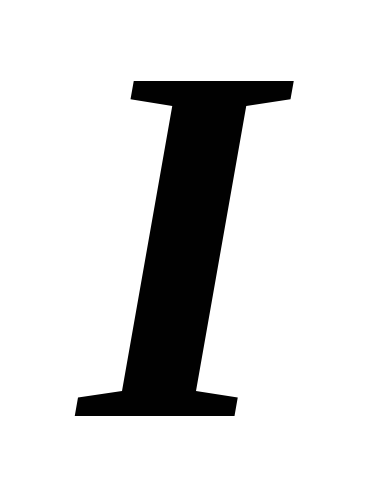 из под знака радикала, записываем
последнее выражение в виде:
из под знака радикала, записываем
последнее выражение в виде:
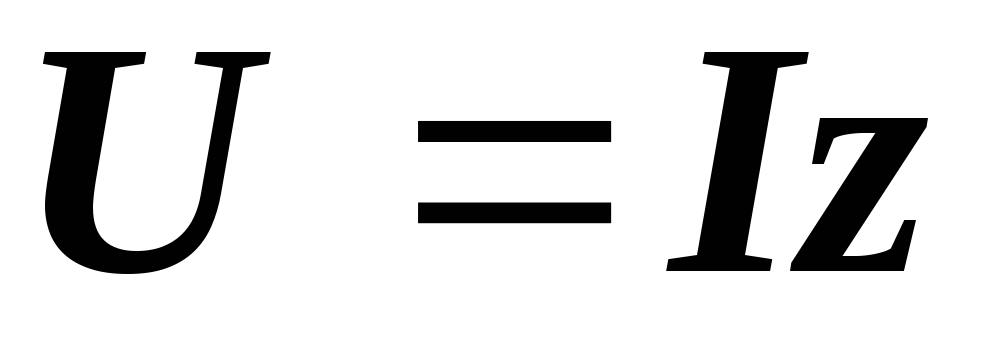 ,
(2.24)
,
(2.24)
где z – полное сопротивление цепи, равное
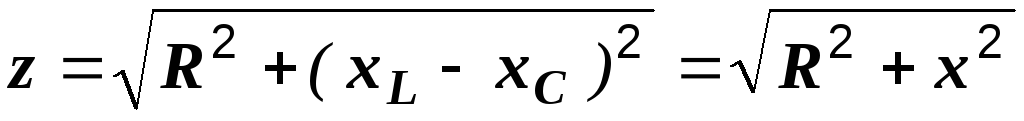 .
(2.25)
.
(2.25)
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = хL – xC. Сами индуктивность и емкость называются реактивными элементами, и их сопротивления хL и xC тоже носят названия реактивных.
Выражение (2.24) называется законом Ома для всей цепи. Оно может быть записано и так:
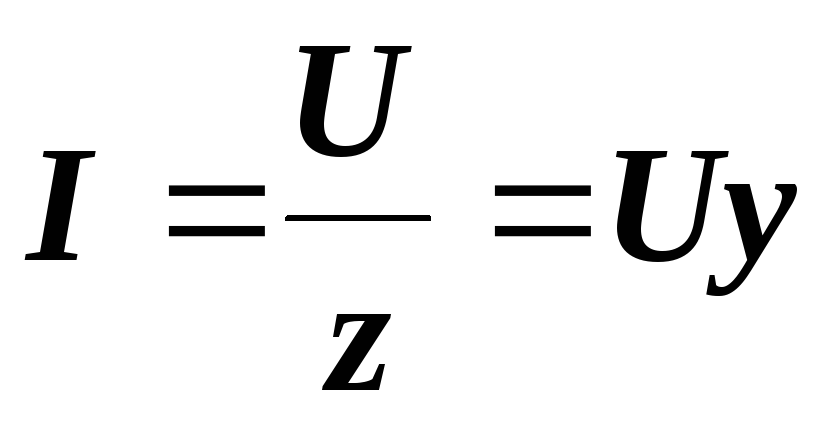 ,
(2.26)
,
(2.26)
где  – полная проводимость цепи, представляющая
величину,
обратную полному сопротивлению:
– полная проводимость цепи, представляющая
величину,
обратную полному сопротивлению: 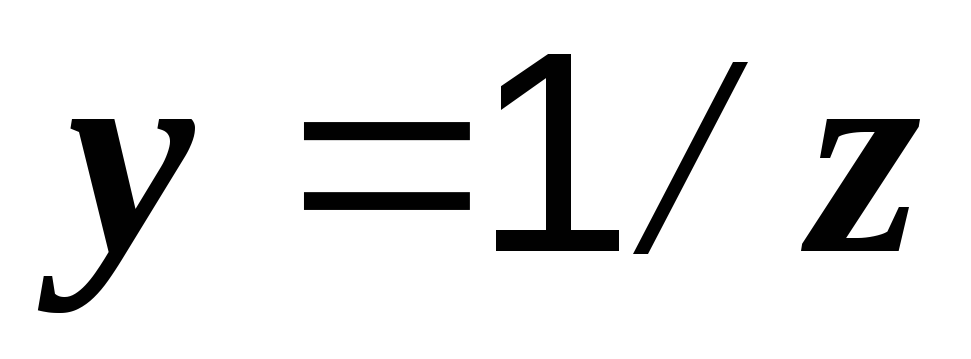 .
.
Если
необходимо определить угол сдвига фаз
между напряжением и током, то это можно
сделать из треугольника напряжений 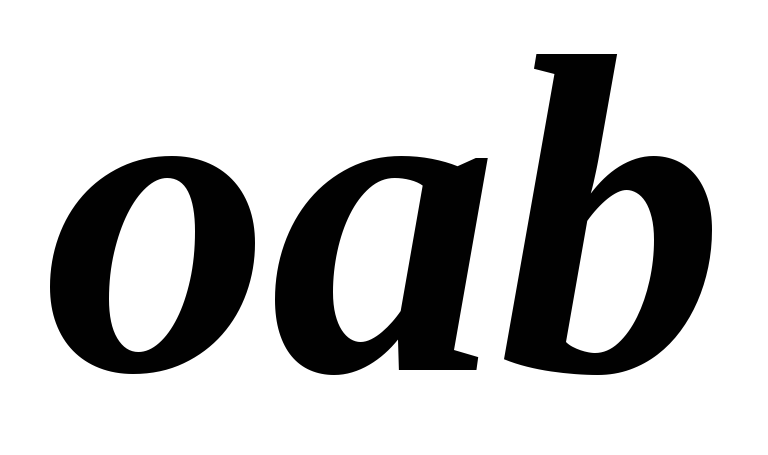 (рис. 2.24):
(рис. 2.24):
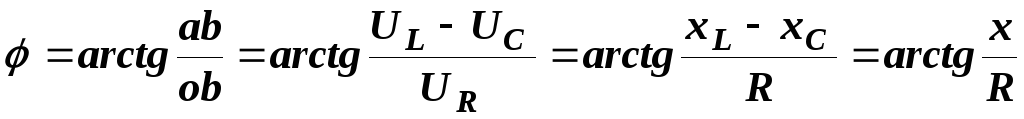 .
.
Векторная
диаграмма на рис. 2.24 построена для
случая, когда 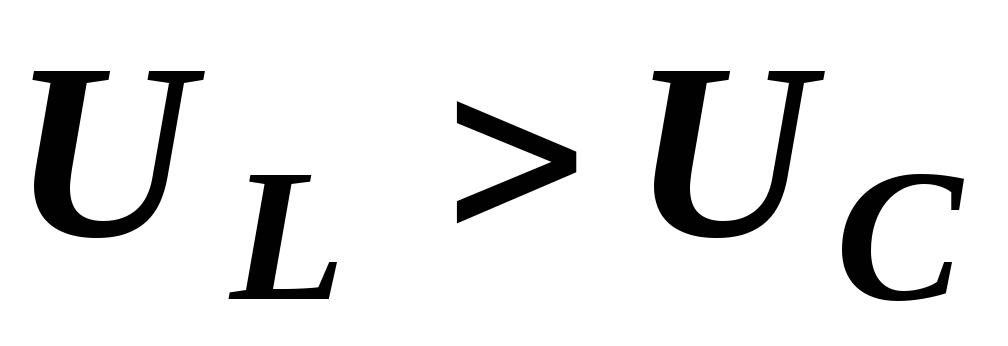 ,
что имеет место при
,
что имеет место при 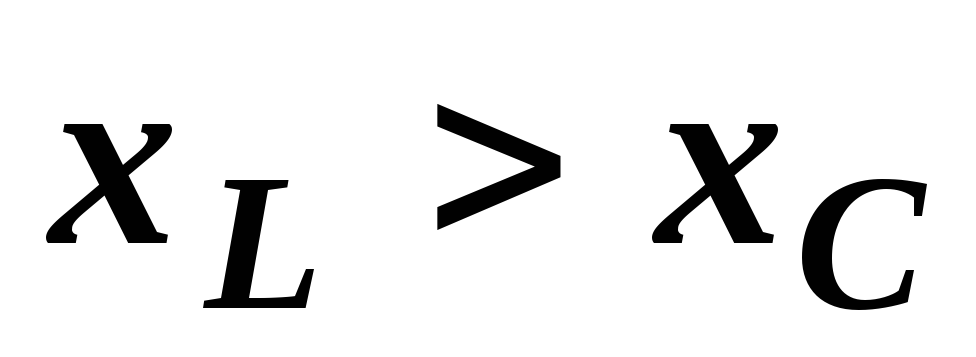 ,
когда в цепи преобладает индуктивность,
и цепь носит активно-индуктивный
характер. Общий ток отстает по фазе от
входного напряжения.
,
когда в цепи преобладает индуктивность,
и цепь носит активно-индуктивный
характер. Общий ток отстает по фазе от
входного напряжения.
Возможны
также режимы, когда 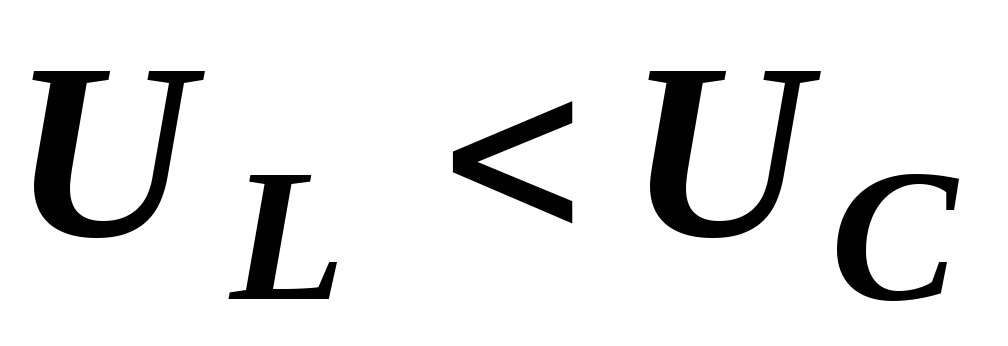 и
и 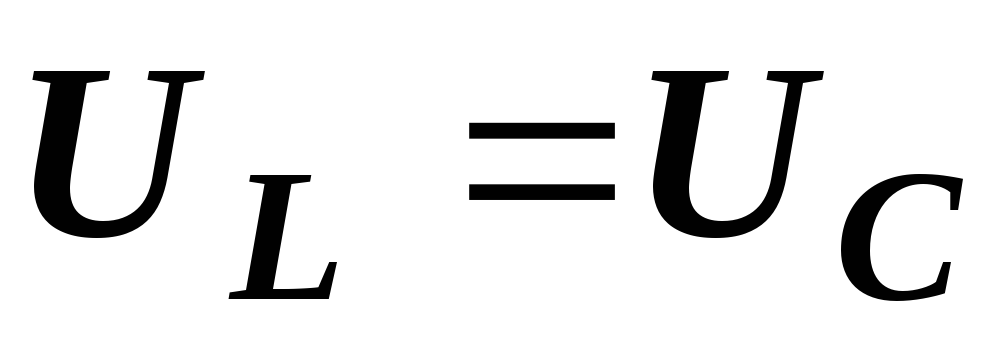 .
.
Пример 2.7. Параметры цепи на рис. 2.23, имеют следующие числовые значения: R = 60 Ом, xL = 40 Ом, xC = 120 Ом, U = 200 В.
Определить ток, напряжения на элементах и угол сдвига фаз между напряжением и током. Построить векторную диаграмму.
Р е ш е н и е. Определяем полное сопротивление цепи
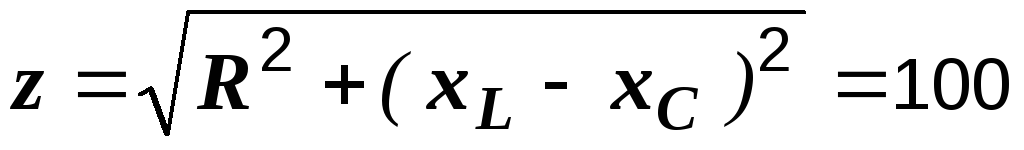 Ом.
Ом.
Действующее
значение тока 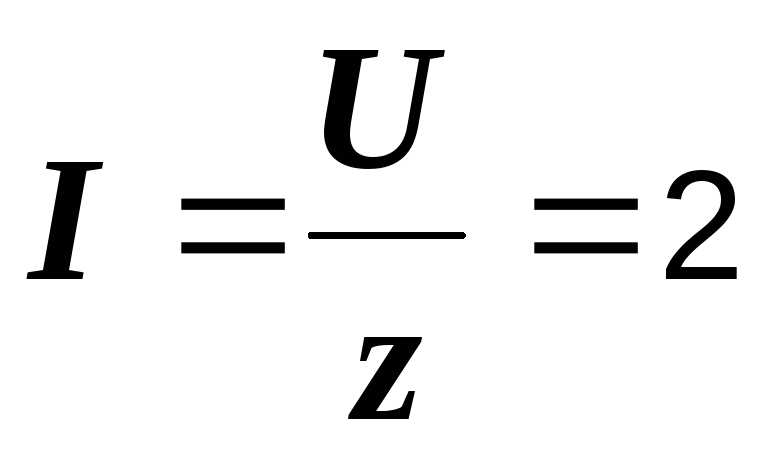 А.
А.
Напряжения на элементах:
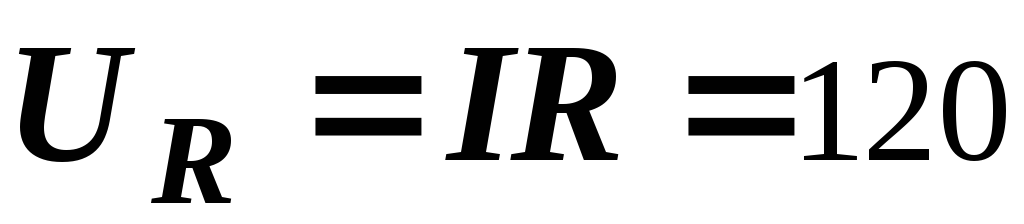 B,
B, 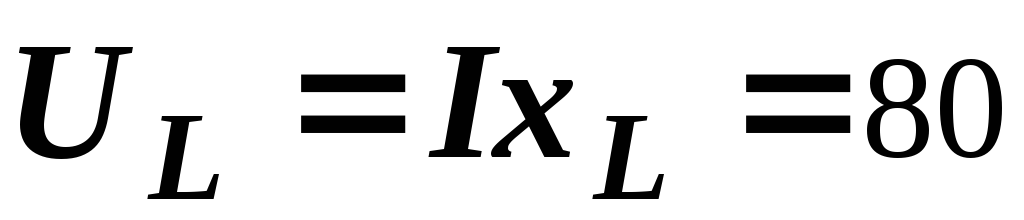 В,
В,  В.
В.

Рис. 2.25. Векторная диаграмма последовательной цепи
Угол сдвига фаз
Векторная
диаграмма показана на рис. 2.25. Так как 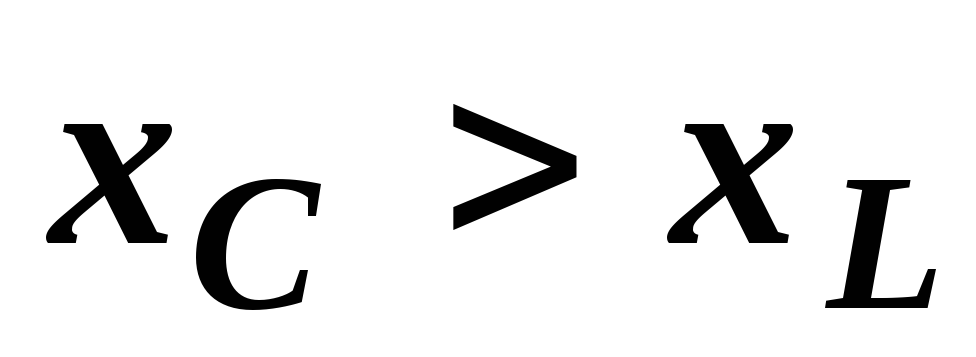 ,
цепь носит активно-емкостный характер,
ток опережает напряжение, угол сдвига
фаз отрицателен и на диаграмме направлен
от тока к напряжению в отрицательном
направлении – по часовой стрелке.
,
цепь носит активно-емкостный характер,
ток опережает напряжение, угол сдвига
фаз отрицателен и на диаграмме направлен
от тока к напряжению в отрицательном
направлении – по часовой стрелке.
Типичным для цепей переменного тока является рассмотренный в задаче режим, когда напряжение на одном из реактивных элементов (в данном случае на емкости) превышает входное напряжение. При определенных соотношениях параметров цепи это превышение может быть довольно значительным – в десятки и сотни раз.
Обратим внимание также на то, что сумма падений напряжений на элементах в вольтах (120 + 80 + 240) не равна 200 – напряжению, приложенному к цепи. Еще раз повторяем, что для численных значений токов и напряжений законы Кирхгофа неприменимы. Они справедливы только для мгновенных значений, векторов и комплексных чисел. Показания приборов в цепях переменного тока складывать нельзя.
Пример 2.8. Определить величины сопротивления R и емкости С, если при частоте f = 50 Гц приборы в схеме на рис. 2.26, а имеют следующие показания: U = 125 В, UR = 100 В, I = 2,5 А.
Р е ш е н и е. По показаниям вольтметра и амперметра определяем величину активного сопротивления
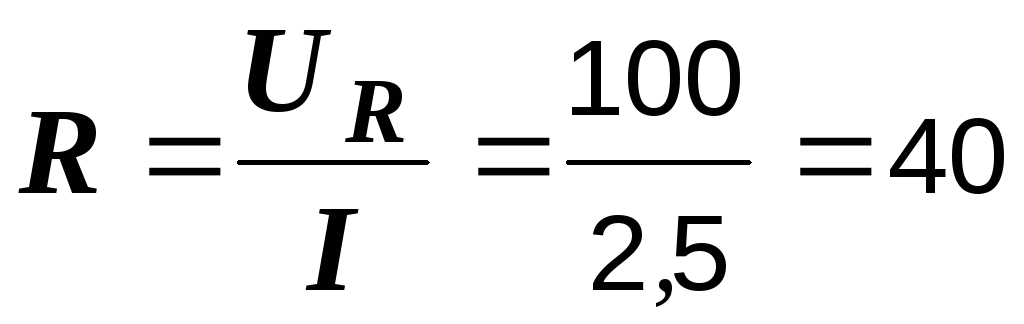 Ом.
Ом.
Для
определения емкости конденсатора
необходимо знать напряжение 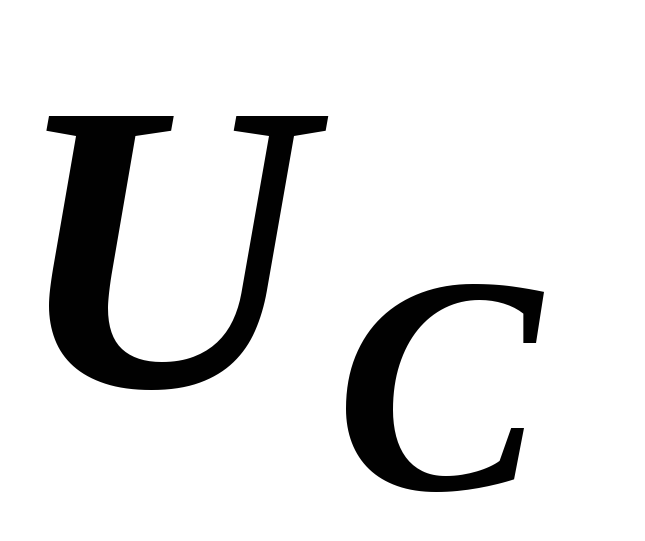 на его зажимах. Его можно найти из
векторной диаграммы (рис. 2.26, б).
При ее построении вектор
на его зажимах. Его можно найти из
векторной диаграммы (рис. 2.26, б).
При ее построении вектор  направляем по вектору тока – они
совпадают по фазе, а вектор
направляем по вектору тока – они
совпадают по фазе, а вектор 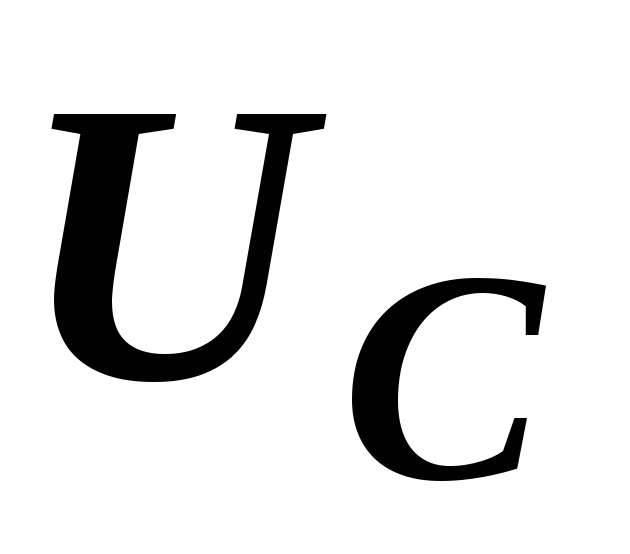 – под углом 90
к току в сторону отставания. Вектор
входного напряжения
– под углом 90
к току в сторону отставания. Вектор
входного напряжения  находим как сумму векторов
находим как сумму векторов 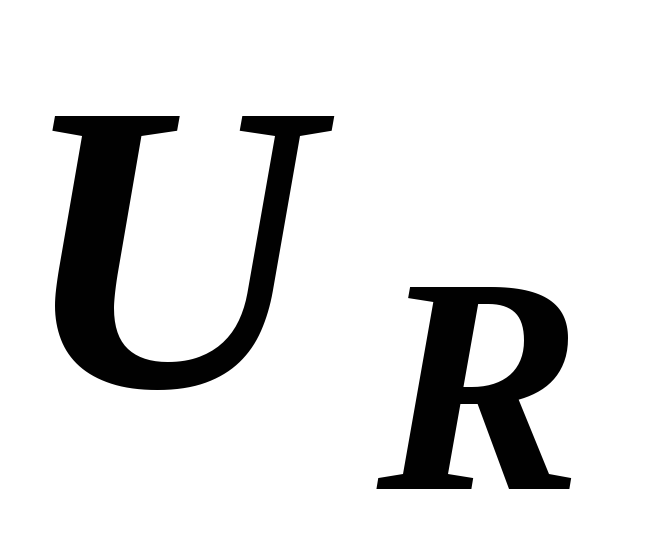 и
и 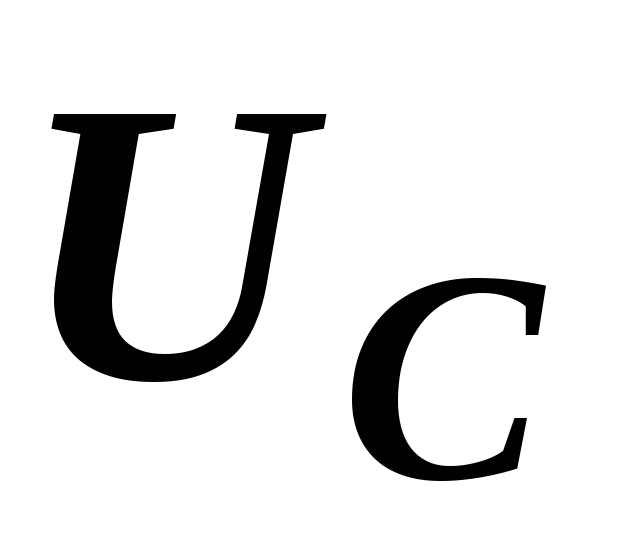 :
: 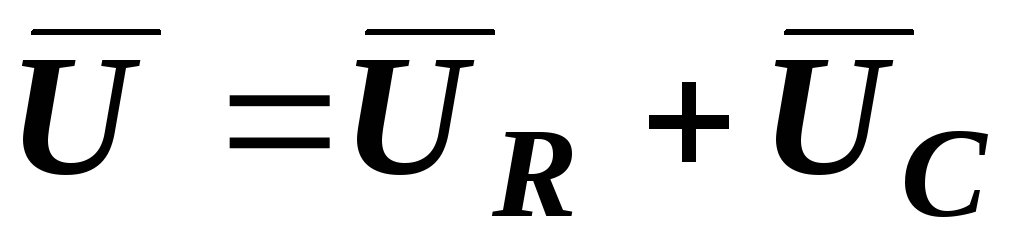 .
.
Из векторной диаграммы определяем напряжение на конденсаторе
 В.
В.
Теперь находим емкостное сопротивление:
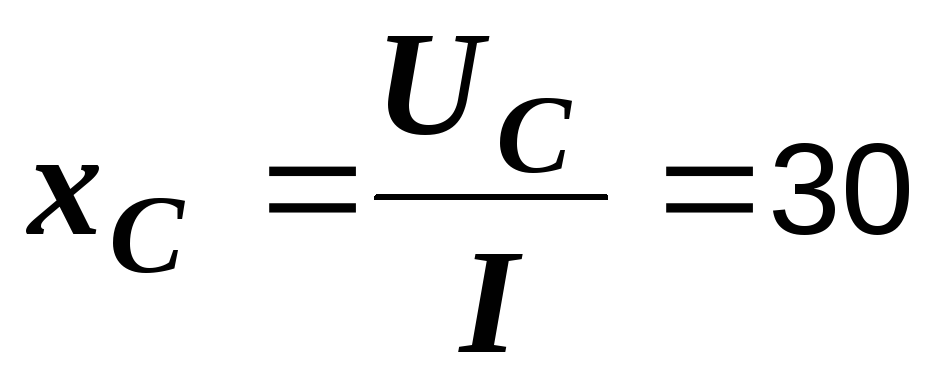 Ом.
Ом.
Из
формулы 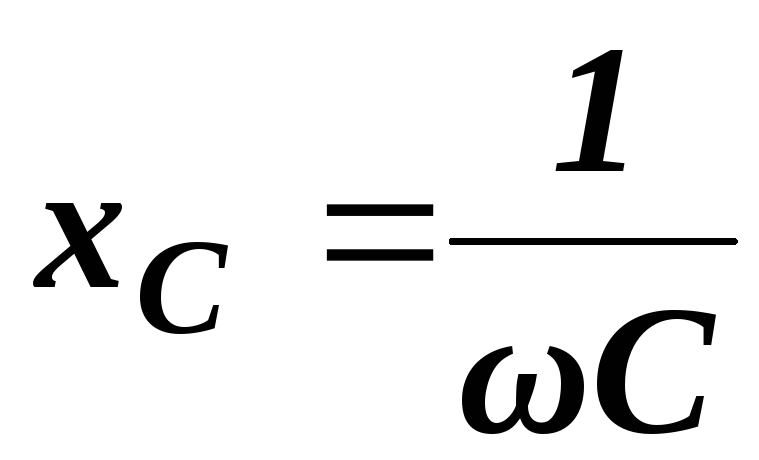 определяем емкость
определяем емкость
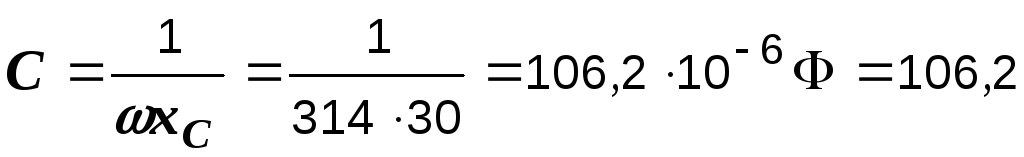 мкФ.
мкФ.
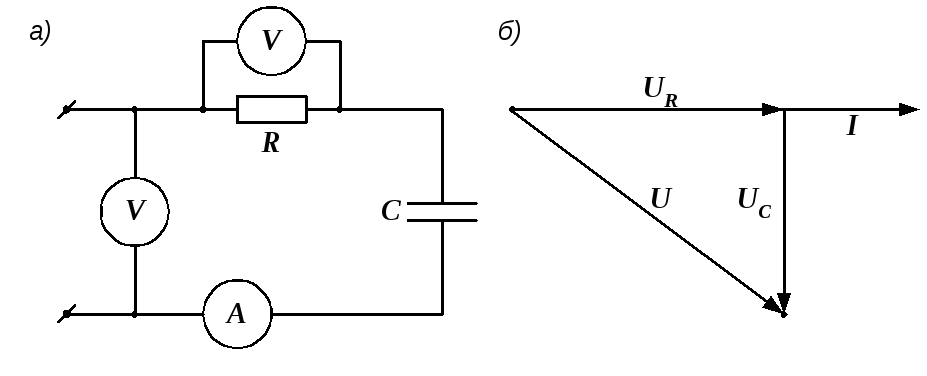
Рис. 2.26. Электрическая цепь и ее векторная диаграмма
Пример
2.9. К
зажимам катушки с параметрами R =
30 Ом и L = 40 мГн приложено напряжение 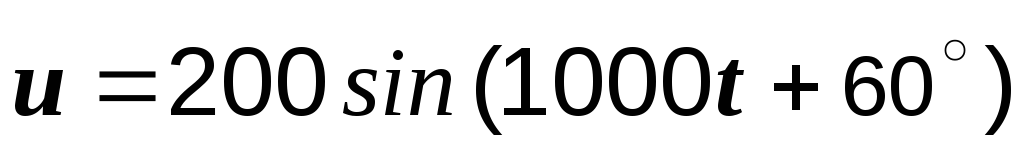 В. Записать выражение мгновенного
значения тока. Каким оно станет, если
частота питающего напряжения уменьшится
вдвое?
В. Записать выражение мгновенного
значения тока. Каким оно станет, если
частота питающего напряжения уменьшится
вдвое?
Р е ш е н и е. Вычисляем индуктивное и полное сопротивления:
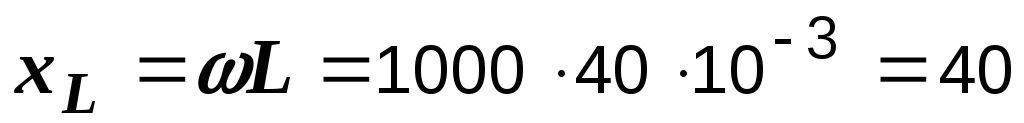 Ом,
Ом, 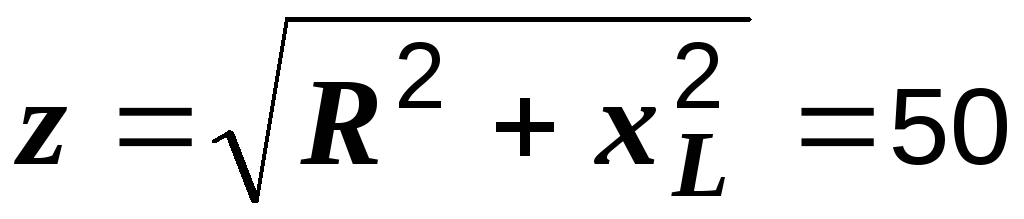 Ом.
Ом.
По закону Ома находим амплитуду тока
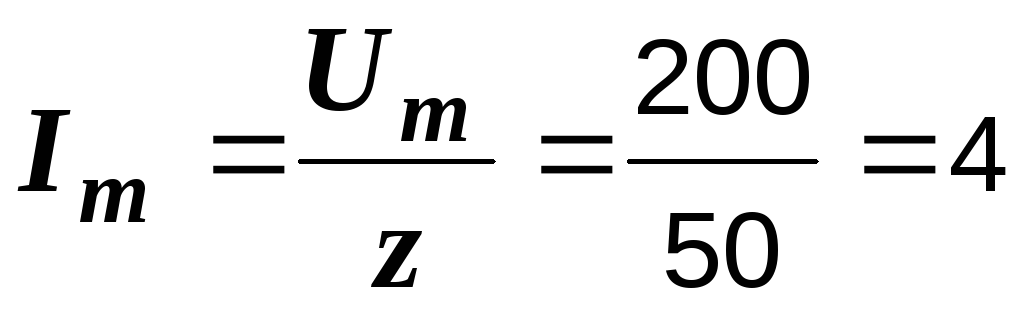 А.
А.
Определяем угол сдвига фаз
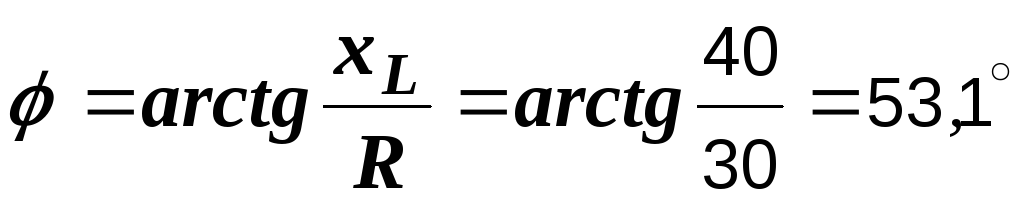 .
.
При отстающем токе (при активно-индуктивном характере цепи) этот угол положителен. Из (2.4) находим начальную фазу тока:
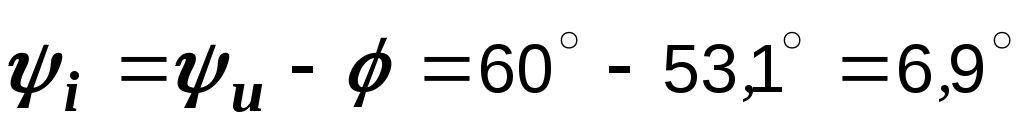 .
.
Итак 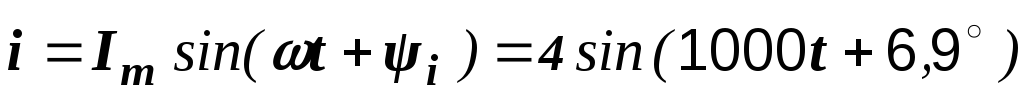 А.
А.
При
уменьшении частоты, т.е. при 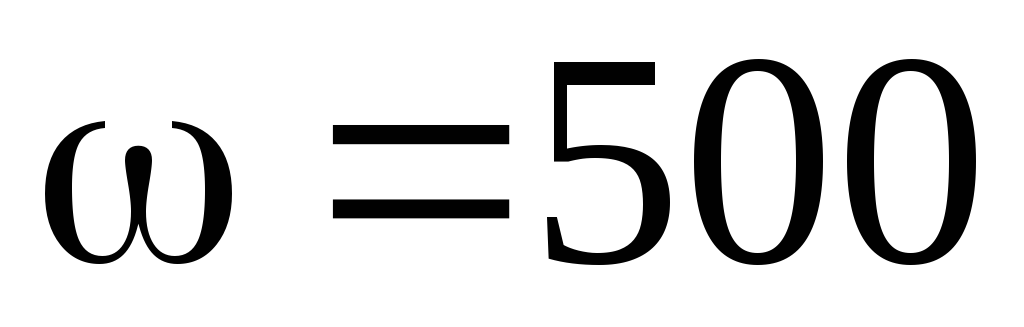 с-1:
с-1:
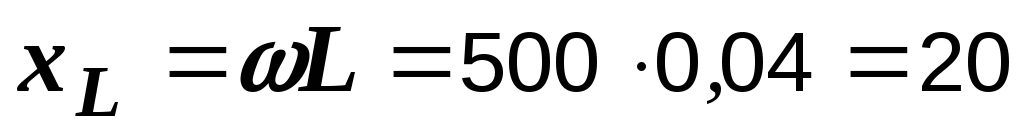 Ом,
Ом, 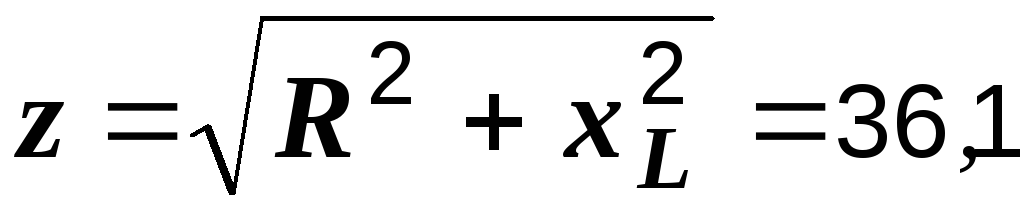 Ом,
Ом,
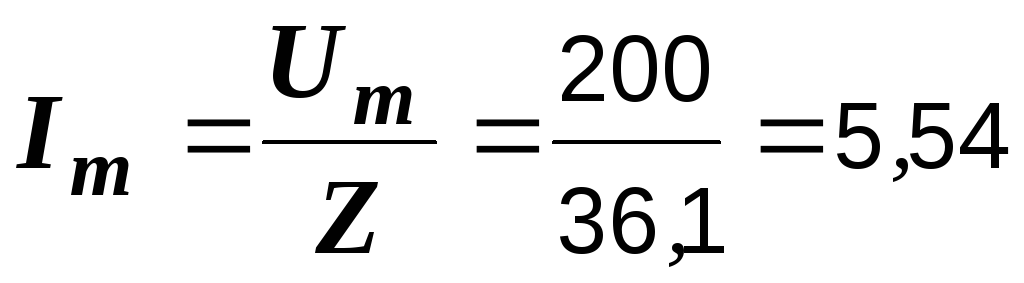 А,
А, 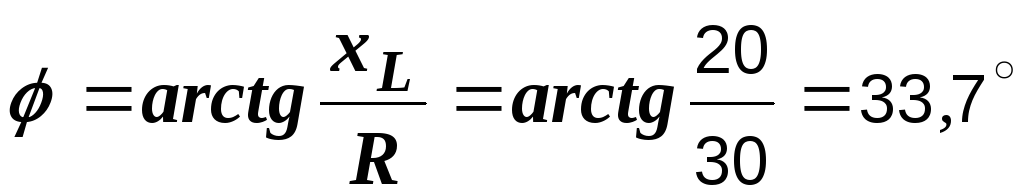 ,
,
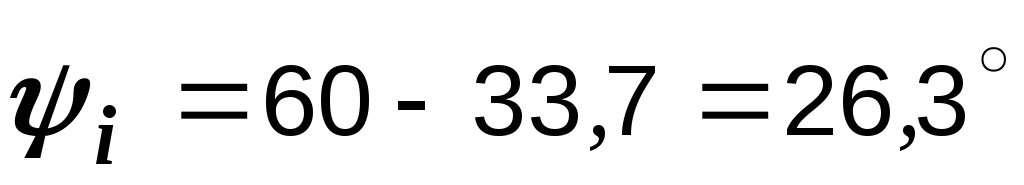 ,
, 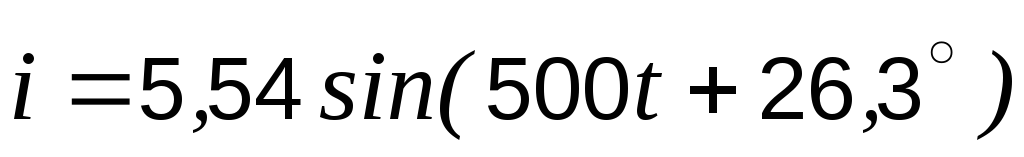 А.
А.
В схемах на рис. 2.27 предлагается определить показание вольтметра V на входе цепи, если во всех случаях показания вольтметров на отдельных элементах составляют V1 = 40 В, V2 = 30 В. Ответы на поставленный вопрос приводятся под каждой схемой.
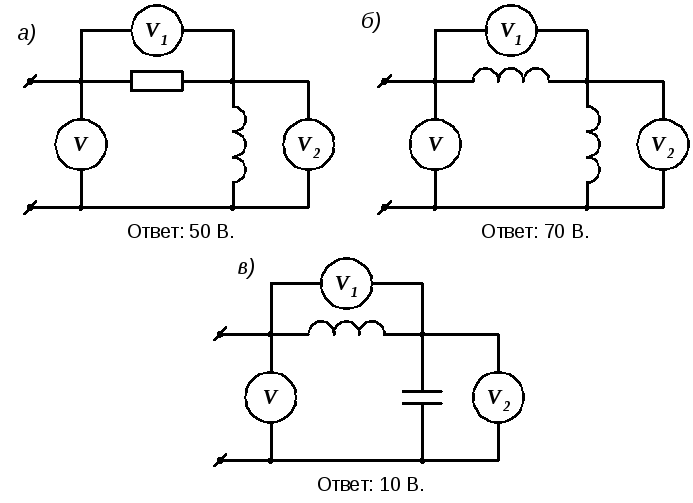
Рис. 2.27. Измерение напряжения в электрической цепи
Предлагаем учащемуся для каждого случая построить векторную диаграмму и проверить правильность приведенных ответов.
Вернемся к векторной диаграмме, представленной на рис. 2.24. Изобразим отдельно треугольник oab, являющийся ее частью (рис. 2.28, а). Этот треугольник называется треугольником напряжений.
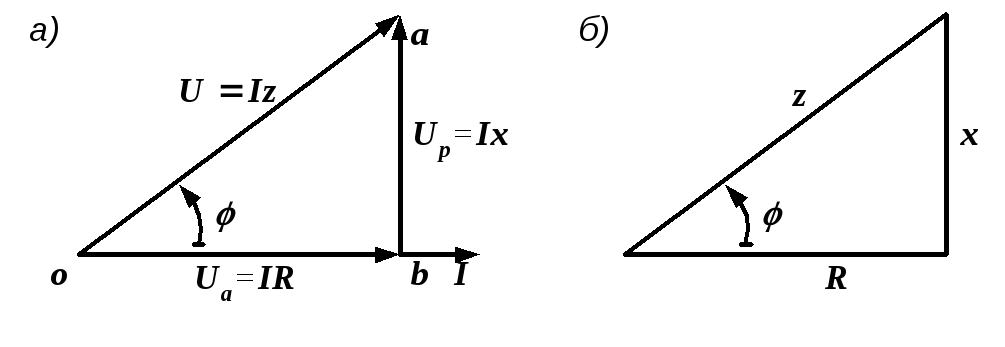
Рис. 2.28. Треугольники напряжений (а) и сопротивлений (б)
Проекция
вектора напряжения на вектор тока
называется активной составляющей
напряжения. Она обозначается Uа и равна падению напряжения на активном
сопротивлении 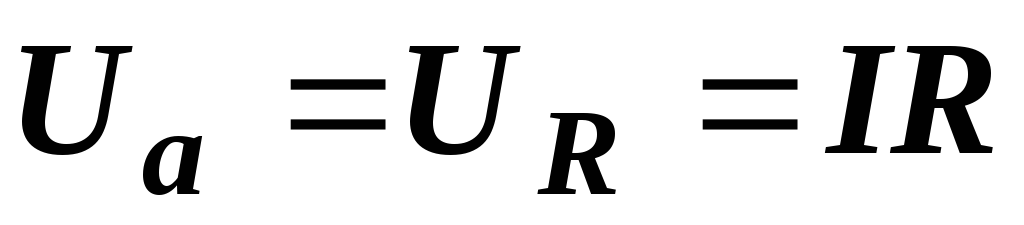 . Реактивная
составляющая напряжения U – это
проекция вектора напряжения на
направление, перпендикулярное вектору
тока. Она равна падению напряжения на суммарном
реактивном сопротивлении цепи
. Реактивная
составляющая напряжения U – это
проекция вектора напряжения на
направление, перпендикулярное вектору
тока. Она равна падению напряжения на суммарном
реактивном сопротивлении цепи 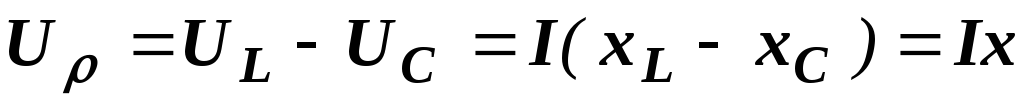 .
Как видно из рис. 2.28, если все стороны
треугольника напряжений разделить на
ток, то получится подобный ему треугольник
сопротивлений (рис. 2.28, б).
Ему соответствуют следующие формулы:
.
Как видно из рис. 2.28, если все стороны
треугольника напряжений разделить на
ток, то получится подобный ему треугольник
сопротивлений (рис. 2.28, б).
Ему соответствуют следующие формулы:
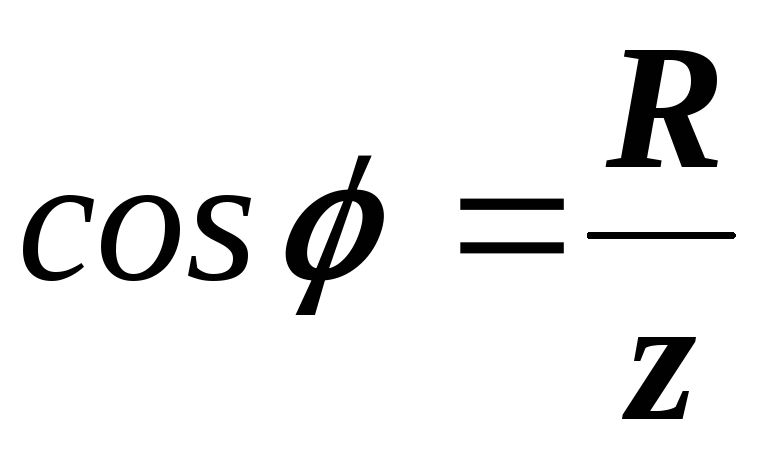 ,
, 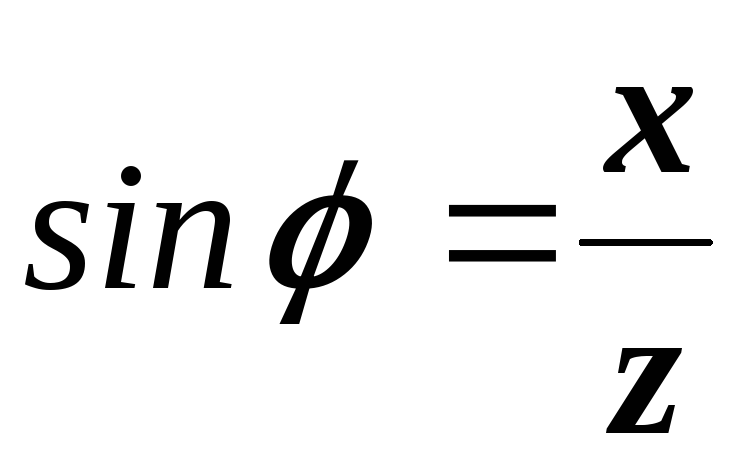 ,
, 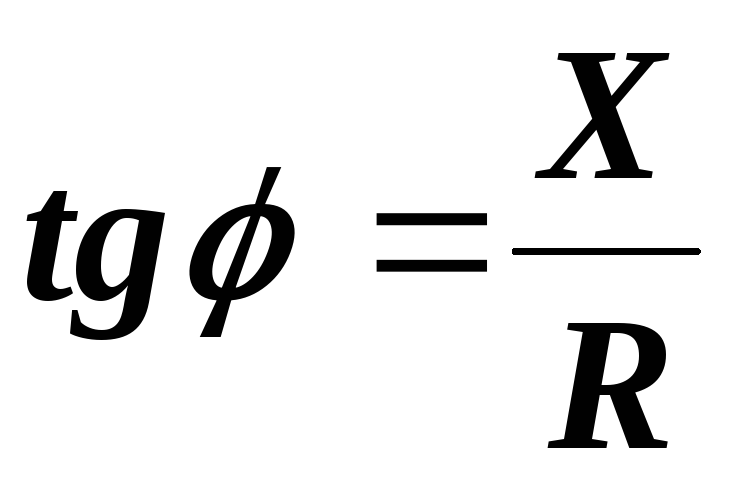 ,
, 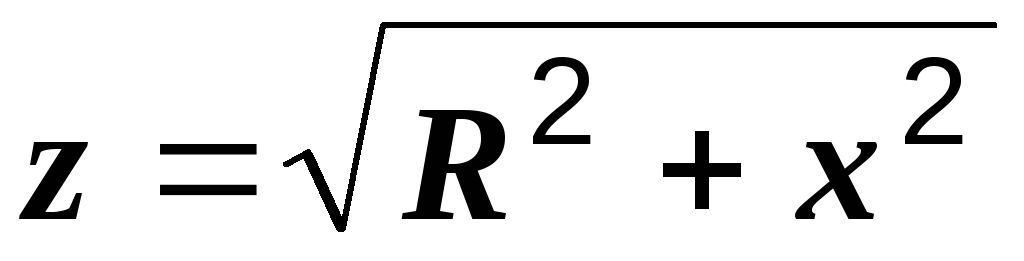 .
(2.27)
.
(2.27)
Решим задачу, поставленную в начале подразд. 2.12, символическим методом.
Запишем для цепи, изображенной на рис. 2.23, второй закон Кирхгофа в символической форме:
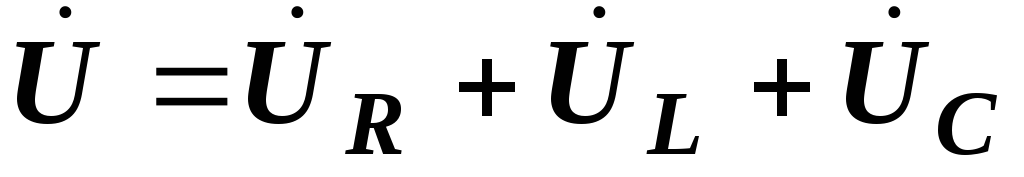 .
.
Подставляя
в него напряжения на элементах, записанные
ранее в комплексных числах 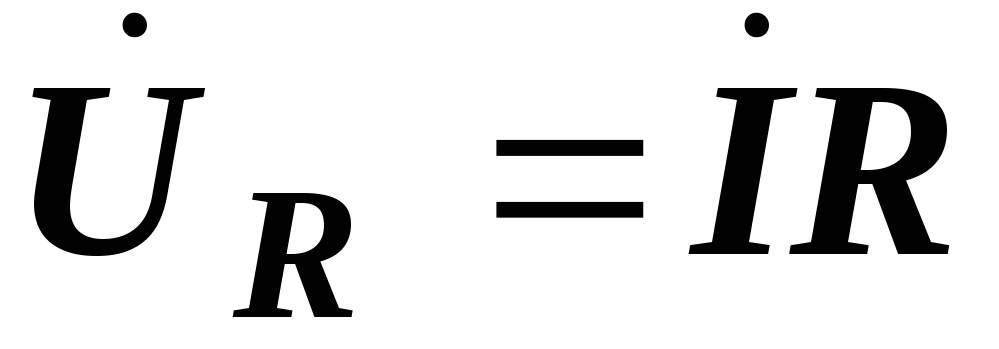 ,
, 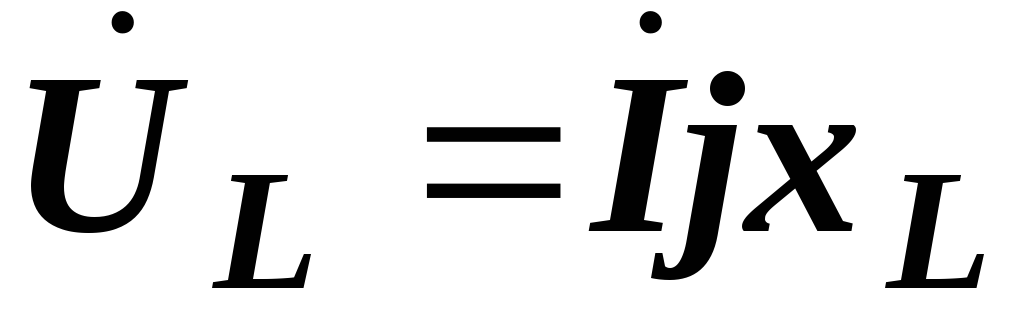 и
и 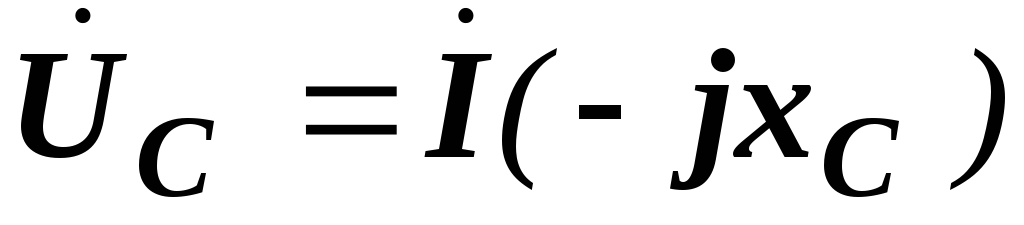 , получим:
, получим:
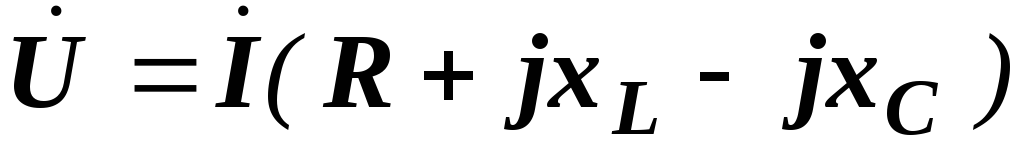 или
или 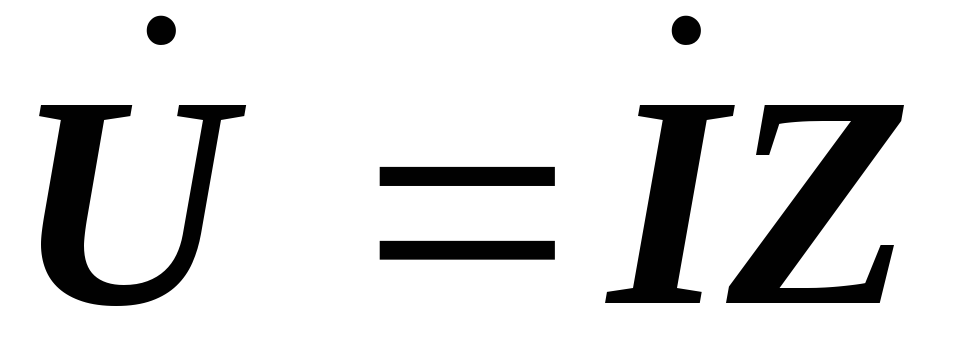 ,
(2.28)
,
(2.28)
где  – комплексное сопротивление цепи,
равное
– комплексное сопротивление цепи,
равное
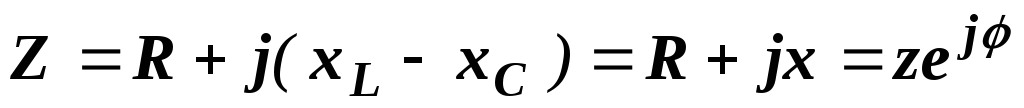 .
.
Выражение (2.28) представляет собой закон Ома в символической форме.
Пример 2.10. Определить показание амперметра в цепи, состоящей из последовательно соединенных сопротивлений – активного R = 60 Ом и индуктивного xL = 80 Ом, если напряжение на входе цепи U = 220 В.
Р е ш е н и е. Комплексное сопротивление цепи равно
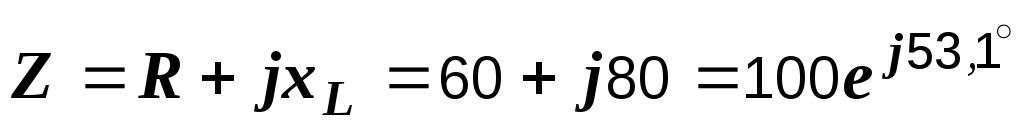 Ом.
Ом.
Для
применения формулы (2.28) входное напряжение необходимо
записать в символической форме, в виде
комплексного числа 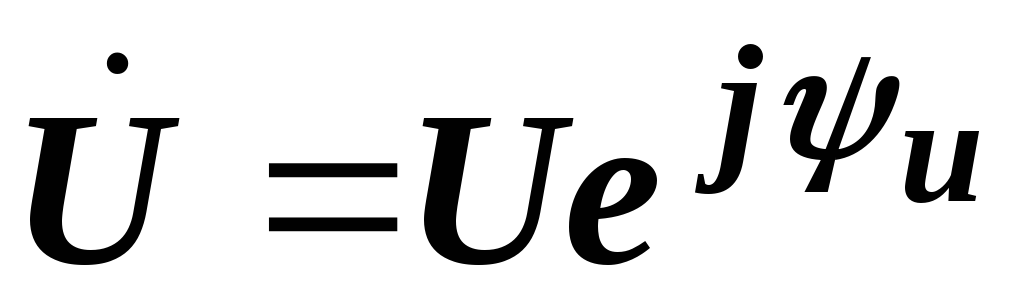 .
Так как нам задано только его численное
значение, начальную фазу (аргумент
комплексного числа
.
Так как нам задано только его численное
значение, начальную фазу (аргумент
комплексного числа 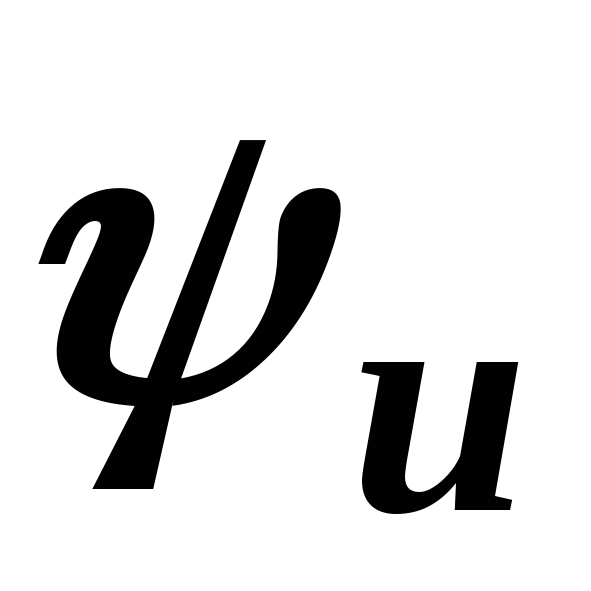 )
мы выбираем по своему усмотрению.
)
мы выбираем по своему усмотрению.
Примем 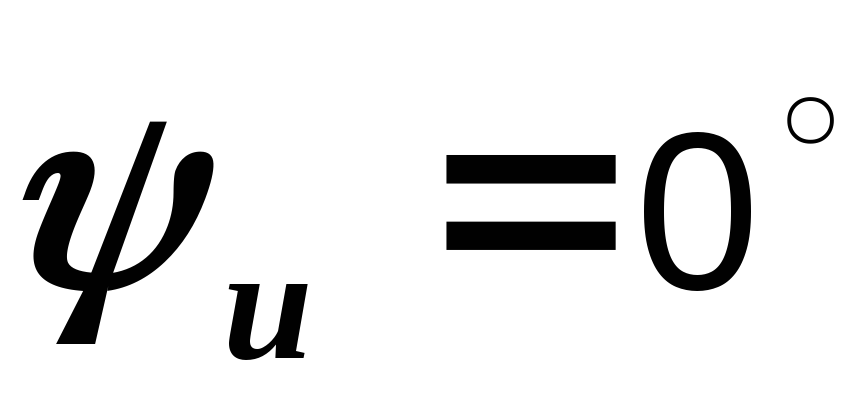 ,
тогда
,
тогда 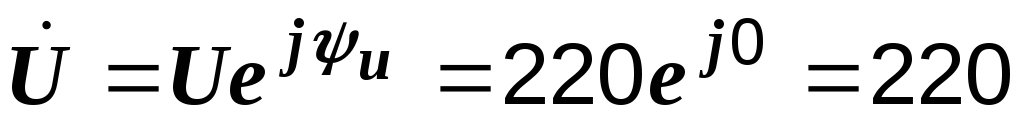 В.
В.
Комплекс действующего значения тока
 A.
A.
Показание
амперметра равно модулю комплексного
числа 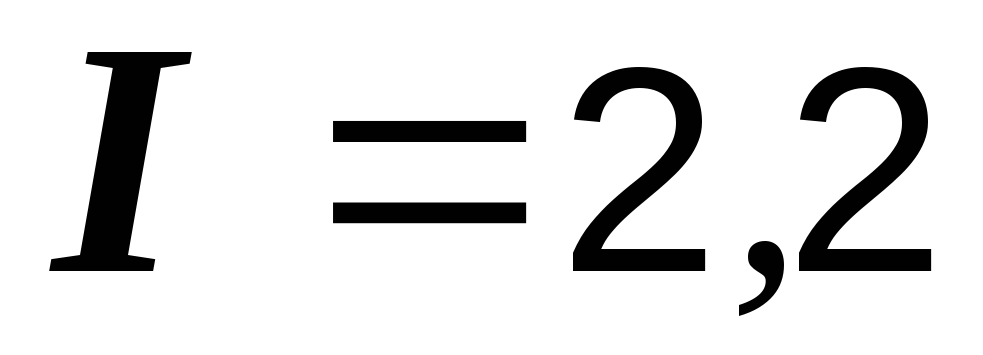 A.
A.
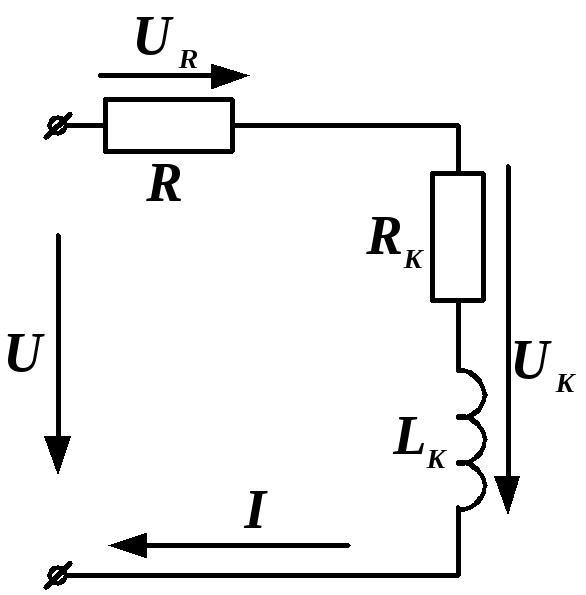
Пример 2.11. В цепи, состоящей из последовательно соединенных активного сопротивления R и катушки с параметрами RK = 34 Ом и хК = LK = 48 Ом (рис. 2.29, а), известны UR = 100 B и UK = 120 В. Требуется найти напряжение на входе цепи U.
а) | б) |
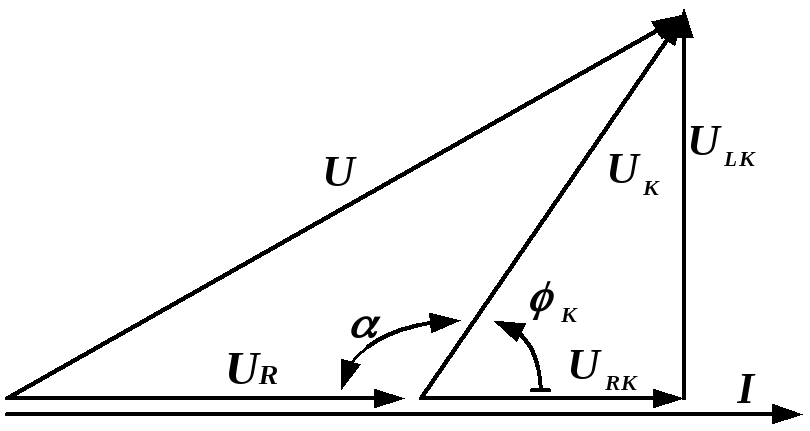
Рис. 2.29. Электрическая цепь и её векторная диаграмма
Р
е ш е н и е начинаем с построения векторной
диаграммы
(рис. 2.29, б).
Вектор напряжения U равен векторной сумме напряжений 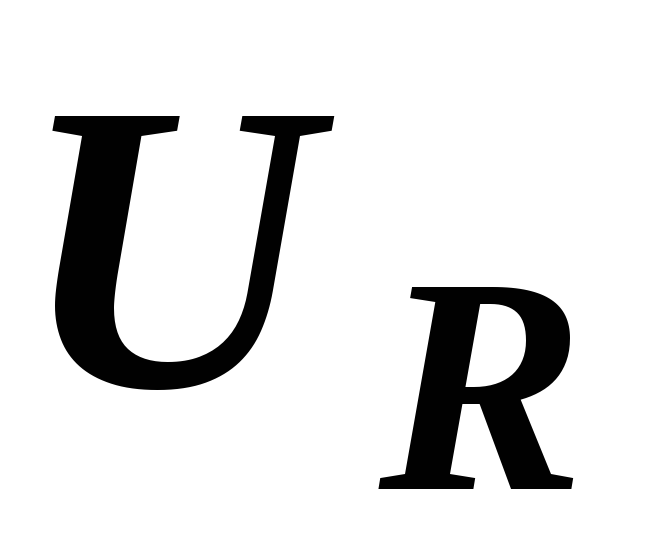 и
и  :
: 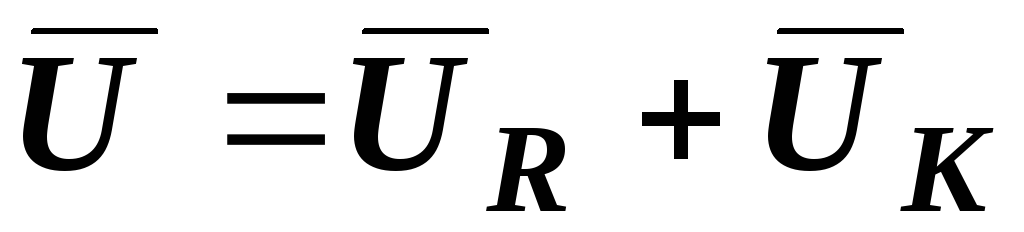 .
Напряжение на катушке
.
Напряжение на катушке  представляем как сумму напряжений на
ее активном и реактивном сопротивлениях
представляем как сумму напряжений на
ее активном и реактивном сопротивлениях  .
Векторы
.
Векторы  и
и 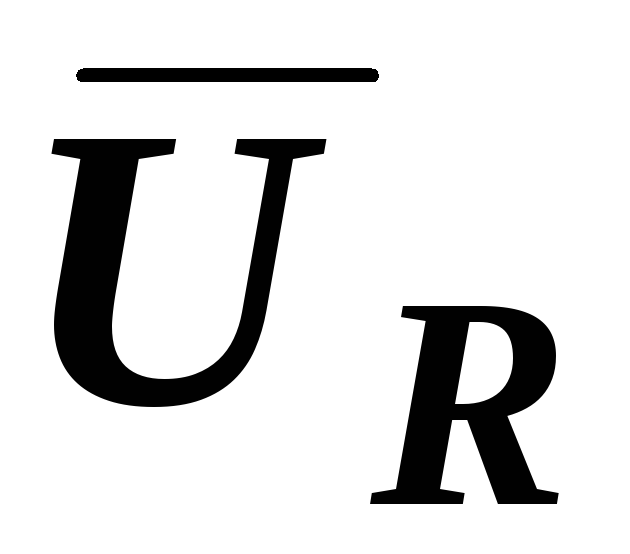 направляем по току, а
направляем по току, а 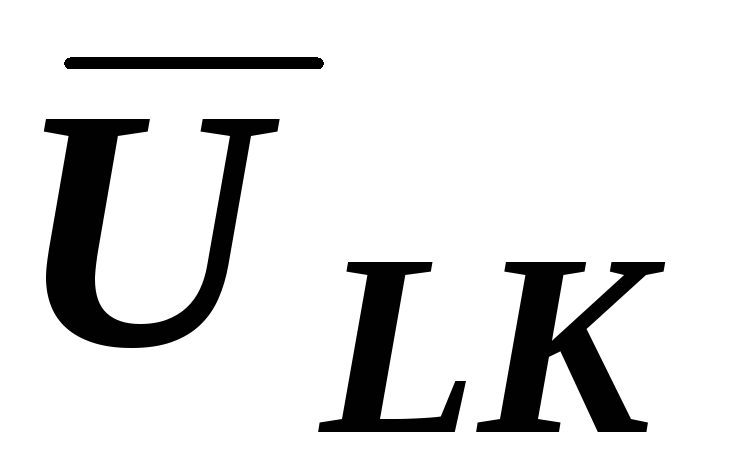 проводим перпендикулярно вверх.
проводим перпендикулярно вверх.
Величину входного напряжения, равную длине вектора U, можно найти одним из трех способов:
а) графически, построив векторную диаграмму в масштабе, для чего предварительно нужно рассчитать следующие величины:
– полное сопротивление катушки
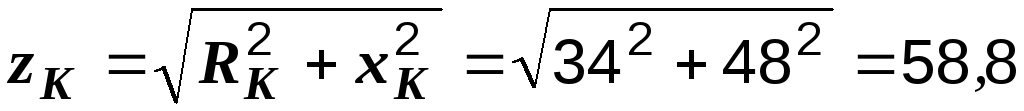 Ом;
Ом;
– ток в цепи
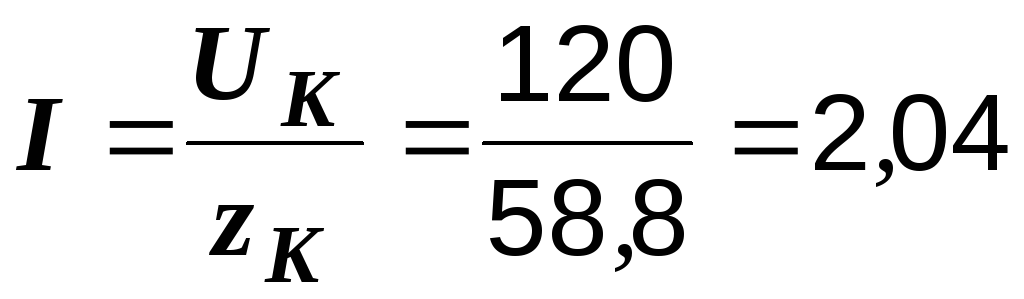 А;
А;
– составляющие напряжения на катушке
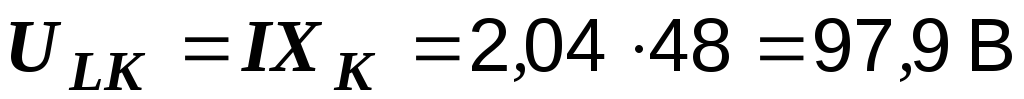 .
.
Измерив длину вектора U и умножив ее на масштаб, получим нужное нам значение;
б)
решением треугольников,
применяя известную из тригонометрии
теорему косинусов: 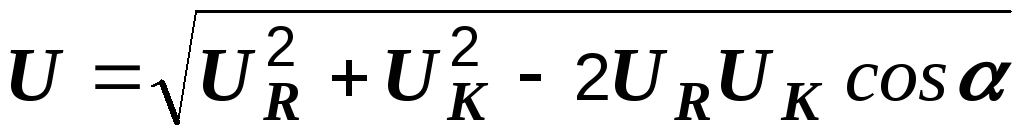 . Угол определяем из векторной диаграммы:
. Угол определяем из векторной диаграммы: 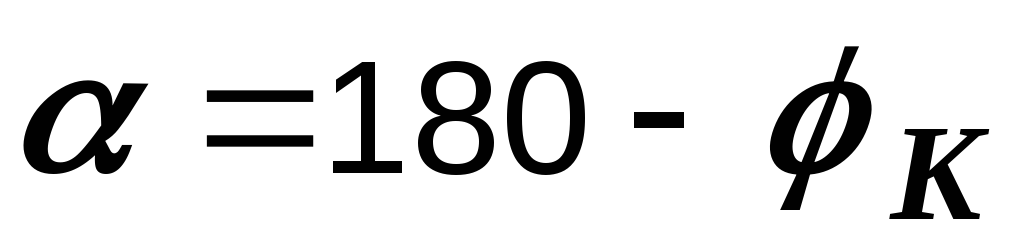 ,
где
,
где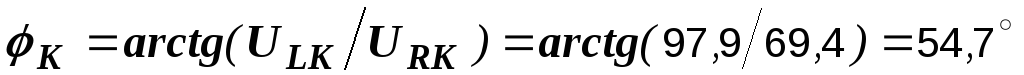 ,
,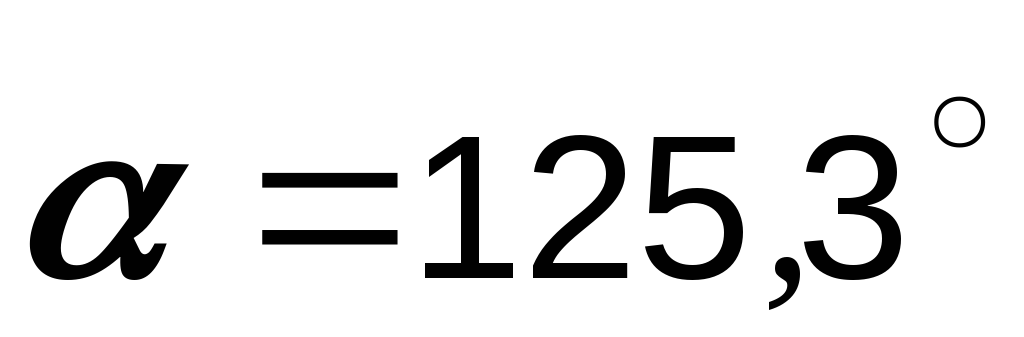 .
.
Вычисляем напряжение:
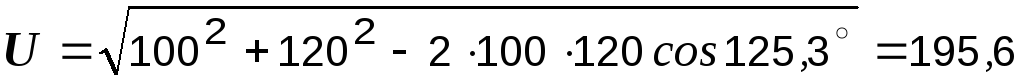 В;
В;
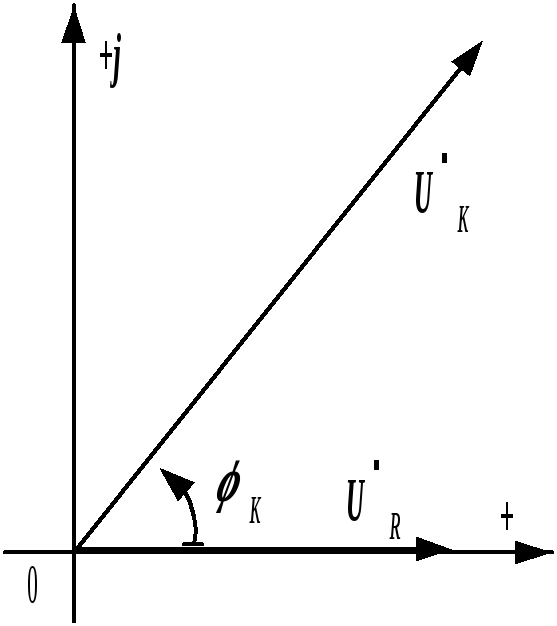
Рис. 2.30. Векторы в комплексной плоскости
в) символическим методом, записав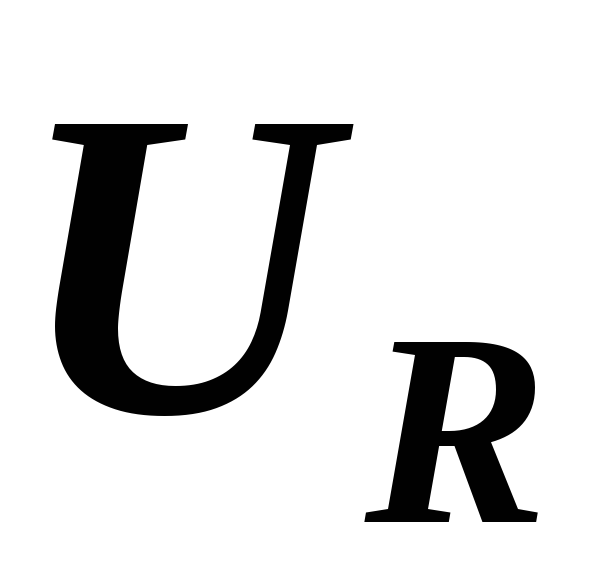 и
и  в комплексном виде и использовав
уравнение второго закона Кирхгофа в
символической форме
в комплексном виде и использовав
уравнение второго закона Кирхгофа в
символической форме 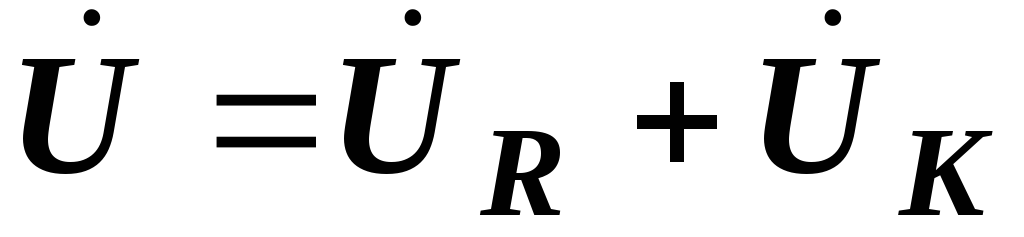 .
Комплексные выражения
.
Комплексные выражения 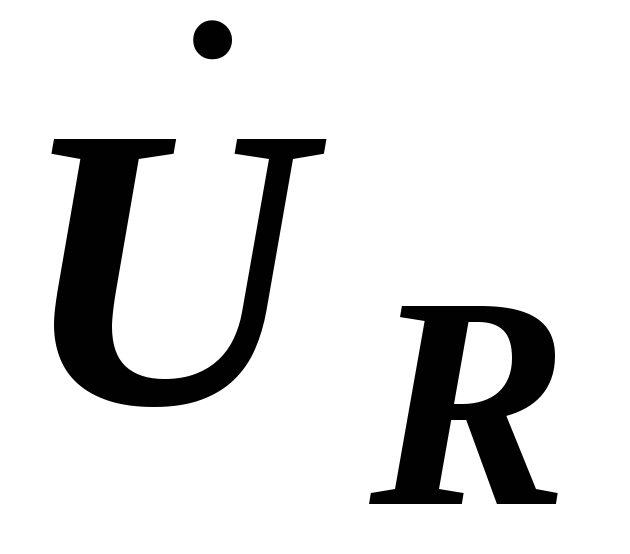 и
и  мы получим, изобразив векторы этих
напряжений в комплексной плоскости,
направив их из одного начала (рис.
2.30):
мы получим, изобразив векторы этих
напряжений в комплексной плоскости,
направив их из одного начала (рис.
2.30): 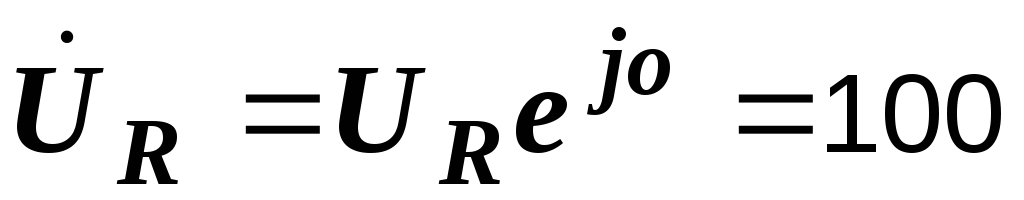 В;
В;
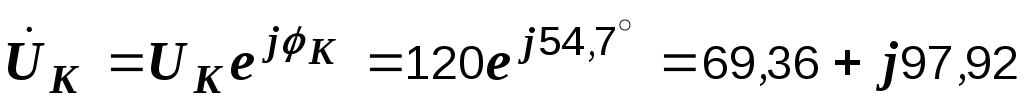 В.
В.
Находим 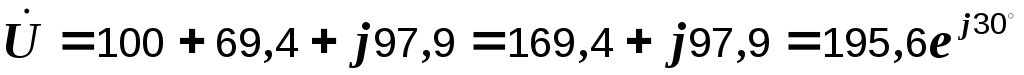 В.
В.
Величина
напряжения 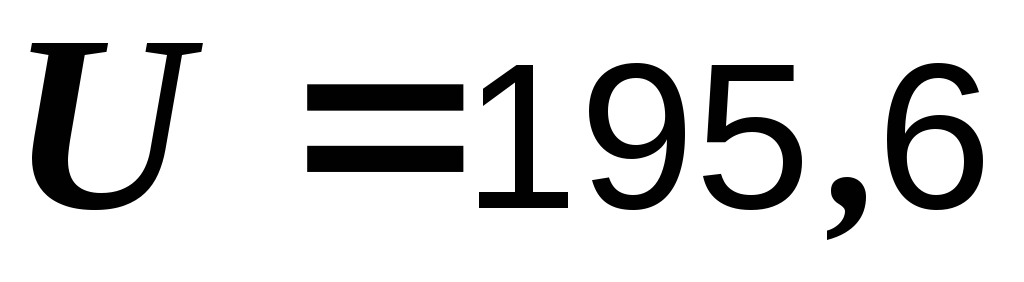 В.
В.
Последовательное соединение сопротивления, индуктивности, емкости
В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 22.1), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах.
При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы.
В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 22.2).
Вообще, направление первого вектора при построении диаграмм произвольно. Оно диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в соответствии со вторым законом Кирхгофа в векторной форме U=UR+UL+UC получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.
Нам известно, что напряжение на активном сопротивлении совпадает по фазе с током, поэтому вектор UR мы направляем по вектору I. К его концу пристраиваем вектор UL и направляем его вверх, так как напряжение на индуктивности опережает ток на 90°. Напряжение UС находится в противофазе с UL, т.е. отстает от тока на тот же угол 90°, поэтому вектор UС, пристроенный к концу вектора UL, направлен вниз. Векторная сумма UR, UL и UС дает вектор приложеного напряжения U.
Величины напряжений на отдельных элементах цепи нам известны:
Из треугольника oab (рис. 22.2) по теореме Пифагора находим:
Вынося из под знака радикала, записываем последнее выражение в виде: U=I*z; где,z — полное сопротивление.
В последней формуле разность индуктивного и емкостного сопротивлений мы обозначили буквой х. Это общее реактивное сопротивление цепи: х = хL – xC. Сами индуктивность и емкость называются реактивными элементами, и их сопротивления хL и xC тоже носят названия реактивных.
Выражение U=Iz называется законом Ома для всей цепи. Оно может быть записано и так: I=U/z=Uy.
где, y– полная проводимость цепи, представляющая величину, обратную полному сопротивлению 1/z
Если необходимо определить угол сдвига фаз между напряжением и током, то это можно сделать из треугольника напряжений oab (рис. 22.2):
Векторная диаграмма на рис. 22.2 построена для случая, когда UL>UC, что имеет место при XL>XC, когда в цепи преобладает индуктивность, и цепь носит активно-индуктивный характер. Общий ток отстает по фазе от входного напряжения.
Возможны также режимы, когда ULC и UL=UC
Последовательное соединение катушки и конденсатора
При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.

Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = Imsinωt.
Требуется определить напряжение на участках цепи и мощность.
Векторная диаграмма и полное сопротивление цели
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
u = u1R + uL + uC + u2R,
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
U = U2R + UL + UC +U2R
Для построения векторной диаграммы находим:
U1R = IR1; U2R = IR2; UL = IXL; UC = IXC.
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.

Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует

где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Из треугольников напряжения и сопротивлений определяют следующие величины:

Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).
2. ХL< ХC Векторная диаграмма изображена на рис. 14.3, где UL<UC , поэтому общее напряжение отстает от тока на угол φ<0.
Реактивное сопротивление цепи носит емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.


Общее напряжение совпадает по фазе с током и равно по величине активной
составляющей напряжения.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
Ток в цепи и общее напряжение связаны формулой
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Энергетический процесс в цепи с последовательном соединении конденсатора и катушки
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:

Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0; при φ<0 Q<0.
Активная мощность положительна при любом угле, так как cosφ = cos(-φ).
Полная мощность также всегда положительна. На основании формул (14.2) можно сделать вывод, что в рассматриваемой цепи совершается преобразование электрической энергии (Р ≠ 0) и обменный процесс между генератором и приемником (Q ≠ 0 при φ ≠ 0).
Энергетические процессы в данном случае сложнее, чем в ранее рассмотренных простых цепях. Усложнение объясняется тем, что наряду с обменом энергией между генератором и приемником совершается обмен энергией внутри приемника, между катушкой и конденсатором.
Особенности энергетического процесса в цепи с последовательным соединением катушки и конденсаторов отражены на рис. 14.5, где показаны графики мгновенной мощности отдельных элементов и цепи в целом при XL = ХС.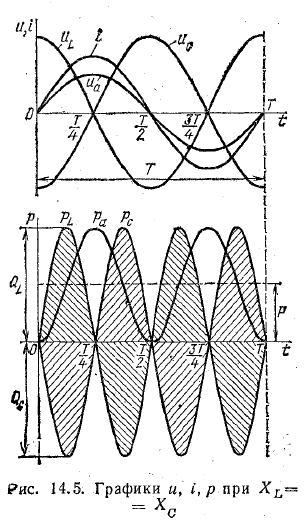

Катушка и конденсатор в течение полупериода накапливают равные количества энергии. Однако в первую четверть периода, когда ток увеличивается, а напряжение на конденсаторе уменьшается, энергия накапливается в магнитном поле катушки и уменьшается в электрическом поле конденсатора, причем скорость изменения энергии (мощность) в любой момент времени одинакова. Это дает основание считать, что обмен энергией происходит только в приемнике между катушками
и конденсатором.
Для преобразования электрической энергии в другой вид приемник получает ее от генератора со средней скоростью (мощностью) Р.
Задачи по теме и пример решения задачи для схемы с последовательным соединением конденсатора и катушки
Последовательное и параллельное соединения индуктивно связанных элементов.
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒Два элемента индуктивно связаны, если изменение тока в одном элементе приводит к появлению э.д.с. в другом элементе.
Две индуктивно связанные катушки с сопротивлениями 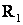 ,
, 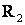 и индуктивностями
и индуктивностями 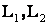 соединены последовательно. Возможны два вида включения: согласное и встречное.
соединены последовательно. Возможны два вида включения: согласное и встречное.
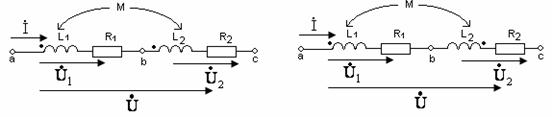
а) б)
Рисунок 10.2
Согласное включение.При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов (рисунок 10.2,а). Поэтому потокосцепления самоиндукции и взаимной индукции в каждом элементе складываются
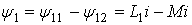 ,
,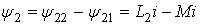 .
.
Индуктивность двух последовательно соединенных индуктивно связанных элементов при согласном включении равна
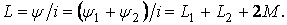 (10.8)
(10.8)
Напряжение на зажимах первой и второй катушках в комплексной форме
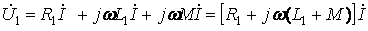 , (10.9)
, (10.9)
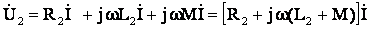 . (10.10)
. (10.10)
Напряжение на зажимах цепи (рисунок 10.2,а)
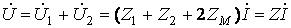 (10.11)
(10.11)
где 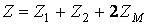 — входное сопротивление цепи при согласном включении;
— входное сопротивление цепи при согласном включении;
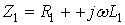 ;
;
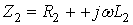 ;
;
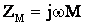 .
.
Встречное включение. При встречном включении токи в обоих элементах в любой момент времени направлены различно относительно одноименных выводов (рисунок 10.2,б). Поэтому потокосцепления самоиндукции и взаимной индукции в каждом элементе вычитаются 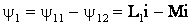 ,
, 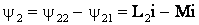 . Индуктивность двух последовательно соединенных индуктивно связанных элементов при встречном включении равна
. Индуктивность двух последовательно соединенных индуктивно связанных элементов при встречном включении равна
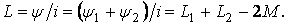 (10.12)
(10.12)
Напряжение на зажимах первой и второй катушках в комплексной форме
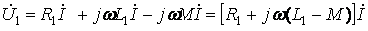 , (10.13)
, (10.13)
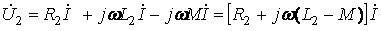 . (10.14)
. (10.14)
Напряжение на зажимах цепи (рисунок 10.2,б)
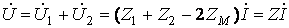 (10.15)
(10.15)
где 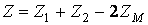 — входное сопротивление цепи при встречном включении;
— входное сопротивление цепи при встречном включении;
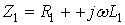 ;
;
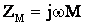
Две индуктивно связанные катушки с сопротивлениями 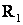 ,
, 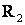 и индуктивностями
и индуктивностями 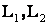 соединены параллельно, причем одноименные выводы присоединены к одному и тому же узлу
соединены параллельно, причем одноименные выводы присоединены к одному и тому же узлу 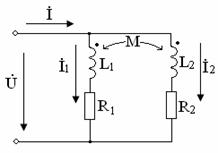 Рисунок 10.4
Рисунок 10.4
Запишем законы Кирхгофа для цепи (рисунок 10.4)
 } (10.16)
} (10.16)
где 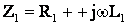 ,
, 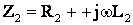 ,
,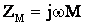 .
.
Решая систему уравнений ( 10.16), получим
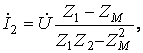
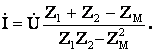 (10.17)
(10.17)
Входное сопротивление цепи
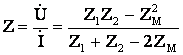 . (10.18)
. (10.18)
Если индуктивно связанные элементы присоединены к узлу разноименными выводами
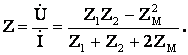 (10.19)
(10.19)
Методы расчета разветвленных индуктивно связанных цепей.
Если изменение тока в одном из элементов цепи приводит к появлению э.д.с. в другом элементе, то эти два элемента индуктивно связаны, а возникающая э.д.с. называется э.д.с. взаимной индукции.
Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи
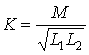 ,
,
где М – взаимная индуктивность элементов цепи,
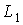 и
и 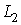 – индуктивности элементов.
– индуктивности элементов.
При расчете цепей с взаимной индуктивностью следует на схеме отметить стрелками выбираемые положительные направления токов в ветвях (или контурных токов). Кроме того, одинаковыми условными значками (звездочками, точками, буквами и т.п.) обозначить одноименные зажимы каждой пары индуктивно связанных катушек.
Одноименными называются такие зажимы, при одинаковом положительном направлении токов относительно которых, магнитные потоки самоиндукции и взаимной индукции складываются.
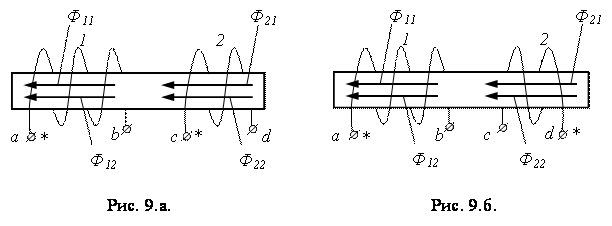
Пример 2.4.1
При направлении тока 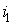 от зажима
от зажима 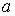 к зажиму
к зажиму 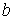 и тока
и тока 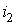 от зажима c к зажиму d магнитные потоки самоиндукции
от зажима c к зажиму d магнитные потоки самоиндукции 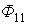 и
и 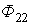 и взаимной индукции
и взаимной индукции 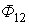 и
и 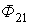 суммируются. Поэтому зажимы а и с одноименные.
суммируются. Поэтому зажимы а и с одноименные.
Для катушек, показанных на Рис. 9б, одноименными будут зажимы a и d.
Комплексное сопротивление взаимной индукции:
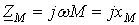 .
.
При последовательном соединении двух индуктивно связанных катушек эквивалентное комплексное число сопротивления определяется по формуле:
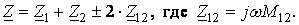
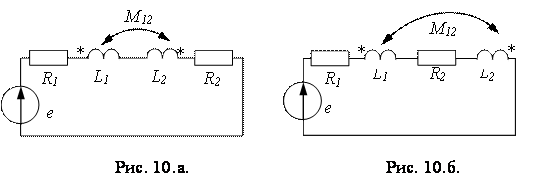
Знак (+) соответствует согласному включению катушек, а знак (-) – встречному (Рис. 10а, 10б).
При параллельном соединении двух индуктивно связанных катушек эквивалентное комплексное сопротивление:
 .
.
Знак (-) ставится при согласном включении, знак (+) – при встречном.
Расчеты разветвленных индуктивно связанных цепей можно вести по законам Кирхгофа или методом контурных токов. При составлении уравнений по второму закону Кирхгофа, э.д.с. взаимной индукции учитывают, как соответствующие напряжения. Знак комплексного напряжения 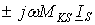 на элементе определяется так: если направление обхода элемента К и направление тока в элементе S одинаковы относительно одноименных зажимов, то берется знак (+), если не одинаковы, то берется знак (-).
на элементе определяется так: если направление обхода элемента К и направление тока в элементе S одинаковы относительно одноименных зажимов, то берется знак (+), если не одинаковы, то берется знак (-).
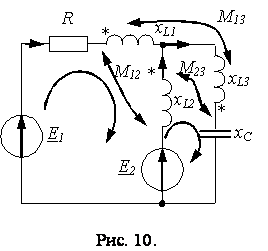
Пример 2.4.2
Составить систему уравнений по законам Кирхгофа для цепи рис. 11:
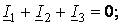

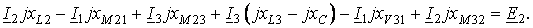
Явление резонанса.
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
Резонанс напряжений.
Резонанс – состояние эл цепи, состоящей из разнохарактерных эл-ов, при к-ой фазовый сдвиг м/у входным током и приложенным напряжением равен нулю
Возникает в последовательном контуре.


при резонансе  , возможно при
, возможно при 
резонансная частота: 
На резонансной частоте комплексное сопротивление носит чисто активный х-р, т.е. 
, ток совпадает по фазе с приложенным напряжением и достигает макс значения  . Реактивные сопротивления контура на резонансной частоте равны друг другу
. Реактивные сопротивления контура на резонансной частоте равны друг другу 
 — характеристическое сопротивление контура – сопротивление реактивнх эл-ов при резонансе
— характеристическое сопротивление контура – сопротивление реактивнх эл-ов при резонансе
Резонансные св-ва контура х-ся добротностью контура:  — во ск-ко раз напряжение на реактивных элементах при резонансе превышают входное напряжение
— во ск-ко раз напряжение на реактивных элементах при резонансе превышают входное напряжение
Коэффициент затухания контура – величина обратная добротности 
Сумма энергий электрического и магнитного полей при резонансе остается постоянной