Определение эквивалентного последовательного сопротивления (ESR) конденсаторов
Добавлено 12 декабря 2019 в 07:16
Рассмотрим подробнее важность ESR (эквивалентного последовательного сопротивления) конденсатора, как его измерить, и какие факторы могут повлиять на ваши измерения.
По мере того, как рабочие частоты увеличиваются, а электронные системы становятся все сложнее и меньше, разработчики должны уделять пристальное внимание ESR (эквивалентному последовательному сопротивлению) конденсатора, поскольку оно влияет на энергопотребление и эффективность.
Знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.
Некоторые производители указывают ESR при конкретных частоте и рабочих условиях, некоторые просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния.
Эквивалентное последовательное сопротивление (ESR) является одной из характеристик неидеального конденсатора, которая может вызывать различные проблемы производительности в электронных схемах.
Высокое значение ESR ухудшает производительность из-за потерь I2R, шума и более высокого падения напряжения.
В некоторых случаях тепло, выделяемое благодаря ESR, невелико и может не вызывать проблем. Однако в некоторых схемах, особенно в приложениях с большим током, рассеиваемое тепло может вызвать значительное повышение температуры, повлиять на работу схемы и вызвать деградирование конденсатора. Кроме того, на сопротивлении происходит значительное падение напряжения, что снижает долю полезной энергии в приложении.
Таким образом, при выборе конденсатора для таких применений, как ВЧ, аккумулирование энергии, схемы фильтров и другие чувствительные схемы, требуется учет и других характеристик, помимо значений емкости и напряжения.
Связанная информация
- Особенности конденсаторов
- Практические аспекты применения конденсаторов
- Чистое питание для каждой микросхемы, часть 2: Выбор и использование блокировочных конденсаторов
Влияние ESR на радиочастотные схемы и схемы аккумулирования энергии
Несмотря на то, что ESR у керамических конденсаторов очень мало, порядка миллиом, это сопротивление может существенно повлиять на такие схемы, как радиочастотные схемы и схемы с низким энергопотреблением.
В переносных радиочастотных передатчиках конденсаторы с высоким ESR в схемах связи или обхода источника питания усилителя потребляют и расходуют больше энергии аккумулятора из-за более высоких потерь I2ESR. Это уменьшает эффективность, выходную мощность и срок службы батареи.
Кроме того, большинство радиочастотных полупроводниковых устройств, изготовленных для согласующих каскадов, построены с очень низким входным сопротивлением. Таким образом, согласующий конденсатор, такой как многослойный керамический чип-конденсатор (MLCC) с высоким ESR, будет представлять собой значительную долю от общего полного сопротивления цепи. Например, если входной импеданс устройства составляет 1 Ом, согласующий конденсатор с ESR 0,8 Ом будет рассеивать около 40 процентов общей мощности, таким образом, уменьшая выходную мощность и эффективность схемы.
Конденсаторы в приложениях по аккумулированию энергии выполняют более важную роль – накапливают заряд от низковольтных источников энергии и быстро и эффективно разряжают эту накопленную энергию для питания нагрузки.
Следовательно, конденсаторы и другие компоненты в цепях аккумулирования энергии должны во время работы потреблять очень мало энергии.
Конденсатор с высоким ESR будет иметь бо́льшие потери I2ESR, поэтому часть полученной энергии в конечном итоге будет потрачена впустую в виде тепла, что приведет к уменьшению выходной энергии конденсатора. Однако разработчики могут предпочесть суперконденсаторы (несмотря на их более высокие ESR и утечку), потому что они предлагают более высокую плотность энергии.
Определение эквивалентного последовательного сопротивления с помощью измерителя ESR
Измеритель ESR является умеренно точным прибором, который доступен и удобен в использовании, особенно при измерении нескольких конденсаторов, когда они находятся в схеме. На конденсатор в схеме делителя напряжения подается переменное напряжение. Частота подаваемого переменного напряжения обычно равна значению, при котором реактивное сопротивление конденсатора незначительно.
Рисунок 1 – Простая модель измерения ESRВо время теста с использованием измерителя ESR ток пропускается через конденсатор в течение очень короткого времени, поэтому конденсатор не заряжается полностью.
Ток создает напряжение на конденсаторе. Это напряжение будет равно произведению тока на ESR конденсатора, плюс незначительное напряжение из-за небольшого заряда в конденсаторе.
Поскольку ток известен, значение ESR рассчитывается путем деления измеренного напряжения на ток. Результаты затем отображаются на показаниях измерителя.
Измерения ESR могут выполняться, когда конденсатор находится и в схеме, и вне схемы. Для конденсаторов, подключенных параллельно, измерение дает в результате общее сопротивление. Если необходимо определить отдельно ESR у конкретных конденсаторов, они должны быть извлечены из схемы. Однако при наличии сотен конденсаторов утомительно вынимать каждый из них, а также существует повышенный риск повреждения конденсаторов или печатной платы во время удаления.
Типовой измеритель ESR использует низкое напряжение около 250 мВ или менее с частотой около 100 кГц. Низкое напряжение является недостаточным для смещения и активации полупроводниковых устройств в окружающих цепях, что гарантирует, что импеданс соседних компонентов не влияет на показания ESR.
Перед проведением измерения конденсатор должен быть разряжен. Некоторые измерители ESR имеют встроенный механизм разряда. Однако может быть важно разрядить конденсатор вручную, особенно если это высоковольтный конденсатор, заряд которого может повредить измеритель ESR.
Несмотря на то, что измеритель ESR может удобно тестировать конденсаторы внутри схемы, он имеет ограничения по частоте, а также по самому низкому уровню сопротивления, который он может точно измерить.
Измерение с помощью коаксиальной резонансной трубы для сверхнизких сопротивлений на высоких частотах
Поскольку значение ESR зависит от рабочей частоты, измерение сверхнизких значений ESR на очень высоких частотах становится проблемой при использовании обычных измерителей ESR.
Для керамических конденсаторов наиболее точным методом определения ESR на высоких частотах (от 100 МГц до 1,3 ГГц) является метод коаксиальной резонансной линии. Этот метод основан на стандартной модели Boonton 34A и используется вместе с генератором высокочастотных сигналов и высокочастотным вольтметром.
Линия коаксиального резонатора выполнена из медной трубки со сплошным медным стержнем в качестве центрального проводника. Тестируемый конденсатор устанавливается последовательно между центральным проводником и проводником экрана.
Перед выполнением измерения ESR конденсатора необходимо определить характеристики ненагруженной линии резонатора. ВЧ возбуждение закороченной коаксиальной линии помогает определить ширину полосы λ/4 и 3λ/4, тогда как ширина полосы λ/2 и λ определяется, когда линия разомкнута (λ – это длина волны; дополнительную информацию см. в этой статье). Эти данные характеризуют резонансную частоту, добротность (Q) ненагруженной резонансной линии и сопротивление крепежного элемента.
Затем тестируемый конденсатор помещается в секцию DUT (device under test, тестируемое устройство), и генератор сигналов настраивается на пиковое резонансное напряжение. Конденсатор вызывает изменение резонансной частоты и добротности, значения которых теперь отличаются от значений ненагруженной коаксиальной линии.
Затем используются расчеты линии передачи, и значение ESR определяется на основе взаимосвязи между новой частотой и добротностью, а также частотой и добротностью исходного состояния без нагрузки.
В настоящее время обычной практикой является использование векторного анализатора цепей для замены как генератора сигналов, так и высокочастотного вольтметра. При использовании векторного анализатора цепей резонансная частота считывается с дисплея. Некоторые модели векторных анализаторов могут экспортировать результаты непосредственно в программу расчета и отображать окончательное значение ESR.
Длина трубки рассчитана на работу в диапазоне частот от 100 МГц до 1,5 ГГц; однако для частот, выходящих за пределы этого диапазона, трубка может быть выполнена произвольной длины.
Факторы, которые влияют на измерения ESR
Ошибки измерения ESR могут возникать в результате проблем с техникой, способа выполнения контакта с конденсатором или отсутствия калибровки измерительного оборудования.
Должны быть приняты во внимание сопротивления, самоиндукция и емкость измерительного прибора и его выводов, особенно на высоких частотах измерения.
Сопротивление и индуктивность измерительных проводов
Сопротивление измерительных проводов является распространенным источником ошибок при измерениях низких сопротивлений. Это сопротивление добавляется к сопротивлению тестируемого устройства.
Кроме того, следует избегать измерительных проводов со спиральной намоткой, поскольку источником ошибки может стать их индуктивность.
Помехи от соседнего оборудования
Измерение следует проводить в местах, удаленных или экранированных от источников значительных электромагнитных помех. В противном случае измерительные провода могут ловить помехи, и это может повлиять на показания.
Заключение
ESR варьируется в зависимости от типа конденсатора и условий эксплуатации, таких как частота и температура. Некоторые производители указывают ESR на определенной частоте и при определенных условиях работы, другие просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния.
Тем не менее, знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.
Тип метода, используемого для определения ESR, зависит от таких факторов, как тип конденсатора, рабочая частота и требуемая точность. В то время как измеритель ESR и другие самодельные измерители подходят для ряда применений на частотах примерно до 100 кГц, они не могут точно определить очень низкие значения ESR на очень высоких частотах. Метод коаксиальной резонансной линии часто является предпочтительным при определении сверхнизких значений ESR на частотах между приблизительно 100 МГц и 1,3 ГГц.
По мере того, как рабочие частоты увеличиваются, а электронные системы становятся меньше и сложнее, необходимо уделять пристальное внимание таким параметрам, как ESR, которые напрямую влияют на характеристики схемы и эффективность энергопотребления.
Оригинал статьи:
- Amos Kingatua. Determining the Equivalent Series Resistance (ESR) of Capacitors
Теги
ESR (эквивалентное последовательное сопротивление)ИзмерениеКерамический конденсаторКонденсаторЭквивалентная схемаЭлектролитический конденсаторЭквивалентное последовательное сопротивление — r
Эквивалентное последовательное
сопротивление (ЭПС, англ.
ESR)
обусловлено главным образом электрическим
сопротивлением материала обкладок и
выводов конденсатора и контакта(-ов)
между ними, а также потерями в диэлектрике.
Обычно ЭПС возрастает с увеличением
частоты тока, протекающего через
конденсатор.
В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсатороввфильтрахимпульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр.,Capacitor plague(англ.)).
Существуют специальные приборы
(ESR-метры) для измерения этого достаточно
важного параметра конденсатора, по
которому можно часто определить
пригодность его дальнейшего использования
в определённых целях. Этот параметр,
кроме собственно ёмкости (ёмкость —
это основной параметр) — часто имеет
решающее значение в исследовании
состояния старого конденсатора, стоит
ли использовать его в определённой
схеме, или он прогнозируемо выйдет за
пределы допустимых отклонений.
Эквивалентная последовательная индуктивность — l
Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности.
Саморазряд
С течением времени конденсатор теряет энергию за счёт саморазряда.
Тангенс угла потерь
Тангенс угла потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости.
Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол , где— угол диэлектрических потерь. При отсутствии потерь. Тангенс угла потерь определяется отношениемактивной мощностиPакреактивнойPрпри синусоидальном напряжении определённой частоты. Величина, обратная, называетсядобротностьюконденсатора. Термины добротности и тангенса угла потерь Температурный коэффициент ёмкости (ТКЕ)
ТКЕ — относительное изменение ёмкости
при изменении температуры окружающей
среды на один градус Цельсия (Кельвина).
,
где ΔT— увеличение температуры в°Cили°Котносительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость ёмкости от температуры, и конденсаторы с большими уходами ёмкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение ёмкости в рабочем диапазоне температур.
Диэлектрическое поглощение
Если заряженный конденсатор быстро
разрядить до нулевого напряжения путём
подключения низкоомной нагрузки, а
затем снять нагрузку и наблюдать за
напряжением на выводах конденсатора,
то мы увидим, что напряжение медленно
повышается. Это явление получило название диэлектрическое
поглощениеилиадсорбция электрического
заряда.
Конденсатор ведёт
себя так, словно параллельно ему
подключено множество последовательных
В зависимости от назначения можно
условно разделить конденсаторы на
конденсаторы общего и специального
назначения. Конденсаторы общего
назначения используются практически
в большинстве видов и классов аппаратуры.
Традиционно к ним относят наиболее
распространённые низковольтные
конденсаторы, к которым не предъявляются
особые требования. Все остальные
конденсаторы являются специальными.
Также различают конденсаторы по форме обкладок: плоские, цилиндрические, сферические и другие.
электричества — Есть ли у конденсатора сопротивление?
спросил
Изменено 5 лет, 10 месяцев назад
Просмотрено 17 тысяч раз
$\begingroup$
Имеет ли конденсатор сопротивление? И почему? Когда я спросил своего учителя физики, он сказал, что нет, но я не понял почему. Кто-нибудь может уточнить? Заранее спасибо.
- электричество
$\endgroup$
1
$\begingroup$
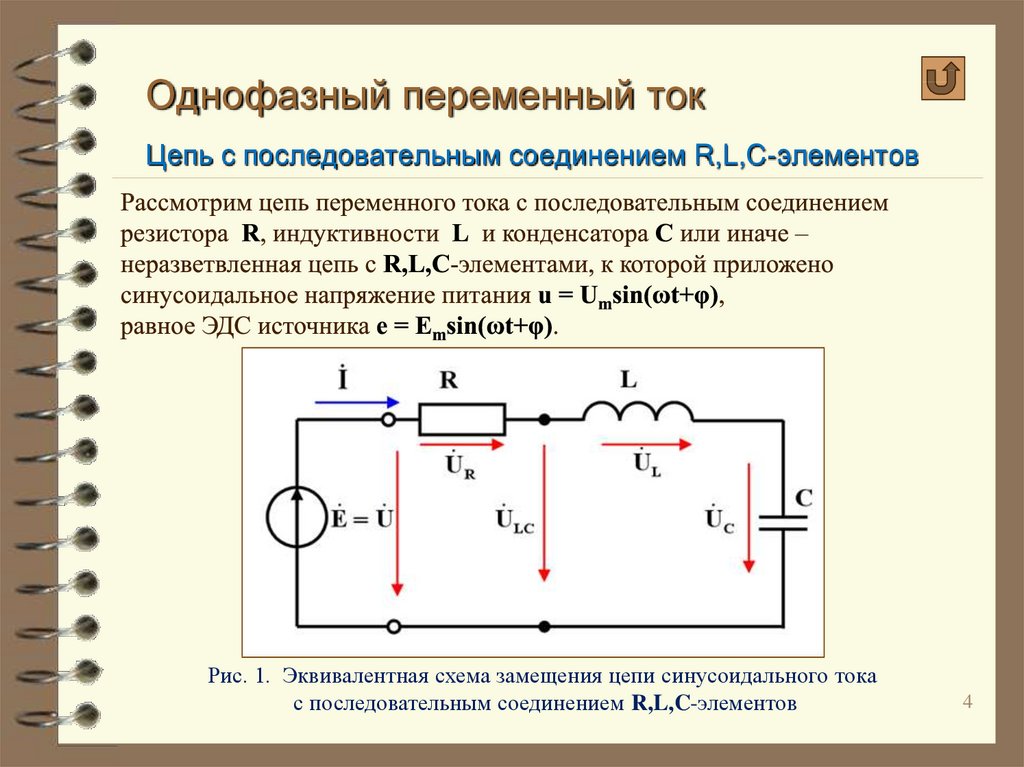
Если вы имеете дело с реальным конденсатором, он наверняка имеет сопротивление паразитов, вы можете моделировать его следующим образом
, где $ rs $ — эквивалентное сопротивление серии, $ rp $.
схема, предназначена для идеального конденсатора, который, конечно, не имеет паразитных сопротивлений.
$\endgroup$
0
$\begingroup$
Вопрос, который вы задали, довольно прямой и честный. Во-первых, сопротивление потоку заряда в проводнике возникает в первую очередь из-за неупругих столкновений электронов с атомами в материальной среде. Вы можете понять это, взглянув на уравнение импульса из теории Друде.
$$dp/dt=qE+ \delta({p}_{коллизия})/{\tau}$$ где $\tau$ относится к среднему времени между двумя столкновениями.
Поскольку конденсатор в основном является накопителем заряда, такого уравнения не существует, поэтому можно сказать, что электрического сопротивления нет.
Но если вы определяете сопротивление в его прямом смысле, конденсатор устойчив к низким частотам, но пропускает токи высокой частоты.
Полное сопротивление (или эквивалентное сопротивление) конденсатора равно $1/\omega C$, где $\omega$ — частота тока, а $C$ — емкость. Для постоянного тока $\omega=0$ и, следовательно, импеданс бесконечен. Но для ненулевых частот он конечен, и, следовательно, могут проходить высокочастотные токи.
$\endgroup$
2
$\begingroup$
Я чувствую, конденсатор имеет бесконечное сопротивление, так как заряд обычно не проходит через конденсатор, он накапливает заряд. Обычно он имеет диэлектрическую среду, которая не проводит электричество. Таким образом, его сопротивление будет таким же, как сопротивление среды. К нему нужно приложить очень высокое напряжение, чтобы протекал ток.
$\endgroup$
6
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Эквивалентные схемы и имитационные модели
Современное измерительное оборудование, такое как анализатор импеданса HP4195A и аналогичные приборы, позволяет компьютеризировать создание эквивалентных схем и их оптимизацию. Постоянные параметры индуктивности L, емкости C и сопротивления R необходимы для моделирования электронных схем. Неправильный подход к определению схемы замещения приводит к ошибочным или некорректным результатам моделирования.
Эквивалентные параметры схемы никоим образом не являются юридически обязывающими, точными наблюдаемыми характеристиками, но показывают пользователю примерное положение основных допусков. Тот факт, что эти данные ранее были недоступны, во многом связан с традициями тестирования и маркетинга, которые в будущем должны быть заменены усилиями по обеспечению удобства для пользователя.
Электронные компоненты, резисторы, конденсаторы, катушки индуктивности, проводники, приближенные к ферритовым материалам и изоляционным материалам могут быть адекватно охарактеризованы параметрами переменного тока.
Условием является то, что их свойства не изменяются заметно при различных уровнях высокого напряжения и тока или чтобы они работали в малом диапазоне сигналов. Затем говорят о линейных компонентах в отличие от нелинейных компонентов, таких как варисторы, диоды, транзисторы и т. д.
Вследствие пространственного размера конструкции компонентов между каждой точкой на поверхности проводника и другой. Проводники генерируют магнитные поля за счет протекания тока и обладают частичной индуктивностью благодаря энергии, запасенной в этих магнитных полях. Конечная проводимость меди, серебра и т. д. или проводимость многослойных резисторов
, генерируемые локально, приводят к частичному сопротивлению. Параллельные проводники также можно рассматривать как участки высокочастотных линий на высоких частотах, обладающие волновым сопротивлением, временем прохождения сигнала и, возможно, затуханием сигнала.
Реальность вообще чрезвычайно сложна. Если бы кто-то захотел нарисовать или даже рассчитать микроскопически тонкую схему со всеми парциальными сопротивлениями, емкостями или индуктивностями, он был бы обречен на неудачу.
К счастью для пользователя, можно легко найти точные эквивалентные схемы для конденсаторов и катушек индуктивности без железных или ферритовых сердечников. Также хорошо описываются аппроксимации других индуктивных составляющих, усредненные параметры которых намного лучше неизвестных характеристик. Реальные значения измерений в виде кривых сравниваются с моделями эквивалентных схем, чтобы продемонстрировать пользователю получение этих значений. Это особенно относится к ферритам ЭМС, с которыми подавляются помехи, но не формируется точная схема.
Конденсаторы → серии резонанс
Рис. 1.39: серии резонансной цепь и импедант на частоту
индуктивность выводов L s (порядка нескольких нГн) и сопротивление дорожек R s (тип. порядка 20 мОм … 100 мОм, для конденсаторов с холодным электролитом до 1 Ом). На низких частотах преобладает емкостная составляющая, на собственной резонансной частоте
сопротивление пути можно измерить.
Выше последовательного резонанса преобладает индуктивная составляющая, на которую в некоторой степени может влиять наличие коротких соединительных длин. Фазовая кривая изменяется от ≈ –90° до ≈ +90° в области резонанса. Таким образом, фазовая точка 0° точно определяет точку резонансной частоты, часто гораздо точнее, чем это возможно при измерении амплитуды. Фазовая кривая также служит для компьютерного определения схемы замещения (1-е приближение).
Индуктивность → Параллельный резонанс
Рис. 1.40: Параллельная схема и импеданс на частоту
Идеальное индуктивное индуктивное давление L P влияет на недоировку для веруния. потери (материал сердечника, потери в обмотке). Для катушек индуктивности желательно бесконечно большое параллельное сопротивление R p , для ЭМС ферритов наоборот очень низкое и широкополосное сопротивление R p — нужный параметр. Индуктивность L p играет меньшую роль и является ключом к преобразованию резистивных потерь в линию.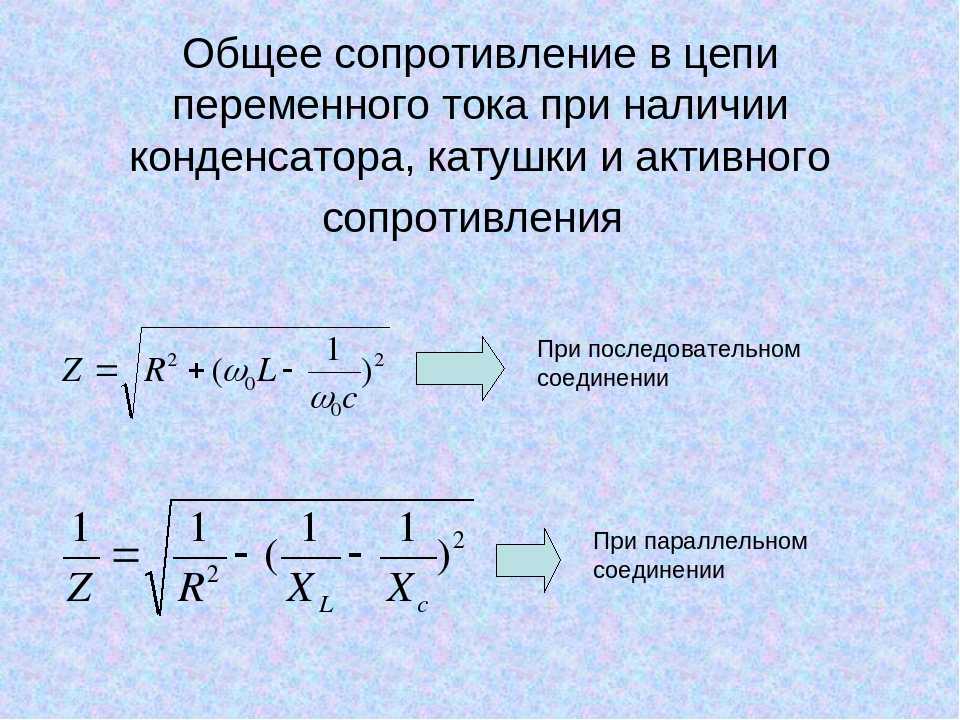
Это означает, что в модели на месте феррита ЭМС разрезана линия и вставлена эквивалентная схема. Компонент точно описывается только всеми тремя параметрами L, C и R. Одного параметра недостаточно, хотя для известных конфигураций можно предсказать другие свойства.
Представьте себе трехмерную систему координат с осями R стр , Л стр , С стр ; компонент представляет собой точку в этом пространстве, а его поле допуска представляет собой прямоугольное тело. Различные компоненты расположены в этом пространстве допусков как разные точки.
Рис. 1.41: Пространство допусков
Эта математическая обработка последовательного и параллельного резонанса может быть резюмирована следующим образом: во все значения L, C и R включены. Стандартизированная расстройка унифицирует параметры добротности и резонансной частоты f РЭС . Это упрощает описание поведения резонансных систем в их диапазоне частот
(Δf … отклонение частоты от резонансной частоты)
Последовательные резонансные контуры:
Рис.
1.42: 1 + jΩ (величина и фаза) в зависимости от Ом
Параллельные резонансные контуры:
5
Параллельный резонанс
Резонансные условия:
для серии резонанса:
для параллельного резонанса:
Нормализованный автономный резонанс:
For Series. v обозначает, насколько резонансный контур расстроен по сравнению с навязанными колебаниями. Вкратце: Мера отклонения частоты (контура) от резонансной частоты (контура).
Нормализованные кривые представлены на рисунках 1.42 и 1.43 для R = 1 (верхняя амплитуда, нижняя фаза).
Подбирая подходящие операнды (нормализация), можно изобразить все характеристики в виде двух стандартных кривых. Они служат для обеспечения общего понимания, тогда как в приложениях оцениваются измеренные резонансные кривые или в компьютерном моделировании числовые значения L, R и C.
Вывод простых эквивалентных схем
В следующих примерах анализируются кривые измерения, полученные с помощью HP 4195.
Однако в принципе не имеет значения, с помощью какого измерительного прибора или конфигурации получаются кривые.
Анализ основан на фундаментальных концепциях теоретического моделирования.
Рис. 1.44: Кривая полного сопротивления катушки с 6 витками на керамическом каркасе ∅ 6 мм
На рисунке 1.44 показано полное сопротивление небольшой воздушной катушки диаметром 6 мм и 6 витками обмотки. Простая оценка индуктивности по значениям на частотах 10 МГц и 100 МГц дала L 63,7 нГн. Поскольку фаза Θ находится в пределах 85°–90°, можно принять чистую индуктивность и получить из |Z| = 4 Ом на частоте 10 МГц и |Z| = 40 Ом на частоте 100 МГц.
Анализатор измеряет L = 58 нГн благодаря более точно сохраненным значениям, чем отображаемые. На рис. 1.44 различимы только две кривые: толстая кривая измерения и одна, построенная анализатором в результате измерения эквивалентной схемы. На самом деле он включает калькулятор эквивалентной схемы. Он вычисляет эквивалентную схему, изображенную на рис.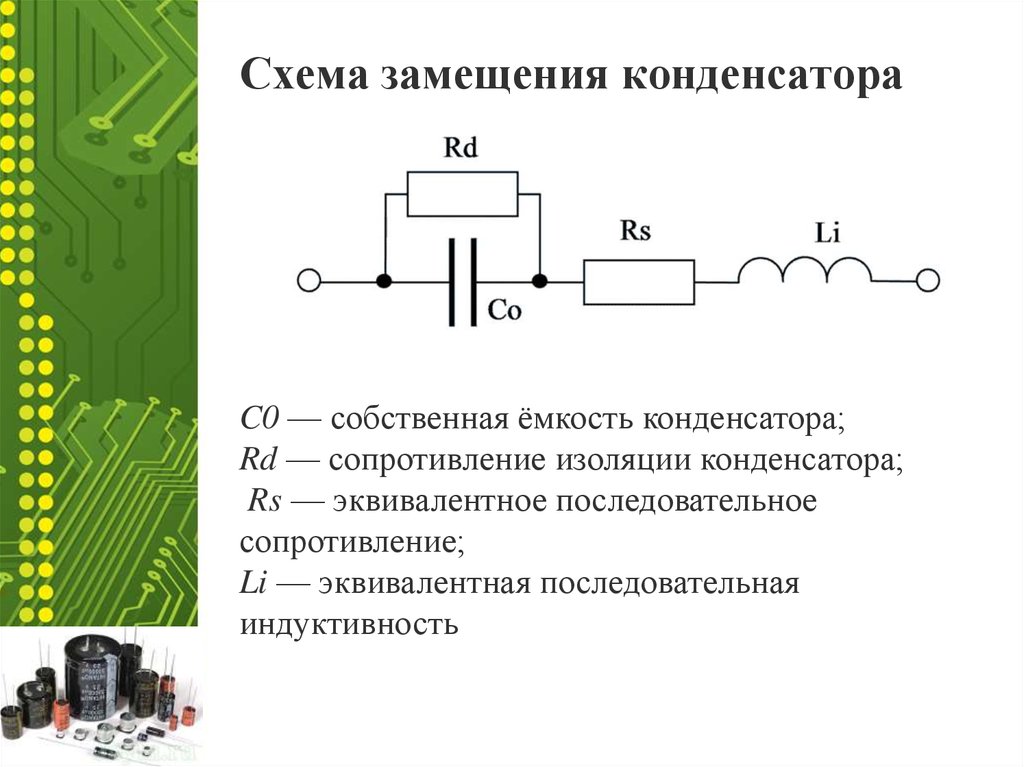
1.44, и записывает рассчитанные значения |Z| и Θ рядом с кривой измерения. Без компьютера пришлось бы довольствоваться лишь грубым расчетом.
В вопросах ЭМС требуются многомерные меры; точность не имеет первостепенного значения.
Рис. 1.45: Кривая полного сопротивления керамического конденсатора емкостью 10 нФ с прибл. Соединительные ножки длиной 5 мм
На рис. 1.45 показана кривая импеданса керамического дискового конденсатора с номинальной емкостью 10 нФ и прибл. Соединительные ножки длиной 5 мм. Читая кривые измерения и вычисляя, можно найти C = 11,37 нФ и L = 9,55 нГн. Из |Z| кривая при Θ = –90° можно рассчитать емкость
, а при Θ = + 90° можно рассчитать индуктивную составляющую
.
|З| 200 кГц = 70 Ом, |Z| 4 МГц ≈ 3,5 Ом, C = 11,37 нФ, |Z| 40 МГц ≈ 2 Ом,
|Z| 200 МГц = 12 Ом и L = 9,55 нГн.
Последовательное сопротивление согласно измерениям составило 33,8 мОм.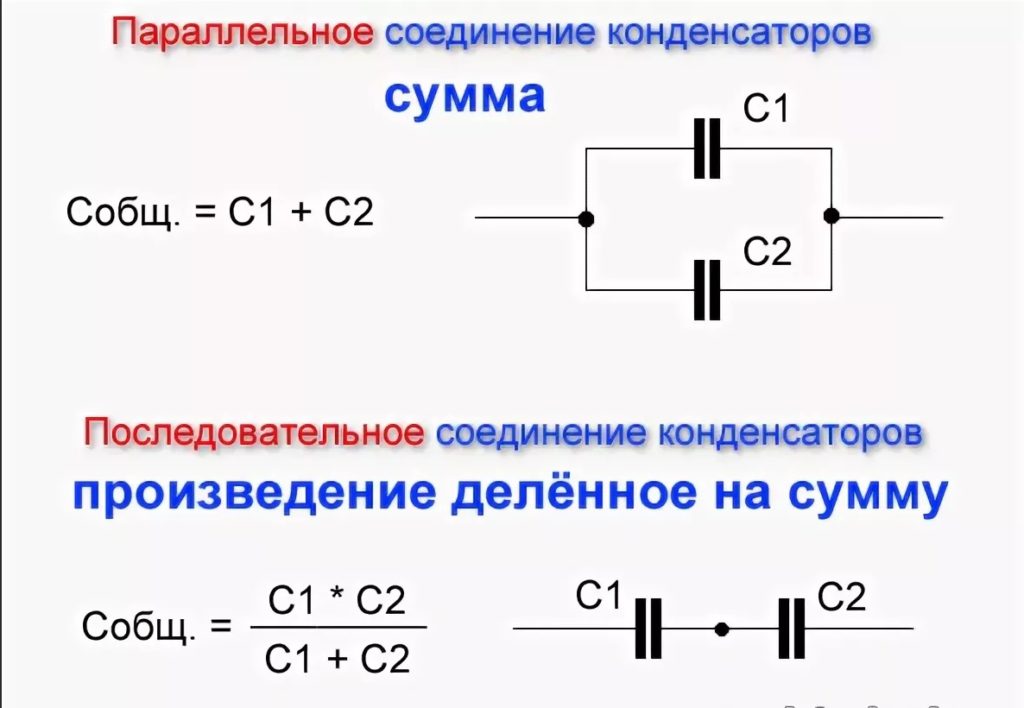
При правильно выбранной схеме замещения (рис. 1.45) анализатор измерил R = 33,7 мОм, C = 11,2 нФ и L = 9 нГн, и совпадающая с ней кривая показала, что никаких дополнительных паразитных параметров схемы замещения, имеющих какое-либо значение, не было. В то время как катушка на рис. 1.45 по-прежнему полезна на частоте 200 МГц, конденсатор
применим только до 30 МГц.
Отсюда видно, насколько важно учитывать линейные индуктивности в связи с блокирующими процессами. Это иллюстрирует пример на рис. 1.46.
Рис. 1.46: Влияние треугольного импульса, возникающего во время фронта переключения в логических схемах, на конденсатор с линейными индуктивностями
Если треугольный импульс достигает «голого» конденсатора без индуктивности, снижение на 25 мВ происходит за 10 нс со скругленным задним фронтом. Индуктивность линии 9Только nH добавляет биполярный импульс с крутым фронтом ±90 мВ, эффект, который наблюдал каждый, кто смотрел на свою линию питания с помощью осциллографа.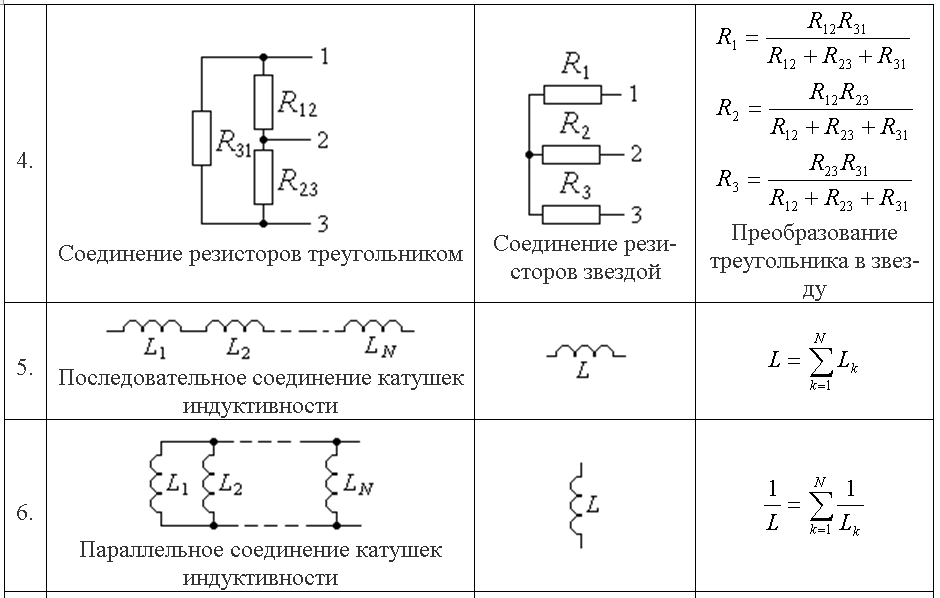
Мало толку заменить 10 нФ на 1 мкФ; если индуктивность остается, шумовое напряжение остается. Чистое изменение заряда конденсатора емкостью 10 нФ за счет треугольного импульса приводит к изменению напряжения ΔU на конденсаторе.
Края тока ΔI/Δt всего при 9 нГн создают биполярный сдвиг напряжения
Рис. 1.47: Кривая импеданса и эквивалентная схема резонансного контура
В качестве примера на Рисунке 1.47 показан резонансный контур, состоящий из катушки и конденсатора, соединенных параллельно с резистором 1 кОм. Анализатор с выбранной структурой A побеждает в эквивалентной схеме. Другие структуры приводят к плохим или бесполезным приближениям. Анализатор в первую очередь пытается приблизиться к фазовой кривой. Можно вручную улучшить параметры и получить новые приближения.
В этом случае индуктивность можно определить по кривой измерения. Емкость может быть найдена только в ограниченной степени. |З| 3 МГц = 4 Ом, |Z| 57,6 МГц = 969 Ом, |Z| 200 МГц = 24 Ом, L p = 207 нГн, R p = 989 Ом, C p = 36,4 пФ.
Тогда помогает условие резонанса:
Результаты анализатора подтверждают расчетные значения.
Рис. 1.48: Эквивалентные типы цепей от HP4195A
Рис. 1.49: Кривые импеданса для параллельного соединения двух разнородных конденсаторов (Легенда об эффективной ВЧ блокировке)
На рис. 1.49 показана кривая импеданса для параллельного соединения 2-х разнородных конденсаторов. Большой конденсатор емкостью 150 нФ был дополнен небольшим конденсатором емкостью 150 пФ для улучшения блокировки по ВЧ. Он должен «сбалансировать» недостаток более длинной линии конденсатора с нагрузкой. Результатом является резонансный пик на частоте 61,57 МГц с Z 59.0 Ом (без нагрузки). Каждый крутой фронт импульса обязательно вызовет длительные затухающие колебания и значительно снизит полезность блокировки.
Получение эквивалентной схемы из |Z| кривых происходит в несколько этапов. Фазовая кривая Q сигнализирует о емкости до 2 МГц (зона I).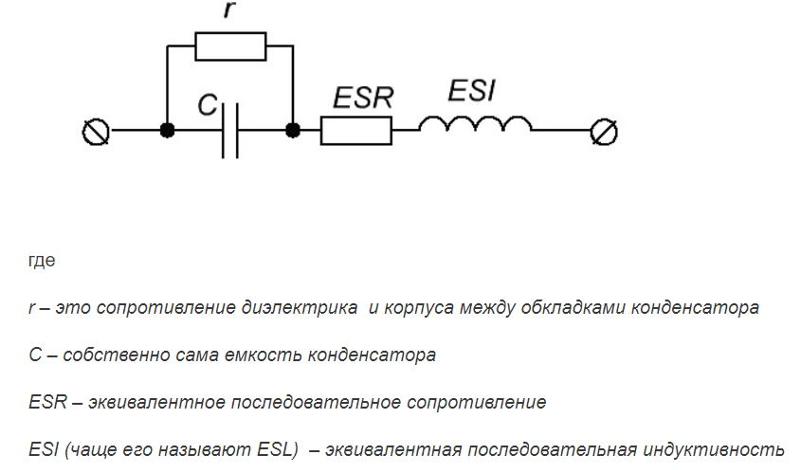
Последовательный резонанс на частоте 2 МГц является следствием прибл. Ножки подключения конденсатора 150 пФ длиной 4 см. Схема индуктивная в зоне II для создания параллельного резонанса с 590 Ом на частоте 60 МГц, где уже нельзя говорить о блокировке. В диапазоне от 30 МГц до 100 МГц (зона III) импеданс превышает 100 Ом и крайне вреден для внутренней связи сигнала. Конденсатор емкостью 150 пФ начинает играть роль за пределами параллельного резонанса и влияет на последовательный резонанс на частоте 154 МГц. Фазовая кривая Q наблюдается в зоне IV.
Расчетные значения
в зоне I |Z| 600 кГц = 2 Ом ∩ 133 нФ,
в зоне II |Z| 20 МГц = 6,5 Ом ∩ 52 нГн,
в зоне III резонанс 61,6 МГц C b = 1/ω 2 · L = 128,6 пФ,
в зоне IV резонанс 154,6 МГц L – 1/ω 2 · C b = 8,25 нГн
Рис. 1.50: Эквивалентная схема двух параллельных подключенных конденсаторов
ABC CLR: Глава L Индукторы Эквивалентные цирки и симуляционные модели — схема Эквивалентные цирмиты и симуляционные модели — схема Эквивалентные цирмиты и симуляционные модели — схема .
