Понятие о переменном токе

Электрический ток бывает постоянным и переменным. Переменный – это ток, в котором среднее значение за период силы и напряжения равно нулю. Такой ток непрерывно изменяется по величине и направлению, и происходят эти изменения через равные промежутки времени.

Периодический переменный ток.

Известно, что, для того чтобы вызвать в цепи переменный ток, используют генераторы переменного тока. В таких генераторах электродвижущая сила (ЭДС) возникает в процессе электромагнитной индукции. В полости цилиндрической формы вращается магнит, называемый ротором, а неподвижный сердечник с его обмоткой называется статором.

Переменный ток применяется в устройствах связи (радио, телевидение, проволочная телефония и пр.), и все это благодаря тому, что напряжение и силу переменного тока можно преобразовывать почти без потери энергии.

Для промышленности и освещения переменный ток вырабатывается генераторами, приводимыми во вращение водяными или паровыми турбинами и двигателями внутреннего сгорания.

Переменный ток бывает однофазным и многофазным. Из многофазных широкое распространение получил трехфазный ток — система переменного тока, состоящая из трех электрических цепей, имеющих одинаковую частоту и электродвижущую силу, сдвинутые по фазе на 120°. Трехфазная система переменного тока применяется в промышленности для питания электродвигателей, электропечей, освещения.

Схема простейшего генератора переменного тока.

При прохождении по проводнику переменный ток выделяет столько же тепла, сколько и постоянный. Время, в течение которого совершается одно колебание, называют периодом (обозначают буквой Т). Состояние переменного тока в отдельные моменты времени называют фазами. А число периодов в секунду – частотой. Единицей частоты является герц (Гц). Если мы говорим, что в одну секунду совершается одно колебание, то частота будет равна 1 Гц.

При помощи выпрямителей переменный ток может быть преобразован в постоянный (для большинства устройств требуется постоянный ток).

Долгое время в электротехнике применялся исключительно постоянный ток. Но потом возникла необходимость в передаче электроэнергии на дальние расстояния. В быту обычно используется переменный ток, поэтому мы расскажем подробнее о нем и его физических характеристиках.

При передаче электроэнергии по проводам в них возникают потери, пропорциональные квадрату тока. Для уменьшения потерь необходимо уменьшить ток. Но для передачи той же мощности при меньшем токе необходимо более высокое напряжение. Поэтому передача электроэнергии на дальние расстояния может быть выполнена только при высоком напряжении.

Преобразование с малыми потерями больших токов низкого напряжения в малые токи высокого напряжения, или наоборот, может производиться лишь посредством электромагнитного аппарата переменного тока — трансформатора. Поэтому в настоящее время преимущественно применяется переменный электрический ток.

Ток, изменяющийся в течение определенного времени по величине и направлению, называется переменным током. Переменный ток, изменяющийся по синусоидальному закону, представляет собой однофазный синусоидальный ток:
i = IM sin (wt + cp),
где IM — амплитудное значение тока.

Промежуток времени, в течение которого осуществляется одно полное колебание, называется периодом Т.

Число периодов в секунду называется частотой, которая выражается формулой

F = 1/Т
Частота измеряется в герцах (Гц).

Величина w = 2яср = 2л/Т называется угловой частотой и измеряется в рад/сек; угол Zwcp называется начальной фазой.

На практике наибольшее распространение получил ток, который изменяется с частотой 50 периодов в секунду, т. е. 50 Гц.

Переменный ток: основные понятия

Господа, мы обсудили основные моменты, касающиеся постоянного тока. Теперь пришло время поговорить про переменный ток. Эта тема немного сложнее постоянного тока и одновременно с этим гораздо интереснее. Сегодня мы коротенечко рассмотрим вопросы, касающиеся переменного тока: что он из себя представляет, как выглядит, чем характеризуется и все в таком духе.

Для начала, призвав на помощь нами всеми любимого капитана Очевидность, введем определение. Как он подсказывает нам,

переменный ток – это такой ток, который изменяется во времени. Изменяться он может по величине, направлению или по тому и другому вместе. Когда мы рассматривали постоянный ток, мы полагали, что в течении всего времени его величина постоянна: если сейчас течет 10 Ампер, то и полчаса назад текло 10 Ампер и через час будет течь 10 Ампер. Если же величина тока меняется (сейчас 10 Ампер в одну сторону, а через некоторое время 5 Ампер в другую сторону), то мы уже имеем дело с током переменным. То есть переменный ток можно рассматривать как некоторую зависимость (функцию) тока от времени: I(t). В каждые моменты времени t

мгн имеет место быть конкретное значение I_мгн=I(t_мгн).

Переменный ток неразрывно связан с переменным напряжением. И если при постоянном токе они были просто связаны между собой через закон Ома, то здесь в общем случае все чуточку сложнее. Как именно сложнее – будем выяснять по ходу новых статей. Нет-нет, не переживайте, если дело касается обычных резисторов, закон Ома все так же продолжает выполняться . Для определенности мы будем в данной статье использовать термин «переменный ток», но все, что здесь сказано, применимо так же и для переменного напряжения: просто меняем I(t) на U(t) и все останется верным.

Переменный ток может быть

периодическим и непериодическим. Периодический – это такой, который через некоторое время, называемое периодом, полностью повторяет свою форму. Ниже на картинках это будет наглядно видно. Непериодический соответственно колбасится как ему вздумается и мы не можем в нем выделить какой бы то ни было период по крайней мере на протяжении времени наблюдения.

На рисунка 1-4 приведены различные виды переменных сигналов. С некоторыми из них позднее мы подробно познакомимся.

Рисунок 1 – Синусоидальный ток

Рисунок 2 – Прямоугольный ток

Рисунок 3 – Треугольный ток

Рисунок 4 – Шум

На всех этих картинках по оси Х у нас время, а по оси Y – величина тока в Амперах.

На рисунке 2 изображен ток, форма которого называется синусом. Такая форма тока является одной из самых важных и мы будем его подробно рассматривать в дальнейшем. А начнем его изучать прямо в этой статье.

На рисунке 3 изображен прямоугольный ток. Он тоже весьма важен и его тоже мы будем потом подробно рассматривать.

На рисунке 4 изображен треугольный ток. И такая форма тока встречается не редко.

На рисунке 5 я изобразил ток хаотичной формы (шумовой). С ним постоянно приходится иметь дело в радиотехнике. В ближайшее время его касаться не планирую, но со временем – вполне возможно.

Это лишь часть возможных форм токов, каждый из которых можно считать переменным. Безусловно, существуют и другие формы, главное, чтобы этот ток менялся во времени.

Знакомство с переменным током мы начнем с синусоидального тока. В общем виде закон изменения этого тока можно описать вот таким вот хитрым выражением

Давайте разберемся что здесь есть что. Для этого взглянем на рисунок 5. Там наглядно все прорисовано.

Рисунок 5 – Синусоидальный ток

А_m называется амплитудой тока. Она показывает, какую максимальную величину имеет синусоидальный ток, а именно величину того «пика», которого достигает синус. Это становится возможным благодаря тому, что

чистый «математический» синус без какого бы то ни было множителя А_m достигает в пике единички. Ясно, что если мы на единичку умножим наше число А_m то получим в пике как раз это самое число А_m. Очевидно, что чем больше А_m, тем большего значения достигает ток.

Величины ω на рисунке 5 нет. Зато на рисунке 5 есть величина f и T. Что же это такое?

Т – это период тока. Это время в секундах, за которое сигнал совершает полный цикл своих изменений. Взглянете на рисунок 5. В точке А ток пересекает ось времени, начинает расти, идет вверх до точки B, где прекращает расти и начинает убывать, снова пересекает ось времени в точке С, идет в отрицательную полуплоскость до точки D, там перестает расти и начинает убывать и становится равным нулю в точке E. Видно, что начиная с точки Е характер изменения тока будет точно таким же, как если бы он начинался с точки А. Посему время, за которое ток изменяется от точки А до точки Е и есть период Т.

Частота f – величина, обратная периоду:

Она показывает сколько периодов (по рисунку 5 – изменений от точки А до точки Е) умещается в одной секунде времени. Соответсвенно чем больше частота, тем меньше пириод и наоборот.

Изменяется частота в герцах. Если частота 1 Гц – это значит, что время изменения тока от точки А до точки Е равно 1 секунда. Если частота, например, 50 Гц (как в наших с вами розетках), это значит, что за 1 секунду успевает произойти 50 полных циклов изменения тока от точки А до точки Е. Если частота 2,4 ГГц (как в некоторых процессорах, и, кроме того, на такой частоте работает всеми нами любимый Wi-Fi), это значит, что за 1 секунду сигнал претерпевает аж 2,4 миллиарда итераций от точки А до точки Е!

С периодом Т (и, соответственно, с частотой f) плотно связана другая величина – как раз та самая ω, которая стоит в нашей формуле под синусом. Называется она круговая частота и связана она следующим образом

 

Ох ты ж блин. Чем дальше – тем хуже. Какие-то π откуда-то повылазили. Откуда они тут вообще и что забыли?! Давайте разберемся.

Господа, надеюсь, вы помните из курса математики, что синус – сама по себе функция периодическая и период синуса как раз равен 2·π радиан. Ну или 360°, что тоже самое, однако я предпочитаю обычно вести расчет в радианах. То есть для простого классического математического синуса расстояние от точки А до точки Е равно 2·π=6,28 радиан. Как же теперь увязать эти радианы со временем и с нашим периодом? Ведь в нашем графике тока у нас по оси Х именно время, а не радианы. Очень просто. Полагаем, что 2·π радианам соответствует наш период Т. Для того же, чтобы посчитать скольки радианам соответствует произвольное время t₁ надо выполнить следующее преобразование: . Знаю, звучит запутанно, поэтому давайте разберем на примере. Давайте запишем зависимость тока от времени для периода Т=4 секунды. Как будет выглядеть преобразованная формула синуса для этого случая? Как-то так

 

Изображаем это на рисунке 6.

Рисунок 6 – Синусоидальный ток с периодом 4 секунды

Видите, все честно, на графике наглядно видно, что период синуса равен, как мы и хотели, четырем секундам.

Итак, с амплитудой разобрались, с круговой частотой вроде тоже. Осталось последнее – φ₀ – начальная фаза. Что же это такое? Все просто, господа. Фаза здесь – это просто сдвиг графика тока по временной оси. То есть график тока будет стартовать не с нуля, а с какого-то другого значения. Действительно, если мы в нашу формулу для зависимости тока от времени подставим время, равное нулю, то получим

Из этого выражения очевидно еще и то, что фаза измеряется в градусах или радианах: только градусы или радианы имеют право стоять под синусом.

Давайте возьмем наш график тока с периодом Т=4 секунды и положим, что начальная фаза равна 30° или, что тоже самое, 0,52 радина. Имеем

Построим график для данного случая на рисунке 7.

Рисунок 7 – Синусоидальный ток с периодом 4 секунды и начальной фазой 30°

Внимательный читатель, посмотрев попристальнее на график, изображенный на рисунке 7, скажет: так фаза вообще какая-то скользкая штука. Она ж зависит от того, где мы поставим нолик, то есть когда начнем наблюдать сигнал. И вообще может быть чуть ли не любой. Господа, замечание абсолютно верно! Сама по себе как таковая фаза достаточно редко когда интересна. Гораздо интереснее разность фаз между несколькими сигналами. Взгляните на рисунок 9. На нем изображены два графика: один зеленый имеет начальную фазу в φ_{0_зелен}=90°, а второй синий – φ_{0_син}=90°. Разность фаз между ними

 

Рисунок 8 – Два сигнала, сдвинутые по фазе

И заметьте, господа, эта разность фаз одна и таже всегда для любой точки этих графиков. Без привязки к нулю и к началу. Вот это уже гораздо интереснее и может много где пригодиться.

Вообще фаза такая штука, что как-то традиционно на нее обращается не очень много внимания, между тем, как на самом деле это очень важная величина. Фазовая модуляция, трехфазные цепи, фазированные антенные решетки, фазовые системы автоподстройки частоты, когерентная обработка сигналов – вот лишь малая область систем, где фаза сигнала является одним из главнейших факторов. Поэтому, господа, постарайтесь с ней подружиться .

На сегоня заканчиваем, господа. Сегодня была вводная статья в мир переменного тока. Дальше будем разбираться в нем более подробно. Всем вам большой удачи, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Понятие о переменном токе — Основы электроники

До сих пор мы рассматривали электрический ток, направ­ление и сила которого оставались постоянными, т. е. не изме­нялись с течением времени. Такой ток мы называли постоян­ным. При постоянном токе электроны движутся по проводнику все время в одном и том же направлении (если не считать хаотического теплового движения электронов), причем количе­ство движущихся электронов и скорость, их движения все время остаются постоянными.

Условное графическое изображение постоянного тока при­ведено на рисунке 1.

Рисунок 1. График переменного тока.

Переменный ток отличается от постоянного тем, что он периодически изменяет свое направление, т. е. течет по про­воднику то в одну, то в другую сторону.

Переменный ток можно получить при помощи очень про­стой схемы, изображенной на рисунке 2а. При каждом передви­жении переключателя изменяется лишь направление тока в цепи, сила же тока при этом остается все время неизменной.

Рисунок 2. Простейший способ получения переменного тока а) и его график б).

Графическое изображение переменного тока, полученного таким способом, приведено на рисунке 2б, где ток, протекающий по проводнику в одном направлении, отложен над горизонтальной осью времени, а ток обратного направления — под осью времени.

Рассмотрим другой, белее распространенный случай пере­менного тока, когда изменяется не только направление тока, но и его сила.

Представим себе проводник, согнутый в виде рамки и вра­щающийся в равномерном магнитном поле (рисунок 3).

Рисунок 3. Рамка вращающаяся в равномерном магнитном поле.

При вращении рамки магнитный поток, охватываемый ею, будет изменяться, следовательно, в рамке возникнет ЭДС индук­ции. В этом случае форма ЭДС индукции возникающей в рамке, а при подключению нагрузки к ней и форма переменного электрического тока текущего по цепи будет иметь вид показанный на рисунке 4, то есть изменение переменного тока будет осуществляться по закону синиуса.

Рисунок 4. График синусоидального переменного тока.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Основные понятия об электрических цепях переменного тока

ЭЛЕКТРИЧЕСКИЕ цепи переменного тока

Урок 5

Тема урока: Получение переменного тока. Основные понятия и определения, изображение переменного тока

Цель урока: формирование знаний по теме, воспитывать познавательный интерес; расширять кругозор учащихся; развивать мышление и память.

Теоретическая часть

Переменный ток, в отличие от тока постоянного, непрерывно изменяется как по величине, так и по направлению, причем изменения эти происходят периодически, т. е. точно повторяются через равные промежутки времени.

Чтобы вызвать в цепи такой ток, используются источники переменного тока, создающие переменную ЭДС, периодически изменяющуюся по величине и направлению. Такие источники называются генераторами переменного тока.

На рисунке показана схема устройства (модель) простейшего генератора переменного тока.

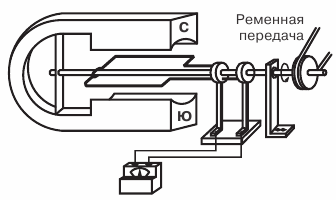
Прямоугольная рамка, изготовленная из медной проволоки, укреплена на оси и при помощи ременной передачи вращается в поле магнита. Концы рамки припаяны к медным контактным кольцам, которые, вращаясь вместе с рамкой, скользят по контактным пластинам (щеткам).

Магнит создает между своими полюсами равномерное магнитное поле, в котором плотность магнитных силовых линий в любой части поля одинаковая. Вращаясь, рамка пересекает силовые линии магнитного поля, и в каждой из ее сторон а и б индуктируются ЭДС.

Стороны в и г рамки — нерабочие, так как при вращении рамки они не пересекают силовых линий магнитного поля и, следовательно, не участвуют в создании ЭДС.

В любой момент времени ЭДС, возникающая в стороне а, противоположна по направлению ЭДС, возникающей в стороне б, но в рамке обе ЭДС действуют согласно и в сумме составляют обшую ЭДС, т. е. индуктируемую всей рамкой. В этом можно убедиться, если использовать для определения направления ЭДС известное как правило правой руки.

Для этого надо ладонь правой руки расположить так, чтобы она была обращена в сторону северного полюса магнита, а большой отогнутый палец совпадал с направлением движения той стороны рамки, в которой мы хотим определить направление ЭДС. Тогда направление ЭДС в ней укажут вытянутые пальцы руки.

Для какого бы положения рамки мы ни определяли направление ЭДС в сторонах а и б, они всегда складываются и образуют общую ЭДС в рамке. При этом с каждым оборотом рамки направление общей ЭДС изменяется в ней на обратное, так как каждая из рабочих сторон рамки за один оборот проходит под разными полюсами магнита.

Величина ЭДС также изменяется, так как изменяется скорость, с которой стороны рамки пересекают силовые линии магнитного поля. Действительно, в то время, когда рамка подходит к своему вертикальному положению и проходит его, скорость пересечения силовых линий сторонами рамки бывает наибольшей, и в рамке индуктируется наибольшая ЭДС. В те моменты времени, когда рамка проходит свое горизонтальное положение, ее стороны как бы скользят вдоль магнитных силовых линий, не пересекая их, и ЭДС не индуктируется.

Таким образом, при равномерном вращении рамки в ней будет индуктироваться ЭДС, периодически изменяющаяся как по величине, так и по направлению. ЭДС, возникающую в рамке, можно измерить прибором и использовать для создания тока во внешней цепи. Используя явление электромагнитной индукции, можно получить переменную ЭДС и, следовательно, переменный ток.

Переменный ток для промышленных целей и для освещения вырабатывается мощными генераторами, приводимыми во вращение паровыми или водяными турбинами и двигателями внутреннего сгорания.

Графическое изображение переменного тока

Построение графиков переменных величин, меняющихся с течением времени, начинают с построения двух взаимно перпендикулярных линий, называемых осями графика. Затем на горизонтальной оси в определенном масштабе откладывают отрезки времени (или угол поворота рамки), а на вертикальной, также в некотором масштабе, — значения той величины, график которой собираются построить (ЭДС, напряжения или тока).

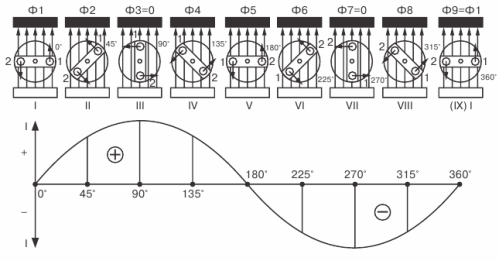
Полученная волнообразная кривая называется синусоидой, а ток, ЭДС или напряжение, изменяющиеся по такому закону, называются синусоидальными.

Синусоидальный характер изменения тока — самый распространенный в электротехнике, поэтому, говоря о переменном токе, в большинстве случаев имеют в виду синусоидальный ток.

Для сравнения различных переменных токов (ЭДС и напряжений) существуют величины, характеризующие тот или иной ток. Они называются параметрами переменного тока.

Переменный ток характеризуется периодом, амплитудой и частотой.

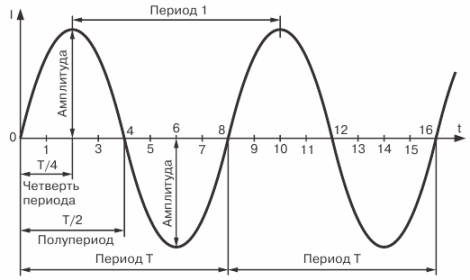
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.

Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока. Общепринятые обозначения амплитуд тока, ЭДС и напряжения — Im, Em и Um.

Значение переменного тока (ЭДС, напряжения), соответствующее любому выбранному моменту времени, называется его мгновенным значением (i, u, е соответственно).

Мгновенное значение тока, как и амплитудное его значение, легко определить с помощью графика. Для этого из любой точки на горизонтальной оси, соответствующей интересующему нас моменту времени, проведем вертикальную линию до точки пересечения с кривой тока; полученный отрезок вертикальной прямой определит значение тока в данный момент, т. е. мгновенное его значение.

Число полных периодов, совершаемых током в 1 секунду, называется частотой переменного тока и обозначается латинской буквой f. Чтобы определить частоту переменного тока, т. е. узнать, сколько периодов своего изменения ток совершил в течение 1 секунды, необходимо 1 секунду разделить на время одного периода f = 1/T. Частота переменного тока измеряется единицей, называемой герцем.

При определении сопротивления различных цепей переменному току использовать еще одна вспомогательную величину, характеризующую переменный ток, так называемую угловую или круговую частоту.

Круговая частота обозначается буквой ω, измеряется в радианах и связана с частотой соотношением

ω = 2πf

В общем виде в момент времени t=0 мгновенное значение переменных величин можно записать в виде:

i = I_m sin ωt ,

u = U_m sin ωt,

е = Е_msin ωt.

При этом начальный период времени t=0 совпадает с нулевыми значениями функций. Но в общем случае на оси времени можно выбрать любой момент отсчета, тогда формулы мгновенных значений будут иметь вид:

i = I_m sin(ωt + φ_i),

u = U_m sin(ωt +φ_u),

е = Е_m sin(ωt +φ_е),

где φ_i,_{φu,φе – начальный фазовый угол или начальная фаза.}

Временно́й сдвиг между максимальными значениями в разных витках определяется разностью фаз:

Если для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если начальные фазы одинаковые и их разность равна 0, то это означает. Что они совпадают по фазе.

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений из-за емких расчетов. Для этих целей ввели понятие действующих значений тока, напряжения.

Действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электрические приборы показывают действующие значения переменных величин, которые обозначаются прописными буквами без индексов (I, U, Е).

; ;

Вопросы для самопроверки:

— Объясните понятие «переменный ток».

— Что такое амплитуда переменного тока?

— Что такое частота тока? Единицы измерения частоты?

— Что такое угловая частота? Единицы измерения угловой частоты?

— Что такое разность фаз?

— В чем разница между действующими и амплитудными значениями синусоидальных величин?

— Запишите и расшифруйте математическое выражение мгновенного синусоидального тока.

— Запишите и расшифруйте математическое выражение мгновенного синусоидального напряжения.

Практическая часть:

Пример 1. Определите угловую частоту, если частота сети равна 50Гц? 60Гц? 1кГц?

Пример 2. Амперметр показывает значение 10А. Определите амплитудное (максимальное) значение тока и запишите мгновенное значение тока (фазовый угол равен нулю).

Пример 3. Мгновенное значение напряжение равно u=282sin(ωt-47). Определить действующее значение и начальную фазу напряжения.

Урок 6

Тема урока: Элементы электрической цепи синусоидального тока.

Цель урока: расширение и обобщение знаний по теме, применение теоретических знаний на практике; развитие памяти и логики.

Теоретическая часть

На любом участке цепи переменного тока одновременно осуществляются необратимые процессы преобразования электрической энергии в другие виды и проявляется действие переменного электромагнитного поля.

При решении большинства электротехнических задач вводят допущения, которые позволяют раздельно учитывать каждое из явлений и упрощают задачу расчета электрических цепей переменного тока.

1. Цепь с идеальным резистивным элементом.

Рассмотрим, например, процессы, происходящие в обыкновенной лампе накаливания, включенной в сеть переменного тока. Между отдельными витками нити накаливания существует электрическая емкость, и нить обладает определенной индуктивностью, но они незначительны. Поэтому считают, что С=0 и L=0. В этом случае при анализе электрической цепи лампу называют идеальным резистивным элементом цепи с сопротивлением R.

Величина сопротивления переменному току больше, чем сопротивлению постоянному току, за счет неравномерного распределения тока в проводе (поверхностный эффект). Поэтому в отличие от сопротивления постоянному току сопротивление в цепи переменного тока называют активным сопротивлением. Активное сопротивление измеряется в омах.

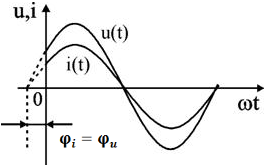
Если напряжение u = U_msinωt),подключить к сопротивлению R, то через него протекает ток

Это показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе: .

Напряжение, совпадающее по фазе с током, называют активным напряжением и обозначают U_a.

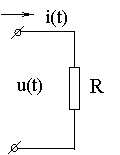
2. Цепь с идеальным индуктивным элементом.

Примером идеального индуктивного элемента может служить индуктивная катушка. Электрическая энергия, выделяемая в катушке за счет нагрева провода обмотки, как правило, невелика, как и межвитковая емкость, и во многих практических случаях ими можно пренебречь (R=0, C=0). При принятых допущениях индуктивную катушку называют идеальным индуктивным элементом цепи или L-элементом.

Параметром идеального индуктивного элемента является индуктивность L, а энергетические процессы в нем определяются только явлениями, происходящими в магнитном поле.

Индуктивность — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур. На электрических схемах используют условные графические обозначения катушек индуктивностей, примеры которых приведены на рисунке.

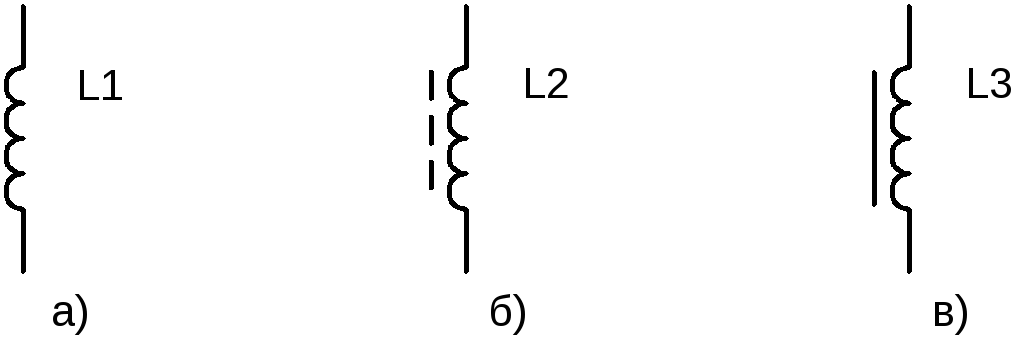
Условные графические обозначения индуктивностей:

а – обозначение катушки индуктивности; б – с магнитодиэлектрическим сердечником;

в – с ферромагнитным сердечником

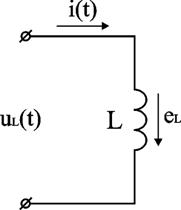
При прохождении электрического тока по катушке, ток создаст переменный магнитный поток Ф. Силовые линии этого потока, пересекая витки катушки, будут индуктировать в ней э.д.с. самоиндукции. По закону электромагнитной индукции

e_L=

Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+e_L=0, т. е. u = -e_L Следовательно, напряжение источника всегда равно по величине и противо-положно по направлению э. д. с. самоиндукции.

Если в формулу подставить значение тока и продифференцировать, то получим:

Обозначим величину ωL· равной амплитуде напряжения U_m. Тогда по закону Ома

Величину называют индуктивным сопротивлением, измеряют в Омах и обозначают

Так как , то начальную фазу напряжения можно представить как φ _u= φ _i+ 90 и, следовательно,

Выведенное соотношение показывает, что если в катушке протекает синусоидальный ток, то напряжение также имеет синусоидальный характер, но при этом оно опережает ток на четверть периода (90).

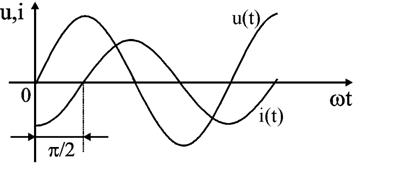
3. Цепь с идеальным емкостным элементом

Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость (С). Этот параметр является коэффициентом пропорциональности между зарядом q (Кл) и прикладываемым напряжением u (В).

q = C·u,

При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток

Идеализированный конденсатор обладает только ёмкостью С (R=0, L=0).

Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом. Пусть напряжение источника изменяется по закону u = Um·sinωt, (φ_u = 0).

В цепи возникает ток

 Из полученного выражения видно, что начальная фаза тока φ_i = . Угол сдвига фаз между напряжением и током составляет

Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол 90. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.

Амплитуда тока будет равна Im = ω·C·Um=.

Величину называют ёмкостным сопротивлением конденсатора и измеряют в Омах 

Xc=1/ ω•C =1/2πfC.

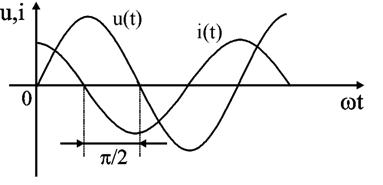
Итак, в цепях переменного тока выделяют следующие виды сопротивлений:

— активное (активным называют сопротивление резистора). Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты сети.

— реактивное (индуктивное X_L и емкостное Х_С). Единицей измерения индуктивного и емкостного сопротивления также является Ом. Величина индуктивного сопротивления линейно зависит от частоты. А величина ёмкостного сопротивления обратнопропорциональна частоте сети. В цепях со смешанным соединением нагрузки (активной, индуктивной, ёмкостной) реактивным сопротивлением цепи называют величину

X = X_L — X_C.

Для того, чтобы найти общее сопротивление электрической цепи со смешанным соединением нагрузки используют понятие полного сопротивления цепи, которое определяется как

Вопросы для самопроверки:

— Объясните физический смысл активного сопротивления проводника переменному току по сравнению с сопротивлением проводника постоянному току?

— Что такое индуктивность катушки? От чего она зависит?

— Что понимается под действующим значением переменного синусоидального тока? Как его рассчитать через амплитудное значение тока?

— Опишите физические явления, наблюдаемые в резисторе в цепи переменного синусоидального тока?

— Запишите математическую связь между мгновенным напряжением, мгновенным током и активным сопротивлением?

— Запишите математические выражения мгновенного напряжения и тока на активном сопротивлении, приняв начальную фазу напряжения φ=45.

— Что понимается под углом сдвига фаз? Чему он равен на участке цепи с резистором? индуктивностью? ёмкостью?

— Как рассчитать индуктивное сопротивление идеальной катушки?

— Запишите математическое выражение мгновенного напряжения на индуктивном сопротивлении, приняв начальную фазу тока φ=45.

— Объясните физический смысл ёмкостного сопротивления. Как рассчитать ёмкостное сопротивление идеального конденсатора?

— Чему равен угол сдвига фаз в ёмкости?

— Что понимается под термином реактивное сопротивление? Как его определить?

— Как в сети переменного тока определяется полное сопротивление?

Практическая часть:

Пример 1. В цепи переменного тока к резистору подведено напряжение u=141sin(t-30)В. Сопротивление идеального резистора равно 100 Ом. Определить амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Пример 2. К идеальной катушке подведено напряжение u=141sin(t+73)В. Частота тока в сети равна 50Гц. Индуктивность катушки равна 12,7 мГн. Определить индуктивное сопротивление катушки, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Пример 3. К идеальному конденсатору подведено напряжение u=282sin(t+30)В. Частота тока в сети равна 50Гц. Ёмкость конденсатора равна 159мкФ. Определить ёмкостное сопротивление конденсатора, амплитуду и начальную фазу тока; записать мгновенное и действующее значение тока.

Урок 7

Тема урока: Неразветвленные цепи переменного тока. Мощность цепи синусоидального тока. Коэффициент мощности.

Цель урока: получение практического навыка расчета элементов цепи переменного тока; расширение знаний о физических явлениях в реальной катушке и реальном конденсаторе.

Теоретическая часть

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и ёмкостное сопротивление.

1. Цепь с активно-индуктивным сопротивлением.

Фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока.

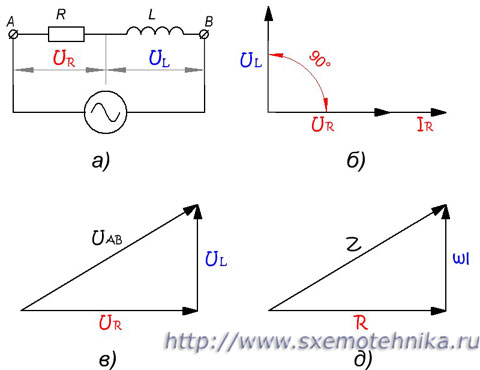
Полное сопротивление цепи с активным сопротивлением и индуктивностью

а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений

Произведем геометрическое сложение радиусов-векторов U_L и U_R. Результирующий вектор U_AB будет являеться гипотенузой прямоугольного треугольника. Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление. Разделим обе части уравнение на

Извлекая квадратный корень из обеих частей этого равенства, получим,

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений

2. Цепь с активно-ёмкостным сопротивлением.

Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений.

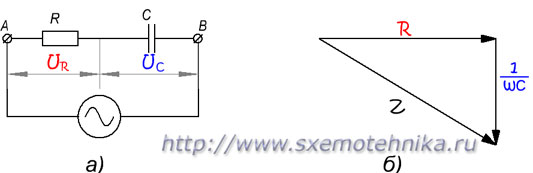
Полное сопротивление цепи с активным сопротивлением и емкостью

а) — схема цепи; б) — треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его

В общем случае, когда цепь содержит все три вида сопротивлений, сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

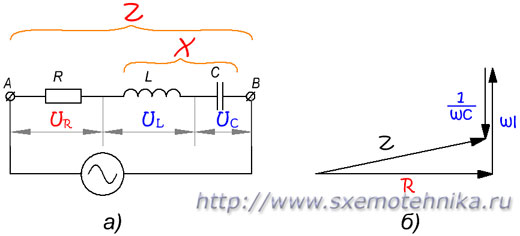
Полное сопротивление цепи содержащей R, L и C

а) — схема цепи; б) — треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений преобладает.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

3. Параллельное соединение активного и реактивного элемента

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно, нужно сначала вычислить проводимость каждой из параллельных ветвей.

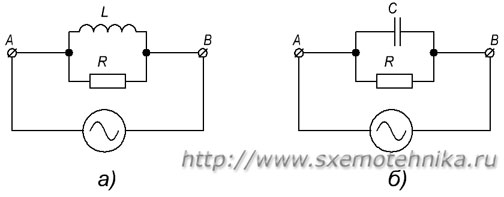
Полное сопротивление цепи при параллельном соединении активного и реактивных элементов

а) — параллельное соединение R и L; б) — параллельное соединение R и C.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

откуда:

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С :

Мощность цепи синусоидального тока

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.

Пусть мгновенные напряжение и ток определяются по формулам:

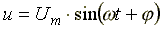
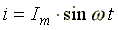
Тогда

Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.

Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе 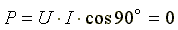, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90. В реактивных элементах не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Реактивная мощность, измеряемая в вольтамперах реактивных (Вар), расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

, ВА

В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Коэффициент мощности и его экономическое значение

Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cosφ = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cosφ = 0,25-0,3).

Коэффициент мощности учитывают при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Коэффициент мощности повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов.

Практическая часть

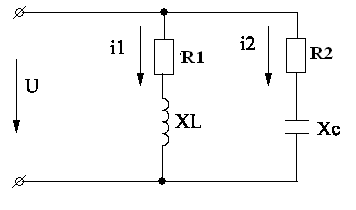
Задача. Катушка с активным сопротивлением R1=200 Ом и индуктивностью L=0,24 Гн соединена параллельно с конденсатором, активным сопротивлением R2=70 Ом и емкостью С=8*10^-6Ф и подключена к источнику переменного тока с частотой f=200 Гц и амплитудным значением напряжения Um=300 В. Определить действующее значение токов в каждой ветке и общее значение тока в цепи, полное сопротивление цепи, полную, активную и реактивную мощности. Построить векторную диаграмму тока и напряжения.