Сумматоры. Полусумматоры и полные сумматоры. Параллельный сумматор с параллельным переносом. Сумматор-вычитатель
3.5 Сумматоры
Комбинационный сумматор – это цифровое устройство, предназначенное для арифметического сложения чисел, представленных в виде двоичных кодов.
Обычно сумматор представляет собой комбинацию одноразрядных сумматоров. При сложении двух чисел в каждом разряде производится сложение трех цифр: цифры первого слагаемого Ai, цифры второго слагаемого Bi и цифры переноса из младшего разряда Pi-1. В результате суммирования на выходных шинах получается сумма S i и перенос в старший разряд P i.
Сумматоры с поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда.
Например, К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8
необходимо взять две микросхемы и соединить их последовательно по цепи
переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации, однако имеет низкое быстродействие. Время выполнения операции зависит от разрядности так как включает в себя затраты времени на вычисление во всех более младших разрядах и выполнение в них переносов.
Для повышения быстродействия используются сумматоры с параллельным переносом.
По числу входов различают: полусумматоры, полные сумматоры.
Полусумматор
Полусумматор (Half Summator) складывает два числа самого младшего разряда A, B без учета переноса. Результат сложения S и перенос в старший разряд P (рис.1) значения, которых представлены в таблице истинности (табл.1).
и его функциональная схема, (б).
Таблица истинности полусумматора Таблица 1
Набор | Первое слагаемое | Второе слагаемое | Результат | |
Перенос | ||||
A | B | S | P | |
1 | 0 | 0 | 0 | 0 |
2 | 0 | 1 | 1 | 0 |
3 | 1 | 0 | 1 | 0 |
4 | 1 | 1 | 0 | 1 |
Из таблицы 1
следует, что, если A = 1
и B = 1, то происходит
переполнение разряда S = 0 и вырабатывается
сигнал переноса в старший разряд P =
1.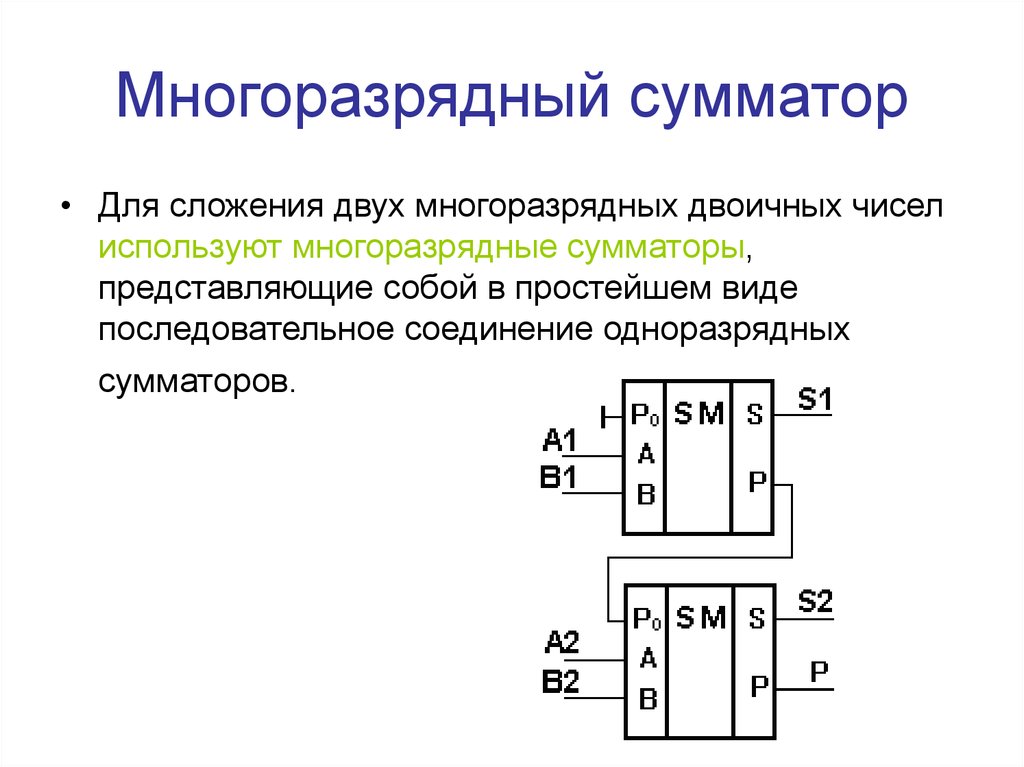
Вывод: максимальное значение результата сложения на полусумматоре с учетом переноса равно: A0 + B0 = 12+12 = 102 = 210, где P0 = 1, S0 = 0.
Аналитические выражения выходных сигналов:
Полный сумматор
Одноразрядный полный сумматор (Summator) имеет три входа: для разряда слагаемого An, разряда слагаемого Bn и входного сигнала переноса из младшего разряда Pn-1.
Результат
сложения Sn и перенос в
старший разряд Pn (рис.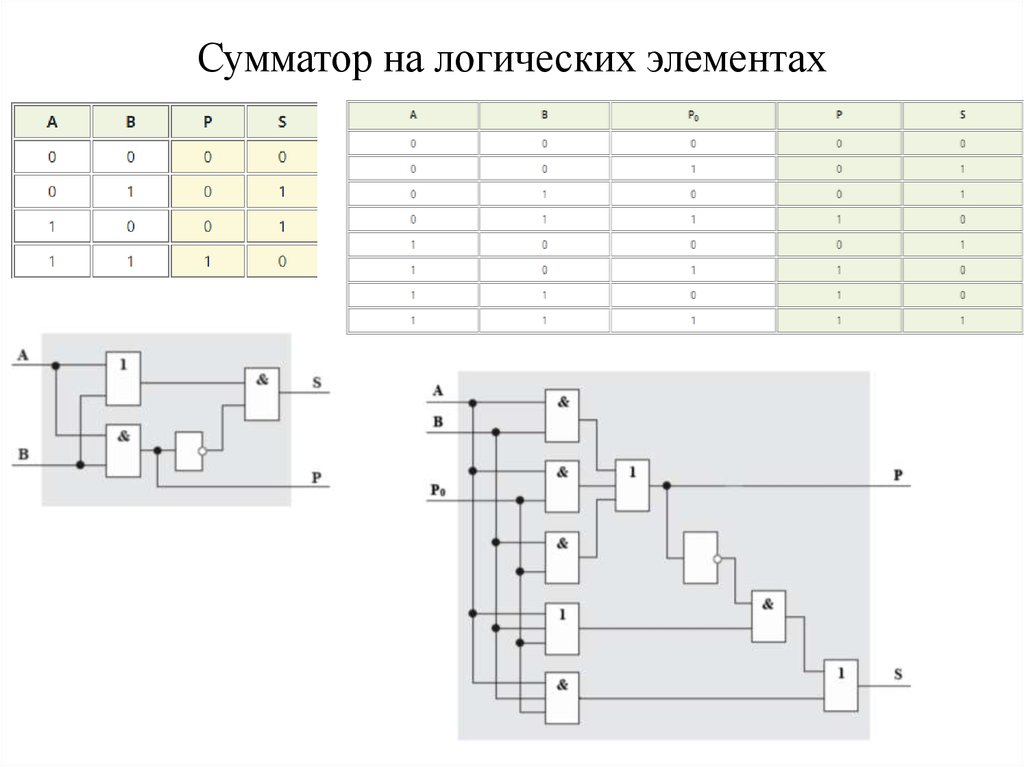
Рис. 2 Обозначение одноразрядного полного сумматора, (а),
и его функциональная схема на полусумматорах, (б).
Вместо элемента 2ИЛИ можно использовать третий полусумматор, у которого S = P n.
Таблица истинности одноразрядного полного сумматора Таблица 2
Набор | Первое слагаемое | Второе слагаемое | Перенос | Результат | |
Сумма | Перенос | ||||
An | B n | S n | P n | ||
1 | 0 | 0 | 0 | 0 | 0 |
2 | 0 | 0 | 1 | 1 | 0 |
3 | 0 | 1 | 0 | 1 | 0 |
4 | 0 | 1 | 0 | 1 | |
5 | 1 | 0 | 0 | 1 | 0 |
6 | 1 | 0 | 1 | 0 | 1 |
7 | 1 | 1 | 0 | 0 | 1 |
8 | 1 | 1 | 1 | 1 | 1 |
Вывод: сложение в двоичной системе производится с учетом переноса из младшего разряда
аналогично «сложению в столбик» в десятичной системе.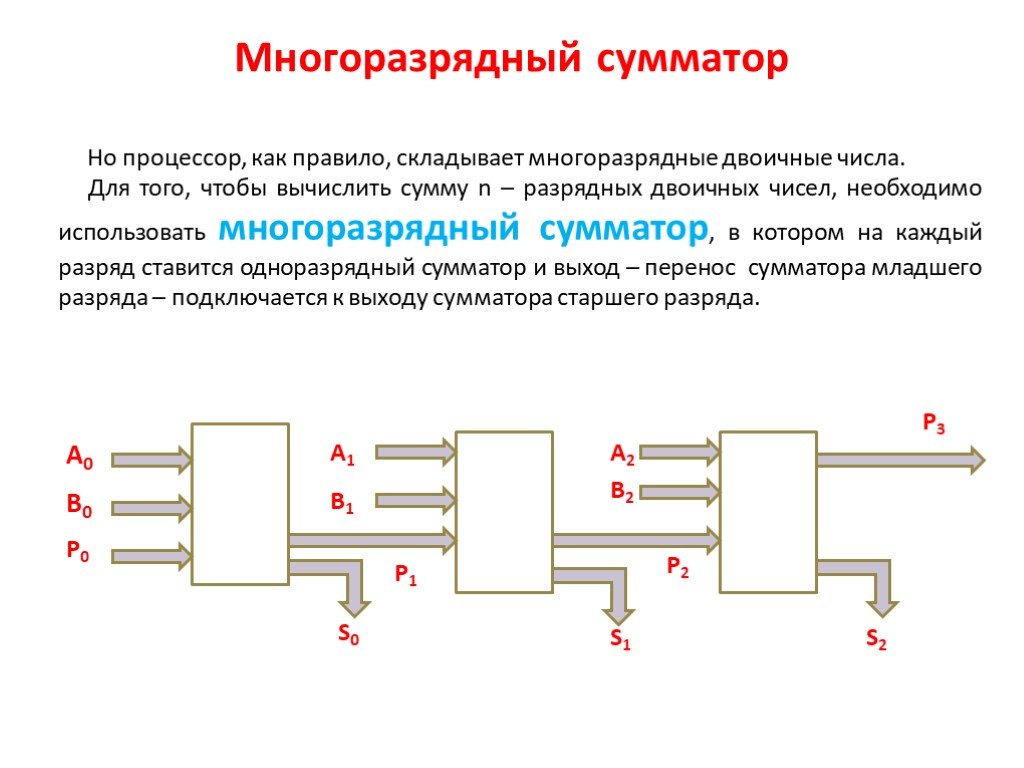 При этом максимальное
значение результата сложения в одном разряде с учетом переносов равно: An + Bn + Pn—1 = 12+12+12 =
112 = 310, где Pn= 1, Sn = 1.
При этом максимальное
значение результата сложения в одном разряде с учетом переносов равно: An + Bn + Pn—1 = 12+12+12 =
112 = 310, где Pn= 1, Sn = 1.
Как видно из карт Карно, функция результата не минимизируется, а функция переноса упрощается (табл. 3), что сделано также в аналитическом виде и реализовано на логических элементах (рис. 3).
Из таблицы истинности следуют выражения для сигналов:
(1)
Карта Карно для Sn Карта Карно для Pn Таблица 3
An Bn Pn-1 | 00 | 01 | 11 | 10 | An Bn Pn-1 | 00 | 01 | 11 | 10 |
0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Рис.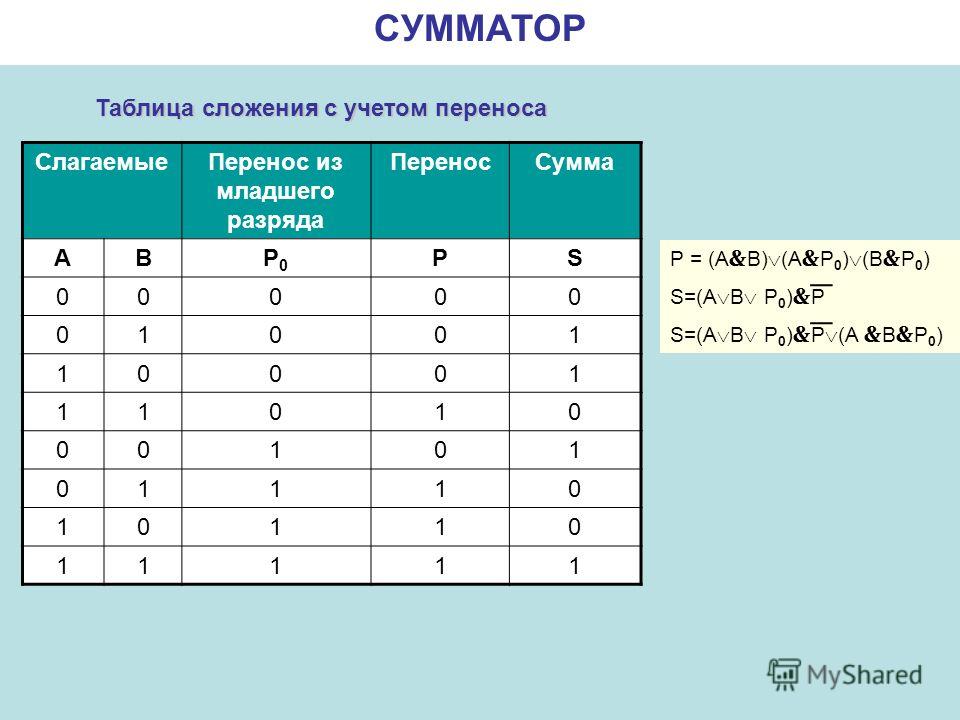 3 Принципиальная
схема одноразрядного полного сумматора
3 Принципиальная
схема одноразрядного полного сумматора
на элементах И, ИЛИ, НЕ: получение суммы (а), и переноса, (б).
Параллельный многоразрядный сумматор состоит из n одноразрядных сумматоров (рис. 4). Входные сигналы подаются на одноразрядные сумматоры одновременно. Если появляются сигналы переноса, то они поступают в старший разряд.
Вывод: пока не состоится сложение в младшем разряде и не определится значение переноса не может быть определена сумма в разряде более старшем.
Максимальное значение результата сложения с учетом переносов: Pn, Sn= 112 = 310.
Рис. 4 Параллельный многоразрядный сумматор
При использовании обратного кода перенос из самого старшего разряда подается на вход переноса самого младшего разряда. В остальных случаях на вход самого младшего разряда подается логический ноль.
Сумматоры с
поразрядным переносом выпускаются в виде микросхем на 2 и 4 разряда.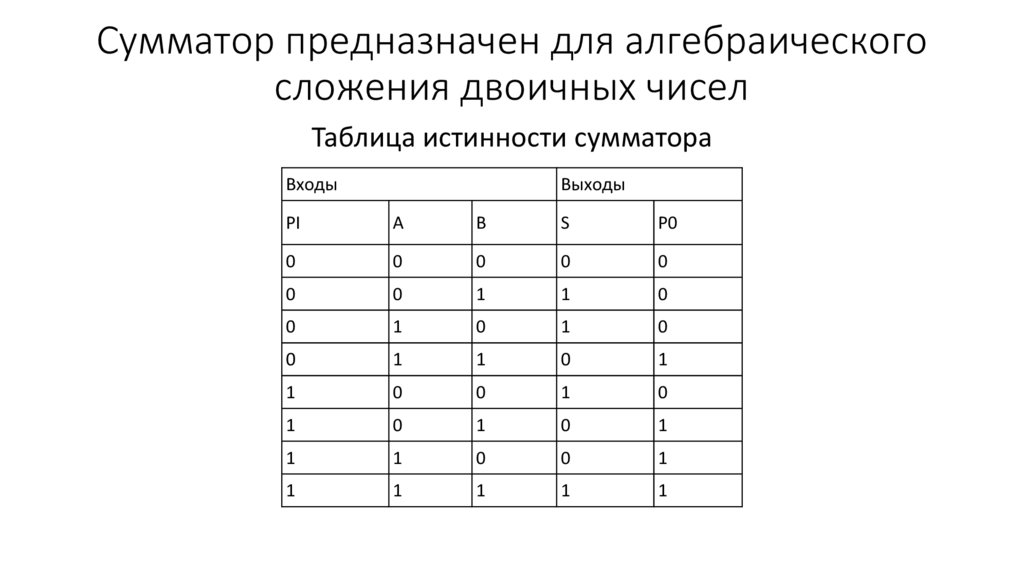 Например,
К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо
взять две микросхемы и соединить их последовательно по цепи переноса.
Например,
К561ИМ1 – сумматор на 4 разряда. Для увеличения разрядности до 8 необходимо
взять две микросхемы и соединить их последовательно по цепи переноса.
Сумматор с поразрядным последовательным переносом наиболее прост с точки зрения схемной реализации.
Быстродействие данного сумматора ограничено временем, за которое сигнал переноса последовательно распространяется через все разряды сумматора.
Этот недостаток отсутствует у параллельных сумматоров с параллельным переносом.
Параллельный сумматор с параллельным переносом
В данных устройствах сигнал переноса формируется с одновременным (параллельным) учетом всех переносов в младших разрядах, по отношению к рассматриваемому разряду.
Для построения сумматора с параллельным переносом используются две вспомогательные функции.
Функция генерации (порождения переноса) – принимает единичное значение, если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса:
Функция прозрачности (транзита
переноса) – принимает единичное значение, если перенос на выходе данного
разряда появляется только при наличии входного переноса.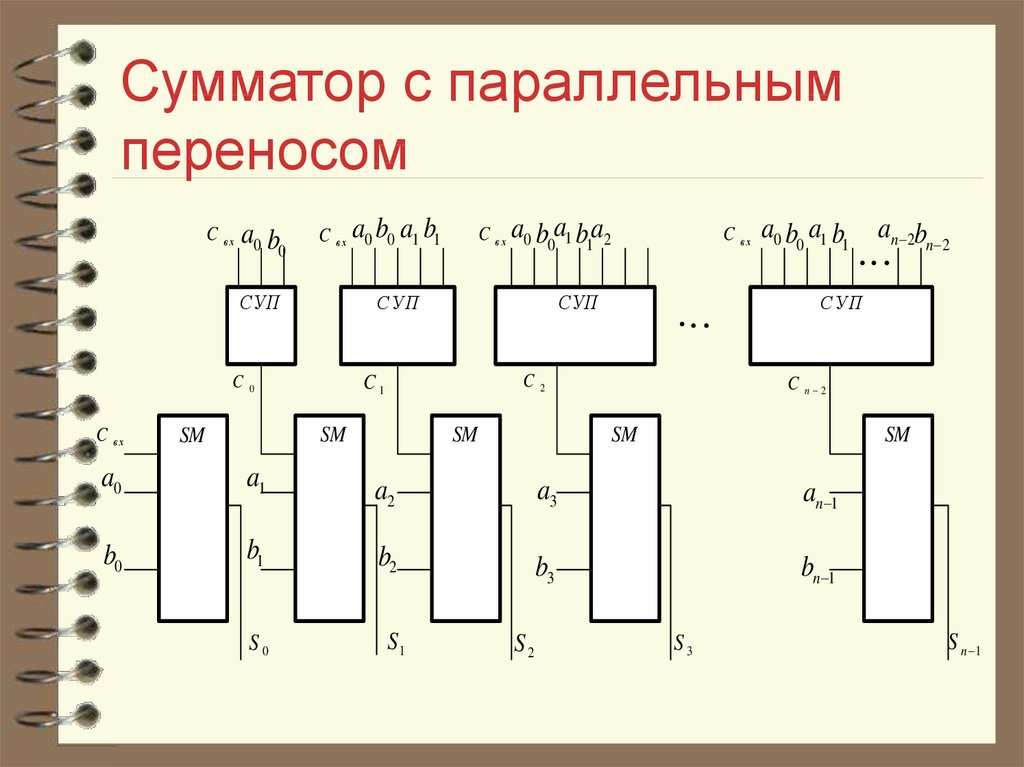 Это следует из
выражения (3.1):
Это следует из
выражения (3.1):
Тогда перенос на выходе младшего разряда:
(2)
что, с учетом выражений для дополнительных функций, соответствует зависимости для определения переноса одноразрядного сумматора (1).
На выходе следующего разряда, согласно (1, 2):
Учебный курс «Информатика»
Арифметико-логическое устройство (АЛУ) является узлом ЭВМ, который выполняет арифметические и логические операции над данными, обрабатываемыми ЭВМ.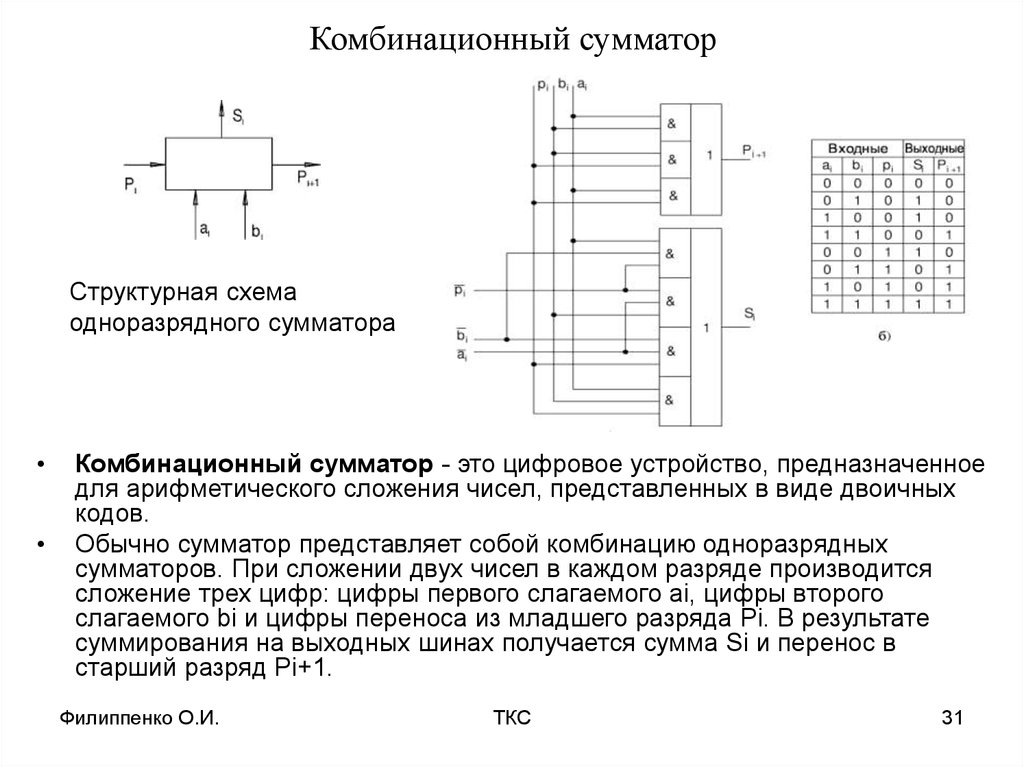 Основной элемент, используемый в АЛУ, называется полусумматором. Функция полусумматора заключается в сложении двух двоичных цифр, в результате чего образуется сумма (S) и перенос в старший разряд (Р) в соответствии с правилами двоичного сложения. Вспомните таблицу сложения двоичных чисел:
Основной элемент, используемый в АЛУ, называется полусумматором. Функция полусумматора заключается в сложении двух двоичных цифр, в результате чего образуется сумма (S) и перенос в старший разряд (Р) в соответствии с правилами двоичного сложения. Вспомните таблицу сложения двоичных чисел:
0+0=0 0+1=1 1+0=1 1+1=10
Таблица результата работы полусумматора:
Условно полусумматор на логических схемах изображается следующим образом:
Очевидно, что полусумматор имеет два входа А и В и два выхода S и Р. Первый столбец результата этой таблицы аналогичен логической операции И, он даёт перенос из данного разряда в следующий. Столбец S даёт значение младшего разряда суммы двух чисел и представляет собой логическую операцию “сложение по модулю 2”. Эта операция эквивалентна арифметическому сложению двух бинарных чисел.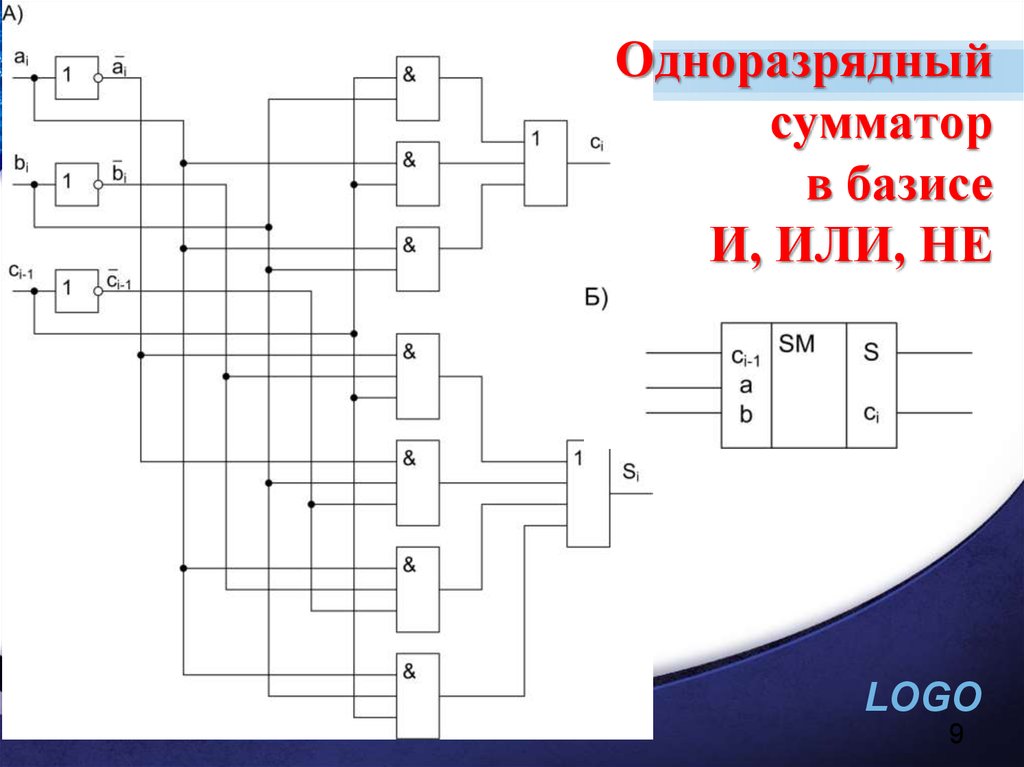
Таблице истинности результата работы полусумматора в аналитической форме соответствуют следующие записи логических функций:
Практическая реализация такого устройства не составит особого труда, так как построение комбинационных схем по логическим функциям уже рассматривалось ранее. Каждая из схем полученных пар записей логических функций будет иметь по 6 логических элементов: 5 для получения значения S и ещё один для формирования сигнала переноса Р. Однако во второй паре функций выражение для значения S можно преобразовать, воспользовавшись вторым законом де Моргана:
Отсюда видно, что для реализации полусумматора будет достаточно четырёх логических элементов:
На данном примере изображена комбинационная схема простейшего «полусумматора», устройства для сложения двух бинарных чисел А и В, где S — результат сложения, а Р — перенос в старший разряд.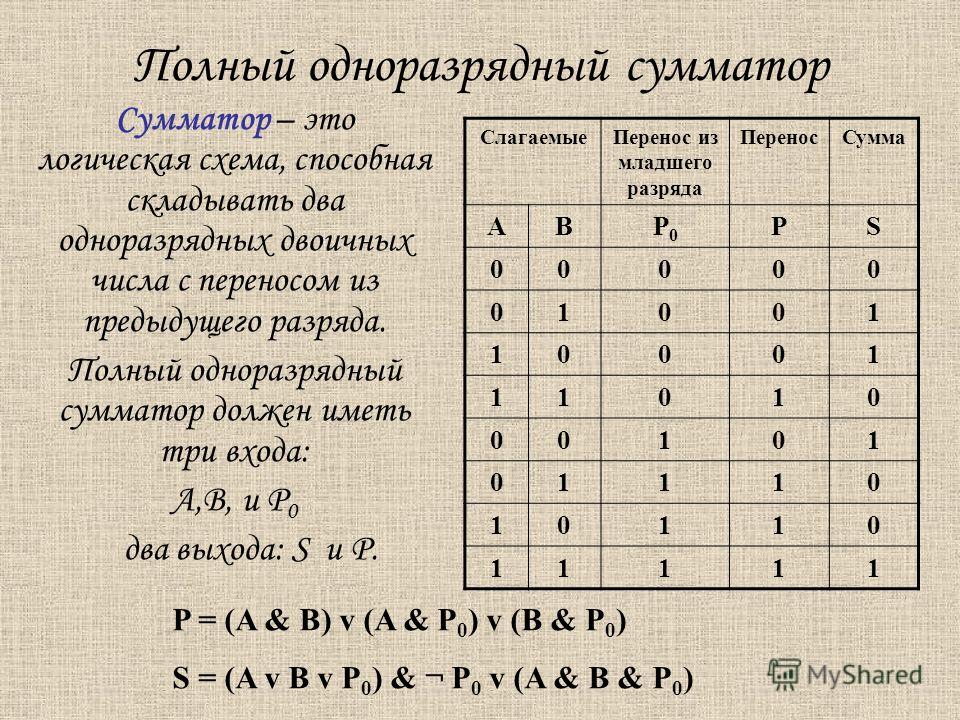 Рассматриваемому устройству дано название “полусумматор” потому, что оно хотя и даёт значение суммы двух величин и переноса в следующий разряд, однако не учитывает сигнал переноса, получаемый в предыдущем (младшем) разряде. Для получения полного двоичного одноразрядного сумматора необходимы два полусумматора. Следовательно, двоичный одноразрядный сумматор должен иметь три входа и два выхода. На логических схемах он условно изображается так:
Рассматриваемому устройству дано название “полусумматор” потому, что оно хотя и даёт значение суммы двух величин и переноса в следующий разряд, однако не учитывает сигнал переноса, получаемый в предыдущем (младшем) разряде. Для получения полного двоичного одноразрядного сумматора необходимы два полусумматора. Следовательно, двоичный одноразрядный сумматор должен иметь три входа и два выхода. На логических схемах он условно изображается так:
На входы А и В подаются соответственно цифры первого и второго слагаемого, а на вход С — цифра переноса из предыдущего разряда. Выходы S и Р так же, как в полусумматоре, соответственно выводят значения суммы и переноса в следующий разряд.
Комбинируя полусумматоры и двоичные одноразрядные сумматоры можно составить сумматор для сложения n-разрядных двоичных чисел. Приведём в качестве примера условную схему так называемого двоичного четырёхразрядного сумматора:
Двоичные n-разрядные сумматоры имеют существенный недостаток — малое быстродействие из-за значительного времени распространения переноса: чем больше разрядность складываемых чисел, тем больше время задержки работы устройства.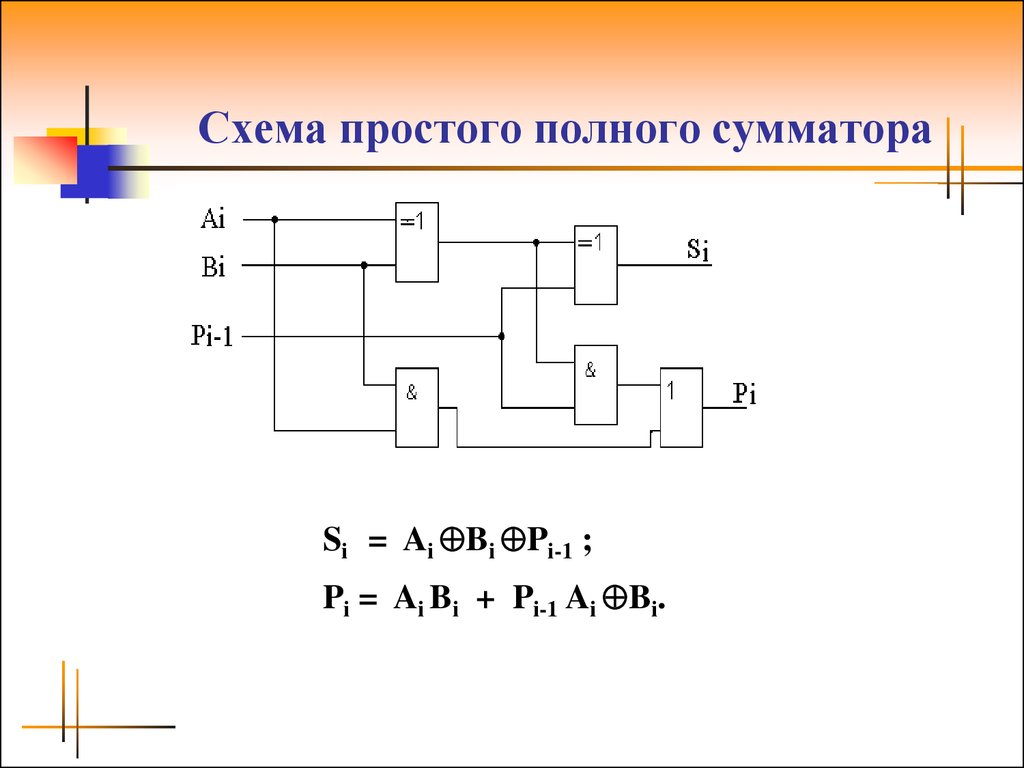 Инженеры схемным путём добиваются увеличения быстродействия работы сумматора, сокращая время распространения переноса, тем самым увеличивая скорость работы АЛУ.
Инженеры схемным путём добиваются увеличения быстродействия работы сумматора, сокращая время распространения переноса, тем самым увеличивая скорость работы АЛУ.
Разница между полусумматорами и полными сумматорами (со сравнительной таблицей)
Основное различие между полусумматорами и полными сумматорами заключается в том, что полусумматор складывает два 1-битных числа , заданные в качестве входных данных, но не добавляет полученный перенос. из предыдущего добавления, в то время как полный сумматор вместе с двумя 1-битными числами также может добавить перенос, полученный из предыдущего добавления.
Полусумматор и полный сумматор, оба представляют собой комбинационную логическую схему , но отличается способом обработки входных данных. Комбинационная схема — это схема, не состоящая из каких-либо элементов памяти; он состоит всего из логических элементов.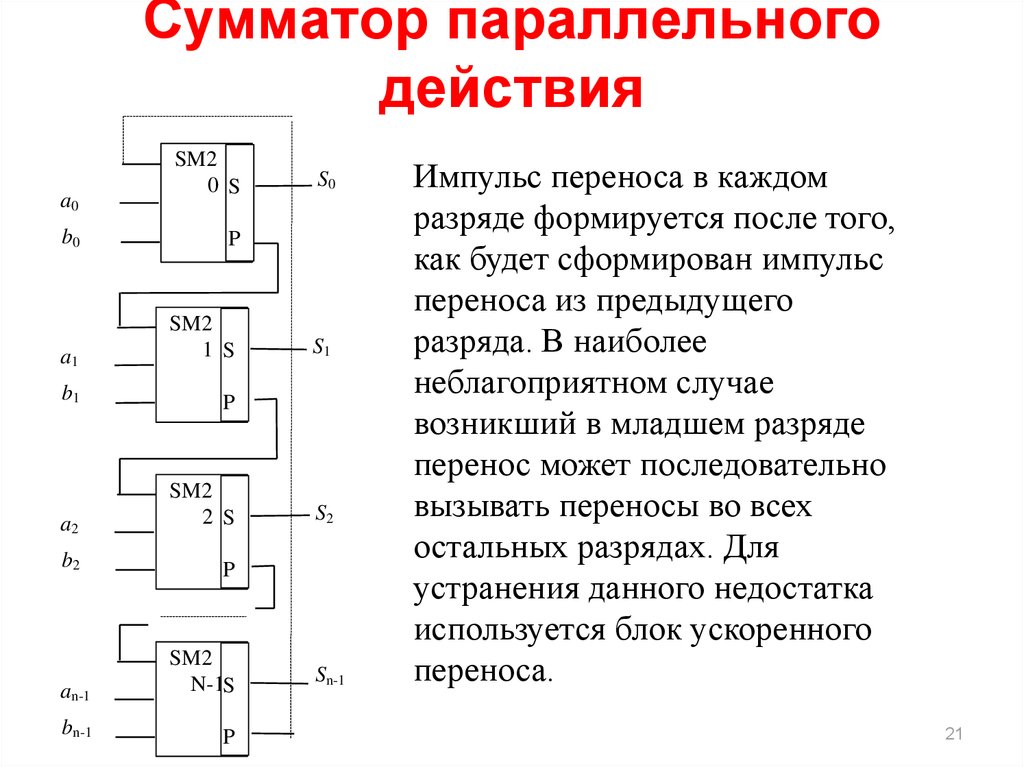
Еще одно существенное различие между Half Adder и Full Adder состоит в том, что Half Adder состоит из одного EX-OR вентиля и одного AND вентиля , в то время как Full Adder состоит из двух EX-OR вентилей, двух вентилей AND и один операционный шлюз. Если в процессе сложения получается какой-либо перенос, он передается полному сумматору в качестве входных данных, и он добавляет эти переносы вместе с другими входными данными. Напротив, полусумматор не берет никакого переноса, полученного в результате предыдущего сложения.
Сумматор является важнейшей цифровой схемой, используемой в компьютерах, цифровой обработке и т. д. Благодаря использованию логических вентилей процесс сложения становится быстрым. Полусумматор и полный сумматор выполняют сложение и широко используются в цифровых схемах для выполнения арифметических функций.
Комплектация: половинный сумматор и полный сумматор
- Сравнительная таблица
- Определение
- Ключевые отличия
- Сходства
- Вывод
Сравнительная таблица
| Параметры | Половинный сумматор | Полный сумматор |
|---|---|---|
| Определение | Полусумматор представляет собой комбинационную логическую схему, которая складывает две однобитовые цифры. | Полный сумматор — это комбинационная схема, которая складывает три однобитных цифры. |
| Добавление переноса | Перенос, созданный в результате предыдущего добавления, не добавляется на следующем шаге. | Перенос, созданный в результате предыдущего добавления, добавляется на следующем шаге. |
| Аппаратные компоненты | Состоит из одного вентиля EX-OR и одного вентиля AND. | Он состоит из двух логических элементов «ИСКЛЮЧАЮЩЕЕ ИЛИ», двух вентилей «И» и одного вентиля «ИЛИ». |
| Применения | Калькуляторы, компьютеры, цифровые измерительные устройства и т. д. | Множественное сложение битов, цифровые процессоры и т. д. |
Определение
Полусумматор
Полусумматор представляет собой комбинационную логическую схему, которая разработана путем соединения одного элемента исключающее ИЛИ и одного элемента И. Он складывает два однобитных числа и генерирует сумму в качестве вывода.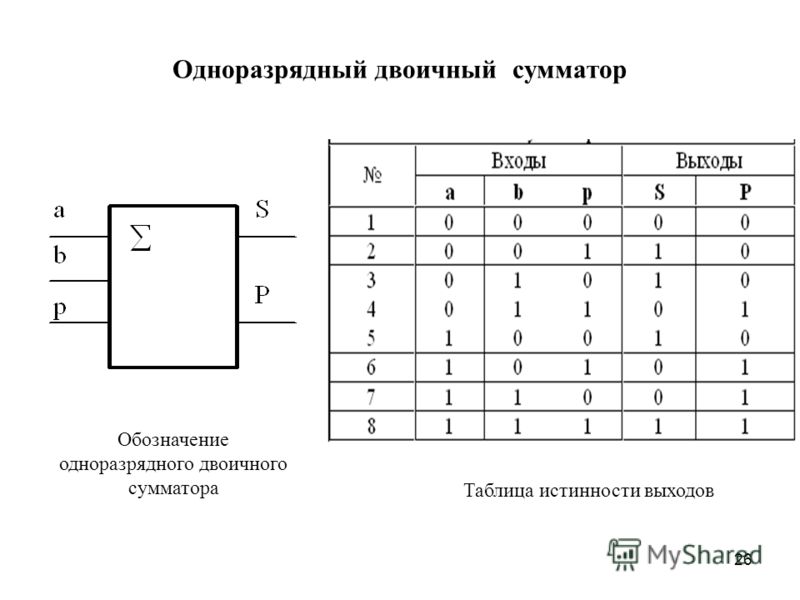
Он состоит из двух входных клемм и двух выходных клемм, одна из которых SUM, а другая — CARRY.
Выход, полученный с помощью логического элемента EX-OR, представляет собой сумму двух чисел, а результат, полученный с помощью логического элемента AND, является переносом. Но перенос, полученный в одном дополнении, не будет перенаправлен в другое дополнение, потому что для его обработки нет логического элемента. Таким образом, это называется схемой полусумматора.
Выходное уравнение обоих вентилей можно записать в виде логической операции, выполняемой логическими вентилями. Уравнение суммы будет записано в виде операции EX-OR, а уравнение переноса — в виде операции AND.
Таблица истинности полусумматора
Таблица истинности полусумматора представляет возможную комбинацию входных данных и возможных выходных данных, полученных из него. Таблица истинности Half Adder приведена ниже.
| Вход | Выход | ||
|---|---|---|---|
| А | Б | СУММА | ПЕРЕНОС |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Выход, полученный от элемента EX-OR, будет равен 1 только тогда, когда либо первый вход равен 1, либо второй вход равен 1, но не оба одновременно.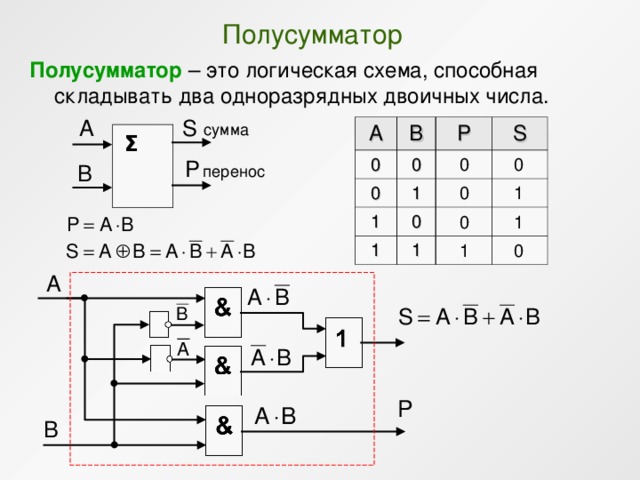 Выход вентиля EX-OR указывает сумму двух битов, начиная с младшего бита и заканчивая старшим битом.
Выход вентиля EX-OR указывает сумму двух битов, начиная с младшего бита и заканчивая старшим битом.
Выход, полученный от логического элемента И, будет единицей только тогда, когда оба входа равны 1, в остальных случаях выходной сигнал будет равен 0. Выходной сигнал, полученный от логического элемента И, указывает перенос, полученный в результате сложения.
Полный сумматор
Полный сумматор — это схема, состоящая из схемы, состоящей из двух вентилей EX-OR, двух вентилей AND и одного вентиля OR.
Добавляет три двоичных разряда, два из которых являются входными, а один — переносом, полученным в результате предыдущего сложения.
Как и полусумматор, полный сумматор также является комбинационной логической схемой, т.е. не имеет запоминающего элемента. Но из-за дополнительных логических вентилей он добавляет предыдущий перенос и генерирует полный вывод. Таким образом, он называется полным сумматором.
Полный сумматор также может быть разработан с использованием двух половинных сумматоров и одного вентиля ИЛИ .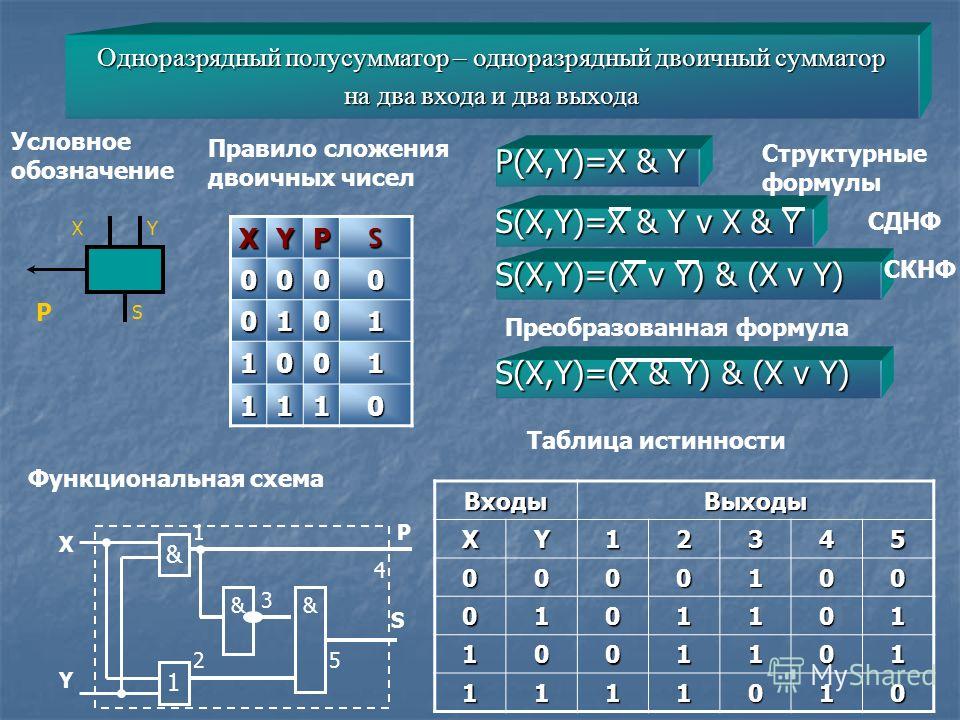 Сумма цифр может быть получена на выходе второго полусумматора, в то время как логический элемент ИЛИ будет генерировать перенос, полученный после сложения.
Сумма цифр может быть получена на выходе второго полусумматора, в то время как логический элемент ИЛИ будет генерировать перенос, полученный после сложения.
Выходное уравнение, полученное вентилем EX-OR, представляет собой сумму двоичных цифр. В то время как выход, полученный логическим элементом И, является переносом, полученным путем сложения. Уравнение можно записать в виде логической операции.
Таблица истинности полного сумматора
Таблица истинности полного сумматора представлена ниже. Таблица истинности состоит из всех возможных комбинаций трех входов, данных полному сумматору, а также суммы и переноса выходов. Он определяет двоичные цифры, полученные после сложения.
| Входы | Выход | |||
|---|---|---|---|---|
| А | В | С | СУММА | ВЫПОЛНИТЬ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Цепь сложения нескольких битов
Мы можем получить сложение нескольких битов, увеличив число полного сумматора.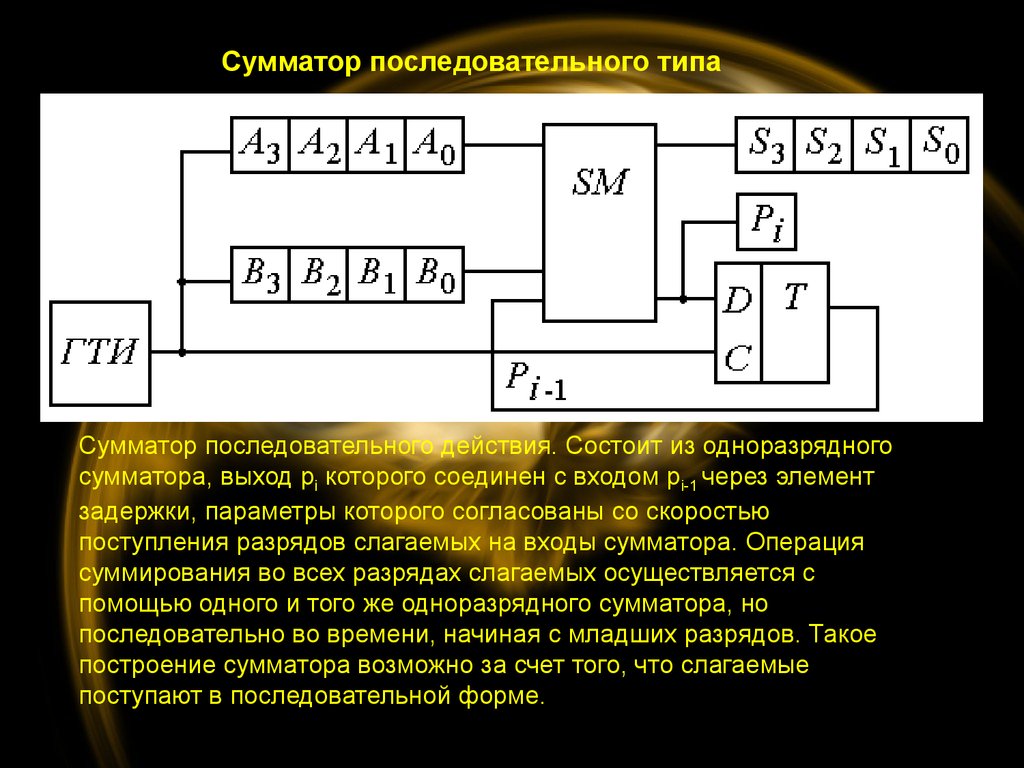
Основные различия между полусумматорами и полными сумматорами
- Полусумматор складывает две двоичные цифры и генерирует сумму и перенос. В то время как полный сумматор складывает три двоичных разряда и генерирует сумму и бит переноса.
- Еще одно существенное различие между полусумматорами и полусумматорами заключается в том, что перенос, полученный в результате предыдущего сложения, не добавляется при следующем сложении в случае полусумматора. Наоборот, полный сумматор добавляет предыдущий перенос вместе с текущими входами.
- Аппаратная архитектура Half Adder и Full Adder также отличается друг от друга. Half Adder состоит только из одного вентиля EX-OR и вентиля AND. В то время как полный сумматор состоит из двух логических элементов EX-OR и AND с одним логическим элементом ИЛИ.
Сходства
- Полусумматор и полный сумматор, оба представляют собой комбинационную цифровую схему .
 Это означает, что в схеме нет элементов памяти, подобных 9.0003 последовательных цепей.
Это означает, что в схеме нет элементов памяти, подобных 9.0003 последовательных цепей. - Вышеуказанные две комбинационные схемы имеют решающее значение для арифметической операции . Обе комбинационные схемы обеспечивают сложение двоичных чисел.
Заключение
Полусумматор и Полный сумматор являются строительными блоками различных цифровых схем, таких как компьютеры, калькуляторы, цифровые измерительные приборы. Преимущество использования сумматоров в том, что они являются частью цифровой схемы. А логические элементы составляют основу цифровой схемы и очень быстро обрабатывают входные данные.
Скорость обработки логическими элементами составляет микросекунды, и нам нужно быстрое вычисление результатов почти в каждом приложении, поэтому мы используем сумматоры.
Разница между половинным сумматором и полным сумматором
Когда дело доходит до компьютерных операций, внутри можно найти множество различных типов компонентов.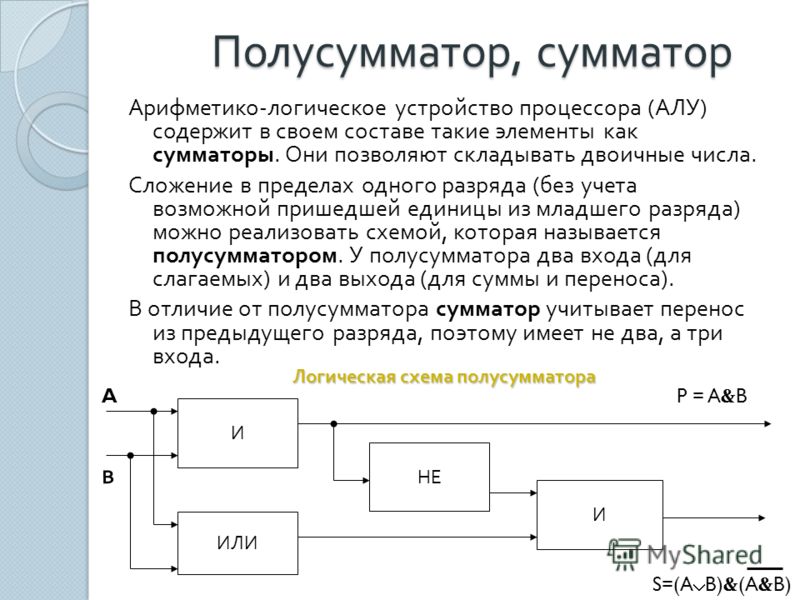 Одним из таких компонентов является сумматор, который отвечает за выполнение дополнительных операций с двоичными данными. Существует два основных типа сумматоров: половинный сумматор и полный сумматор. В этой статье мы обсудим различия между этими двумя типами сумматоров. Следите за обновлениями!
Одним из таких компонентов является сумматор, который отвечает за выполнение дополнительных операций с двоичными данными. Существует два основных типа сумматоров: половинный сумматор и полный сумматор. В этой статье мы обсудим различия между этими двумя типами сумматоров. Следите за обновлениями!
Что такое полусумма?
Полусумматор — это цифровая схема, выполняющая сложение двух двоичных чисел. Он имеет два входа и один выход. Два входа — это добавляемые операнды, а выход — сумма двух операндов.Что такое полный сумматор?
Полный сумматор — это цифровая схема, выполняющая сложение трех двоичных чисел. Он имеет три входа и один выход. Три входа — это добавляемые операнды, а выход — сумма трех операндов.Ключевая разница между половинным сумматором и полным сумматором
Основное отличие полусумматора от полного сумматора состоит в том, что полусумматор может складывать только два операнда, а полный сумматор может складывать три операнда.| Критерии | Полугадюка | Полный сумматор |
| Основы | Полусумматор имеет два входа и один выход | Полный сумматор имеет три входа и один выход |
| Вход | В полусумматоре два входных операнда | В полном сумматоре три входных операнда |
| Выход | Полусумматор выдает сумму двух входных операндов на выходе | Полный сумматор выдает сумму трех входных операндов на выходе |
| Эксплуатация | Полусумматор складывает два входных операнда и выводит их сумму | Полный сумматор складывает три входных операнда и выводит их сумму |
| Аппаратная архитектура: | Полусумматор — это цифровая схема, которую можно реализовать с помощью логических элементов | .Полный сумматор — это цифровая схема, которую можно реализовать с помощью логических элементов | .
| Применение | Полусумматор используется для сложения двух двоичных чисел | Полный сумматор используется для сложения трех двоичных чисел |
| Логическое выражение | Логическое выражение для полусумматора: A XOR B | Логическое выражение для полного сумматора: (A AND B) OR (C AND (A XOR B)) |
| Преимущества | Полусумматор имеет простую аппаратную архитектуру | Полный сумматор можно использовать для сложения трех двоичных чисел |
| Недостатки | Полусумматор может складывать только два операнда | Полный сумматор имеет сложную аппаратную архитектуру |
| Приложения | Полусумматор используется в цифровых схемах | Полный сумматор используется в АЛУ, регистрах ЦП и модулях памяти |
Заключение
Полусумматор складывает два однобитовых двоичных числа, а полный сумматор также может обрабатывать заимствования и переносы между битами.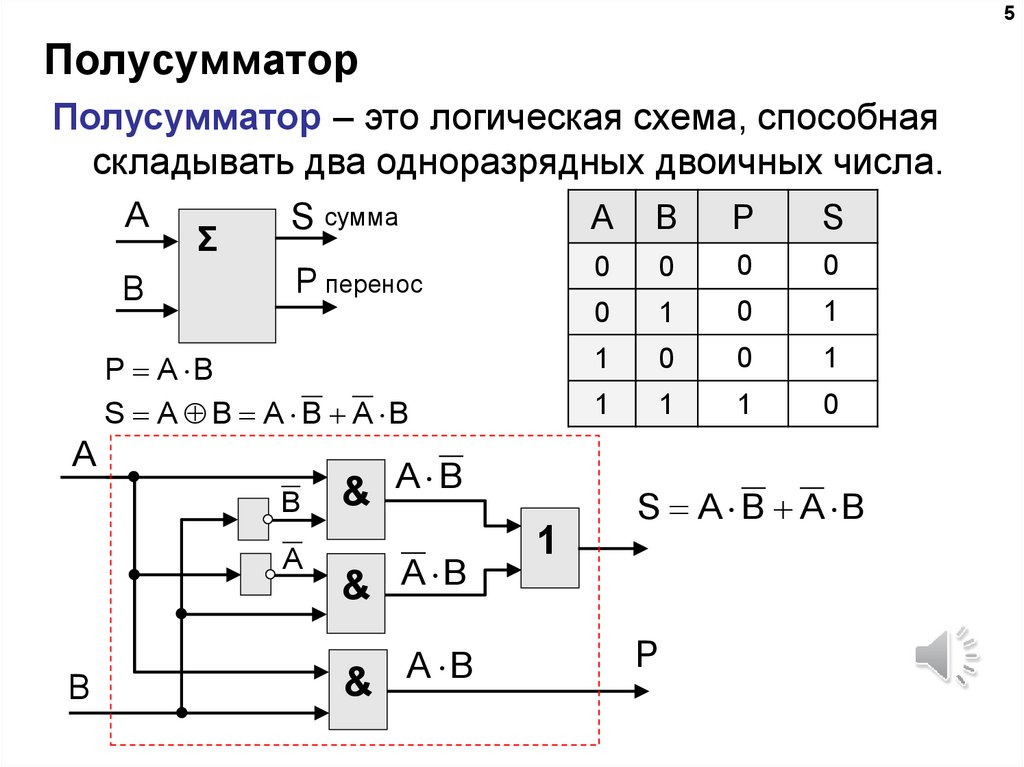


 Это означает, что в схеме нет элементов памяти, подобных 9.0003 последовательных цепей.
Это означает, что в схеме нет элементов памяти, подобных 9.0003 последовательных цепей.