Примесные полупроводники
Примесные полупроводники
Примесный полупроводник - это полупроводник, электрофизические свойства которого определяются, в основном, примесями других химических элементов. Процесс введения примесей в полупроводник называется легированием полупроводника, а сами примеси называют легирующими. Для равномерного распределения легирующей примеси в объеме полупроводника легирование осуществляется в процессе выращивания монокристалла полупроводника из жидкой или газообразной фазы. Локальное легирование части объема полупроводника, например, приповерхностной области, производится методом диффузии при сильном нагреве полупроводника или низкотемпературными методами ионного легирования.
Роль примесей могут играть и всевозможные дефекты структуры кристаллической
решетки полупроводника, такие как вакансии,
междуузельные атомы, дислокации.
При малой концентрации примесей (1021…1023 м-3) примесные атомы создают дополнительные дискретные энергетические уровни в запрещенной зоне полупроводника. Такой полупроводник называется невырожденным. Повышение концентрации примесных атомов в полупроводнике до 1024…1025 м-3 сопровождается появлением в запрещенной зоне полупроводника вместо дискретных уровней зон примесных уровней. Такие полупроводники называют вырожденными.
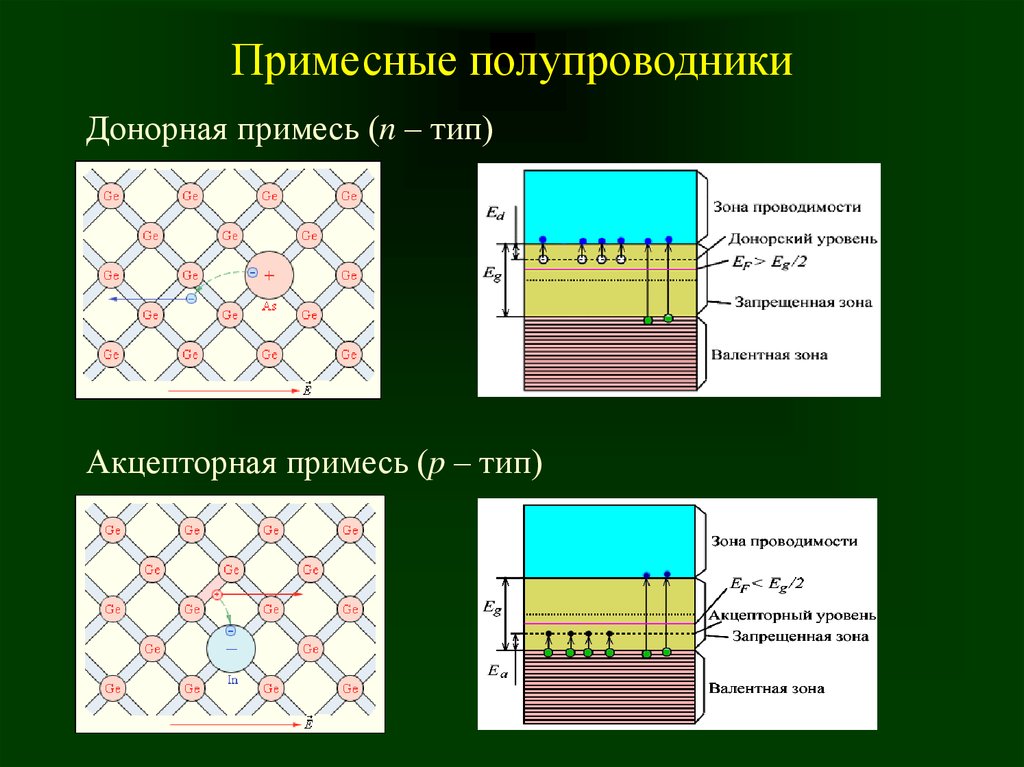
Различают два основных вида примесей, которые используются для преднамеренного легирования полупроводников и создающих преимущественно электронный или дырочный тип проводимости. Примеси, введение которых в полупроводник создает электронный тип проводимости, называются

Электронные полупроводники. Полупроводник, легированный донорной примесью, называют полупроводником электронного типа (n-типа) проводимости или электронным полупроводником.
Электронная проводимость появляется в результате легирования полупроводника
элементами, имеющими большую валентность, чем валентность атомов из которых состоит полупроводник. Например,
для Si и Ge, являющимися
элементами 4 группы таблицы Менделеева, в качестве донорных примесей применяют элементы 5
группы, как правило это
Замещая узлы кристаллической решетки полупроводника, атомы донорной примеси отдают часть своих валентных электронов
для создания ковалентных связей с атомами основного вещества и участвуют
в создании дополнительных энергетических уровней в запрещенной зоне полупроводника,
как показано на рис. 1.25.
При образовании химической связи с атомом кремния один из пяти валентных электронов атома примеси оказывается «лишним» и переходит на стационарную орбиту вблизи атома примеси (рис. 1.25, а). У этого электрона существует слабая электростатическая связь с примесным атомом за счет кулоновского взаимодействия. Энергия кулоновской связи DWd составляет всего 0,03…0,05 эВ. Поэтому для перехода «лишнего» электрона в свободное состояние достаточно небольшой энергии, которую электрон может получить за счет тепловых колебаний кристаллической решетки. В результате атом донорной примеси становится положительно заряженным ионом.
Рассмотрим энергетическую зонную диаграмму полупроводника
с электронным типом проводимости, изображенную на рис. 1.25, б.
Как уже отмечалось, для того, чтобы пятый валентный электрон
стал свободным, необходимо затратить энергию значительно меньшую,
чем для разрыва ковалентной связи.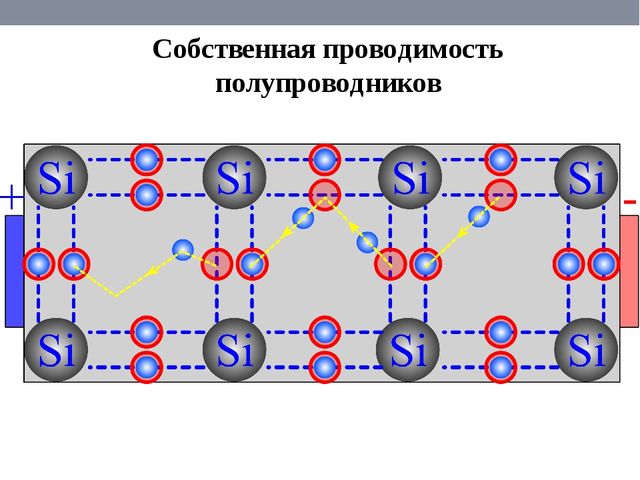 В соответствии с этим энергетический
уровень пятого валентного электрона на зонной диаграмме должен
располагаться в запрещенной зоне вблизи дна зоны проводимости, образуя
дополнительный энергетический уровень донорной
примеси с энергией
В соответствии с этим энергетический
уровень пятого валентного электрона на зонной диаграмме должен
располагаться в запрещенной зоне вблизи дна зоны проводимости, образуя
дополнительный энергетический уровень донорной
примеси с энергией
Дырочные полупроводники. Полупроводник, легированный акцепторной примесью, называют полупроводником дырочного типа (р-типа) проводимости или дырочным полупроводником.
Дырочная проводимость создается в результате легирования полупроводника
элементами, имеющими меньшую валентность, чем валентность атомов, из которых
состоит полупроводник. Например,
для Si и Ge, являющимися
элементами четвертой группы таблицы Менделеева, в качестве
акцепторных примесей применяют элементы третьей группы, как правило это 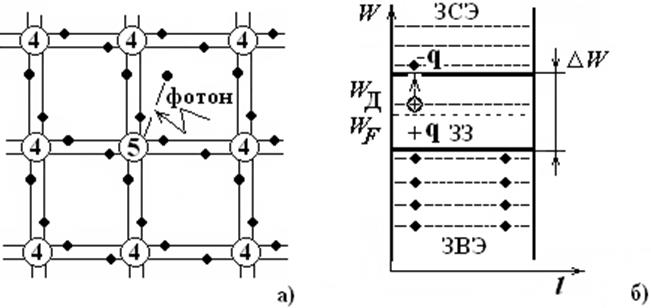
Замещая узлы кристаллической решетки полупроводника, атомы акцепторной примеси захватывают валентный электрон от соседнего атома кремния для создания ковалентных связей с атомами основного вещества, превращаясь при этом в отрицательно заряженные ионы, и участвуют в создании дополнительных энергетических уровней в запрещенной зоне полупроводника, как показано на рис. 1.26.
Механизм появления дырочной проводимости иллюстрируется на рис.
1.26, а. При образовании химической
ковалентной связи с атомами Si или Ge все три валентных электрона атома акцепторной примеси
участвуют в образовании ковалентных связей. Для создания четвертой
(незавершенной) химической связи
может быть захвачен электрон из ковалентных связей одного из ближайших
соседних атомов кремния. У этого атома, в свою очередь, появляется
незавершенная связь с соседним атомом кремния, которая называется
дыркой.
У дырки существует слабая электростатическая связь с атомом кремния. Энергия этой кулоновской связи DWa, как и в случае электронных полупроводников, невелика и составляет всего 0,01…0,07 эВ. Поэтому для захвата дыркой электрона из ковалентной связи соседнего атома достаточно небольшой энергии, которую электрон может получить за счет тепловых колебаний кристаллической решетки. В результате обмена электронами между соседними атомами дырка может перемещаться по кристаллу полупроводника, осуществляя при приложении внешнего электрического поля дырочную проводимость.
На рис. 1.26, б
представлена энергетическая зонная диаграмма дырочного полупроводника, из
которой следует, что ионизация акцепторного атома происходит в результате
захвата электрона из валентной зоны полупроводника на энергетический уровень
акцепторной примеси с энергией Wa. Поскольку, как уже отмечалось выше,
энергия образования свободной дырки невелика, то локальные энергетические
уровни акцепторной примеси
Поскольку, как уже отмечалось выше,
энергия образования свободной дырки невелика, то локальные энергетические
уровни акцепторной примеси
56. Какой полупроводник называется примесным и чем объясняется его широкое применение.
Примесный полупроводник — это полупроводник, электрофизические свойства которого определяются, в основном, примесями других химических элементов.
Примесные
полупроводники получают
в результате внедрения в собственный
полупроводник атомов примеси с
валентностью большей или меньшей, чем
у атомов собственного полупроводника.
При наличии в полупроводниках примесей
в них наряду с собственной проводимостью
возникает дополнительная примесная
проводимость. Примесные
полупроводники обладают
более высокой электрн ческой проводимостью,
чем полупроводники с собственной
проводимостью. В полупроводниковых
приборах используются главным образом
полупроводники, содержащие донорные
или акцепторные примеси.
Материал этой примеси выбирается так, чтобы разрешенные уровни ее электронов находились вблизи “дна” зоны проводимости (рис. 3.2). За счет значительно меньшего удаления от зоны проводимости вероятность перехода электронов примеси в зону проводимости уже при комнатной температуре резко увеличивается по сравнению с электронами валентной зоны (см. рис. 3.2, пунктир). Свободные носители в зоне проводимости в основном будут обусловлены электронами примеси, а их число намного больше дырок в валентной зоне. Такой полупроводник называется
nn >> pn. (3.3)
В
отличие от электронов, уходящих из
валентной зоны, электроны примеси,
перешедшие в зону проводимости, дырок
не образуют, поскольку при малой
концентрации примеси расстояние между
ее атомами настолько велико, что переход
электрона от одного атома примеси на
освободившийся уровень у другого атома
становится невозможным, поэтому атом
примеси, потерявший электрон, становится
положительно заряженным ионом, не
способным передвигаться в твердом теле.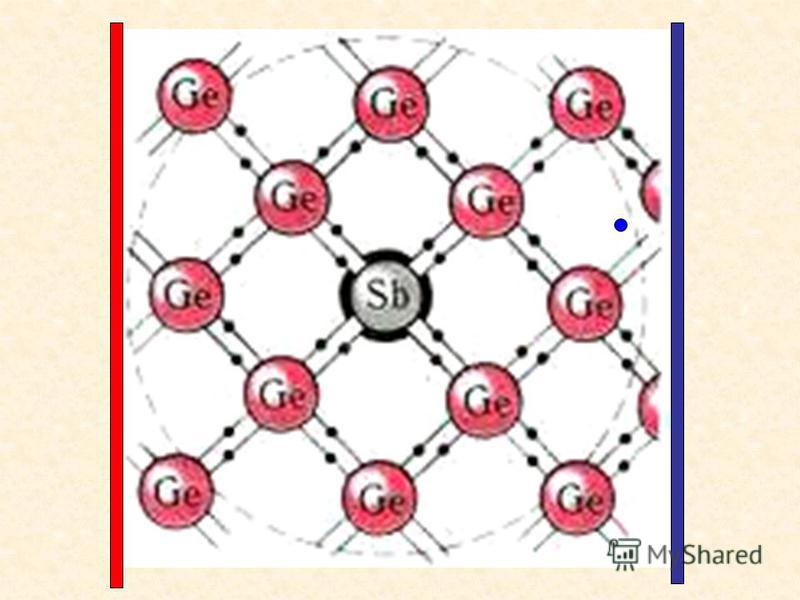
Концентрация носителей в примесном полупроводнике подчиняется закону
nn pn=ni2. (3.4)
Соотношение (3.4) означает, что увеличение объема примеси, с одной стороны, приводит к увеличению основных носителей, но, с другой стороны, возрастает и вероятность их рекомбинации, когда электрон из зоны проводимости возвращается на свободные уровни примеси, деионизируя ее атомы. В результате этих процессов и наступает равновесие, определяемое соотношением (3.4).
Поскольку уже при комнатной температуре практически все атомы примеси становятся ионизированными, число основных носителей от температуры практически не зависит (nn const).
Согласно соотношению (3.4)
,
а
это означает, что число неосновных
носителей очень сильно зависит от температуры из-за аналогичной зависимости от
температуры числа собственных носителей ni .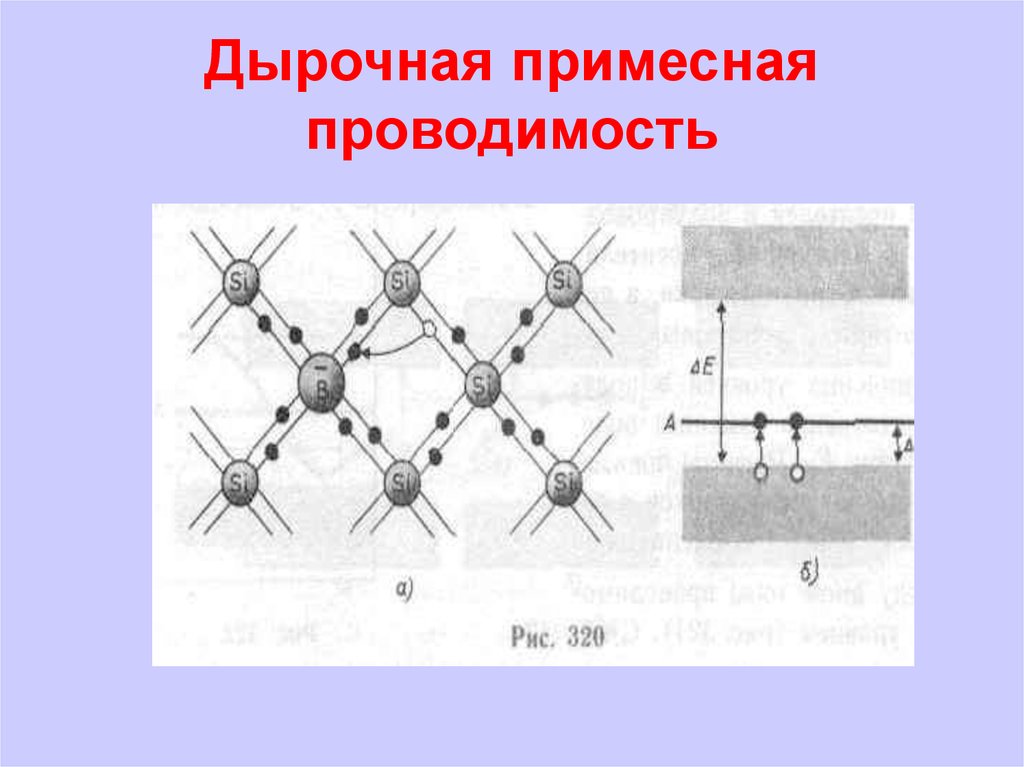
При
повышении температуры число свободных
электронов, образовавшихся при ионизации
примеси, остается практически неизменным,
а число электронов, переходящих из
валентной зоны, как это было и в собственном
полупроводнике, экспоненциально
нарастает. Поскольку число атомов
исходного полупроводника на несколько
порядков превышает число атомов примеси,
число “собственных” электронов в зоне
проводимости становится много больше
электронов от примеси. В полупроводнике
снова устанавливается практическое
равенство свободных электронов и дырок
(см. формулу 3.1): примесный
характер проводимости практически
исчезает. Такой полупроводник называется вырожденным.
Поскольку примесный характер проводимости
является для многих приборов главным
условием функционирования, критическая
температура, при которой происходит
вырождение, является важнейшей
характеристикой полупроводника,
определяющей его температурный “потолок”
нормальной работы. Важное значение в
теории электропроводности полупроводника
играет такое понятие, как уровень
Ферми (F).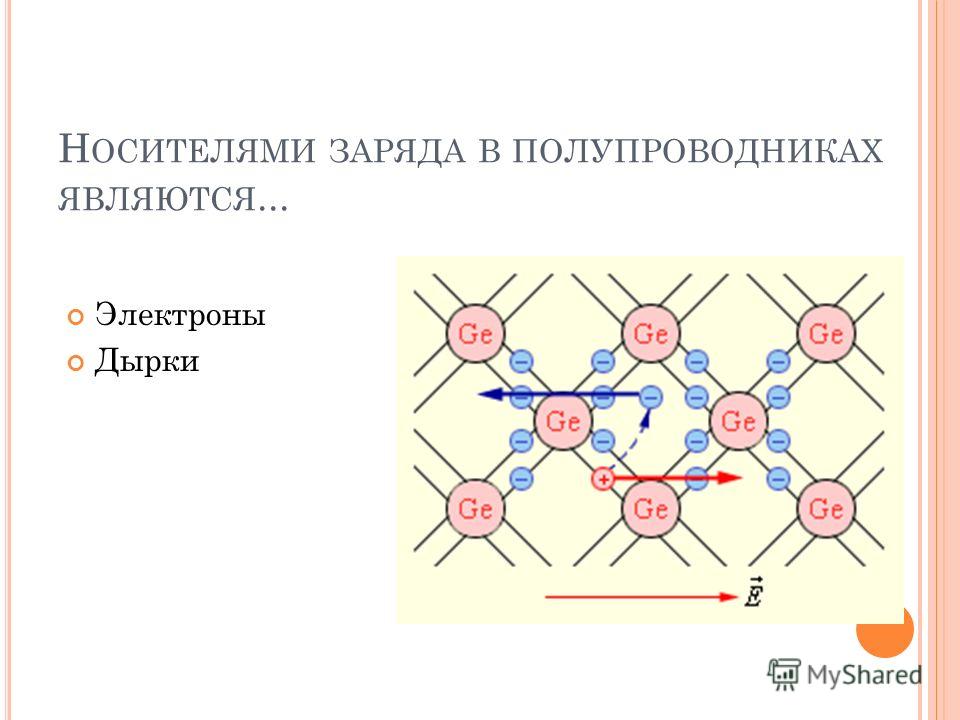 Уровень
Ферми – это сумма химического потенциала,
обеспечивающего диффузию носителей в
объеме твердого тела и электрического
потенциала, обеспечивающего дрейф
носителей. Движение носителей
(электропроводность) возможно лишь при
наличии градиента или химического, или
электрического потенциала. В равновесном
состоянии, когда направленного движения
носителей в твердом теле нет, градиент
уровня Ферми равен нулю, т. е. F=const.
Уровень
Ферми – это сумма химического потенциала,
обеспечивающего диффузию носителей в
объеме твердого тела и электрического
потенциала, обеспечивающего дрейф
носителей. Движение носителей
(электропроводность) возможно лишь при
наличии градиента или химического, или
электрического потенциала. В равновесном
состоянии, когда направленного движения
носителей в твердом теле нет, градиент
уровня Ферми равен нулю, т. е. F=const.
Уровень Ферми является функцией концентрации свободных носителей:
, (3.5)
где 0 — потенциал середины запрещенной зоны.
Для собственного полупроводника, у которого согласно (3.1) n=ni:
F = 0,
т.е. уровень Ферми расположен в середине запрещенной зоны.
Для
электронного полупроводника, согласно
(3. 3) и (3.4), nn>ni и
3) и (3.4), nn>ni и
F > 0,
т. е. уровень Ферми перемещается выше середины запрещенной зоны.
Примесный полупроводник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Примесные полупроводники обладают более высокой электрн ческой проводимостью, чем полупроводники с собственной проводимостью, если концентрация атомов донорной Лгд или акцепторной NZ примеси превышает концентрацию собственных носителей заряда. [1]
Примесные полупроводники получают в результате внедрения в собственный полупроводник атомов примеси с валентностью большей или меньшей, чем у атомов собственного полупроводника. При наличии в полупроводниках примесей в них наряду с собственной проводимостью возникает дополнительная примесная проводимость. [2]
Примесный полупроводник называется электронным или полупроводником я-типа, если атомы примесей слабее удерживают свои электроны.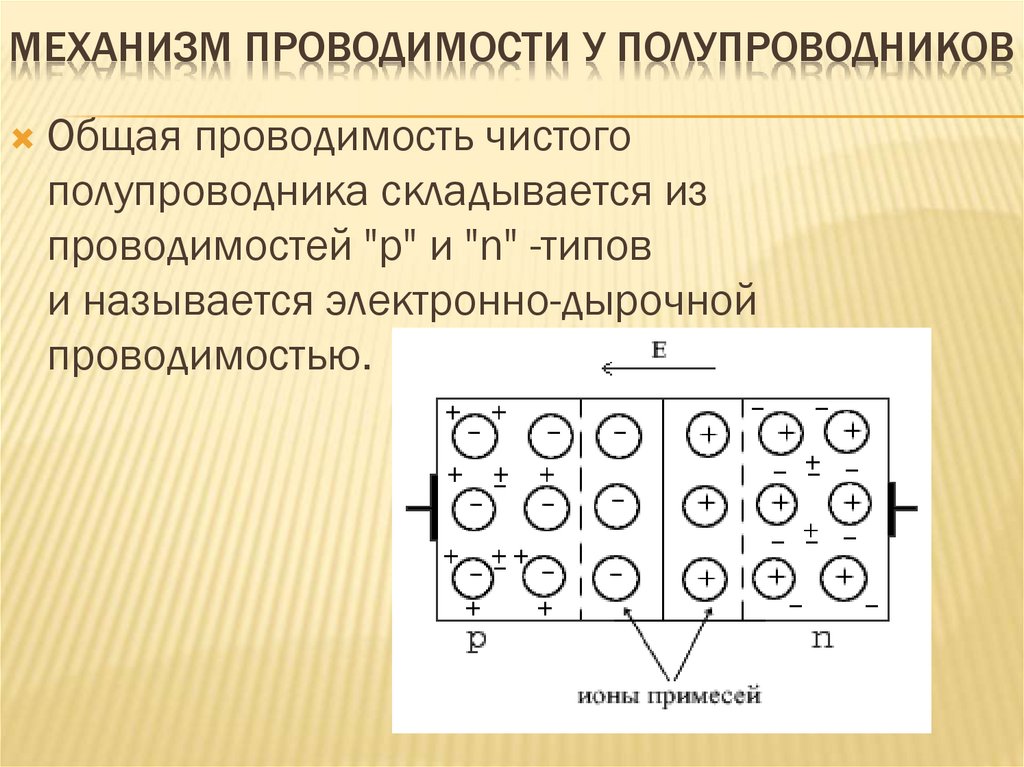 Ясно, что в таком полупроводнике обычно наблюдается электронная проводимость. Подвижные дырки в нем почти не образуются. Положительно заряжаются примеси, которые длительно остаются ионизированными, будучи не в силах отобрать недостающие электроны у основных атомов. Дырочная проводимость в полупроводниках — типа или электронная проводимость в полупроводниках р-типа заметны обычно лишь в тех случаях, когда в полупроводники соответствующие подвижные заряды вносятся какими-либо посторонними источниками.
[3]
Ясно, что в таком полупроводнике обычно наблюдается электронная проводимость. Подвижные дырки в нем почти не образуются. Положительно заряжаются примеси, которые длительно остаются ионизированными, будучи не в силах отобрать недостающие электроны у основных атомов. Дырочная проводимость в полупроводниках — типа или электронная проводимость в полупроводниках р-типа заметны обычно лишь в тех случаях, когда в полупроводники соответствующие подвижные заряды вносятся какими-либо посторонними источниками.
[3]
Примесные полупроводники применяются для изготовления полупроводниковых приборов. [4]
Примесные полупроводники бывают двух типов. D от примесного уровня до дна зоны проводимости невелико, то при повышении температуры электроны переходят с примесных уровней в зону проводимости, следствием чего является ненулевая проводимость при Т 0, осуществляемая электронами зоны проводимости. Примеси, которым соответствуют уровни описанного типа, носят название доноров. Донорами являются, например, примеси фосфора или мышьяка в германии.
[5]
Донорами являются, например, примеси фосфора или мышьяка в германии.
[5]
Примесные полупроводники, электропроводность которых определяется примесями, обладают резко выраженной электронной или дырочной электропроводностя-ми. Эффект повышения электрической проводимости объясняется присутствием в кристалле полупроводника атомов элементов иной валентности. Примеси с валентностью, большей четырех, дающие избыток свободных электронов, называются донорными; примеси с валентностью, меньшей четырех, увеличивающие количество дырок, называются акцепторными. Схема кристалла кремния, в котором один атом основного вещества замещен атомом пятивалентного мышьяка, приведена на рис. 3.2, а. Мышьяк образует четыре ковалентные связи с соседними атомами кремния, а его пятый валентный электрон оказывается лишним. При низких температурах ( О К) этот электрон еще удерживается около ядра мышьяка, но уже при небольшом повышении температуры сила связи ослабляется, электрон отрывается и становится носителем отрицательного заряда, а атом1 мышьяка превращается в положительный неподвижный ион. В целом кристалл остается электрически нейтральным, так как положительные заряды ионов уравновешиваются отрицательными зарядами электронов проводимости.
[6]
В целом кристалл остается электрически нейтральным, так как положительные заряды ионов уравновешиваются отрицательными зарядами электронов проводимости.
[6]
Примесный полупроводник — полупроводник электронной ( n — типа) или дырочной ( р-типа) проводимости. При одновременном введении в полупроводник и донорной и акцепторной примесей происходит компенсация их влияний и эффект на проводимость оказывает только избыток одного типа примеси над другим. [7]
Примесный полупроводник также называется легированным полупроводником. В зависимости от примеси полупроводник может быть / г-типа и / ьтипа. Буква п обозначает электронную проводимость, а р — дырочную. [8]
Примесные полупроводники бывают двух типов. D от примесного уровнядо дна зоны проводимости невелико, то при повышении температуры электроны переходят с примесных уровней в зону проводимости, следствием чего является ненулевая проводимость при Т 0, осуществляемая электронами зоны проводимости. Примеси, которым соответствуют уровни описанного типа, носят название доноров. Донорами являются, например, примеси фосфора или мышьяка в германии.
[9]
Примеси, которым соответствуют уровни описанного типа, носят название доноров. Донорами являются, например, примеси фосфора или мышьяка в германии.
[9]
| Энергетические спектры примесных пол vii ро пол i. 11 ков. [10] |
Примесный полупроводник, у которого электропроводность при росте Т сначала уменьшается, а потом растет, называется полуметаллом. [11]
Примесными полупроводниками называются такие, которые превращаются в полупроводники при наличии в них определенных примесей. [12]
Примесными полупроводниками называются такие кристаллические тела, которые становятся полупроводниками при наличии в них примесей, нарушающих обычное кристаллическое строение. [13]
Рассмотрим примесный полупроводник, содержащий, например, донорные примеси. Концентрацию примесей будем считать малой по сравнению с критической концентрацией 7VC, при которой происходит моттовский переход металл — диэлектрик ( см.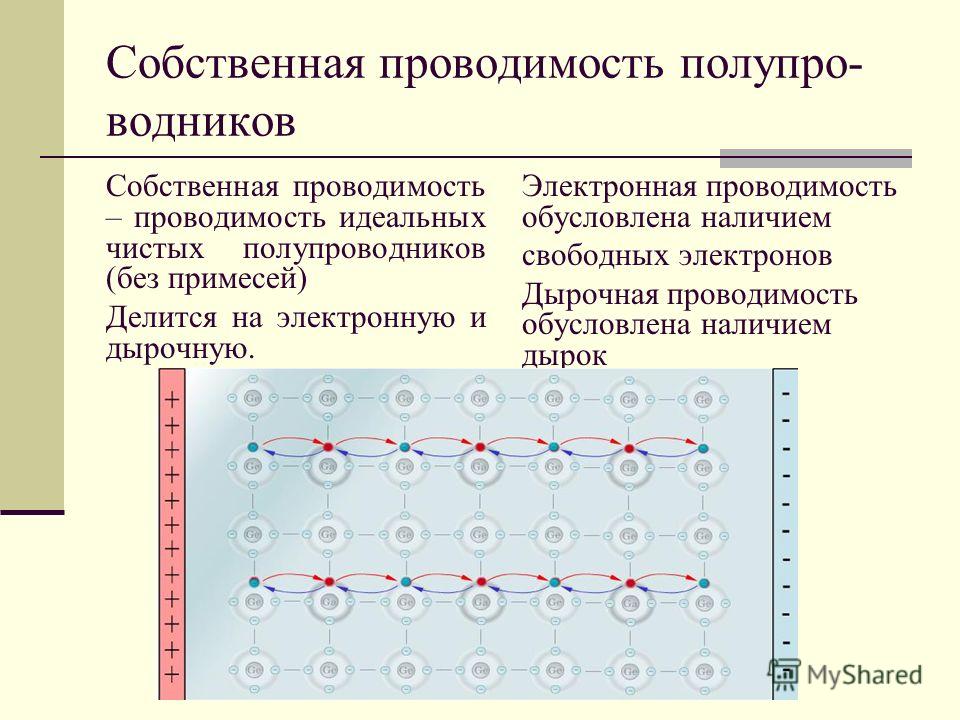 гл. При этих условиях перекрытие электронных оболочек соседних примесных атомов мало. Поэтому каждый донор можно рассматривать как изолированный водородоподобный атом, внешний электрон которого находится на расстоянии порядка а Б от ядра и имеет энергию связи порядка Е Б ( гл. Допустим, что температура столь низка, что тепловой энергии колеблющихся атомов недостаточно, чтобы отрывать электроны от доноров. Как же осуществляется при этом электропроводность.
[14]
гл. При этих условиях перекрытие электронных оболочек соседних примесных атомов мало. Поэтому каждый донор можно рассматривать как изолированный водородоподобный атом, внешний электрон которого находится на расстоянии порядка а Б от ядра и имеет энергию связи порядка Е Б ( гл. Допустим, что температура столь низка, что тепловой энергии колеблющихся атомов недостаточно, чтобы отрывать электроны от доноров. Как же осуществляется при этом электропроводность.
[14]
Такие примесные полупроводники называются электронными или полупроводниками п-типа. [15]
Страницы: 1 2 3 4
1.3. Электропроводность примесных полупроводников | Электротехника
Химически чистые полупроводники используют в полупроводниковой технике в основном в качестве исходного материала, на базе которого получают примесные полупроводники. За счет введения примеси можно значительно улучшить электропроводность полупроводника, создав в нем существенное преобладание одного какого-либо типа подвижных носителей заряда – дырок или электронов. В зависимости от валентности атомов примеси получают полупроводники с преобладанием либо электронной, либо дырочной электропроводности. Сочетание областей с разным типом электропроводности позволяет придать полупроводниковым приборам различные свойства. Примесь вводится в очень малом количестве: один атом примеси на 106 – 108 атомов исходного полупроводника. При этом атомная кристаллическая решетка не нарушается.
В зависимости от валентности атомов примеси получают полупроводники с преобладанием либо электронной, либо дырочной электропроводности. Сочетание областей с разным типом электропроводности позволяет придать полупроводниковым приборам различные свойства. Примесь вводится в очень малом количестве: один атом примеси на 106 – 108 атомов исходного полупроводника. При этом атомная кристаллическая решетка не нарушается.
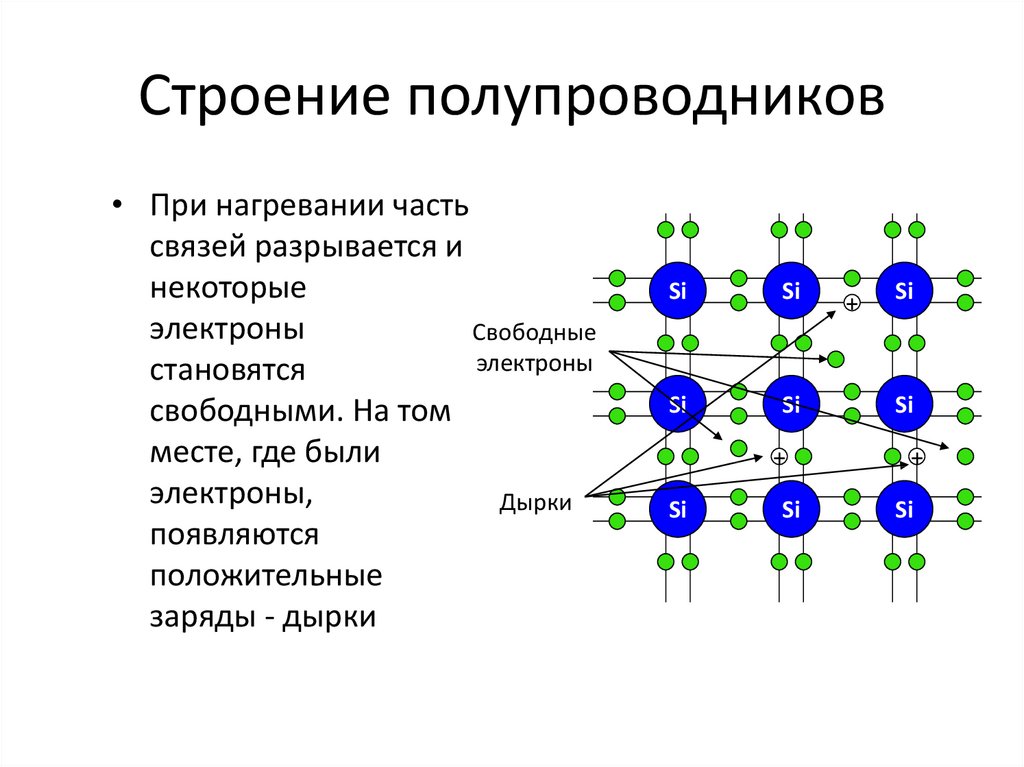
При введении в четырехвалентный полупроводник, например кристалл кремния или германия, примеси пятивалентного химического элемента (мышьяка, сурьмы, фосфора) атомы примеси замещают атомы исходного вещества в некоторых узлах кристаллической решетки (рис. 1.6, а). Четыре валентных электрона атома примеси создают ковалентные связи с четырьмя соседними атомами исходного полупроводника, а пятый электрон, не занятый в связи, оказывается избыточным и легко отрывается от атома. На его отрыв требуется затратить существенно меньшую энергию, чем на разрыв ковалентной связи, так что уже при комнатной температуре избыточные электроны атомов примеси становятся свободными.
Атом примеси, потерявший один электрон, превращается в неподвижный положительный ион, связанный в узле кристаллической решетки, т.е. происходит ионизация атомов примеси. Положительный заряд иона примеси компенсируется отрицательным зарядом свободного электрона, и слой полупроводника с примесью остается электрически нейтральным, если свободный электрон не уходит из этого слоя. В случае ухода электрона в другие слои полупроводникового кристалла неподвижные заряды ионов примеси образуют нескомпенсированный положительный объемный заряд.
Примесь, атомы которой отдают электроны, называют донорной, При введении донорной примеси концентрация электронов в кристалле резко возрастает. Она определяется в основном концентрацией атомов примеси. Одновременно происходит генерация пар «электрон – дырка», но количество электронов, возникающих при этом, значительно меньше, чем количество электронов, отдаваемых донорами. Поэтому концентрация электронов становится значительно выше концентрации дырок:
nn>> pn.
Электрический ток в таком полупроводнике создается в основном электронами, т.е. преобладает электронная составляющая тока. Полупроводник, обладающий преимущественно электронной электропроводностью, называют полупроводником n-типа. В таком полупроводнике электроны являются основными носителями заряда, а дырки – неосновными носителями заряда.
Поскольку содержание примесей невелико, атомы примеси можно рассматривать, как отдельные, не взаимодействующие друг с другом. Тогда их энергетические уровни соответствуют уровням отдельного атома и не расщепляются в кристалле на зоны. Такие местные уровни называют локальными.
На энергетической диаграмме полупроводника n-типа (рис. 1.6, б) введение донорной примеси отражается появлением в запрещенной зоне вблизи зоны проводимости близко друг от друга расположенных локальных уровней энергии, занятых избыточными валентными электронами атомов доноров при температуре абсолютного нуля. Число этих локальных уровней энергии равно числу атомов примеси в кристалле. На рисунке эти уровни показаны штрихами.
На рисунке эти уровни показаны штрихами.
Ширина зоны ∆Wд равна разности между энергией нижнего уровня зоны проводимости и локального валентного уровня донора в запрещенной зоне. Она очень мала и составляет 0,01 – 0,07 эВ в зависимости от выбранного полупроводника и материала примеси. Этим объясняется то, что при комнатной температуре почти все электроны с локальных донорных уровней переходят в зону проводимости и могут участвовать в создании электрического тока.
При введении в кристалл кремния или германия примеси трехвалентного химического элемента (например, индия, алюминия, бора или
галлия) атом примеси, войдя в узел кристаллической решетки, образует своими тремя валентными электронами только три ковалентные связи с соседними атомами четырехвалентного полупроводника (рис. 1.7, а). Для четвертой связи у него не хватает одного электрона; она оказывается
незаполненной, т.е. создается дырка. Для заполнения этой связи атом примеси может захватить электрон из ковалёнтной связи соседнего атома, так как требуемая для перехода электрона энергия в этом случае невелика. В результате присоединения лишнего валентного электрона атом примеси превращается в неподвижный отрицательный ион, а в соседней ковалентной связи, откуда этот электрон ушел, появляется дырка.
В результате присоединения лишнего валентного электрона атом примеси превращается в неподвижный отрицательный ион, а в соседней ковалентной связи, откуда этот электрон ушел, появляется дырка.
Положительный заряд дырки компенсирует отрицательный заряд иона примеси, и слой кристалла остается электрически нейтральным. В случае прихода в данный слой электрона из другого слоя и рекомбинации его с дыркой неподвижные заряды ионов примеси создают нескомпенсированный отрицательный объемный заряд.
Примесь, атомы которой захватывают электроны соседних атомов, называют акцепторной. Введение акцепторной примеси приводит к образованию избыточного числа дырок, концентрация которых значительно превышает концентрацию электронов, возникающих вследствие разрушения ковалентных связей полупроводника:
рp > np.
В электрическом токе, возникающем в таком полупроводнике, преобладает дырочная составляющая. Полупроводник с преобладанием дырочной электропроводности называют полупроводником р-типа.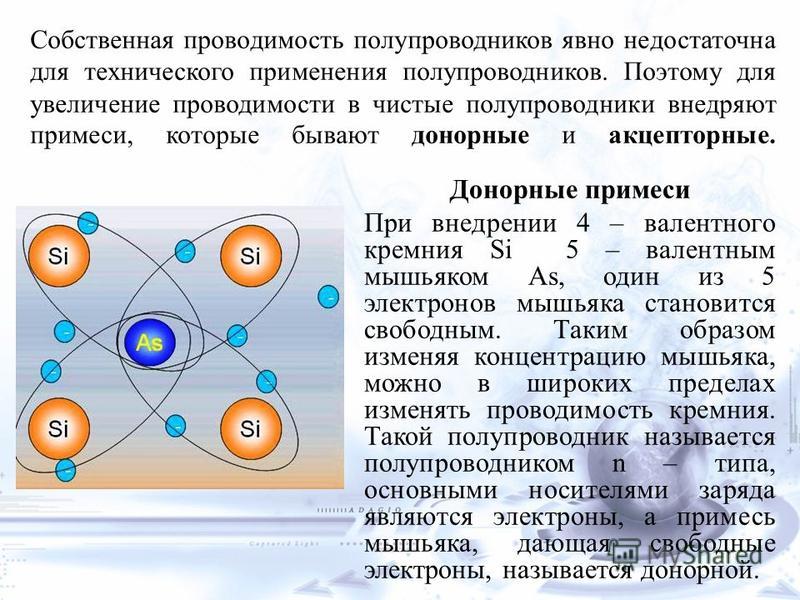 В таком полупроводнике дырки являются основными носителями заряда, а электроны – неосновными носителями заряда.
В таком полупроводнике дырки являются основными носителями заряда, а электроны – неосновными носителями заряда.
Энергетическая диаграмма полупроводника р-типа представлена на рис. 1.7, б. Локальные уровни энергии атомов акцепторной примеси (показаны штрихами) расположены в запрещенной зоне вблизи валентной зоны исходного полупроводника. Все эти уровни свободны при температуре абсолютного нуля, а число их соответствует количеству атомов примеси в кристалле. Величина энергии ∆Wд равна разности между энергией акцепторного уровня и верхнего уровня валентной зоны. Она, как и величина ∆Wд для полупроводников n-типа, мала и составляет 0,01 – 0,07 эВ в зависимости от материала исходного полупроводника и примеси. Поэтому при комнатной температуре все акцепторные уровни энергии оказываются занятыми электронами, которые переходят на них из валентной зоны. В результате в валентной зоне появляется большое количество вакантных уровней – дырок.
Таким образом, в примесных полупроводниках основные носители заряда появляются главным образом за счет атомов примеси, а неосновные – за счет разрушения ковалентных связей и вызванной этим генерации пар носителей заряда. Концентрация основных носителей заряда превышает на два-три порядка концентрацию неосновных носителей. При этом удельная электрическая проводимость примесного полупроводника превышает удельную проводимость собственного полупроводника в сотни тысяч раз.
Концентрация основных носителей заряда превышает на два-три порядка концентрацию неосновных носителей. При этом удельная электрическая проводимость примесного полупроводника превышает удельную проводимость собственного полупроводника в сотни тысяч раз.
Кроме кремния и германия в качестве исходных полупроводниковых материалов в промышленности применяют арсенид галлия, селен, оксиды, карбиды и другие химические соединения элементов III и V групп, а также II и VI групп периодической системы Менделеева.
3.3. Примесные полупроводники. 3. Полупроводниковые материалы. Химия радиоматериалов. Курс лекций
3.3.1. Донорные примеси
3.3.2. Акцепторные примеси
3.3.3. Основные и неосновные носители зарядов
Для большинства полупроводниковых приборов используются примесные полупроводники. Поэтому в практике важное значение имеют такие полупроводниковые материалы, у которых ощутимая концентрация собственных носителей заряда наблюдается при достаточно высокой температуре, т. е. с большой шириной запрещенной зоны. Поставщиками свободных носителей зарядов в рабочем интервале температур в таких ПП являются примеси.
е. с большой шириной запрещенной зоны. Поставщиками свободных носителей зарядов в рабочем интервале температур в таких ПП являются примеси.
Примесями в простых полупроводниках являются чужеродные атомы. В химических же соединениях это не только чужеродные атомы, но и атомы тех самых элементов, избыточные по стехиометрическому составу. Кроме того, роль примесей играют дефекты кристаллической решетки.
Рассмотрим роль примесей, атомы которых создают дискретные энергетические уровни в запрещенной зоне полупроводника.
3.3.1. Донорные примеси
Если в кристаллическую решетку IV валентного элемента ввести атом элемента с валентностью V, то четыре электрона на его внешней оболочке свяжутся с четырьмя атомами IV валентного элемента, а один электрон становится избыточным, слабосвязанным со своим атомом. Он под вличнием тепловой энергии начнет свободно блуждать по полупроводнику, а под воздействием электрического поля он станет направленно перемещаться (электропроводность типа n ), а атом, отдавший электрон, будет неподвижно находиться в данном месте решетки полупроводника.
Рис. 3.2 Схематическое изображение кристаллической решетки Ge с донорной примесью мышьяка.
С точки зрения энергетических диаграмм донорные примеси образуют заполненные энергетические уровни в запрещенной зоне вблизи дна зоны проводимости. При этом энергия активации примесных атомов меньше ширины запрещенной зоны, поэтому при нагреве тела переброс электронов примеси будет опережать возбуждение электронов решетки.
Рис. 3.3. Энергетическая диаграмма донорного полупроводника.
3.3.2. Акцепторные примеси
Если в решетку IV валентного полупроводника ввести III элемент, например, бор, то он установит три ковалентные связи с атомами германия, для связи с четвертым атомом германия у атома бора нет электрона. Таким образом, у нескольких атомов германия будет по одному электрону без ковалентной связи. Достаточно теперь небольших внешних воздействий, чтобы эти электроны покинули свои места, образовав дырки у атомов германия. Освободившиеся электроны, захваченные атомами бора, не могут создать электрический ток. А дырки у атомов германия позволяют электронам с соседних атомов перейти на них, освобождая другие дырки. Т.о., положительно заряженная дырка будет перемещаться по кристаллу, а под действием поля возникает примесный дырочный ток.
Освободившиеся электроны, захваченные атомами бора, не могут создать электрический ток. А дырки у атомов германия позволяют электронам с соседних атомов перейти на них, освобождая другие дырки. Т.о., положительно заряженная дырка будет перемещаться по кристаллу, а под действием поля возникает примесный дырочный ток.
Рис. 3.4. Схематическое изображение кристаллической решетки Ge с акцепторной примесью In.
С точки зрения зонной теории, акцепторная примесь образует незаполненные энергетические уровни в запрещенной зоне вблизи потолка валентной зоны. Тепловое возбуждение будет в первую очередь перебрасывать электроны из валентной зоны на эти энергетические уровни. Ввиду разобщенности атомов примеси, электроны, заброшенные на примесные уровни, не участвуют в образовании электрического тока. Такой полупроводник будет иметь концентрацию дырок, большую концентрации электронов, перешедших из валентной зоны в зону проводимости. И его относят к полупроводнику p-типа.
Рис. 3.5. Энергетическая диаграмма акцепторного полупроводника.
3.3.3. Основные и неосновные носители зарядов
Те носители, концентрация которых в данном полупроводнике больше, носят название основных, а те, которых меньше – неосновных. Так, в полупроводнике n-типа электроны являются основными носителями зарядов, а дырки – неосновными (nn и pn соответственно). Концентрация свободных электронов в зоне проводимости может быть различной. В большинстве случаев используются слаболегированные полупроводники; электроны в этом случае заполняют незначительную часть уровней в зоне проводимости. Такое состояние называют невырожденным. В полупроводнике p-типа основные носители – дырки (pp), а неосновные – электроны (np). Примесная электропроводность для своего появления требует меньших энергетических воздействий (сотые или десятые доли электронвольта), чем собственная, поэтому она обнаруживается при более низкой температуре, чем собственная электропроводность полупроводника. В примесном полупроводнике при данной температуре справедливо соотношение:
В примесном полупроводнике при данной температуре справедливо соотношение:
p·n = ni2 (3.5)
При нормальной температуре можно считать, что все примеси ионизированы. Тогда, например, в электронном полупроводнике концентрация основных носителей:
nn » Nд, а pn » ni2/Nд
а в дырочном:
pp » Na, a np » ni2/Na.
Полупроводниковая электроника
Главная / Учёба / Учебный план / Полупроводниковая электроника
Содержание разделов дисциплины
1. Состояния электронов в твердом теле.Приближение Борна — Оппенгеймера. Фононы. Одноэлектронное уравнение с периодическим потенциалом. Функция Блоха. Квазиволновой вектор. Зона Бриллюэна. Понятие энергетической зоны. Заполнение одноэлектронных уровней носителями. Понятие дырки. Полупроводники, металлы, диэлектрики. Зонная структура Ge, Si, GaAs. Приближение эффективной массы. Уравнения для медленных амплитуд. Границы применимости приближения эффективной массы. Дно зоны проводимости в Ge, Si и GaAs (Случай простой зоны). Эффективная масса электрона. Потолок валентной зоны в Ge, Si, GaAs. Гамильтониан Латтинджера. Акцепторы и доноры. Понятие мелкой примеси.
Понятие дырки. Полупроводники, металлы, диэлектрики. Зонная структура Ge, Si, GaAs. Приближение эффективной массы. Уравнения для медленных амплитуд. Границы применимости приближения эффективной массы. Дно зоны проводимости в Ge, Si и GaAs (Случай простой зоны). Эффективная масса электрона. Потолок валентной зоны в Ge, Si, GaAs. Гамильтониан Латтинджера. Акцепторы и доноры. Понятие мелкой примеси.
Статистика электронов и дырок. Плотность состояний. Положение уровня Ферми в собственных полупроводниках. Положение уровня Ферми в легированных (некомпенсированных и компенсированных) полупроводниках.
3. Теория рассеяния.Релаксация характеристики пробной частицы. Времена релаксации энергии и импульса. Рассеяние на примесях. Межэлектронное рассеяние. Рассеяние на DO, PO, DA и PA фононах. Зависимость времен релаксации от энергии частицы.
4. Твердое тело в слабых внешних полях.
Уравнение Больцмана. Интеграл столкновений. Приближение времени релаксации. Закон Ома. Зависимость подвижности от температуры. Подвижность и диффузия. Соотношение Эйнштейна. Эффект Холла. Магнитосопротивление.
5. Носители заряда в сильном электрическом поле.Электронная температура. Горячие носители. Квазиуровни Ферми. Амбиполярная диффузия и дрейф. Эффект убегания. Межзонный и примесный пробой. Эффект Ганна. Явление стриминга в p-Ge. NEMAG. Лазер на дырках в p Ge в скрещенных Е, Н полях.
6. Явления в контактах. Диоды. Транзисторы.Энергия электронного сродства и работа выхода. Диод Шотки. Контактная разность потенциалов. Область пространственного заряда. Вольт — амперные и вольт — фарадные характеристики. Антизапорный контакт. Токи ограниченные пространственным зарядом. Полупроводниковые диоды. Контакт двух полупроводников из одного материала с разным типом легирования (p-n переход). Контактная разность потенциалов.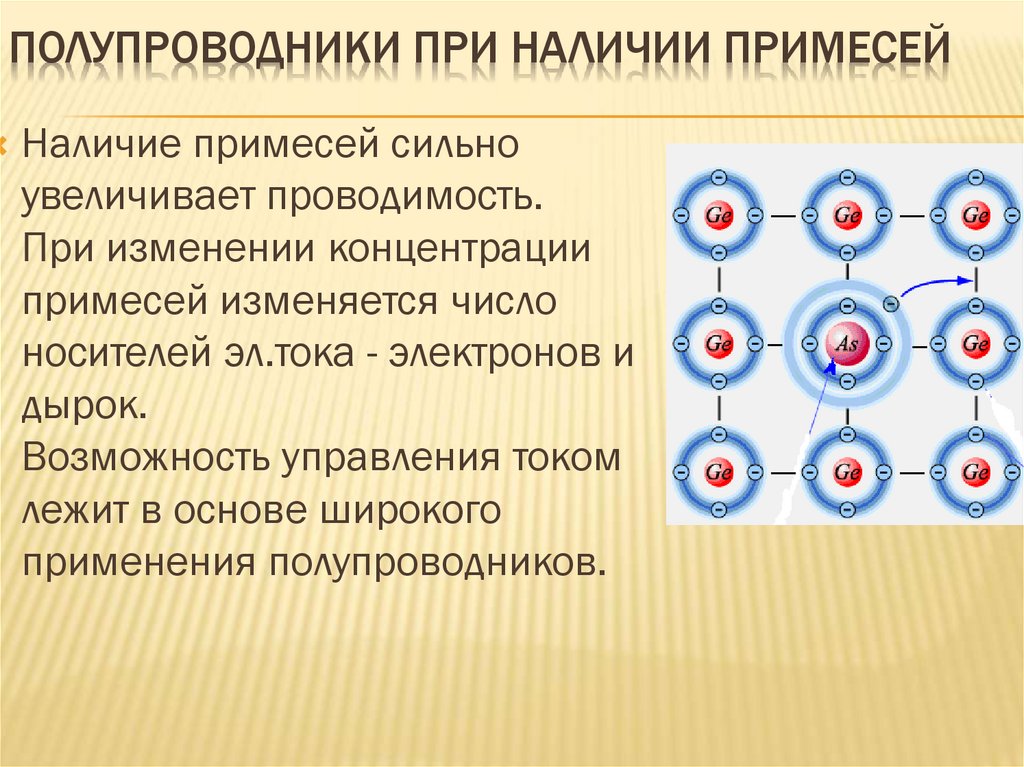 Выпрямляющие свойства. Биполярный транзистор. Гетеропереход. Разрыв зон. Гетеропереходы 1-го и 2- го рода. Граница твердого тела. Поверхностные состояния. Эффект поля. МДП и МОП структуры. Полевой транзистор
Выпрямляющие свойства. Биполярный транзистор. Гетеропереход. Разрыв зон. Гетеропереходы 1-го и 2- го рода. Граница твердого тела. Поверхностные состояния. Эффект поля. МДП и МОП структуры. Полевой транзистор
Оптические свойства полупроводников. Межзонное и примесное поглощение света. Поглощение в сильном электрическом поле. Полупроводниковые лазеры. Гетеролазеры с двойной гетероструктурой. Квантовые каскадные лазеры.
Рекомендуемая литература
Основная литература
- В.Л. Бонч-Бруевич, С. Г. Калашников. Физика полупроводников. // М.: Наука. 1977, 672 с
- Ю.Питер, Мануэль Кардона. Основы физики полупроводников// М.: Физматлит, 2002, 560 с.
- Ч. Киттель. Введение в физику твердого тела.// М.: Наука. 1978, 791
Дополнительная литература
- В.Я. Демиховский, Г. А. Вугальтер. Физика квантовых низкоразмерных структур.// М, «Логос», 2000, 248 с.
- В.
 Н. Мурзин. Субмиллиметровая спектроскопия коллективных и связанных состояний носителей тока в полупроводниках.// М.: Наука. 1985, 264 с.
Н. Мурзин. Субмиллиметровая спектроскопия коллективных и связанных состояний носителей тока в полупроводниках.// М.: Наука. 1985, 264 с.
Вопросы для контроля
- Приближения используемые для описания состояний электронов в твердом теле. Одноэлектронное уравнение с периодическим потенциалом.
- Функция Блоха. Квазиволновой вектор. Зона Бриллюэна. Понятие энергетической зоны. Заполнение одноэлектронных уровней носителями. Полупроводники, металлы, Диэлектрики.
- Уравнения для медленных амплитуд. Границы применимости приближения эффективной массы.
- Дно зоны проводимости в Ge, Si и GaAs (Случай простой зоны). Эффективная масса электрона.
- Приближение эффективной массы для вырожденной зоны. Потолок валентной зоны в Ge, Si, GaAs.
- Акцепторы и доноры. Понятие мелкой примеси. Применение приближения эффективной массы для описания мелких примесных состояний.
- Статистика электронов и дырок. Плотность состояний.
 Положение уровня Ферми в собственных полупроводниках.
Положение уровня Ферми в собственных полупроводниках. - Положение уровня Ферми в легированных полупроводниках.
- Рассеяние носителей заряда. Времена релаксации энергии и импульса.
- Рассеяние на примесях.
- Межэлектронное рассеяние.
- Рассеяние на DO, PO, DA и PA фононах.
- Зависимость времен релаксации от энергии частицы.
- Полупроводник в слабом внешнем поле. Уравнение Больцмана. Интеграл столкновений.
- Приближение времени релаксации. Время релаксации импульса и энергии
- Закон ома. Зависимость подвижности от температуры.
- Подвижность и диффузия. Соотношение Эйнштейна.
- Эффект Холла. Магнитосопротивление
- Полупроводник в сильных полях. Электронная температура. Горячие носители.
- Эффект убегания.
- Межзонный и примесный пробой.
- Эффект Ганна.
- Контакт двух твердых тел. Условие равновесия. Энергия электронного сродства и работа выхода.
 Контактная разность потенциалов. Разрывы зон.
Контактная разность потенциалов. Разрывы зон. - Контакт металл — полупроводник. Диод Шотки. Размеры области пространственного заряда.
- Воль- амперная характеристика диода Шотки. Контактная емкость.
- Контакт металл — полупроводник. Антизапорный контакт. Токи ограниченные пространственным зарядом.
- Контакт двух полупроводников из одного материала с разным типом легирования (p-n переход). Контактная разность потенциалов. Выпрямляющие свойства.
- Гетеропереход. Разрыв зон. Гетеропереходы 1-го и 2- го рода.
- Биполярный транзистор.
- Поверхностные состояния. Эффект поля. МДП и МОП структуры. Полевой транзистор
- Оптические свойства полупроводников. Межзонное и примесное поглощение света. Поглощение в сильном электрическом поле.
- Полупроводниковые.лазеры. Гетеролазеры с двойной гетероструктурой.
Легирование: n- и p-полупроводники — Основы — Технология полупроводников от А до Я
- Deutsch
- Скачать в формате PDF
- Легирование
- n-легирование
- p-легирование
- Электронная зонная структура в легированных полупроводниках
Легирование означает введение примесей в полупроводниковый кристалл с определенной модификацией проводимости.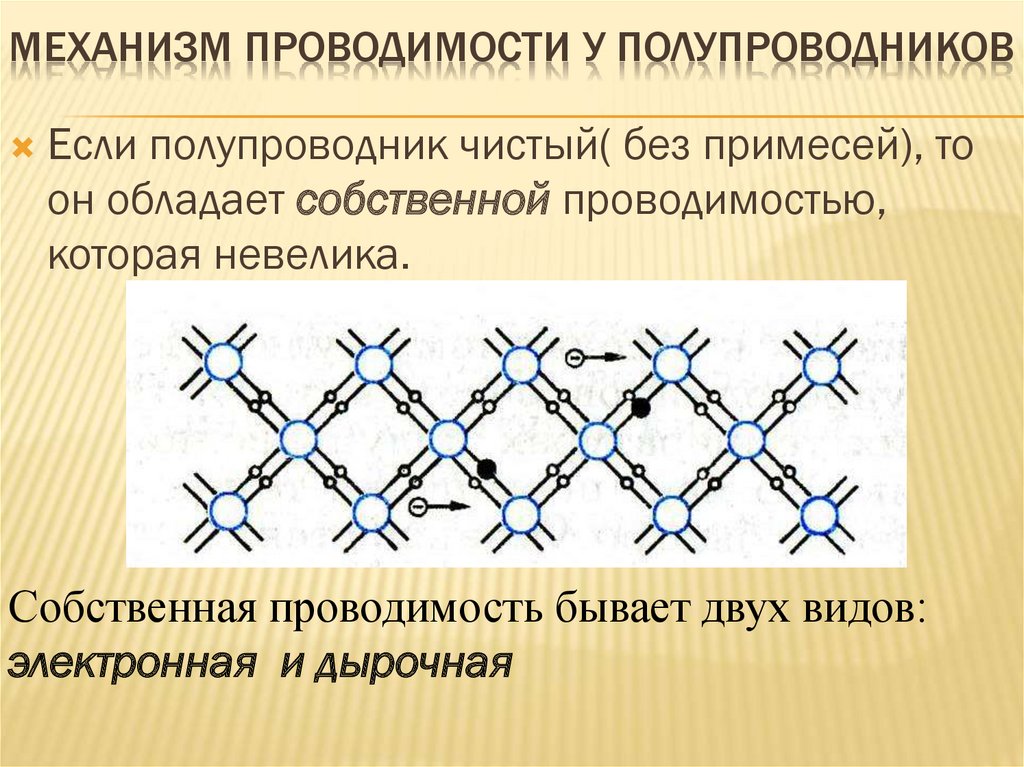 Двумя наиболее важными материалами, которыми можно легировать кремний, являются бор (3 валентных электрона = 3-валентный) и фосфор (5 валентных электронов = 5-валентный). Другими материалами являются алюминий, индий (3-валентный) и мышьяк, сурьма (5-валентный).
Двумя наиболее важными материалами, которыми можно легировать кремний, являются бор (3 валентных электрона = 3-валентный) и фосфор (5 валентных электронов = 5-валентный). Другими материалами являются алюминий, индий (3-валентный) и мышьяк, сурьма (5-валентный).
Легирующая добавка интегрируется в структуру решетки полупроводникового кристалла, количество внешних электронов определяет тип легирования. Элементы с 3 валентными электронами используются для легирования p-типа, 5-значные элементы для n-легирования. Проводимость преднамеренно загрязненного кристалла кремния может быть увеличена в 10 6 раз.
Пятивалентная примесь имеет на один внешний электрон больше, чем атомы кремния. Четыре внешних электрона соединяются с одним атомом кремния, а пятый электрон свободен в движении и служит носителем заряда. Этот свободный электрон требует гораздо меньше энергии для подъема из валентной зоны в зону проводимости, чем электроны, которые вызывают собственную проводимость кремния. Легирующая примесь, испускающая электрон, известна как донор электронов (donare, лат. = отдавать).
Легирующая примесь, испускающая электрон, известна как донор электронов (donare, лат. = отдавать).
Легирующие примеси заряжены положительно за счет потери отрицательных носителей заряда и встроены в решетку, двигаться могут только отрицательные электроны. Легированные полуметаллы, проводимость которых основана на свободных (отрицательных) электронах, относятся к n-типу или n-легированным. Из-за большего количества свободных электронов они также называются основными носителями заряда, а свободные подвижные дырки называются неосновными носителями заряда.
n-легирование фосфором
Мышьяк используется в качестве альтернативы фосфору, поскольку его коэффициент диффузии ниже. Это означает, что диффузия примеси во время последующих процессов меньше, чем у фосфора, и, таким образом, мышьяк остается в том положении, в котором он был первоначально введен в решетку.
В отличие от свободного электрона из-за легирования фосфором эффект трехвалентной легирующей примеси прямо противоположен.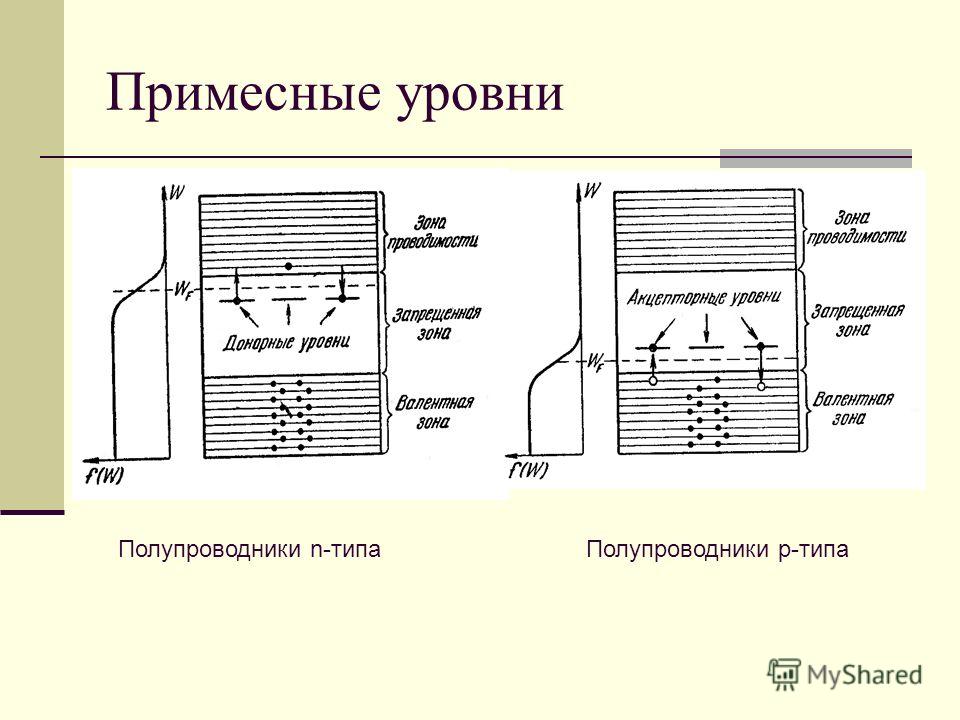 Трехвалентные примеси могут захватывать дополнительный внешний электрон, оставляя дырку в валентной зоне атомов кремния. Поэтому электроны в валентной зоне становятся подвижными. Дырки движутся в направлении, противоположном движению электронов. Энергия, необходимая для подъема электрона на энергетический уровень индия в качестве легирующей примеси, составляет всего 1 % энергии, необходимой для подъема валентного электрона кремния в зону проводимости.
Трехвалентные примеси могут захватывать дополнительный внешний электрон, оставляя дырку в валентной зоне атомов кремния. Поэтому электроны в валентной зоне становятся подвижными. Дырки движутся в направлении, противоположном движению электронов. Энергия, необходимая для подъема электрона на энергетический уровень индия в качестве легирующей примеси, составляет всего 1 % энергии, необходимой для подъема валентного электрона кремния в зону проводимости.
При включении электрона легирующая примесь заряжается отрицательно, такие примеси называются акцепторами (acceptare, лат. = прибавлять). Опять же, примесь закреплена в кристаллической решетке, двигаться могут только положительные заряды. Из-за положительных дырок эти полупроводники называются p-проводящими или p-легированными. По аналогии с n-легированными полупроводниками дырки являются основными носителями заряда, свободные электроны являются неосновными носителями заряда.
р-легирование бором
Легированные полупроводники электрически нейтральны. Термины легированные n- и p-типа относятся только к основным носителям заряда. Каждый положительный или отрицательный носитель заряда принадлежит фиксированной отрицательно или положительно заряженной легирующей примеси.
Термины легированные n- и p-типа относятся только к основным носителям заряда. Каждый положительный или отрицательный носитель заряда принадлежит фиксированной отрицательно или положительно заряженной легирующей примеси.
Полупроводники, легированные N и p, ведут себя примерно одинаково по отношению к протекающему току. С увеличением количества примесей в полупроводниковом кристалле увеличивается число носителей заряда. Здесь требуется только очень небольшое количество легирующих примесей. Слаболегированные кристаллы кремния содержат только 1 примесь на 1 000 000 000 атомов кремния, высоколегированные полупроводники, например, содержат 1 посторонний атом на 1000 атомов кремния.
При введении легирующей примеси с пятью внешними электронами в n-легированных полупроводниках электрон в кристалле не связан и, следовательно, может перемещаться с относительно небольшой энергией в зону проводимости. Таким образом, в n-легированных полупроводниках уровень энергии донора близок к краю зоны проводимости, ширина запрещенной зоны, которую необходимо преодолеть, очень мала.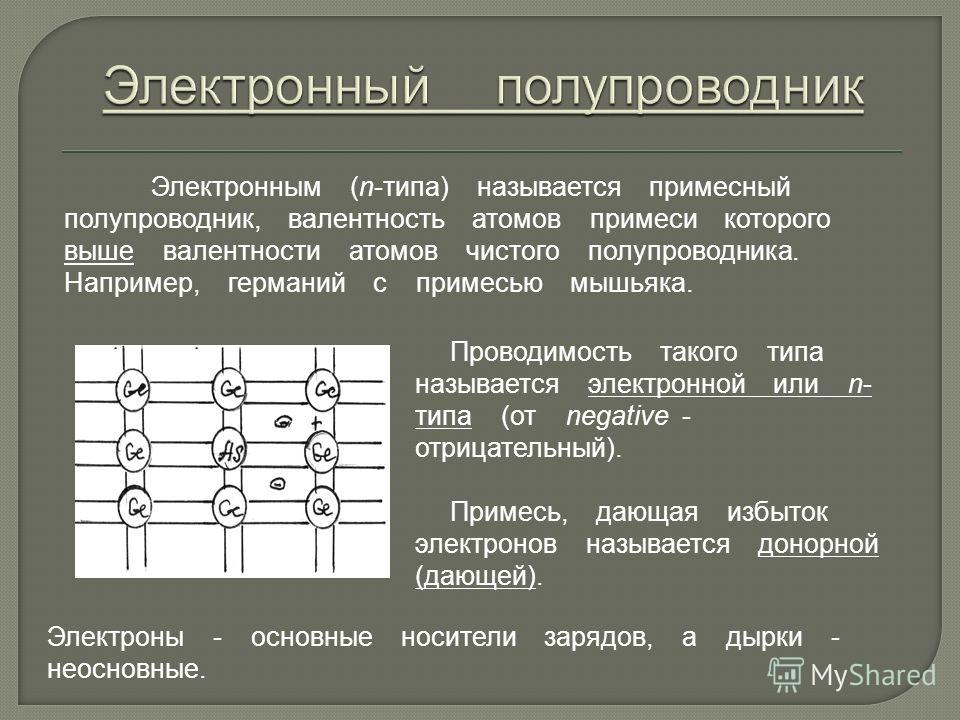
Аналог, при введении 3-валентной примеси в полупроводник появляется дырка, которая уже при низкой энергии может быть занята электроном из валентной зоны кремния. Для p-легированных полупроводников энергетический уровень акцептора близок к валентной зоне.
Ленточная модель легированных полупроводников
- Далее: p-n переход
Вдыхание
- Атомная структура
- Элементы периодической таблицы
- Химические связи
- Благородные газы
- Проводники – Изоляторы – Полупроводники
- Легирование: n- и p-полупроводники
- p-n переход
- Полевые транзисторы
- Биполярные транзисторы
- Строительство FinFET
В производстве полупроводников легирование относится к процессу преднамеренного введения примесей в чрезвычайно чистый (также называемый собственным ) полупроводником с целью изменения его электрических свойств. Некоторые примеси обычно добавляются по мере выращивания (обычно кремниевой) були, что придает каждой пластине почти однородное начальное легирование. Чтобы определить элементы схемы, выбранные области (обычно контролируемые фотолитографией) [1] дополнительно легируются такими процессами, как диффузия [2] и ионная имплантация, причем последний метод более популярен в больших производственных циклах из-за его лучшей управляемости. . Количество атомов легирующей примеси, необходимое для создания разницы в способности полупроводника к проводимости, очень мало. Когда добавляется сравнительно небольшое количество атомов легирующей примеси (порядка 1 на каждые 100 000 000 атомов), то легирование называется низким или легким. Дополнительные рекомендуемые знания
Легирующие элементыПолупроводники группы IV Для полупроводников группы IV, таких как кремний, германий и карбид кремния, наиболее распространенными легирующими добавками являются элементы группы III или группы V. (Номер группы относится к римским цифрам столбцов в периодической таблице элементов. При легировании чистого кремния элементами группы V, такими как фосфор, добавляются дополнительные валентные электроны, которые отсоединяются от отдельного атома (UTC) и позволяют соединению быть электропроводящим полупроводником n-типа. Легирование элементами группы III, такими как бор, у которых отсутствует четвертый валентный электрон, создает «разорванные связи» или дыры в решетке кремния, которые могут свободно двигаться. Это электропроводящий полупроводник p-типа. В этом контексте говорят, что элемент группы V ведет себя как электрон донор , а элемент группы III как акцептор . КомпенсацияВ большинстве случаев присутствуют многие типы примесей. Если в полупроводнике присутствует равное количество доноров и акцепторов, дополнительные остовные электроны, обеспечиваемые первыми, будут использоваться для удовлетворения разорванных связей из-за вторых, так что легирование не создает свободных носителей ни одного типа. Это явление известно как компенсация и происходит на p-n переходе в подавляющем большинстве полупроводниковых устройств. Частичная компенсация, когда доноров больше, чем акцепторов, или наоборот, позволяет производителям устройств неоднократно изменять тип данной части материала путем последовательного применения все более высоких доз легирующих примесей. Хотя компенсация может использоваться для увеличения или уменьшения количества доноров или акцепторов, подвижность электронов и дырок всегда уменьшается при компенсации, поскольку на подвижность влияет сумма донорных и акцепторных ионов. Легирование органических проводников
Проводящие полимеры могут быть «легированы» путем добавления химических реагентов для окисления (или иногда восстановления) системы, чтобы вытолкнуть электроны на проводящие орбитали внутри уже (потенциально) проводящей системы. Причина, по которой легирование встречается гораздо реже, заключается в том, что атмосфера Земли богата кислородом, что создает окислительную среду. ИсторияДопинг был первоначально разработан Джоном Робертом Вудъярдом, работавшим в компании Sperry Gyroscope во время Второй мировой войны. [3] Требования его военной работы над радаром лишили Вудьярда возможности продолжить это направление исследований, но после войны его патент стал основанием для обширных судебных разбирательств со стороны Сперри Рэнд. [4] . Связанная работа была проделана в Bell Labs Тилом и Спарксом. [5] См. также
| |
| Эта статья находится под лицензией GNU Free Documentation License. Он использует материал из статьи Википедии «Допинг_(полупроводник)». Список авторов есть в Википедии. |
9.7: Полупроводники и легирование — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4546
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описать изменения энергетической структуры полупроводника из-за к допингу
- Различают полупроводники n-типа и p-типа
- Опишите эффект Холла и объясните его значение
- Рассчитать заряд, дрейфовую скорость и количество носителей заряда плотность полупроводника с использованием информации об эффекте Холла эксперимент
В предыдущем разделе мы рассмотрели только вклад в
электрический ток из-за того, что электроны занимают состояния в
зона проводимости. Однако перемещение электрона из валентной зоны
в зону проводимости выходит из незанятого состояния или дырка в энергетической структуре валентной зоны,
куда может двигаться ближайший электрон. Поскольку эти дыры заполнены
другие электроны, создаются новые дырки. Электрический ток
связанное с этим заполнением, можно рассматривать как коллективное движение
множества отрицательно заряженных электронов или движение
положительно заряженные электронные дырки.
Однако перемещение электрона из валентной зоны
в зону проводимости выходит из незанятого состояния или дырка в энергетической структуре валентной зоны,
куда может двигаться ближайший электрон. Поскольку эти дыры заполнены
другие электроны, создаются новые дырки. Электрический ток
связанное с этим заполнением, можно рассматривать как коллективное движение
множества отрицательно заряженных электронов или движение
положительно заряженные электронные дырки.
Для иллюстрации рассмотрим одномерную решетку на рис.
\(\PageIndex{1}\). Предположим, что каждый атом решетки вносит один
валентный электрон к току. Так как отверстие справа
заполнено, это отверстие перемещается влево. Течение можно интерпретировать
как поток положительного заряда влево. Плотность отверстий,
или количество отверстий на единицу объема, представлено как стр . Каждый электрон, перешедший в зону проводимости
оставляет после себя дыру. Если полоса проводимости изначально пуста,
плотность электронов проводимости p равна дырочной
плотность, т. е. \(n = p\).
е. \(n = p\).
Как уже упоминалось, полупроводник представляет собой материал с заполненным валентная зона, незаполненная зона проводимости и относительно небольшой энергетический зазор между полосами. Избыточные электроны или дырки могут быть вводится в материал путем замещения в кристалле решетки примесного атома, представляющего собой атом слегка другое число валентности. Этот процесс известен как легирование. За Например, предположим, что мы добавили атом мышьяка в кристалл кремния. (Рисунок \(\PageIndex{2a}\)).
Рисунок \(\PageIndex{2}\): (а) донорная примесь и (б) акцепторная примесь. Введение в примеси и акцепторы в полупроводник существенно изменяет электронную свойства этого материала. У мышьяка пять валентных электронов, тогда как у кремния только
четыре. Поэтому этот дополнительный электрон должен перейти в проводимость
зоне, так как в валентной зоне нет места. Ион мышьяка
оставленный позади имеет чистый положительный заряд, который слабо связывает
делокализованный электрон. Связывание слабое, потому что окружающие
атомная решетка экранирует электрическое поле иона. В результате
энергия связи дополнительного электрона составляет всего около 0,02 эВ. В
Другими словами, энергетический уровень примесного электрона находится в
ширина запрещенной зоны ниже зоны проводимости на 0,02 эВ, гораздо меньшее значение
чем энергия щели 1,14 эВ. При комнатной температуре это
примесный электрон легко возбуждается в зону проводимости и
поэтому вносит вклад в проводимость (рис.
\(\PageIndex{3a}\)). Примесь с дополнительным электроном называется донорная примесь , а легированный полупроводник
называется полупроводником типа n , потому что
первичные носители заряда (электроны) отрицательны.
Ион мышьяка
оставленный позади имеет чистый положительный заряд, который слабо связывает
делокализованный электрон. Связывание слабое, потому что окружающие
атомная решетка экранирует электрическое поле иона. В результате
энергия связи дополнительного электрона составляет всего около 0,02 эВ. В
Другими словами, энергетический уровень примесного электрона находится в
ширина запрещенной зоны ниже зоны проводимости на 0,02 эВ, гораздо меньшее значение
чем энергия щели 1,14 эВ. При комнатной температуре это
примесный электрон легко возбуждается в зону проводимости и
поэтому вносит вклад в проводимость (рис.
\(\PageIndex{3a}\)). Примесь с дополнительным электроном называется донорная примесь , а легированный полупроводник
называется полупроводником типа n , потому что
первичные носители заряда (электроны) отрицательны.

Добавляя больше донорных примесей, мы можем создать примесная полоса , новая энергетическая полоса, созданная легирование полупроводников, как показано на рисунке \(\PageIndex{3b}\). Уровень Ферми теперь находится между этой зоной и зоной проводимости. В комнатной температуре, многие примесные электроны термически возбуждены в зону проводимости и вносят свой вклад в проводимость. Тогда проводимость может возникать и в примесной зоне, так как вакансии там создаются. Обратите внимание, что изменение энергии электрона соответствуют изменению движения (скорости или кинетической энергии) этих носителей заряда с полупроводником, а не с массой движение самого полупроводника.
Легирование также может быть выполнено с использованием примесных атомов, которые
обычно имеют на 90 272 меньше 90 273 валентных электронов, чем
полупроводниковые атомы. Например, Al, имеющий три валентности.
электроны, можно заменить Si, как показано на рисунке
\(\PageIndex{2b}\). Такая примесь называется акцепторная примесь , а легированный полупроводник
называется полупроводником p типа , потому что
первичные носители заряда (дырки) положительны. Если отверстие
рассматривается как положительная частица, слабо связанная с примесным узлом,
затем в запрещенной зоне чуть выше
валентная полоса. Когда это состояние заполняется электроном
термически возбуждается из валентной зоны (рис.
\(\PageIndex{1a}\)), в валентной зоне создается подвижная дырка.
Добавляя больше акцепторных примесей, мы можем создать примесную полосу,
как показано на рисунке \(\PageIndex{1b}\).
Если отверстие
рассматривается как положительная частица, слабо связанная с примесным узлом,
затем в запрещенной зоне чуть выше
валентная полоса. Когда это состояние заполняется электроном
термически возбуждается из валентной зоны (рис.
\(\PageIndex{1a}\)), в валентной зоне создается подвижная дырка.
Добавляя больше акцепторных примесей, мы можем создать примесную полосу,
как показано на рисунке \(\PageIndex{1b}\).
Электрический ток легированного полупроводника может быть обусловлен
движение основного носителя , в котором отверстия
вклад примесного атома или из-за меньшинства носитель , в котором отверстия созданы исключительно за счет теплового
возбуждения электронов через энергетическую щель. В n Полупроводник типа , основными носителями являются свободные электроны
вклад примесных атомов, а неосновные носители свободны
электроны, произведенные тепловыми возбуждениями из валентной в
зона проводимости.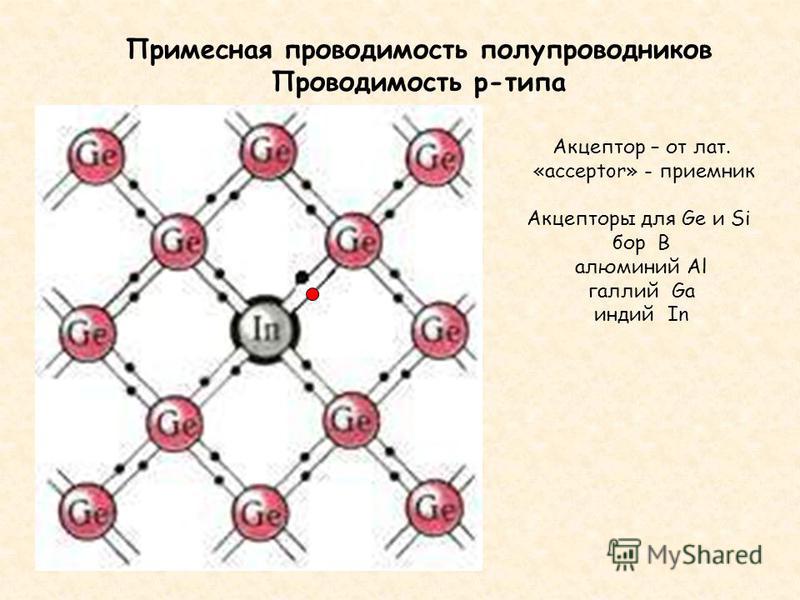 В полупроводнике типа р большинство
носителями являются свободные дырки, вносимые примесными атомами, а неосновные
носители — это свободные дыры, оставленные заполнением состояний из-за
тепловое возбуждение электронов через щель. В целом,
число мажоритарных перевозчиков намного превышает количество мажоритарных перевозчиков.
будет использоваться понятие мажоритарных и миноритарных перевозчиков.
следующий раздел, чтобы объяснить работу диодов и
транзисторы.
В полупроводнике типа р большинство
носителями являются свободные дырки, вносимые примесными атомами, а неосновные
носители — это свободные дыры, оставленные заполнением состояний из-за
тепловое возбуждение электронов через щель. В целом,
число мажоритарных перевозчиков намного превышает количество мажоритарных перевозчиков.
будет использоваться понятие мажоритарных и миноритарных перевозчиков.
следующий раздел, чтобы объяснить работу диодов и
транзисторы.
При изучении легирования p — и n Естественно задаться вопросом: действительно ли «электронные дырки» ведут себя как частицы? существование дырок в легированном полупроводнике типа p продемонстрировано Эффект Холла. Эффект Холла – это возникновение потенциального разница из-за движения проводника через внешнюю магнитное поле. Схема эффекта Холла показана на рисунке. \(\PageIndex{5a}\).
Рисунок \(\PageIndex{5}\): Эффект Холла. (а) Положительно заряженные электронные дырки притягиваются влево однородное магнитное поле, направленное вниз.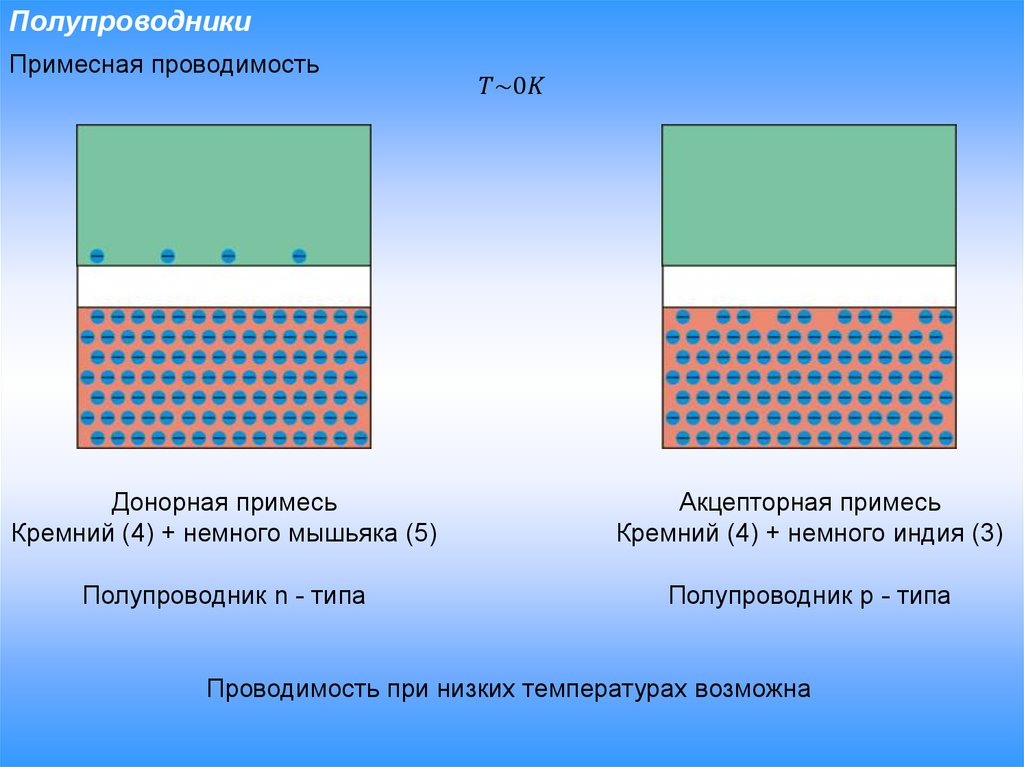 Электрическое поле
генерируется вправо. б) Отрицательно заряженные электроны притягиваются к
слева магнитным полем, направленным вверх. Электрическое поле
генерируется слева.
Электрическое поле
генерируется вправо. б) Отрицательно заряженные электроны притягиваются к
слева магнитным полем, направленным вверх. Электрическое поле
генерируется слева.Полупроводниковая полоска находится в однородном магнитном поле. (который указывает на бумагу). Когда электронные дырки движутся слева прямо через полупроводник силы Лоренца движут эти заряды к верхнему концу полосы. (Напомним, что движение положительно заряженных носителей определяется Правило правой руки.) Положительный заряд продолжает накапливаться на верхней края полосы до тех пор, пока сила, связанная с движением вниз электрическое поле между верхним и нижним краями полосы (\(F_E = E_q\)) просто уравновешивает направленную вверх магнитную силу (\(F_B = qvB\)). Приравнивая эти силы друг к другу, имеем \(E = ВБ\). Таким образом, напряжение, возникающее на полосе, равно
\[V_H = vBw, \номер \]
где \(V_H\) — напряжение Холла; \(v\) — дырка дрейфовая скорость , или средняя скорость частицы
который движется частично случайным образом; Б это
напряженность магнитного поля; а w — ширина полосы.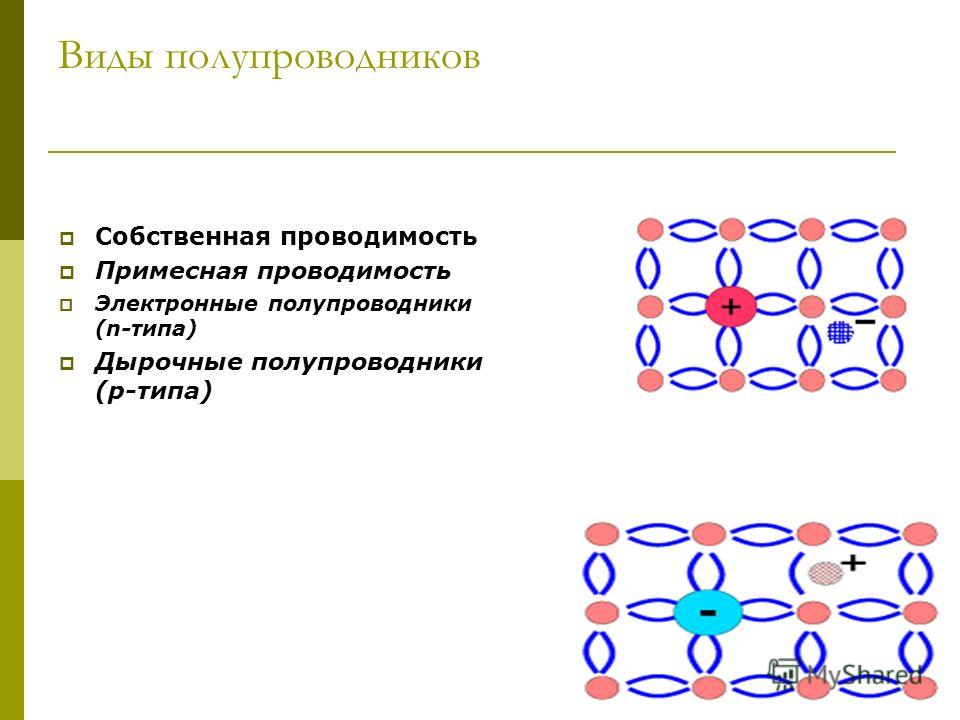 Обратите внимание, что напряжение Холла поперечно напряжению, которое
первоначально производит ток через материал. Измерение
знак этого напряжения (или разности потенциалов) подтверждает
набор отверстий на верхней стороне полосы. Величина
напряжение Холла дает скорость дрейфа ( v )
большинство перевозчиков.
Обратите внимание, что напряжение Холла поперечно напряжению, которое
первоначально производит ток через материал. Измерение
знак этого напряжения (или разности потенциалов) подтверждает
набор отверстий на верхней стороне полосы. Величина
напряжение Холла дает скорость дрейфа ( v )
большинство перевозчиков.
Дополнительную информацию также можно получить из Холла Напряжение. Обратите внимание, что плотность электронного тока (количество ток на единицу площади поперечного сечения полупроводниковой ленты) равно
\[j = nqv, \label{eq3} \]
, где q — величина заряда, n —
количество носителей заряда в единице объема, а v равно
скорость дрейфа. Плотность тока легко определяется по формуле
делим общий ток на площадь поперечного сечения
полоса, q — заряд дырки (величина
заряд одного электрона), а u определяется выражением
Уравнение \ref{eq3}. Следовательно, приведенное выше выражение для электрона
плотность тока дает количество носителей заряда на единицу
том, n .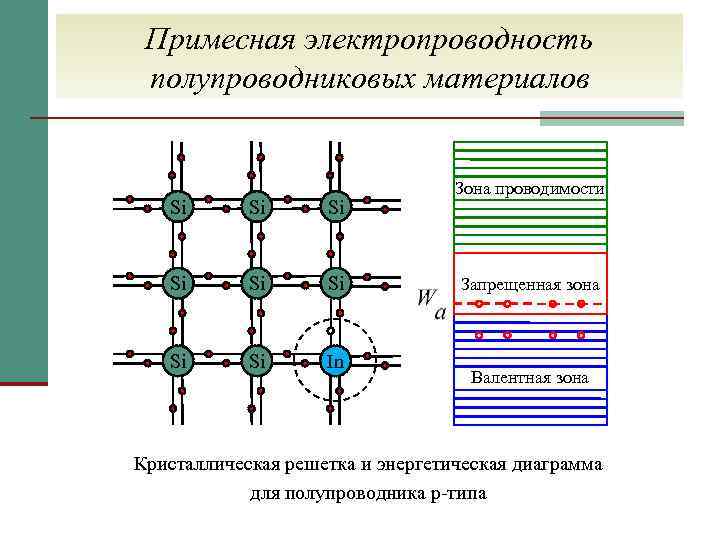 Аналогичный анализ можно провести для
отрицательно заряженные носители в материале типа n (см.
Рисунок \(\PageIndex{5}\)).
Аналогичный анализ можно провести для
отрицательно заряженные носители в материале типа n (см.
Рисунок \(\PageIndex{5}\)).
Эта страница под названием 9.7: Полупроводники и допинг распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Метки
- акцепторная примесь
- донорная примесь
- допинг
- скорость дрейфа
- отверстие
- примесный атом
- примесная полоса
- мажоритарная несущая
- малый перевозчик
- полупроводник n-типа
- полупроводник p-типа
- источник@https://openstax.
 org/details/books/university-physics-volume-3
org/details/books/university-physics-volume-3
Объяснение урока: Легированные полупроводники | Нагва
В этом объяснении мы узнаем, как описать эффект легирования полупроводник влияет на его электрические свойства.
Для начала вспомним некоторые основные сведения о полупроводниках. Полупроводники обладают проводящими свойствами, которые находятся где-то между изоляторами. и проводники. Специализированные свойства полупроводников позволяют нам контролировать их проводимость некоторыми уникальными и полезными способами. Напомним, что чистый полупроводник состоит из одного типа элемента, чаще всего из кремния, и не содержит другие примеси.
Нейтральный атом кремния имеет четыре электрона на внешней электронной оболочке, и
когда они сгруппированы вместе, атомы образуют решетку, разделяя ковалентные связи с
соседние атомы. Эта конфигурация решетки показана на диаграмме ниже.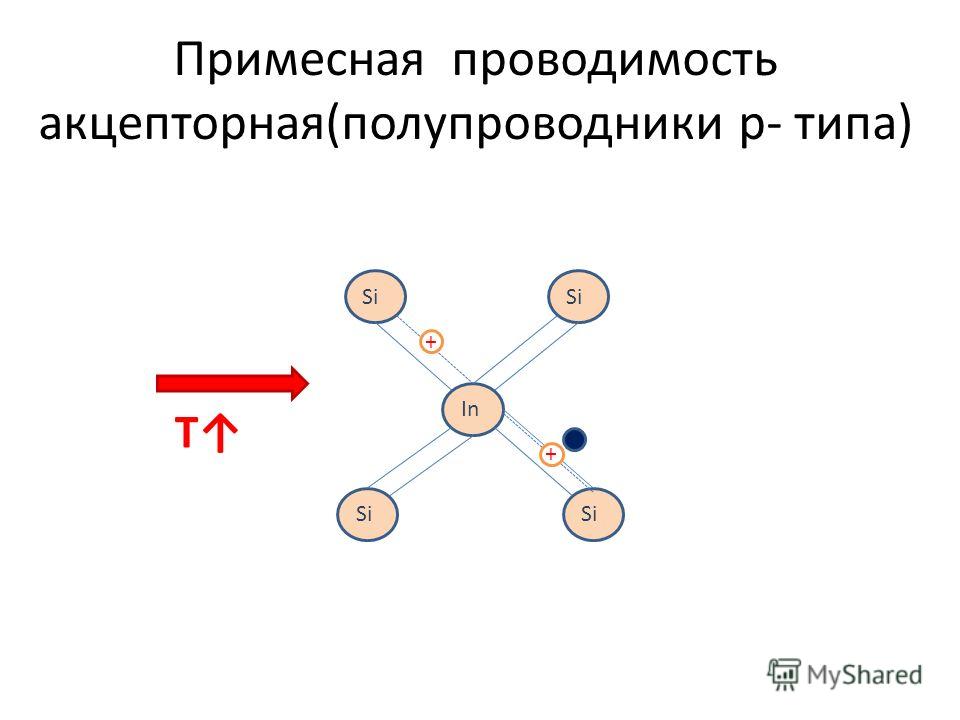 Примечание
что показаны только самые внешние электроны для каждого атома.
Примечание
что показаны только самые внешние электроны для каждого атома.
Любой внутренний или центральный атом имеет соседний атом сверху, снизу, слева, и правильно, поэтому его окружают четыре пар электронов. Это общее из восьми электронов заполняет внешнюю оболочку атома. Атомы с более полным самые внешние электронные оболочки более изолирующие, поэтому мы полагаемся на определенные методы сделать полупроводник более проводящим.
Одним из способов увеличения проводимости чистого полупроводникового материала является
повысить его температуру. В этом случае, если достаточно тепловой энергии передается в
электрон, он может преодолевать свою атомную связь и двигаться по решетке как
свободный электрон. Когда электрон освобождается, он оставляет после себя дырку или вакансию.
который имеет эффективный положительный заряд. Когда другой свободный электрон из
решетки приблизится к вакансии, электрон заполнит дырку, потеряв
энергии и связывается с атомом. Этот процесс представляет собой цикл
передача энергии между свободными и связанными электронами и дырками. Такой
свободное движение заряда — это то, как чистый полупроводник способен проводить
электричество.
Этот процесс представляет собой цикл
передача энергии между свободными и связанными электронами и дырками. Такой
свободное движение заряда — это то, как чистый полупроводник способен проводить
электричество.
Следует особо отметить, что для чистого полупроводника в тепловом равновесия любая электронная дырка соответствует свободному электрону, покинувшему дырку на своем месте. Таким образом, количество свободных электронов, представленное 𝑛, равно число электронных дырок, 𝑝, так что атомная решетка остается электрически нейтральный.
Если температура полупроводника увеличивается, его проводимость также увеличивается потому что больше электронов могут получить энергию, необходимую им для освобождения. Другой, более эффективный способ увеличить проводимость полупроводника состоит в том, чтобы «одурить» его, что мы и рассмотрим в оставшейся части этого объяснения.
Легировать полупроводник означает ввести еще один элемент в атомную решетку.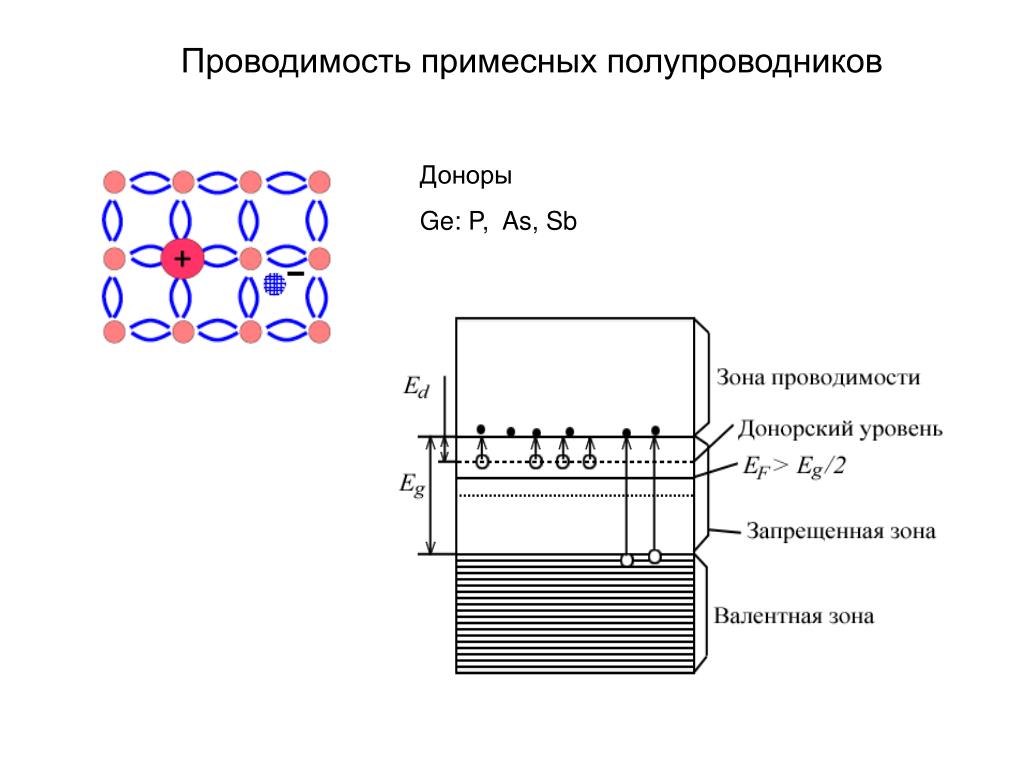 Таким образом, мы добавляем в материал «примеси», чтобы он больше не
«чистый» или состоящий из одного элемента. Мы видели, что
нейтральный атом кремния имеет четыре крайних электрона, что позволяет создать решетку
образование, в котором каждый внутренний атом Si имеет полную внешнюю электронную оболочку. В этом объяснении мы исследуем, что происходит, когда внутренний атом кремния
заменяется другим элементом с другим числом
крайние электроны, в частности, либо на один больше, либо на один меньше. Таким образом,
мы будем использовать элемент, который (когда он нейтрален) имеет либо три, либо пять
крайние электроны.
Таким образом, мы добавляем в материал «примеси», чтобы он больше не
«чистый» или состоящий из одного элемента. Мы видели, что
нейтральный атом кремния имеет четыре крайних электрона, что позволяет создать решетку
образование, в котором каждый внутренний атом Si имеет полную внешнюю электронную оболочку. В этом объяснении мы исследуем, что происходит, когда внутренний атом кремния
заменяется другим элементом с другим числом
крайние электроны, в частности, либо на один больше, либо на один меньше. Таким образом,
мы будем использовать элемент, который (когда он нейтрален) имеет либо три, либо пять
крайние электроны.
Для простоты мы сосредоточимся на одном атоме каждого типа; мы будем использовать фосфор (P) как атом с пятью крайними электронами. На приведенной ниже диаграмме показан нейтральный атом фосфора.
И мы будем использовать бор (B) в качестве атома с тремя крайними электронами.
на диаграмме ниже показан нейтральный атом бора.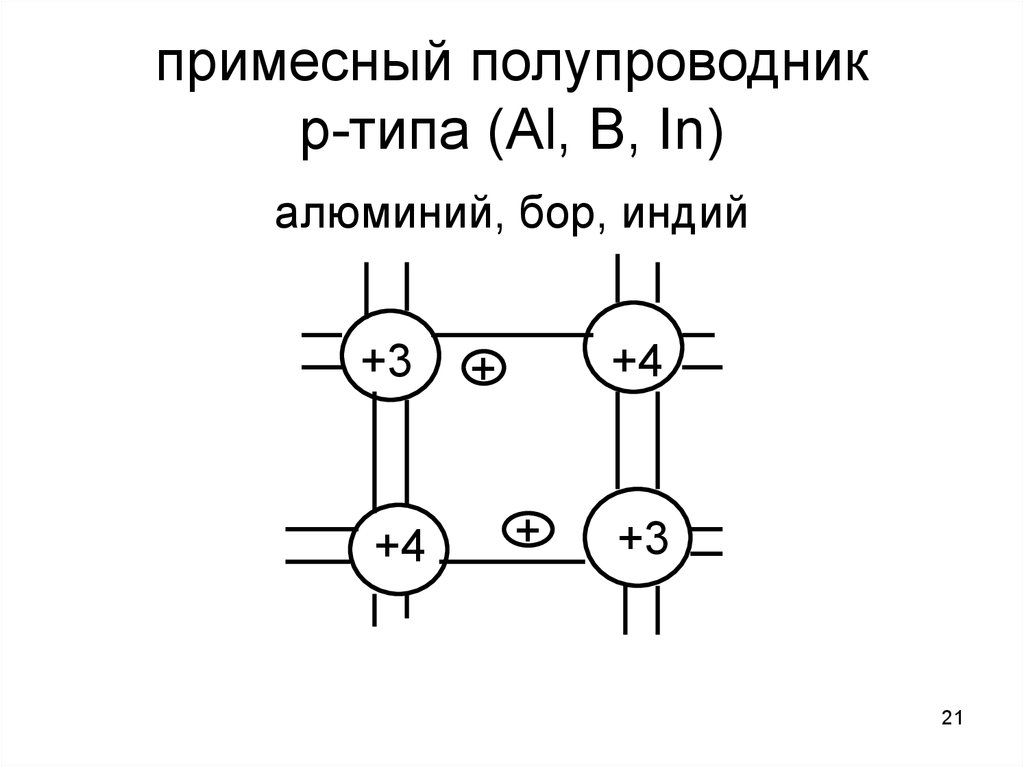
Следует отметить, что количество электронов на самой внешней оболочке определяет, как это влияет на проводимость, что мы рассмотрим ниже. Мы будем исследовать эффекты легирования фосфором и бором по отдельности.
Для начала давайте сосредоточимся на эффектах замены центрального атома кремния в решетки с атомом фосфора, как показано на схеме в примере ниже.
Вместо четырех крайних электронов, как у кремния, нейтральный фосфор атом входит в решетку с пятью крайними электронами. До восьми электронов может занимать самую внешнюю оболочку, поэтому четыре электрона атома фосфора разделены ковалентными связями, как мы видели раньше. Тем не менее, фосфор атом пришел с пятью электронами, так что есть один дополнительный электрон, который не помещается в оболочку. Таким образом, лишний электрон не связан и не участвует в ковалентная связь, поэтому вместо этого он движется по атомной решетке как свободный электрон.
Четыре из пяти электронов, с которыми пришел атом фосфора, связаны с
ядро, а один электрон теперь свободен и просто не связан ни с одним атомом. Таким образом, каждый атом фосфора, введенный в решетку, дает один свободный
электрон к материалу. Наличие большего количества свободных зарядов увеличивает проводимость
материала, поэтому мы знаем, что легирование полупроводника атомами P увеличивает
электропроводность материала в целом.
Таким образом, каждый атом фосфора, введенный в решетку, дает один свободный
электрон к материалу. Наличие большего количества свободных зарядов увеличивает проводимость
материала, поэтому мы знаем, что легирование полупроводника атомами P увеличивает
электропроводность материала в целом.
Давайте рассмотрим некоторые способы количественного выражения этого понятия.
Пример 1. Понимание электронов в легированном полупроводнике
На диаграмме показана решетка атомов кремния, которой Добавлено в. Атом фосфора имеет пять валентных электронов. Атом кремния имеет четыре валентных электрона.
- Сколько ковалентных связей образует атом фосфора с атомами кремния рядом с ним?
- Сколько свободных электронов добавляется к решетке при добавлении атома фосфора?
- Каков суммарный относительный атомный заряд фосфора?
после добавления в решетку?
- +4
- +1
- 0
- −1
- -4
Ответ
Часть 1
. атомов: по одному сверху, снизу, слева и справа. Таким образом, внутренний атом в
решетке, такой как атом фосфора, показанный выше, может иметь четыре набора ковалентных связей.
связи с соседними атомами. Напомним, что каждая ковалентная связь состоит из
два электрона — это дает в общей сложности восемь электронов, окружающих
атом, который завершает внешнюю электронную оболочку.
атомов: по одному сверху, снизу, слева и справа. Таким образом, внутренний атом в
решетке, такой как атом фосфора, показанный выше, может иметь четыре набора ковалентных связей.
связи с соседними атомами. Напомним, что каждая ковалентная связь состоит из
два электрона — это дает в общей сложности восемь электронов, окружающих
атом, который завершает внешнюю электронную оболочку.
Таким образом, атом фосфора образует 4 ковалентные связи с соседним кремнием атомы.
Часть 2
Нейтральный атом фосфора имеет пять электронов на внешней оболочке. Таким образом, когда атом P вводится в решетку, он имеет четыре соседних атома Si образовывать ковалентные связи с. Таким образом, четыре из пяти электронов, Атом P стал связан с соседними атомами.
На внешней оболочке атома P может находиться до восьми электронов. Поскольку имеется четыре ковалентных связи (и, следовательно, восемь электронов) сразу
окружающая атом, самая внешняя оболочка заполнена и не может вместить последнюю
электрон, с которым пришел атом фосфора.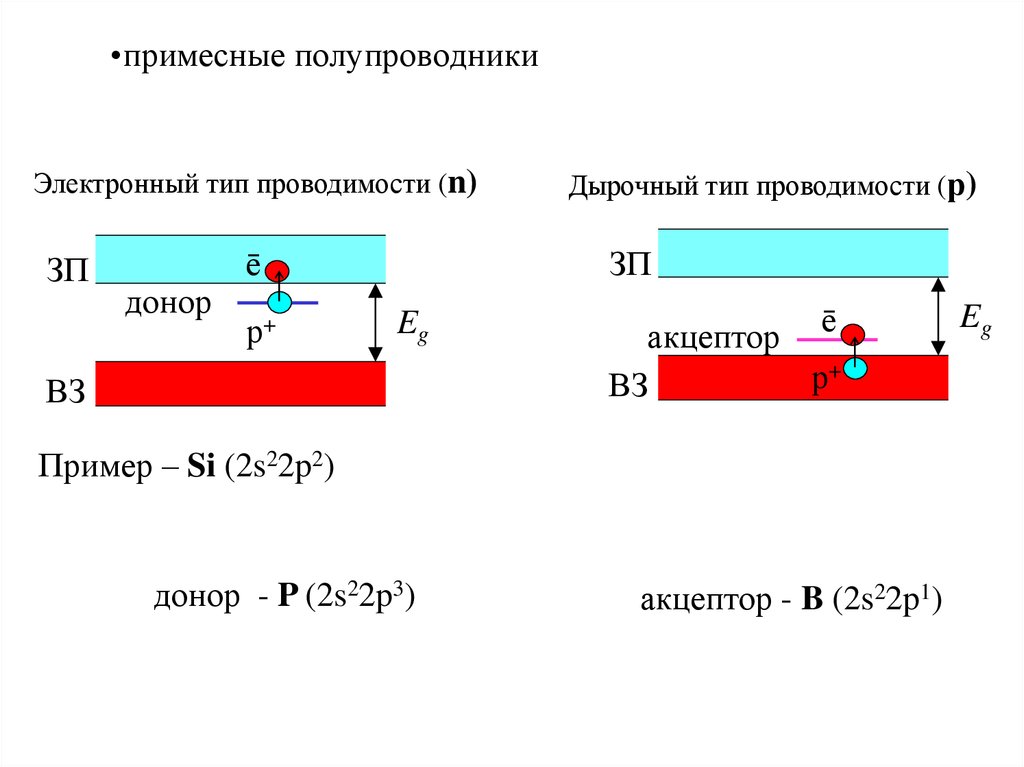 Поскольку один лишний электрон
не может быть связан с атомом P, теперь это свободный электрон.
Поскольку один лишний электрон
не может быть связан с атомом P, теперь это свободный электрон.
Следовательно, атом фосфора добавляет к решетке 1 свободный электрон.
Часть 3
Атом фосфора потерял один электрон, с которым он пришел. Так как фосфор атом потерял один электрон, который имеет относительный заряд -1, мы можем сказать что заряд -1 был вычтен из атома, что привело к чистой положительный заряд.
Таким образом, суммарный относительный заряд атома фосфора равен +1, и ответ вариант Б правильный.
Прежде чем мы продолжим, давайте быстро установим несколько ключевых словарных терминов: мы будем
используйте термины трехвалентный , четырехвалентный ,
и пятивалентный для описания атома числом электронов в его внешней оболочке. Например, вспомним, что у кремния на внешней оболочке четыре электрона.
поэтому он считается четырехвалентным, поскольку «тетра-» означает «четыре». Кроме того, атом бора имеет три крайних электрона, поэтому он трехвалентен.
а фосфор пятивалентен, потому что у него пять крайних электронов. Окончательно,
любой атом, используемый для легирования образца, называется «легирующей примесью».
Кроме того, атом бора имеет три крайних электрона, поэтому он трехвалентен.
а фосфор пятивалентен, потому что у него пять крайних электронов. Окончательно,
любой атом, используемый для легирования образца, называется «легирующей примесью».
Приведенный выше пример объясняет, почему нейтральный атом фосфора присоединяется к нейтральному атому кремния. Решетка имеет чистый относительный заряд +1. Из-за этого чистого положительного заряда мы можем назвать этот атом фосфора (или любой пятивалентный атом, используемый для легирования) как «положительный донорный ион». Выражаем концентрацию положительного донора ионов с символом 𝑁D, где 𝑁 дает количество, D означает «донор», (поскольку атом «отдал» материалу электрон), а + знак относится к общему положительному заряду иона фосфора в решетке. Таким образом, концентрация фосфора в материале определяется как 𝑁D.
Помните, что в чистом нелегированном полупроводнике каждый свободный электрон создает
электронная дырка в решетке.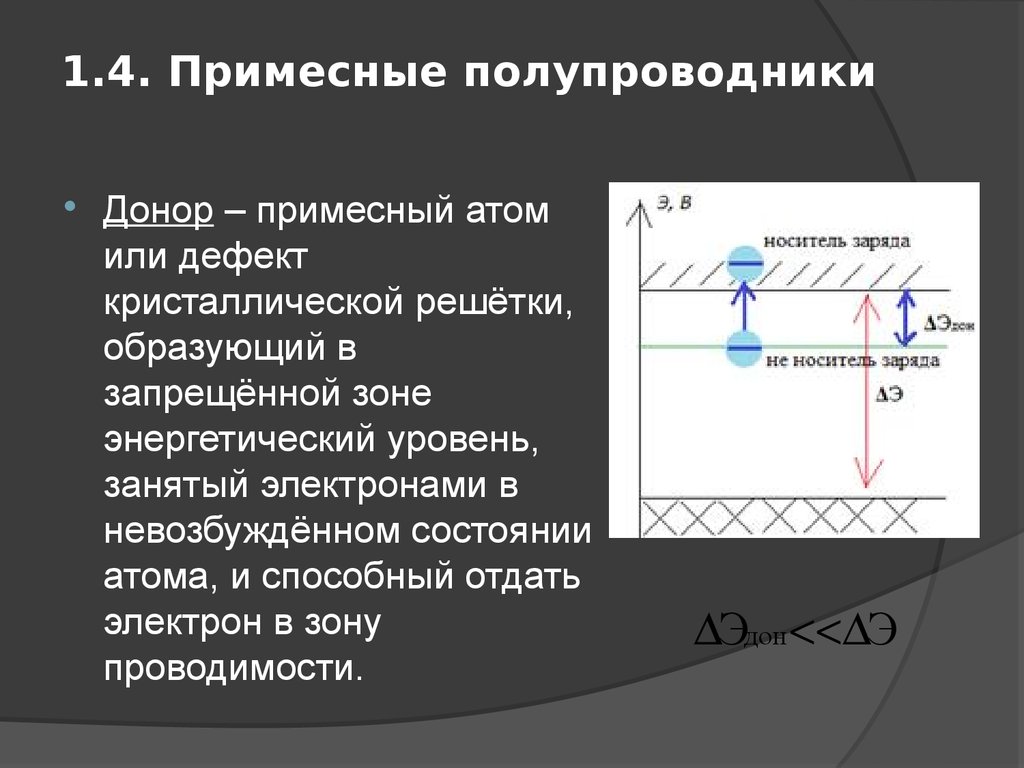 Напротив, когда ион-донор добавляет свободный электрон
к решетке, это не создает отверстия. Это важно, поскольку, когда мы видим
свободный электрон в материале с пятивалентной примесью, мы знаем, что он мог
происходят из одного из двух мест: либо положительный донорный ион, либо оборванный ковалентный
связь в четырехвалентном атоме, таком как кремний.
Напротив, когда ион-донор добавляет свободный электрон
к решетке, это не создает отверстия. Это важно, поскольку, когда мы видим
свободный электрон в материале с пятивалентной примесью, мы знаем, что он мог
происходят из одного из двух мест: либо положительный донорный ион, либо оборванный ковалентный
связь в четырехвалентном атоме, таком как кремний.
По мере легирования образца положительными донорными ионами мы увеличиваем значение 𝑁D, и поэтому мы можем сказать, что плотность свободных электронов 𝑛 будет больше плотности электронов и дырок 𝑝. По этой причине, мы можем назвать его полупроводником «𝑛-типа», который просто относится к Дело в том, что свободных электронов больше, чем электронных дырок. Это определяет один из два основных типа легированных полупроводников.
𝑛-Type Semiconductors
Полупроводниковый материал, легированный положительными донорными ионами, известен как
полупроводник 𝑛-типа. Это связано с тем, что плотность свободных электронов
𝑛 больше плотности электронов дырок 𝑝,
следуя уравнению
𝑛=𝑝+𝑁,D
где 𝑁D представляет собой плотность положительных донорных ионов.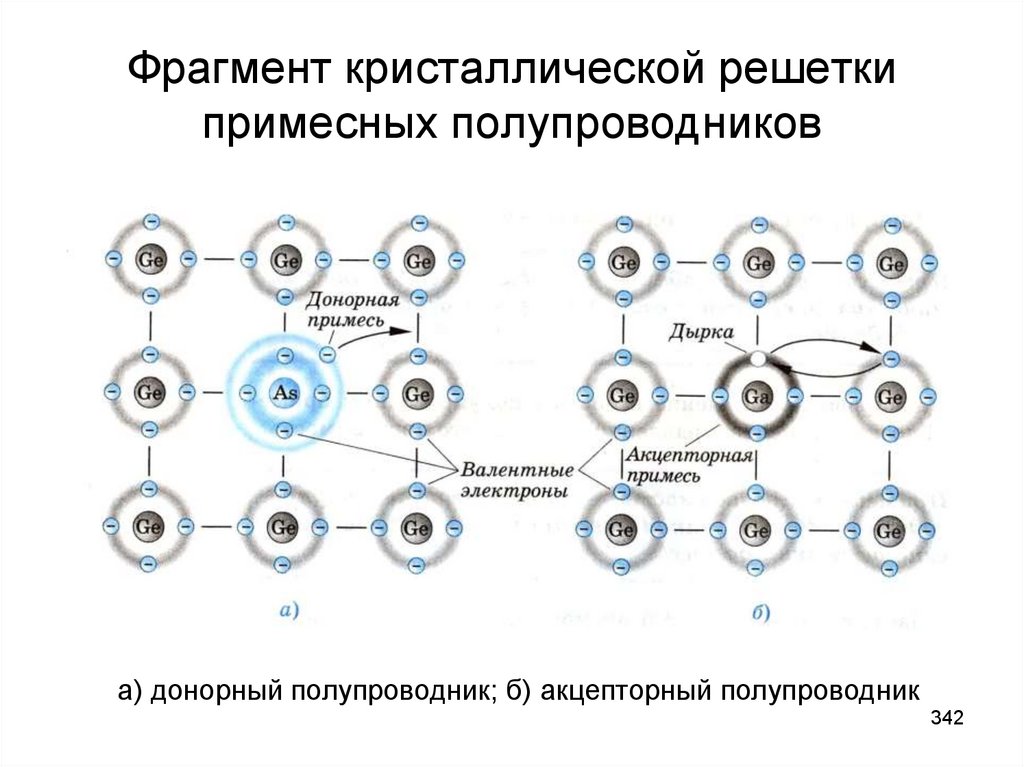
Пример 2. Концентрация свободных электронов для полупроводника 𝑛-типа
Легированный полупроводник, содержащий донорные ионы и находящийся в тепловом равновесии, моделируется с использованием трех переменных. Плотность свободных электронов в полупроводнике представлен 𝑛. Плотность донорных ионов в полупроводник представлен 𝑁D. Плотность вакансии в полупроводнике обозначены 𝑝. Какая из следующих формул правильно представляет связь между эти переменные в полупроводнике?
- 𝑛 = 𝑁 — 𝑝d
- 𝑛 = 𝑝 -𝑁d
- 𝑛 = 𝑝+𝑁d
- 𝑛 = 𝑝𝑁D
- 𝑛 = 𝑁𝑝D
Ответ
Вспользователь , для чистого полупроводника каждый свободный электрон создает и покидает за дырой в решетке. Таким образом, перед добавлением донорных ионов плотность свободных электронов равна плотности дырок, или 𝑛=𝑝.
Однако, когда мы легируем образец, донорные ионы вносят свободные электроны
без создания электронных дыр, и, следовательно, 𝑛 не равно
к 𝑝.
Когда мы добавляем больше свободных электронов через донорные ионы, плотность свободных электронов равно 𝑝 (количество до легирования) плюс 𝑁D (количество добавленных новых электронов). Это представлен в формуле 𝑛=𝑝+𝑁.D
Следовательно, правильный вариант ответа C.
Таким образом, мы видели, как введение пятивалентных атомов или атомов с еще одним самый внешний электрон, чем у кремния, к решетке Si увеличивает общее проводимость путем создания полупроводника 𝑛-типа.
Теперь рассмотрим другой тип легированного полупроводника, который можно
достигается путем введения атомов с одним внешним электроном меньше, чем у кремния, в
Си решетка. Еще раз напомним, что нейтральный атом кремния в решетке образует
ковалентные связи с соседними атомами, которые заполняют его внешнюю электронную оболочку. Теперь мы исследуем эффекты замены внутреннего атома кремния на
нейтральный атом бора, который имеет три крайних электрона.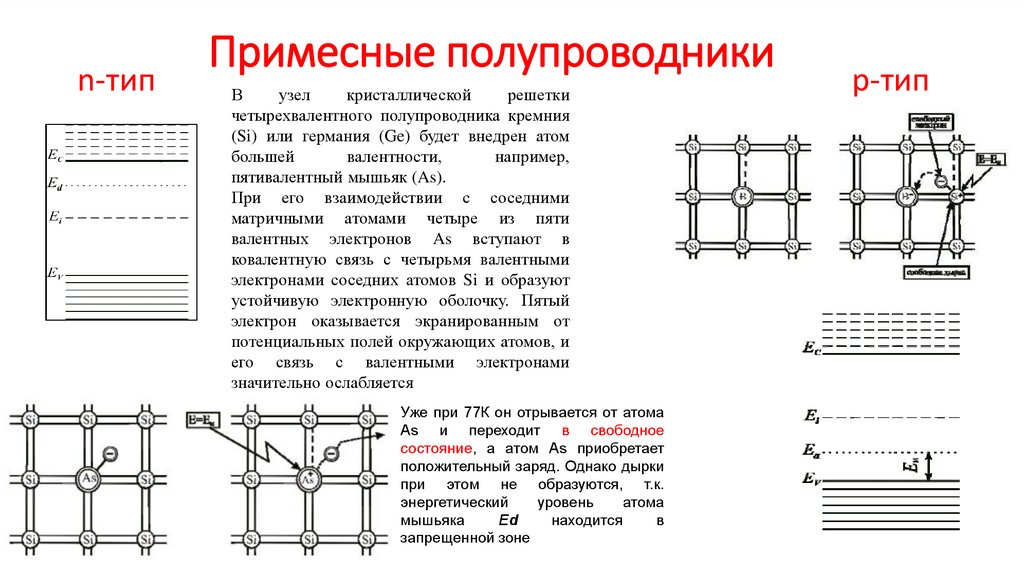
Пример 3. Электроны в легированном полупроводнике
На схеме показана решетка атомов кремния, содержащая один атом бора.
- Какое число электронов ковалентно связывает атом бора с атомы кремния, которые его окружают?
- Какое число электронов может быть ковалентно связано с атомом кремния? который занимает положение атома бора?
Ответ
Часть 1
Нейтральный атом бора имеет три из восьми возможных электронов на самом внешнем оболочка. Поскольку внутренний атом образует ковалентные связи с четырьмя соседними атомами, внутренний атом бора окружен этими четырьмя общими электронами, плюс три электрона, с которыми он пришел.
Таким образом, атом бора имеет 7 электронов, ковалентно связывающих его с соседние атомы кремния.
Часть 2
Напомним, что нейтральный атом кремния имеет четыре из восьми возможных электронов в
его внешняя оболочка.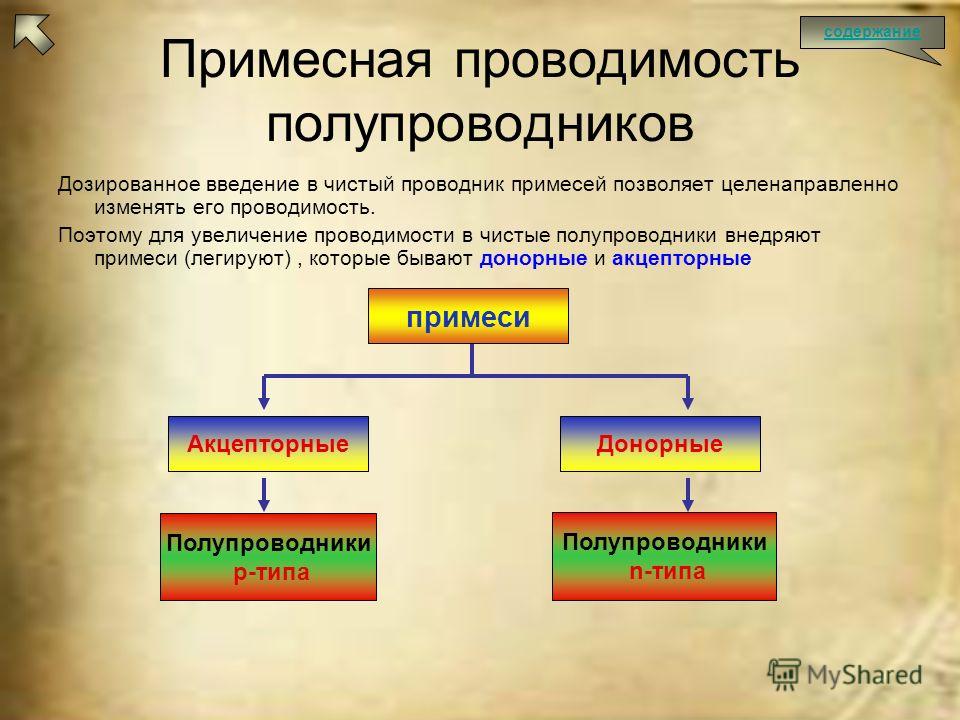 Было бы четыре атома Si, окружающие внутренний Si
атома, поэтому каждая пара атомов будет иметь общую пару электронов в ковалентной связи.
Было бы четыре атома Si, окружающие внутренний Si
атома, поэтому каждая пара атомов будет иметь общую пару электронов в ковалентной связи.
Поскольку атом Si будет иметь четыре набора ковалентных связей, будет 8 электронов ковалентно связывают его с решеткой.
В приведенном выше примере показано, как атом бора в решетке кремния имеет семь
из восьми возможных электронов, окружающих его, через ковалентные связи. Так как это делает
не содержит полных восьми электронов, которые сделали бы оболочку полной, мы можем
говорят, что в скорлупе одна дырка. Наличие этого отверстия означает, что
атом бора, скорее всего, «примет» ближайший свободный электрон в свою
самая внешняя оболочка. Таким образом, мы можем обратиться к атому бора (или любому трехвалентному атому, используемому
для легирования) как «отрицательный акцепторный ион». Мы связываем этот атом с
отрицательный заряд, потому что он попал в нейронную решетку, а с тремя
электроны, но как только он принимает свободный электрон в дырку в своем внешнем
оболочки, он становится отрицательно заряженным. Символ, часто используемый для обозначения
концентрация этих отрицательных акцепторных ионов равна 𝑁A, где
𝑁 указывает количество, A означает
«акцептор», а знак «-» указывает на отрицательный заряд
атом после того, как он примет свободный электрон.
Символ, часто используемый для обозначения
концентрация этих отрицательных акцепторных ионов равна 𝑁A, где
𝑁 указывает количество, A означает
«акцептор», а знак «-» указывает на отрицательный заряд
атом после того, как он примет свободный электрон.
Когда мы легируем материал отрицательными акцепторными ионами, мы знаем, что электрон плотность дырок 𝑝 будет больше, чем плотность свободных электронов плотность 𝑛. По этой причине можно сказать, что у нас есть Полупроводник «𝑝-типа», который просто относится к факту что электронных дырок больше, чем свободных электронов. Это определяет второй основной тип легированного полупроводника.
Полупроводники 𝑝-типа
Полупроводниковый материал, легированный отрицательными акцепторными ионами,
известный как полупроводник 𝑝-типа. Это связано с тем, что плотность электронов и дырок
𝑝 больше плотности свободных электронов
𝑛, следуя уравнению
𝑝=𝑛+𝑁,A
где 𝑁A представляет собой плотность отрицательных акцепторных ионов.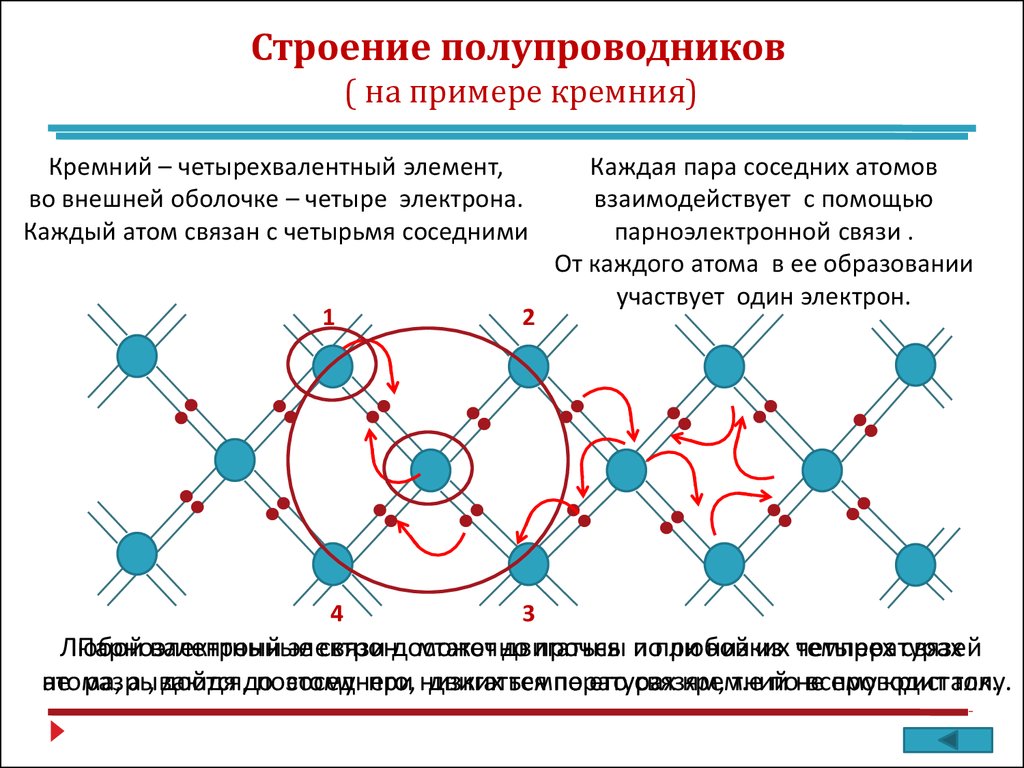
Пример 4. Концентрация электронных дырок для полупроводника 𝑝-типа
Легированный полупроводник, содержащий акцепторные ионы и находящийся в тепловом равновесии, моделируется с использованием трех переменных. Плотность свободных электронов в полупроводнике представлен 𝑛. Плотность акцепторных ионов в полупроводник представлен 𝑁A. Плотность вакансий в полупроводнике представлен 𝑝. Который из перечисленных формулы правильно представляют связь между этими переменными в полупроводник?
- 𝑝 = 𝑁+𝑛a
- 𝑝 = 𝑛 -𝑁a
- 𝑝 = 𝑁 — 𝑛a
- 𝑝 = 𝑛𝑁a
- 𝑝 = 𝑁𝑛a
Ответ
Вспользователь , для чистого нелегированного полупроводника каждая электронная дырка была
созданный и оставленный свободным электроном. Таким образом, перед акцепторными ионами
добавляются, плотность дырок равна плотности свободных электронов, или
𝑝=𝑛.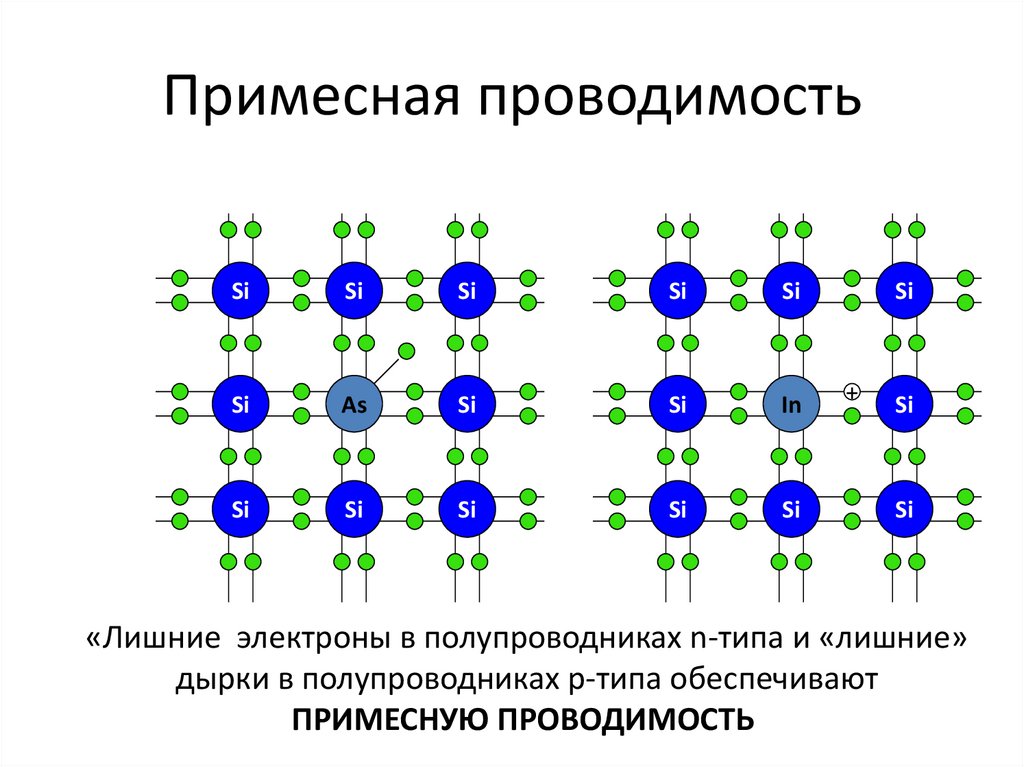
Однако, когда мы легируем образец, каждый акцепторный ион вносит одну дырку потому что есть семь из восьми возможных электронов, окружающих легирующая примесь. Поэтому, когда мы видим дырку в полупроводнике, легированном акцепторными ионами, это могло произойти либо от самой примеси, либо от разорванной ковалентной связь между исходными атомами чистого полупроводника.
Когда мы добавляем больше дырок с помощью акцепторных ионов, общая плотность дырок равна 𝑛 (сумма до допинга) плюс 𝑁A (количество новых добавленных отверстий). Это представлено в формуле 𝑝=𝑛+𝑁,A и, следовательно, вариант ответа А является правильным.
Итак, мы увидели, как создавать и описывать как 𝑛-тип, так и 𝑝-типа полупроводники.
Мы можем сделать вывод, что легирование полупроводника является более эффективным способом
чтобы обеспечить поток заряда, чем просто повышение температуры чистого образца.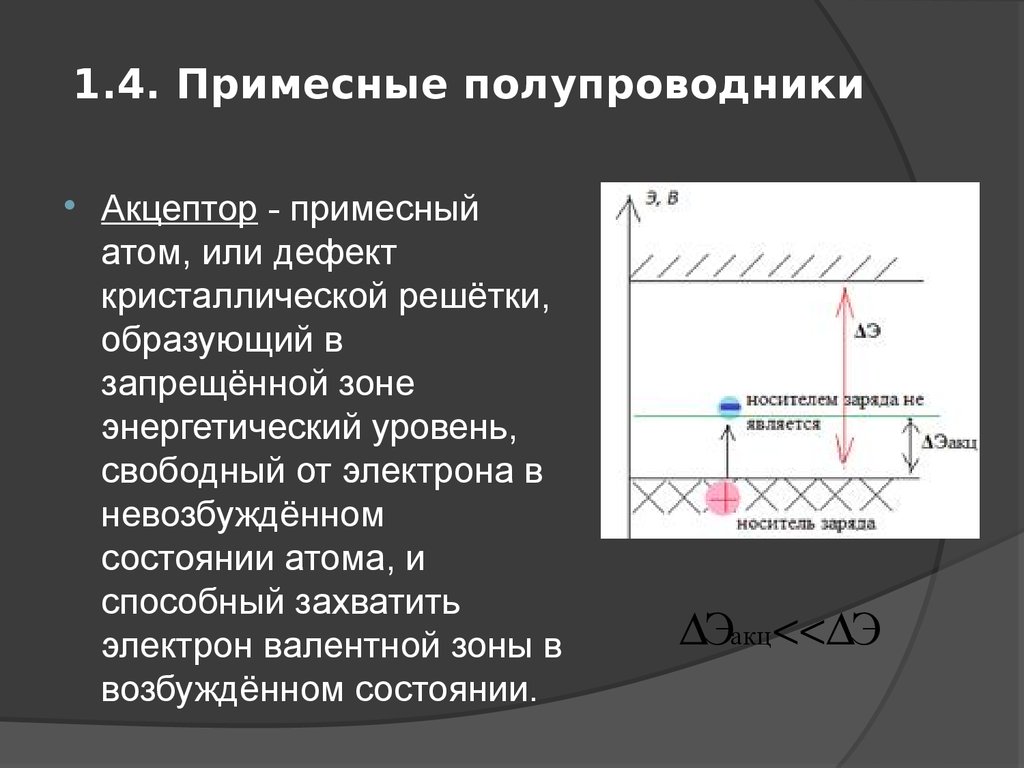 Благодаря этому мы можем применить некоторые приближения к паре уравнений
мы установили ранее.
Благодаря этому мы можем применить некоторые приближения к паре уравнений
мы установили ранее.
Во-первых, потому что добавление положительных донорных ионов намного перевешивает создание свободных электронов и дырок, созданных разрывом ковалентных связей (как мы видим в чистом образце) можно сказать, что для полупроводника 𝑛-типа 𝑛=𝑝+𝑁≈𝑁.DD
Это означает, что подавляющее большинство свободных электронов в нашем полупроводнике обусловлены легированием, поэтому величина 𝑁D намного больше, чем 𝑝.
Точно так же мы можем применить эту концепцию к случаю полупроводников 𝑝-типа: 𝑝=𝑛+𝑁≈𝑁.AA
Проще говоря, подавляющее большинство электронных дырок в нашем полупроводнике возникает из-за легирования, поэтому 𝑁A намного больше, чем 𝑛.
Давайте теперь установим еще один способ математического описания полупроводников,
используя формулу, которая хорошо резюмирует наше обсуждение как чистого, так и легированного
полупроводники.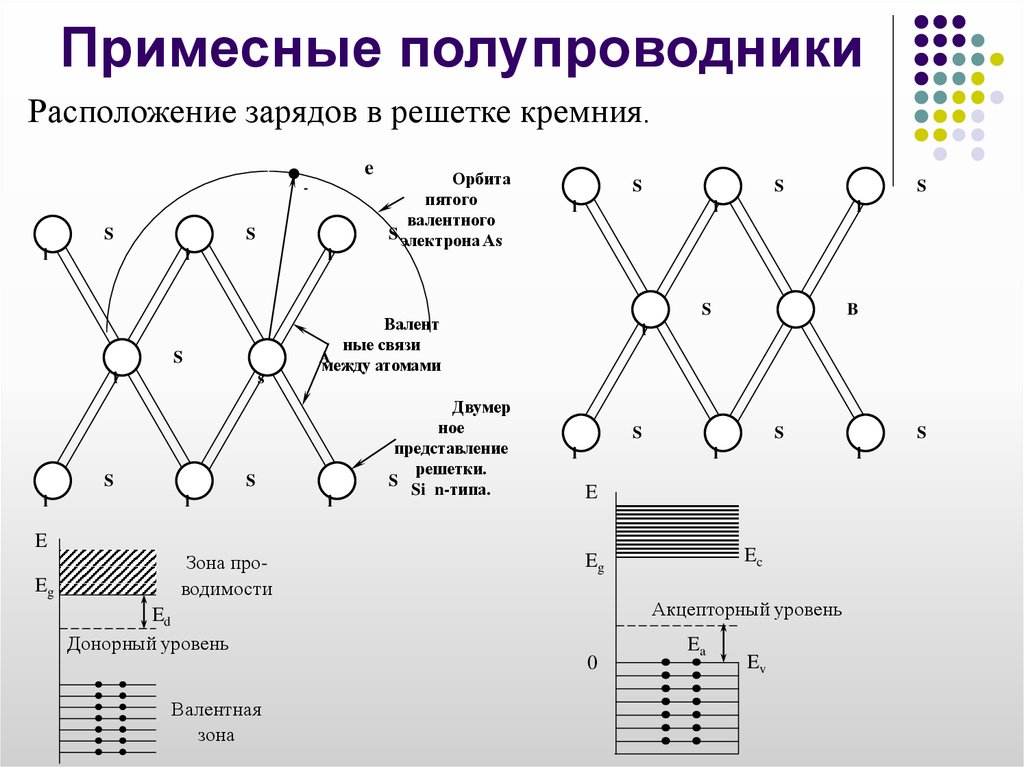 В качестве краткого обзора напомним, что для легированного полупроводника
𝑛 не обязательно должен быть равен 𝑝, но для
чистый полупроводник, эти две величины равны.
В качестве краткого обзора напомним, что для легированного полупроводника
𝑛 не обязательно должен быть равен 𝑝, но для
чистый полупроводник, эти две величины равны.
Чистые полупроводники также называются собственными полупроводниками, и мы можем использовать термин 𝑛 (где 𝑖 означает «внутренний») при их описании. Для чистый полупроводник, 𝑛 часто используется для обозначения концентрации свободных электронов и/или концентрации дырок одновременно, поскольку эти два количества равны. То есть для чистого полупроводника величины 𝑛, 𝑝 и 𝑛 равны. Мы можем разработать интересный результат от этих значений.
Ранее мы видели, что 𝑛 и 𝑝 меняются при добавлении сэмпла. Следующее уравнения помогут нам определить новые, обновленные значения этих величин.
Для начала возведем член в квадрат 𝑛. Обратите внимание, что если мы возведем в квадрат 𝑛, мы можем
говорят, что 𝑛 также эффективно представляет произведение плотности свободных
электронов, 𝑛, и плотность дырок, 𝑝,
который можно записать как 𝑛𝑝. Таким образом, мы можем установить связь между
𝑛 и 𝑝 с использованием 𝑛:
𝑛𝑝=𝑛.
Таким образом, мы можем установить связь между
𝑛 и 𝑝 с использованием 𝑛:
𝑛𝑝=𝑛.
Интересным результатом этого уравнения является то, что оно справедливо для всех полупроводников. в тепловом равновесии, а не только чистые полупроводники.
Мы уже установили, что для любого легированного полупроводника 𝑛≠𝑝. Уравнение выше описывает обратную пропорцию между этими двумя количества. Если 𝑛 увеличивается, 𝑝 должно уменьшаться, как мы видели в нашем обсуждении полупроводников 𝑛-типа. Аналогично, если 𝑝 увеличивается, 𝑛 должно уменьшаться, как мы видели в случае материалов 𝑝-типа.
В конечном счете, не имеет значения, является ли полупроводник 𝑛-типом, 𝑝-типа или полностью чистый; величина 𝑛 всегда постоянна для данного материала при данной температуре. Этот факт однозначно позволяет исследовать некоторые свойства легированных полупроводников.
Для полупроводников 𝑛-типа мы можем связать 𝑛 с плотностью
электронных дырок, 𝑝. Напомним, что добавление положительных донорных ионов
к решетке увеличивает количество свободных электронов. С большим количеством свободных электронов
дыры заполняются с большей скоростью, что снижает общую
концентрация отверстий. Мы можем найти результирующую концентрацию дырок по формуле
используя уравнение, введенное выше,
𝑛𝑝=𝑛.
Напомним, что добавление положительных донорных ионов
к решетке увеличивает количество свободных электронов. С большим количеством свободных электронов
дыры заполняются с большей скоростью, что снижает общую
концентрация отверстий. Мы можем найти результирующую концентрацию дырок по формуле
используя уравнение, введенное выше,
𝑛𝑝=𝑛.
Помните, что мы работаем в предположении, что 𝑛=𝑁D, поэтому мы можем сделать замену в формуле 𝑁𝑝=𝑛.D
Теперь мы можем найти 𝑝, разделив уравнение на 𝑁Д: 𝑝=𝑛𝑁.D
Это уравнение связывает величину 𝑛 с плотностью электронные дырки, 𝑝, для полупроводника 𝑛-типа.
Концентрация электронных дырок для полупроводника 𝑛-типа
Концентрация электронных дырок, 𝑝, для 𝑛-типа
полупроводник
𝑝=𝑛𝑁,D
где 𝑁D – концентрация положительных донорных ионов и
𝑛 — концентрация свободных электронов и дырок для
нелегированный образец.
Мы будем использовать аналогичный метод, чтобы связать 𝑛 с плотностью свободные электроны 𝑛 в полупроводнике 𝑝-типа. Напомним, что добавление отрицательных акцепторных ионов в решетку увеличивает количество дырок. При наличии большего количества дырок электроны могут заполнять дырки с большей скоростью, что уменьшается общая концентрация свободных электронов. Мы можем найти результирующая концентрация свободных электронов, начиная с уравнения 𝑛𝑝=𝑛.
В случае легирования отрицательными акцепторными ионами мы используем приближение 𝑝=𝑁А. Мы будем использовать это, чтобы заменить 𝑝-член из это уравнение так, что мы имеем 𝑛(𝑁)=𝑛.A
Находя 𝑛, формула принимает вид 𝑛=𝑛𝑁.A
Это уравнение описывает плотность свободных электронов, 𝑛, для полупроводника 𝑝-типа.
Концентрация свободных электронов для полупроводника 𝑝-типа
Концентрация свободных электронов, 𝑛, для полупроводника
полупроводник 𝑝-типа
данный
𝑛=𝑛𝑁,A
где 𝑁A — концентрация отрицательных акцепторных ионов и
𝑛 — концентрация свободных электронов и дырок для нелегированного
образец.
Завершим обсуждение легированных полупроводников резюмированием некоторых важные понятия.
Ключевые моменты
- Мы можем увеличить проводимость чистого полупроводника, повысив его температуры или путем легирования.
- Легирование включает добавление «примесей» в решетку путем добавления атомов с тремя (трехвалентными) или пятью (пятивалентными) крайними электроны.
- полупроводники 𝑛-типа, легированные пятивалентными атомами или положительными донорные ионы, концентрация которых представлена 𝑁D. Концентрация свободных электронов определяется как 𝑛=𝑝+𝑁D и равна примерно равно 𝑁D.
- полупроводники 𝑝-типа легированы трехвалентными атомами или отрицательным акцептором ионов, концентрация которых представлена 𝑁A. Концентрация дырок определяется как 𝑝=𝑛+𝑁A и приблизительно равна равно 𝑁A.
- Как для чистых, так и для легированных полупроводников 𝑛𝑝=𝑛, где
𝑛 — концентрация свободных электронов и дырок для нелегированного
образец.
 В результате концентрация электронных дырок для 𝑛-типа
полупроводник определяется как 𝑝=𝑛𝑁D. Так же и концентрация
свободных электронов для полупроводника 𝑝-типа определяется выражением
𝑛=𝑛𝑁А.
В результате концентрация электронных дырок для 𝑛-типа
полупроводник определяется как 𝑝=𝑛𝑁D. Так же и концентрация
свободных электронов для полупроводника 𝑝-типа определяется выражением
𝑛=𝑛𝑁А.
Легирование полупроводников
Электропроводность полупроводников можно увеличить, а в некоторых случаях и уменьшить во много раз. порядков за счет добавления примесей или легирующих примесей. Однокомпонентный полупроводники из столбца IV с чистой валентностью четыре. Есть два возможности для легирующей примеси:
- Донор (n-тип): Если примесь из столбца В можно заменить
в узел решетки, и дополнительный валентный электрон может диссоциировать от
своего родительского атома электрон получает возможность свободно перемещаться по всей кристаллической решетке.
 Это активация донора, добавляющая в решетку один дополнительный отрицательный носитель.
Реакция активации донора:
9-$ Такая примесь известна как донор или $n-типа$ (отрицательный). Примеры $n$-типа
примесями являются P и As в Si или Ge.
Это активация донора, добавляющая в решетку один дополнительный отрицательный носитель.
Реакция активации донора:
9-$ Такая примесь известна как донор или $n-типа$ (отрицательный). Примеры $n$-типа
примесями являются P и As в Si или Ge. - Акцептор (p-тип): Если замещена примесь из колонки III на узел решетки, и недостающий валентный электрон компенсируется одним из электронное море, 9+$ Такая примесь известна как акцептор или $p-типа$ (положительный). Примеры Примесями $p$-типа являются B, Al, Ga, In в Si и Ge.
Атом-донор вводится в кристалл (например, путем добавления в расплав Si)
для того, чтобы он отдал свой дополнительный электрон для проводимости. При нулевой температуре,
электрон проводимости остается связанным; для диссоциации требуется конечная тепловая энергия
электрон от донора. Порядок величины энергии активации может быть
оценивается, если предположить, что электрон как бы связан с ядром в (однократно
заряженный) атом водорода. Вспоминая энергию связи или электрон в атоме водорода
(постоянная Ридберга),
92$, постоянная Ридберга в вакууме составляет $\mathbb{R} = 13,6 эВ$. Эффект от размещения примеси внутри кристалла-хозяина
заключается в увеличении диэлектрической проницаемости в $\epsilon_r$ раз, что ослабляет кулоновское
притяжение за счет экранирования и уменьшение кинетической энергии электрона за счет
перенормировочный коэффициент эффективной массы, $m’$. Предполагая, что $n = 1$, формула связывания
затем становится
92_r}$
При нулевой температуре,
электрон проводимости остается связанным; для диссоциации требуется конечная тепловая энергия
электрон от донора. Порядок величины энергии активации может быть
оценивается, если предположить, что электрон как бы связан с ядром в (однократно
заряженный) атом водорода. Вспоминая энергию связи или электрон в атоме водорода
(постоянная Ридберга),
92$, постоянная Ридберга в вакууме составляет $\mathbb{R} = 13,6 эВ$. Эффект от размещения примеси внутри кристалла-хозяина
заключается в увеличении диэлектрической проницаемости в $\epsilon_r$ раз, что ослабляет кулоновское
притяжение за счет экранирования и уменьшение кинетической энергии электрона за счет
перенормировочный коэффициент эффективной массы, $m’$. Предполагая, что $n = 1$, формула связывания
затем становится
92_r}$
Тот же подход актуален для активации легирующей примеси p-типа, $\Delta E_A$, где можно было бы
подставить эффективную массу отверстия.
Нейтральность заряда: полная и неполная ионизация
По закону Гаусса образец при нулевом электрическом поле должен поддерживать нейтральный заряд без чистая плотность заряда. Условие нейтральности заряда для легированных полупроводников 9-_A = N_A$ (p-тип)
где концентрации $N_A$ и/или $N_D$ контролируются концентрацией примесей добавлен. Это означает, соответственно, для материала n- и p-типа,$n \simeq N_D$ (тип n)      $p \simeq N_A$ (тип p)
Мы можем использовать функции распределения Ферми-Дирака для учета неполной ионизации примеси. Помните, что $f(E)$ дает вероятность заполнения данного состояния электрон. Для заданного уровня $E_i$ $f(E_i) \rightarrow 0$, если $\mu \llless E_i$ и $f(E_i) \rightarrow 1$, если $\mu \gggtr E_i$.
 Опять же, мы можем рассмотреть два случая:
9+_D = N_D(1 — 1/(exp(\frac{E_g-\Delta E_D — \mu}{k_BT})+1))$
Опять же, мы можем рассмотреть два случая:
9+_D = N_D(1 — 1/(exp(\frac{E_g-\Delta E_D — \mu}{k_BT})+1))$Симулятор кремния при комнатной температуре
$\Дельта E_A$ (мэВ): 100
Т (К): 300
Трехмерное изображение отдельных атомов легирующей примеси в оксидном полупроводнике в атомном масштабе
1. Coll M, et al. На пути к оксидной электронике: дорожная карта. заявл. Серф. науч. 2019; 482:1–93. doi: 10.1016/j.apsusc.2019.03.312. [Перекрестная ссылка] [Академия Google]
заявл. Серф. науч. 2019; 482:1–93. doi: 10.1016/j.apsusc.2019.03.312. [Перекрестная ссылка] [Академия Google]
2. Queisser HJ, Haller EE. Дефекты полупроводников: некоторые фатальные, некоторые жизненно важные. Наука. 1998; 281:945–950. doi: 10.1126/science.281.5379.945. [PubMed] [CrossRef] [Google Scholar]
3. Holstad TS, et al. Свойства электронного объема и доменных стенок в гексагональном ErMnO, легированном B-сайтами 3 . физ. Ред. Б. 2018; 97:85143. doi: 10.1103/PhysRevB.97.085143. [CrossRef] [Google Scholar]
4. Tufte ON, Chapman PW. Подвижность электронов в полупроводниковом титанате стронция. физ. Откр. 1967;155:796–802. doi: 10.1103/PhysRev.155.796. [CrossRef] [Google Scholar]
5. Salluzzo, M. et al. Происхождение интерфейсного магнетизма в гетероструктурах BiMnO 3 /SrTiO 3 и LaAlO 3 /SrTiO 3 . Физ. Преподобный Письмо . 111 , 087204 (2013). [PubMed]
6. Li D, et al. Сверхпроводимость в никелате с бесконечным слоем. Природа. 2019; 572: 624–627. doi: 10.1038/s41586-019-1496-5. [PubMed] [CrossRef] [Академия Google]
Li D, et al. Сверхпроводимость в никелате с бесконечным слоем. Природа. 2019; 572: 624–627. doi: 10.1038/s41586-019-1496-5. [PubMed] [CrossRef] [Академия Google]
7. Gunkel F, Christensen DV, Chen YZ, Pryds N. Кислородные вакансии: (не)видимый друг оксидной электроники. заявл. физ. лат. 2020;116:120505. doi: 10.1063/1.5143309. [CrossRef] [Google Scholar]
8. He Q, et al. Антиузельные дефекты в слоистом мультиферроике CuCr 0,9 In 0,1 P 2 S 6 . Наномасштаб. 2015;7:18579–18583. doi: 10.1039/C5NR04779J. [PubMed] [CrossRef] [Google Scholar]
9. Hor YS, Checkelsky JG, Qu D, Ong NP, Cava RJ. Сверхпроводимость и неметалличность, индуцированные легированием топологических изоляторов Bi 2 Se 3 и Bi 2 Te 3 . Дж. Физ. хим. Твердые вещества. 2011; 72: 572–576. doi: 10.1016/j.jpcs.2010.10.027. [CrossRef] [Google Scholar]
10. Kubicek M, et al. Электрохимические свойства тонких пленок La 0,6 Sr 0,4 CoO 3-δ исследованы методами комплементарной импедансной спектроскопии и глубинного профилирования изотопного обмена. Твердотельный ион. 2014; 256:38–44. doi: 10.1016/j.ssi.2013.12.016. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Твердотельный ион. 2014; 256:38–44. doi: 10.1016/j.ssi.2013.12.016. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
11. Посмотрите, округ Колумбия. Обзор измерений эффекта Холла и магнитосопротивления в материалах и устройствах GaAs. Дж. Электрохим. соц. 1990; 137: 260–266. дои: 10.1149/1.2086379. [CrossRef] [Google Scholar]
12. Fauveau A, et al. Сравнение методов измерения концентраций легирующих примесей в компенсированном кремнии n-типа. Энергетическая процедура. 2016;92:691–696. doi: 10.1016/j.egypro.2016.07.045. [CrossRef] [Google Scholar]
13. Исикава Р., Лупини А.Р., Финдли С.Д., Танигучи Т., Пенникук С.Дж. Трехмерное определение местоположения одной легирующей примеси с атомарной точностью с помощью сканирующей просвечивающей электронной микроскопии с коррекцией аберраций. Нано Летт. 2014;14:1903–1908. doi: 10.1021/nl500564b. [PubMed] [CrossRef] [Google Scholar]
14. Paulauskas T, et al. Исследование с атомным разрешением EDX, HAADF и EELS сплавов GaAs 1-x Bi x . Наномасштаб Res. лат. 2020;15:121. doi: 10.1186/s11671-020-03349-2. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Наномасштаб Res. лат. 2020;15:121. doi: 10.1186/s11671-020-03349-2. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
15. Småbråten DR, Nakata A, Meier D, Miyazaki T, Selbach SM. Исследование из первых принципов топологически защищенных вихрей и сегнетоэлектрических доменных стенок в гексагональном YGaO 3 . физ. Ред. Б. 2020; 102:144103. doi: 10.1103/PhysRevB.102.144103. [CrossRef] [Google Scholar]
16. Schoenherr P, et al. Наблюдение нескомпенсированных связанных зарядов на несобственных сегнетоэлектрических доменных стенках. Нано Летт. 2019;19:1659–1664. doi: 10.1021/acs.nanolett.8b04608. [PubMed] [CrossRef] [Google Scholar]
17. Yeoh, W.K. et al. Прямое наблюдение локального изменения калия и его корреляции с электронной неоднородностью в (Ba 1-x K x )Fe 2 Как 2 прыщи. Физ. Преподобный Письмо . 106 , 247002 (2011). [PubMed]
18. Giddings AD, et al. Промышленное применение атомно-зондовой томографии в полупроводниковых приборах. Скр. Матер. 2018;148:82–90. doi: 10.1016/j.scriptamat.2017.09.004. [CrossRef] [Google Scholar]
Промышленное применение атомно-зондовой томографии в полупроводниковых приборах. Скр. Матер. 2018;148:82–90. doi: 10.1016/j.scriptamat.2017.09.004. [CrossRef] [Google Scholar]
19. Gault, B., Moody, M., Cairney, J. & Ringer, S. Atom Probe Tomography (Springer, 2012).
20. Эль-Зока А.А. и соавт. Возможность проведения анализа замороженной воды в масштабе, близком к атомному. Науч. Дополнение . 6 , eabd6324 (2020). [Бесплатная статья PMC] [PubMed]
21. Fontaine, A. La et al. Картирование состава в атомарном масштабе выявляет богатый Mg аморфный фосфат кальция в зубной эмали человека. науч. Дополнение . 2 , e1601145 (2016 г.). [Бесплатная статья PMC] [PubMed]
22. Ji Z, Li T, Yaghi OM. Секвенирование металлов в многомерных металлоорганических каркасах. Наука. 2020; 369: 674–680. doi: 10.1126/science.aaz4304. [PubMed] [CrossRef] [Академия Google]
23. Голт Б. и др. Атомно-зондовая томография. Нац. Rev. Методы Прим. 2021; 1:1–30. [Google Scholar]
Нац. Rev. Методы Прим. 2021; 1:1–30. [Google Scholar]
24. Comes, R. B., Perea, D. E. & Spurgeon, S. R. Гетерогенные двухфазные столбы в эпитаксиальных нанокомпозитах NiFe 2 O 4 -LaFeO 3 . Доп. Матер. Интерфейсы 4 , 1700396 (2017 г.).
25. Sarker J, Bhuiyan AFMAU, Feng Z, Zhao H, Mazumder B. Прямое наблюдение за заменой легирующей примеси в легированном Si (Al 9)0866 x Ga 1-x ) 2 O 3 методом атомно-зондовой томографии. Дж. Физ. Д. Заявл. физ. 2021;54:8. doi: 10.1088/1361-6463/abe334. [CrossRef] [Google Scholar]
26. Maier J, Pfeiffer B, Volkert CA, Nowak C. Трехмерная микроструктурная характеристика оксида лития-марганца с помощью атомно-зондовой томографии. Энергетика. 2016;4:1565–1574. doi: 10.1002/ente.201600210. [CrossRef] [Google Scholar]
27. Mundy JA, et al. Функциональные электронные инверсионные слои на сегнетоэлектрических доменных границах. Нац. Матер. 2017; 16: 622–627. doi: 10.1038/nmat4878. [PubMed] [CrossRef] [Академия Google]
Нац. Матер. 2017; 16: 622–627. doi: 10.1038/nmat4878. [PubMed] [CrossRef] [Академия Google]
28. Lottermoser T, Fiebig M, Fröhlich D, Leute S, Kohn K. Магнитная структура гексагональных манганитов RMnO 3 (R = Sc, Y, Ho, Er, Tm, Yb, Lu) J. Magn. Магн. Матер. 2001; 226–230:1131–1133. doi: 10.1016/S0304-8853(00)00707-1. [CrossRef] [Google Scholar]
29. Holtz ME, et al. Топологические дефекты в гексагональных манганитах: внутренняя структура и возникающая электростатика. Нано Летт. 2017;17:5883–5890. doi: 10.1021/acs.nanolett.7b01288. [PubMed] [CrossRef] [Академия Google]
30. Skjærvø, S.H. et al. Междоузельный кислород как источник p-типа проводимости в гексагональных манганитах. Нац. Коммуна . 7 , 13745 (2016). [Бесплатная статья PMC] [PubMed]
31. Småbråten DR, et al. Подвижность доменных стенок и огрубение в легированных сегнетоэлектрических гексагональных манганитах. физ. Преподобный Рез. 2020;2:033159. doi: 10. 1103/PhysRevResearch.2.033159. [CrossRef] [Google Scholar]
1103/PhysRevResearch.2.033159. [CrossRef] [Google Scholar]
32. Yan Z, et al. Выращивание высококачественных гексагональных монокристаллов ErMnO 3 методом плавающей зоны под давлением. Дж. Крист. Рост. 2015;409: 75–79. doi: 10.1016/j.jcrysgro.2014.10.006. [CrossRef] [Google Scholar]
33. Дабковска Х.А., Дабковски А.Б., Германн Р., Приде Дж. и Гербет Г. в Handbook of Crystal Growth: Bulk Crystal Growth: Second Edition Ch. 8 (Эльзевир, 2015).
34. Coakley J, et al. Характеристика наноразмерных осадков в титановом сплаве с помощью лазерной атомно-зондовой томографии. Матер. Характер. 2018; 141:129–138. doi: 10.1016/j.matchar.2018.04.016. [Перекрестная ссылка] [Академия Google]
35. Sanford NA, et al. Лазерная атомно-зондовая томография пленок Ti/TiN, нанесенных на Si. Микрон. 2017;94:53–65. doi: 10.1016/j.micron.2016.12.001. [PubMed] [CrossRef] [Google Scholar]
36. Jin S, Su H, Sha G. Анализ атомно-зондовой томографии порошков TiC x , синтезированных методом СВС в системах Al/Fe/Cu-Ti-C. Матер. 2019;12:4095. doi: 10.3390/ma12244095. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Матер. 2019;12:4095. doi: 10.3390/ma12244095. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
37. Verberne R, et al. Анализ природного рутила (TiO 2 ) с помощью лазерной атомно-зондовой томографии. микроск. Микроанал. 2019;25:539–546. doi: 10.1017/S1431927618015477. [PubMed] [CrossRef] [Google Scholar]
38. Kirchhofer R, et al. Количественная оценка однородности состава Pb(Zr, Ti)O 3 с помощью атомно-зондовой томографии. Варенье. Керам. соц. 2014; 97: 2677–2697. дои: 10.1111/jace.13135. [CrossRef] [Google Scholar]
39. Флейшманн С., Паредис К., Мелконян Д., Вандерворст В. Выявление трехмерной формы кончиков атомных зондов с помощью атомно-силовой микроскопии. Ультрамикроскопия. 2018;194: 221–226. doi: 10.1016/j.ultramic.2018.08.010. [PubMed] [CrossRef] [Google Scholar]
40. Zhang S, et al. Электронное проявление магнитных моментов, индуцированных катионными вакансиями, в прозрачном оксидном полупроводнике: Анатаз Nb:TO 2 . Доп. Матер. 2009;21:2282–2287. doi: 10.1002/adma.200803019. [CrossRef] [Google Scholar]
Доп. Матер. 2009;21:2282–2287. doi: 10.1002/adma.200803019. [CrossRef] [Google Scholar]
41. Hellsvik J, et al. Пошаговая настройка мультиферроичности в CuO путем легирования. физ. Преподобный Б. Конденс. Материя Матер. физ. 2014;90:014437. doi: 10.1103/PhysRevB.90,014437. [CrossRef] [Google Scholar]
42. Thompson K, et al. Индивидуальная подготовка образцов in situ для атомно-зондовой томографии. Ультрамикроскопия. 2007; 107: 131–139. doi: 10.1016/j.ultramic.2006.06.008. [PubMed] [CrossRef] [Google Scholar]
43. Marquis EA, Gault B. Определение температуры иглы в лазерной атомно-зондовой томографии с использованием распределения зарядового состояния. Дж. Заявл. физ. 2008;104:84914. doi: 10.1063/1.3006017. [CrossRef] [Google Scholar]
44. Bachhav M, Danoix F, Hannoyer B, Bassat JM, Danoix R. Исследование обогащенного O-18 гематита (α-Fe 2 O 3 ) с помощью лазерной атомно-зондовой томографии. Междунар. Дж. Масс-спектр. 2013; 335:57–60. doi: 10.1016/j.ijms.2012.10.012. [CrossRef] [Google Scholar]
doi: 10.1016/j.ijms.2012.10.012. [CrossRef] [Google Scholar]
45. Кинно Т., Томита М., Окубо Т., Такено С., Хоно К. Лазерная атомно-зондовая томография тонкой пленки оксида, обогащенного 18 О, для количественного анализа кислорода. заявл. Серф. науч. 2014; 290:194–198. doi: 10.1016/j.apsusc.2013.11.039. [CrossRef] [Google Scholar]
46. Geiser BP, Kelly TF, Larson DJ, Schneir J, Roberts JP. Карты пространственного распределения для атомно-зондовой томографии. микроск. Микроанал. 2007; 13: 437–447. дои: 10.1017/S1431927607070948. [PubMed] [CrossRef] [Google Scholar]
47. Жубер Д. От ультрамягких псевдопотенциалов к проекторному методу дополненной волны. физ. Преподобный Б. Конденс. Материя Матер. физ. 1999; 59: 1758–1775. doi: 10.1103/PhysRevB.59.1758. [CrossRef] [Google Scholar]
48. Крессе Г., Фуртмюллер Дж. Эффективные итерационные схемы для неэмпирических расчетов полной энергии с использованием базиса плоских волн. физ. Преподобный Б. Конденс. Материя Матер.


 Н. Мурзин. Субмиллиметровая спектроскопия коллективных и связанных состояний носителей тока в полупроводниках.// М.: Наука. 1985, 264 с.
Н. Мурзин. Субмиллиметровая спектроскопия коллективных и связанных состояний носителей тока в полупроводниках.// М.: Наука. 1985, 264 с.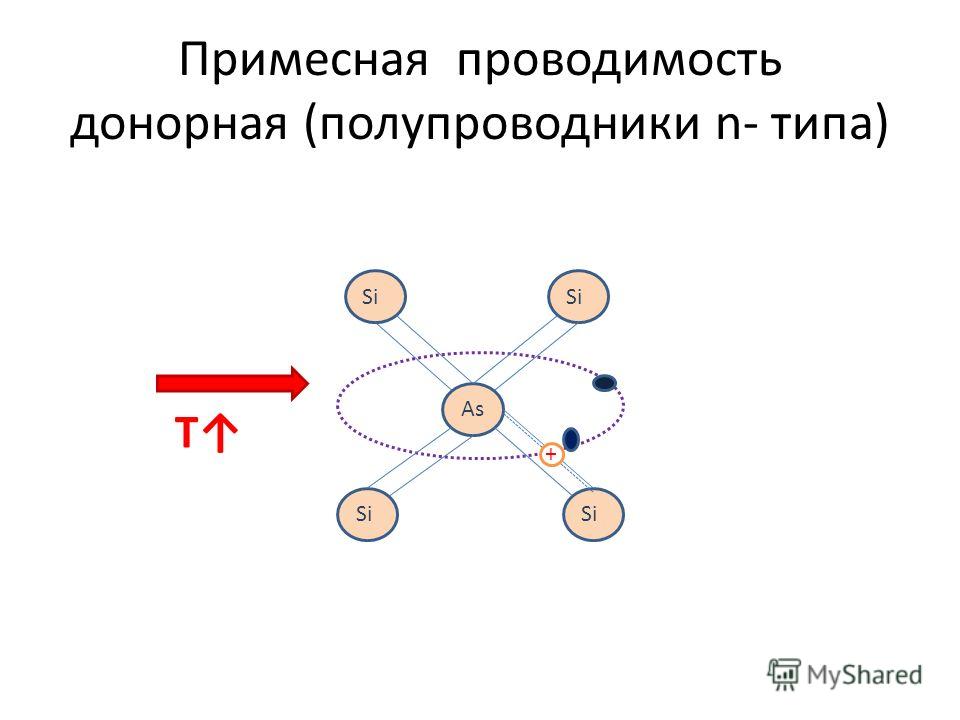 Положение уровня Ферми в собственных полупроводниках.
Положение уровня Ферми в собственных полупроводниках.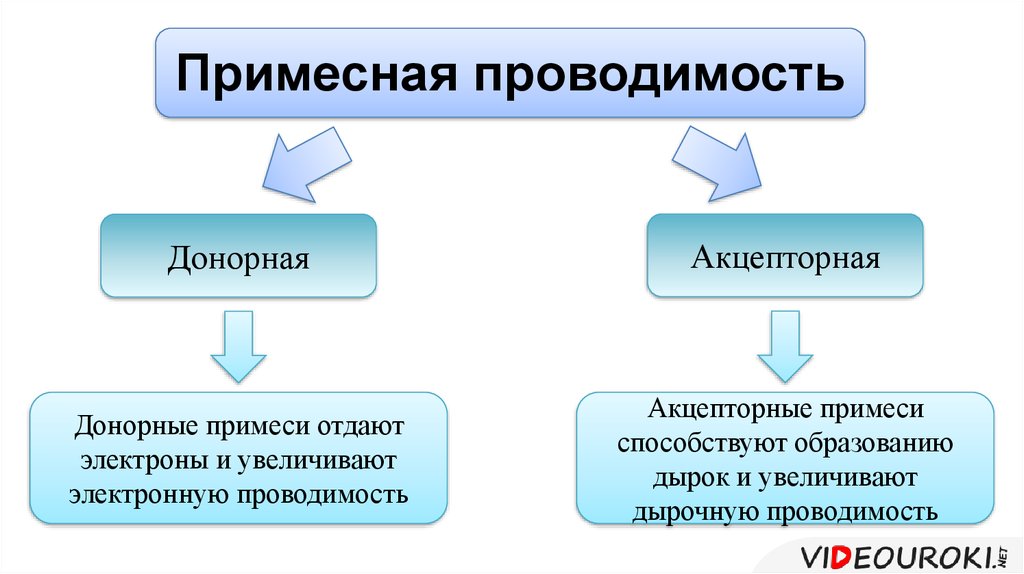 Контактная разность потенциалов. Разрывы зон.
Контактная разность потенциалов. Разрывы зон. Примеси зависят от типа полупроводника. Слабо и умеренно легированные полупроводники называются внешний . Полупроводник, легированный до такого высокого уровня, что он действует скорее как проводник, чем как полупроводник, называется вырожденным .
Примеси зависят от типа полупроводника. Слабо и умеренно легированные полупроводники называются внешний . Полупроводник, легированный до такого высокого уровня, что он действует скорее как проводник, чем как полупроводник, называется вырожденным .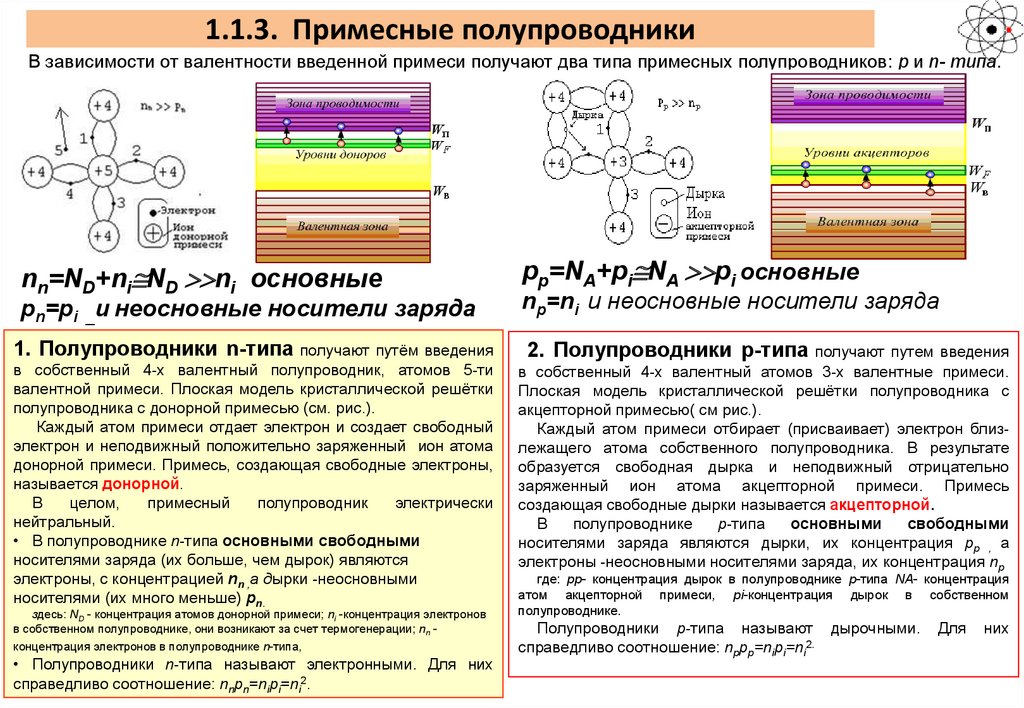 Если добавлено намного больше (порядка 1 на 10 000), то легирование называется тяжелым или высоким. Это часто обозначается как n+ для легирующей примеси n-типа или p+ для легирующей примеси p-типа. Более подробное описание механизма легирования можно найти в статье о полупроводниках.
Если добавлено намного больше (порядка 1 на 10 000), то легирование называется тяжелым или высоким. Это часто обозначается как n+ для легирующей примеси n-типа или p+ для легирующей примеси p-типа. Более подробное описание механизма легирования можно найти в статье о полупроводниках.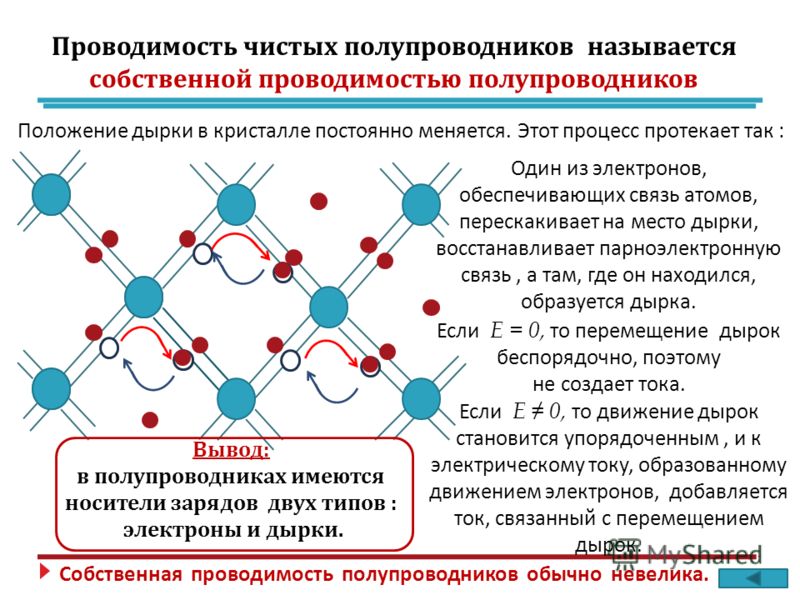 ) Бор, мышьяк, фосфор и иногда галлий используются для легирования кремния. Бор является предпочтительной легирующей примесью p-типа для производства кремниевых интегральных схем, поскольку он диффундирует со скоростью, позволяющей легко контролировать глубину перехода. Фосфор обычно используется для объемного легирования кремниевых пластин, в то время как мышьяк используется для диффузии переходов, поскольку он диффундирует медленнее, чем фосфор, и поэтому более управляем.
) Бор, мышьяк, фосфор и иногда галлий используются для легирования кремния. Бор является предпочтительной легирующей примесью p-типа для производства кремниевых интегральных схем, поскольку он диффундирует со скоростью, позволяющей легко контролировать глубину перехода. Фосфор обычно используется для объемного легирования кремниевых пластин, в то время как мышьяк используется для диффузии переходов, поскольку он диффундирует медленнее, чем фосфор, и поэтому более управляем.
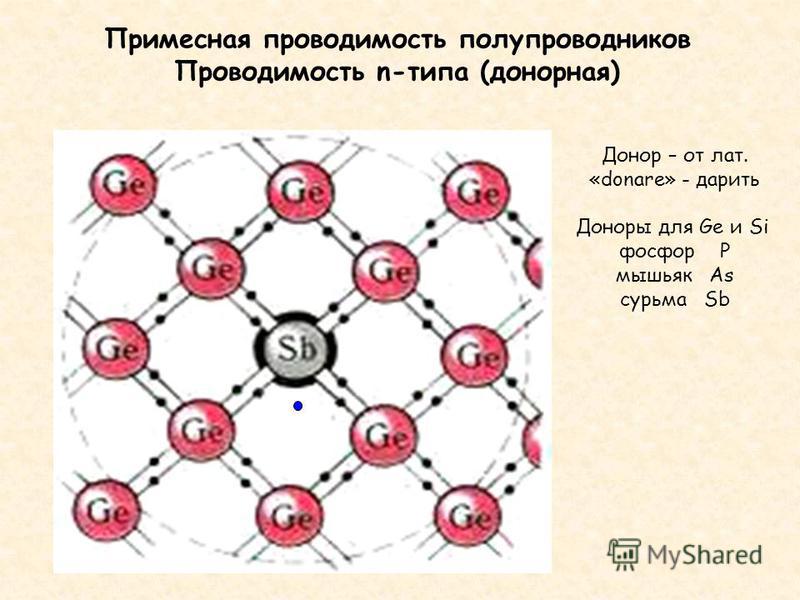 (Начнем с того, что в кремниевой решетке система далека от проводимости!) Существует два основных метода легирования проводящего полимера, оба через окислительно-восстановительный (окислительно-восстановительный) процесс. Первый метод, химическое легирование, включает воздействие на полимер, такой как меланин (обычно тонкая пленка), окислителем (обычно йод или бром) или восстановителем (гораздо реже, но обычно включает щелочные металлы). Второй – электрохимическое легирование, при котором покрытый полимером рабочий
электрод подвешен в растворе электролита, в котором полимер нерастворим вместе с отдельными противоэлектродами и электродами сравнения. Между электродами создается разность электрических потенциалов, которая заставляет заряд (и соответствующий противоион из электролита) проникать в полимер в форме добавления электронов (n-легирование) или удаления (p-легирование).
(Начнем с того, что в кремниевой решетке система далека от проводимости!) Существует два основных метода легирования проводящего полимера, оба через окислительно-восстановительный (окислительно-восстановительный) процесс. Первый метод, химическое легирование, включает воздействие на полимер, такой как меланин (обычно тонкая пленка), окислителем (обычно йод или бром) или восстановителем (гораздо реже, но обычно включает щелочные металлы). Второй – электрохимическое легирование, при котором покрытый полимером рабочий
электрод подвешен в растворе электролита, в котором полимер нерастворим вместе с отдельными противоэлектродами и электродами сравнения. Между электродами создается разность электрических потенциалов, которая заставляет заряд (и соответствующий противоион из электролита) проникать в полимер в форме добавления электронов (n-легирование) или удаления (p-легирование).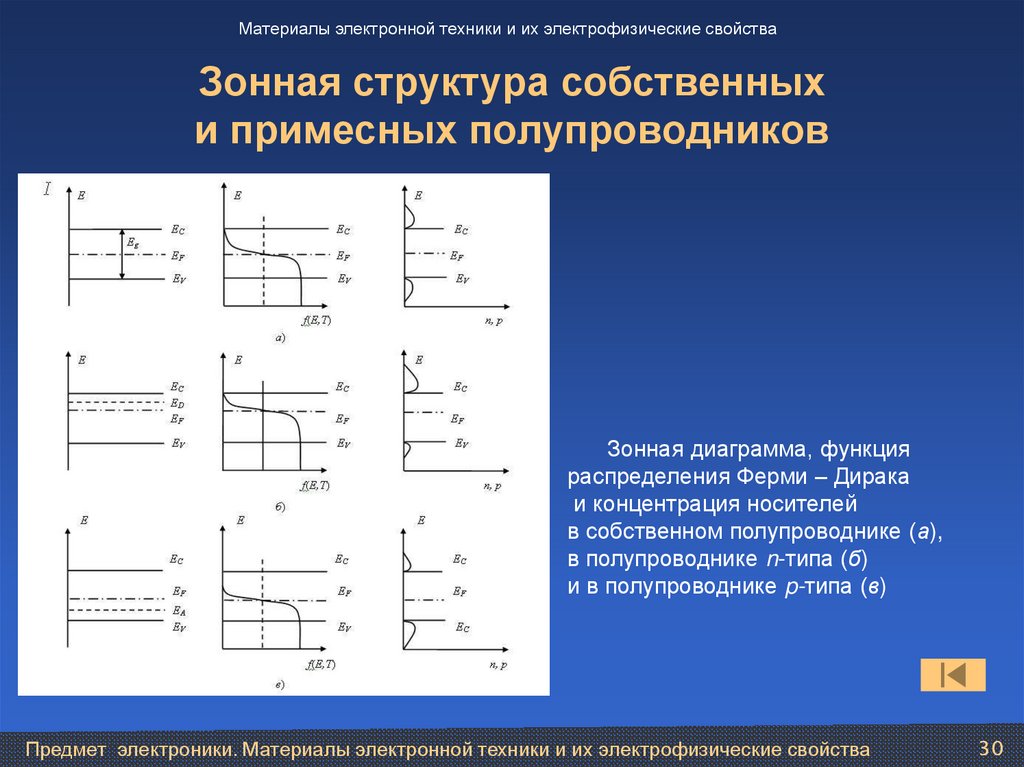 Богатый электронами n-допированный полимер будет немедленно реагировать с элементарным кислородом, деактивируя (повторно окисляя до нейтрального состояния) полимер. Таким образом, химическое n-легирование необходимо проводить в среде инертного газа (например, аргона). Электрохимическое n-допирование гораздо более распространено в исследованиях, так как легче исключить кислород из растворителя в запаянной колбе; однако, вероятно, нет коммерческих проводящих полимеров, легированных n.
Богатый электронами n-допированный полимер будет немедленно реагировать с элементарным кислородом, деактивируя (повторно окисляя до нейтрального состояния) полимер. Таким образом, химическое n-легирование необходимо проводить в среде инертного газа (например, аргона). Электрохимическое n-допирование гораздо более распространено в исследованиях, так как легче исключить кислород из растворителя в запаянной колбе; однако, вероятно, нет коммерческих проводящих полимеров, легированных n.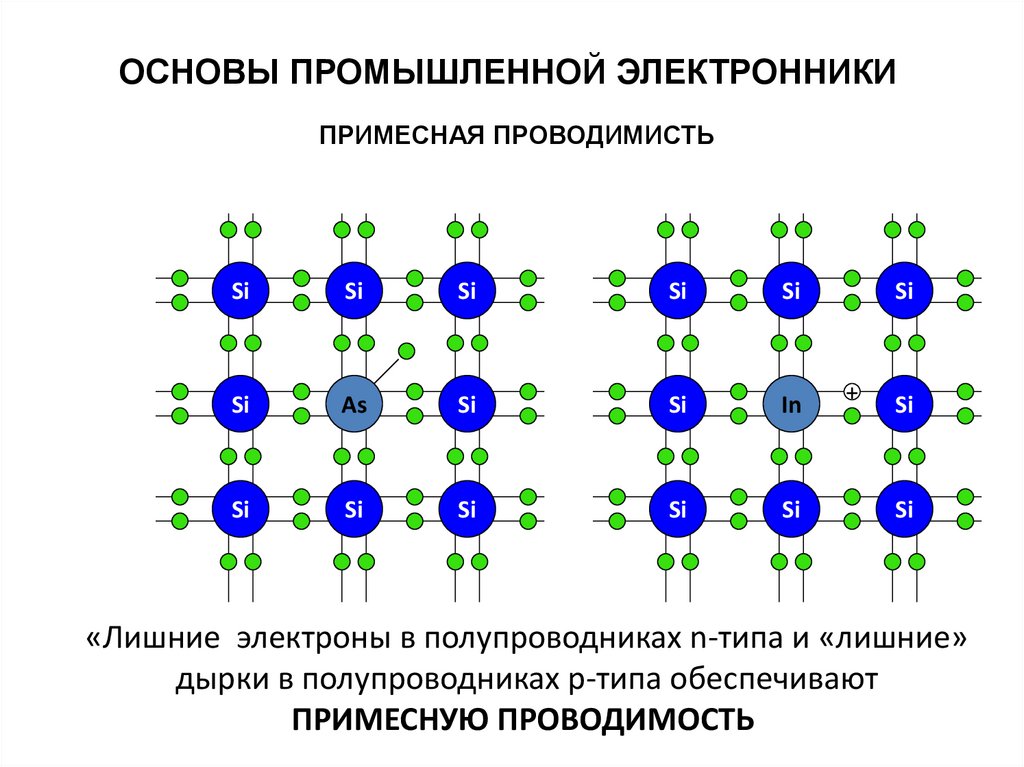 «Метод создания PN-переходов в полупроводниковых материалах», патент США 2 631 356 (подана 15 июня 1950 г., выдана 17 марта 1953 г.)
«Метод создания PN-переходов в полупроводниковых материалах», патент США 2 631 356 (подана 15 июня 1950 г., выдана 17 марта 1953 г.)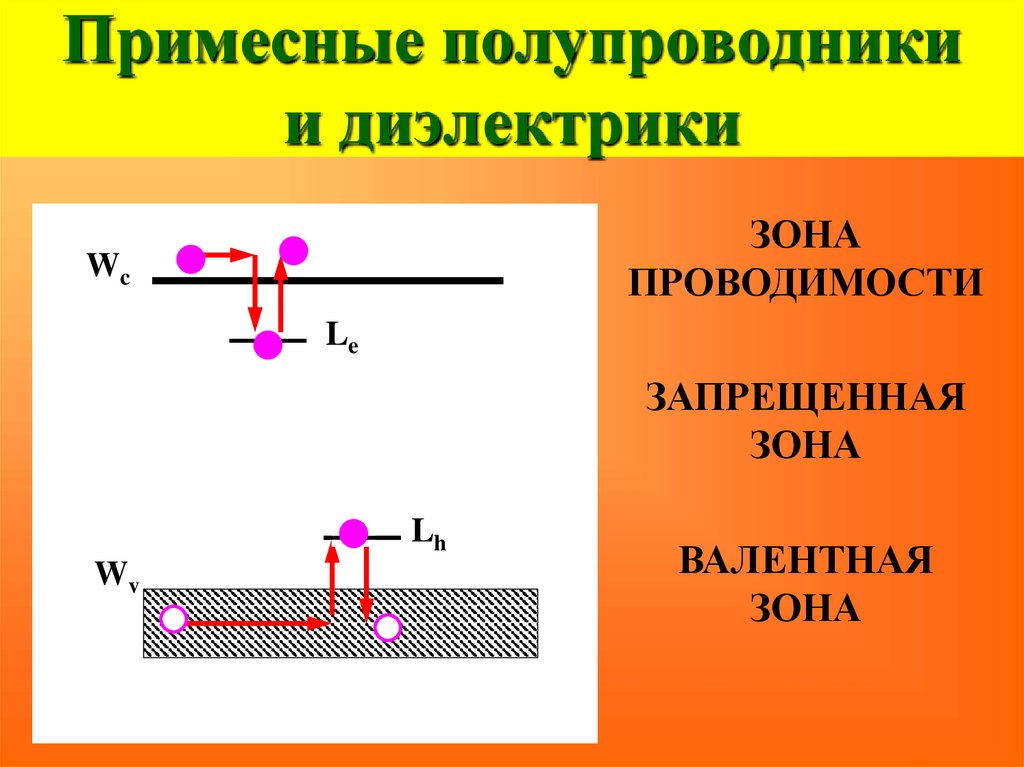 org/details/books/university-physics-volume-3
org/details/books/university-physics-volume-3