Ученые МФТИ объяснили «танцы» вейлевских частиц на поверхности кристаллов

Ученые из МФТИ исследовали поведение вейлевских частиц захваченных на поверхность полуметаллов Вейля. Соответствующая статья была опубликована в Physical Review В, в престижном разделе Rapid Communications.

        

Иллюстрация: Электронный спектр в объеме вейлевского полуметалла описывается совокупностью четного числа конусов («долин»), центрированных в особых точках импульсного пространства (в таких конических точках скрыта нетривиальная топология, и их называют также «дьявольскими»).

Существование вейлевских фермионов (таково строгое название вейлевских частиц), было предсказано немецким физиком Германом Вейлем ещё в начале 20 века. Однако титанические усилия по их обнаружению в природе долгое время были безуспешными. Лишь в 2015 году они были обнаружены на опыте, и не в огромных коллайдерах, как ожидалось, а в миниатюрных кристаллах, получивших название вейлевских полуметаллов.

Исследования этих материалов стремительно развиваются и являются одной из самых «горячих» точек современной физики.

Вейлевский полуметалл считается трехмерным аналогом графена, двумерного кристалла с уникальными свойствами, за открытие которого выпускники МФТИ Андрей Гейм и Константин Новоселов получили Нобелевскую премию по физике в 2010 г.  Электроны в  графене и полуметаллах Вейля  считаются безмассовыми частицами, как фотоны, но в отличие от последних обладают электрическим зарядом, с чем связаны перспективы применений в электронике. Важно, что свойства электронов в этих и ряде других материалов обладают, как недавно выяснилось, качественно новыми особенностями, описываемыми топологической теорией. Интересно отметить, что за внедрение общих топологических представлений в физику конденсированного состояния группа ученых получила Нобелевскую премию по физике 2016 года.

В теоретическом исследовании, проведенном аспирантом МФТИ Жанной Девизоровой под руководством профессора МФТИ Владимира Волкова, рассматривались поверхностные состояния вейлевских фермионов, то есть, на другом языке, поведение электронов вблизи поверхности кристалла, являющегося вейлевским полуметаллом.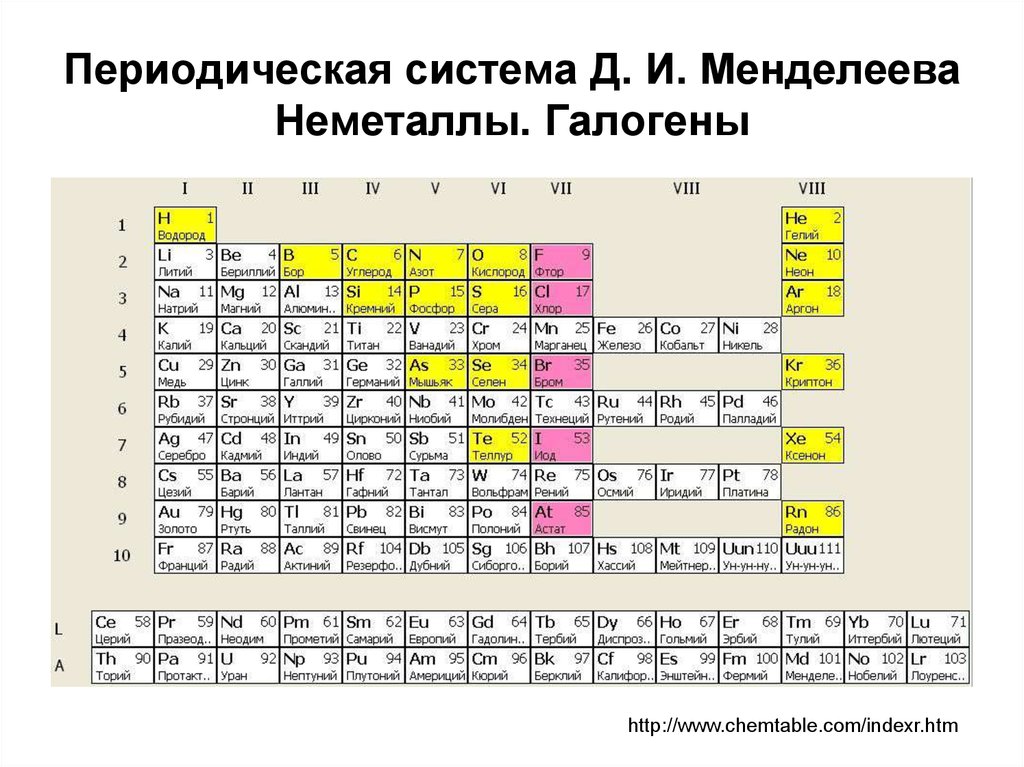 Особые состояния электронов на поверхности кристалла – поверхностные состояния – были предсказаны и теоретически исследованы в простейших моделях будущими нобелиатами Игорем Таммом (СССР) и, позже,  Вильямом Шокли (США) еще в 30-е годы 20 века, но стали интенсивно изучаться  экспериментально сравнительно недавно. О практической важности этих исследований говорит тот факт, что вся современная микроэлектроника основана на эксплуатации токопроводящих приповерхностных каналов на кремнии, который, впрочем, не является топологическим материалом.

Поведение любой частицы во внешних полях определяется законом дисперсии — зависимостью энергии частицы от ее импульса. Именно закон дисперсии электронов (синоним: электронный спектр) определяет электронные свойства кристалла, например, электропроводность. Электронный спектр в объеме вейлевского полуметалла описывается совокупностью четного числа конусов — «долин», центрированных в особых точках импульсного пространства.

Замечательными особенностями обладает поверхность такого кристалла. Экзотическая форма закона дисперсии частиц, заселяющих поверхностные состояния в вейлевских полуметаллах, является визитной карточкой вейлевских полуметаллов. Точки спектра, соединяющие состояния с одинаковой энергией необычны:: они не замкнуты и имеют форму дуг в двумерном импульсном пространстве. Дуги связывают принадлежащие разным долинам конические точки в электронном спектре  и называются ферми-арками (для обычных электронов эти контуры замкнуты и похожи на окружность). Теоретическое описание ферми-арок до сих пор было основано на очень сложных («первопринципных») и не прозрачных компьютерных расчетах. Ученые из МФТИ учли, что далеко от границы вейлевские фермионы в каждой долине подчиняются дифференциальным уравнениям Вейля, и сумели вывести граничные условия, которые впервые корректно учитывают междолинное взаимодействие на поверхности полуметалла. Систему уравнений Вейля для двух долин с этими граничными условиями удалось решить «вручную» и, поэтому, аналитически найти форму ферми-арок.

(adsbygoogle = window.adsbygoogle || []).push({}); Результат описывает опытные данные не только качественно, но и количественно, и доказывает, что основной причиной формирования ферми-арок является сильное междолинное взаимодействие при рассеянии вейлевских фермионов на поверхности кристалла.

Использование вейлевских полуметаллов может оказаться чрезвычайно полезным при создании сверхбыстрой электроники.  Сейчас разрабатывается, пока теоретически, новое поколение электронных приборов на основе вейлевских полуметаллов. Аналитический подход, разработанный учеными из МФТИ, позволяет сравнительно просто учитывать влияние на вейлевские фермионы электрических и магнитных полей. Эвристический потенциал разработанного метода может существенно облегчить продвижение в приборном направлении.

Обнаружен новый тип полуметаллов

Поведение электронов в любом твердом теле (металле, полупроводнике, диэлектрике) определяется законом дисперсии – зависимостью энергии частицы от ее импульса. Внутри кристаллической решетки твердого тела электроны и другие частицы ведут себя иначе, чем в свободном состоянии. Например, в графене (двумерной модификации графита) закон дисперсии таков, что эффективная масса носителей заряда обращается в ноль, и этим объясняются уникальные проводящие свойства этого материала. Известны также полуметаллы Вейля, электронный спектр которых является трехмерным аналогом спектра графена. Носители заряда в них называются фермионами Вейля. Авторы исследования обнаружили новый тип полуметалла, закон дисперсии в котором отличается от всех ранее известных.

Ученые из Физико-технического института имени А.Ф. Иоффе совместно с коллегой из Университета Уотерлу (Канада) выполнили первопринципные вычисления (то есть расчеты, не использующие упрощающих моделей) электронной структуры моносилицида кобальта (CoSi). Оказалось, что это соединение относится к совершенно новому типу полуметаллов – веществ, занимающих промежуточное положение между металлами и полупроводниками.

«Моносилицид кобальта давно известен как перспективный для термоэлектрических применений полуметалл. В первоначальных исследованиях предполагалось, что энергетический спектр электронов соответствует типичным полуметаллам. Однако тип и симметрия кристаллической решетки этого соединения указывают на то, что этот материал может иметь топологически нетривиальную электронную структуру. Это обстоятельство явилось для нас основанием для теоретических и экспериментальных исследований моносилицида кобальта», — рассказал Александр Бурков, один из авторов исследования, заведующий лабораторией физики термоэлементов физико-технического института им. А.Ф. Иоффе.

Необычные топологические свойства электронной структуры могут возникать только при определенной симметрии кристаллической решетки полуметалла. Исследование электронной структуры моносилицида кобальта показало, что носители заряда в нем имеют свойства, отчасти подобные свойствам фермионов Вейля. Однако электронный спектр в новом материале значительно отличается от свойств полуметаллов Вейля, и других известных полуметаллов, поэтому носители заряда в таких материалах называют «новыми фермионами».

Фото: спектральная функция (Фермиевские дуги) поверхностных состояний моносилицида кобальта. Источник: Александр Бурков

В дальнейших исследованиях ученые надеются определить возможные практические применения нового типа материала и экспериментально исследовать его топологические свойства. Предварительные экспериментальные исследования электронных и тепловых свойств соединения при низких температурах уже позволили обнаружить ряд необычных особенностей, которые могут быть связаны с необычной топологией электронной структуры.

«Сейчас мы исследуем транспортные свойства моносилицида кобальта и его сплавов с железом. Ведется подготовка экспериментального исследования электронной структуры с помощью фотоэлектронной спектроскопии с угловым разрешением. Кроме того, с практической точки зрения, важным является исследование природы высокой для полуметаллов термоэлектродвижущей силы в данном материале, ее зависимости от температуры и состава при образовании изоструктурных твердых растворов с замещением атомов кобальта на атомы железа и никеля», — добавил ученый.

Теги

СМИ о Фонде, Физика и космос, Спецпроект

Полуметаллы Вейля, дуги Ферми и киральные аномалии

• Опубликовано: 25 октября 2016 г.

• Шуан Цзя ¹ ,
• Су-Ян Сюй ² и
• М. Захид Хасан ³  

Природные материалы том 15 , страницы 1140–1144 (2016)Цитировать эту статью

• 24 тыс. обращений

• 209 цитирований

• 59 Альтметрический

• Сведения о показателях

Предметы

• Электронные свойства и материалы
• Квантовая механика
• Квантовая физика
• Топологическая материя

Физики открыли новую топологическую фазу вещества, полуметалл Вейля, поверхность которого имеет незамкнутую поверхность Ферми, а низкоэнергетические квазичастицы в объеме возникают как фермионы Вейля. Представлен краткий обзор этих событий и перспективы дальнейших шагов.

Полуметаллы Вейля — это полуметаллы или металлы, квазичастичное возбуждение которых представляет собой фермион Вейля, частица, сыгравшая решающую роль в квантовой теории поля, но не наблюдаемая как фундаментальная частица в вакууме ^{1,2,3,4,5,6 ,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24} . Фермионы Вейля имеют определенную хиральность, либо левую, либо правую. В полуметалле Вейля хиральность можно понимать как топологически защищенный хиральный заряд. Узлы Вейля противоположной хиральности разделены в импульсном пространстве и связаны только через границу кристалла экзотическим незамкнутым поверхностным состоянием — дугами Ферми. Примечательно, что фермионы Вейля устойчивы при переносе токов, что обеспечивает исключительно высокую подвижность. Их спины привязаны к их направлениям импульса из-за их характера конфигурации магнитного монополя импульс-пространство. Из-за хиральной аномалии наличие параллельных электрических и магнитных полей может нарушить кажущееся сохранение хирального заряда, делая металл Вейля, в отличие от обычных немагнитных металлов, более проводящим с увеличением магнитного поля. Эти новые топологические явления за пределами топологических изоляторов делают новую физику доступной и предлагают потенциальные приложения, несмотря на раннюю стадию исследования 9.0010 25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46 .

Это предварительный просмотр содержимого подписки, доступ через ваше учреждение

Соответствующие статьи

Статьи открытого доступа со ссылками на эту статью.

• Столкновение преимуществ Weyl со светом

  • Сяому Ван
  • и Донг Сун

  Свет: наука и приложения Открытый доступ 02 марта 2023 г.

• Энергонезависимое переключение хиральности за счет полностью оптического перемагничивания в ферромагнитном полуметалле Вейля Co3Sn2S2

  • Наотака Йошикава
  • , Казума Огава
  •  … Рё Шимано

  Физика коммуникаций Открытый доступ 20 декабря 2022 г.

• Визуализация дискретных поверхностей Ферми и возможной узловой линии эволюции состояния Вейля в ZrSiTe

  • Ци Бянь
  • , Шаоцзянь Ли
  •  … Мингху Пан

  npj Квантовые материалы Открытый доступ 26 мая 2022 г.

Варианты доступа

Подпишитесь на этот журнал

Получите 12 печатных выпусков и онлайн-доступ

269,00 € в год

всего 22,42 € за выпуск

Узнать больше

Взять напрокат или купить эту статью

Получайте только эту статью до тех пор, пока она вам нужна

$39,95

Узнать больше

Цены могут облагаться местными налогами, которые рассчитываются во время оформления заказа

. Рисунок 2: Наблюдение фермионов Вейля и топологических дуг Ферми. Рисунок 3: Электронный и оптический контроль фермионов Вейля.

Ссылки

1. Weyl, H. Z. Phys. 56 , 330–352 (1929).

   Артикул Google Scholar

2. Сельдь, C. Phys. Ред. 52 , 365–373 (1937).

   Артикул КАС Google Scholar

3. Мураками С. New J. Phys. 9 , 356 (2007).

   Артикул Google Scholar

4. Ван Х., Тернер А. М., Вишванат А. и Саврасов С. Ю. Физ. B 83 , 205101 (2011).

   Артикул Google Scholar

5. Ян, К.-Ю., Лу, Ю.-М., Ран, Ю. Phys. Ред. B 84 , 075129 (2011 г.).

   Артикул Google Scholar

6. Бурков А. А., Баленц Л. Phys. Преподобный Летт. 107 , 127205 (2011).

   Артикул КАС Google Scholar

7. Сюй, Г. и др. Физ. Преподобный Летт. 107 , 186806 (2011).

   Артикул Google Scholar

8. Воловик, Г. Э. Вселенная в капле гелия (Oxford Univ. Press, 2009).

   Книга Google Scholar

9. Ciudad, D. Nat. Матер. 14 , 863 (2015).

   Артикул КАС Google Scholar

10. Хасан М.З., Сюй С.-Ю., Белопольски Б. и Хуанг С.-М. Год. Преподобный Конд. Мат. физ. (в печати).

11. Хасан М.З., Сюй С.-Ю. и Биан, Г. Phys. Скрипта 164 , 014001 (2015).

    Артикул Google Scholar

12. Сюй, С.-Ю. и другие. Наука 332 , 560–564 (2011).

    Артикул КАС Google Scholar

13. Сингх Б. и др. Физ. Ред. B 86 , 115208 (2012 г.).

    Артикул Google Scholar

14. Хуан С. М., Сюй С.-Ю. и другие. Нац. коммун. 6 , 7373 (2015).

    Артикул КАС Google Scholar

15. Сюй, С.-Ю. и другие. Наука 349 , 613–617 (2015).

    Артикул КАС Google Scholar

16. Сюй, С.-Ю. и другие. Наука 347 , 294–298 (2015).

    Артикул КАС Google Scholar

17. Weng, H. et al. Физ. X 5 , 011029 (2015 г.).

    Google Scholar

18. Лв, Б.К. и др. Физ. Ред. X 5 , 031013 (2015 г.).

    Google Scholar

19. Huang, X. et al. Физ. Ред. X 5 , 031023 (2015 г.).

    Google Scholar

20. Zhang, C. et al. Нац. коммун. 7 , 10735 (2016).

    Артикул КАС Google Scholar

21. Сюй, С.-Ю. и другие. Нац. физ. 11 , 748–754 (2015).

    Артикул КАС Google Scholar

22. Лю, З. и др. Нац. Матер. 15 , 27–31 (2016).

    Артикул КАС Google Scholar

23. Лв, Б.К. и др. Нац. физ. 11 , 724727 (2015).

    Артикул Google Scholar

24. Белопольски И. и др. Физ. Преподобный Летт. 116 , 066802 (2016).

    Артикул Google Scholar

25. Hasan, M. Z. & Kane, C.L. Rev. Mod. физ. 82 , 3045–3067 (2010).

    Артикул КАС Google Scholar

26. Хасан, М. З. и Мур, Дж. Э. Annu. Преподобный Конд. Мат. физ. 2 , 55 (2011).

    Артикул КАС Google Scholar

27. МСКД; https://icsd.fiz-karlsruhe.de/search/basic.xhtml

28. Чанг Г. и др. Науч. Доп. 2 , e1600295 (2016).

    Артикул Google Scholar

29. Хуан С.-М. и другие. Проц. Натл акад. науч. США 113 , 1180–1185 (2016).

    Артикул КАС Google Scholar

30. Солуянов А.А. и др. Природа 527 , 495–498 (2015).

    Артикул КАС Google Scholar

31. Sun, Y. et al. Препринт на http://arxiv.org/abs/1508.03501 (2015 г.).

32. Чанг Т.-Р. и другие. Нац. коммун. 7 , 10639 (2016).

    Артикул КАС Google Scholar

33. Wang, Z. et al. Физ. Преподобный Летт. 117 , 056805 (2016).

    Артикул Google Scholar

34. Сюй, С.-Ю. и другие. Препринт на https://arxiv.org/abs/1603.07318 (2016).

35. Белопольски И. и др. Физ. Ред. B 94 , 085127 (2016).

    Артикул Google Scholar

36. Хуанг, Л. и др. Нац. Матер. http://dx.doi.org/10.1038/nmat4685 (2016 г.).

37. Xiong, J. et al. Наука 350 , 413–416 (2015).

    Артикул КАС Google Scholar

38. Li, Q. et al. Нац. физ. 12 , 550–554 (2016).

    Артикул Google Scholar

39. Ву, Р. и др. Физ. X 6 , 021017 (2016 г.).

    Google Scholar

40. Zhang, Y. et al. Препринт на http://arxiv.org/abs/1602.03576 (2016 г.).

41. Parameswaran, S.A. et al. Физ. X 4 , 031035 (2014 г.).

    Google Scholar

42. Potter, A.C. et al. Нац. коммун. 5 , 5161 (2014).

    Артикул КАС Google Scholar

43. Chan, C.-K., Lee, P.A., Burch, K.S., Han, J.H. & Ran, Y. Phys. Преподобный Летт. 116 , 026805 (2016).

    Артикул Google Scholar

44. Ван Ю. -Х. и другие. Наука 342 , 453–457 (2013).

    Артикул КАС Google Scholar

45. Чан, С.-К., Линднер, Н.Х., Рафаэль, Г. и Ли, П.А. Препринт на http://arxiv.org/abs/1607.07839 (2016).

46. Биан Г. и др. Нац. коммун. 7 , 10556 (2016).

    Артикул КАС Google Scholar

Скачать ссылки

Благодарности

Благодарим И. Белопольски, С.-М. Хуан, Г. Биан, Н. Алидуст и М. Неупан за комментарии, а также Д. Холдейн, И. Клебанов и Э. Виттен за обсуждение в рамках Принстонской летней школы по новым взглядам на квантовую материю в рамках «Перспективы в теоретической науке». Программа по физике в IAS. С.Дж. поддерживается Национальной программой фундаментальных исследований Китая (грант № 2014CB239302 и № 2013CB921901). Работа в Принстоне С.-Ю.Х. и М.З.Х. поддерживается Министерством энергетики США в области фундаментальных энергетических наук (грант № DOE / BES DE-FG-02-05ER46200 и № DE-AC02-05Ch21231 в Advanced Light Source в LBNL) и фондами Принстонского университета. М.З.Х. выражает признательность за поддержку пользователей Visiting Scientist со стороны Национальной лаборатории Лоуренса в Беркли, PRISM и частичную поддержку со стороны Фонда Мура.

Информация об авторе

Авторы и организации

1. Шуан Цзя работает в Международном центре квантовых материалов Школы физики Пекинского университета и в Совместном инновационном центре квантовой материи, Пекин 100871, Китай,

   Shuang Jia

2. Факультет физики, Su-Yang Xu работает в Лаборатории топологической квантовой материи и спектроскопии (B7) Принстонского университета, Нью-Джерси 08544, США,

   Su-Yang Xu

3. Факультет физики, М. Захид Хасан работает в Лаборатории топологической квантовой материи и спектроскопии (B7) Принстонского университета и в Принстонском институте науки и технологии материалов (PRISM), Принстон , Нью-Джерси 08544, США,

   М. Захид Хасан

Авторы

1. Шуан Цзя

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

2. Su-Yang Xu

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

3. М. Захид Хасан

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Академия

Авторы переписки

Переписка с Шуан Цзя или М. Захид Хасан.

Права и разрешения

Перепечатка и разрешения

Об этой статье

Эта статья цитируется

• Столкновение преимуществ Weyl со светом

  • Сяому Ван
  • Донг Сун

  Свет: наука и приложения (2023)

• Энергонезависимое переключение хиральности за счет полностью оптического перемагничивания в ферромагнитном полуметалле Вейля Co3Sn2S2

  • Наотака Йошикава
  • Казума Огава
  • Ре Шимано

  Физика связи (2022)

• Визуализация дискретных поверхностей Ферми и возможной узловой линии эволюции состояния Вейля в ZrSiTe

  • Ци Бянь
  • Шаоцзянь Ли
  • Минху Пан

  нпдж Квантовые материалы (2022)

• Надежная фаза двойного топологического изолятора в NaZnBi

  • Хёнгын Ли
  • Юн-Гу Кан
  • Ки Джу Чан

  NPG Азия Материалы (2022)

• Поток векторного поля кривизны Берри

  • Ондржей Стейскал
  • Мартин Вейс
  • Ярослав Хамрле

  Научные отчеты (2022)

Полуметалл Weyl от AdS/CFT с ароматом

B. Yan and C. Felser, Топологические материалы: полуметаллы Weyl , Энн. Преподобный Конденс. Мат. физ. 8 (2017) 337.

Артикул Google Scholar

М.З. Хасан, С.-Ю. Сюй, И. Белопольски и С.-М. Huang, Открытие полуметаллов с фермионами Вейля и состояний топологической ферми-дуги , Ann. Преподобный Конденс. Мат. физ. 8 (2017) 289.

Артикул Google Scholar

А. Буркова, Weyl metals , Ann. Преподобный Конденс. Мат. физ. 9 (2018) 359.

Артикул Google Scholar

Н.П. Армитаж, Э.Дж. Меле и А. Вишванат, Полуметаллы Вейля и Дирака в трехмерных твердых телах , Rev. Mod. физ. 90 (2018) 015001 [arXiv:1705.01111] [INSPIRE].

Артикул MathSciNet Google Scholar

Х. Гао, Дж.В. Вендербос, Ю. Ким и А.М. Rappe, Топологические полуметаллы из первых принципов , Annual Review of Materials Research 49 (2019) 153.

Статья Google Scholar

С.Ю. Xu et al., Открытие полуметалла Вейля Фермиона и топологических дуг Ферми , Science 349 (2015) 613 [arXiv:1502.03807] [INSPIRE].

Артикул Google Scholar

L. Lu et al., Экспериментальное наблюдение точек Вейля , arXiv:1502.03438 [INSPIRE].

Б.К. Lv et al., Экспериментальное открытие полуметалла Вейля TaAs , Phys. X 5 (2015) 031013 [arXiv:1502.04684] [INSPIRE].

Google Scholar

Б.К. Lv et al., Наблюдение узлов Вейля в TaAs , Nature Phys. 11 (2015) 724 [arXiv:1503.09188].

Артикул Google Scholar

Z. Liu et al., Эволюция поверхности Ферми полуметаллов Вейля в семействе пниктидов переходных металлов , Nat. Матер. 15 (2016) 27.

Артикул Google Scholar

С.-Ю. Xu et al., Открытие фермионного состояния Вейля с дугами Ферми в арсениде ниобия , Nature Phys. 11 (2015) 748.

Артикул Google Scholar

I. Belopolski et al., Критерии прямого обнаружения топологических дуг Ферми в полуметаллах Вейля , Phys. Преподобный Летт. 116 (2016) 066802 [arXiv:1601.04327] [INSPIRE].

Артикул Google Scholar

Н. Морали и др., Разнообразие Ферми-АРК на поверхностных конечностях магнитной Вейл Семметальной СО ₃ SN ₂ S ₂ , Science 365 (2019).

Артикул Google Scholar

Д.Ф. Liu et al., Магнитная полуметаллическая фаза Вейля в кристалле Кагоме , Science 365 (2019) 1282 [arXiv:1909.09580].

Артикул Google Scholar

I. Belopolski et al., Открытие топологических фермионных линий Вейля и поверхностных состояний барабана в магните комнатной температуры , Science 365 (2019) 1278 [arXiv:2004.00004].

Артикул Google Scholar

X. Ван, А.М. Тернер, А. Вишванат и С.Ю. Саврасов, Топологические полуметаллические и ферми-дуговые поверхностные состояния в электронной структуре иридатов пирохлора , Физ. B 83 (2011) 205101 [arXiv:1007.0016] [INSPIRE].

Артикул Google Scholar

Х.Б. Нильсен и М. Ниномия, Отсутствие нейтрино на решетке: 2. Интуитивное топологическое доказательство , Nucl. физ. B 193 (1981) 173 [ВДОХНОВЕНИЕ].

Ф.Д.М. Холдейн, Кривизна Берри на поверхности Ферми: аномальный эффект Холла как топологическое свойство ферми-жидкости , Физ. Преподобный Летт. 93 (2004) 206602 [cond-mat/0408417] [INSPIRE].

Д. Колладей и В.А. Костелецкий, Лоренц, нарушающий расширение стандартной модели , Phys. Ред. D 58 (1998) 116002 [hep-ph/9809521] [INSPIRE].

А.Г. Грушин, Последствия реализации КЭД Лоренца в конденсированных средах в полуметаллах Вейля , Физ. Ред. D 86 (2012) 045001 [arXiv:1205. 3722] [INSPIRE].

Артикул Google Scholar

П. Госвами и С. Тевари, Аксионная теория поля (3+1)-мерных полуметаллов Вейля , Phys. B 88 (2013) 245107 [arXiv:1210.6352] [INSPIRE].

Артикул Google Scholar

Б. Рой, П. Госвами и В. Юричич, Взаимодействующие фермионы Вейля: фазы, фазовые переходы и глобальная фазовая диаграмма , Физ. B 95 (2017) 201102 [arXiv:1610.05762] [INSPIRE].

Артикул Google Scholar

J.M. Maldacena, Большой предел N суперконформных теорий поля и супергравитации , Int. Дж. Теор. физ. 38 (1999) 1113 [hep-th/9711200] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

С. С. Губсер, И.Р. Клебанов и А.М. Поляков, Корреляторы калибровочной теории из некритической теории струн , Phys. лат. B 428 (1998) 105 [hep-th/9802109] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

E. Witten, Пространство анти-де Ситтера и голография , Adv. Теор. Мат. физ. 2 (1998) 253 [hep-th/9802150] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

С.С. Губсер, И.Р. Клебанов и А.В. Peet, Энтропия и температура черных 3-бран , Phys. Ред. D 54 (1996) 3915 [hep-th/9602135] [INSPIRE].

Артикул MathSciNet Google Scholar

Э. Виттен, Пространство анти-де Ситтера, тепловой фазовый переход и конфайнмент в калибровочных теориях , Доп. Теор. Мат. физ. 2 (1998) 505 [hep-th/9803131] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

U. Gürsoy, V. Jacobs, E. Plauschinn, H. Stoof and S. Vandoren, Голографические модели для нелегированных полуметаллов Вейля , JHEP 04 (2013) 1209PI2:127 [arXiv2:127] ].

Артикул Google Scholar

В.П.Дж. Джейкобс, П. Бетциос, У. Гюрсой и Х.Т.К. Stoof, Электромагнитный отклик взаимодействующих полуметаллов Вейля , Phys. B 93 (2016) 195104 [arXiv:1512.04883] [INSPIRE].

Артикул Google Scholar

Т. Фолкнер и Дж. Полчински, Полуголографические жидкости Ферми , JHEP 06 (2011) 012 [arXiv:1001.5049] [INSPIRE].

Артикул МАТЕМАТИКА Google Scholar

У. Гюрсой, Э. Плаушинн, Х. Стооф и С. Вандорен, Голография и правила сумм ARPES , JHEP 05 (2012) 018 [arXiv:17412.5PI].

Артикул Google Scholar

K. Landsteiner and Y. Liu, Голографический полуметалл Вейля , Phys. лат. Б 753 (2016) 453 [arXiv:1505.04772] [ВДОХНОВЕНИЕ].

Артикул МАТЕМАТИКА Google Scholar

К. Ландштейнер, Ю. Лю и Ю.-В. Sun, Квантовый фазовый переход между топологическим и тривиальным полуметаллом из голографии , Phys. Преподобный Летт. 116 (2016) 081602 [arXiv:1511.05505] [INSPIRE].

Артикул Google Scholar

C. Copetti, J. Fernández-Pendás and K. Landsteiner, Осевой эффект Холла и универсальность голографических полуметаллов Вейля , JHEP 02 (2017) 138 [arXiv:1611. 08125].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

Ю. Лю и Дж. Чжао, Переход полуметалла/изолятора Вейля из голографии , JHEP 12 (2018) 124 [arXiv:1809.08601] [ВДОХНОВЕНИЕ].

Артикул MathSciNet Google Scholar

К. Ландштейнер, Ю. Лю и Ю.-В. Sun, Голографические топологические полуметаллы , Sci. Китай физ. мех. Астрон. 63 (2020) 250001 [arXiv:1911.07978] [INSPIRE].

Артикул Google Scholar

В. Юричич, И. Салазар Ландеа и Р. Сото-Гарридо, Фазовые переходы в голографическом мультивейлевском полуметалле , JHEP 07 (2020) 052 [arXiv:2005.10387] [INSPIRE].

Артикул MathSciNet Google Scholar

М. Аммон, М. Хайнрих, А. Хименес-Альба и С. Мокель, Поверхностные состояния в голографических полуметаллах Вейля , Phys. Преподобный Летт. 118 (2017) 201601 [arXiv:1612.00836] [INSPIRE].

Артикул Google Scholar

К. Ландштейнер, Ю. Лю и Ю.-В. Sun, Нечетная вязкость в квантовой критической области голографического полуметалла Вейля , Phys. Преподобный Летт. 117 (2016) 081604 [arXiv:1604.01346] [INSPIRE].

Артикул Google Scholar

М. Баджоли, Б. Падхи, П.В. Филлипс и К. Сетти, Гипотеза о скорости бабочки при квантовом фазовом переходе , JHEP 07 (2018) 049 [arXiv:1805.01470] [ВДОХНОВЕНИЕ].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

G. Grignani, A. Marini, F. Pena-Benitez and S. Speziali, AC проводимость для голографического Weyl Semimetal , JHEP 03 (2017) 125 [arXiv:14612.0INSPI] .

Артикул MathSciNet Google Scholar

М. Аммон, М. Баджоли, А. Хименес-Альба и С. Мекель, Размазанный квантовый фазовый переход в неупорядоченной голографии , JHEP 04 (2018) 068 [arXiv:1802.08650] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

Ю. Лю и Ю.-В. Sun, Топологические инварианты для голографических полуметаллов , JHEP 10 (2018) 189 [arXiv:1809.00513] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

М. Баджоли и Д. Джатаганас, Обнаружение топологических квантовых фазовых переходов с помощью c-функции , Phys. Ред. D 103 (2021) 026009 [arXiv:2007.07273] [INSPIRE].

Артикул MathSciNet Google Scholar

А. Карч и Э. Кац, Добавление вкуса к AdS/CFT , JHEP 06 (2002) 043 [hep-th/0205236] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

K. Hashimoto, S. Kinoshita, K. Murata and T. Oka, Голографические состояния Флоке I: сильно связанный полуметалл Вейля ].

Артикул MathSciNet Google Scholar

С. Киношита, К. Мурата и Т. Ока, Голографические состояния Флоке II: Флоке-конденсация векторных мезонов в неравновесной фазовой диаграмме ].

Артикул Google Scholar

вечера Чеслер и А. Вуоринен, Диффузия тяжелых ароматов в слабо связанных N = 4 супертеория Янга-Миллса , JHEP 11 (2006) 037 [hep-ph/0607148] [INSPIRE].

Дж. Эрдменгер, Н. Эванс, И. Кирш и Э. Трелфолл, Мезоны в калибровочных/гравитационных двойниках — обзор , Eur. физ. J. A 35 (2008) 81 [arXiv:0711.4467] [INSPIRE].

Артикул Google Scholar

С.Р. Дас, Т. Нисиока и Т. Такаянаги, Зондовые браны, зависящие от времени связи и термализация в AdS/CFT , JHEP 07 (2010) 071 [arXiv:1005.3348] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

C. Hoyos, T. Nishioka and A. O’Bannon, Хиральный магнитный эффект от AdS/CFT с ароматом , JHEP 10 (2011) 084 [arXiv:1106.4030].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

Дж. Полчински, Теория струн. Том. 2: Теория суперструн и не только , Кембриджские монографии по математической физике, издательство Кембриджского университета, Великобритания (2007) [DOI] [INSPIRE].

Германия Харзеев и Х.-У. Yee, Хиральная спираль в AdS/CFT с ароматом , Phys. Ред. D 84 (2011) 125011 [arXiv:1109.0533] [INSPIRE].

Артикул Google Scholar

Y. Bu and S. Lin, Голографическая намагниченная киральная волна плотности , Chin. физ. C 42 (2018) 114104 [arXiv:1807.00330] [INSPIRE].

Артикул Google Scholar

Д. Матеос, Р.К. Майерс и Р.М. Thomson, Голографические фазовые переходы с фундаментальной материей , Phys. Преподобный Летт. 97 (2006) 0

[hep-th/0605046] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

C. Hoyos-Badajoz, K. Landsteiner and S. Montero, Плавление голографических мезонов , JHEP 04 (2007) 031 [hep-th/0612169] [INSPIRE].

Артикул Google Scholar

A. Karch and A. O’Bannon, Metallic AdS/CFT , JHEP 09 (2007) 024 [arXiv:0705.3870] [INSPIRE].

Артикул MathSciNet Google Scholar

K. Hashimoto and T. Oka, Вакуумная нестабильность в электрических полях через AdS/CFT: лагранжева и планковская термализация Эйлера-Гейзенберга , JHEP 10 (2013) 113 [arXiv.7:4RE] .

Артикул Google Scholar

К. Хашимото, Т. Ока и А. Сонода, Магнитная нестабильность в AdS/CFT: эффект Швингера и лагранжиан Эйлера-Гейзенберга суперсимметричной КХД , JHEP 06 (2014) 085 [arXiv:1403. 6336] [INSPIRE].

Артикул Google Scholar

К. Хашимото, Т. Ока и А. Сонода, Электромагнитная нестабильность в голографической КХД , JHEP 06 (2015) 001 [arXiv:1412.4254] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

А. О’Бэннон, Холловская проводимость ароматических полей AdS/CFT , Phys. Ред. D 76 (2007) 086007 [arXiv:0708.1994] [INSPIRE].

Артикул Google Scholar

В.Г. Филев, С.В. Джонсон, Р.К. Рашкова и К.С. Viswanathan, Калибровочная теория ароматизированного азота во внешнем магнитном поле , JHEP 10 (2007) 019 [hep-th/0701001] [INSPIRE].

Артикул Google Scholar

М. Крученски, Д. Матеос, Р.К. Майерс и Д.Дж. Winters, Мезонная спектроскопия в AdS/CFT с ароматом , JHEP 07 (2003) 049 [hep-th/0304032] [INSPIRE].

Артикул Google Scholar

А. Карч и А. О’Бэннон, Хиральный переход N = 4 супер Ян-Миллс с ароматом на 3-сфере , Физ. Ред. D 74 (2006) 085033 [hep-th/0605120] [INSPIRE].

Артикул MathSciNet Google Scholar

Д. Матеос, Р.К. Майерс и Р.М. Thomson, Термодинамика браны , JHEP 05 (2007) 067 [hep-th/0701132] [INSPIRE].

Артикул MathSciNet Google Scholar

В.П. Фролов, А.Л. Ларсен и М. Кристенсен, Доменная стенка, взаимодействующая с черной дырой: новый пример критических явлений , Физ. Ред. D 59 (1999) 125008 [hep-th/9811148] [INSPIRE].

Артикул Google Scholar

В.П. Фролов, Переходы слияния в системах брана-черная дыра: критичность, скейлинг и самоподобие , Phys. Ред. D 74 (2006) 044006 [gr-qc/0604114] [INSPIRE].

А. Карч, А. О’Бэннон и Л.Г. Yaffe, критических показателя от AdS/CFT со вкусом , JHEP 09 (2009) 042 [arXiv:0906.4959] [INSPIRE].

Артикул MathSciNet Google Scholar

К. Битагсир Фадафан, Дж. Круз Рохас и Н. Эванс, Голографическое описание цветовой сверхпроводимости , Физ. Ред. D 98 (2018) 066010 [arXiv:1803.03107] [INSPIRE].

Артикул MathSciNet Google Scholar

А. Черман, Т. Д. Коэн и А. Неллор, A Граница скорости звука из голографии , Phys. Ред. D 80 (2009) 066003 [arXiv:0905.0903] [INSPIRE].

Артикул Google Scholar

А. Кунду, Эффективная теплофизика в голографии: краткий обзор , arXiv:1812.09447 [INSPIRE].

А. Кунду, Стационарные состояния, теплофизика и голография , Доп. Физика высоких энергий. 2019 (2019) 2635917 [ВДОХНОВЕНИЕ].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

J. Sonner, Голографический эффект Швингера и геометрия запутанности , Phys. Преподобный Летт. 111 (2013) 211603 [arXiv:1307.6850] [INSPIRE].

Артикул Google Scholar

А. О’Бэннон, Дж. Пробст, Р. Роджерс и К.Ф. Улеманн, Первый закон скорости запутывания из голографии , Phys. Ред. D 96 (2017) 066028 [arXiv:1612.07769] [INSPIRE].

Артикул MathSciNet Google Scholar

C.V. Johnson, D-brane primer , in Институт перспективных теоретических исследований физики элементарных частиц (TASI 99): Strings, Branes and Gravity , (2000) DOI [hep-th/0007170] [INSPIRE].

С. Накамура, Отрицательное дифференциальное сопротивление из голографии , Прог. Теор. физ. 124 (2010) 1105 [arXiv:1006.4105] [INSPIRE].

Артикул МАТЕМАТИКА Google Scholar

Д. Т. Сон и Б. З. Спивак, Хиральная аномалия и классическое отрицательное магнитосопротивление металлов Вейля , Phys. B 88 (2013) 104412 [arXiv:1206. 1627] [INSPIRE].

Артикул Google Scholar

М. Аммон, Т.Х. Нго и А. О’Бэннон, Перенос голографического аромата в произвольных постоянных фоновых полях , JHEP 10 (2009) 027 [arXiv:0908.2625] [INSPIRE].

Артикул Google Scholar

А. Баумгартнер, А. Карч и А. Лукас, Магнитосопротивление в релятивистской гидродинамике без аномалий , JHEP 06 (2017) 054 [arXiv:1704.01592] [INSPIRE].

Артикул MathSciNet МАТЕМАТИКА Google Scholar

A. Karch, A. O’Bannon and K. Skenderis, Голографическая перенормировка зондовых D-бран в AdS/CFT , JHEP 04 (2006) 015 [hep-th/0512125] ВДОХНОВЛЯТЬ].

Артикул MathSciNet Google Scholar

К.