|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.
2.5. Полоса пропускания Амплитудно-частотная
характеристика последовательного
контура характеризуется тем, что на
резонансной частоте она имеет максимальное
значение. На частотах, отстоящих
значительно от резонансной частоты,
значения амплитудно-частотной
характеристики близки к нулю. Если к
контуру прикладывать сигналы одинаковой
амплитуды, но с разными частотами, то
сигналы с частотой, равной резонансной
частоте, будут создавать большой ток в
контуре и большие напряжения на реактивных
элементах. В этом случае говорят, что
контур пропускает этот сигнал. Если
частота сигнала значительно отличается
от
Полосой
пропускания называется интервал частот, включающий
резонансную частоту контура, на границах
которого значение тока контура меньше
значения тока на резонансной частоте
в заданное число раз.
Как правило, за исключением особой аппаратуры, требуется, чтобы на границе полосы пропускания ток контура был меньше тока на резонансной частоте враз.
На рис.3.10 показано определение полосы пропускания с помощью АЧХ. В соответствии с заданным уровнем подавления на границе полосы пропускания должно выполняться условие:
. (3.31)
Значит на границах полосы пропускания АЧХ должна иметь значение:
. (3.32) Исходя из этого, на рис.3.10 найдена полоса пропускания, границы которой обозначаются частотами 1 и 2. Полоса пропускания обозначается как и измеряется в единицах измерения частоты. Тогда полоса пропускания будет равна:
. (3.33)
В
зоне полосы пропускания АЧХ практически
симметрична относительно резонансной
частоты. Поэтому интервалы между
резонансной частотой и границами полосы
пропускания обозначим как ∆.
, .
С учетом этого выражение для полосы пропускания (3.33) принимает вид:
. (3.34)
Рассмотренный способ определения полосы пропускания возможен только при наличии графика АЧХ. Это не всегда удобно.
Найдем аналитическое выражение для определения полосы пропускания. Для этого воспользуемся формулой (3.29) определения АЧХ.
. (3.35)
Найдем, какой имеет вид (3.35) для границ полосы пропускания. Для этого предварительно найдем выражение в круглых скобках формулы (3.35) для 1 и 2.
Для =1 получаем:
В контурах радиоаппаратуры полоса пропускания узкая и составляет единицы килогерц, а резонансная частота высокая и составляет сотни килогерц. Это позволяет пренебречь величиной ∆ в числителе и знаменателе. Тогда рассматриваемое соотношение принимает вид:
Для =2, с учетом сказанного получаем:
Из
приведенного анализа видно, что
рассматриваемая часть формулы (3.
35) на
граничных частотах 1 и 2 имеет
одинаковые выражения, отличающиеся
только знаком. Но так как рассмотренное
соотношение в формуле (3.35) находится в
квадрате, то эта формула для обеих границ
полосы пропускания имеет один и тот же
вид:
(3.36)
При решении задачи о полосе пропускания в общем виде вводится понятие коэффициента неравномерности . Он показывает, какую часть от резонансного тока принимает ток контура на границах полосы пропускания и имеет разные значения в зависимости от вида аппаратуры (0.707; 0.1; 0.01 и т. д.) Тогда, в соответствии с понятием полосы пропускания, приравняем (3.36) к коэффициенту неравномерности:
Решаем это уравнение относительно 2∆ и с учетом (3.34) находим:
.
При коэффициенте неравномерности полоса пропускания одиночного последовательного контура определяется формулой:
(3.
37)
1. Мощность, потребляемая контуром на границах полосы пропускания, в 2 раза меньше мощности, потребляемой контуром на резонансной частоте.
Действительно, на резонансной частоте мощность, потребляемая контуром, выражается через действующее значение тока контура известным соотношением:
Обозначим действующее значение тока на границе полосы пропускания через I. Тогда, с учетом (3.31), мощность, потребляемая контуром на каждой из границ полосы пропускания, равна:
2. На границах полосы пропускания сопротивление резистора контура R равно модулю суммы его реактивных элементов:
На резонансной частоте ток в контуре равен:
На границах полосы пропускания ток контура в общем виде (для =1 и =2) определяется формулой:
С
учетом (3.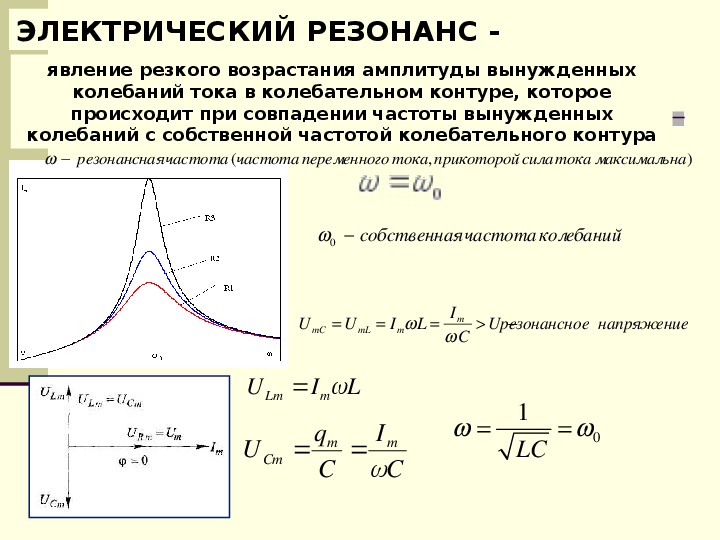
31) приравняем эти токи:
После несложных преобразований находим:
(3.38)
3. На границах полосы пропускания фаза тока контура относительно входного сигнала равна 45.
Комплексное значение тока контура равно:
.
Фаза тока равна:
. (3.39)
Исходя из (3.38), модуль аргумента (3.39) на границах полосы пропускания равен 1. Исходя из свойств ФЧХ, на частотах <0 контур имеет емкостные свойства (Х<0) и, следовательно:
.
На частотах >0 контур имеет индуктивные свойства (Х > 0), следовательно:
4. На границах полосы пропускания обобщенная расстройка .
Из (3.36) видно, что обобщенная расстройка, с учетом ранее выполненного анализа для 1 и 2 имеет вид:
,
где
«плюс» имеет место для 2,
а «минус» — для 1.
Тогда, учитывая (3.34) и (3.37), получаем:
.
5. На границе полосы пропускания модуль полного сопротивления контура равен:
.
Это легко проверить, учитывая второе из рассмотренных свойств (3.38). Из выражения модуля полного сопротивления контура находим:
.
Параллельный контур без диссипаций в реактивных ветвях – полное сопротивление, резонанс в контуре, напряжение на контуре и токи в ветвях, векторная диаграмма.
Параллельные колебательные контура
Параллельные
одиночные колебательные контура
характеризуются тем, что основные
элементы их — конденсатор и индуктивность
соединены между собой параллельно.
Резисторы могут быть включены как
параллельно с реактивными элементами,
так и последовательно. В первом случае
диссипация энергии в параллельных
ветвях, содержащих реактивные элементы,
отсутствует.
Во втором случае в этих
ветвях имеют место диссипативные
процессы. Рассмотрим каждый из названных
видов параллельных контуров.
3.3.1. Параллельный колебательный контур без диссипации в реактивных ветвях
Общие соотношения. В параллельном колебательном контуре без диссипации в реактивных ветвях резистор включен параллельно с конденсатором и индуктивностью, которые здесь считаются идеальными (рис.3.18). Их диссипации могут быть учтены в резисторе по параллельной схеме замещения (рис.1.4).
Сопротивление контура. Для рассмотрения свойств контура определим его полное сопротивление K (рис.3.18,в). Представим контур в виде параллельно соединенных реактивных и резистивного сопротивлений (рис.3.18,б).
Воспользуемся проводимостями этих элементов:
; ; ; .
Как
известно, эквивалентная проводимость
параллельно соединенных элементов
равна сумме проводимостей этих элементов.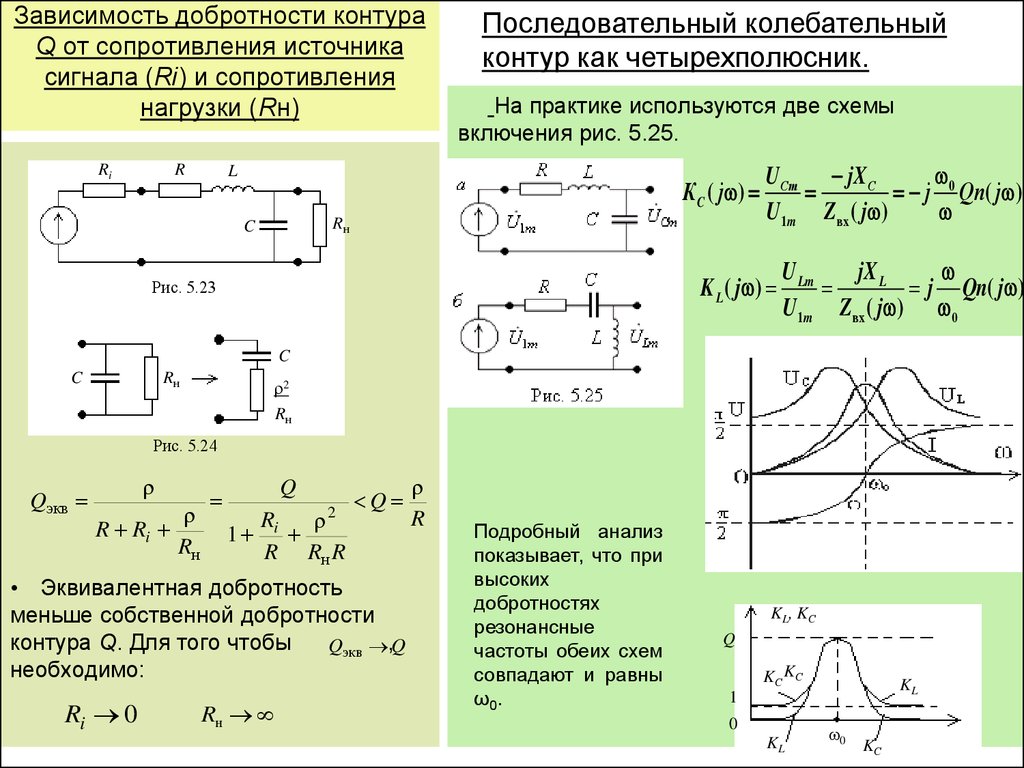
Тогда эквивалентная проводимость
контура имеет вид:
.
Отсюда находим величину эквивалентного сопротивления контура, выделяя в нем вещественную и мнимую составляющие:
(3.50)
Представим сопротивление контура в показательной форме:
, (3.51)
где ;.
Напряжение на контуре. В отличие от последовательного контура, в параллельном контуре входным параметром является ток контура iК(t), а выходным — напряжение на контуре uК(t). Это связано с особенностью функционирования параллельных контуров в радиотехнических устройствах, таких как резонансные усилители, резонансные фильтры и др. В связи с этим задаем ток с определенной амплитудой и нулевой фазой, который в гармонической форме записи и в комплексной форме имеет виды:
; .
Напряжение на контуре определяется в соответствии с законом Ома:
, (3.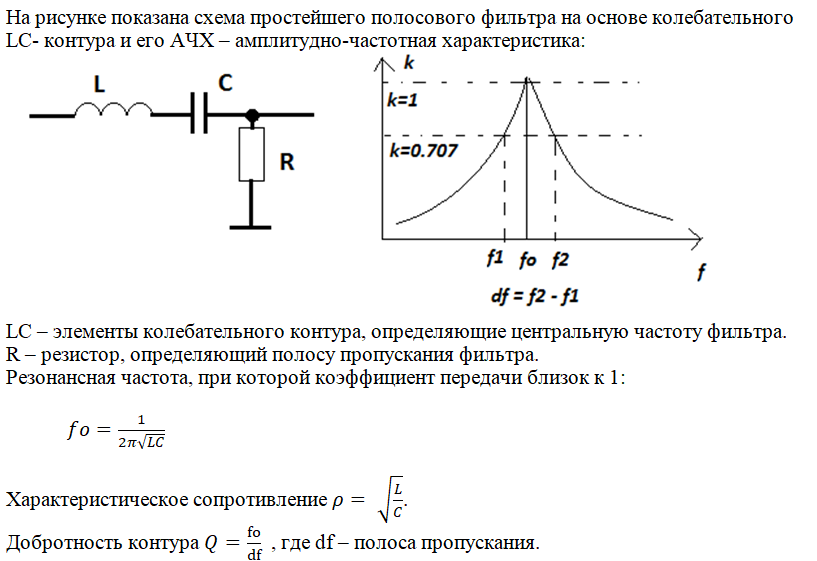
52)
где , .
Токи в контуре. Определим токи во всех ветвях контура. Напряжение на контуре, а, значит, напряжение, приложенное к каждой из ветвей, имеет вид:
. (3.53)
Токи в ветвях определяются по закону Ома:
,где.
, где (3.54)
,где
Резонанс в контуре. Условие резонанса и резонансная частота. Как отмечалось, признаком резонанса являются максимальные значения тока и напряжения в схеме при определенной частоте сигнала. При этом в полном сопротивлении цепи мнимая составляющая равна нулю. Это мы видели в последовательном одиночном колебательном контуре. Воспользуемся этим условием. Тогда из выражения (3.50) видно, что условием резонанса в контуре является выполнение следующего равенства:
. (3.55)
Это значит, что при резонансе сопротивления конденсатора и катушки индуктивности равны:
.
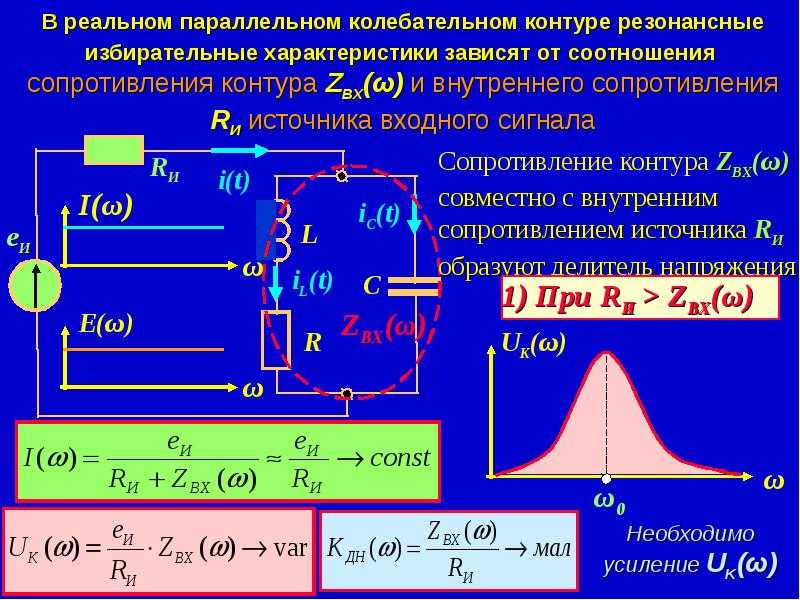
Решая (3.55) относительно частоты, находим выражение для резонансной частоты контура:
. (3.56)
Определим сопротивление контура, напряжение на контуре и токи в ветвях на резонансной частоте.
Сопротивление контура на резонансной частоте можно определить из (3.51). С учётом условия резонанса (3.55) видно, что на резонансной частоте модуль и фаза сопротивления контура принимают значения:
, .
Напряжение на контуре при резонансе определяется из (3.53) с учётом равенства нулю фазы сопротивления контура на резонансной частоте
где , (3.57)
.
Токи в ветвях контура при резонансе определяются из (3.54) с учётом (3.55) и (3.57):
, где ;
,
где
;
(3.
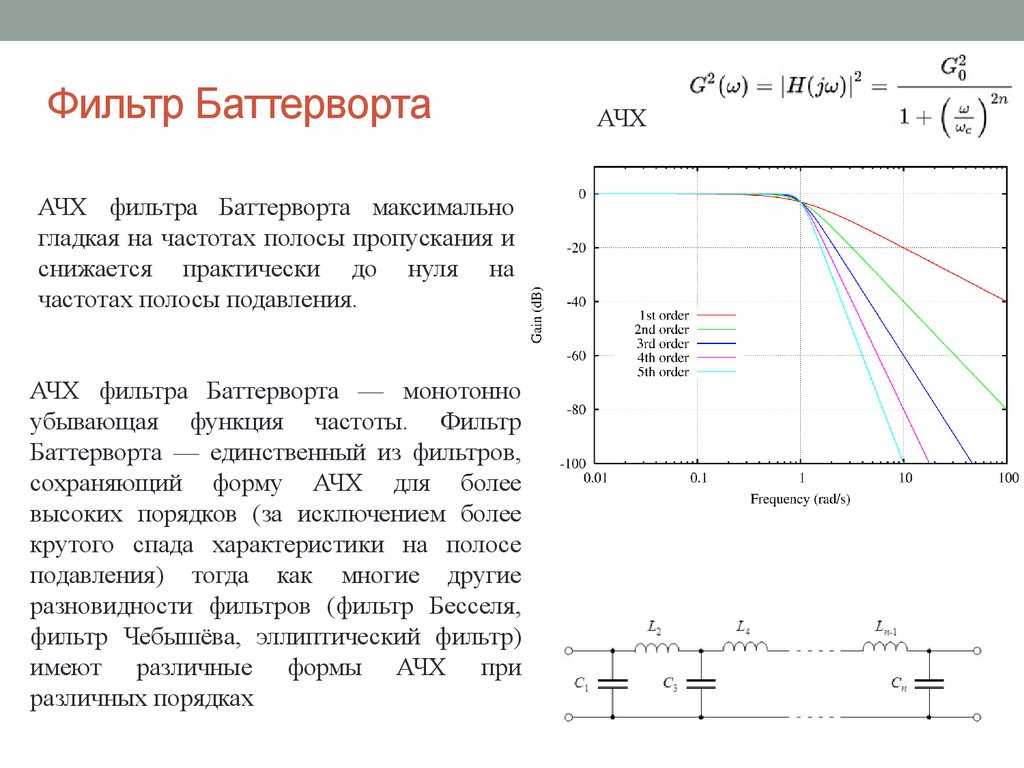58)
, где.
В силу равенства видно, что токи в ветвях с индуктивностью и конденсатором равны по величине, а по фазе отличаются друг от друга на 180. Это хорошо видно на векторной диаграмме (рис.3.19). Совершенно очевидно,
что в соответствии с первым законом Кирхгофа контурный ток равен сумме токов ветвей контура:
.
Однако, как видно из векторной диаграммы, токи и при суммировании уничтожают друг друга и контурный ток определяется током, протекающим через резистор:
. (3.59)
В силу рассмотренных свойств параллельного контура, резонанс в параллельном контуре еще называют резонансом токов.
Мощности в контуре. Мгновенная мощность контура определяется как произведение мгновенного тока контура на мгновенное напряжение:
На резонансной частоте , тогда
.
Средняя мощность, потребляемая контуром, равна:
.
С учетом (3.58) выражение для средней мощности контура принимает вид:
.
В полученном выражении мгновенной мощности контура на резонансной частоте отсутствует реактивная составляющая мощности. Однако под действием контурного напряжения через конденсатор и индуктивность протекают токи. Определим мгновенные мощности на этих элементах так, как это делали при анализе идеальных емкостного и индуктивного двухполюсников.
Для емкостной ветви и индуктивной ветви получим:
,
. (3.60)
При резонансе . Из (3.60) следует, что мгновенные мощности на конденсаторе и индуктивности равны по величине и противоположны по фазе.
Добротность
контура.
Добротность контура, как и прежде, найдем
из отношения амплитуды реактивной
мощности контура к средней мощности.
Для этого воспользуемся амплитудными
значениями мощностей на конденсаторе
и индуктивности (3.60). После очевидных
преобразований имеем:
. (3.61)
Из (3.61) видно, что добротность контура без диссипации в параллельных ветвях (рис.3.18) тем выше, чем больше величина R, и тем меньше затухают колебания в контуре.
С учетом полученного выражения для добротности полное сопротивление контура (3.50) примет вид:
(3.62)
Последнее выражение для сопротивления контура позволяет рассмотреть зависимость от частоты его модуля и фазы:
,. (3.63)
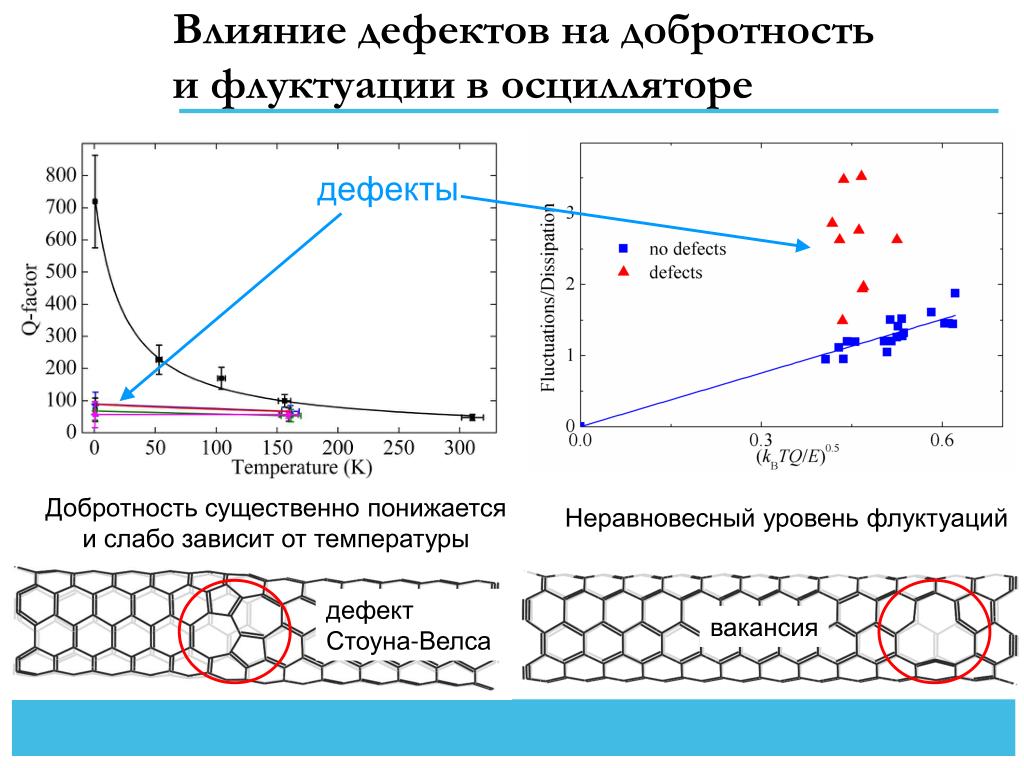
На
рис.3.20 представлены эти зависимости.
Модуль сопротивления контура имеет
наибольшее значение на резонансной
частоте. Если R имеет конечное значение
(присутствует в контуре), то ZК0=R
(график 1). Если R стремится к бесконечности
(резистор отсутствует), то ZК0 также стремится к бесконечности (график
2).
Фазовая характеристика сопротивления контура позволяет установить его свойства на различных частотах. Если воспользоваться треугольником сопротивления, то видно, что на низких частотах (слева от резонансной частоты) контур должен иметь свойства реального индуктивного двухполюсника, а на высоких частотах (справа от резонансной частоты) контур должен иметь свойства реального емкостного двухполюсника.
Сравним амплитуды токов IL и IC с амплитудой тока IR. Используя соотношения (3.58), находим:
; .
Амплитудно-частотной характеристикой (АЧХ) параллельного контура называется зависимость от частоты модуля напряжения на контуре.
Как
и для последовательного контура, удобно
АЧХ для параллельного контура рассматривать
в приведенном виде. Для этого необходимо
найти модуль отношения напряжения на
контуре в комплексной форме при
произвольной частоте к напряжению на
контуре при резонансной частоте.
Напряжение на контуре при произвольной частот и на резонансной частоте находятся по закону Ома:
; .
Для удобства рассмотрения АЧХ здесь напряжение на контуре и сопротивление контура на резонансной частоте обозначены, соответственно как и.
Берем отношение этих напряжений и, с учетом (3.58) и что, получаем:
. (3.64)
Модуль полученного выражения (3.60) является амплитудно-частотной характеристикой параллельного контура.
. (3.65)
На рис.3.21 представлены графики АЧХ параллельного контура для двух значений добротности. Увеличение добротности делает график АЧХ более крутым.
Фазо-частотной характеристикой параллельного контура называется зависимость от частоты фазы напряжения на контуре.
Как
видно из (3.52), фаза напряжения на контуре
равна фазе комплексного сопротивления
контура.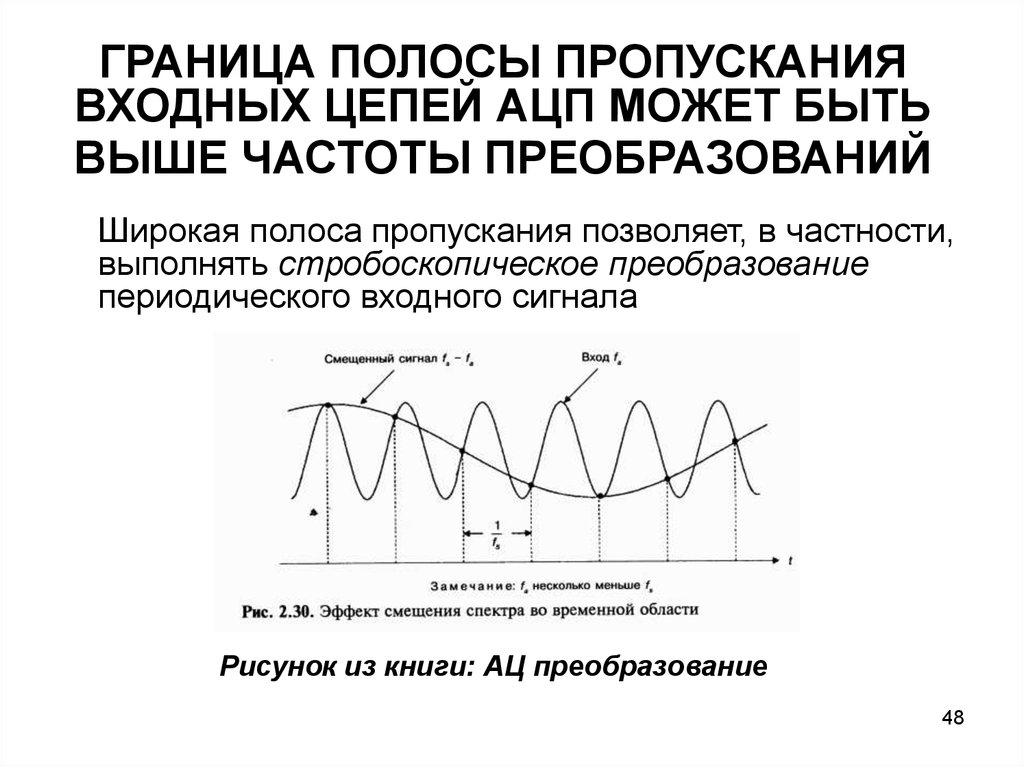
Учитывая (3.63), фазо-частотная
характеристика параллельного контура
принимает вид:
. (3.66)
На рис.3.22 представлен график ФЧХ параллельного контура. Так как фаза контурного тока равна нулю, то ФЧХ контура показывает, в каком фазовом соотношении (опережает, совпадает, отстает) находится напряжение по отношению к току. Эта информация позволяет судить о свойствах контура. Так, на резонансной частоте фаза контурного напряжения равна нулю. Значит на резонансной частоте напряжение контура и ток совпадают по фазе. Исходя из теории двухполюсников, этим свойством обладает резистивный двухполюсник. Следовательно, на резонансной частоте контур может быть заменен резистором. Об этом свойстве контура уже говорилось.
На
низких частотах (слева от резонансной
частоты) фаза контурного напряжения
положительная. Значит, в этом интервале
частот напряжение опережает ток контура.
Из теории двухполюсников известно, что
этим свойством обладает реальный
индуктивный двухполюсник.
Следовательно,
на низких частотах параллельный контур
может быть заменен последовательно
соединенными резистором и индуктивностью.
На высоких частотах (справа от резонансной
частоты) фаза контурного напряжения
отрицательная. Значит, в этом интервале
частот контурное напряжение отстает
от контурного тока. Следовательно, на
этом интервале частот контур обладает
свойствами реального емкостного
двухполюсника, и может быть заменен
последовательно соединенными резистором
и конденсатором. Необходимо отметить,
что величины индуктивности и емкости
в схемах замещения контура индуктивным
и емкостным двухполюсниками не равны
значениям индуктивности и ёмкости
контура и на различных частотах будут
иметь различные значения.
Полоса
пропускания.
Физический смысл полосы пропускания
резонансных контуров рассматривался
для последовательного одиночного
колебательного контура. Для параллельного
контура физический смысл полосы
пропускания совершенно аналогичен.
Отличительная особенность параллельного
контура состоит в том, что выходным
сигналом является контурное напряжение,
и АЧХ отображает его зависимость от
частоты.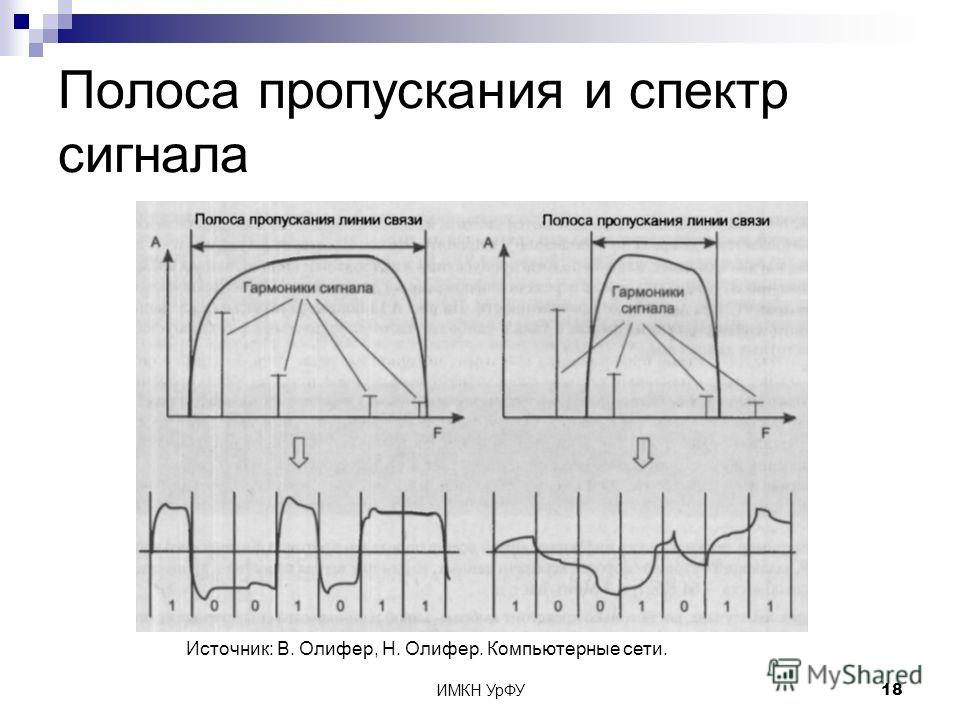
Полосой пропускания параллельного одиночного колебательного контура называется интервал частот, включающий резонансную частоту контура, на границах которого значение напряжения контура меньше значения напряжения на резонансной частоте в раз.
Это требование для значения напряжения на границе полосы пропускания можно выразить так:
; .
Последнее соотношение позволяет определить границы полосы пропускания и ее величину по АЧХ контура (рис.3.23):
.
Пользуясь полученными соотношениями для последовательного колебательного контура, АЧХ для параллельного контура на границах полосы пропускания примет вид, аналогичный (3.36):
.
(3.
67)
Приравнивая (3.67) к коэффициенту неравномерности и решая полученное уравнение относительно 2∆ω, находим:
; .
Как отмечалось, для широкого круга приемно-передающих устройств коэффициент неравномерности берется равным:
.
С учетом этого находим выражение для полосы пропускания одиночного параллельного резонансного контура:
. (3.68)
Коэффициент добротности в зависимости от полосы пропускания в октавном полосовом фильтре -3 дБ Формула расчета коэффициента добротности Коэффициент качества Q в полосу пропускания Фильтр преобразования ширины октавы в полосу пропускания Фильтр преобразования в октаву полосы пропускания Наклон мастеринга вибрации в октаве дБ/октава Крутизна фильтра эквалайзера Частота среза эквалайзера
Коэффициент добротности в зависимости от полосы пропускания в октавном полосовом фильтре — Калькулятор прохода 3 дБ Расчетная формула Коэффициент качества Q в полосу пропускания Фильтр преобразования ширины октавы BW Фильтр октавы BW Наклон мастеринга вибрации дБ/октава Крутизна фильтра эквалайзера Частота среза эквалайзера — sengpielaudio Sengpiel Berlin| Немецкая версия |
Bandpass Filter ( BPF ) and EQ Filter
● Relation between Q factor and bandwidth BW ●
Расчет
Фильтр преобразование : ‘ пропускная способность в октавах ‘ N в добротность Q
and Q factor to ‘bandwidth in octaves’ N (octave width) Q = f 0 / BW
Полоса пропускания BW = f 2 − f 1 = f 0 / Q Эквалайзер Эквалайзер полосовой фильтр фильтр
Коэффициент добротности = коэффициент качества Полоса пропускания BW полосы фильтра f 0 = Центральная частота
Мультипликативная обратная или обратная
Коэффициент качества 1/ Q называется Фактор диссипации D ( демпфирование )
Часто ‘Q’ и ‘Bandwidth’ используются взаимосвязанными, хотя они, хотя они » и ‘и’ Bandwidth ‘ нет.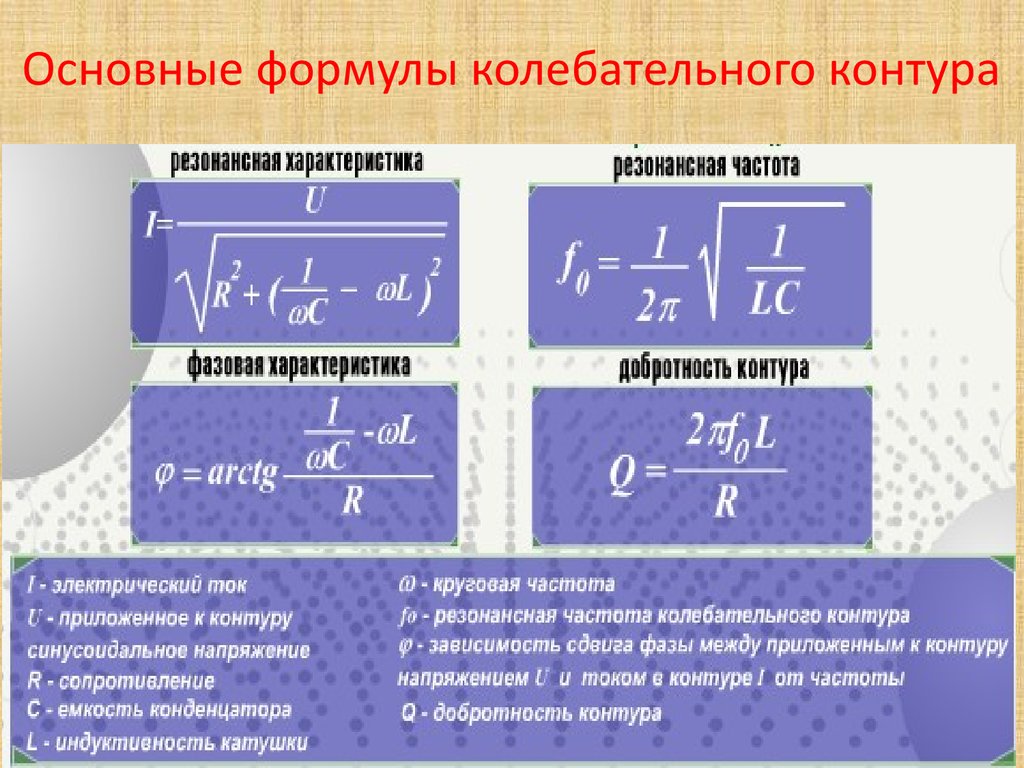
Q не 1/ Н .
Определение полосы пропускания как точки −3 дБ не может быть правильным для усиления усиления 3 дБ или меньше.
The Center frequency f 0 is the geometric mean of f 1 and f 2
f 1 and f 2 is the cut-off frequency = corner frequency = crossover frequency
= half — частота мощности = частота 3 дБ = частота разрыва .
| Используемый браузер не поддерживает JavaScript. Вы увидите программу, но функция не будет работать.  |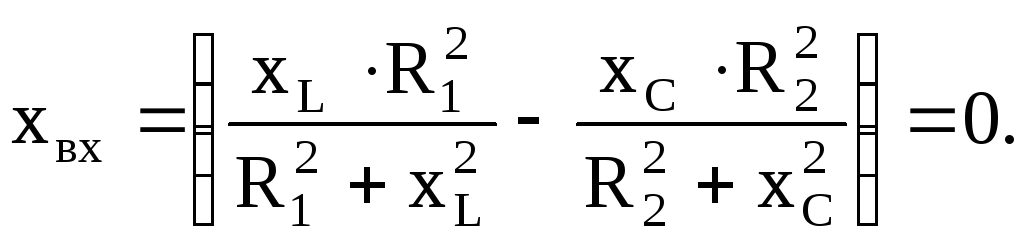
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны от знака ↔ . |
BW = Δf = f 0 / 9
Q Q = f 0 / BW f 0 = BW × Q = √ ( f 1 × f 2 )
BW = f 2 − f 1 f 1 = f 0 2 / f 2 = f 2 − БВ f 2 = f 0 2 / 0008 f 1 = f 1 + BW 33
33
Формула преобразования: «октавная полоса пропускания» N в добротность Q :
Формула преобразования: добротность Q в «ширину октавы» N :
Также известна эта более длинная формула с 4 Q; см.
его разработку по адресу:
Полоса пропускания в октавах по сравнению с Q в полосовых фильтрах — RaneNote 170
Отношение частот октавы:
Формула для преобразования добротности Q в «полосу пропускания в октавах» N ,
но с натуральный логарифм :
И очень короткая формула для преобразования добротности Q
на «полосу пропускания в октавах» N , но с sinh -1 :
Преобразование полосы пропускания в ответ на интервал, отличный от октавы, например индикация
«полосы пропускания как функции квинты» с интервалом 2/3 или 1/2 октавы необычно.
| Учитывая точки -3 дБ, чтобы найти полосу пропускания BW и добротность Q . BW = f 0 / Q Q = f 0 / BW f 0 =√ ( f 1 × f 2 ) 9 Н − 1) По заданной добротности Q найти полосу пропускания в октавах N . N = log(1 + 1 / (2 × Q 2 ) + sqr(((2 + 1 / ( Q 2 )) 2 ) / 4 − 1)) / журнал(2) |
Таблица или таблица преобразования
‘полоса пропускания в октавах’ N до добротности Q
| BW в октавы | Фильтр Q | BW в октавы | Фильтр Q | BW в октавы | Фильтр Q | BW в октавы | Фильтр Q | |||
| 1/80 | 115,4 | 1 | 1,41 | 4 | 0,267 | 7 | 0,089 | |||
| 1/60 | 86,6 | 1 1/4 | 1. 12 | 4 1/4 | 0,242 | 7 1/4 | 0,082 | |||
| 1/50 | 72,1 | 1 1/3 | 1,04 | 4 1/3 | 0,234 | 7 1/3 | 0,079 | |||
| 1/40 | 57,7 | 1 1/2 | 0,92 | 4 1/2 | 0,220 | 7 1/2 | 0,075 | |||
| 1/30 | 43,3 | 1 2/3 | 0,82 | 4 2/3 | 0,207 | 7 2/3 | 0,071 | |||
| 1/25 | 36,1 | 1 3/4 | 0,78 | 4 3/4 | 0,200 | 7 3/4 | 0,068 | |||
| 1/20 | 28,9 | 2 | 0,67 | 5 | 0,182 | 8 | 0,063 | |||
| 1/16 | 23,1 | 2 1/4 | 0,58 | 5 1/4 | 0,166 | 8 1/4 | 0,058 | |||
| 1/12 | 17,3 | 2 1/3 | 0,56 | 5 1/3 | 0,161 | 8 1/3 | 0,056 | |||
| 1/10 | 14,4 | 2 1/2 | 0,51 | 5 1/2 | 0,152 | 8 1/2 | 0,053 | |||
| 1/8 | 11,5 | 2 2/3 | 0,47 | 5 2/3 | 0,143 | 8 2/3 | 0,050 | |||
| 1/6 | 8,65 | 2 3/4 | 0,45 | 5 3/4 | 0,139 | 8 3/4 | 0,048 | |||
| 1/5 | 7. 20 | 3 | 0,40 | 6 | 0,127 | 9 | 0,044 | |||
| 1/4 | 5,76 | 3 1/4 | 0,36 | 6 1/4 | 0,116 | 9 1/4 | 0,041 | |||
| 1/3 | 4.32 | 3 1/3 | 0,35 | 6 1/3 | 0,113 | 9 1/3 | 0,039 | |||
| 1/2 | 2,87 | 3 1/2 | 0,33 | 6 1/2 | 0,106 | 9 1/2 | 0,037 | |||
| 2/3 | 2. 14 | 3 2/3 | 0,30 | 6 2/3 | 0,100 | 9 2/3 | 0,035 | |||
| 3/4 | 1,90 | 3 3/4 | 0,29 | 6 3/4 | 0,097 | 9 3/4 | 0,034 | |||
| 10 | 0,031 |
Q коэффициент как функция ширины полосы в октавах N
| Пропускная способность в октавы N | Фильтр Q коэффициент |
| Ширина 3,0 | 0,404 низкий |
| 2,0 | 0,667 |
| 1,5 | 0,920 |
| 1,0 | 1,414 |
| 2/3 | 2,145 |
| 1/2 | 2,871 |
| 1/3 | 4,318 |
| 1/6 | 8,651 |
| 1/12 малый | 17,310 высокий |
| Уведомление: Низкий коэффициент добротности дает широкополосную (широкую) полосу пропускания или высокая добротность дает узкую (маленькую) полосу пропускания. |
| Высокое качество фильтра означает узкополосную фильтрацию (режим) с большой добротностью. Это приводит к крутым фронтам фильтра с небольшой полосой пропускания. Низкое качество фильтра означает широкополосную фильтрацию с небольшой добротностью. Это приводит к плоским фронтам фильтра с большой полосой пропускания. Чем больше Q, тем уже резонансный пик. Чем меньше Q, тем шире резонансный пик. |
Режекторные фильтры имеют большую добротность (Q), соответствующую небольшой полосе пропускания.
| Коэффициент добротности или пропускная способность не скажешь «крутизну» в дБ/окт. |
| Наклон в дБ/октава = крутизна фронтов фильтра |
| Примечание: Коэффициент добротности (добротность) или полоса пропускания не могут быть преобразованы в «наклон» в дБ/окт. Встречаются мастеринговые эквалайзеры с ложной информацией о настройке фильтра как «Наклон в дБ/октава», а не добротность (ширина), см.: Наклон или крутизна фильтра (дБ/октава) не является полосой пропускания = Наклон в дБ/октава или крутизна фильтра склоны — это не пропускная способность. |
| При заданной добротности и центральной частоте – найти граничные частоты по уровню 3 дБ0009 Formulas for conversion of bandwidth in octaves to quality factor Questions on «Parametric filter adjustment» Conversion table Q to N and N to Q for parametric filters Excel преобразование − добротность Q в полосу пропускания в октавах N Фильтр Наклон или крутизна (дБ/октава) не является полосой пропускания Добавление децибел третьоктавных полос к уровню одной октавной полосы |
| Под «качеством» не подразумевается ценность сигнала. Имеется в виду качество фильтра. Если фильтр имеет плоские наклоны, многие частоты оказывают влияние на частоту среза. Таким образом, фильтр имеет более широкую полосу пропускания, а так называемый коэффициент качества Q определяется как низкий. число. Если фильтр имеет крутые наклоны, его полоса пропускания меньше. Здесь затрагиваются несколько частот ниже и выше его частоты среза, и качество фактор Q указывается как старший номер. |
| Почему полоса пропускания и частота среза находятся на уровне «−3 дБ»? Почему мы всегда снижаем усиление фильтра на 3 дБ? Полная ширина на полувысоте (FWHM). Ответ: Это точка, в которой энергия (мощность) падает до значения ½ или 0,5 = 50 процентов от начальной мощности в виде энергии. величина, эквивалентная (−)3 дБ = 10×log(0,5). Падение мощности (-)3 дБ представляет собой уменьшение на 50 % до значения 50 %. Там напряжение падает до значения √(½) или 0,7071 = 70,71 процента от начального напряжения, так как величина поля эквивалентна (-) 3 дБ = 20 × log (0,7071). Падение напряжения (-)3 дБ представляет собой уменьшение на 29,29 % до значения 70,71 %. |
| (-)3 дБ означает ½ электрической мощности, а поскольку мощность пропорциональна
квадрат напряжения, значение будет 0,7071 или 70,71 % напряжения полосы пропускания. √½ = 1/√2 = √0,5 = 0,7071. P ~ V 2 , то есть 0,5 ~ 0,7071 2 . |
| Звукорежиссеры и звукорежиссеры («люди со слухом») в основном используют обычное (звуковое) количество полей . Вот почему говорят: Частота среза устройства (микрофона, усилителя, громкоговорителя) — это частота, при которой уровень выходного напряжения снижается до значения на (-)3 дБ ниже уровня входного напряжения (0 дБ). ● (−)3 дБ соответствует коэффициенту √½ = 1/√2 = 0,7071, что составляет 70,71 % входного напряжения. Акустикам и звукозащитникам («борцам с шумом»), кажется, больше нравится количество (звука) энергии. Нам говорят: Частота среза устройства (микрофона, усилителя, громкоговорителя) — это частота, при которой уровень выходной мощности уменьшился до значения на (-)3 дБ ниже уровня входной мощности (0 дБ). ● (−)3 дБ соответствует коэффициенту ½ = 0,5, что составляет 50 % входной мощности (половина значения). |
| Примечание: Усиление мощности (усиление мощности) не является обычным явлением в аудиотехнике. Даже усилители мощности для громкоговорителей не усиливают мощность. Они усиливают звуковое напряжение, которое перемещает звуковую катушку. |
| Величины звукового поля Звуковое давление, скорость звука или частиц, смещение частицы или амплитуда смещения, (напряжение, ток, электрическое сопротивление). Закон обратного расстояния 1/ r | Количество звуковой энергии Сила звука, плотность звуковой энергии, звуковая энергия, акустическая мощность. (электричество). Закон обратных квадратов 1/ r ² |
| Примечание: Величина звукового поля (звуковое давление p , электрическое напряжение В ) не является звуковой энергией
количество (сила звука I , мощность звука P ак ). I ~ p 2 или P ~ V 2 . Иногда вы можете услышать
утверждение: Частота среза находится там, где уровень L уменьшается на (-)3 дБ. Что бы пользователь ни хотел сказать нам так точно: уровень есть уровень или дБ есть дБ. |
| задняя часть | Поисковая система | дом |
Передаточная функция, полоса пропускания и добротность в цепях RLC
Определение передаточной функции для последовательных цепей RLCПередаточная функция {H(w)} равна выходному напряжению В out , деленному на входное напряжение В в , что может быть далее записано как:
График представляет амплитуду в зависимости от частоты. На схеме показаны три различные передаточные функции. Изменение сопротивления внутри цепи изменяет ширину передаточной функции; увеличение сопротивления увеличивает ширину, действующую как полосовой фильтр. Полосовой фильтр позволяет пропускать только определенную полосу частот, подавляя все частоты за пределами полосы.
На схеме видно, что это очень узкополосный фильтр, который пропускает частотные составляющие только в резонансной частоте. Таким образом, если предположить, что f o является резонансной частотой с величиной передаточной функции 1,0, мы можем сказать, что в этой точке V R = V s , это означает, что мы можем передать всю мощность в пределах этой частоты на выход нашего схема. Например, если у вас есть мощность или сигнал в пределах этой узкой полосы, он будет перемещен на выход; однако, если у вас есть сигнал за пределами этой полосы, он будет ослаблен цепью. Таким образом, эта схема действует как полосовой фильтр.
Как мы можем иметь передаточную функцию 1,0 для контура на резонансной частоте?
На резонансной частоте эти импедансы (L и C), эквивалентные импедансы Z LC, , станут равными нулю. В принципе, на резонансной частоте эквивалентная схема этой сети будет иметь только сопротивление, как показано на рисунке 2. Следовательно, V R становится равным V s .
При определенной частоте мощность, рассеиваемая резистором, составляет половину максимальной мощности, тогда амплитуда напряжения на резисторе становится равной 1/√2 максимального напряжения.
На этой диаграмме представлена передаточная функция, и мы определили две точки w1 и w2. Амплитуда этой точки составляет 1/√2 максимального напряжения. Максимальная передаточная функция находится в точке А, где V R = V с , максимальная мощность, которая может быть достигнута на выходе. Мощность будет меньше в любой другой точке на графике, показанном, поскольку коэффициент усиления меньше 1. Разница между двумя частотами w1 и w2 называется пропускной способностью.
Теперь мы можем увидеть взаимосвязь между резистором, катушкой индуктивности и пропускной способностью. Следовательно, это причина, по которой на рисунке 3 для серии RLC сопротивление увеличивается с увеличением полосы пропускания.
Коэффициент качества определяется как отношение резонансной частоты (f r ) к ширине полосы; однако это определение верно только при наличии резонанса (L и C) в цепи.
Общепринятое определение добротности – это отношение энергии, запасенной в колебательном резонаторе, к энергии, рассеиваемой за цикл.
Здесь потери мощности связаны с резистором, и у нас нет потерь мощности в катушке индуктивности или конденсаторе (как обсуждалось в разделе активной и реактивной мощности). Катушка индуктивности и конденсатор рассеивают или генерируют реактивную мощность, но когда мы говорим о потере мощности, это активная мощность, связанная с резистором в цепи. Если у нас больше потери мощности, то у нас будет низкая добротность (Q). Сети с низкой добротностью неэффективны из-за больших потерь мощности. Таким образом, цель состоит в том, чтобы иметь высокую добротность в цепях.
Как найти коэффициенты качества в цепях RLC?
Как мы знаем, эта добротность есть отношение резонансной частоты к ширине полосы; поэтому мы можем написать уравнение для цепи RLC как:
- Когда передаточная функция сужается, добротность высока.
- Добротность увеличивается с уменьшением R.
- Пропускная способность уменьшалась с уменьшением R.
Таблица для последовательных и параллельных уравнений RLC:
Узнайте больше по этой теме, пройдя полный курс «Теория и принципы проектирования радиочастот — RAHRF203» 916. Посмотрите видеокурсы для более подробного понимания. Также ознакомьтесь с другими курсами по радиочастотным системам и проектированию интегральных схем на https://rahsoft.com/courses/ Rahsoft также предоставляет сертификат по радиочастотам.
