Общее сопротивление цепи переменного тока с конденсатором



Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.

Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным. На практике все это надо обязательно учитывать, потому что возможны ситуации (обычно связанные с ростом частоты сигнала), когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности

. При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про емкостное сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления .

Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).

Рисунок 1 – Конденсатор в цепи переменного тока

К его обкладкам приложено некоторое переменное напряжение U(t), и через него течет некоторый ток I(t). Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока , там мы про все это довольно подробно говорили.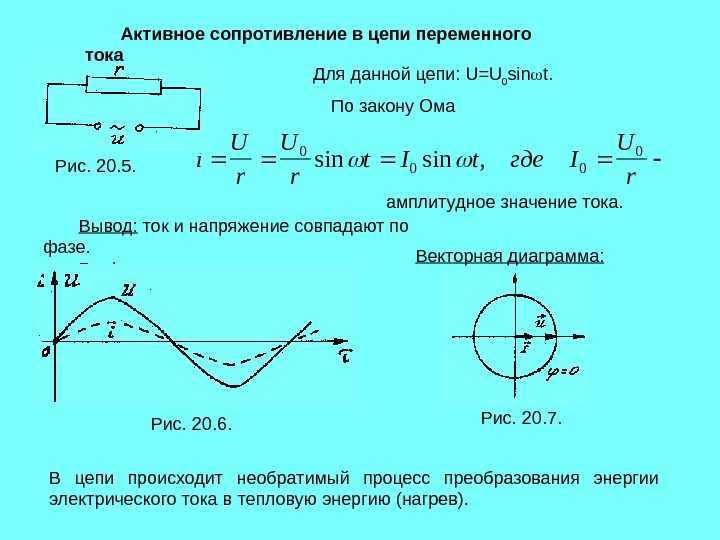 Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так

В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом

Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья ? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида

то его можно представить в показательной форме вот так

Почему это так, откуда взялось, что здесь какая буковка значит – обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.

Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого

Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала. Сейчас как раз такой момент. Поэтому полагаем t=0 и получаем комплексную амплитуду напряжения

Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.

Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида

Что мы вообще такое записали? Правильно, комплексную амплитуду тока через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид

Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике , не зря ж я ее писал

. Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:

Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид

Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим

Как мы помним из статьи про закон Ома , у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение – переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току:

Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное. Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье .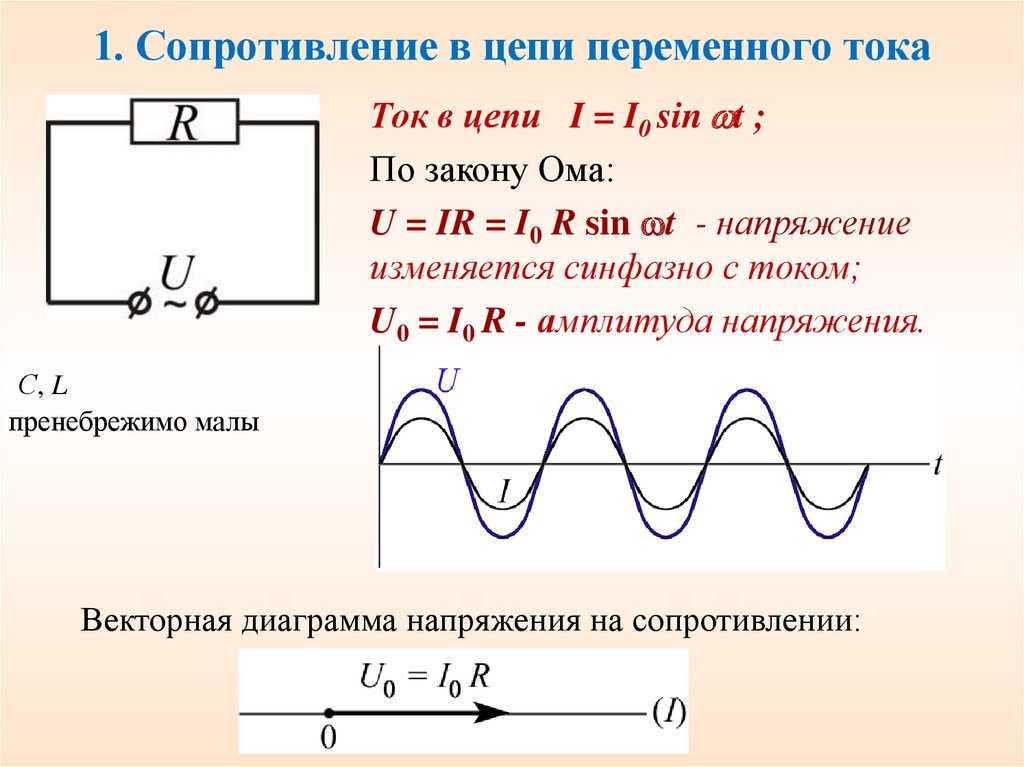 Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент

. Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.

Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно.

Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения.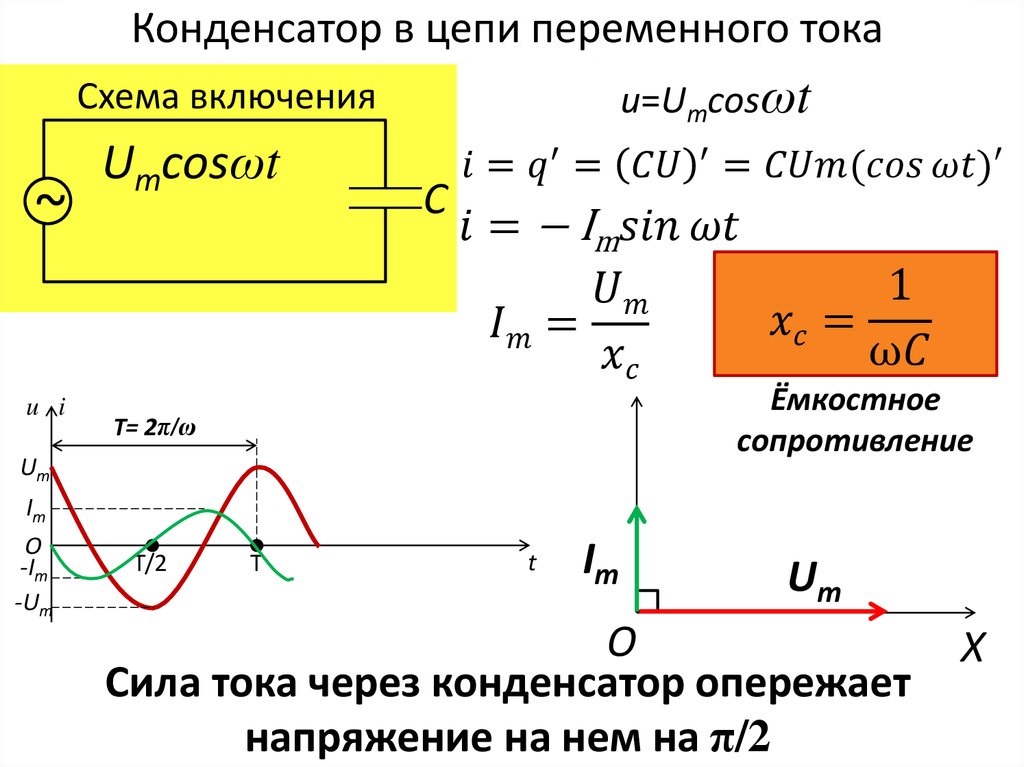 Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует, то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:

Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора (а именно его емкости), но и от частоты протекающего тока. Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты (разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров). Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения.

Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току.

По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах . Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным. И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.

Рисунок 2 (кликабельно) – Зависимость сопротивления конденсатора от частоты

На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.

При стремлении частоты к нулю (то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим.

При стремлении частоты к бесконечности, сопротивление конденсатора стремится к нулю. Это все в теории, конечно. На практике реальный конденсатор обладает рядом паразитных параметров (в частности, паразитная индуктивности и сопротивление утечки), из-за чего сопротивление уменьшается только лишь до некоторой определенной частоты, а потом начинает наоборот расти. Но об этом более подробно в другой раз.

Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет.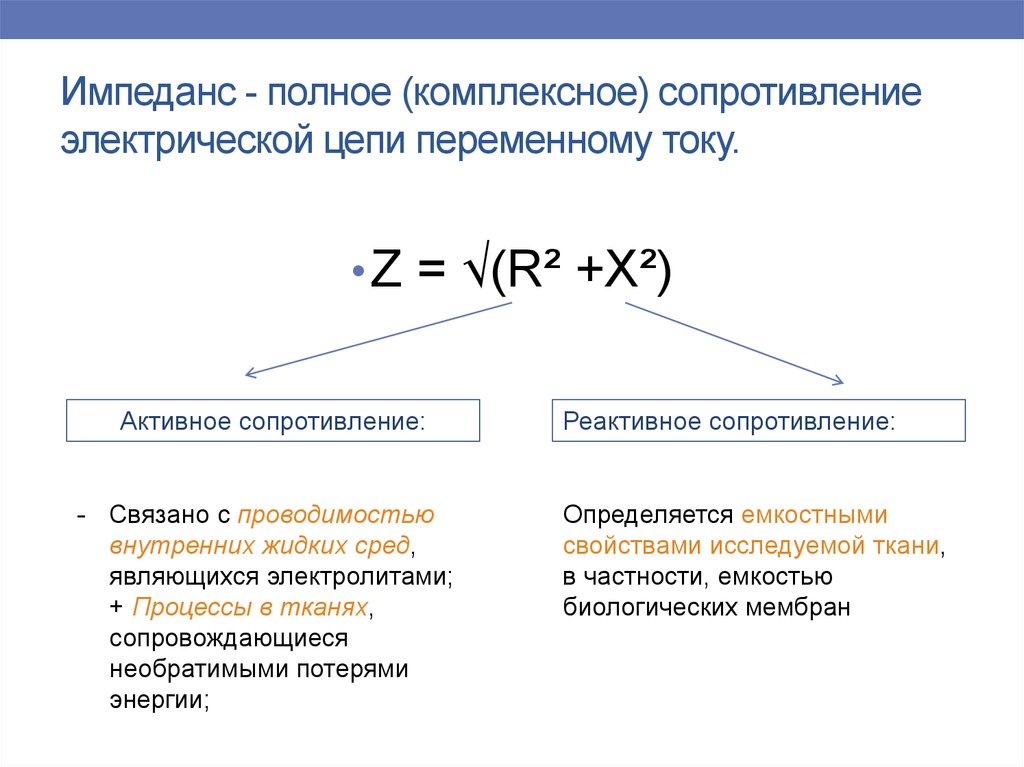 Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая – емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам.

Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ. Требуется определить его сопротивление на частоте f₁=50 Гц и на частоте f₂=1 кГц. Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна U_m=50 В. Ну и построить графики напряжения и тока.

Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f₁=50 Гц сопротивление, равное

А для частоты f₂=1 кГц сопротивление будет

По закону Ома находим величину амплитуды тока для частоты f₁=50 Гц

Аналогично для второй частоты f₂=1 кГц

Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f₁=50 Гц следующим образом

А для второй частоты f₂=1 кГц вот так

Дальше мы помним, что ток в конденсаторе опережает напряжение на

. Поэтому с учетом этого можем записать закон изменения тока через конденсаторы для первой частоты f₁=50 Гц

и для частоты f₂=1 кГц

Графики тока и напряжения для частоты f₁=50 Гц представлены на рисунке 3

Рисунок 3 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f₁=50 Гц

Графики тока и напряжения для частоты f₂=1 кГц представлены на рисунке 4

Рисунок 4 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f₂=1 кГц

Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров.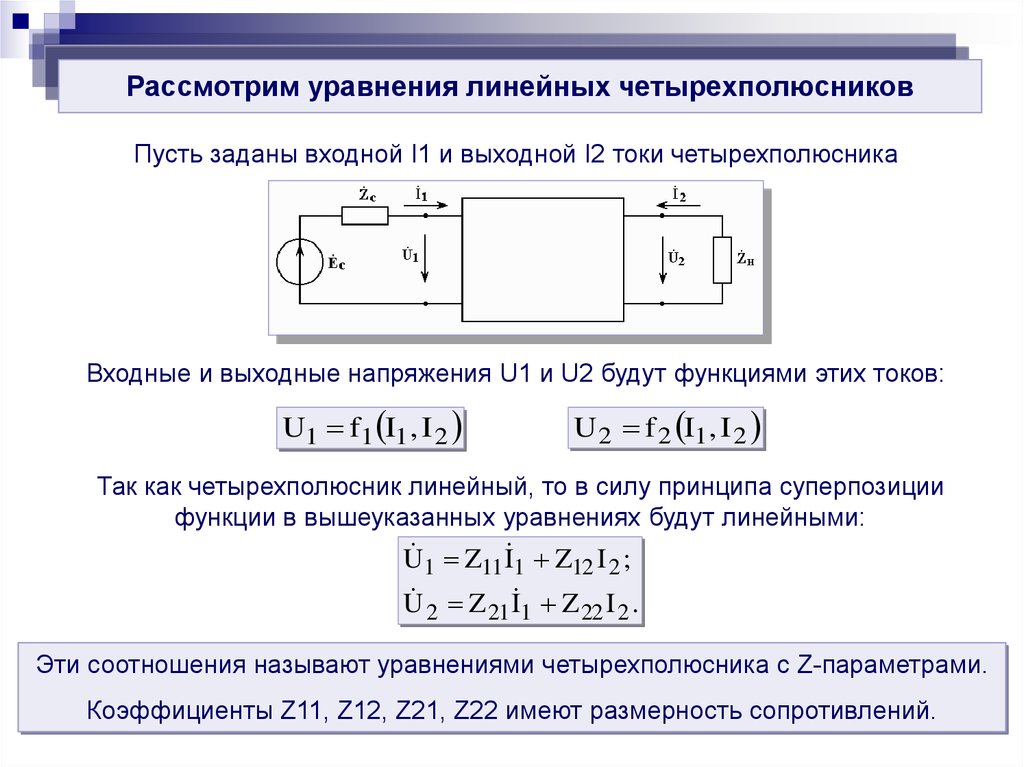 На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Источник

Цепь переменного тока с R, L и С сопротивлениями

Цепь переменного тока с R, L и С сопротивлениями

Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

 На рис. 60, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением Х_L и емкость С, обладающая емкостным сопротивлением Х_c.

Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 60, б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока 

I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения откладываем по вектору тока.
Напряжение на индуктивности опережает ток на угол φ = 90°. Поэтому вектор  откладываем вверх под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол φ = 90°. Поэтому вектор откладываем на диаграмме вниз под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы  и . Для этого отнимем от большего вектора  вектор  и получим вектор  — , выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( — ) и . Суммой этих векторов будет диагональ параллелограмма — вектор , изображающий общее напряжение на зажимах цепи.

На основании теоремы Пифагора из треугольника напряжений АОБ следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I, выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А′О′Б′ (рис. 59, в). Его сторонами являются сопротивления r, (Х_L — Х_c) и полное сопротивление цепи 

Z. Пользуясь теоремой Пифагора, можно написать, что

Z² =r² + (Х_L — Х_c)².

Отсюда полное сопротивление цепи

Формула (70) может применяться и в частных случаях, когда Х_L = 0 или Х_c = 0.
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома:

На векторной диаграмме (рис. 59, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

Из треугольника сопротивлений

Главная страница

Подписаться на: Сообщения (Atom)

Что такое реактивное сопротивление и полное сопротивление в цепи переменного тока?

17 мая 2020 г. от администратора

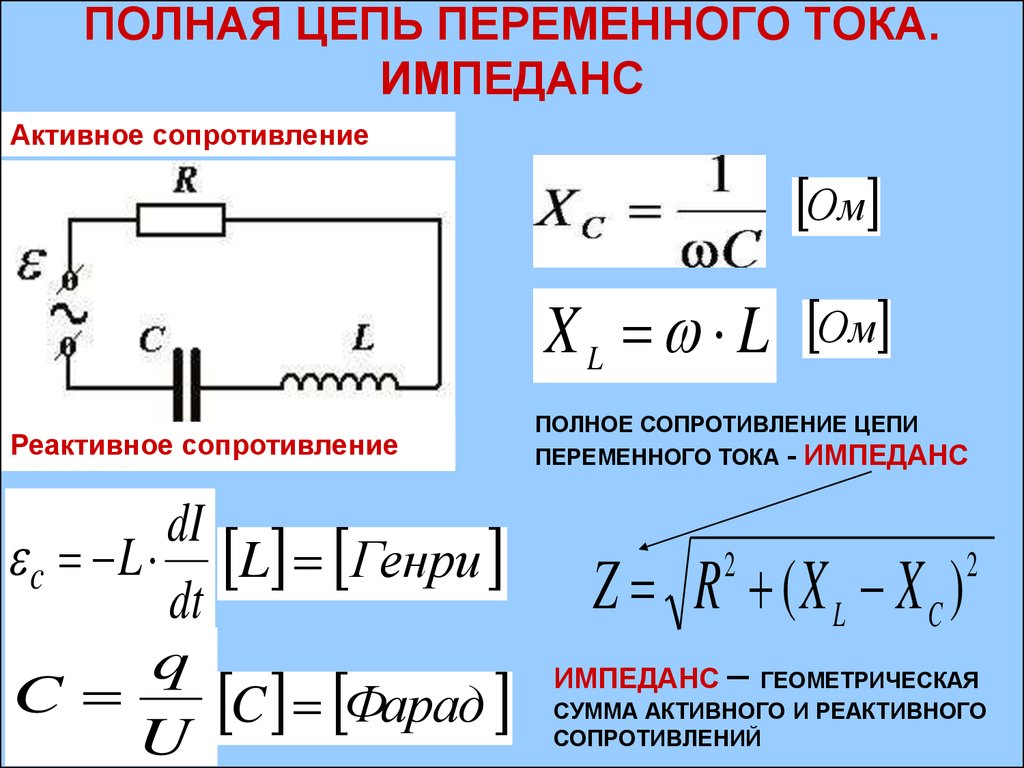
Реактивное сопротивление определяется электрической величиной, благодаря которой переменному току противодействует катушка индуктивности или конденсатор или их комбинация в цепи. Импеданс — это чистый противодействующий фактор переменному току. Реактивное сопротивление также можно назвать импедансом, обеспечиваемым катушкой индуктивности или конденсатором. Реактивное сопротивление обозначается X, а импеданс Z. В этой статье мы подробно обсудим реактивное сопротивление и импеданс.

Что такое реактивное сопротивление?

Реактивное сопротивление – это сопротивление, предлагаемое протеканию переменного тока. Это противодействие может быть вызвано катушкой индуктивности (L) или конденсатором (C). Значение реактивного сопротивления из-за индуктора, имеющего индуктивность L, равно ωL, тогда как его значение равно (1/ωC) для конденсатора, имеющего емкость C.

Объяснение реактивного сопротивления:

Давайте рассмотрим схему для лучшего понимания. В схеме катушка индуктивности L Генри подключена к источнику переменного тока V = V _м Синωт. Здесь ω — угловая частота в радианах/с. ω = 2πf, где f — частота питания в Гц. Ток в цепи равен I.

Ток I, протекающий по цепи, равен [В _м Sin(ωt – π/2) / (ωL)]. Следовательно, максимальное значение этого тока дана как

I _M = (V _M / ωl)

= (V _M / X _L )

, где X _L = ωL

Внимательно изучите приведенное выше выражение для тока и сравните его с законом Ома (I = V/R). Вы заметите, что здесь X _L выполняет работу R. То есть X _L = ωL противодействует потоку тока точно так же, как сопротивление. Это причина; это называется реактивным сопротивлением. Так как оно обеспечивается катушкой индуктивности, оно называется индуктивным реактивным сопротивлением и обозначается символом X _L .

Теперь рассмотрим другую схему, состоящую из конденсатора и переменного источника, как показано ниже.

Ток в цепи равен (В _m ωC)Sin(ωt+π/2). Следовательно, максимальное значение тока будет иметь место, когда Sin(ωt+π/2) = 1, и это значение указано ниже.

I _M = V _M / (1 / ωc)

= V _M / x _C

При сравнении выше среднего значения тока I _M с законом OHM (OHM’S (OHM’S (OHM’S (OHM’S (OHM’S (OHM) I = V/R), ясно, что X _C противостоит потоку тока и действует как сопротивление. Это X _C = (1/ωC) называется емкостным реактивным сопротивлением.

Что такое импеданс?

Полное сопротивление в цепи переменного тока определяется как чистый противодействующий фактор протеканию тока. Это противостояние может быть связано с сопротивлением и индуктивностью или сопротивлением и емкостью или сопротивлением, индуктивностью и емкостью.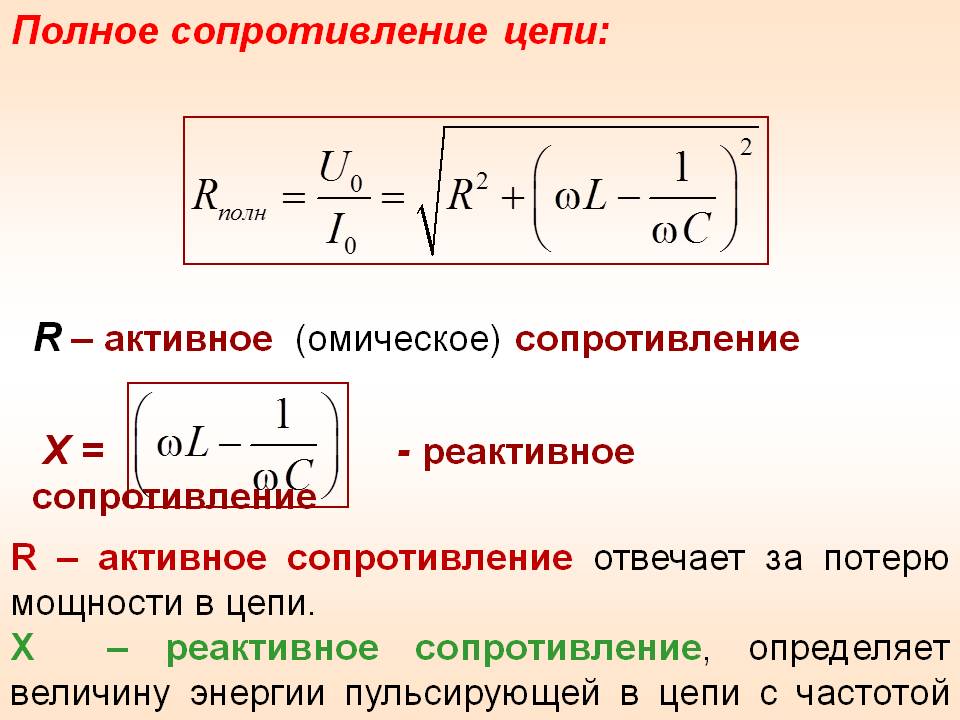 Он обозначается символом Z. Z часто выражается как Z = R + jX, где X — реактивное сопротивление.

Объяснение импеданса:

Чтобы иметь кристально ясное представление об импедансе, давайте рассмотрим схему, показанную ниже. В этой цепи чистое сопротивление R и чистая индуктивная катушка с индуктивностью L соединены последовательно.

Пусть, V = среднеквадратичное значение приложенного напряжения

I = среднеквадратичное значение тока цепи

В _R = падение напряжения на R

В _L = падение напряжения на катушке быть эталонным фазовращателем. Падение напряжения на сопротивлении будет синфазно с током I. Однако падение напряжения в катушке индуктивности будет опережать ток I на 90°. Эти падения напряжения показаны в треугольнике напряжений OAB.

Векторы OA, AB и OB представляют падение напряжения на сопротивлении (V _R ), индуктивное падение напряжения (V _L ) и напряжение питания (V) соответственно. Напряжение питания (V) является гипотенузой этого треугольника напряжений. Следовательно, напряжение питания можно рассчитать, как показано ниже.

Величина Z представляет собой абсолютное сопротивление цепи переменного тока. Из треугольника напряжения можно также записать напряжение питания с помощью оператора j. Это показано ниже.

V = (IR) + j(IX _L )

I = V / (R+jX _L )

   = V/Z

Таким образом, полное сопротивление Z = R+1050 9,0 Таким образом, импеданс является комплексной величиной. Угол, который Z образует с эталонным вектором, рассчитывается из тангенса Ɵ = (X/R).

Комплексное сопротивление

Комплексное сопротивление

Обработка импеданса цепи переменного тока с несколькими компонентами быстро становится неуправляемой, если для представления напряжений и токов используются синусы и косинусы. Математическая конструкция, облегчающая эту трудность, — использование сложных экспоненциальных функций. Основные части стратегии следующие: Математические отношения, лежащие в основе метода Соотношение Эйлера Полярная форма комплексного числа Действительная часть сложной экспоненциальной функции может использоваться для представления переменного напряжения или тока. Затем импеданс можно выразить как комплексную экспоненту. Комбинации импедансов Векторные диаграммы Полное сопротивление отдельных элементов схемы может быть выражено в виде чистых действительных или мнимых чисел. Комбинации RL и RC Пример для параллельных элементов

Алфавитный указатель Концепции цепей переменного тока

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Использование комплексного импеданса является важным методом работы с многокомпонентными цепями переменного тока. Если используется комплексная плоскость с сопротивлением вдоль действительной оси, то реактивные сопротивления конденсатора и катушки индуктивности рассматриваются как мнимые числа. За ряд комбинаций компонентов, таких как Комбинации RL и RC, значения компонентов добавляются, как если бы они были компонентами вектора. Здесь показана декартова форма комплексного импеданса. Они также могут быть записаны в полярной форме. Импедансы в этой форме можно использовать в качестве строительных блоков для расчета импедансов комбинированных цепей, таких как параллельная цепь RLC. Полное сопротивление Поведение катушки индуктивности при переменном токе Поведение конденсатора при переменном токе

Индекс Концепции цепей переменного тока

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Здесь показаны векторные диаграммы и выражения комплексного импеданса для цепей RL и RC в полярной форме. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника