Полное сопротивление цепи — определение, принципы, проблемы

Расчет выходных характеристик цепи, т.е. значений тока и напряжения, требует знания общего сопротивления всей замкнутой цепи. Другими словами, все элементы от источника питания до нагрузки заменяются эквивалентными резисторами. Для схемы сначала вычисляется значение полного сопротивления, а затем рассчитывается желаемая характеристика. Относительно источника тока, нагрузку и другие элементы, каждый резистор может быть подключен:

Содержание

Полное сопротивление цепи – принципы, формулы и примеры расчета

Протекание электрического тока через проводник Зависит от его проводимости.. Этот параметр пропорционален силе тока. Другими словами, он определяет способность вещества проводить через себя электрический ток без потерь. Проводимость зависит от физических свойств материала, температуры и степени приложенных внешних сил. Обратной величиной является сопротивление – характеристика проводника, показывающая его способность сопротивляться протеканию тока.

Связь между основными параметрами электрического тока была установлена экспериментально Симоном Омом. Он заявил, что ток в замкнутой цепи пропорционален разности потенциалов (напряжению) и обратно пропорционален сопротивлению: I = U / R. Таким образом, если R равно нулю, ток будет бесконечным.

Способность веществ препятствовать протеканию электрического тока используется при построении электрических цепей. Например, радиоэлемент, который называется резистором, помещенный в определенную точку электрической цепи, позволяет заряду получить нужное напряжение или ток. Радиоэлемент – это биполярный элемент, который имеет фиксированное значение сопротивления или может его изменять.

Настоящий замкнутый контур состоит из нескольких активных и пассивных радиочастотных элементов. Каждый из них имеет определенное значение сопротивления. В данном случае речь идет о внутреннем сопротивлении устройства.

Расчет выходных характеристик цепи, т.е. значений тока и напряжения, требует знания общего сопротивления всей замкнутой цепи. Другими словами, все элементы от источника питания до нагрузки заменяются эквивалентными резисторами. Для схемы сначала вычисляется значение полного сопротивления, а затем рассчитывается желаемая характеристика. Относительно источника тока, к источнику тока, нагрузке и другим элементам, каждый резистор может быть подключен

• в серии;
• параллельно.

Тип соединения влияет на общее сопротивление. Формула для ее нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще всего вычисления проводят в несколько этапов, соединяя один или несколько элементов на каждом этапе.

I – ток в цепи AB. Он одинаков во всей цепи и равен силе тока I₁ и I₂ в каждом из резисторов. Поэтому его можно записать:
IR = IR₁ + IR₂,
IR = I(R₁ + R₂).

Рассмотрим участок AB цепи, который представляет собой последовательное соединение двух резисторов сопротивлением R₁ и Р₂.

Согласно закону Ома, полное сопротивление этой цепи равно U = IRгде U – общее напряжение в цепи AB, равное сумме напряжений на каждом резисторе: U = U₁ + U₂.

I – ток в участке AB цепи. Он одинаков во всей цепи и равен силе тока I₁ и I₂ в каждом из резисторов. Поэтому мы можем написать:
IR = IR₁ + IR₂,
IR = I(R₁ + R₂).

Следовательно, R = R₁ + R₂.

Общее сопротивление цепи, соединенной последовательно, равно сумме сопротивлений отдельных проводников.

Когда несколько проводников соединены последовательно, общее сопротивление цепи равно сопротивлению отдельных проводников: R = R₁ + R₂ + … Rn.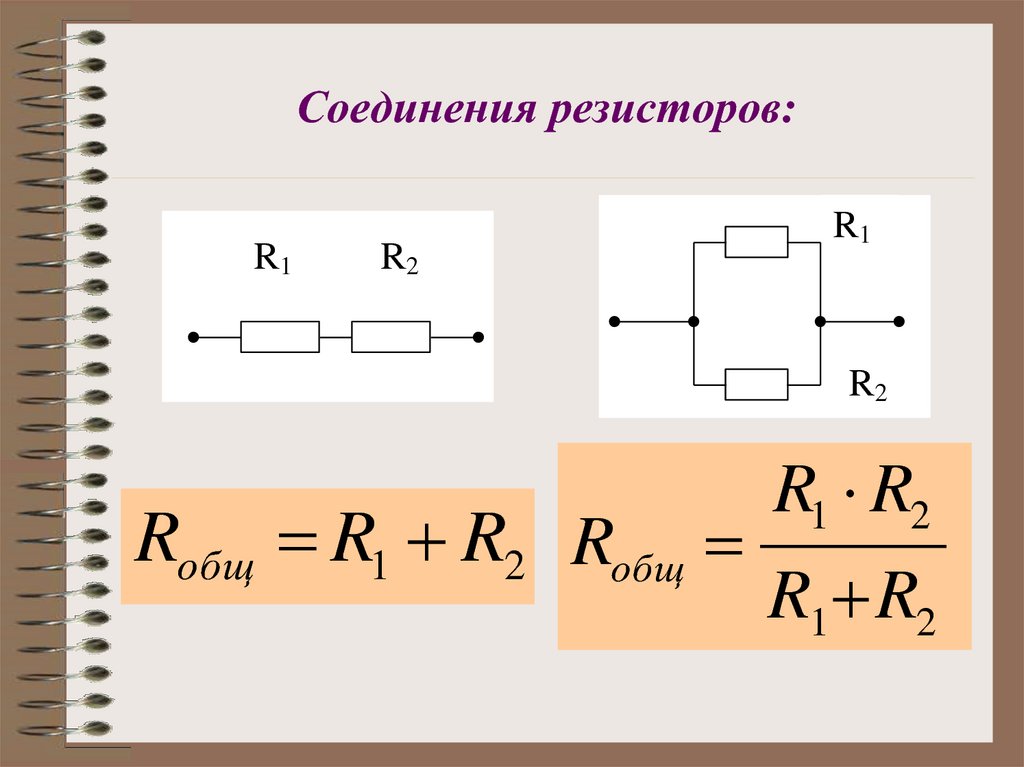

Метод соединения последовательных участков цепи реализуется в действии реостата, о котором говорилось в предыдущих уроках. Перемещая ползунок реостата, мы увеличиваем или уменьшаем количество витков провода, последовательно соединенных в цепи. Это увеличивает или уменьшает сопротивление цепи соответственно.

При последовательном соединении проводов их общая длина увеличивается. Поэтому сопротивление цепи становится больше, чем сопротивление любого из проводников.

СОПРОТИВЛЕНИЕ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ

Рассмотрим участок цепи CD, который представляет собой параллельное соединение двух резисторов с сопротивлениями R₁ и Р₂.

Согласно закону Ома I = U/Rгде R – полное сопротивление данного участка цепи; U – полное напряжение участка цепи CD, равное напряжениям U₁ и U₂ на каждом из резисторов; I – ток в цепи CD, он равен сумме токов в каждом из резисторов: I = I₁ + I₂.

Поэтому мы можем написать:

где R₁ и Р₂ – сопротивление первого и второго резистора соответственно.

Принимая во внимание, что U = U₁ = U₂получаем

Следовательно,

Для случая двух параллельно соединенных резисторовПолное сопротивление цепи можно рассчитать по формуле

Поэтому общее сопротивление цепи, если несколько резисторов соединены параллельно, можно рассчитать по формуле

Уменьшение общего сопротивления параллельно соединенных проводников связано с тем, что общая площадь поперечного сечения проводников в цепи увеличивается.

В электрических цепях, используемых на практике, часто бывает так, что проводники соединены как последовательно, так и параллельно. При расчете таких схем сначала рассчитываются необходимые значения для каждого участка схемы, а затем находятся общие параметры схемы.

Вы изучали тему “Сопротивление при последовательном и параллельном соединении проводников” на уроке физики в 8 классе. .

Закон Ома для электрической цепи утверждает, что сила тока (I) в цепи прямо пропорциональна на напряжение (U) на концах цепи и обратно пропорциональна его его устойчивость (R).

Закон Ома для полной цепи

Закон Ома для полной цепи утверждает, что текущий в цепи пропорциональна электродвижущей силе (ЭМПи обратно пропорциональна сумме сопротивление в цепи и внутреннее сопротивление источника.

Онлайн-калькулятор

Найдите текущий

ЭДС: ε = V
Сопротивление всех внешних элементов в цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом

Формула

Пример

Если ЭДС источника напряжения составляет ε = 12 В, сопротивление всех внешних элементов цепи равно R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то

Сила тока I = 12 /₄₊₂ = 2 А

Найти ЭМП

Сила тока: I = A
Сопротивление всех внешних элементов цепи: R = Ом
Внутреннее сопротивление источника напряжения: r = Ом

Формула

Пример

Если ток в цепи равен I = 2A, сопротивление всех внешних элементов в цепи равно R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то

ЭМП ε = 2 ⋅ (4+2) = 12 В

Найдите внутреннее сопротивление источника напряжения

Сила тока: I = A
ЭДС: ε = V
Сопротивление всех внешних элементов цепи: R = Ом

Внутреннее сопротивление источника напряжения: r =

Формула:

Пример

Если ток в цепи равен I = 2A, сопротивление всех внешних элементов в цепи равно R = 4 Ом, а ЭДС источника напряжения равна ε = 12 В, то

Внутреннее сопротивление источника напряжения r = 12/2 – 4 = 2 Ом

Найдите сопротивление всех внешних элементов в цепи

Сила тока: I = A
ЭДС: ε = V
Внутреннее сопротивление источника напряжения: r = Ом

Сопротивление всех внешних элементов цепи: R =

Формула

Пример

Если ток в цепи I = 2А, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:

Емкостной тип можно рассчитать по формуле: Xc = 1/ ωC, где C – емкость радиоэлемента.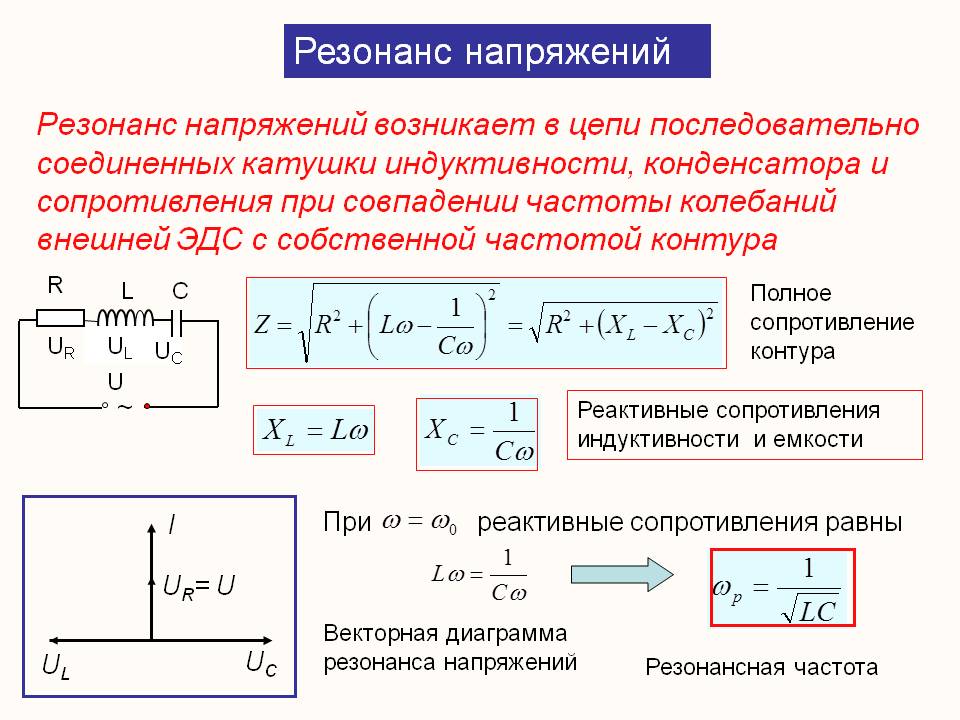 Здесь все наоборот. Если частота увеличивается, емкость конденсатора уменьшается по отношению к напряжению. Отсюда следует, что для цепи постоянного тока конденсатор является бесконечно большим R.

Как определить общее сопротивление цепи по формуле

Из закона Ома следует, что полное сопротивление равно полному напряжению, деленному на полный ток в цепи. При параллельном соединении напряжение, как уже говорилось, везде одинаковое, поэтому необходимо знать его значение в каждой части цепи. С током сложнее, так как на каждой ветви его значение различно и зависит от конкретного R.

Также обратите внимание, что могут быть параллельные соединения с нулевым значением R. Если в ветви нет резистора или подобного элемента, то весь ток будет протекать через него, и общее значение для цепи станет равным нулю. На практике это происходит при отказе резистора или коротком замыкании. Такая ситуация может привести к повреждению других элементов из-за протекания большого тока.

Таблица удельных значений для различных проводников

Количество элементов не имеет значения, правило, которое мы используем для определения общего сопротивления, будет работать в любом случае ? И если при последовательном соединении все резисторы равны ( R_1 = R_2 = . = R ), то общее сопротивление цепи будет:

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

А для токов справедливо следующее выражение:

Это означает, что общий ток разветвляется на две составляющие и его значение равно сумме всех составляющих. Согласно закону Ома:

За основу этих выражений возьмем формулу для полного тока:

A в соответствии с законом Ома ток:

Приравняйте эти выражения, и вы получите формулу для полного сопротивления цепи:

Эту формулу можно записать и несколько иначе:

Таким образом, Когда проводники соединены параллельно, обратное полное сопротивление цепи равно сумме обратных сопротивлений параллельно соединенных проводников.

Аналогичная ситуация возникает при параллельном соединении большего количества проводников:

Чтобы рассчитать общую цепь, вычислите внутреннее сопротивление (RRin) источника:

Как рассчитать общее сопротивление цепи

При расчете применяются правила, формулы и проверки, описанные выше. Рекомендуется сначала описать схему в упрощенном виде, соединив отдельные цепи вместе. Затем рассчитайте эквивалентные сопротивления отдельных групп. При необходимости можно определить токи в цепях, найти напряжения в точках измерения.

Метод 1 Последовательное соединение

Для таких соединений используется простое суммирование, показанное выше:

R общий = R1 + R2 + … + Rn.

Ток в замкнутой цепи не изменяется. Проверка мультиметром в любом зазоре покажет одно и то же значение. Однако каждый резистор будет иметь разное падение напряжения при разных номиналах элементов. Согласно второму постулату Кирхгофа, результат расчета проверяется суммированием:

Uacb = U1 + U2 + Un.

Примечание. В показанной схеме несложно рассчитать делитель напряжения на определенном уровне, учитывая известные рабочие параметры источника питания постоянного тока.

Метод 2 Параллельное подключение

При таком способе подключения удобно использовать обратную величину сопротивления, т. е. проводимость. В качестве альтернативы можно также использовать следующее уравнение:

1/Rcomm = 1/R1 + 1/R2 = 1/(1/R1 + 1/R2) = R1*R2/R1 + R2.

В узле входной ток распределяется по отдельным цепям пропорционально номиналам отдельных резисторов. На выходе происходит обратное преобразование. Расчет проверяется в соответствии с принципами первого постулата Кирхгофа.

Метод 3 Комбинация

Сложные схемы упрощаются. Параллельный контур рассчитывается отдельно. Затем из последовательных элементов создается неразветвленная цепь.

При необходимости схема может быть преобразована из треугольного соединения резисторов в звездообразное или наоборот. Ниже приведены формулы для расчета эквивалентных сопротивлений в цепях после преобразования.

Метод 4 Формулы, включающие мощность

Результат можно легко рассчитать по одной из соответствующих формул:

Входные параметры выводятся из предварительных расчетов или определяются по результатам измерений. Можно использовать расчетные диаграммы с токами в цепях или напряжениями на отдельных резисторах (группах элементов, соединенных последовательно).

Читайте далее:

• Как найти напряжение источника.
• Законы Кирхгофа таковы. Что такое законы Кирхгофа?.
• Разветвленные цепи. Правило обхода цепи – Электричество и магнетизм – Киберфорум.
• Топология электрической цепи (Лекция N 2).
• Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
• Полное сопротивление цепи переменного тока – Основы электроники.
• Расчет цепи постоянного тока с конденсаторами.

Замер полного сопротивления цепи «фаза-нуль»

Замер полного сопротивления цепи «фаза-нуль»

В этой статье поговорим о проверке согласования параметров петли «фаза-нуль» с характеристиками аппаратов защиты и непрерывности защитных проводников, нормативных требованиях предъявляемых к измеренным величинам и периодичности измерения сопротивления петли «фаза-нуль»

Получить КП и смету за 2 часа

Измерение сопротивления изоляции выполняют для проверки диэлектрических свойств изоляционных материалов проводов и кабельных линий. Сопротивление изоляции — важная характеристика кабельных изделий. По ней можно сделать вывод о наличии механических повреждений изоляции или степени ее износа, обусловленного естественным старением и несоблюдением условий эксплуатации и, соответственно, пригодности кабеля к дальнейшей эксплуатации. Если сопротивление ниже нормы, такой кабель нуждается в замене или ремонте. Первоначально сопротивления изоляции необходимо измерять при сдаче объекта в эксплуатацию в ходе приемосдаточных испытаний, и измеренные значения должны соответствовать требованиям ПУЭ. Затем, на этапе эксплуатации, эти работы регулярно выполняют в рамках эксплуатационных испытаний для профилактики возникновения дефектов, и проверяют измеренные значения на соответствие требованиям ПТЭЭП.

Периодичность замера сопротивления петли «фаза-нуль»

В ПТЭЭП нет прямого указания на периодичность проверки петли «фаза-ноль». В соответствии с прил. 3, п. 28.4, эти работы выполняют как после капитального или текущего ремонта электроустановки, так и при межремонтных, т. е. эксплуатационных испытаниях. На практике, как правило, ответственный за электрохозяйство принимает решение о периодичности эксплуатационных испытаний, исходя из требований по проверки сопротивления изоляции, например, 1 раз в 3 года. С этой периодичностью проводятся весь комплекс межремонтных испытаний: и проверка сопротивления цепи «фаза-ноль», и проверка металлосвязи, и испытания УЗО.

Исключения составляют электроустановки, расположенные во взрывоопасных зонах — для них установлена периодичность не реже, чем 1 раз в 2 года.

В электроустановках напряжением до 1000 В с глухозаземленной нейтралью (системы ТN) при капитальном, текущем ремонтах и межремонтных испытаниях, но не реже 1 раза в 2 года должно измеряться полное сопротивление петли фаза-ноль электроприемников, относящихся к данной электроустановке и присоединенных к каждой сборке, шкафу и т.д., и проверяться кратность тока КЗ, обеспечивающая надежность срабатывания защитных устройств.

 

ПТЭЭП, гл. 3.4, п. 3.4.12

Из чего складывается сопротивление цепи «фаза-нуль»

На рис. 1 схематично изображен путь, который проходит электрический ток от трансформатора до нагрузки. Каждый участок цепи защищает свой автоматический выключатель: автомат на подстанции защищает питающую сеть на участке до ВРУ; автомат в ВРУ защищает распределительную сеть до групповых щитов; автоматы в групповых щитах защищают групповую сеть до нагрузки. Полное сопротивление цепи «фаза-нуль» складывается из сопротивлений жил кабеля, а также переходных сопротивлений в местах соединений, подключения к коммутационным аппаратам. Поэтому, двигаясь от ТП в сторону конечных потребителей, сопротивление цепей «Ф-0» должно увеличиваться.

На величину сопротивления петли «фаза-нуль» влияют следующие факторы:

• удаленность точки измерения от ТП;
• длина и сечение отрезков кабелей, входящих в проверяемую цепь;
• количество и качество соединений и коммутаций в цепи.

Измерить сопротивление петли, как правило, можно в разных точках, но рекомендуется проводить замер в наиболее удаленной от проверяемого аппарата защиты, поскольку сопротивление в этой точке будет максимальным, а ток КЗ, наоборот, минимальным.

Проверка срабатывания защиты при системе питания с заземленной нейтралью (TN—C, TN—C—S, ТN—S): проверяется непосредственным измерением тока однофазного короткого замыкания с помощью специальных приборов или измерением полного сопротивления петли фаза-нуль с последующим определением тока короткого замыкания.
У электроустановок, присоединенных к одному щитку и находящихся в пределах одного помещения, допускается производить измерения только на одной, самой удаленной от точки питания установке.
У светильников наружного освещения проверяется срабатывание защиты только на самых дальних светильниках каждой линии. Проверку срабатывания защиты групповых линий различных приемников допускается производить на штепсельных розетках с защитным контактом.

ПТЭЭП, прил. 3, табл. 28, п. 28.4

Электрические сети должны иметь защиту от токов короткого замыкания, обеспечивающую по возможности наименьшее время отключения и требования селективности.
Защита должна обеспечивать отключение поврежденного участка при КЗ в конце защищаемой линии: одно-, двух- и трехфазных — в сетях с глухозаземленной нейтралью; двух- и трехфазных — в сетях с изолированной нейтралью.
Надежное отключение поврежденного участка сети обеспечивается, если отношение наименьшего расчетного тока КЗ к номинальному току плавкой вставки предохранителя или расцепителя автоматического выключателя будет не менее значений, приведенных в 1.7.79 и 7.3.139.

ПУЭ, п. 3.1.8

Каким должно быть сопротивление цепи «фаза-нуль»?

Сопротивление должно быть таким, чтобы время срабатывания аппарата защиты при КЗ уложилось в рамки, устанавливаемые ПУЭ и ПТЭЭП. Поэтому прежде всего имеет смысл разобраться с требованиями ко времени срабатывания, а затем переходить к величине тока и сопротивления.

В системе TN время автоматического отключения питания не должно превышать значений, указанных в табл.1.7.1.

Таблица 1.7.1 Наибольшее допустимое время защитного автоматического отключения для системы TN
Номинальное фазное напряжение 127В — Время отключения, 0,8 с
Номинальное фазное напряжение 220В — Время отключения, 0,4 с
Номинальное фазное напряжение 380В — Время отключения, 0,2 с
Номинальное фазное напряжение >380В — Время отключения, 0,1 с

Приведенные значения времени отключения считаются достаточными для обеспечения электробезопасности, в том числе в групповых цепях, питающих передвижные и переносные электроприемники и ручной электроинструмент класса 1.

В цепях, питающих распределительные, групповые, этажные и др. щиты и щитки, время отключения не должно превышать 5 с.

ПУЭ,п. 1.7.79

Таким образом для питающей и распределительной сетей время автоматического отключения должно быть не более 5 сек., а в групповых сетях — не более 0,4 сек.

Для обеспечения этих условий наименьший ток КЗ в конце линии, защищенной автоматом с электромагнитным расцепителем, должен составлять не менее 1,1 верхнего значения тока срабатывания расцепителя.

Для модульных автоматов с характеристиками «B», «C» и «D» это будут соответственно: 5,5Iн для «B», 11Iн для «C» и 22Iн для «D». При таких токах автомат гарантированно отключит цепь за 0,02 сек.

Если ток КЗ не превышает 1,1 верхнего значения тока срабатывания выключателя, то необходимо определять время срабатывания расцепителя с использованием время-токовой характеристики.

Важно! Для того, чтобы сравнить измеренное значение Iкз с номинальным значением Iн и проверить кратность, необходимо знать Iн. Но если в щите нет однолинейной схемы или какой-либо другой формы адресации, т.е. если непонятно, с каких автоматов на какие потребители уходят кабельные линии, то проводить замеры бесполезно. Интерпретировать результаты замеров и сделать выводы будет невозможно.

Проверка срабатывания защиты при системе питания с заземленной нейтралью (TN—C, TN—C—S, ТN—S): при замыкании на нулевой защитный рабочий проводник ток однофазного короткого замыкания должен составлять не менее:

• трехкратного значения номинального тока плавкой вставки предохранителя;
• трехкратного значения номинального тока нерегулируемого расцепителя автоматического выключателя с обратнозависимой от тока характеристикой;
• трехкратного значения уставки по току срабатывания регулируемого расцепителя автоматического выключателя обратнозависимой от тока характеристикой;
• 1,1 верхнего значения тока срабатывания мгновенно действующего расцепителя (отсечки).

ПТЭЭП, прил. 3, табл. 28, п. 28.4

Почему сопротивление петли «фаза-нуль» больше допустимого?

Иногда полученные значения сопротивления и тока КЗ не укладываются в рамки ПУЭ и ПТЭЭП. Причины две:

• проектировщик получил неправильное расчетное значение сопротивления цепи «фаза-нуль», неправильно рассчитал ток КЗ и, как следствие, ошибся с выбором номинала автомата;
• за время эксплуатации объекта переходные сопротивления в контактных соединениях возросли и сопротивление петли «Ф-0» увеличилось настолько, что перестало удовлетворять требованиям нормативных документов.

Если в результате электроизмерений выяснилось, что автомат своевременно не обесточит кабельную линию, то начать следует с поиска плохих контактов: почистить и протянуть контакты автоматов и шин, пропаять скрутки (если уж такие имеются), проверить клеммники, убрать пыль и грязь в местах соединений. Если эти меры не помогли уменьшить сопротивление петли, значит, пора задуматься о внесении изменений в проект и установке автомата меньшего номинала или прокладке кабеля большего сечения.

Подробнее о допустимых значениях сопротивления петли вы можете прочитать в этой статье. Там же, в конце статьи, вы найдете калькулятор расчета допустимых значений сопротивлений и токов КЗ для автоматических выключателей.

Вывод о необходимости проверки сопротивления цепи «фаза-нуль»?

Регулярное проведение замеров сопротивления петли «фаза-нуль» позволяет обнаружить линии с неудовлетворительным временем срабатывания аппарата защиты и заблаговременно разобраться с проблемой, не дожидаясь возникновения КЗ. Делать замеры следует в соответствии с графиком ППР, но не реже, чем 1 раз в 3 года. Для электроустановок во взрывоопасных зонах — не реже1 раза в 2 года.

Результаты измерений будут оформлены в виде протокола проверки согласования параметров цепи «фаза-нуль» с характеристиками аппаратов защиты и непрерывности защитных проводников, который подшивается в технический отчет о проведении испытаний электроустановки и хранится на объекте до проведения очередных периодических электроизмерений.

Остались вопросы?

Проконсультируем вас по вопросам проведения

замеров полного сопротивления цепи!

Связаться с нами

Файлы для скачивания

ПУЭ, глава 1.8

Нормы приемо-сдаточных испытаний

ПТЭЭП, прил. 3, табл. 28

Электроустановки, аппараты, вторичные цепи, нормы испытаний которых не определены в разделах 2–27, и электропроводки напряжением до 1000 В

Отзывы клиентов и рекомендательные письма

Ознакомьтесь с перечнем выполненных работ, отзывами, рекомендательными и благодарственными письмами наших клиентов

Посмотреть отзывы

Мы заслуживаем ваше доверие!

Наша компания ООО «Контур» была учреждена в далеком 1996 году для проведения электромонтажных, электротехнических, проектно-изыскательских, научно-исследовательских и строительных работ

Узнать подробнее

© 2022 ООО Контур. Все права защищены.

Получите бесплатную смету и КП в течении дня!

Наш специалист перезвонит вам, уточнит объемы работ и подготовит предложение в течении часа

Отправляя сведения через электронную форму, Вы даете согласие на обработку, сбор, хранение и передачу третьим лицам представленной Вами информации на условиях Политики обработки персональных данных.

+7 (863) 247 14 90    

[email protected]

Что такое импеданс цепи RLC? | Блог Advanced PCB Design

Ключевые выводы

• Узнайте, что такое импеданс цепи RLC.

• Узнайте, как рассчитать полное сопротивление последовательной и параллельной цепи RLC.

• Узнайте, как анализировать сложные цепи RLC.

Цепь RLC серии A (Источник)

Цепи RLC являются основными строительными блоками более сложных аналоговых систем и обеспечивают множество полезных функций. Пассивное усиление, фильтрация, согласование импеданса и многое другое могут быть выполнены с помощью цепей RLC. Кроме того, схемы RLC используются в качестве фундаментальных моделей для более сложных частей электрических систем, таких как PDN на печатной плате.

Во всех этих областях разработчику необходимо знать импеданс цепи RLC при создании своего проекта. В этой статье мы рассмотрим, как определить этот импеданс как для последовательных, так и для параллельных цепей RLC.

Какое сопротивление цепи RLC?

Во-первых, давайте проясним несколько определений:

Полное сопротивление — это термин, описывающий характеристики электронного компонента при сопротивлении протеканию тока. Звучит похоже на сопротивление, но импеданс пропорционален изменению частоты.   Цепь RLC состоит из резистора, катушки индуктивности и конденсатора. Термин RLC относится к условному обозначению соответствующих компонентов, а именно: Р — Резистор L — Индуктор С — Конденсатор

Цепи RLC часто используются в качестве примеров для базового анализа импеданса.

В то время как резистор является чистым компонентом постоянного тока, катушки индуктивности и конденсаторы имеют различные импедансы в зависимости от частоты сигнала. Общий импеданс цепи RLC определяется импедансом каждого компонента.

Вот как полное сопротивление резисторов, катушек индуктивности и конденсаторов выражается по величине и фазовому углу:

Результирующий полный импеданс существует в комплексной плоскости. Импеданс RLC выражается комплексными числами или представляется величиной и углом вектора. Лучше всего это визуализировать с помощью векторной диаграммы, описывающей взаимосвязь между импедансом всех трех компонентов.

Векторная диаграмма импеданса RLC. (Источник)

Как определить импеданс RLC-цепи

Последовательное и параллельное расположение компонентов RLC проще всего решить, поскольку общие формулы для эквивалентного сопротивления можно использовать с импедансом RLC-элементов. Для моделирования цепей RLC необходимы всего 3 простых математических инструмента:

• Действующий закон Кирхгофа
• Закон напряжения Кирхгофа
• Закон Ома

Более сложные цепи RLC могут не иметь той же формы уравнения импеданса, что и последовательные и параллельные цепи. Это связано с тем, что цепь не может быть сведена к простому уравнению с использованием правил последовательного и параллельного соединения, но законы Кирхгофа и закон Ома все еще могут использоваться для определения мощности, рассеиваемой в цепи.

Давайте сначала рассмотрим обычные последовательные и параллельные схемы, так как они распространены во многих системах.

Серийная RLC-цепь

В последовательной RLC-цепи, показанной ниже, импеданс можно легко определить с помощью закона напряжения Кирхгофа.

Полное сопротивление цепи RLC. Источник

Согласно закону тока Кирхгофа ток в каждом элементе последовательной RLC-цепи одинаков. Используя закон Ома, мы можем написать характеристическое дифференциальное уравнение для этой цепи и решить его в частотной области. Формула импеданса этой цепи показана ниже:

Для расчета амплитуды и фазового угла последовательного импеданса RLC приведенное выше уравнение решается следующим образом.

Обратите внимание, что это тот же импеданс, который вы бы нашли, если бы использовали правило последовательностей для расчета эквивалентного импеданса.

Эта схема представляет собой демпфирующий генератор, в котором демпфирование обеспечивается последовательным резистором. Когда схема имеет недостаточное демпфирование, возникает резонансная частота, которая возникает при минимальном импедансе. В этой схеме (или любой другой частотно-зависимой схеме) резонансная частота определяется путем вычисления критических точек для функции импеданса и решения для частоты.

В этом случае импеданс минимизируется на резонансной частоте последовательной RLC-цепи.

Параллельная цепь RLC

На приведенной ниже схеме показана параллельная цепь RLC. В этом случае импеданс легко определить, рассчитав общий ток, протекающий в цепи, по закону тока Кирхгофа. Полное сопротивление каждого элемента и эквивалентное полное сопротивление всей цепи можно определить с помощью закона Ома.

Сопротивление параллельной цепи RLC. Источник

Полный импеданс параллельной цепи RLC описывается следующим уравнением.

С некоторой алгеброй приведенное выше уравнение может быть решено для его модуля и фазового угла следующим образом.

Эта формула сложнее, чем формула для последовательного контура, и в этом контуре тоже есть резонансная частота. Для заданного набора значений R, L и C параллельная и последовательная цепи RLC будут иметь одинаковую резонансную частоту.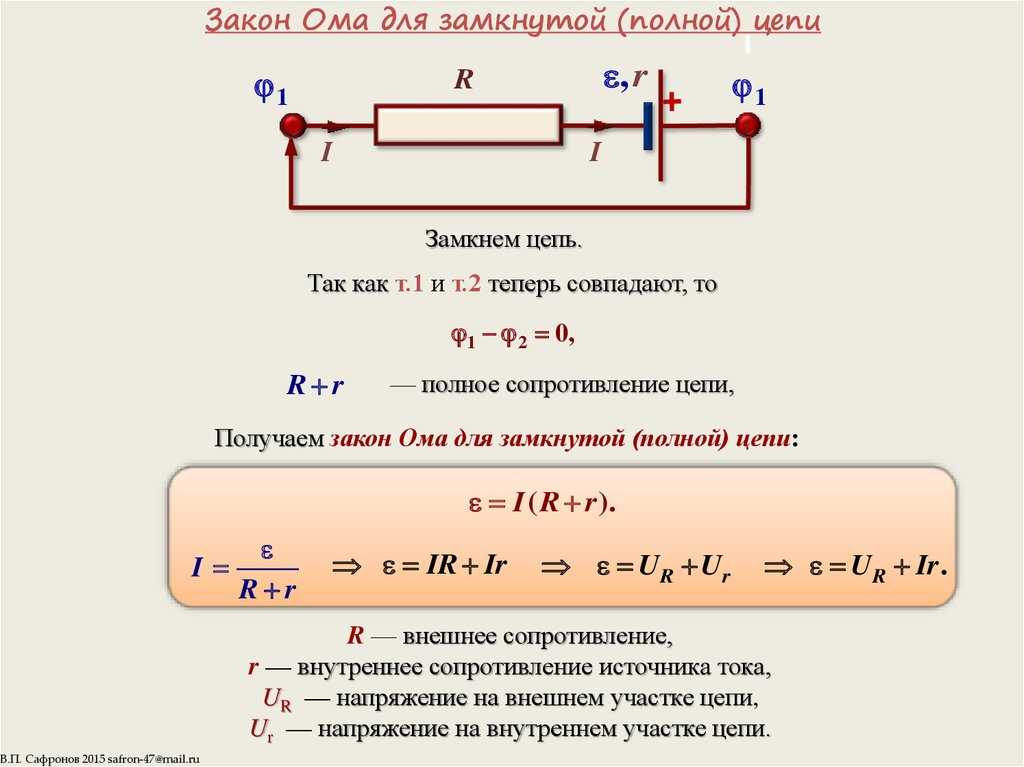 Однако импеданс в параллельной RLC-цепи максимален при резонансе, тогда как в последовательной RLC-цепи он минимален при резонансе. Таким образом, два типа цепей RLC обеспечивают два разных режима фильтрации: полосовой фильтр и режекторный фильтр.

Полосно-заграждающая фильтрация в сравнении с полосовой фильтрацией

Приведенное ниже уравнение представляет собой значение резонансной частоты в последовательной или параллельной цепи RLC. Что интересно, хотя два типа цепей устроены по-разному, они имеют одинаковую резонансную частоту. Это связано с тем, что резонанс возникает, когда мощность, подаваемая разряжающимся конденсатором, уравновешивается мощностью, генерируемой катушкой индуктивности. Таким образом, резистор остается единственным оставшимся элементом, обеспечивающим рассеяние полезной мощности в каждой цепи.

Резонансная частота последовательного и параллельного RLC

В таблице ниже показано, как резонанс в каждом типе схемы связан с режимом фильтрации, обеспечиваемым схемой.

Из этой таблицы и из подстановки значения резонансной частоты видно, что импеданс обоих контуров равен R при резонансе.

	Параллельный	Серия
Тип фильтрации	Режущая лента	Полосовой фильтр
Полный импеданс при резонансе	Максимальная, равна руб.	Минимальный, равен руб.
Полное сопротивление части LC	Бесконечность	Ноль

И последнее замечание: полезно увидеть физически, как каждый тип контура обеспечивает фильтрацию. При резонансе в последовательной цепи элементы L и C имеют одинаковое и противоположное реактивное сопротивление, поэтому их полное сопротивление равно нулю, и они не дают реактивной мощности. В параллельной цепи чистый ток, втекающий в эти два элемента и вытекающий из них при резонансе, равен нулю, поэтому единственный путь возврата к земле с низким импедансом проходит через резистор.

Более сложные цепи RLC

Сложные цепи, включающие элементы RLC, могут не иметь таких простых характеристик импеданса. Они могут состоять из следующих элементов:

• Нелинейные компоненты, включая диоды и транзисторы.
• Смешанное последовательное и параллельное расположение компонентов.
• Каскадные группы каскадов фильтрации или усиления.

Эти возможности затрудняют анализ некоторых цепей RLC, и они могут не иметь ни одного резонанса. Для изучения более сложных схем следует использовать симулятор на основе SPICE. Этот тип симулятора позволит вам исследовать схему во временной или частотной области, и вы можете использовать такие функции, как развертка параметров, для оптимизации проектирования более сложных схем.

Когда вы будете готовы создавать схемы для своего нового проекта и исследовать их электрическое поведение, используйте интерфейсные функции проектирования от Cadence для создания и моделирования ваших схем. Полный набор функций моделирования в PSpice Simulator позволяет создавать подробные файлы моделирования, моделировать практически любой аспект электрического поведения и оптимизировать поведение схемы с помощью развертки параметров. Когда вы будете готовы создать печатную плату для своих схем, просто сохраните свои схемы в виде пустого макета и используйте утилиты компоновки платы Cadence, чтобы завершить свой дизайн.

Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов.

Свяжитесь с нами

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions

УЧИТЬ БОЛЬШЕ

4.3: Последовательно-параллельный импеданс — Технические тексты LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25260

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

Правила объединения резисторов, конденсаторов и катушек индуктивности в последовательно-параллельных цепях переменного тока аналогичны правилам, установленным для объединения резисторов в цепях постоянного тока. Очевидно, первым пунктом является определение реактивных сопротивлений конденсаторов и катушек индуктивности. В этот момент можно идентифицировать простые серии и параллельные комбинации. Каждая из этих комбинаций сводится к комплексному импедансу. Как только это будет завершено, сеть снова исследуется, чтобы увидеть, можно ли идентифицировать эти новые комплексные импедансы как части новых последовательных или параллельных подсхем и упростить. Этот процесс повторяется до тех пор, пока не останется один комплексный импеданс. Опять же, полезно помнить, что фазовые углы реактивных компонентов могут иногда приводить к удивительным результатам, например, когда последовательная подсхема имеет величину импеданса меньше, чем ее наибольший компонент — то, что никогда не произойдет с сетью, состоящей только из резисторы. Важность использования векторных вычислений невозможно переоценить.

Начнем с относительно простой последовательно-параллельной сети RLC, где значения реактивного сопротивления уже найдены.

Пример \(\PageIndex{1}\)

Определите эквивалентный импеданс сети, показанной на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): пример сети \(\PageIndex{1}\).

Глядя с левой стороны, мы видим, что катушка индуктивности и резистор 33 кОм (\Омега\) параллельны, поскольку они оба связаны с одними и теми же двумя узлами. Также мы видим, что конденсатор включен последовательно с резистором 8,2 кОм (\Омега\). Эта последовательная комбинация, в свою очередь, параллельна двум другим параллельным компонентам. Таким образом, имеет смысл сначала найти комбинацию серий. 9{\circ} \Omega \nonumber \]

Очевидно, что здесь доминирует индуктор. Параллельный резистор примерно на два порядка больше индуктивного сопротивления и оказывает минимальное влияние на параллельную комбинацию. Кроме того, комплексный импеданс, полученный из комбинации конденсатор/резистор, также значительно больше, и, учитывая, что он имеет отрицательный (емкостной) фазовый угол, он частично компенсирует индуктивное реактивное сопротивление. Это оставляет нам величину немного большую, чем у одного лишь индуктивного реактивного сопротивления, и фазовый угол, сдвинутый в резистивную сторону.

Последовательные и параллельные комбинации могут быть намного сложнее, чем в предыдущей сети. Лестничные сети, например, имеют набор секций, которые загружают другие секции, что приводит к повторяющимся последовательностям, а затем к параллельным упрощениям. В этой ситуации лучше всего начинать работу с самого дальнего от интересующих узлов конца. Следующий пример проиллюстрирует это в скромном масштабе.

Пример \(\PageIndex{2}\)

Определите эквивалентный импеданс сети, показанной на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\): Пример сети \(\PageIndex{2}\).

Заглянув с правой стороны, сразу видим резистор 750\(\Омега\). Это последовательно с подсхемой, состоящей из оставшихся пяти компонентов. Эту подсхему можно рассматривать как конденсатор \(-j800 \Omega \) параллельно другой подсхеме, содержащей остальные четыре компонента. Эта четырехкомпонентная подсхема состоит из катушки индуктивности, соединенной последовательно с еще одной подсхемой, состоящей из двух последних резисторов и конденсатора. Эта подсхема из трех элементов состоит из резистора 2,2 кОм \(\Омега\), соединенного параллельно с последовательной комбинацией резистора 1 кОм (\Омега\) и конденсатора \(-j400 \Омега\). 9{\circ} \Omega \nonumber \]

В прямоугольной форме это 1443 \(−j422,3 \Omega \), что означает, что эта цепь эквивалентна резистору 1443 \(\Omega\), включенному последовательно с емкостным реактивное сопротивление \(−j422,3 \Omega \).

Методы последовательно-параллельного упрощения

подходят не для всех цепей. Для некоторых сетей, таких как конфигурации «треугольник» или «мост», требуются другие методы, которые будут рассмотрены в последующих главах.

---

Эта страница под названием 4.3: Последовательно-параллельный импеданс распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М.