Электричество и магнетизм

Повышения емкости проводника можно достигнуть не только увеличением его размеров, но и за счет приближения к нему другого проводника. Примерами могут служить плоский конденсатор, сферический конденсатор и др. Мы вычислим их емкости, исходя из данных определений и геометрии конденсатора.

Плоский конденсатор (рис. 2.11). 

Рис. 2.12.  Электрическое поле идеального плоского конденсатора

Идеальный плоский конденсатор предста­вляет собой две металлические параллельные пластины, линейные размеры которых много больше расстояния  между ними. Пусть площадь каждой из пластин равна  (рис. 2.12). На одну пластину помещен заряд , на другую —  Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.

Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью.

Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:

Рис. 2.12.  Электрическое поле идеального плоского конденсатора

Видео 2.9. Геометрия реального плоского конденсатора и распределение заряда на его пластинах.

Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью . Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними: 

(2.10)

Поле, создаваемое двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями, является одно­родным, и его напряженность равна   (см. (2.3)).

Напряженность поля в пространстве, окружающем пластины, можно считать равной нулю, если пренебречь краевыми эффектами. Интегрируя вдоль силовой линии (которые ортогональны пластинам), получаем

(2.11)

Отсюда находим емкость плоского конденсатора:

(2.12)

Цилиндрический конденсатор. Цилиндрический конденсатор представляет собой два коаксиальных длинных проводящих цилиндра радиусами  и  и длиной . Предполагая, что , мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна . Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):

(2. 13)

Электрическое поле направлено по радиусу цилиндров. Интегрируя по этому пути от одной обкладки к другой, находим разность потенциалов между обкладками:

(2.14)

Отсюда следует выражение для емкости цилиндрического конденсатора:

(2.15)

В случае, когда зазор между обкладками  , можно использовать первый член разложения логарифма в ряд Тейлора

 

что приводит к выражению

(2.16)

В скобках стоит произведение длины окружности цилиндра на его высоту, что равно площади поверхности цилиндра (площади обкладок).

Т. о. мы воспроизвели в этом пределе выражение (2.12) для емкости плоского конденсатора.

Сферический конденсатор. Сферический конденсатор образуется двумя концентрическими сферами радиусам  и . Интегрируя вдоль радиуса уже хорошо знакомое выражение

 

получаем разность потенциалов между обкладками:

(2.17)

откуда

(2.18)

Если внешний радиус бесконечно велик  (физически  это значит, что ), то вычитаемым в знаменателе можно пренебречь, и мы приходим к формуле (2.9) для емкости уединенной сферы. В обратном случае, когда зазор между обкладками  можно положить в числителе  Замечая, что  есть площадь обкладок, мы снова приходим к формуле (2. 12).

Видео 2.10. Влияние диэлектрика на распределение зарядов на проводнике и его емкость.

Задача. Конденсатор, используемый в чипе запоминающего устрой­ства компьютера, имеет емкость  и заряжается до разности потенциалов . Каково число  избыточных электронов на его отрицательной обкладке? В какой массе воды полное число всех атомных электронов равно ?

Решение. Заряд конденсатора равен . Чтобы найти число избыточных электронов, надо разделить  на заряд электрона:  Почти два миллиона электронов, много это или мало? Для этого найдем массу воды с тем же числом электро­нов. Молекула воды  содержит два атома  и один атом , то есть всего 10 электронов. Стало быть, в интересующей нас массе воды должно содержаться молекул. Число молекул в одном моле равно  то есть надо взять моля. Молярный вес воды равен  кг/кмоль, так что искомая масса составляет кг, то есть крайне мала.   Миллион частиц — много в мире электронов, но совсем мало в масштабах нашего мира.

Плоский конденсатор

Уединенный проводник.

Это проводник, расположенный относительно других тел на расстоянии во много раз большем, чем его размеры.

Электрическая емкость (электроемкость) уединенного проводника. (С)

Это физическая величина, равная отношению заряда проводника к потенциалу этого проводника.
В Си электроемкость измеряется в Фарадах:	.
Электроемкость не зависит от величины заряда на проводнике, а зависит от геометрических размеров проводника, его формы и диэлектрической проницаемости среды, в которую он помещен.

Основная задача для электрической ёмкости проводника.

Вычисление потенциала проводника по известной величине заряда на нем,
или наоборот, вычисление заряда на проводнике по известной величине его потенциала.

Емкость уединенного проводящего шара.

Так как потенциал шара можно вычислить по формуле , то ёмкость уединенного проводящего шара может быть вычислена по формуле:

Конденсатор.

Конденсатор – это система двух близко расположенных проводников, расстояние между которыми мало по сравнению с их размерами. При этом проводники разделены диэлектриком, который не дает возможности разноимённым зарядам соединиться и нейтрализовать друг друга.

Обкладки конденсатора.

Образующие конденсатор проводники называют обкладками конденсатора . Обкладки конденсатора берутся такой формы и располагаются на таком расстоянии друг от друга, чтобы создаваемое зарядами конденсатора электрическое поле было сосредоточено между обкладками и не рассеивалось в окружающее пространство. В этом случае окружающие тела не оказывают влияние на ёмкость конденсатора. В зависимости от формы обкладок конденсаторы бывают сферические, цилиндрические и плоские.

Заряд конденсатора.

Под зарядом конденсатора понимают модуль заряда одной из обкладок.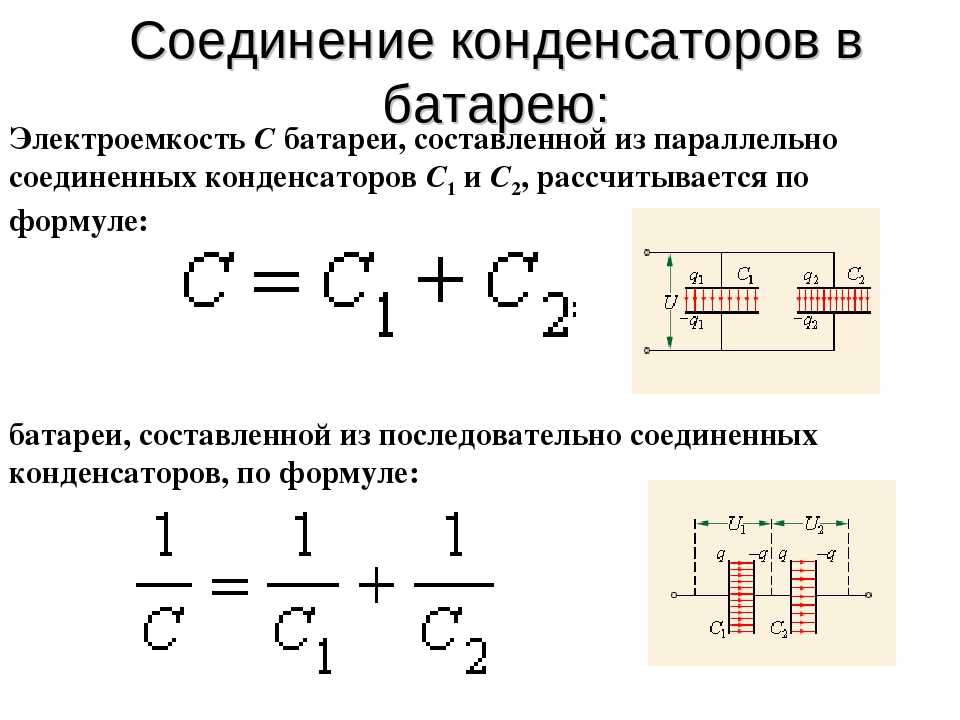 При сообщении заряда конденсатору его обкладки приобретают одинаковые по модулю, но противоположные по знаку заряды. Так как разноимённые заряды притягиваются, они располагаются на внутренних поверхностях обкладок с большей плотностью.

Электроемкость конденсатора

это физическая величина, численно равная величине заряда, который необходимо перенести с одной электрически нейтральной обкладки конденсатора на другую для того, чтобы между ними образовалось электрическое поле с разностью потенциалов между обкладками 1 Вольт .
Электроемкость конденсатора не зависит от величины его заряда, а зависит от геометрических размеров и формы его обкладок, а также диэлектрической проницаемости среды между обкладками, так как диэлектрик поляризуется в поле конденсатора, и его связанные заряды уменьшают разность потенциалов между его обкладками.

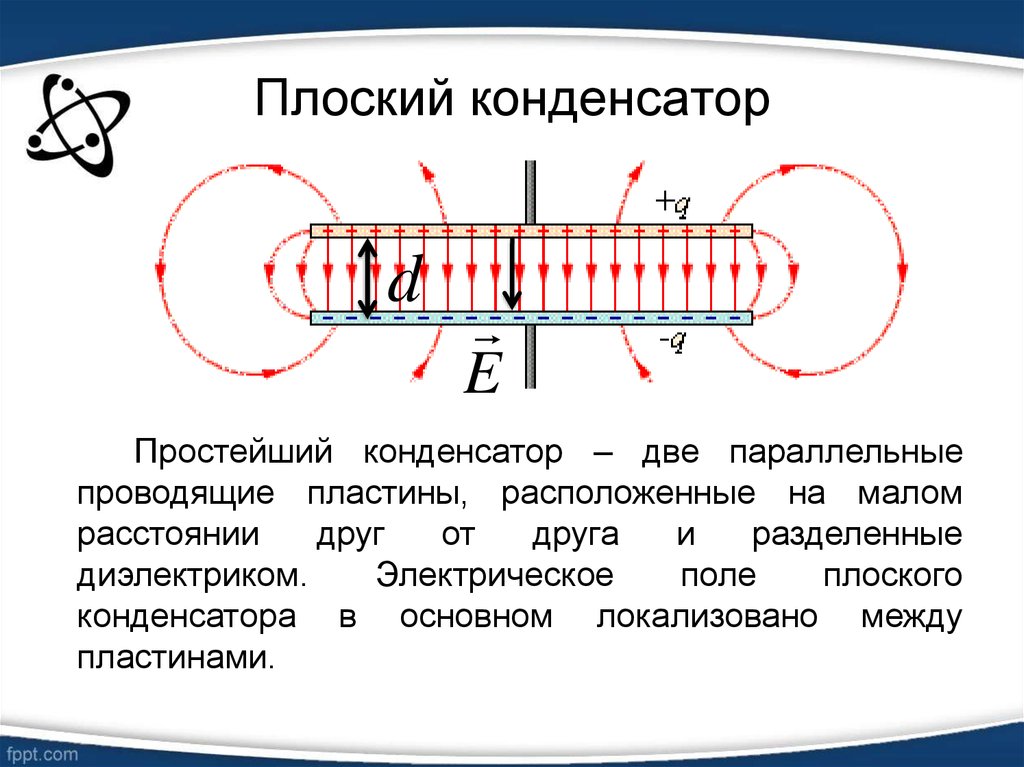
это система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
	Вблизи краев пластин и в окружающем пространстве также возникает
сравнительно слабое электрическое поле, которое называют полем рассеяния.
В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками

Напряженность электростатического поля плоского конденсатора.

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением:	;
Согласно принципу суперпозиции напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:
Учитывая направление векторов напряженностей каждой пластины, избавимся от векторов.
Внутри конденсатора, между пластинами, поля имеют одинаковое направление напряженностей:
, тогда
Снаружи конденсатора вектора напряженностей направлены противоположно друг другу: ,
поэтому

Напряженность электростатического поля плоского конденсатора.
Внутри конденсатора	Снаружи конденсатора

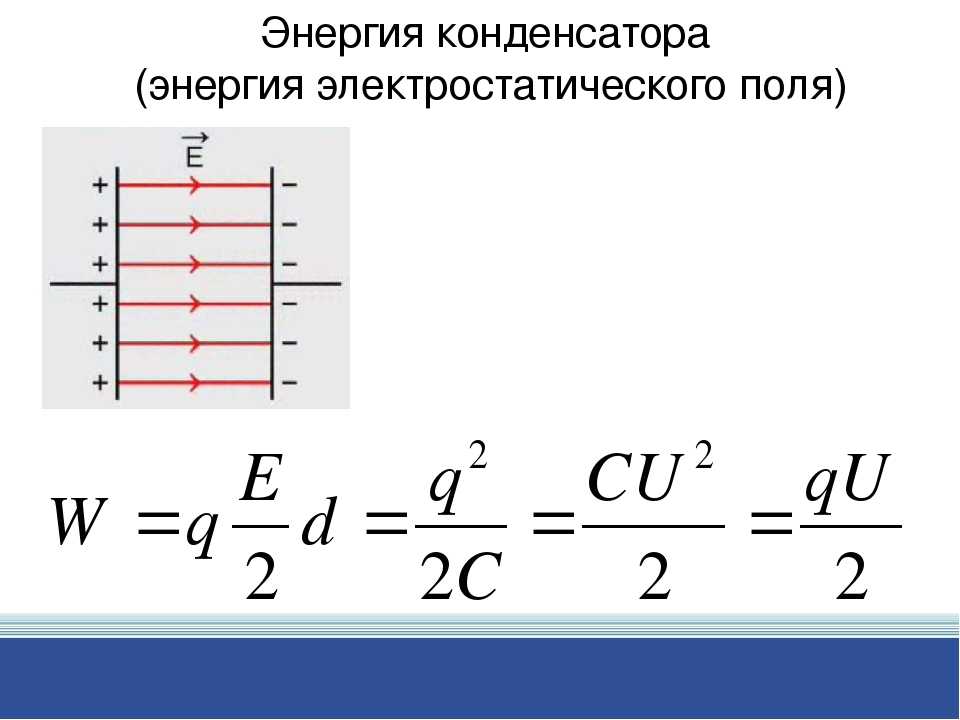
Электроемкость плоского конденсатора.

По определению поверхностная плотность заряда пластин равна: где q – заряд, S – площадь каждой пластины.

Разность потенциалов между пластинами в однородном электрическом поле равна:

где d – расстояние между пластинами,

Е-напряженность поля конденсатора.

Из определения электроемкости конденсатора можно получить формулу для расчета электроемкости плоского конденсатора.

Электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними, а если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз.

Сферический конденсатор
это система из двух концентрических проводящих сфер радиусами R1 и R2, с диэлектрической средой между этими сферами.
Электроемкость сферического конденсатора можно вычислить по формуле:

Цилиндрический конденсатор

это система из двух соосных проводящих цилиндров радиусами R1 и R2 и длины L с диэлектрической средой между цилиндрами. Электроемкость цилиндрического конденсатора можно вычислить по формуле:

Конденсаторы переменной ёмкости.

Конденсаторы, устройство которых позволяет изменять один из параметров, от которого зависит электроёмкость конденсатора. Например, у плоского конденсатора емкость можно увеличить, если увеличить площадь его пластин, так как .

Последовательное соединение конденсаторов

Соединение, при котором первая обкладка каждого следующего конденсатора соединяется со второй обкладкой предыдущего.

При последовательном соединении конденсаторы имеют одинаковый заряд, так как в результате явления электростатической индукции на обкладках соседних конденсаторов происходит разделение заряда.

Общая разность потенциалов равна сумме разностей потенциалов на каждом конденсаторе.

₀ — _{n =} (₀ — ₁)+( ₁— ₂)+( ₂— ₃)+…+( _n-1 — _n)

Поделив обе части выражения на величину заряда конденсатора, получим:

Учитывая, что ёмкость конденсатора , запишем получившееся выражение в новой форме.

При последовательном соединении всегда выполняется условие: (электроемкость батареи конденсаторов меньше, чем минимальная емкость одного из конденсаторов).

Последовательное соединение n конденсаторов различной емкости.
Разность потенциалов	Заряд	Эквивалентная электроемкость батареи
0—n=(0 — 1)+(1 — 2)+ +( 2 — 3)+…+( n-1 — n)	q1= q2= q3=…= qn

Последовательное соединение двух конденсаторов различной емкости.
Разность потенциалов	Заряд	Эквивалентная электроемкость батареи
0 — 2 = (0 — 1)+(1 — 2)	q1= q2	

Последовательное соединение n конденсаторов одинаковой ёмкости.
Разность потенциалов	Заряд	Эквивалентная электроемкость батареи
0 — n =n(0 — 1)	q1= q2= q3=…= qn

5.

23: Конденсатор с тонкими параллельными пластинами

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

6324

• Стивен У. Эллингсон
• Политехнический институт Вирджинии и Государственный университет через Инициативу открытого образования Технологических библиотек Вирджинии

Давайте теперь определим емкость конденсатора общего типа, известного как тонкий конденсатор с параллельными пластинами , показанный на рисунке \(\PageIndex{1}\). Этот конденсатор состоит из двух плоских пластин, каждая из которых имеет площадь \(A\), разделенных расстоянием \(d\). Для облегчения обсуждения поместим начало системы координат в центр нижней пластины с осью \(+z\), направленной к верхней пластине так, чтобы верхняя пластина лежала в \(z=+d\). ) самолет.

Рисунок \(\PageIndex{1}\): Конденсатор с тонкими плоскими пластинами

Ниже мы найдем емкость, предполагая определенный заряд на одной пластине, используя граничное условие на плотность электрического потока \({\bf D}\), чтобы связать эту плотность заряда с внутренним электрическим полем, а затем интегрируя по электрическое поле между пластинами, чтобы получить разность потенциалов. Тогда емкость представляет собой отношение предполагаемого заряда к результирующей разности потенциалов.

Основная трудность в этом подходе заключается в нахождении электрического поля. Чтобы понять проблему, сначала учтите, что если бы площадь пластин была бесконечной, то электрическое поле было бы очень простым; он будет начинаться на положительно заряженной пластине и простираться в перпендикулярном направлении к отрицательно заряженной пластине (раздел 5.19).). Кроме того, поле было бы постоянным везде между пластинами. Это становится очевидным только из симметрии. Однако, когда площадь пластины конечна, мы ожидаем появления краевого поля . Окантовочное поле — это просто термин, применяемый к неоднородному полю, возникающему у края пластин. Поле в этой области неоднородно, поскольку в этой области значительное влияние оказывают граничные условия на внешних (обращенных наружу) поверхностях пластин. Однако в центральной области конденсатора поле мало чем отличается от поля, существующего в случае бесконечной площади пластины.

В любом плоскопараллельном конденсаторе, имеющем конечную площадь пластин, некоторая часть энергии будет запасаться примерно однородным полем центральной области, а остальная часть — краевым полем. Мы можем сделать последнее пренебрежимо малым по сравнению с первым, сделав конденсатор очень «тонким» в том смысле, что наименьший идентифицируемый размер пластины намного больше \(d\). При этом условии мы можем получить хорошее приближение емкости, просто пренебрегая краевым полем, так как там запасается незначительная доля энергии.

Наложение «тонкого» условия приводит к трем дополнительным упрощениям. Во-первых, можно считать, что распределение поверхностного заряда по поверхности пластины примерно однородно, что значительно упрощает анализ. Во-вторых, форма тарелок становится неактуальной; они могут быть круглыми, квадратными, треугольными и т. д. При расчете емкости в «тонком» корпусе важна только площадь пластины \(A\). В-третьих, толщина каждой из пластин становится неактуальной.

Теперь мы готовы определить емкость тонкого плоского конденсатора. Вот шаги: 92\)).

Из граничного условия на нижней поверхности верхней пластины \({\bf D}\) на этой поверхности равно \(-\hat{\bf z}\rho_{s,+}\).

Общий заряд на нижней пластине, \(Q_-\), должен быть равен и противоположен общему заряду на верхней пластине; т. е. \(Q_-=-Q_+\). Точно так же поверхностная плотность заряда на верхней поверхности нижней пластины \(\rho_{s,-}\) должна быть равна \(-\rho_{s,+}\).

Из граничного условия на верхней поверхности нижней пластины (раздел 5.18) \({\bf D}\) на этой поверхности равно \(+\hat{\bf z}\rho_{s,-}\) . Так как \(+\hat{\bf z}\rho_{s,-}=-\hat{\bf z}\rho_{s,+}\), \({\bf D}\) на противоположных сторонах пластин равны.

Снова прибегая к «тонкому» условию, мы предполагаем, что \({\bf D}\) между пластинами имеет примерно такую ​​же структуру, какую мы видели бы, если бы площадь пластины была бесконечной. Поэтому мы вправе предположить, что \({\bf D}\приблизительно-\шляпа{\bf z}\rho_{s,+}\) везде между пластинами. (Вы также можете видеть, что это очевидно из определения \({\bf D}\) как плотности потока электрического заряда (раздел 2.4).)

Имея в руках выражение для электрического поля, мы можем теперь вычислить разность потенциалов \(V\) между пластинами следующим образом (раздел 5.8): \begin{aligned} 9{d}\left(-\hat{\mathbf{z}} \frac{\rho_{s,+}}{\epsilon}\right) \cdot(\hat{\mathbf{z}} d z) \\
&=+\frac{\rho_{s,+} d}{\epsilon}
\end{выровнено}

Наконец, \[C = \frac{Q_+}{V} = \frac{\rho_{s,+}~A}{\rho_{s,+}~d/\epsilon} = \frac{\epsilon A}{d} \номер\]

Обобщение: \[\boxed{ C \приблизительно \frac{\epsilon A}{d} } \label{m0070_eTPPC} \]

Емкость конденсатора с параллельными пластинами, расстояние между пластинами которого намного меньше размера пластин, определяется уравнением \ref{m0070_eTPPC}. Это приближение, потому что краевым полем пренебрегается. 92\) разделить на m дает F. Стоит также отметить влияние различных параметров:

Емкость увеличивается пропорционально диэлектрической проницаемости и площади пластины и уменьшается пропорционально расстоянию между пластинами.

Пример \(\PageIndex{1}\): Емкость печатной платы. используется для распределения напряжения питания постоянного тока (см. «Дополнительные сведения» в конце этого раздела). Эти плоскости разделены диэлектрическим материалом, и полученная структура обладает емкостью. Эту емкость можно рассматривать как эквивалентный дискретный конденсатор, включенный параллельно источнику питания. Значение этого эквивалентного конденсатора может быть либо незначительным, значительным и полезным, либо значительным и вредным. Итак, полезно знать значение этого эквивалентного конденсатора. 92\) и \(d \cong 1,6\) мм. Используя уравнение \ref{m0070_eTPPC}, значение эквивалентного конденсатора составляет \(62,3\) пФ.

Дополнительное чтение:

• «Печатная плата» в Википедии.

---

Эта страница под названием 5.23: Конденсатор с тонкими параллельными пластинами распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Стивеном В. Эллингсоном (Инициатива открытого образования технических библиотек Вирджинии) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Стивен В. Эллингсон

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   Инициатива открытого образования технических библиотек Вирджинии

   Показать оглавление

   нет

2. Теги

   1. окантовочное поле
   2. Пластинчатый конденсатор
   3. источник@https://doi.org/10.21061/electromagnetics-vol-1
   4. тонкий конденсатор с плоскими пластинами

Конденсаторы

Конденсаторы
Далее: Уравнение Пуассона Вверх: Электростатика Предыдущий: Граничные условия на Мы можем хранить электрические заряд на поверхности проводника. Однако, электрические поля будут генерироваться непосредственно над этой поверхностью. Проводник может успешно накапливать заряд только в том случае, если он электрически изолирован. из его окружения. Воздух очень хороший изолятор. К сожалению, воздух перестает быть изолятором, когда напряженность электрического поля через него превышает некоторое критическое значение, которое составляет около вольт на метр. Этот явление, которое называется пробой , связан с образованием искр. Наиболее известный пример распада воздух во время молнии забастовка. Ясно, что хорошее устройство хранения заряда — это то, которое вмещает большое количество заряда, но генерирует только небольшие электрические поля. Такое устройство называется конденсатор .

Рассмотрим два тонких параллельных проводящих пластины с площадью поперечного сечения, которые разделены небольшое расстояние ( т.е. , ). Предположим, что каждая пластина несет равный и противоположный заряд. Мы ожидаем, что этот заряд равномерно распределить по пластинам, чтобы обеспечить эффективную плотность заряда листа на каждой тарелке. Предположим, что верхняя пластина несет положительный заряд, а нижняя пластина несет отрицательный заряд. Согласно с уравнения (624) и (625) поле, создаваемое верхней пластиной, перпендикулярно пластине и величины

			(638)
			(639)

Точно так же поле, создаваемое нижней пластиной, равно

			(640)
			(641)

Заметим, что мы пренебрегаем «утечкой» поля на краях пластин. Это разумно, если пластины расположены близко друг к другу. Общее поле – это сумма двух полей, создаваемых верхней и нижней пластинами. Таким образом, чистое поле нормальна к пластинам и имеет величину

			(642)
			(643)

Поскольку электрическое поле однородно, разность потенциалов между тарелки просто

(644)

Общепринято измерять емкость проводника или группы проводников, хранить заряд, но генерировать небольшие электрические поля с точки зрения параметра называется емкость . Это обычно обозначают. Емкость накопителя заряда устройство — это просто отношение накопленного заряда к разности потенциалов генерируемый зарядом. Таким образом,

(645)

Ясно, что хорошее устройство накопления заряда имеет большую емкость. Кстати, емкость измеряется в кулонах на вольт или фарадах. Это довольно громоздкий единица, так как хорошие конденсаторы обычно имеют емкость, которая составляет всего около одной миллионной фарада. Для конденсатора с плоскими пластинами ясно, что

(646)

Обратите внимание, что емкость зависит только от геометрических величин, таких как площадь и расстояние между пластинами. Это следствие суперпозитивности электрические поля. Если мы удвоим заряд проводников, мы удвоим электрические поля, генерируемые вокруг них, и мы, таким образом, удваиваем потенциал разница между проводниками. Таким образом, разность потенциалов между проводники всегда прямо пропорциональны переносимому заряду: постоянная пропорциональности (обратной емкости) может зависеть только от геометрии.

Предположим, что заряд на каждой пластине накапливается постепенно путем переноса небольшие количества заряда от одной пластины к другой. Если мгновенный заряд на пластинах равен , а бесконечно малое количество положительный заряд переносится с отрицательно заряженной пластины на положительно пластина заряда, то работа , где мгновенный разница напряжений между пластинами. Обратите внимание, что разница в напряжении такова что он препятствует любому увеличению заряда на любой пластине. Суммарная работа, совершенная при зарядке конденсатора является

(647)

где использовалось уравнение (645). Энергия, запасенная в конденсаторе, равна работе, необходимой для зарядить конденсатор. Таким образом,

(648)

Это общий результат, справедливый для всех типов конденсаторов.

Энергия заряженная параллель пластина конденсатор фактически сохраняется в электрическом поле между пластинами. Это поле имеет примерно постоянную величину и занимает область объема. Таким образом, учитывая плотность энергии электрического поле, , энергия, запасенная в электрическое поле

(649)

где использовалось уравнение (646). Обратите внимание, что уравнения. (647) и (649) совпадают. Все мы знаем, что если подключить конденсатор через клеммы батареи, то переходный ток течет, поскольку конденсатор заряжается. Затем конденсатор можно поместить в сторону, и через некоторое время накопленный заряд можно использовать: например, для кратковременного зажигания лампочки в электрическая цепь. Здесь интересно то, что энергия, запасенная в конденсатор хранится в виде электрического поля, поэтому мы можем думать о конденсаторе как о устройство, которое либо накапливает энергию или извлекает энергию из электрического поле.

Идея, которую мы обсуждали ранее, о том, что электрическое поле оказывает отрицательное давление на проводниках сразу наводит на мысль, что две пластины конденсатора с параллельными пластинами притягиваются друг к другу с взаимная сила

(650)

Нет необходимости иметь два противоположно заряженных проводника для изготовления конденсатора. Рассмотрим изолированный сфера радиуса которой несет заряд. Радиальное электрическое поле, создаваемое вне сферы, равно данный

(651)

Разность потенциалов между сферой и бесконечностью, или, более реалистично, какой-то большой, относительно удаленный резервуар заряда, такой как Земля,

(652)

Таким образом, емкость шара

(653)

Энергия сферы, когда она несет заряд, снова определяется выражением . Легко показать, что это действительно энергия, содержащаяся в электрическом поле вокруг сферы.

Предположим, что у нас есть две сферы радиусов и , соответственно, которые соединены электрическим проводом. Провод позволяет заряду перемещаться вперед и назад между сферы, пока они не достигнут того же потенциала (относительно бесконечности). Пусть — заряд на первой сфере и заряд на вторая сфера. Конечно, общий заряд, переносимый двумя сферами, сохраняется. количество. Это следует из уравнения (652) что

			(654)
			(655)

Обратите внимание, что если одна сфера намного меньше другой, , например. , , то большая сфера захватывает большую часть заряда:

(656)

Отношение электрических полей, генерируемых непосредственно над поверхностями двух сфер следует из уравнений (651) и (656):

(657)

Если , то поле над меньшей сферой намного больше, чем над большей сферой. Уравнение (657) является простым примером гораздо более общего правила. Электрическое поле над некоторой точкой поверхность проводника обратно пропорциональна локальный радиус кривизны поверхности.

Ясно, что если мы хотим накопить значительное количество заряда на проводнике то поверхность проводника необходимо сделать как можно более гладкой. Любой острый шипы на поверхности неизбежно имеют сравнительно малый радиус кривизны. Сильные локальные электрические поля генерируются в этих регионах. Они могут легко превысить критическое поле для пробоя воздуха, что приводит к искрению и возможной потере заряда на проводнике. Искрение также может быть очень разрушительным, поскольку связанное электрические токи протекают через очень локализованные области, вызывающие интенсивный омический нагрев.

В качестве последнего примера рассмотрим два коаксиальных проводящие цилиндры радиусов и , куда . Предположим, что заряд на единицу длины, переносимый наружный и внутренний цилиндры соответственно.