Соединение резисторов — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Тема урока: «Соединение резисторов»

2. Что такое сопротивление?

Сопротивление проводника
можно характеризовать, как
свойство препятствовать
прохождению тока.

3. Почему обмотку электротехнических устройств выполняется из меди? Почему при расчете сопротивления проводника нужно учитывать

удельное
сопротивление материала проводника?

4. Материалы, с малым удельным сопротивлением

5.

Материалы, с большим удельным сопротивлением

6. Задача 1 Сечение проволоки из нихрома 1,5 мм². Из неё изготовили десять спиралей для электронагревательного устройства.

Сопротивление каждой из них равно
150 Ом. Определить длину
проволоки, использованной для этих
спиралей.

7. Дано: S = 1,5 мм² R = 150 Ом = 1 Ом ∙ мм²/м Найти ℓ -? Решение: = RS/ = 150 ∙ 1,5 / 1 = 225 м; для 10 спиралей потребуется 2250

м проволоки.

8. Задача 2 Определите удельное сопротивление провода и материал из которого он изготовлен, если длина провода 69,79 м,

сопротивление 6 Ом и
площадь поперечного сечения
5 мм².

9. Дано: = 69,79 м R = 6 Ом S = 5 мм² _____________ Найти: -? Материал провода? Решение: R = ∙ /S = R∙S/ = 6∙5 /69,79 =0,42

10. Устройства, обладающие электрическим сопротивлением, называются резисторами.

11. Переменный и постоянный резистор

Переменный
резистор
Постоянный
резистор

12. Реостат

14.

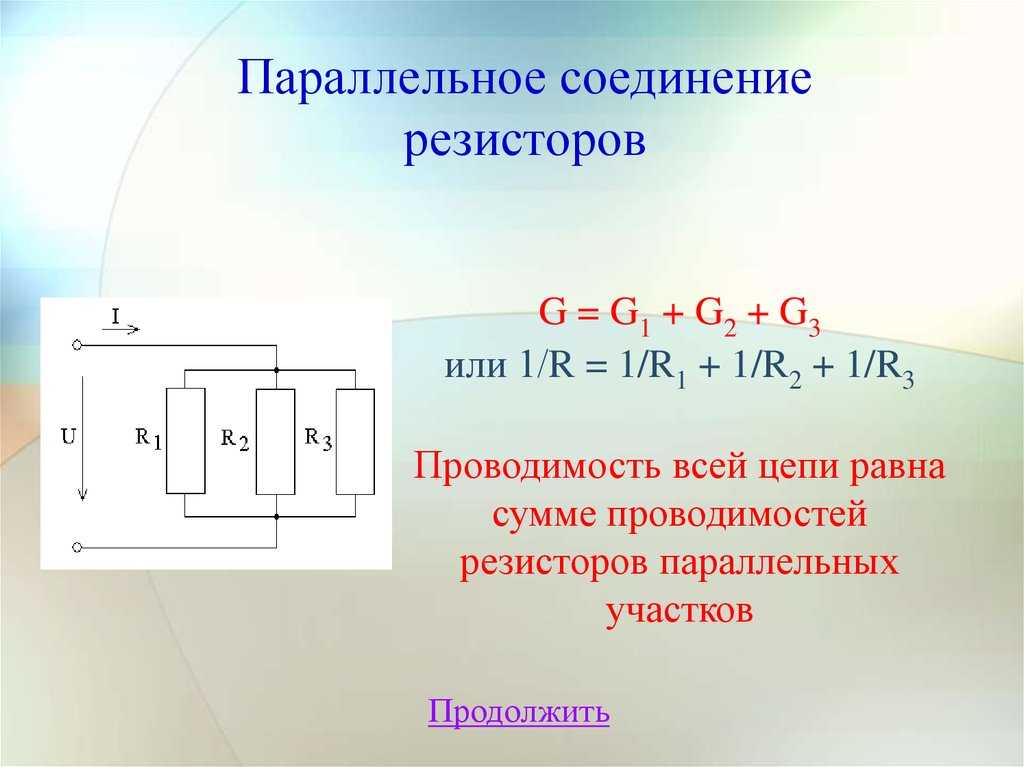Соединение резисторовПоследовательное
Параллельное
Смешанное

15. При последовательном соединении нескольких резисторов с разными сопротивлениями r общ находится по формуле: r общ = r1 + r2 +

r3 + … + r n
С одинаковыми сопротивлениями r общ находится по формуле:
r общ = r ∙ n
Пример:
Дано: R1 = 10 Ом
R2 = 12 Ом
Rобщ = R1+ R2
Rобщ = 10+12= 22 Ом
Вывод: при последовательном соединении R общ
всегда будет больше, чем большее из сопротивлений
включённых в цепь.

16. Недостатки последовательного соединения: 1) выключение одного из приёмников приводит к прекращению работы всех остальных. 2)

все приёмники должны иметь
одинаковое сопротивление (или
мощность), так как иначе создаётся
неравномерное распределение
напряжения на зажимах.
3) нельзя включать последовательно
большое число приёмников, так как
придётся подавать на зажимы большое
напряжение.

17. При параллельном соединении резисторов с разными сопротивлениями Rобщ находится по формуле: 1/r общ = 1/r1 + 1/r2 + 1/r3 + … +

1/r n
С одинаковыми сопротивлениями находится по формуле:
r общ = r/n
для двух параллельно соединённых находится по формуле:
r общ = r1 ∙ r2 / r1 + r2
Пример:
R1 = 8 Ом
R2 = 4 Ом
R3 = 2 Ом
1/R общ = 1/R1 + 1/R2 + 1/R3R общ = 1/R общ = 1/R1 + 1/R2 + 1/R3R1 + 1/R общ = 1/R1 + 1/R2 + 1/R3R2 + 1/R общ = 1/R1 + 1/R2 + 1/R3R3
1/R общ = 1/R1 + 1/R2 + 1/R3R общ = 1/R общ = 1/R1 + 1/R2 + 1/R38 + 1/R общ = 1/R1 + 1/R2 + 1/R34 + 1/R общ = 1/R1 + 1/R2 + 1/R32 = 1+2+4/R общ = 1/R1 + 1/R2 + 1/R38 = 7/R общ = 1/R1 + 1/R2 + 1/R38 = 8/R общ = 1/R1 + 1/R2 + 1/R37 = 1,14 Ом
Вывод: при параллельном соединении Rобщ будет меньше,
чем величина наименьшего сопротивления включённого в
цепь.

18. Смешанное соединение приёмников электроэнергии. Определение r общ смешанного соединения сводится к постепенному упрощению схемы

путём нахождения общего
сопротивления отдельных ветвей и участков, содержащих чисто
последовательное или чисто параллельное соединения.

19. Дано : R1 = 24 Ом R2 = 36 Ом R3 = 12 Ом R4 = 4 Ом R5 = 60 Ом R6 = 4 Ом Найти Rобщ — ?

21. Составьте соответствие

1 По какой формуле можно
определить Rобщ трёх общ трёх
резисторов соединённых
смешанно
1 Величину сопротивления нельзя
изменять
2 Формула по которой
определяют полное
сопротивление проводника
2 ВЛЭП, обмотки трансформатора,
электродвигателя
3 Единица измерения удельного
сопротивления материала
проводника
3 Rобщ трёх общ = Rобщ трёх 1 + Rобщ трёх 2 ∙ Rобщ трёх 3/Rобщ трёх 2+Rобщ трёх 3
4 Материалы, обладающие
малым удельным
сопротивлением
4 Электронагревательные устройства
5 Материалы, обладающие
большим удельным
сопротивлением
5 Величину сопротивления можно
изменять в определённых пределах
6 В переменных резисторах
6 Ом ∙ мм 2 / м
7 В постоянных резисторах
7 Rобщ трёх = p ∙ l/S

22.

Задание

English     Русский Правила

Параллельное соединение резисторов таблица. Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой.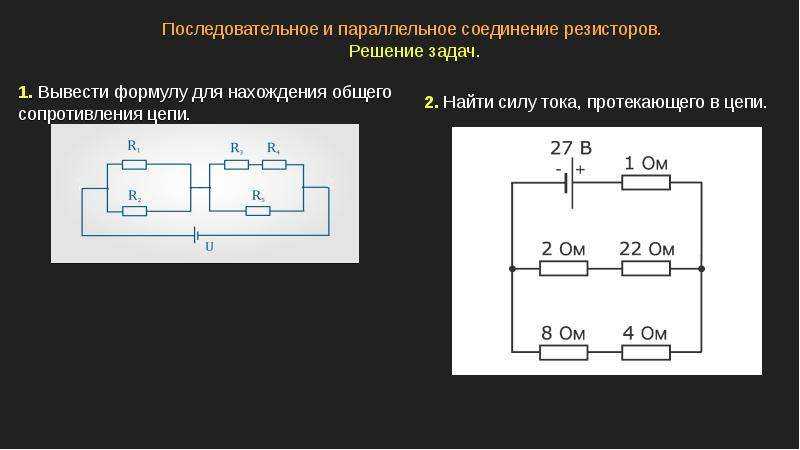 Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь

потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.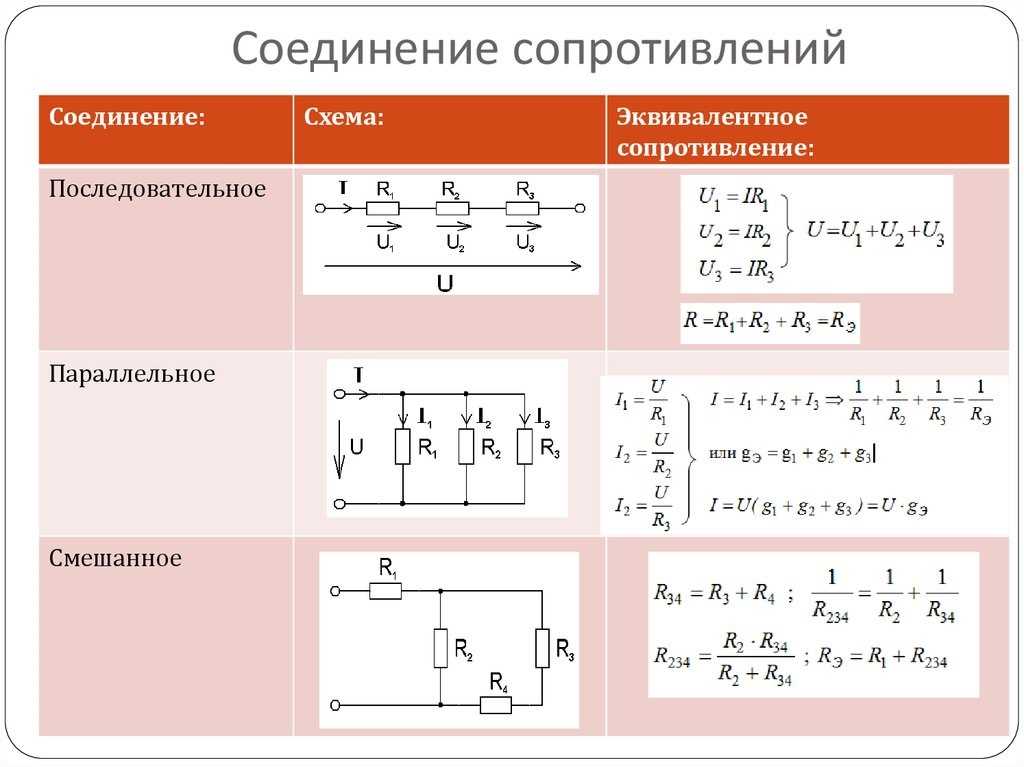

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель

, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчета

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом.

Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте

определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Заключение

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.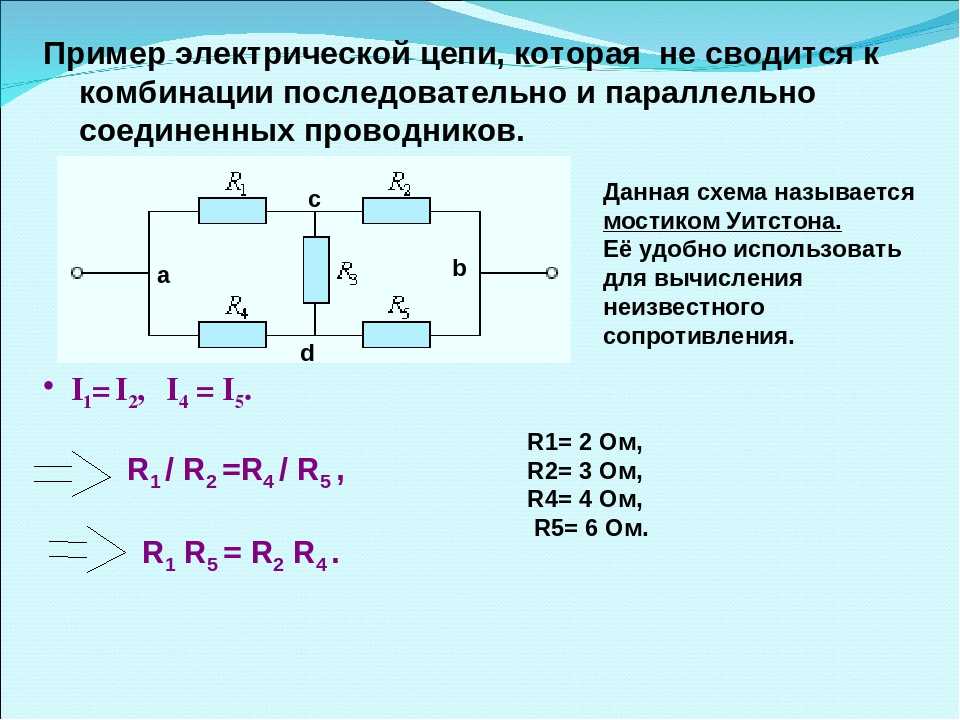

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление — ρ Ом·м/мм 2 . Все металлы — хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник — серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S — площадь сечения; l — длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

и нагрев проводника

Для практических расчётов режимов работы проводников применяется понятие плотности тока — δ А/мм 2 , она вычисляется по формуле:

δ = I/S, I — ток, S — сечение.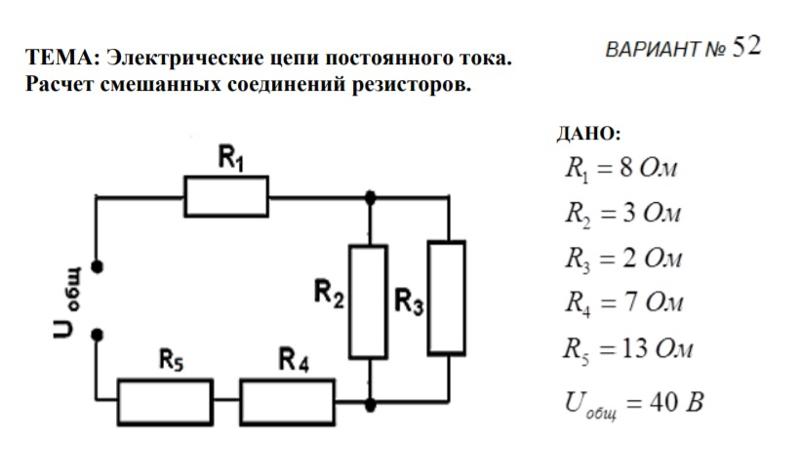

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой — последовательное соединение.

На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .

Второй способ более сложный — параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.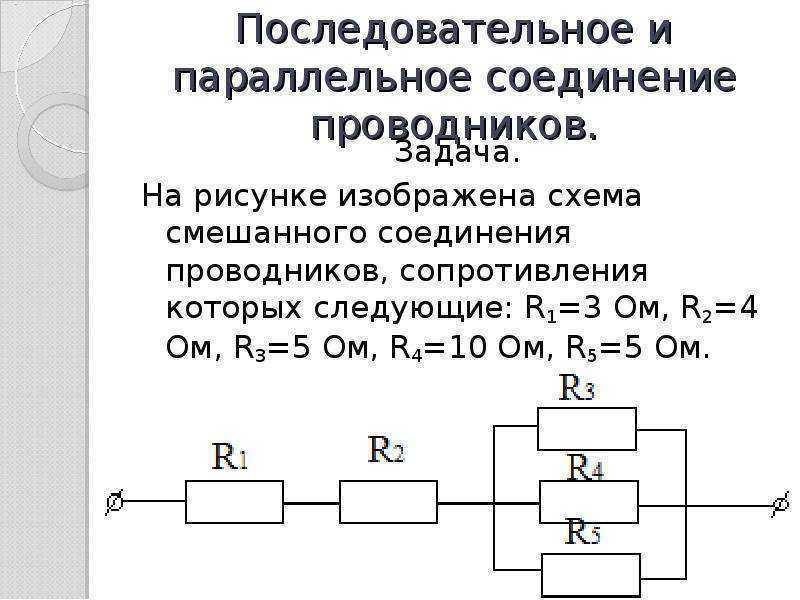

Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный — смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

R2,3,4 = R2,3 · R4/(R2,3 + R4).

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода.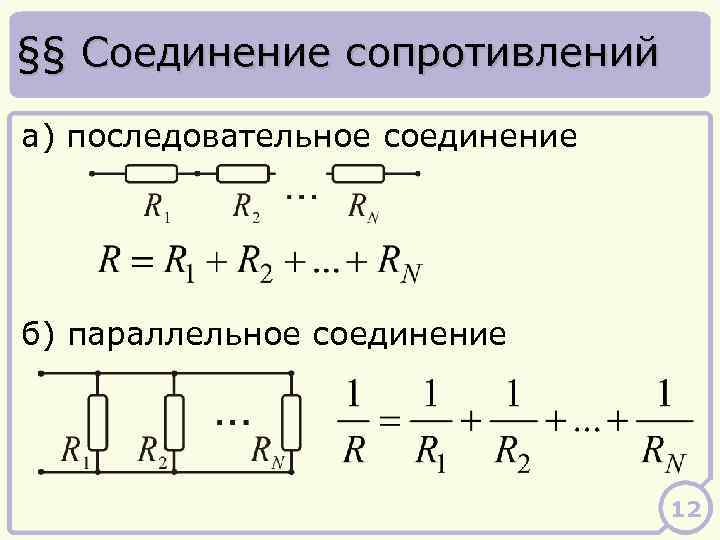 Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.

R л = ρ · 2L/S,

Здесь S — сечение провода линии, мм 2 .

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.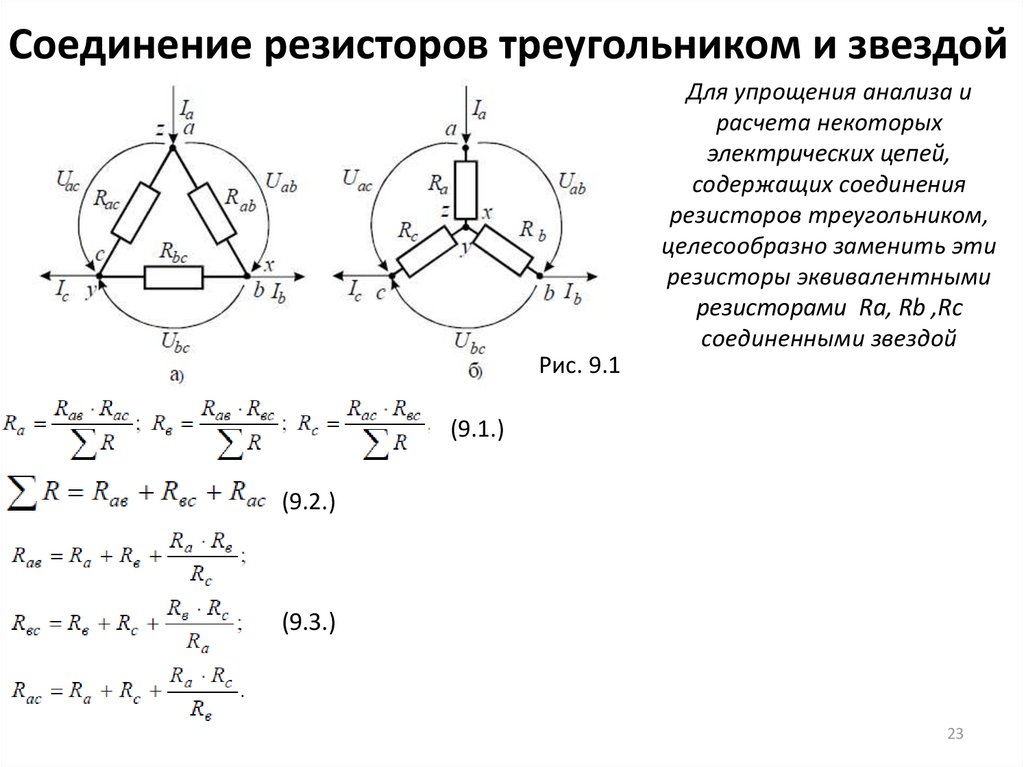

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.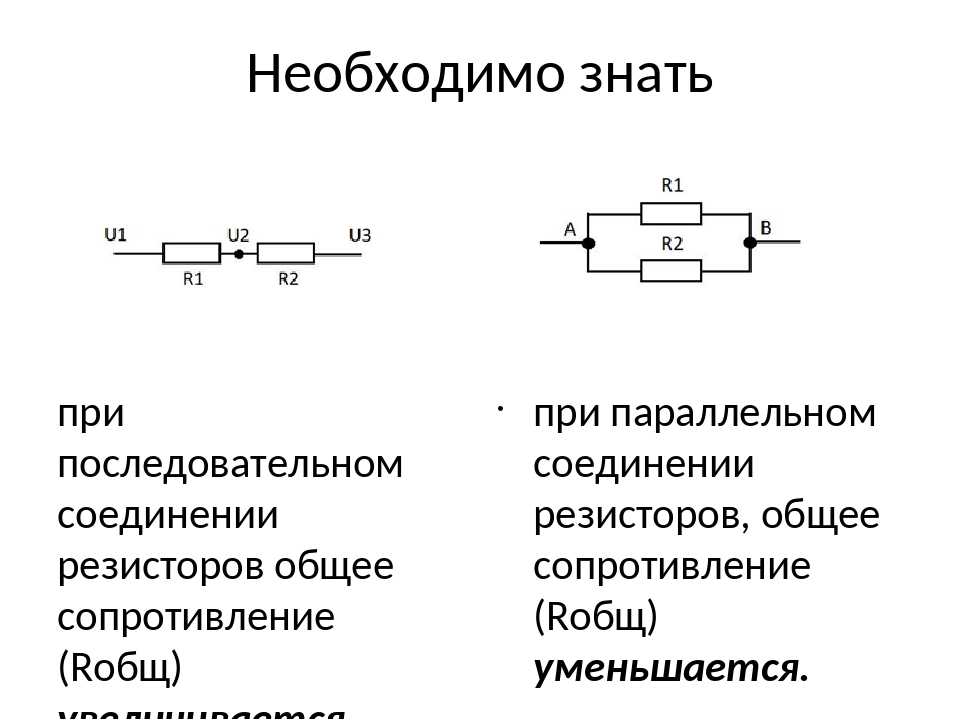

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку.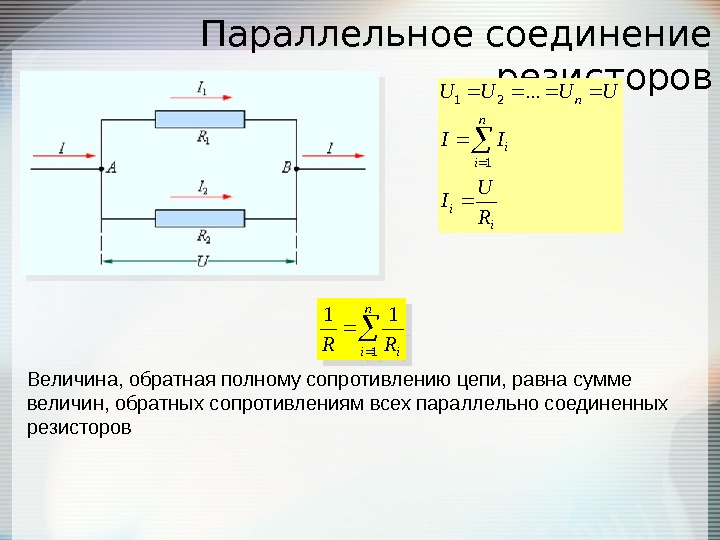 Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.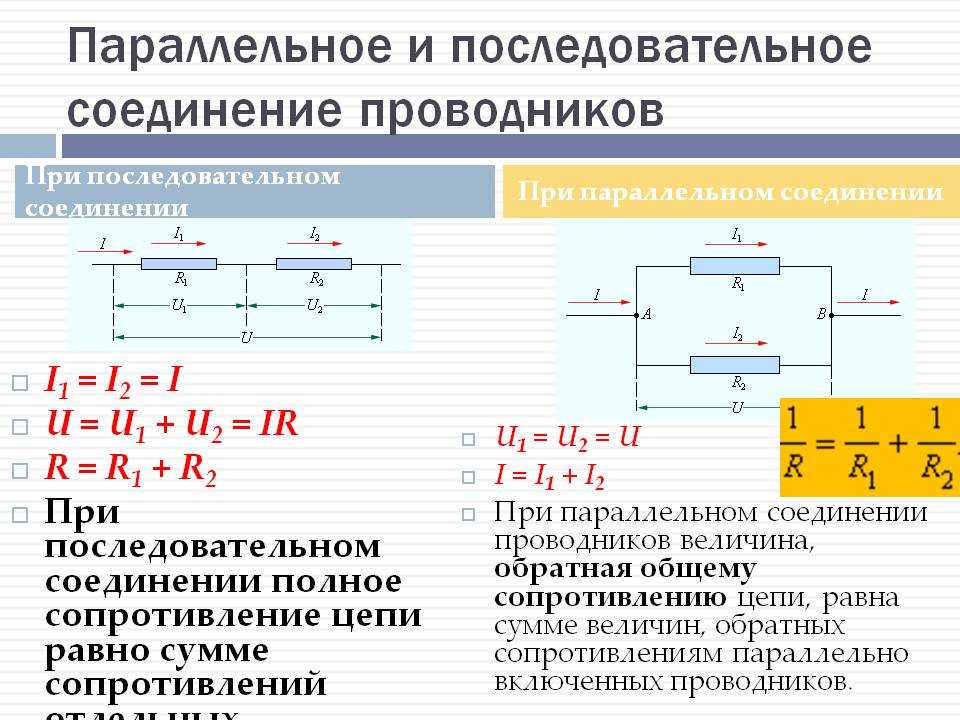

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.

С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.

Виды соединений

Резистор — пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:

1. Постоянные.
2. Переменные.

Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление.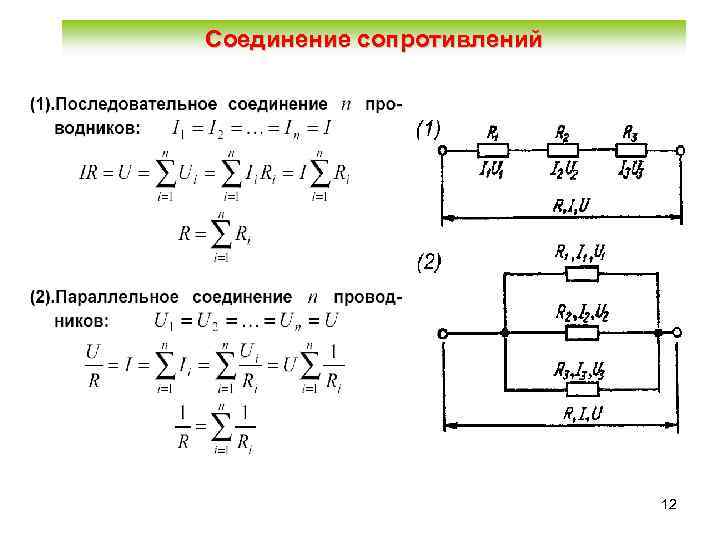 А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:

1. Последовательное.
2. Параллельное.
3. Смешанное.

Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.

Последовательное соединение проводников

В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.

Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.

Примером последовательного соединения проводников в быту является ёлочная гирлянда.

Параллельное соединение резисторов

При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.

Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.

В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.

Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.

Примеры параллельного соединения проводников:

1. Освещение.
2. Розетки в квартире.
3. Производственное оборудование.

Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.

Смешанное соединение проводников

Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно.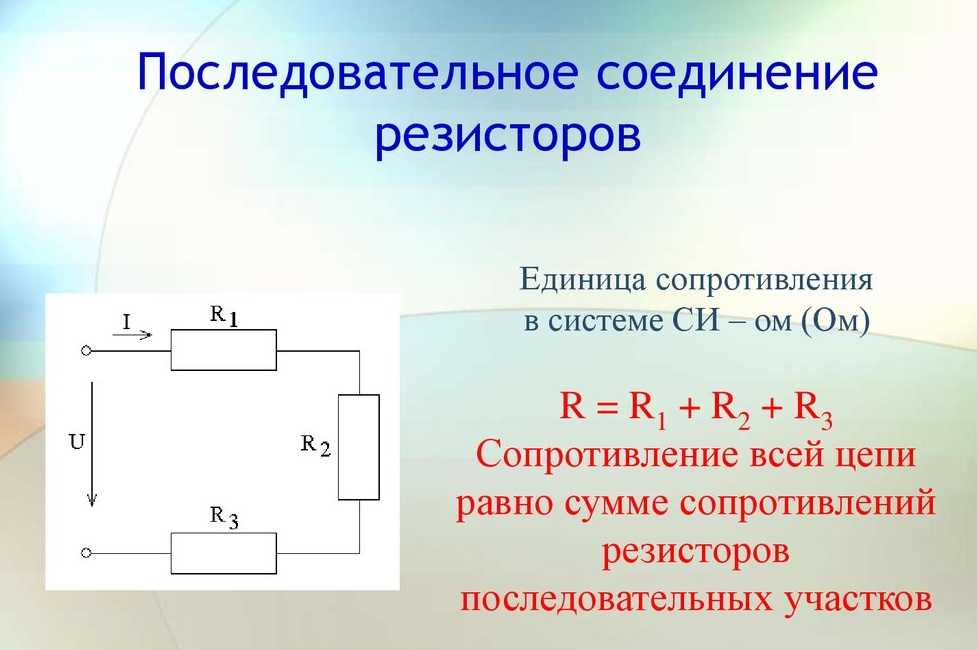 Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.

Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.

Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.

В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.

Серия

и параллельные резисторные схемы

Электронные компоненты соединяются разными способами.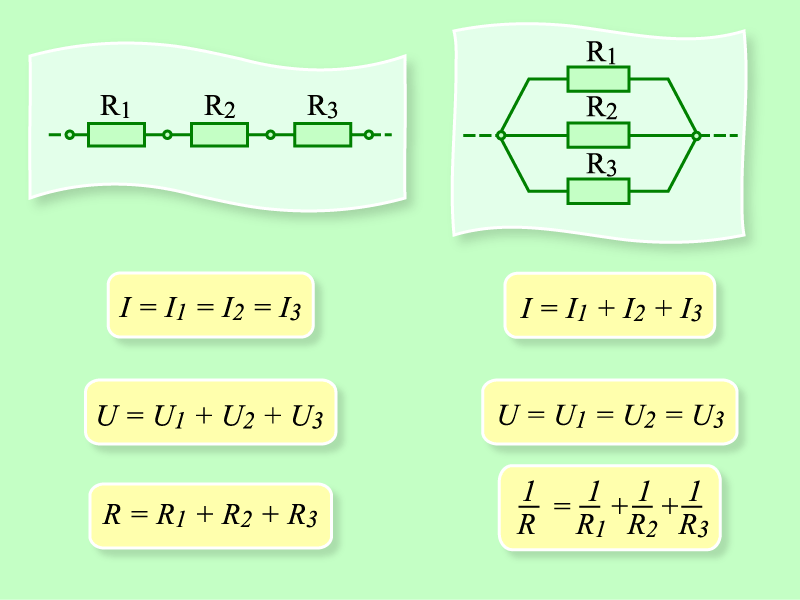 Две простейшие формы соединений — последовательное и параллельное. соединения.

Если компоненты соединены в цепи последовательно, то цепь называется последовательной. Если резисторы соединены последовательно в цепи, то цепь называется цепью последовательного резистора.

Если компоненты соединены в цепи параллельно, то цепь называется параллельной. Если резисторы соединены в цепи параллельно, то цепь называется параллельной цепью резисторов.

Серийный резистор цепь

А Цепь последовательного резистора представляет собой электронную схему, в которой все резисторы подключены один за другим по одному и тому же пути чтобы через каждый и каждый резистор.

полное сопротивление такой цепи получается просто суммирование значений сопротивления отдельных резисторов.

Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ ……..и т. д.

Для Например, если пять резисторов соединены последовательно. Тогда полное сопротивление цепи равно:

Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ + R ₅

Все ток, протекающий через первый резистор, не имеет другого путь идти. Следовательно, он также должен пройти через второй резистор, третий резистор, четвертый резистор и так далее.

Пример:

А Схема последовательного резистора показана на рисунке ниже. Этот схема состоит из пяти резисторов, соединенных последовательно и источник постоянного напряжения.

Если значения пяти резисторов: R ₁ = 4 Ом, R ₂ = 4 Ом, R ₃ = 2 Ом, R ₄ = 2 Ом, R ₅ = 3 Ом и батарея постоянного тока = 15 В, тогда

Общее сопротивление это Р _Т = Р ₁ + Р ₂ + Р ₃ + Р ₄ + R ₅ = 4 + 4 + 2 + 2 + 3 = 15 Ом.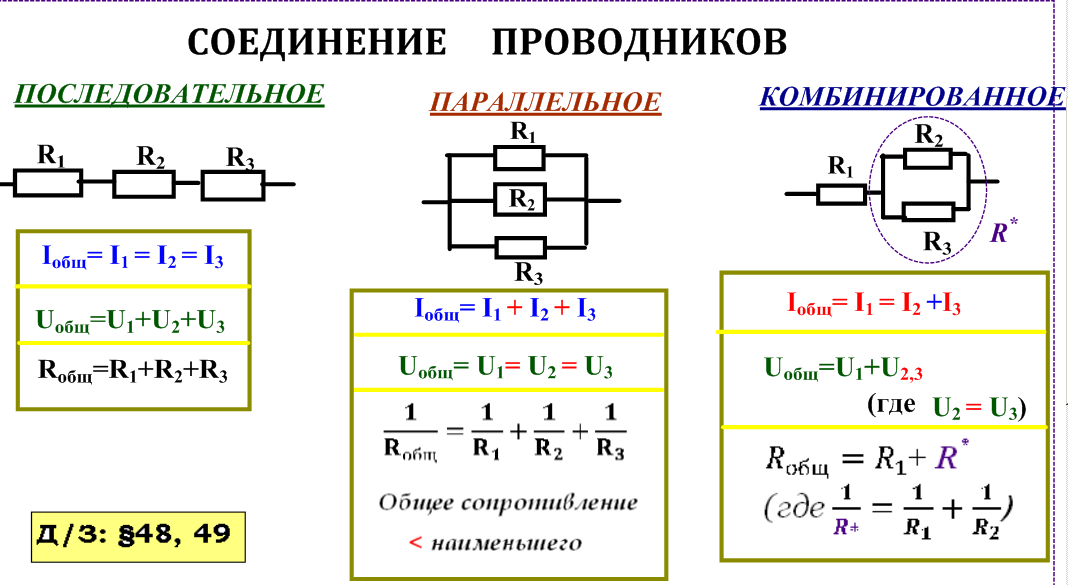

Вспомните формулу закона Ома, V = I R

Зная любые две переменные в приведенное выше уравнение, мы можем легко найти оставшееся неизвестное переменная.

Нам известно значение полного сопротивления Т.е. R _T = 15 Ом и значение напряжения I.e. V = 15 В

Теперь нам нужно найти оставшееся неизвестное значение тока I.

Текущий ток через каждый резистор будет 1 А.

Напряжение на каждый резистор в последовательной цепи отличается. Если все резисторы в последовательной цепи имеют одинаковое значение сопротивления тогда напряжение через каждый резистор одинаковый. С другой стороны, если каждый резистор имеет другое значение сопротивления, то напряжение на каждом резисторе разный.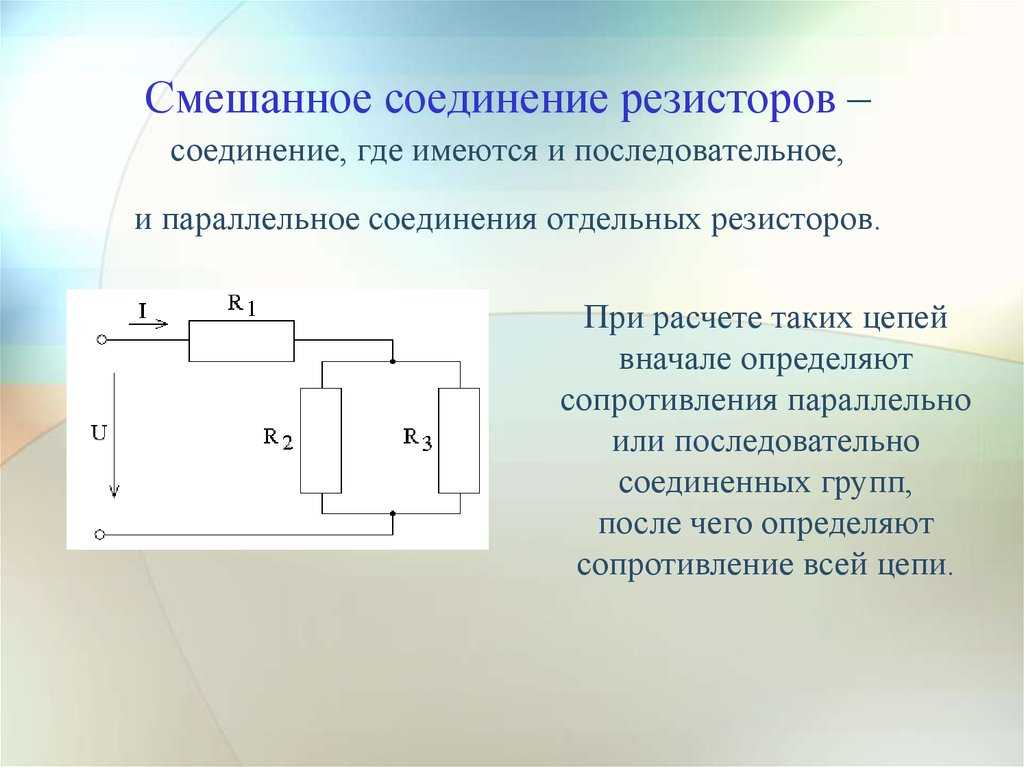

Напряжение на резистор (R ₁ ) есть V ₁ = I × R ₁ = 1 × 4 = 4 В

Напряжение на резистор (R ₂ ) равен В ₂ = I × R ₂ = 1 × 4 = 4 В

Напряжение на резистор (R ₃ ) равен В ₃ = I × R ₃ = 1 × 2 = 2 В

Напряжение на резистор (R ₄ ) составляет В ₄ = I × R ₄ = 1 × 2 = 2 В

Напряжение на резистор (R ₅ ) равен В ₅ = I × R ₅ = 1 × 3 = 3 В

Общее напряжение в последовательная цепь равна сумме всех отдельных суммарные напряжения

Т.е. В _Т = В ₁ + В ₂ + В ₃ + V ₄ + ……….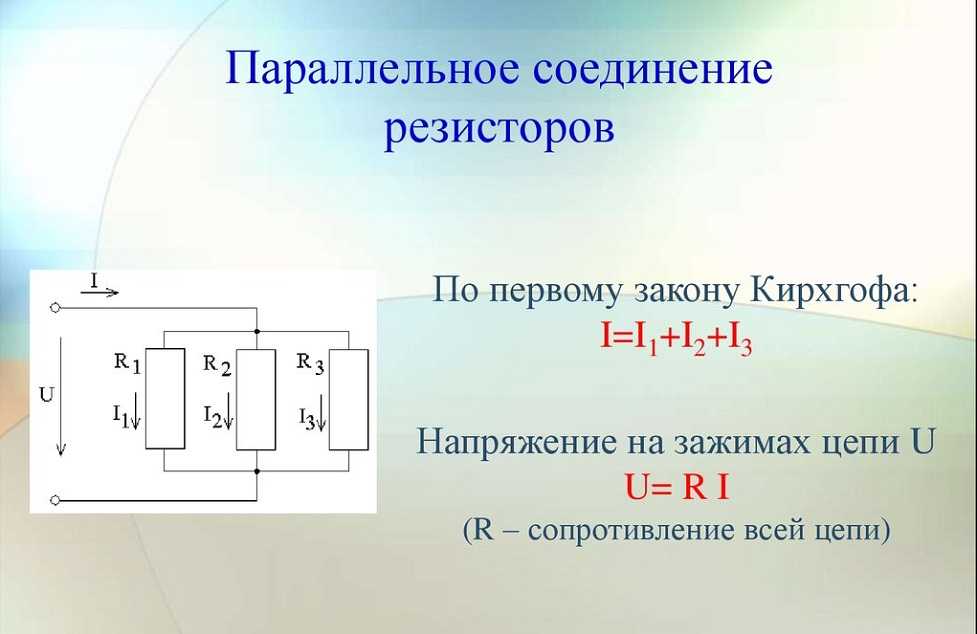 +V _N

В нашей схеме общее напряжение равно сумме разностей потенциалов по Р _1, , _{Р 2 , Р 3 , R 4 и R 5 .}

Т.е. В _Т = В ₁ + В ₂ + В ₃ + В ₄ + В ₅ = 4 + 4 + 2 + 2 + 3 = 15 В.

Параллельно цепь резистора

А Цепь параллельных резисторов представляет собой электронную схему, в которой все резисторы соединены рядом в разные пути, чтобы один и тот же ток не протекал через каждый резистор. Параллельная схема показывает несколько путей к протекать электрический ток.

ток в параллельной цепи распадается, при этом некоторый ток протекающие по каждой параллельной ветви и воссоединяющиеся, когда ветви встречаются снова. Следовательно, электрический ток через каждый резистор будет другим. Однако напряжение на каждый резистор одинаковый.

полное сопротивление параллельной цепи резистора получается по формуле суммируя обратные величины (1/R) значений сопротивления отдельные резисторы, а затем взяв обратную величину общее количество.

Для Например, если три резистора соединены параллельно. затем общее сопротивление цепи

Пример:

А Схема параллельного резистора показана на рисунке ниже. Этот схема состоит из трех резисторов, соединенных параллельно и источник постоянного напряжения.

Если значения трех резисторов: R ₁ = 8 Ом, R ₂ = 8 Ом, R ₃ = 4 Ом и батарея постоянного тока = 14 В, затем

общее сопротивление

Суммарный ток течет по цепи

Как напряжение на каждом резисторе параллельно схема, мы можем использовать омы закон найти ток отдельной ветви следующим образом.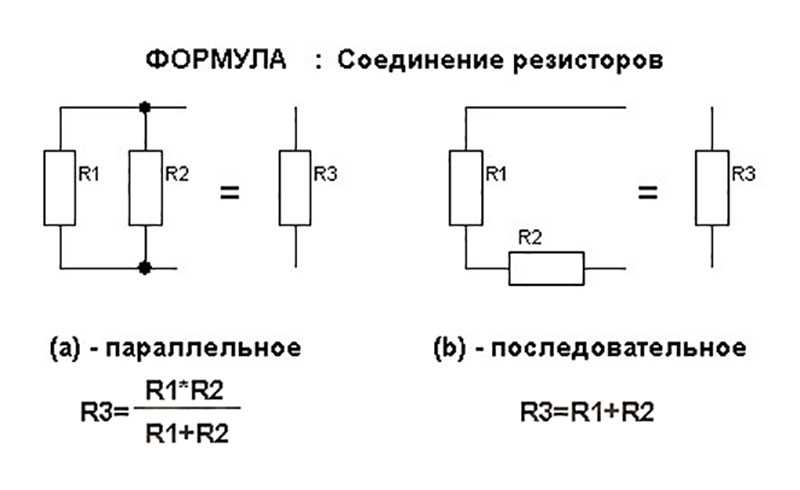

ток через резистор (R ₁ ) _{is I 1 = В / Р 1 = 14 / 8 = 1,75 А}

ток через резистор (R ₂ ) _{это я 2 = В / Р 2 = 14 / 8 = 1,75 А}

ток через резистор (R ₃ ) _{is I 3 = В / Р 3 = 14 / 4 = 3.5 А}

Тогда сумма ток равен сумме токов отдельных ветвей

т.е. Я _Т = Я ₁ + I ₂ + I ₃ = 1,75 + 1,75 + 3,5 = 7 А

Почему резисторы, соединенные последовательно и параллельно, имеют решающее значение в электрических цепях

Инженеры-электрики и электронщики соединяют компоненты в цепи параллельно или последовательно для создания некоторых важных цепей.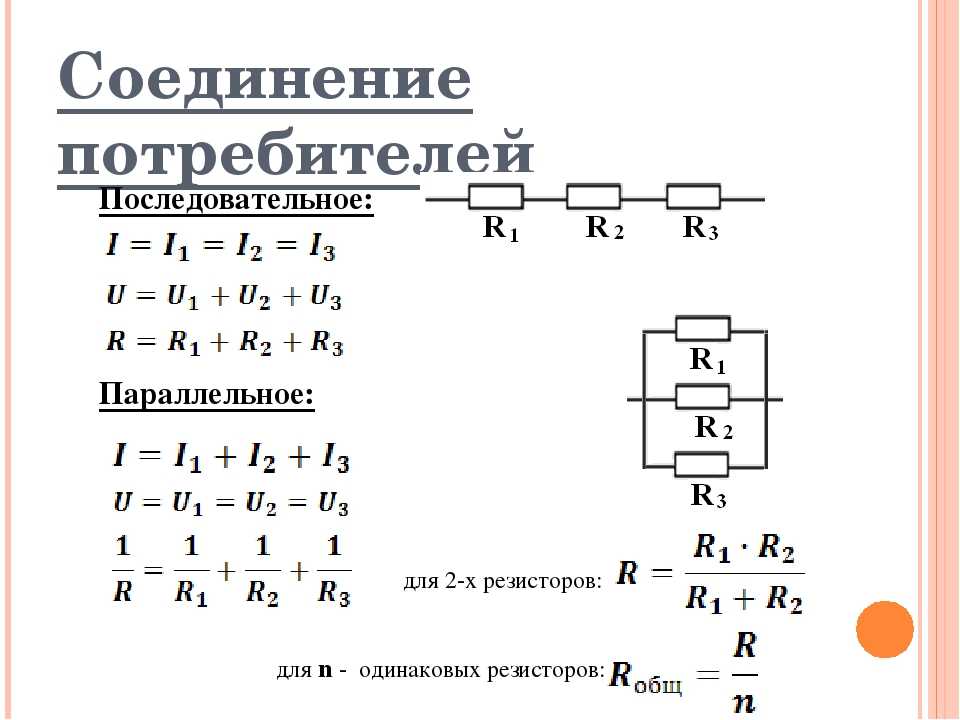 Также мы можем рассчитать сопротивление, напряжение и ток в этих цепях. Мы можем соединить резисторы вместе в ряде параллельных и последовательных комбинаций для создания резистивных цепей. Резистор, включенный последовательно и параллельно, является предметом обсуждения среди инженеров. В этой статье мы прольем больше света на резисторы, включенные последовательно и параллельно.

Что такое последовательные резисторы?

Резисторы — это компоненты, ограничивающие поток заряда в цепи. Таким образом, когда резисторы соединены один за другим, это просто называется последовательным соединением. Ток через каждый резистор одинаков при последовательном соединении резисторов.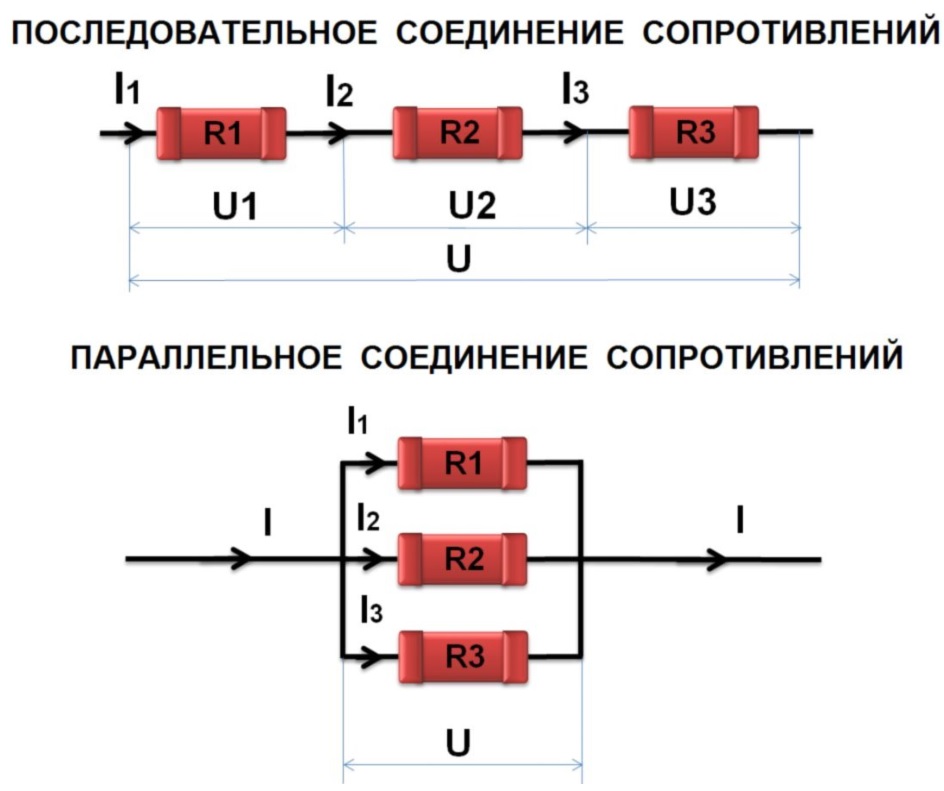 Кроме того, при последовательном соединении резисторов происходят различные изменения. Напряжение на всех резисторах равно точной сумме напряжений на каждом резисторе.

Это означает, что напряжение, окружающее цепь, в сумме равно напряжению источника питания. Кроме того, совокупное сопротивление некоторых резисторов, соединенных последовательно, равно сумме сопротивлений каждого из них. Кроме того, резисторы соединяются последовательно, когда они соединены через гирляндную цепь в одну линию. Это приводит к протеканию тока через эти резисторы.

Отдельные разъемы можно соединять параллельно или последовательно. Это также может быть комбинация обоих соединений. Это поможет генерировать сложные цепи резисторов. Кроме того, резистор преобразует ток в напряжение или наоборот. Вы можете по-разному взвешивать преобразованное напряжение, регулируя значение резистора. Следовательно, это позволяет интегрировать его в схемы опорного напряжения.

Вы можете использовать импеданс или один эквивалентный резистор для замены сложных цепей резисторов, независимо от сложности или комбинации соединений резисторов.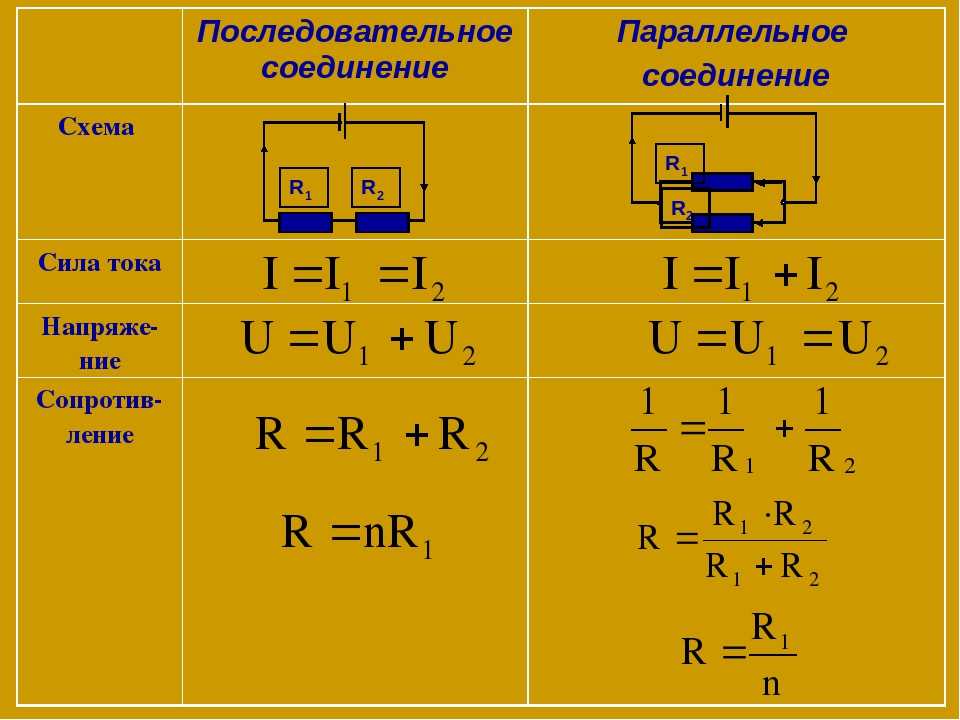 Это связано с тем, что резисторы должны соответствовать некоторым фундаментальным правилам. Закон Ома и Законы Кирхгофа о цепях являются такими законами.

Последовательно соединенные резисторы имеют общий ток, протекающий через них, поскольку ток, проходящий через один резистор, должен проходить через другие резисторы. Следовательно, величина тока, проходящего через последовательные резисторы, будет одинаковой в каждой точке сети последовательных резисторов.

Величина тока, протекающего через некоторые последовательно соединенные резисторы, будет одинаковой во всех узлах сети с последовательными резисторами.

Например,

I _R1 = I _R2 = I _R3 = I _AB = 1MA

Резисторы в параллеле , когда это находится в параллеле

, когда резисторы находятся в параллеле

. все резисторы полностью соединены друг с другом.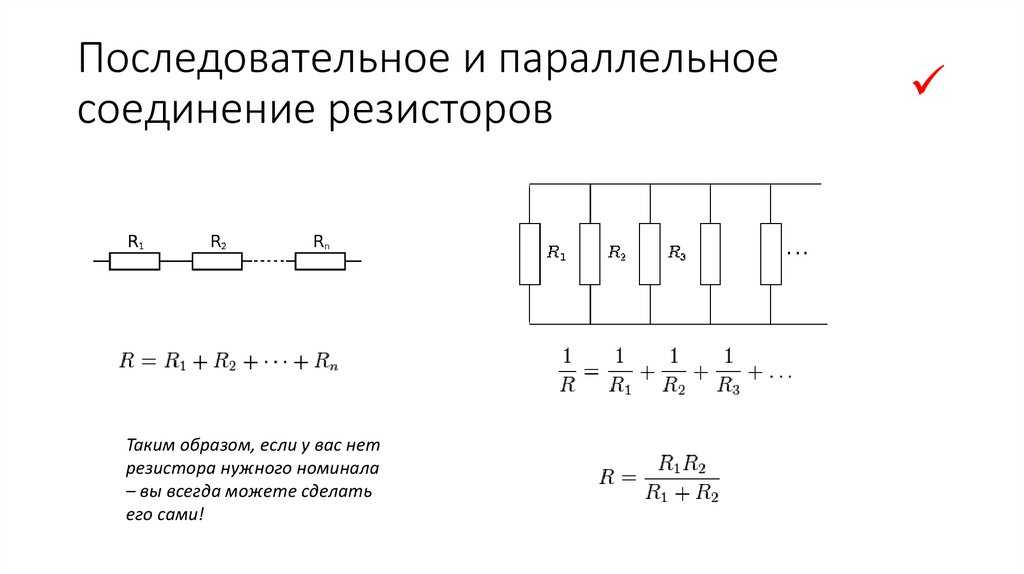 Происходит это через провод пренебрежимо малого сопротивления. Кроме того, параллельные резисторы указывают на то, что резисторы соединены бок о бок. Кроме того, резисторы параллельны, когда их выводы соответственно соединены с каждым выводом других резисторов.

В отличие от резисторов, соединенных последовательно, ток в цепи резисторов, соединенных параллельно, протекает по нескольким путям. Поэтому резисторы, включенные параллельно, обычно рассматриваются как делители тока. Кроме того, ток может быть неодинаков, поскольку ток питания протекает по нескольким путям. Но, падение напряжения на всех резисторах параллельно одинаковое.

Под параллельной резистивной цепью понимается цепь, в которой резисторы подключены к одним и тем же узлам. Кроме того, вы можете идентифицировать эту цепь, поскольку она имеет несколько путей тока, связанных с одним и тем же источником напряжения. Например, в приведенном ниже параллельном резисторе напряжение на резисторе R1 такое же, как и напряжение на резисторе R2, которое также эквивалентно напряжению на резисторе R3.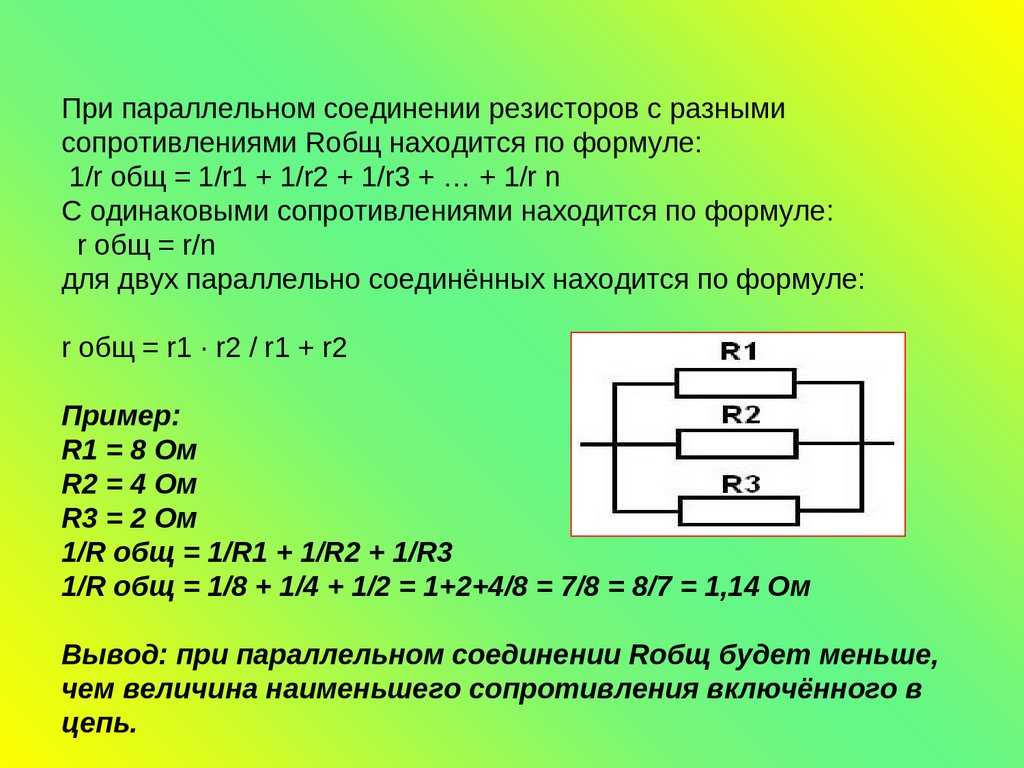 Это, наконец, сводится к напряжению питания.

Формула цепи параллельных резисторов:

VR1 = VR2 = VR3 +12 В

В этом примере R1, R2 и R3 хорошо соединены параллельно.

Общее сопротивление двух параллельно соединенных резисторов можно рассчитать с помощью этого уравнения.

1/R = 1/R1 + 1/R2

Если параллельно три резистора, вы добавите в уравнение третий резистор. например,

1/R равно 1/R1+1/R2+1/R3

Резисторы в последовательном и параллельном соединении

Существуют резисторы в последовательном и параллельном соединении. Кроме того, вы можете соединить отдельные разъемы в параллельном или последовательном соединении. Это может быть комбинация обоих подключений. Здесь наше основное внимание сосредоточено на сочетании обоих соединений.

Кроме того, последовательное и параллельное соединение различных резисторов помогает создавать более сложные резистивные цепи. Вопрос здесь в том, как мы это делаем?

Резисторные цепи, в которых последовательно и параллельно соединены резисторы, обычно называют цепями со смешанными резисторами или комбинацией резисторов. Кроме того, резисторы, соединенные последовательно, пропускают одинаковую величину тока, а резисторы, соединенные параллельно, обычно имеют одинаковое напряжение на них.

Например, рассчитайте I _T  (общий ток), полученный от источника питания 12 В.

Глядя на это, может показаться сложным. Однако при ближайшем рассмотрении мы поймем, что R2 и R3 оба связаны вместе в последовательной комбинации. Следовательно, можно создать эквивалентное сопротивление. Таким образом, сопротивление для этой комбинации будет

R2 + R3 + 8 Ом + 4 Ом = 12 Ом

. Следовательно, указанные выше резисторы R2 и R3 можно заменить одним резистором с сопротивлением 12 Ом. Теперь в схеме есть один резистор, включенный параллельно резистору R4. Кроме того, мы можем минимизировать эту параллельную комбинацию до эквивалентного значения резистора, используя эту формулу:

R(экв.)=1/RA + 1/R4 = 1/12 + 1/12 = 0,1667

R(комбинация) = 1/R(экв.) =1/0,1667 = 6 Ом

Теперь мы можем видеть, что R1 и R(гребенка) соединяются последовательно.