Векторный элемент площади — Энциклопедия по машиностроению XXL
Векторный элемент площади nda боковой поверхности 22, очевидно, равен [c.327]Векторный элемент площади р , поверхности резания Р равен [c.445]
Криволинейные интегралы в (1а), (2й) берутся по произвольному замкнутому контуру (их наз. циркуляциями векторных полей), а стоящие в правых частях поверхностные интегралы — по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура (11) связано с направлением нормали к 3 (вектор й5) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (5) в (За), (4а) направление вектора элемента площади 5 совпадает с наружной нормалью к поверхности V — объём, ограниченный замкнутой поверхностью 5. [c.34]
Векторное обозначение элемента площади поверхности указывает его ориентацию в пространстве. Прим. ред.)
Обилий интеграл этой системы (х, у, г) —F (x, у, 2 )==Сз определяет искомые векторные линии постоянные интегрирования j и с-2 вычисляются заданием одной точки. Элементарный поток поля а через элемент площади Au/, на поверхности а определяется как a nJ Aa , где —вектор а, [c.67]
Граничную поверхностную ячейку (в трехмерном пространстве) элемента площади dS(x) следует каждый раз отличать от двумерной ячейки (элемента dA x)), так как dS x) не является плоским в X, хотя является плоским и ограниченным ортами ( i, Сг) в Z (рис. 8.2, в). Снова используя известное соотношение векторной алгебры [c.210]
Элемент площади вычисляется по формуле векторного произведения векторов
Уравнения для элементов возмущенного движения. Рассмотрим один из возможных способов получения дифференциальных уравнений для элементов возмущенного движения [47], С этой целью воспользуемся векторными интегралами площадей (2.2.5) и Лапласа (2.2.22) [c.337]
М — присоединенная масса, йзр — векторный элемент поверхности частицы, % — площадь контакта. [c.188]
Плотность электрического тока J—векторная величина, равная пределу отношения силы тока сквозь некоторый элемент поверхности, нормальный к направлению движения носителей заряда, к площади этого элемента поверхности, когда этот элемент поверхности стремится к пулю. Модуль плотности тока
Мы придем к этому, рассматривая давление на стенку сосуда (которое экспериментально может быть измерено, например, посредством манометра) как эффект среднего числа бесчисленных и беспрестанных ударов, которые молекулы газа в их движении производят на стенку выражаясь точнее, мы введем понятие удельного давления как некоторой величины (векторной), которая имеет размерность силы, деленной на площадь, и определяется следующим образом. Рассмотрим произвольный элемент До стенки и результирующую импульсов, которые она испытывает со стороны молекул газа в течение элемента времени At, следующего за произвольным моментом t. Удельным давлением называется отношение названной результирующей к произведению До Ы. Обозначим через п нормаль, направленную наружу по отношению к сосуду.
Плотность электрического тока. Плотностью электрического тока 6 называют векторную величину, численно равную отношению силы тока dl к элементу dS площади поперечного сечения проводника [c.75]
Введем в рассмотрение вектор йъ, часто используемый в векторном анализе, абсолютная величина которого равна площади элемента поверхности, а направление совпадает с положительным направлением нормали п. Положительное направление нормали п выбирается следующим образом. Если площадка йз является элементом замкнутой поверхности, ограничивающей какой-то объем, то за положительное направление ее нормали обычно принимается направление из объема наружу, т. е. направление внешней нормали. Если рассматривается изолированный элемент поверхности, на который падает неширокий пучок лучей, то за положительное направление принимается направление, составляющее острый угол с направлением падающего пучка. В других случаях положительное направление нормали следует оговаривать особо.
Далее, следуя [ ] и используя последнюю формулу, с помощью теоремы Нансона можно получить следующее уравнение, связывающее векторные элементы площади (1А и с1А
Перемещаясь в толще материала заготовки, векторный элемент площади с1Рр охватывает объем, равный [c.441]
Классик, подход к спину. Векторное произведение в З-мерном евклидовом пространстве порождает скобку Пуассона ф-ций на нём. Симплектик. слои в данном примере — концентрич. сферы, снабжённые элементом площади. Вращений группа сохраняет площади и потому действует на сфере потоками гамильтоновых векторных полей. Гамильтонианы действия — линейные ф-ции в пространстве. Квантование этого действия возможно лишь на сферах целочисленной площади (в единицах h) и приводит к неприводимым представлениям группы вращений — как векторный , так и спинорным .
Но по теореме Гаусса в векторном поле w интеграл по замкнутой поверхности от потока w-б/А через элемент площади dk = SidA равен количеству вещества, поступившему из находящихся внутри этой поверхности источников с интенсивностью на единицу объема, равной div w, или [c.166]
Рассмотрим теперь алгебру Ли, образованную векторными полями дивергенции нуль на торе с однозначной функцией тока. Соответствующая группа SoDiffJ состоит из оставляюищх на месте центр тяжести тора и сохраняющих элемент площади диффеоморфизмов. Она вложена в группу SDiff всех сохраняющих элемент площади диффеоморфизмов как вполне геодезическое подмногообразие (т. е. такое подмногообразие, что каждая его геодезическая является геодезической в объемлющем многообразии).
Отметим, что зависимость вектора g(x) от деформации ф определяется двумя факторами во-первых, формулой, связывающей элементы площади в обеих конфигурациях, и, во-вторых, возможной зависимостью плотности g от деформации ф. Векторное поле g . Г] характеризует плотность приложенных поверхностных сил на единицу плои1,ади в отсчётной конфигурации оно вводится таким образом, чтобы вектор g x)da был равен элементу поверхностной силы (х ) приложенной к соответствующему элементу площади в точке л = ф (х) (рис. 2.6-1). [c.109]
Закон дистрибутивности является следствием теоремы о сложении моментов плоскостных элементов, доказанной в предыдущем параграфе. Действительно, векторное произведение с не изменится, если мы произвольным способом преобразуем векторы а и Ь, не изменяя их взаимного расположения, от которого зависит положительное направление обхода контура параллелограмма, а также сохраняя величину площади параллсмюграмма А B D. Следовательно, параллелограмм А B D всегда мо К ю заыенш ь эквивалентным прямоугольником. [c.33]
Добавление 1.3. Решим задачу об изменении площади элемента поверхности в теле при его деформации. Для этого рассмотрим два вектора daj и dttj, исходящих из одной и той же точки о. Площадь элементарного параллелограмма, построенного на векторах йа, и равна модулю векторного произведения daiXda2 = d5o- В декартовой системе компоненты вектора dS определяются по формуле (см. приложение I)
По способу приложения различают силы сосредоточенные и распределенные. Сосредоточенные силы считают приложенными в точке, и они являются векторной величиной. Так как сила возникает в результате взаимодействия тел и давление между телами передается через площадку больших или меньших размеров, то в действительности сосредоточенных сил не суп1,ествует. В тех случаях, когда размеры площадки малы по сравнению с разме-рами элемента конструкции, силу можно считать приложенной в точке, являющейся центром площадки касания тел. Такое допущение значительно упрощает расчеты. К сосредоточенным силам относят, например, давление вала на опоры, действие колеса на рельс. Сосредоточенные силы измеряют в ньютонах. Распределенными называют силы, действующие на некоторой сравнительно большой площади поверхности конструкции. Эти нагрузки измеряют в паскалях (1 Па = 1 Н/м ). Если силы распределены по длине, то единицы силы относят к единице длины. К распределенным нагрузкам относятся давление воды на плотину, газа на стенки сосуда.
Результат измерения параметров случайного скалярного или векторного поля, характеризуемого своими пространственно-временными статистическими характеристиками, определяется помимо приборных (систематических) погрешностей, также погрешностями, связанными с эффектами взаимодействия измерительного элемента с исследуемым полем. Так, результаты измерений временных параметров поля зависят от инерционных характеристик измерителя (тепловой инерции нити термоанемометра, собственной частотной характеристики преобразователя давления), а пространственных параметров-от соотношений масштабов измерительного прибора и исследуемого поля. Масштабы эти в зависимости от физического содержания процедуры измерения могут быть пропорциональны L», (и = 1, 2, 3). Например, измерения пульсационной компоненты скорости /, М2 или Мз зависят от соотношения между длиной термонити Ь и характерным масштабом пульсации 1и , 1и ц) или / (С) измерения пульсаций давления на поверхности обтекаемого тела определяются соотношением между площадью преобразователя 5 LlL2 и площадкой, образованной
Давление векторная или скалярная величина? Раньше считал скалярным, но в ответах мнения разделяются.
скалярная. Т. к определять направление смысла нет, действует всегда нормально поверхности
Вообще это тензор
Давление — скалярное. Но вот СИЛА, которую это давление прикладывает к стенкам — уже векторная.
Ёпт… Ну посмотри на уравнение для движения жидкости. Там градиент давления фигурирует. Само давление — это скаляр. Сила — это разница давлений, из направления максимальной разницы и забирает направление. А чё, на ответах русскую википедию забанили? . <img src=»//otvet.imgsmail.ru/download/188030775_ebcf4380b76f04b31638878ef577b20d_800.png» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/188030775_ebcf4380b76f04b31638878ef577b20d_120x120.png» data-big=»1″>
При выполнении закона Паскаля в статике вполне можно обойтись и скалярной величиной — давлением. Для более сложных случаев есть всякие другие величины — напр., тензор напряжений.
Давле́ние — физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы действующей на малый элемент поверхности, к его площади. Определение не раскрывает физический смысл явления. Представьте сосуд с криволинейной поверхностью. Для простоты сферической. На каждую точку этой поверхности перпендикулярно поверхности в этой точке действует маленькая сила (маленький вектор). Строим эпюру сил. Каждая сила это вектор. При чём векторы все одинаковой длины. Имеем, что сумма векторов равна нулю. Сила это вектор, а давление это сумма величин сил перпендикулярных к поверхности. Давление в замкнутом сосуде скалярная величина. По другому, если бы давление было векторной величиной мы получили бы движение с ускорением. В замкнутом сосуде движения сосуда нет. В случае например ракетного двигателя, когда сосуд не замкнут, мы имеем силу тяги равную давлению в сосуде умноженному на площадь критического сечения (без учёта диффузора). Но при этом мы используем понятие силы, а не давления. Хотя можно условно сказать, что давление в КС имеет вектор, потому что на критическое сечение давление не действует и сумма векторов всех сил больше нуля. При этом есть наличие движения. Ещё пример: испытание кирпиче на разрушение. На кирпич давят прессом на одну его грань и определяют именно давление на см^2 при котором он разрушится. Вот тут все силы направлены в одну сторону векторы совпадают. Значит давление имеет вектор. Но говорить что давление векторная величина это кощунство и за это будут поругать, могут даже и обозвать обидно.
Зря ты читаешь этого безграмотного ушлёпка Замятина. Давление даже больше, чем вектор — это тензор второго ранга.
Давление в точке в общем случае описывается тензором 2-го ранга. Просто для невязкой жидкости (воды) оно имеет характер гидростатического (одинакового по всем направлениям) давления, описываемого шаровым тензором напряжений. Компоненты последнего записываются в квадратную матрицу 3х3, у которой все элементы нули, кроме диагональных (все 3 равны p): Tik=dik * p, где dik — дельта Кронекера. В этом частном случае можно сказать, что давление скаляр. Если же рассматривать давление, действующее на определённую площадку, то это уже вектор.
Вектор обладает как модулем (то есть значением), так и направлением. Проекция силы имеет направление. Проекция силы — векторная величина. На плоскости проекция силы имеет знак + или -, что и характеризует направление. То что проекция силы — скаляр — это скорее ахинея. Если мы разложим, на пример вектор скорости под углом к горизонту на вектор перемещения по вертикальной и горизонтальной оси, то они будут проекциями, но естественно они будут иметь направление.
Бесконечно малый элемент — поверхность
Бесконечно малый элемент — поверхность
Cтраница 1
Бесконечно малый элемент поверхности характеризуется вектором dS, модуль которого равен площади элемента поверхности и направлен по нормали к поверхности, принятой за положительную. [1]
Выделим на поверхности проводника бесконечно малый элемент поверхности dS ( рис. 21) и обозначим поверхностную плотность заряда на нем через о. В данном случае нужно рассматривать бесконечно малый элемент поверхности проводника, так как в общем случае о меняется от точки к точке поверхности. Высота цилиндра должна быть также бесконечно малой, потому что в случае проводника произвольной формы силовые линии будут перпендикулярными к поверхности проводника только в непосредственной близости от нее. [3]
Элементарные тепловые потоки на бесконечно малом элементе поверхности dF, вычисленные через разность локальных температур, dQ a kt dF ( рис. 2 — 2, в), или через разность средних температур, dQ aAtdF ( рис. 2 — 3), естественно равны друг другу. В то же время средний для всей поверхности FT коэффициент а является, естественно, величиной постоянной для данного теплообменника. Таким образом, для конкретного теплообменника с поверхностью FT коэффициенты а, и-о — могут быть одновременно постоянны: коэффициент а — как средний для Ft, а а — — вдоль поверхности F при постоянстве параметров гидродинамического режима. В то же время численно коэффициенты а и а могут сильно отличаться друг от друга. [4]
В данном случае нужно рассматривать бесконечно малый элемент поверхности проводника, так как в общем случае о меняется от точки к точке поверхности. Высота цилиндра должна быть также бесконечно малой, потому что в случае проводника произвольной формы линии смещения будут перпендикулярными к поверхности проводника только в непосредственной близости от нее. [6]
А — давление, действующее на бесконечно малый элемент поверхности контакта, а г — расстояние от этого элемента до рассматриваемой точки. Интегрирование должно распространяться по всей области поверхности контакта. [7]
Принимается, что сила, действующая на бесконечно малый элемент поверхности dS, имеет вид F dS, где F — некоторый конечный вектор. Точное математическое содержание этого положения определяется совершенно аналогично тому, как это указано в замечании в конце § 1 относительно объемных сил. [8]
Каждый луч, упавший от светящего тела на бесконечно малый элемент поверхности матированного светильника ( см. рис. 7.33), при прохождении через него рассеивается. Следовательно, ЭО имеет неравномерную яркость лучей и размеры, большие размеров светящего тела относительно рассматриваемой точки. Размеры и распределение яркости лучей ЭО по существу должны быть такими же, как и для матированной отражающей поверхности. [9]
Вихревыми нитями я называю части жидкой массы, которые выделяются из нее, если через все точки контура бесконечно малого элемента поверхности провести соответственные вихревые линии. [10]
Длина вектора потока тепла в данной точке — это количество тепловой энергии, проходящее за единицу времени и в пересчете на единицу площади сквозь бесконечно малый элемент поверхности, перпендикулярный к направлению потока. Вектор указывает направление потока ( фиг. [11]
Ротация скоростного поля в точке А равна предельному значению, к которому приближается линейный интеграл ( отнесенный к единице поверхности делением на площадь элемента поверхности) от вектора скорости вдоль кривой, заключающей бесконечно малый элемент поверхности, перпендикулярный к направлению ротации. [12]
Ротация скоростного поля в точке А равна предельному значению, к которому приближается линейный интеграл ( отнесенный к единице поверхности делением на площадь элемента поверхности) от вектора скорости вдоль кривой, заключающей бесконечно малый элемент поверхности, перпендикулярный к направлению ротации. [13]
Выделим бесконечно малый элемент поверхности — цилиндр — высотой dz и радиусом г и найдем элементарный расход через боковую поверхность этого цилиндра. [14]
Интеграл по поверхности ( двумерной) в 4-пространстве. Аналогично в 4-пространстве бесконечно малый элемент поверхности определяется антисимметричным тензором второго ранга dfik — dxfdx k — dxkdx l t его компоненты равны проекциям площади элемента на координатные плоскости. [15]
Страницы: 1 2
13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
Векторным произведениемвектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
|
рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведениедвух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
a × b = | i | j | k | = i(aybz — azby) — j(axbz — azbx) + k(axby — aybx) |
ax | ay | az | ||
bx | by | bz |
a × b = {aybz— azby; azbx— axbz; axby— aybx}
Свойства векторного произведения векторов
Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал= a × b]
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
Смешанным
произведением 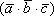 некомпланарныхвекторов
некомпланарныхвекторов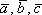 ,взятых в данном порядке, называетсяобъём параллелепипеда, построенного
на данных векторах, снабжённый знаком
«+», если базис
,взятых в данном порядке, называетсяобъём параллелепипеда, построенного
на данных векторах, снабжённый знаком
«+», если базис правый,
и знаком «–», если базис
правый,
и знаком «–», если базис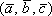 левый.
левый.
1.
Смешанное
произведение не меняется при циклической
перестановке его сомножителей (не
меняется ни объем параллелепипеда, ни
ориентация его ребер): 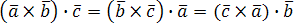 .
.
2.
Смешанное
произведение не меняется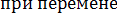 знаков
векторного и скалярного умножения:
знаков
векторного и скалярного умножения: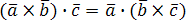 ,
поэтому смешанное произведение записывают
,
поэтому смешанное произведение записывают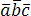 .
.
3.
Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей: 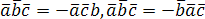 ,
,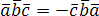 .
.
4.
Смешанное
произведение ненулевых векторов 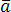 ,
,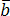 и
и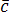 равно
нулю тогда и только тогда, когда они
компланарны:
равно
нулю тогда и только тогда, когда они
компланарны: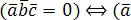 ,
, ,
,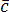 –
компланарны
–
компланарны .
.
Доказательство. Предположим, что векторы 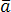 ,
,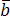 и
и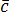 –
не компланарны. Тогда можно построить
параллелепипед имеющий объем
–
не компланарны. Тогда можно построить
параллелепипед имеющий объем ,
т.е.
,
т.е.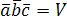 ,
но это противоречит условию, согласно
которого,
,
но это противоречит условию, согласно
которого,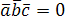 .
Следовательно, векторы
.
Следовательно, векторы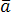 ,
,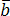 и
и –
компланарны.
–
компланарны.
Обратно,
пусть 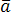 ,
, и
и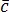 –
компланарны. Тогда вектор
–
компланарны. Тогда вектор и
перпендикулярен плоскости, в которой
находятся векторы
и
перпендикулярен плоскости, в которой
находятся векторы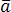 ,
,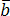 и
и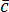 ,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
например
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
например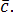 Это
значит, что
Это
значит, что
 .
.
Смешанное произведение векторов, заданных своими проекциями в декартовой системе координат.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат:
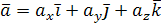 ,
, 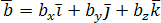 и
и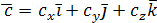 .
.
Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
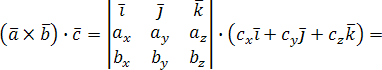
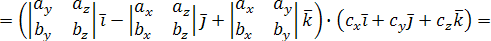
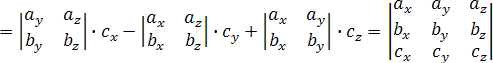 .
.
Итак,
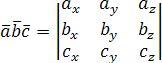 .
.
Приложения смешанного произведения:
1. Определение взаимной ориентации векторов в пространстве.
Если 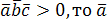 ,
,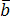 и
и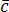 –
правая тройка, если
–
правая тройка, если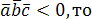 левая.
левая.
2. Установление компланарности векторов:
(
(
(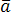 ,
, ,
,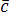 –
компланарны).
–
компланарны).
3. Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):
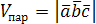 ,
, 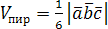 .
.
Пример.
Компланарны ли векторы 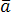 ,
, и
и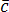 ,
если
,
если
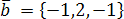
 .
.
Решение. Вычислим смешанное произведение векторов:
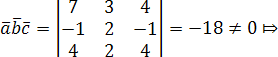 векторы
векторы 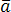 ,
, и
и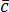 не
компланарны.
не
компланарны.
Пример.
Доказать, что векторы 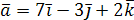 ,
,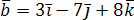 и
и компланарны.
компланарны.
Решение.
Рассмотрим матрицу, составленную из
координат векторов  ,
,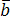 и
и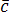
 ,
т. к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
,
т. к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
Пример.
Вычислить объем тетраэдра с вершинами
в точках 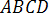 и
его высоту, опущенную из вершины
и
его высоту, опущенную из вершины на
грань
на
грань ,
если
,
если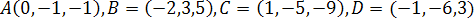
Решение. Найдем координаты векторов:
 ,
, 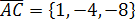 ,
,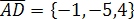 .
.
Вычислим объем:
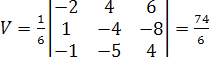 .
.
Поскольку
объем тетраэдра 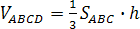 ,
то высота
,
то высота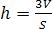 .
.
Вычислим площадь основания тетраэдра
 .
.
Итак,
высота 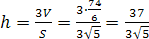 .
.
ИСПОЛЬЗОВАНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ ДЛЯ ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕКОТОРЫХ ГЕОМЕТРИЧЕСКИХ ФИГУР Исследовательская работа по математике ученика 10 Б класса МОУ СОШ №73 Перевозникова Михаила
Использование векторного произведения ВЕКТОРОВ
для вычисления площади
некоторых геометрических фигур
Исследовательская работа по математике
Ученика 10 Б класса
МОУ СОШ №73
Перевозникова Михаила
Руководители:
Ассистент каф. математического анализа механико-математического факультета СГУ им. Н.Г. Чернышевского Бердников Глеб Сергеевич
Саратов, 2015
Содержание
Введение.
1. Теоретический обзор.
1.1. Векторы и вычисления с векторами.
1.2. Использование скалярного произведения векторов в решении задач
1.3 Скалярное произведение векторов в координатах
1.4. Векторное произведение векторов в трёхмерном Евклидовом пространстве: определение понятия.
1.5. Координаты векторного произведения векторов.
2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма. Выведение формулы и геометрический смысл векторного произведения векторов.
2.2. Зная только координаты точек, найти площадь треугольника. Доказательство теоремы
2.3. Проверка на примерах правильности формулы.
2.4. Практическое использование векторной алгебры и произведения векторов.
Заключение
Введение
Как известно, многие геометрические задачи имеют два ключевых способа решения – графический и аналитический. Графический метод связан с построением графиков и чертежей, а аналитический предполагает решение задач преимущественно с помощью алгебраических действий. В последнем случае алгоритм решений задач связан с аналитической геометрией. Аналитическая геометрия – это область математики, а точнее линейной алгебры, которая рассматривает решение геометрических задач средствами алгебры на основе метода координат на плоскости и в пространстве. Аналитическая геометрия позволяет анализировать геометрические образы, исследовать линии и поверхности, важные для практических приложений. При этом в этой науке для расширения пространственного понимания фигур помимо скалярного произведения векторов иногда применяется векторное произведение векторов.
В связи с широким распространением трехмерных пространственных технологий, изучение свойств некоторых геометрических фигур с использованием векторного произведения представляется актуальным.
В связи с этим была обозначена цель данного проекта – использование векторного произведения векторов для вычисления площади некоторых геометрических фигур.
В связи с поставленной целью решались следующие задачи:
1. Теоретически изучить необходимые основы векторной алгебры и дать определение векторному произведению векторов в системе координат;
2. Проанализировать наличие связи векторного произведения с площадью треугольника и параллелограмма;
3. Вывести формулу площади треугольника и параллелограмма в координатах;
4. Проверить на конкретных примерах верность выведенной формулы.
1. Теоретический обзор.
Векторы и вычисления с векторами
Вектором называется направленный отрезок, для которого указано его начало и конец:
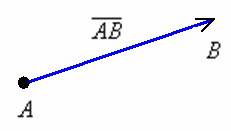
В данном случае началом отрезка является точка А, концом отрезка – точка В. Сам вектор обозначен через  или
или  . Чтобы найти координаты вектора
. Чтобы найти координаты вектора  , зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки:
 = {Bx — Ax ; By — Ay}
= {Bx — Ax ; By — Ay}
Коллинеарными называются векторы, лежащие на параллельных прямых или на одной прямой. При этом вектор отрезок, характеризующийся длиной и направлением.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
.
Длина вектора | | в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
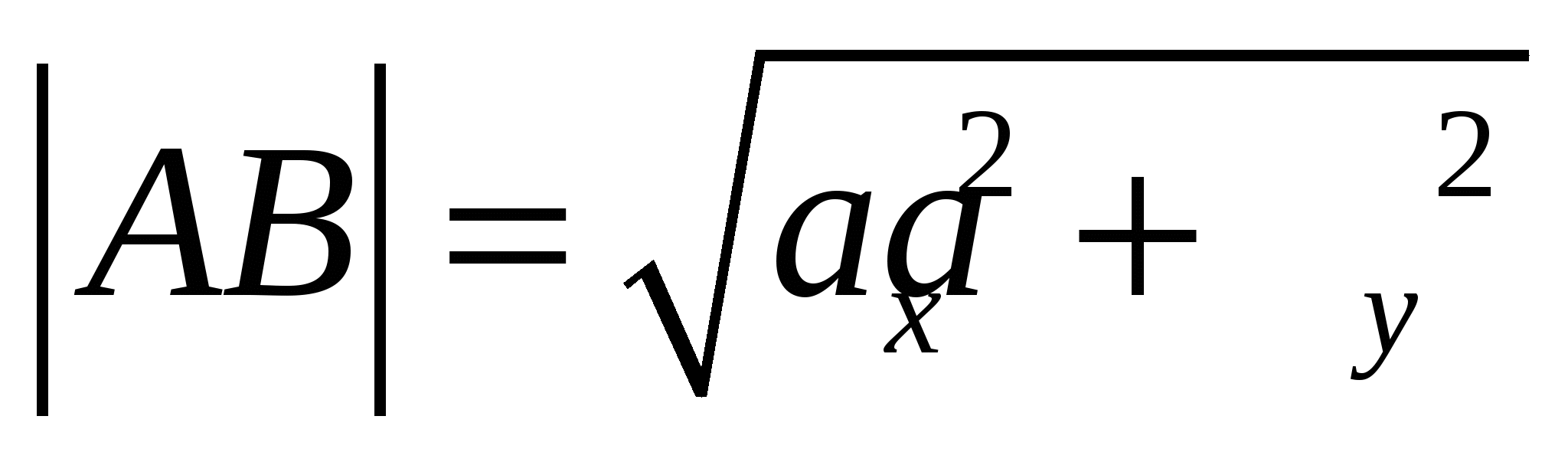
С векторами можно совершать различные действия.
Например, сложение. Чтобы их сложить, нужно провести сначала второй вектор из конца первого, а потом соединить начало первого с концом второго (рис. 1). Суммой векторов является другой вектор с новыми координатами.
Сумму векторов 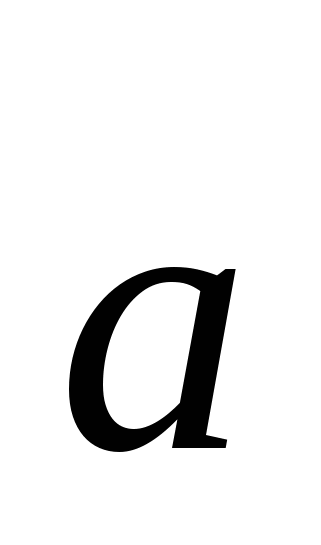 = {ax ; ay} и
= {ax ; ay} и  = {bx ; by} можно найти воспользовавшись следующей формулой:
= {bx ; by} можно найти воспользовавшись следующей формулой:
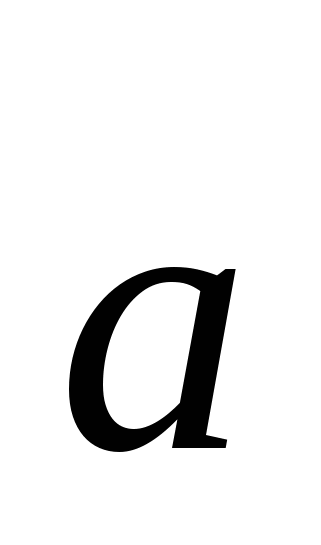 +
+  = {ax + bx; ay + by}
= {ax + bx; ay + by}
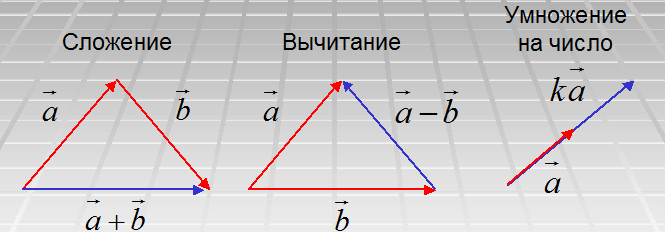
Рис. 1. Действия с векторами
Вычитая векторы, нужно сначала провести их из одной точки, а потом соединить конец второго с концом первого.
Разность векторов 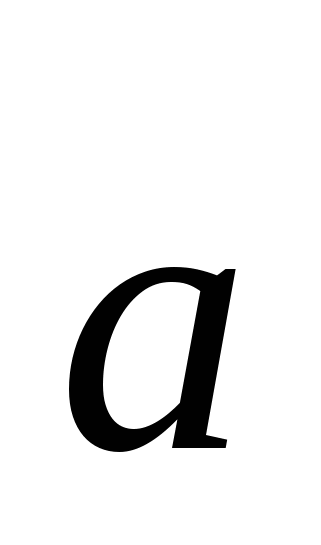 = {ax ; ay} и
= {ax ; ay} и 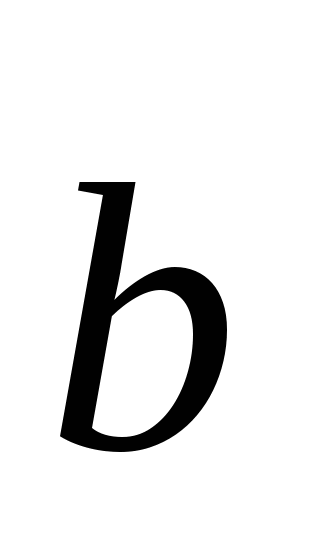 = {bx ; by} можно найти по формуле:
= {bx ; by} можно найти по формуле:

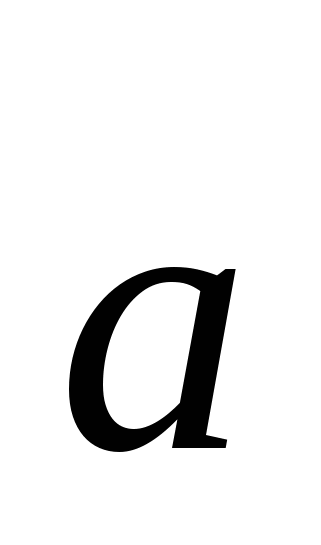 —
— 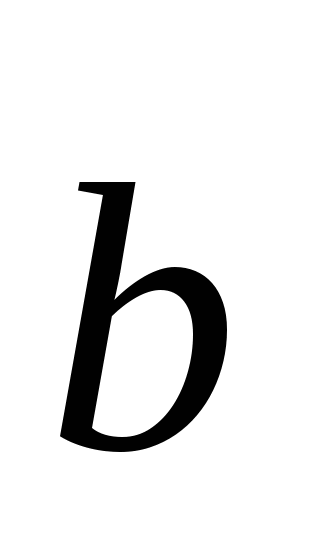 = {ax — bx; ay — by}
= {ax — bx; ay — by}
Также, векторы можно умножать на число. Результатом также будет вектор, который в k раз больше (или меньше) данного. Его направление будет зависеть от знака k: при положительном k векторы сонаправлены, а при отрицательном – противоположно направлены.
Произведение вектора 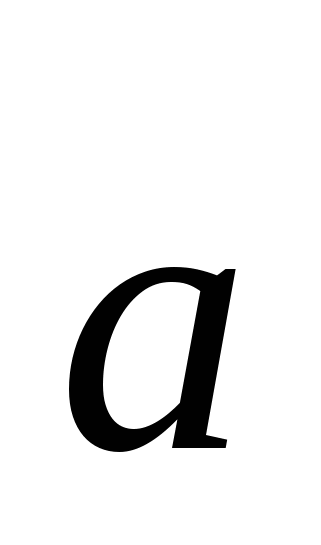 = {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
= {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
k · 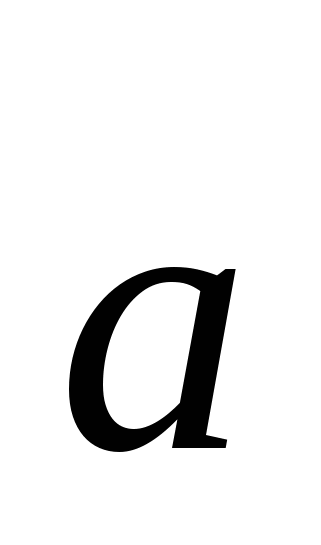 = {k · ax; k · ay}
= {k · ax; k · ay}
А можно ли умножать вектор на вектор? Конечно, и даже двумя вариантами!
Первый вариант – скалярное произведение.

Рис. 2. Скалярное произведение в координатах
Для нахождения произведения векторов можно использовать угол между данными векторами, показанный на рисунке 3.
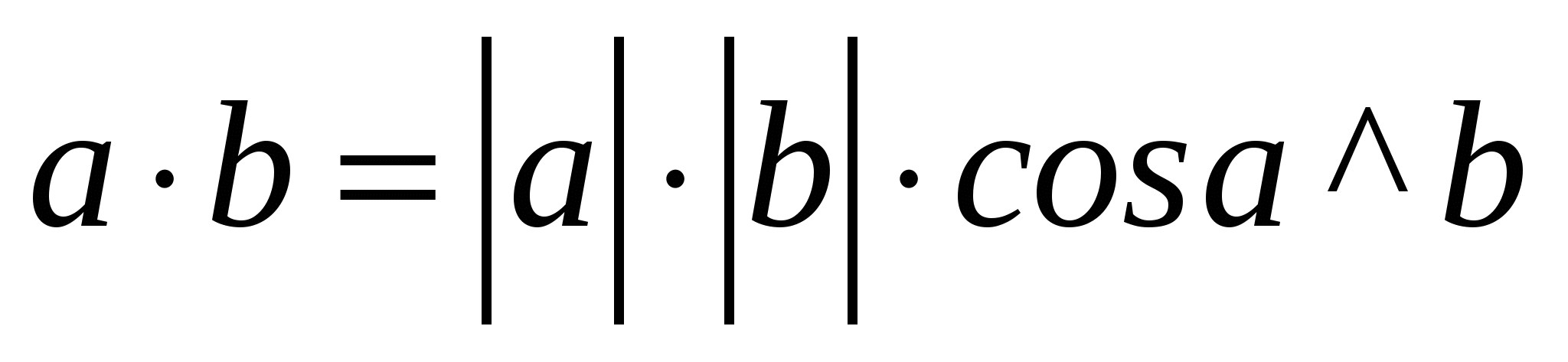
Из формулы следует, что скалярное произведение равно произведению длин данных векторов на косинус угла между ними, его результатом является число. Важно, что если векторы перпендикулярны, то их скалярное произведение равно нулю, т.к. косинус прямого угла между ними равен нулю.
В координатной плоскости вектор также имеет координаты. Вектора, их координаты и скалярное произведение являются одними из самых удобных методов вычисления угла между прямыми (или их отрезками), если введена система координат. И если координаты 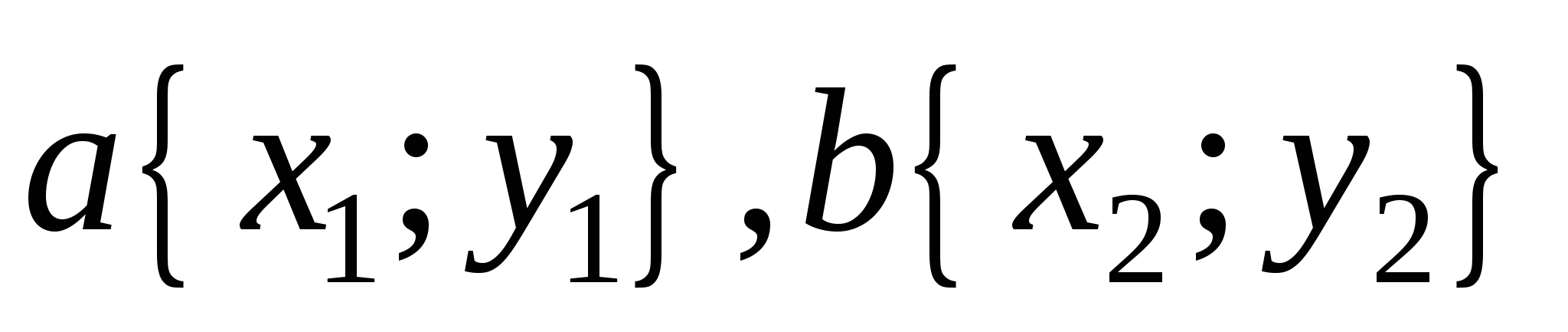 , то их скалярное произведение равно:
, то их скалярное произведение равно:
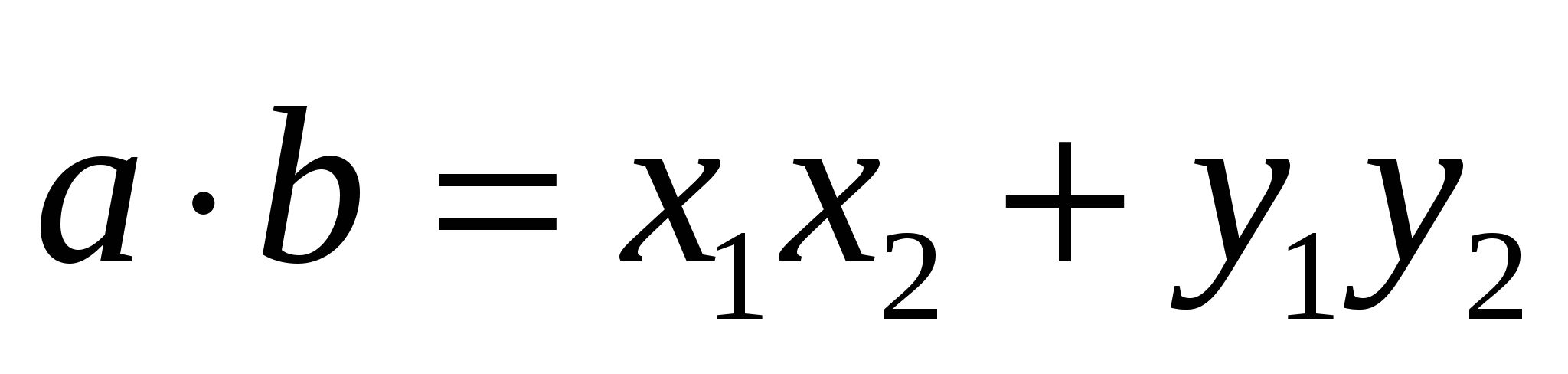
В трехмерном пространстве существует 3 оси и, соответственно, у точек и векторов в такой системе будет по 3 координаты, а скалярное произведение векторов вычисляется по формуле:
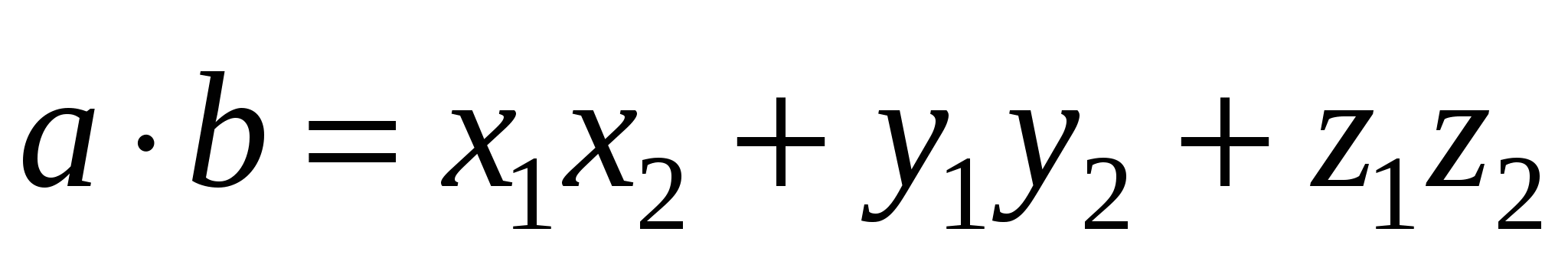 .
.
1.2. Векторное произведение векторов в трехмерном пространстве.
Вторым вариантом вычисления произведения векторов является векторное произведение. Но, чтобы его определить требуется уже не плоскость, а трехмерное пространство, в котором начало и конец вектора имеют по 3 координаты.
В отличие от скалярного произведения векторов в трёхмерном пространстве операция «векторное умножение» над векторами приводит к иному результату. Если в предыдущем случае скалярного умножения двух векторов результатом было число, то в случае векторного умножения векторов результатом будет другой вектор, перпендикулярный обоим вступившим в произведение векторам. Поэтому это произведение векторов называется векторным.
Очевидно, что при построении результирующего вектора  , перпендикулярного двум, вступившим в произведение —
, перпендикулярного двум, вступившим в произведение — 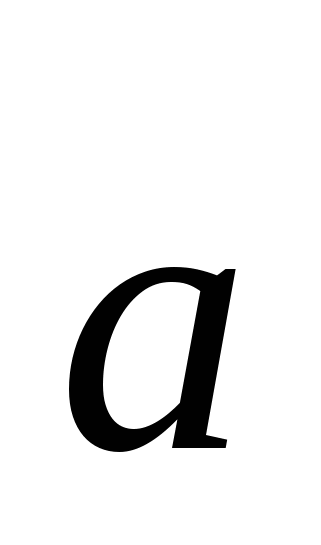 и
и 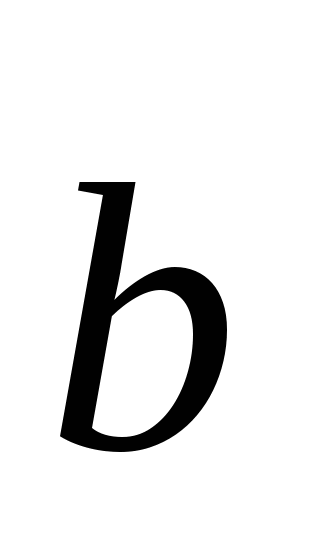 , может быть выбрано два противоположных направления. При этом направление результирующего вектора
, может быть выбрано два противоположных направления. При этом направление результирующего вектора 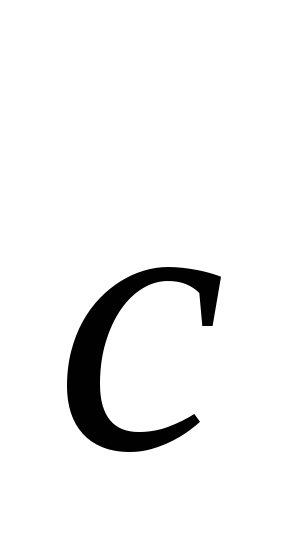 определяется по правилу правой руки, или правилу буравчика. Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
определяется по правилу правой руки, или правилу буравчика. Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, а четыре пальца правой руки показывали направление вращения (как бы охватывая вращающийся цилиндр), то оттопыренный большой палец покажет направление вектора-произведения (рис. 7).
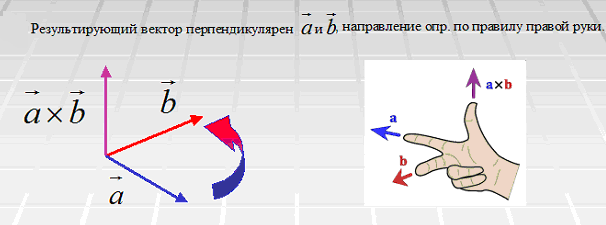
Рис. 7. Правило правой руки
1.3. Свойства векторного произведения векторов.
Длина результирующего вектора определяется по формуле
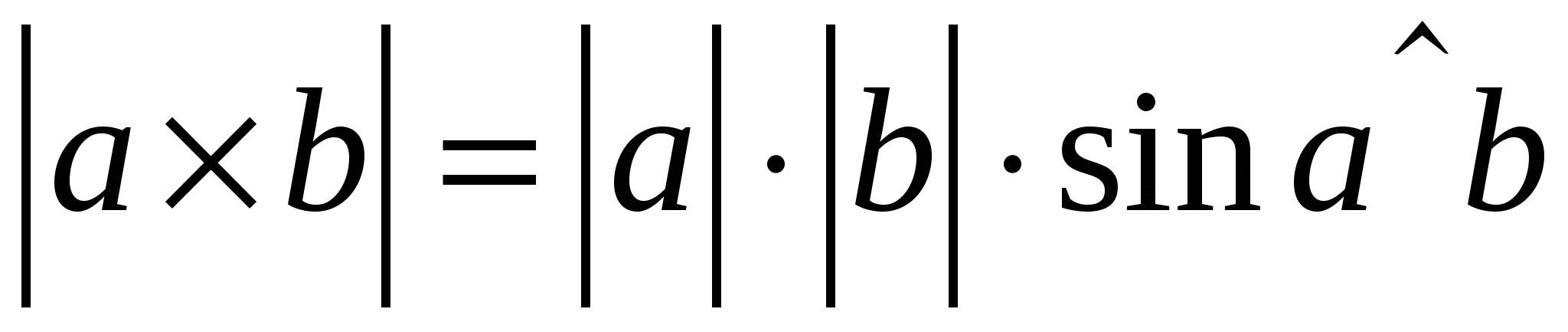 .
.
При этом 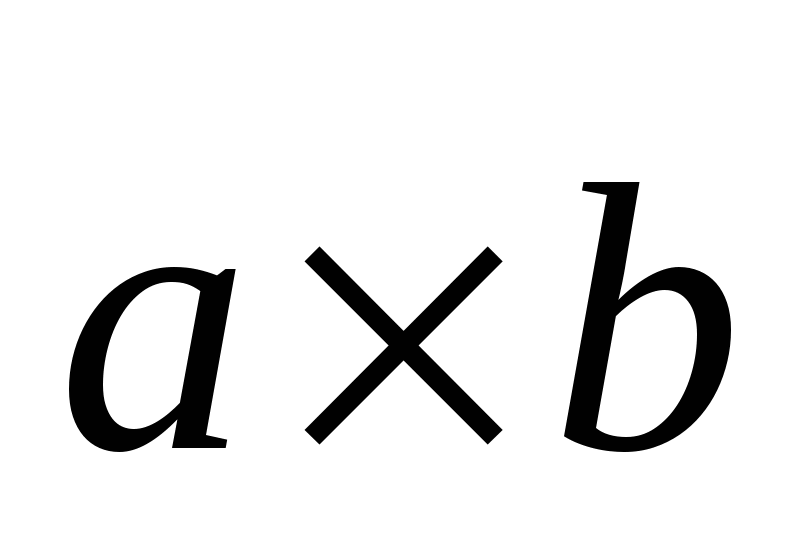 векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен
векторное произведение. Как было сказано выше, результирующий вектор будет перпендикулярен 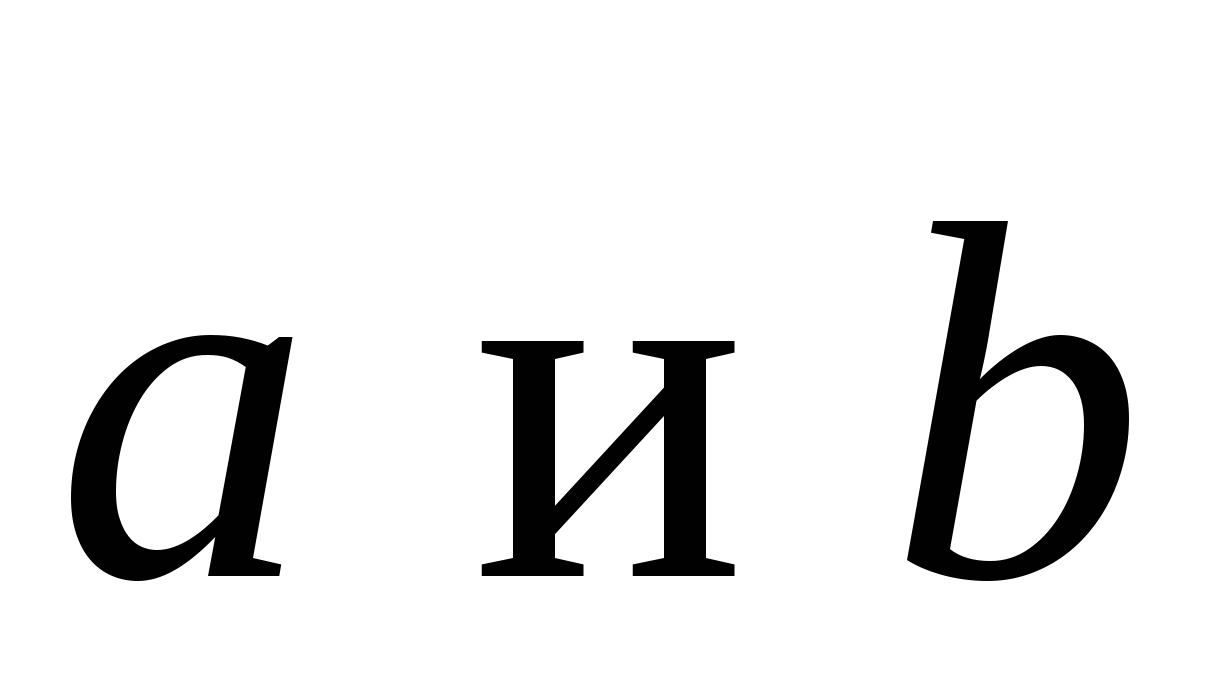 , а его направление определяется по правилу правой руки.
, а его направление определяется по правилу правой руки.
Векторное произведение зависит от порядка сомножителей, именно:
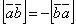 .
.
Векторное произведение ненулевых векторов равно 0, если они коллинеарны, тогда синус угла между ними будет равен 0.
Координаты векторов в трехмерном пространстве выражаются следующим образом: 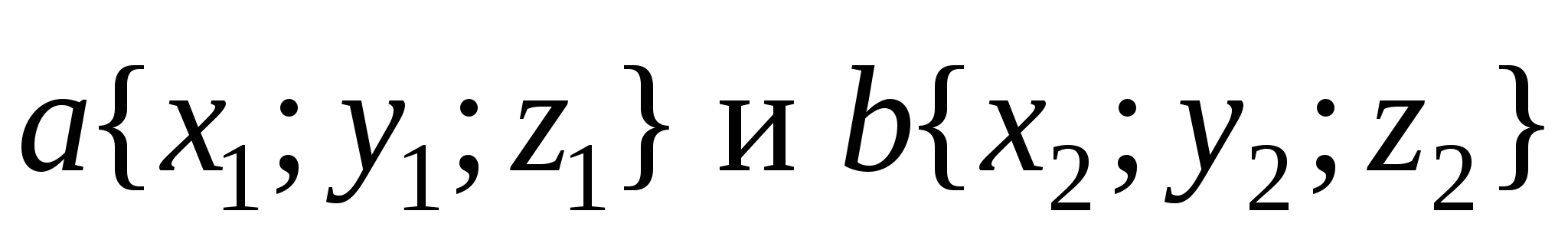 . Тогда координаты результирующего вектора находим по формуле
. Тогда координаты результирующего вектора находим по формуле
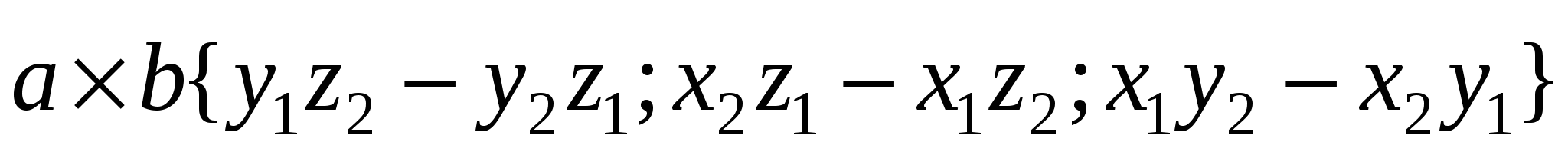 .
.
Длина результирующего вектора находится по формуле:
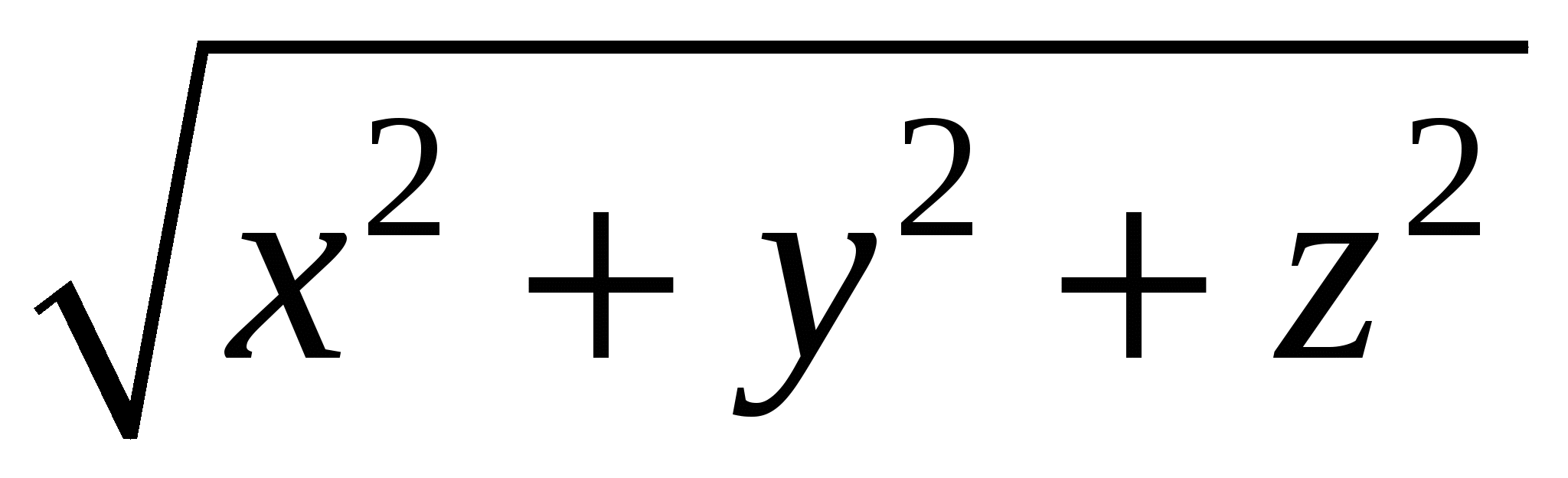 .
.


2. Практическая часть.
2.1. Связь векторного произведения с площадью треугольника и параллелограмма в плоскости. Геометрический смысл векторного произведения векторов.
Пусть нам дан треугольник ABC (рис. 8). Известно, что 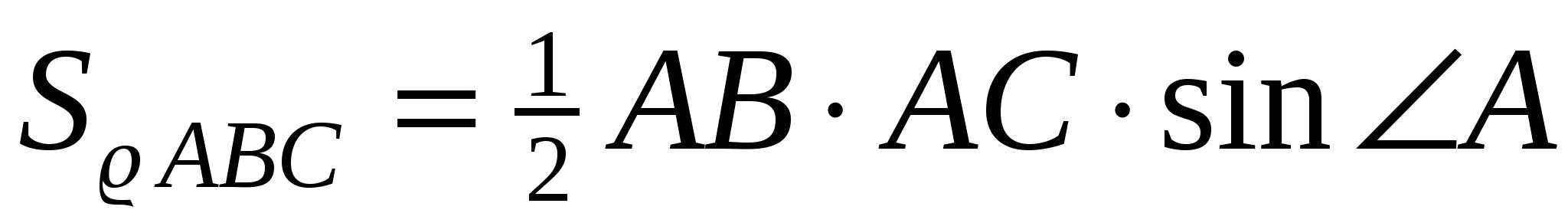 .
.
Если представить стороны треугольника АВ и АС в виде двух векторов, то в формуле площади треугольника мы находим выражение векторного произведения векторов:
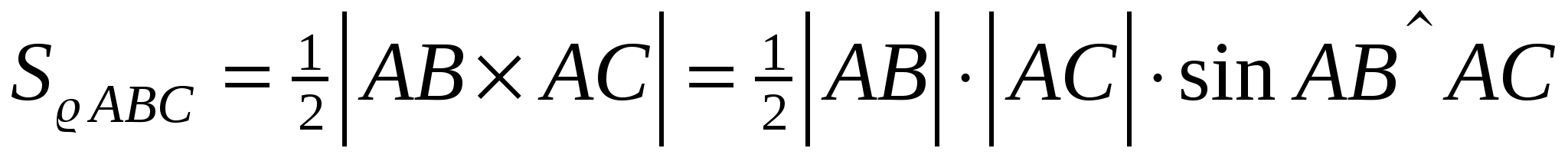
Из выше сказанного можно определить геометрический смысл векторного произведения (рис. 9):
длина векторного произведения векторов равна удвоенной площади треугольника, имеющего сторонами векторы 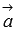 и
и 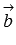 , если их отложить от одной точки.
, если их отложить от одной точки.
Другими словами, длина векторного произведения векторов 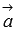 и
и 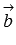 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах 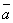 и
и  , со сторонами
, со сторонами  и
и 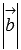 и углом между ними, равным
и углом между ними, равным  .
.
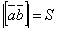 .
.
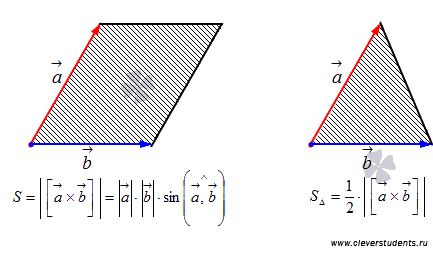
Рис. 9. Геометрический смысл векторного произведения векторов
В связи с этим, можно привести еще одно определение векторного произведения векторов:
Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 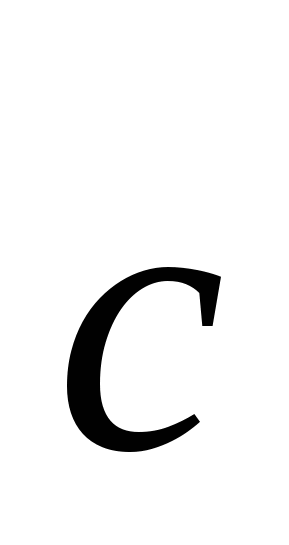 , длина которого численно равна площади параллелограмма построенного на векторах
, длина которого численно равна площади параллелограмма построенного на векторах 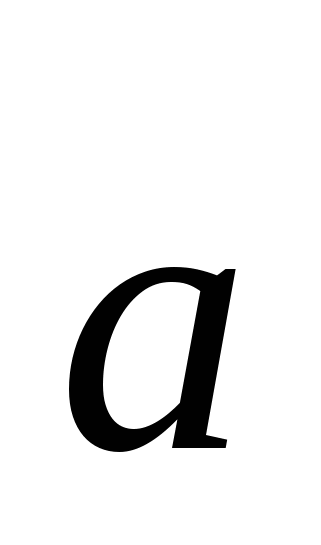 и
и  , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от
, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от 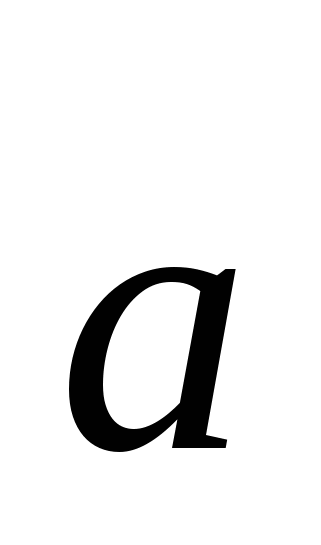 к
к 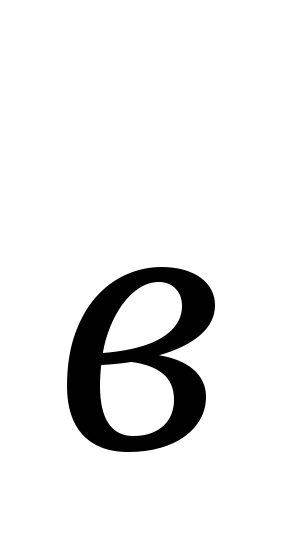 вокруг вектора
вокруг вектора 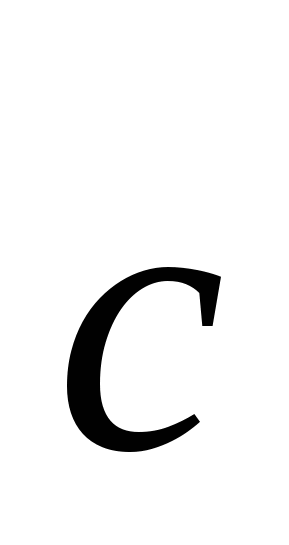 осуществлялось против часовой стрелки, если смотреть с конца вектора
осуществлялось против часовой стрелки, если смотреть с конца вектора 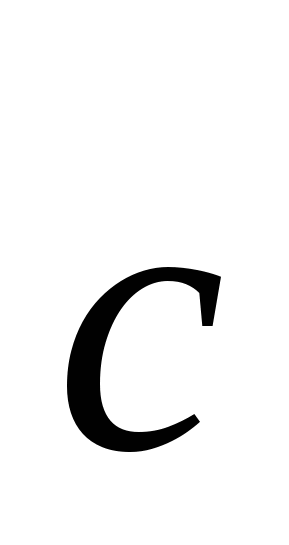 (рис. 10).
(рис. 10).
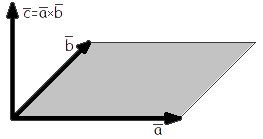
Рис. 10. Определение векторного произведения векторов
с использованием параллелограмма
2.2. Вывод формулы для нахождения площади треугольника в координатах.
Итак, нам дан треугольник АВС в плоскости и координаты его вершин. Найдем площадь этого треугольника (рис. 11).

Рис. 11. Пример решения задачи на нахождение площади треугольника по координатам его вершин
Решение.
Для начала, рассмотрим координаты вершин в пространстве и вычислим координаты векторов АВ и АС.
По данной прежде формуле подсчитаем координаты их векторного произведения. Длина этого вектора равна 2 площадям треугольника АВС. Площадь треугольника равна 10.
Более того, если мы рассмотрим треугольник на плоскости, то первые 2 координаты векторного произведения всегда будут равны нулю, поэтому мы можем сформулировать следующую теорему.
Теорема: Пусть дан треугольник АВС и координаты его вершин 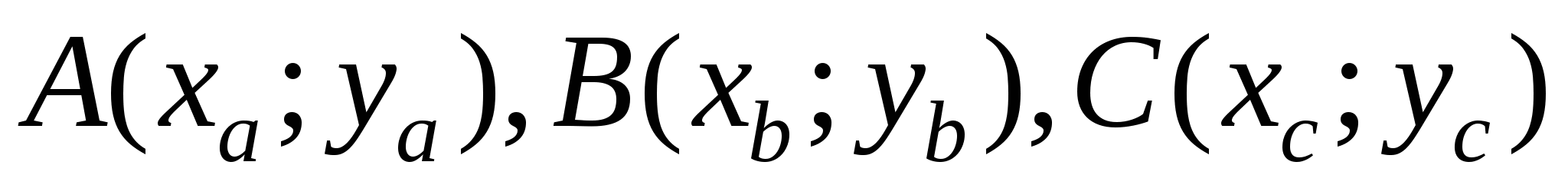 (рис. 12).
(рис. 12).
Тогда 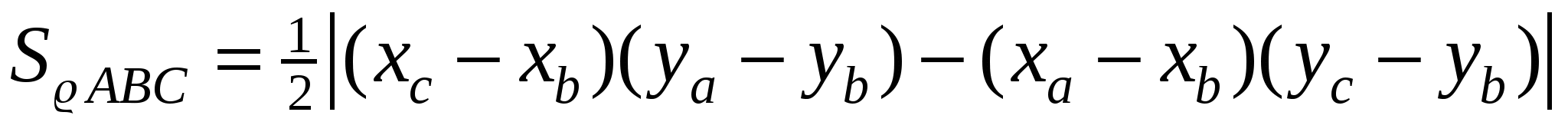 .
.
 Рис. 12. Доказательство теоремы
Рис. 12. Доказательство теоремы
Доказательство.
Рассмотрим точки в пространстве и вычислим координаты векторов ВС и ВА. 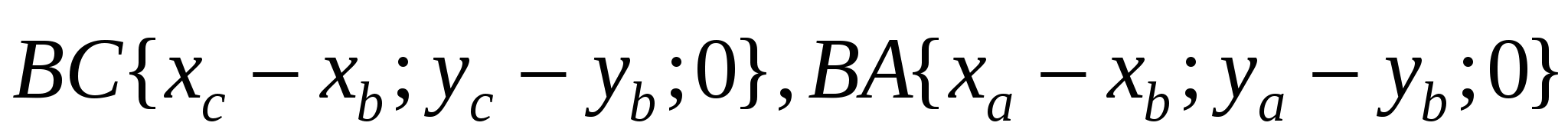 . По приведенной раньше формуле вычислим координаты векторного произведения этих векторов. Обратим внимание, что все члены, содержащие z1 или z2, равны 0, т.к. z1и z2 = 0. УБРАТЬ!!!
. По приведенной раньше формуле вычислим координаты векторного произведения этих векторов. Обратим внимание, что все члены, содержащие z1 или z2, равны 0, т.к. z1и z2 = 0. УБРАТЬ!!!
Итак, следовательно,
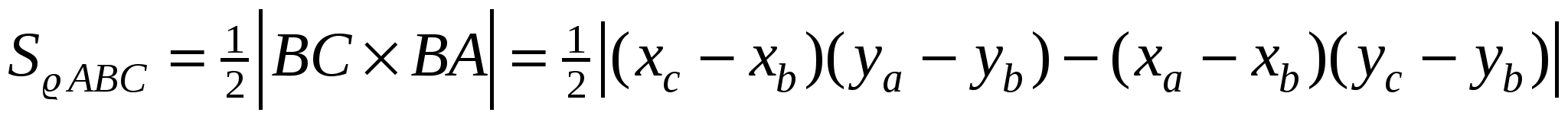
2.3. Проверка правильности формулы на примерах
Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
a × b=
i
j
k
=
-1
2
-2
2
1
-1
= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
1
|a × b| =
1
√02 + 52 + 52 =
1
√25 + 25 =
1
√50 =
5√2
2
2
2
2
2
Ответ: SΔ = 2.5√2.
Заключение
2.4. Приложения векторной алгебры
и скалярного и векторного произведения векторов.
Где же нужны векторы? Векторное пространство и векторы носят не только теоретический характер, но и имеют вполне реальное практическое применение в современном мире.
В механике и физике многие величины имеют не только численное значение, но и направление. Такие величины называются векторными. Вместе с использованием элементарных механических понятий, опираясь на их физический смысл, многие величины рассматриваются как скользящие векторы, а их свойства описываются как аксиомами, как это принято в теоретической механике, так и при помощи математических свойств векторов. Наиболее яркими примерами векторных величин являются скорость, импульс и сила (рис. 12). Например, момент импульса и сила Лоренца математически записываются с помощью векторов.
В физике важны не только сами вектора, но в большой степени важны и их произведения, которые помогают вычислять некоторые величины. Векторное произведение полезно для определения коллинеарности векторов модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы сонаправленны или противоположно направленны.
Еще один пример: скалярное произведение используется для вычисления работы по приведенной ниже формуле, где F – вектор силы, а s – вектор перемещения.
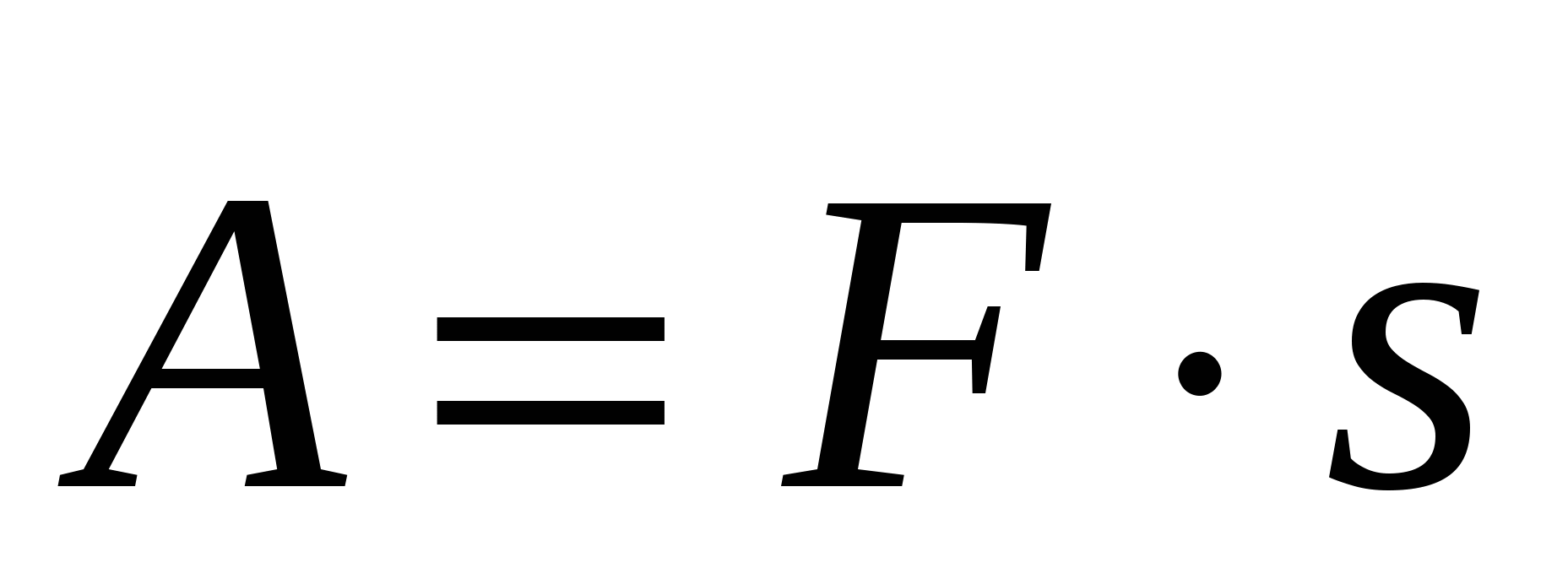
Одним из примеров использования произведения векторов является момент силы, равный произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
Многое из того, что вычисляется в физике по правилу правой руки является векторным произведением. Найти подтверждения, привести примеры.
Стоит еще заметить, что двухмерным и трехмерным пространством не исчерпываются возможные варианты векторных пространств. Высшая математика рассматривает пространства большей размерности, в которых также определяются аналоги формул для скалярного и векторного произведения. Несмотря на то, что пространства большей размерности, чем 3, человеческое сознание неспособно представить визуально, они удивительным образом находят себе приложения во многих областях науки и промышленности.
В то же время результатом векторного произведения векторов в трёхмерном Евклидовом пространстве является не число, а результирующий вектор со своими координатами, направлением и длиной.
Направление результирующего вектора определяется по правилу правой руки, что является одним из самых удивительных положений аналитической геометрии.
Векторное произведение векторов может быть использовано в нахождении площади треугольника или параллелограмма по заданным координатам вершин, что было подтверждено выведением формулы, доказательством теоремы и решением практических задач.
Векторы широко используются в физике, где такие показатели как скорость, импульс и сила могут быть представлены в виде векторных величин и вычисляются геометрически.
Список использованных источников
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 7-9 классы: учебник для общеобразовательных организаций. М.: Просвещение, 2013. 383 с.
Атанасян Л.С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10-11 классы: учебник для общеобразовательных организаций: базовый и профильный уровни. М.: Просвещение, 2013. 255 с.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
????Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, Физматлит, 1998.
Аналитическая геометрия.
http://a-geometry.narod.ru/problems/problems_32.htm
Математика. Клевер.
http://www.cleverstudents.ru/vectors/vector_product_of_vectors.html
——Изучение математики онлайн.
http://ru.onlinemschool.com/math/library/vector/multiply1/
Сайт В. Глазнева.
http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm
——Википедия.
https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5
Скалярные и векторные поля. Изображение полей. Примеры скалярных и векторных полей
До сих пор мы рассматривали отдельные векторы или скаляры. Рассмотрим более сложный случай, когда с каждой точкой пространства связывается значение некоторого скаляра или вектора. Рассматриваемая часть пространства называется тогда полем, скалярным или векторным.
Так, например, в атмосфере мы имеем скалярное поле давления, т.к. каждой точке атмосферы отвечает некоторое значение давления. В реке мы имеем векторное поле скорости; вокруг передающей радиоантенны – векторное электромагнитное поле.
Аналитически задание скалярной функции 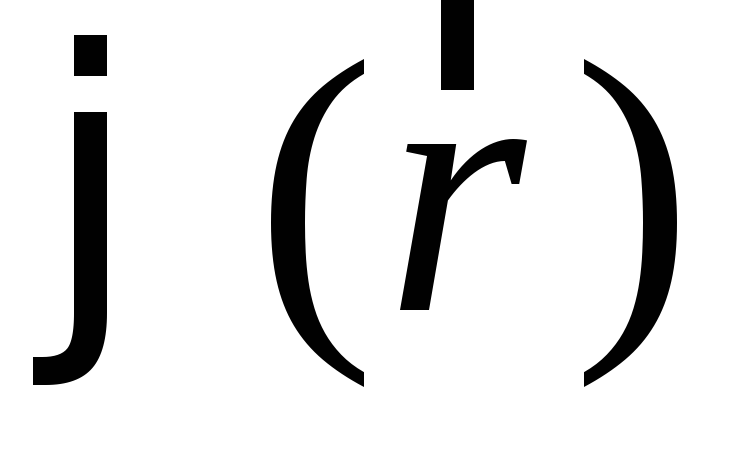 сводится к заданию функции
сводится к заданию функции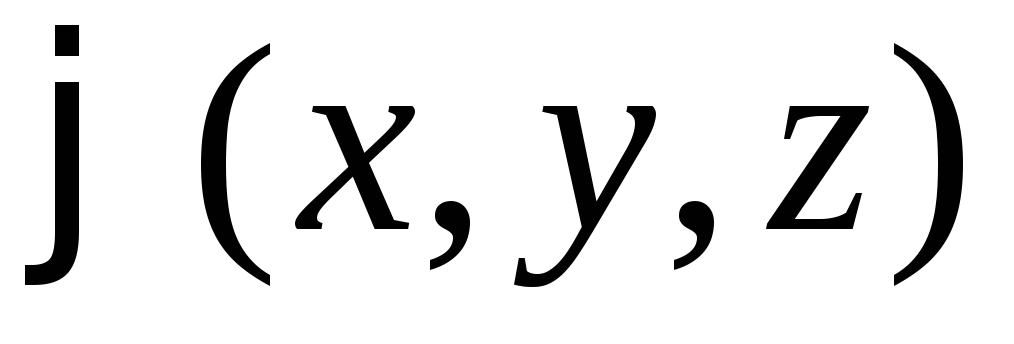 от
трех координат точки, задание векторной
функции
от
трех координат точки, задание векторной
функции равносильно заданию трех скалярных
функций
равносильно заданию трех скалярных
функций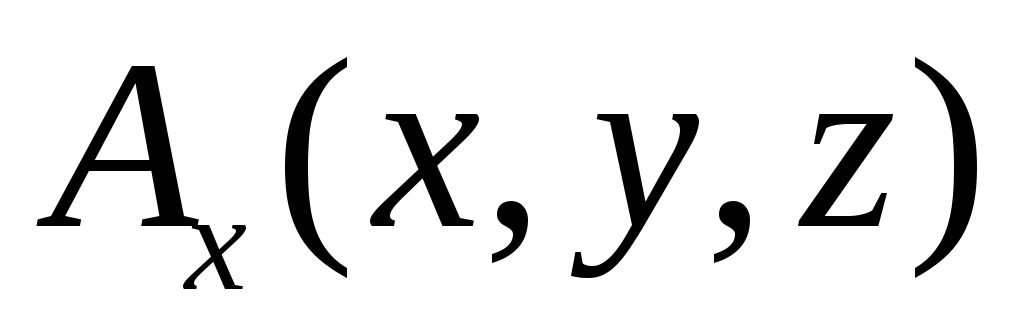 ,
, ,
,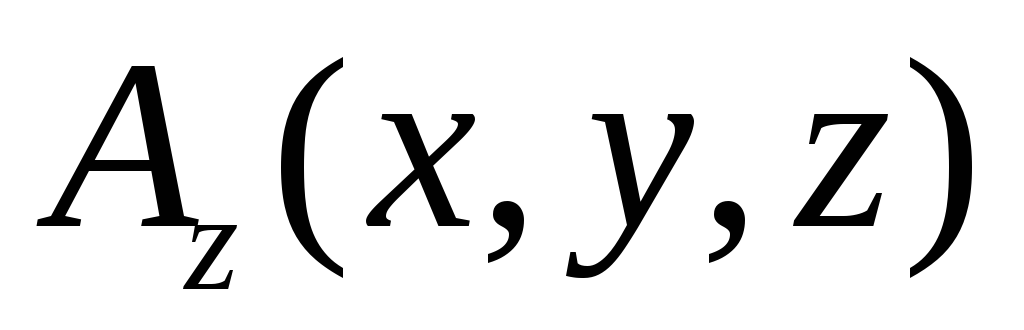 ,
дающих компоненты вектора
,
дающих компоненты вектора .
.
Очень часто приходится рассматривать
скалярные или векторные функции,
изменяющиеся с течением времени:  ,
, .
Соответствующие им поля называются
тогда переменными или нестационарными.
.
Соответствующие им поля называются
тогда переменными или нестационарными.
Для наглядности большое значение имеет
графическое представление полей. Проще
всего обстоит дело с двумерными скалярными
полями: они изображаются в виде карт,
контурных диаграмм, поверхностей и т.п.
Примеры таких изображений приведены
на рисунке Рисунок 6 ; следует иметь в
виду, что здесь изображено «плоское»
скалярное поле двух координат 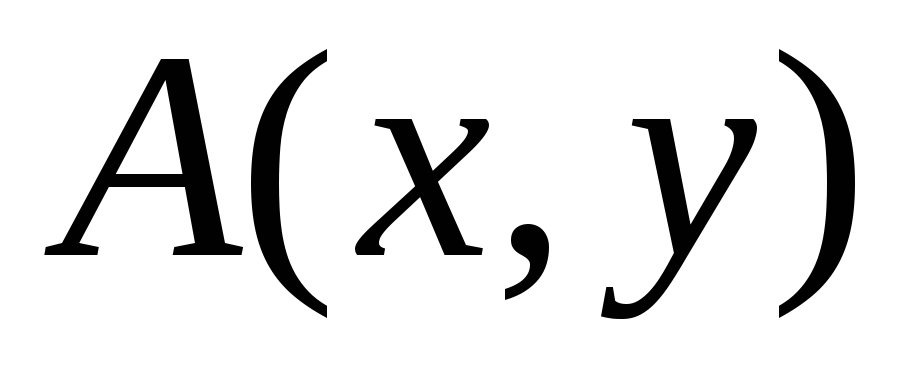 ,
для поля трех координат приходится
строить семейство поверхностей или
карт.
,
для поля трех координат приходится
строить семейство поверхностей или
карт.


карта контурная диаграмма
цветная поверхность сетчатая поверхность
−Изображение скалярных полей
Рассмотрим теперь векторное поле. Наиболее просто нанести на поле равномерную сетку и в каждом узле сетки изобразить вектор обычным образом, т.е. в виде направленного отрезка (рисунок ).

− Изображение векторного поля векторами на сетке
Однако для более наглядного изображения векторного поля удобно использовать векторные линии, предложенные Фарадеем, т.е., такие линии, во всякой точке которых вектор будет иметь направление касательное к линии (рисунок Рисунок 8 ).

−Построение векторных линий
Приближенно мы можем построить эти линии следующим образом. Выберем какую-нибудь точку поля и отложим вдоль отвечающего этой точке вектора отрезок малой длины. В конце этого отрезка поступим аналогично, и будем продолжать так дальше. В результате будет получена ломаная линия, которая тем ближе будет представлять нашу векторную линию, чем короче отрезки берутся.
Однако задание векторных линий и их ориентировка дает нам только направление вектора во всякой точке поля, величину же вектора мы должны графически изобразить каким-либо другим способом. Обычно величина вектора характеризуется густотой проводимых линий, как показано на рисунке Рисунок 9 .

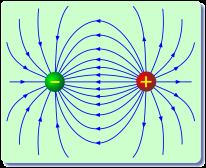
−Векторные линии
Лекция 2. Используемые понятия и законы векторного анализа. Заряды и токи. Векторы электромагнитного поля.
Циркуляция вектора и поток вектора через поверхность
Пусть нам задано векторное поле вектора  ;
возьмем какую-нибудь кривую,
соединяющую две точки
;
возьмем какую-нибудь кривую,
соединяющую две точки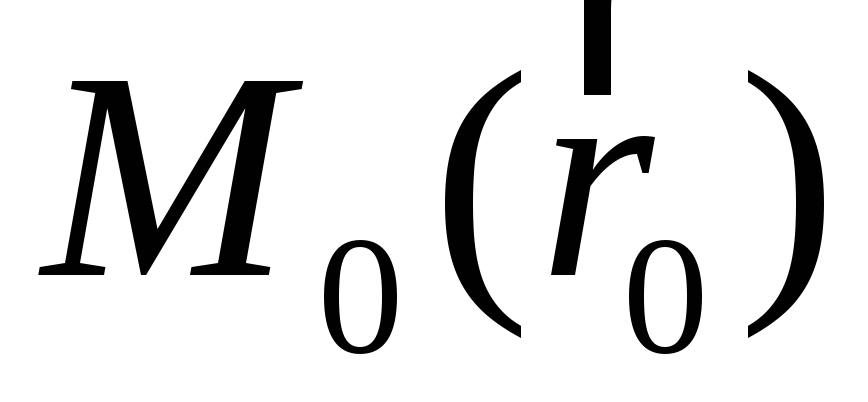 и
и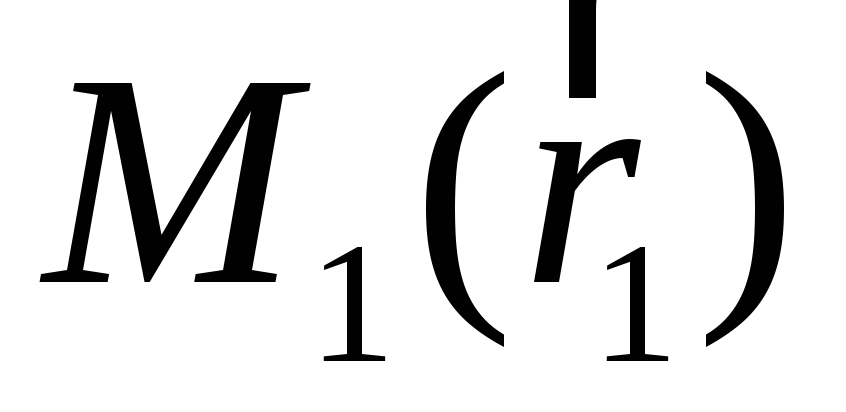 ,
разобьем ее на бесконечно малые элементы,
которые заменим хордами
,
разобьем ее на бесконечно малые элементы,
которые заменим хордами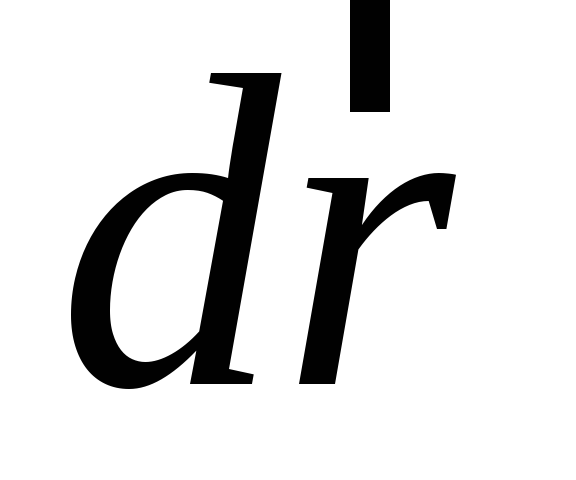 ,
составим далее скалярные произведения
,
составим далее скалярные произведения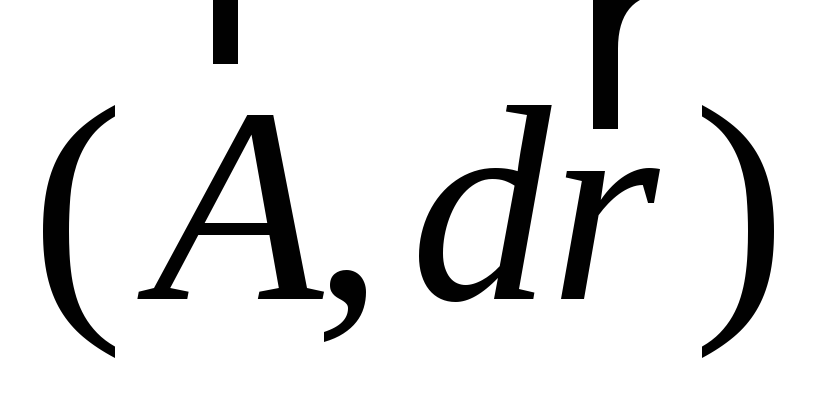 ,
где
,
где есть вектор поля, отвечающий началу
вектора
есть вектор поля, отвечающий началу
вектора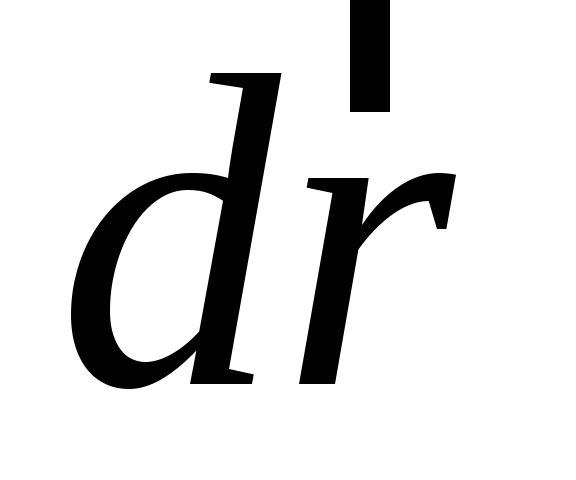 .
Составим далее сумму всех таких скалярных
произведений и перейдем к пределу,
устремив все элементы
.
Составим далее сумму всех таких скалярных
произведений и перейдем к пределу,
устремив все элементы к нулю. Полученный предел называется
линейным интегралом вектора
к нулю. Полученный предел называется
линейным интегралом вектора вдоль кривой
вдоль кривой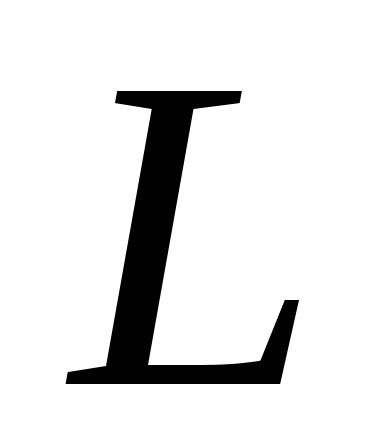 и обозначается через
и обозначается через
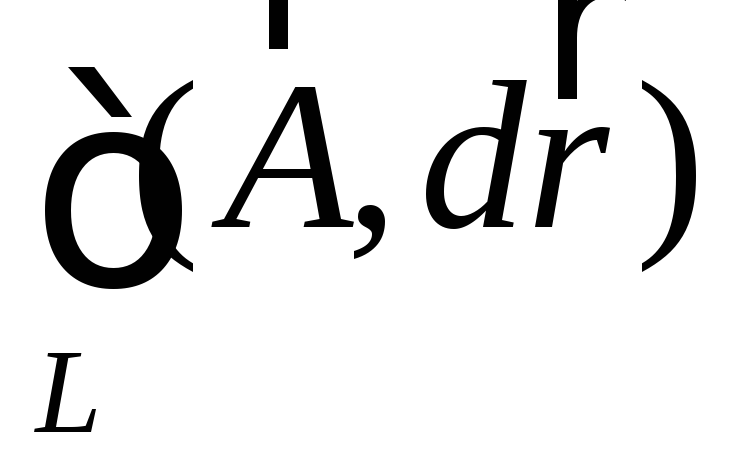

− К определению линейного интеграла вектора
Линейный интеграл вычисляется через
интегрирование проекций вектора  на оси координат:
на оси координат:
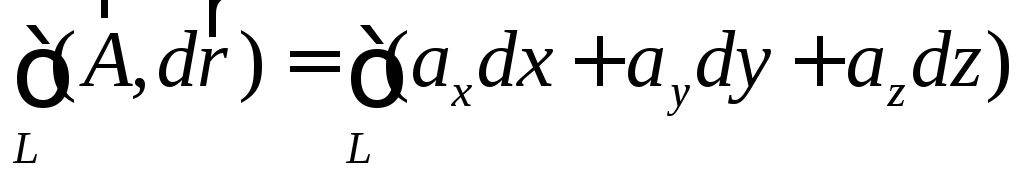
Если кривая  замкнута, то линейный интеграл вектора
называется циркуляцией вектора по этой
кривой. К знаку интеграла в этом случае
добавляется кружок:
замкнута, то линейный интеграл вектора
называется циркуляцией вектора по этой
кривой. К знаку интеграла в этом случае
добавляется кружок: .
.
С помощью векторов можно изображать не
только направленные отрезки, но и
направленные площади. Для этого вернемся
к определению векторного произведения:
там нам тоже встретилась площадь в виде
параллелограмма, построенного на
векторах  и
и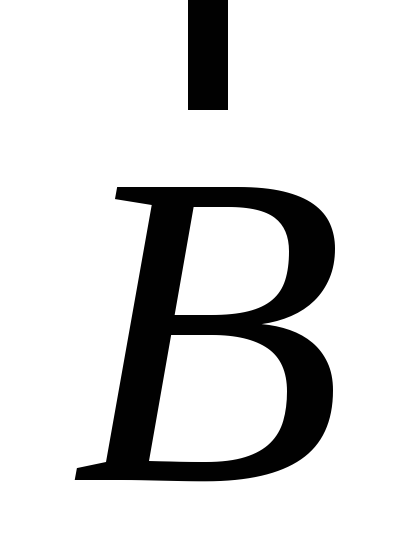 ,
причем был важен порядок, в котором
следовали вектора. Откладывая сначала
вектор
,
причем был важен порядок, в котором
следовали вектора. Откладывая сначала
вектор ,
а затем
,
а затем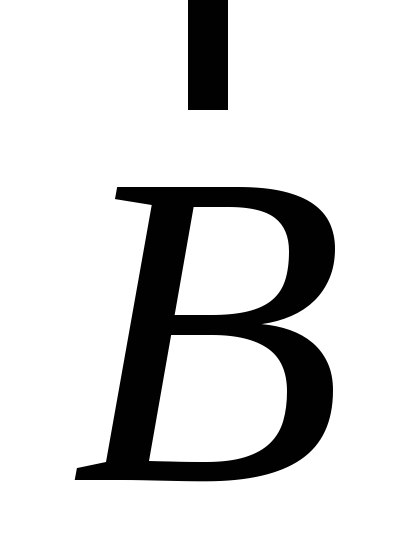 ,
получим определенное направление
контура параллелограмма.
,
получим определенное направление
контура параллелограмма.
Представление площадей векторами
необходимо для введения понятия потока
вектора через поверхность. Поток вектора через поверхность является поверхностным
интегралом вектора
через поверхность является поверхностным
интегралом вектора по поверхности
по поверхности .
Определим его следующим образом. В
каждой точке поверхности проведем
единичный вектор нормали
.
Определим его следующим образом. В
каждой точке поверхности проведем
единичный вектор нормали .
Если
.
Если − значение вектора в некоторой точкеMповерхностиS,
то проекция
− значение вектора в некоторой точкеMповерхностиS,
то проекция на единичный
на единичный определяется через скалярное произведение
(рисунок Рисунок 11 ):
определяется через скалярное произведение
(рисунок Рисунок 11 ):
 .
.
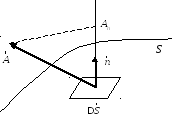
−К определению потока вектора через поверхность
Разделим теперь поверхность Sна большое число малых элементов, каждый
из них изображается, как мы определили
выше, вектором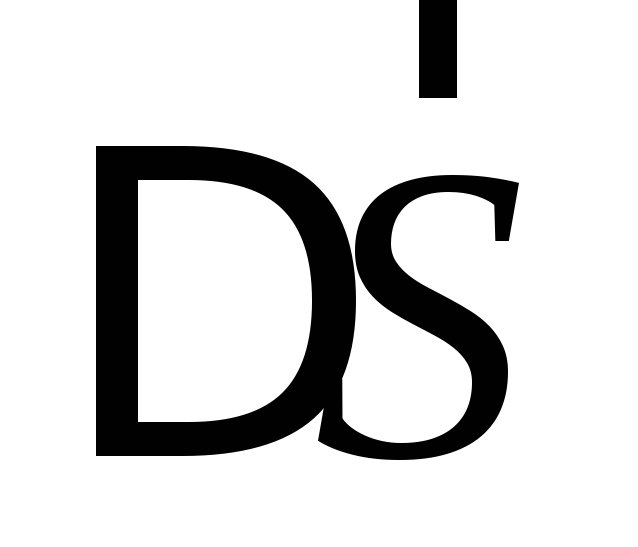 .
Размерность будет выражаться в единицах
измерения площади – м2.Например, если мы впишем в поверхностьSмногогранную
поверхность, то каждая ее грань будет
изображаться вектором, направленным
по нормали к этой грани и равным по
величине площади грани. Составим для
каждого элемента скалярное произведение
.
Размерность будет выражаться в единицах
измерения площади – м2.Например, если мы впишем в поверхностьSмногогранную
поверхность, то каждая ее грань будет
изображаться вектором, направленным
по нормали к этой грани и равным по
величине площади грани. Составим для
каждого элемента скалярное произведение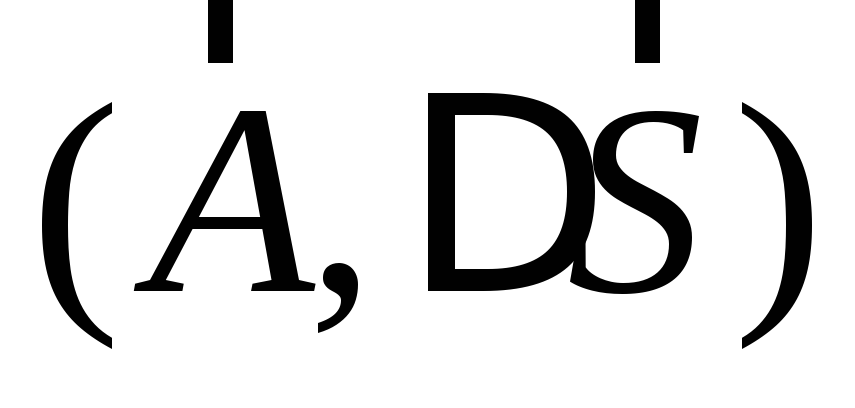 и образуем сумму
и образуем сумму ,
распространенную по всем элементам
поверхности. Эта сумма стремится к
пределу, когда все элементы поверхности
стремятся к нулю. Получаемый предел
обозначается как
,
распространенную по всем элементам
поверхности. Эта сумма стремится к
пределу, когда все элементы поверхности
стремятся к нулю. Получаемый предел
обозначается как
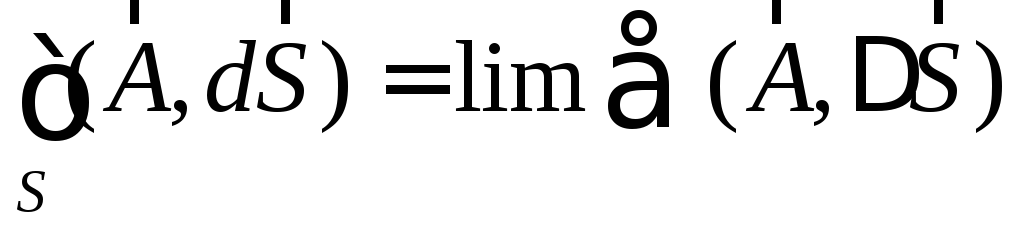 ,
,
и называется поверхностным интегралом
вектора по поверхностиSили
потоком вектора
по поверхностиSили
потоком вектора через поверхностьS.
Вычисление потока выполняется следующим
образом:
через поверхностьS.
Вычисление потока выполняется следующим
образом:
 .
.
Поток вектора положителен, если силовые
линии выходят из поверхности Sнаружу, и отрицателен, если они входят
внутрь – потому что угол между и
и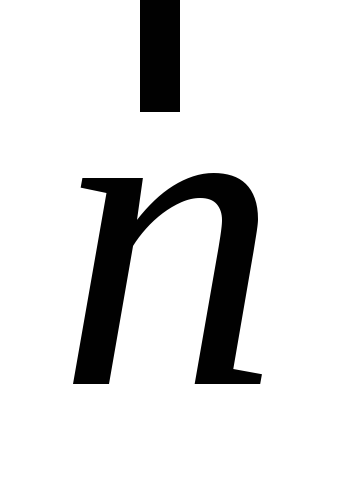 в первом случае острый, и косинус больше
нуля, а во втором – тупой.
в первом случае острый, и косинус больше
нуля, а во втором – тупой.
Если поверхность 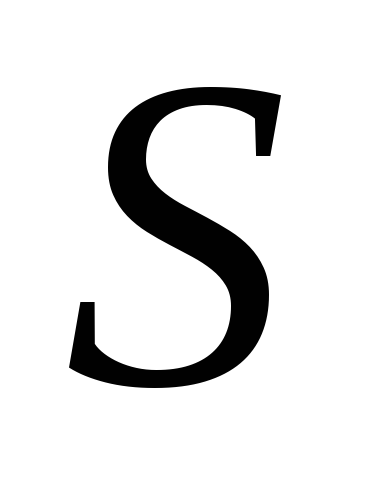 замкнутая, то к знаку интеграла добавляется
кружок:
замкнутая, то к знаку интеграла добавляется
кружок:
Понятие потока вектора появилось в
гидродинамике, которая развилась раньше
теории электричества. Если через 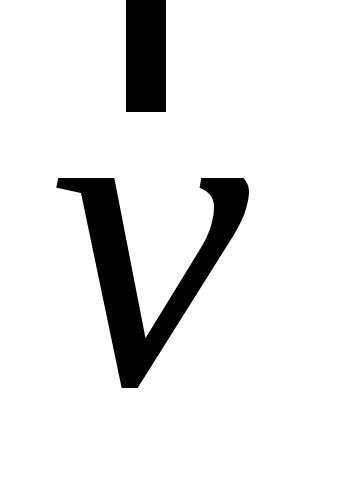 обозначить вектор скорости течения
жидкости, то выражение
обозначить вектор скорости течения
жидкости, то выражение
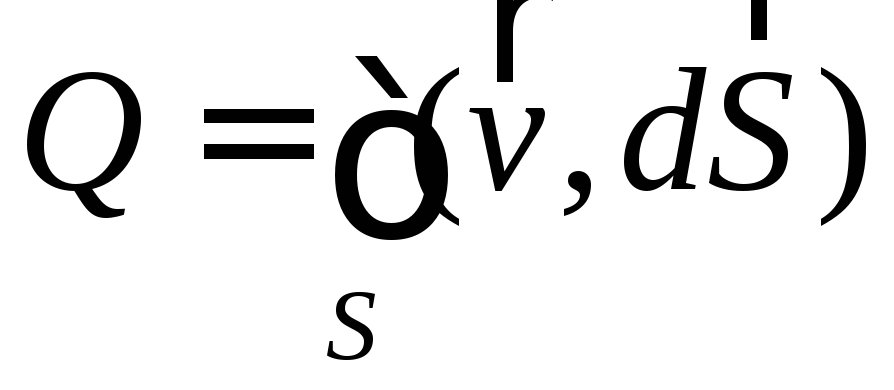
будет представлять собой количество жидкости, проходящее через эту поверхность в единицу времени, т.е., действительно поток. Следует отметить, что в применении к векторам электромагнитного поля слово «поток» имеет только математическое значение, подчеркивающее сходство формул, но никак не сходство физических явлений.
Скалярное поле — Википедия
Если каждой точке M{\displaystyle M} заданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое (обычно — действительное) число u{\displaystyle u}, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rn{\displaystyle \mathbb {R} ^{n}} в R{\displaystyle \mathbb {R} } (скалярная функция точки пространства).
Чаще других в приложениях встречаются:
- Функция трёх переменных: u=u(r)=u(x,y,z){\displaystyle u=u(\mathbf {r} )=u(x,y,z)} (скалярное поле на (в) трёхмерном пространстве, называемое иногда[1] пространственным полем).
- Функция двух переменных: u=u(r)=u(x,y){\displaystyle u=u(\mathbf {r} )=u(x,y)} (скалярное поле на (в) двумерном пространстве, называемое иногда[1] плоским полем).
Обычно от скалярной функции требуется непрерывность или дифференцируемость достаточное количество раз (то есть, функция должна принадлежать Cm{\displaystyle \mathbb {C} ^{m}}).
Примеры скалярных полей на трёхмерном пространстве:
Примеры плоских (двумерных) скалярных полей:
- глубина моря, отмеченная каким-либо образом на плоской карте;
- плотность заряда на плоской поверхности проводника.
Обычно под скалярным полем понимается поле, инвариантное при преобразованиях координат (иногда, и нередко — при определенном классе преобразований координат, например, при преобразованиях, сохраняющих объем, ортогональных преобразованиях и т. п.; но не менее редко имеется в виду инвариантность скалярного поля при произвольных преобразованиях координат, ограниченных, быть может, только гладкостью). (См. скаляр).
В этом смысле далеко не каждая вещественнозначная функция координат является скалярным полем. Простейший пример: в этом смысле не является скалярным полем одна из координатных компонент векторного поля, так как при изменении выбора координат (например, при повороте координатных осей) она не останется неизменной (то есть, не является инвариантом преобразований координат).
В физике и многих других приложениях поле, вообще говоря, зависит также от времени[2]:
- u=u(x,y,z,t){\displaystyle u=u(x,y,z,t)},
при этом операции над полем (такие, как градиент) используются по-прежнему 3-мерные, то есть, несмотря на добавление еще одной независимой переменной, по существу при этом поле рассматривается как поле в пространстве размерности 3, а не 4. Те же соображения касаются случаев, когда поле зависит, кроме пространственных координат, ещё от каких-то других параметров: эти параметры могут быть явно указаны в функциональной зависимости, что, однако, не меняет размерности основного пространства, в котором рассматривается поле.
В современной теоретической физике принято явным образом рассматривать время как координату, формально равноправную трем пространственным[3], а совокупность пространства и времени рассматривается явно как единое четырёхмерное пространство (называемое пространством-временем). Таким образом, говоря о скалярном поле в современной теоретической физике, по умолчанию подразумевают поле на четырёхмерном пространстве или многообразии, т. е. функцию, зависимую от четырёх формально равноправных координат:
- u=u(xi)=u(x0,x1,x2,x3){\displaystyle u=u(x_{i})=u(x_{0},x_{1},x_{2},x_{3})}
(одна из этих четырёх координат xi{\displaystyle x_{i}} равна или пропорциональна времени), более того, при этом, если используют термин скалярное поле, еще и подразумевается, что u{\displaystyle u} — лоренц-инвариантно. Все операции над полем (такие, как градиент) при этом используются в их четырёхмерном виде.
Под скалярным полем в современной теоретической физике понимается обычно (если речь идёт о фундаментальных полях) фундаментальное поле скаляра пространства Минковского (лоренц-инвариантное поле) или поле, инвариантное относительно общекоординатных преобразований, (обычно первое и второе практически совпадает).
Практическими синонимами термина скалярное поле в этом смысле являются термины поле спина ноль, частица спина ноль, скалярная частица (последние, всё же несколько разводя эти близкие понятия, называют также возбуждениями скалярного поля).
Единственной экспериментально открытой скалярной частицей является бозон Хиггса.
Скалярные поля играют немалую роль в теоретических построениях. Их наличие (наряду с векторными и тензорными полями, понимаемыми в том же смысле и наблюдаемыми реально) необходимо для полноты классификации фундаментальных полей.
В новых физических теориях (таких, как например теория струн) часто имеют дело с пространствами и многообразиями разной размерности, в том числе и достаточно высокой (больше четырёх), и полями, в том числе скалярными полями, на таких пространствах.
Скалярное поле можно представить графически с помощью поверхностей уровня (также называемой изоповерхностями).
Поверхностью уровня скалярного поля u=u(x,y,z){\displaystyle u=u(x,y,z)} называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением u(x,y,z)=c{\displaystyle u(x,y,z)=c}. Изображение набора поверхностей уровня для разных c{\displaystyle c} дает наглядное представление о конкретном скалярном поле, для которого они построены (изображены)[4], кроме того, представление о поверхностях уровня дает определенный дополнительный геометрический инструмент для работы со скалярным полем, который может использоваться для вычислений, доказательства теорем и т. п. Пример: эквипотенциальная поверхность.
Для поля на двумерном пространстве аналогом поверхности уровня является линии уровня. Примеры: изобата, Изотерма, изогипса (линия равных высот) на географической карте и прочие изолинии.
Поверхностями уровня для скалярного поля на пространстве большей размерности являются гиперповерхности с размерностью на единицу меньшей, чем размерность пространства.
Направление скорейшего возрастания поля u=u(r)=u(x,y,z){\displaystyle u=u(\mathbf {r} )=u(x,y,z)} указывает вектор градиента, обозначаемый стандартно:
- grad u{\displaystyle \mathbf {grad} \ u},
или иное обозначение:
- ∇u{\displaystyle \nabla u},
с компонентами:
- (∂u∂x, ∂u∂y, ∂u∂z){\displaystyle \left({\frac {\partial u}{\partial x}},\ {\frac {\partial u}{\partial y}},\ {\frac {\partial u}{\partial z}}\right)}.
Здесь приведена формула для трёхмерного случая, на другие размерности она обобщается прямо и тривиально.
- Если координаты не декартовы (базис не ортонормирован) существенно заметить, что приведенные выше компоненты градиента есть компоненты ковариантные, то есть градиент скалярного поля есть ко-векторное поле. Для ортономированных базисов это не существенно, так как для них понятие вектора и ко-вектора можно считать совпадающими, как и ковариантные и контравариантные координаты.
Абсолютная величина вектора градиента u есть производная u по направлению скорейшего роста (скорость роста u при движении с единичной скоростью в этом направлении).
Градиент всегда перпендикулярен поверхностям уровня (в двумерном случае — линиям уровня). Исключение — особые точки поля, в которых градиент равен нулю.
- ↑ 1 2 Плоское поле — Метеорологический Словарь
- ↑ Будем во избежание путаницы в этом параграфе говорить только о поле на трёхмерном пространстве.
- ↑ На это есть достаточно серьёзные причины, сводящиеся к тому, что в физике не только можно делать формальные преобразования (так называемые преобразования Лоренца, которые можно охарактеризовать как пространственно-временные повороты), смешивающие пространственные координаты с временной, но оказывается, что никакие физические эксперименты и наблюдения, насколько известно на сегодня, не могут выявить различия между уравнениями физики, записанными в той или другой из двух повернутых так друг относительно друга пространственно-временных системах координат.
- ↑ «Картинка» таких поверхностей, конечно же, в целом трёхмерная (сами поверхности двумерны, но вообще говоря не плоские и располагаются в трёхмерном пространстве), однако её можно, в простых случаях и нетрудно вообразить[что?], а также каким-то образом построить одну или несколько двумерных проекций или сечений такой трёхмерной картинки.


