3.Закон Ома для участка цепи, не содержащего эдс:
I = U/R . (1.4)
Рассмотрим участок цепи с ЭДС (Error: Reference source not found).
Рис.1.5. Линейный участок цепи, содержащий ЭДС
Из состава сложной электрической цепи выделим ветвь, содержащую источник энергии и потребитель. Для определенности примем, что направления тока и источника ЭДС совпадают. При условно выбранных положительных направлениях тока и ЭДС в ветви имеем:
1 > a 1 – a = IR, 0(1.5)
2 > a 2 – a =
 0(1.6)
0(1.6)Вычтем из уравнения ( 1 .5) уравнение ( 1 .6) и тогда получим:
1 – 2 = IR – E = U12;
. 0(1.7)
Полученное выражение представляет собой закон Ома для участка цепи с ЭДС. В случае несовпадения направления тока в ветви с направлениями напряжения и ЭДС перед ними появляется знак «минус».
Первый закон Кирхгофа алгебраическая сумма токов в узле равна нулю:
. 0(1.8)
Второй закон Кирхгофа алгебраическая сумма падений напряжений вдоль замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре:
0(1.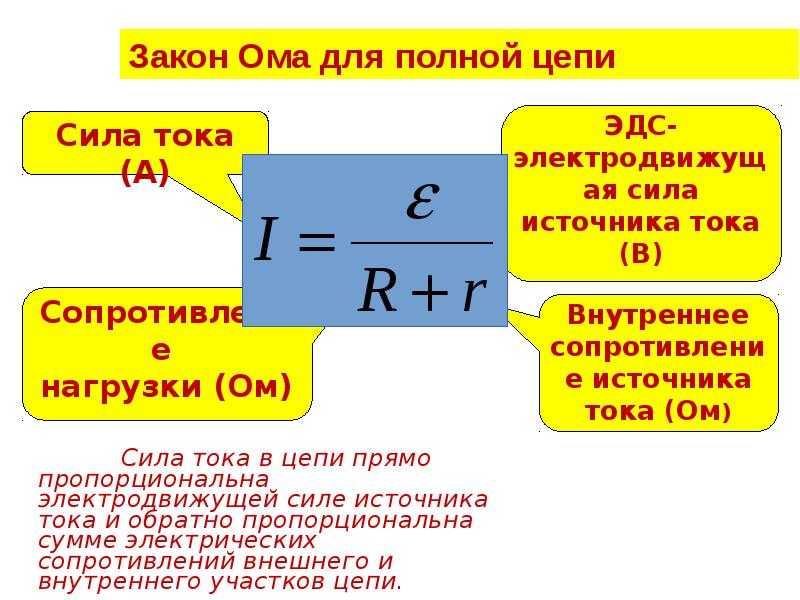 9)
9)
Второй закон Кирхгофа работает как для замкнутого, так и для разомкнутого контура.
Уравнение баланса мощности:
0 (1.10)
В левой части этого уравнения стоит арифметическая сумма мощностей, которые выделяются на сопротивлениях от токов, которые по ним протекают. В правой части – мощность, отданная источниками в сеть.
При этом возможна такая ситуация, когда одно из слагаемых суммы справа может оказаться отрицательным. Это будет означать, что в данной ситуации источник становится потребителем. Она возникает в случае, когда ток, протекающий по источнику, направлен встречно направлению ЭДС.
Закон
Джоуля — Ленца — физический
закон,
дающий количественную
оценку теплового действия электрического
тока. Установлен в 1841
году Джеймсом
Джоулем и
независимо от него в 1842
году Эмилием
Ленцом[1].
Установлен в 1841
году Джеймсом
Джоулем и
независимо от него в 1842
году Эмилием
Ленцом[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивлению участка
В математической форме этот закон имеет вид
где dQ —
количество теплоты, выделяемое за
промежуток времени dt, I —
сила тока, R —
сопротивление, Q —
полное количество теплоты, выделенное
за промежуток времени от t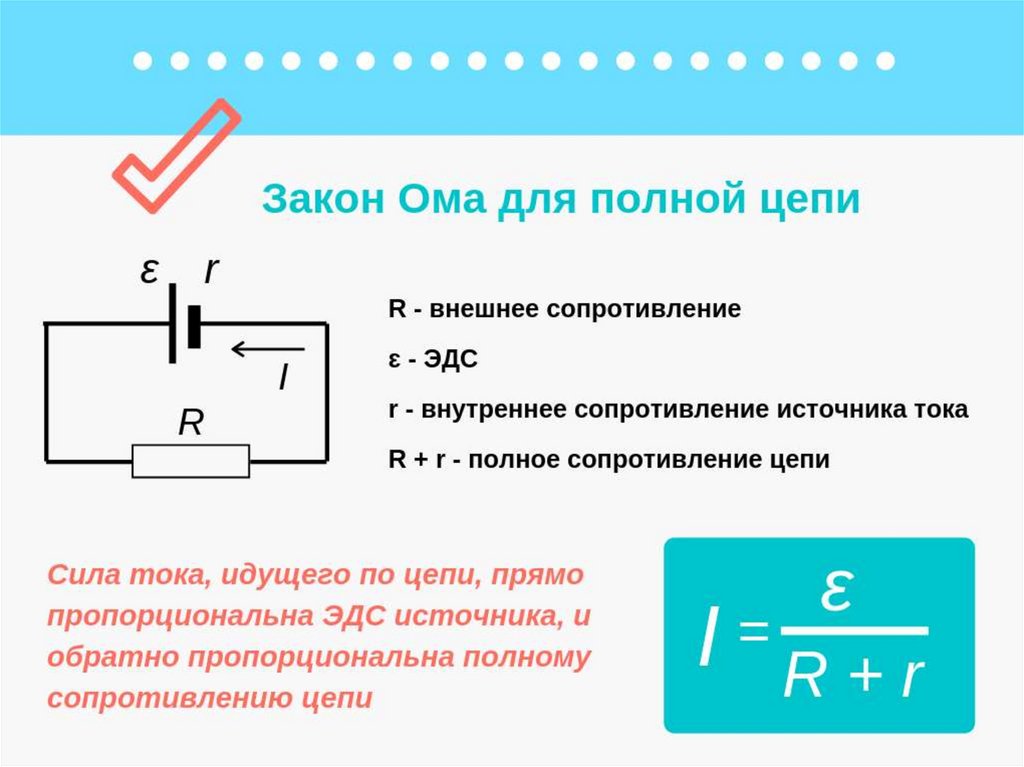 В случае постоянных силы тока и
сопротивления:
В случае постоянных силы тока и
сопротивления:
4.
5.
6. Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Закон Ома для полной цепи. Школьный курс физики
Главная | Физика 11 класс | Закон Ома для полной цепи
Закон ома для полной цепи.
Ранее мы изучили закон Ома для участка цепи, не содержащего источник тока. Теперь рассмотрим простейшую полную (замкнутую) электрическую цепь (рис. 1.41), состоящую из источника тока (например, гальванического элемента или аккумулятора) и резистора с сопротивлением
Рис. 1.41
Источник тока, имеющий ЭДС , обладает сопротивлением r. Его называют внутренним сопротивлением источника, в отличие от сопротивления R цепи, называемого внешним сопротивлением.
Например, в генераторе r — это сопротивление его обмоток (медных проводов), в гальваническом элементе или аккумуляторе это сопротивление раствора электролита и электродов.
Для вывода закона Ома для полной цепи воспользуемся законом сохранения энергии. Пусть за время Δ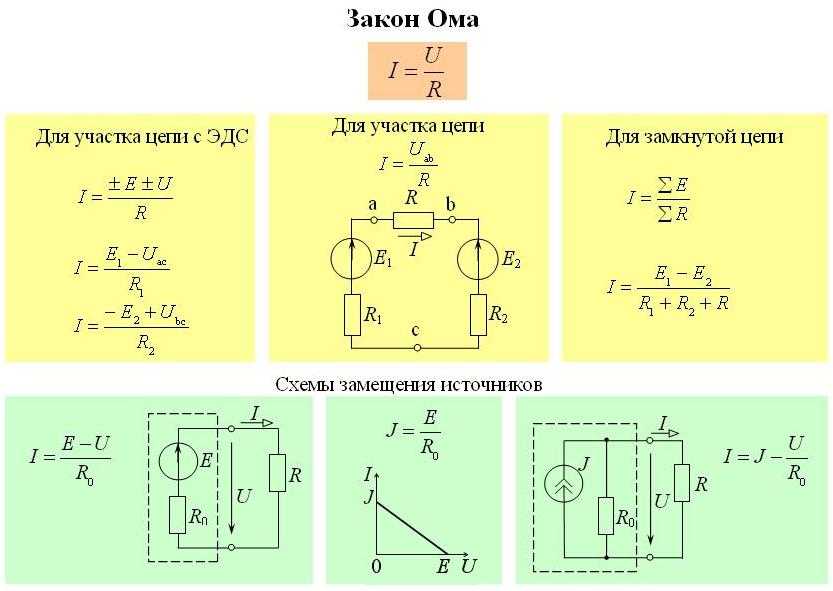 Источники тока«), работа сторонних сил при перемещении заряда q равна
Источники тока«), работа сторонних сил при перемещении заряда q равна
Аст = q.
Из определения силы тока I получим q = IΔt. C учётом этого
Аст = IΔt.
Благодаря работе сторонних сил при прохождении тока в цепи на её внешнем и внутреннем участках выделяется количество теплоты, равное по закону Джоуля—Ленца
Q = I2RΔt + I2rΔt.
Согласно закону сохранения энергии, Аст = Q, поэтому
Произведение силы тока на сопротивление участка цепи называют падением напряжения на этом участке. Таким образом, ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи:
= U + U0,
где U = IR — падение напряжения на внешнем участке; U0 = Ir — падение напряжения на внутреннем участке цепи.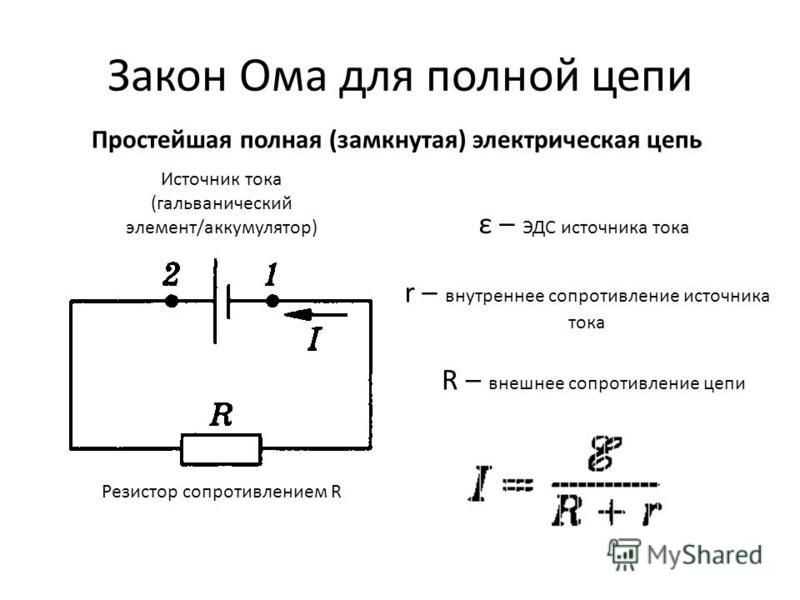
Из равенства (1) запишем:
Это и есть закон Ома для полной цепи.
Сила тока в полной цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.
Внутреннее сопротивление источника тока, если оно мало по сравнению с внешним сопротивлением (r << R), оказывает незначительное влияние на силу тока. Но при коротком замыкании, когда R ≈ 0, сила тока очень велика, так как r мало. Например, при = 2 В и r = 0,1 — 0,004 Ом сила тока короткого замыкания Iкз
1 Напомним, что при перегрузках и коротких замыканиях электрическую сеть защищает специальное устройство — предохранитель. Он состоит из проволоки, изготовленной из легкоплавкого металла. Проволока помещена в стеклянную трубку, имеющую на концах металлические наконечники, и рассчитана на определённую силу тока. Если сила тока превышает допустимое значение, то проволока плавится и цепь размыкается.
Проволока помещена в стеклянную трубку, имеющую на концах металлические наконечники, и рассчитана на определённую силу тока. Если сила тока превышает допустимое значение, то проволока плавится и цепь размыкается.
Если цепь содержит несколько последовательно соединённых источников тока (рис. 1.42),
Рис. 1.42
то полная ЭДС в цепи равна алгебраической сумме ЭДС отдельных элементов:
Определим знак ЭДС отдельных элементов. При выбранном (произвольно) направлении обхода против часовой стрелки для цепи, схема которой изображена на рисунке 1.42, 1 > 0, 2 < 0 и 3 > 0, поэтому
Внутреннее сопротивление батареи, состоящей из последовательно соединённых элементов, равно сумме внутренних сопротивлений элементов:
Если батарея состоит из N одинаковых последовательно соединённых элементов с одинаковыми знаками ЭДС, то из формул (2) и (3) следует, что
где 6 и r6 — ЭДС и внутреннее сопротивление батареи; э и rэ — ЭДС и внутреннее сопротивление одного элемента.
Таким образом, последовательное соединение увеличивает общую ЭДС и увеличивает внутреннее сопротивление батареи.
Если цепь содержит несколько параллельно соединённых элементов (рис. 1.43),
Рис. 1.43
то можно записать следующие формулы:
где N — число одинаковых ЭДС в цепи.
Таким образом, параллельное соединение N одинаковых источников тока не изменяет ЭДС батареи, если сравнивать с включённым в эту цепь одним источником тока с той же ЭДС. Однако при таком включении внутреннее сопротивление источника уменьшается в N раз.
Закон Oмa для участка цепи, содержащего ЭДС.
Наиболее общую форму имеет закон Ома для участка цепи, содержащего ЭДС (иногда его называют обобщённым законом Ома).
Рассмотрим участок цепи, содержащий гальванические элементы или аккумулятор, т. е. участок, на котором действуют сторонние силы. Таким участком является, например, участок ab (рис. 1.44).
1.44).
Рис. 1.44
Внутренние сопротивления источников 1, и 2 равны соответственно r1 и r2. Сила тока на участке равна I, ток течёт от точки а к точке b.
За время Δt через поперечное сечение проводника проходит заряд q = IΔt. При этом электрическое поле совершает работу Aπ = (φa — φb)q = (φa — φb)IΔt. Источники тока совершают работу Acт = |1|q — |2|q = (|1| — |2|)IΔt. За время Δt на участке цепи выделяется количество теплоты Q = I2(r1 + r2 + R1 + R2)Δt. Согласно закону сохранения энергии Aп + Aст = Q, поэтому
Сформулируем закон Ома для участка цепи, содержащего ЭДС.
Разность потенциалов на концах участка цепи равна падению напряжения на участке минус ЭДС этого участка.
Если неразветвленный участок цепи содержит п источников тока и N резисторов, то
Применяя закон Ома для участка цепи, содержащего ЭДС, придерживаются правила знаков.
1. Сила тока в правой части уравнения (5) считается положительной, если направление тока совпадает с направлением от a к b.
2. ЭДС считается положительной, если работа сторонних сил при перемещении единичного положительного заряда на данном участке цепи в направлении от а к Ь положительна. В случае гальванического элемента или аккумулятора ЭДС положительна, если этот заряд внутри источника перемещается от отрицательного электрода к положительному. C учётом этого в правой части уравнения (5) записывается сумма всех ЭДС по правилу знаков.
Применив закон Ома к участку 1—2 цепи, показанной на рисунке 1. 41, получим φ1 — φ2 = Ir — . При разомкнутой цепи I = 0 и, следовательно, = φ2 — φ1. Таким образом, ЭДС элемента равна разности потенциалов между его полюсами при разомкнутой цепи.
41, получим φ1 — φ2 = Ir — . При разомкнутой цепи I = 0 и, следовательно, = φ2 — φ1. Таким образом, ЭДС элемента равна разности потенциалов между его полюсами при разомкнутой цепи.
Реостат.
Реостат представляет собой резистор с регулируемым сопротивлением (рис. 1.45).
Рис. 1.45
Пусть часть цепи состоит из электрической лампы накаливания и последовательно соединённого с ней реостата (рис. 1.46).
Рис. 1.46
C помощью реостата можно изменять общее сопротивление цепи: от максимального сопротивления, равного сумме сопротивлений реостата и лампы, до минимального, равного только сопротивлению лампы.
В общем случае
Если контакт 3 совпадает с контактом /, то
Если контакт 3 совпадает с контактом 2, то
где R12 — сопротивление реостата.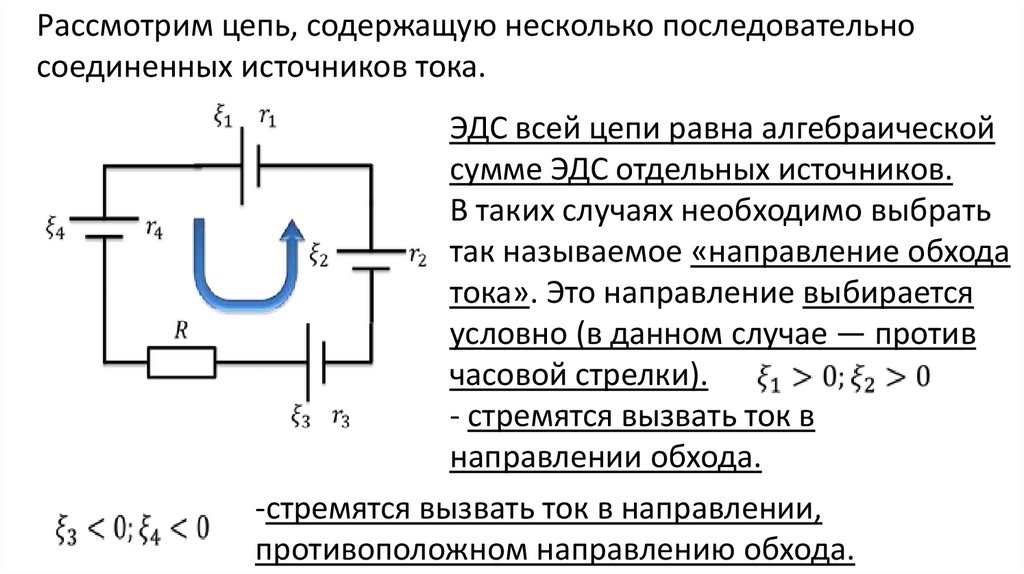
Таким образом, реостат позволяет плавно регулировать значение силы тока в цепи и в данном случае изменять степень накала нити лампы, включённой в цепь.
Потенциометр.
Потенциометр (делитель напряжения) — устройство, предназначенное для получения плавно изменяемого напряжения U от источника постоянного напряжения U0:
U ≤ U0 (рис. 1.47).
Рис. 1.47
Точка D на схеме представляет собой скользящий контакт. При этом
URmin = 0 (когда контакт D соединён с точкой А),
URmax = U0 (когда контакт D соединён с точкой В).
Таким образом, потенциометр позволяет получать различные значения напряжения на нагрузке, которой в данном случае является резистор с сопротивлением R.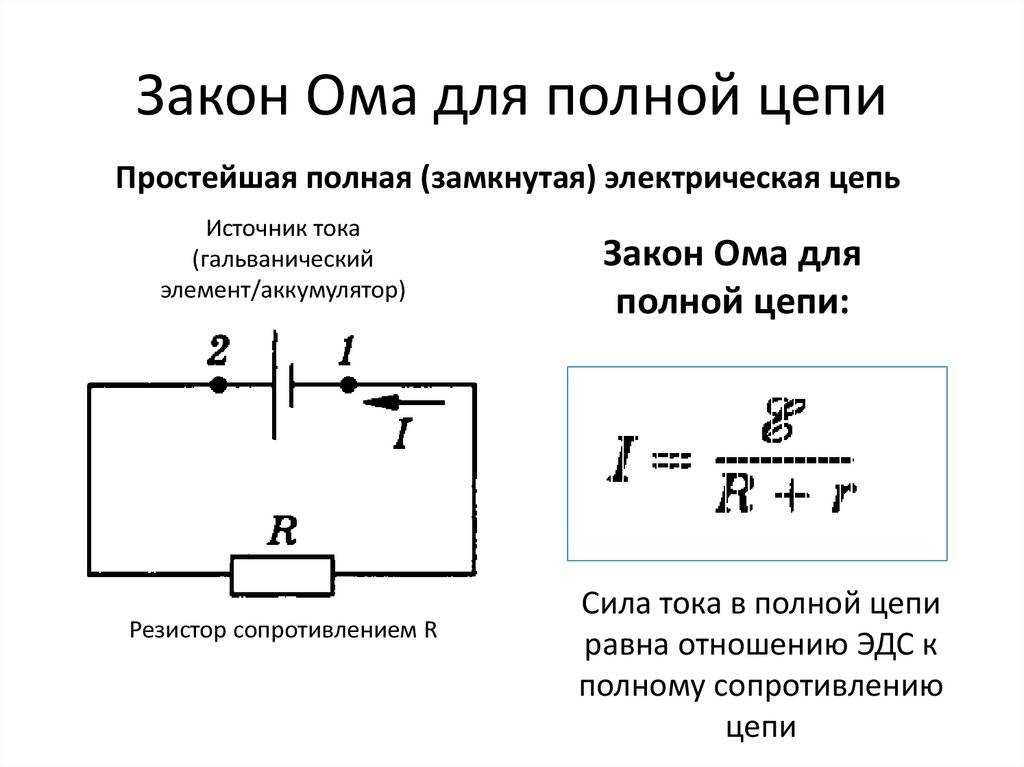
Вопросы:
1. Какое сопротивление называют:
а) внутренним;
б) внешним?
2. Чем определяется падение напряжения на участке цепи?
3. Сформулируйте и запишите закон Ома для полной цепи.
4. Как определить ЭДС и внутреннее сопротивление батареи, содержащей несколько:
а) последовательно соединённых элементов;
б) параллельно соединённых элементов?
5. Сформулируйте и запишите закон Ома для участка цепи, содержащего ЭДС.
6. Для чего используют:
а) реостат;
б) потенциометр?
Вопросы для обсуждения:
Почему при коротком замыкании напряжение на клеммах источника тока близко к нулю, хотя сила тока в цепи имеет наибольшее значение?
Пример решения задачи
Сила тока через аккумулятор в конце зарядки I1 = 4 А. При этом разность потенциалов на его клеммах U1 = 12,6 В.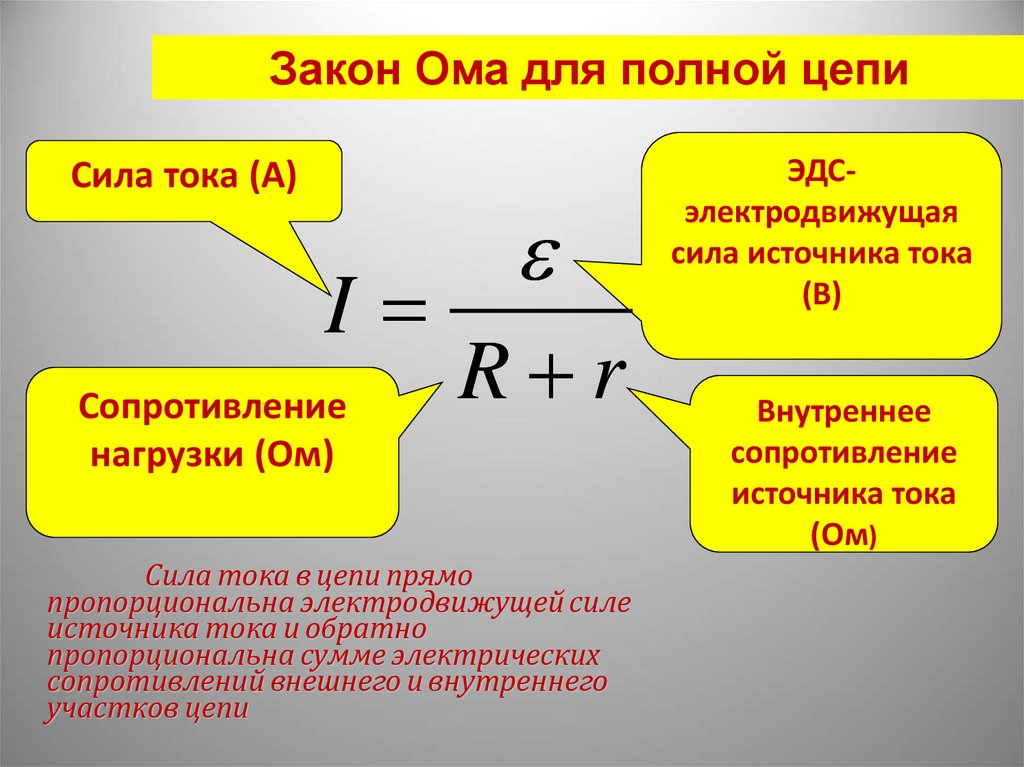 Сила тока короткого замыкания Iкз = 305 А. В начале разрядки того же аккумулятора сила тока I2 = 6 А. Какова при этом разность потенциалов U2 на его клеммах?
Сила тока короткого замыкания Iкз = 305 А. В начале разрядки того же аккумулятора сила тока I2 = 6 А. Какова при этом разность потенциалов U2 на его клеммах?
Рис. 1.48
Сила тока при коротком замыкании аккумулятора (рис. 1.48, б)
Схема разрядки аккумулятора на внешнюю нагрузку показана на рисунке 1.48, в. По закону Ома для участка цепи, содержащего ЭДС:
Из уравнений(1)и(2)найдём:
Подставим данные выражения в уравнение (3):
C учётом числовых данных получим
Ответ: U2 ≈ 12,2 В.
Упражнения:
1. К источнику тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён резистор с сопротивлением 5 Ом. Найдите силу тока в цепи и напряжение на зажимах источника.
2. Чему равно внутреннее сопротивление источника тока, если его ЭДС составляет 1,2 В и при внешнем сопротивлении 5 Ом сила тока в цепи равна 0,2 А?
3. Определите разность потенциалов между точками A и B электрической цепи, схема которой приведена на рисунке 1.49. ЭДС каждого источника тока равна 1,5 В, внутреннее сопротивление каждого источника составляет 0,1 Ом.
Определите разность потенциалов между точками A и B электрической цепи, схема которой приведена на рисунке 1.49. ЭДС каждого источника тока равна 1,5 В, внутреннее сопротивление каждого источника составляет 0,1 Ом.
Рис. 1.49
4. Два одинаковых источника тока с ЭДС и внутренним сопротивлением r соединены так, как показано на рисунке 1.50. Определите показания приборов. Сопротивление амперметра принять равным нулю, а сопротивление вольтметра — бесконечно большим.
Рис. 1.50
Предыдущая страницаСледующая страница
Электрический ток — физика
Батарея
Батарея — это устройство, которое непосредственно преобразует химическую энергию в электрическую.
Цели обучения
Описать функции и определить основные компоненты батареи
Основные выводы
Ключевые моменты
- Батарея накапливает электрический потенциал в результате химической реакции.
 Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи.
Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи. - Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q, перемещенного из точки 1 в точку 2, деленное на заряд.
- Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за поток заряда через цепь, известную как электрический ток.
Ключевые термины
- батарея : Устройство, вырабатывающее электричество в результате химической реакции между двумя веществами.
- ток : Скорость потока электрического заряда во времени.
- напряжение : Величина электростатического потенциала между двумя точками в пространстве.
Символ батареи на принципиальной схеме : Это символ батареи на принципиальной схеме. Он возник как схематический рисунок самого раннего типа батареи, вольтовой батареи. Обратите внимание на положительный катод и отрицательный анод. Эта ориентация важна при рисовании принципиальных схем, чтобы изобразить правильный поток электронов.
Обратите внимание на положительный катод и отрицательный анод. Эта ориентация важна при рисовании принципиальных схем, чтобы изобразить правильный поток электронов.
Батарея — это устройство, которое непосредственно преобразует химическую энергию в электрическую. Он состоит из ряда гальванических элементов, соединенных последовательно проводящим электролитом, содержащим анионы и катионы. Одна полуэлемент включает электролит и анод или отрицательный электрод; другая половина элемента включает электролит и катод или положительный электрод. В окислительно-восстановительной (восстановительно-окислительной) реакции, которая питает аккумулятор, катионы восстанавливаются (присоединяются электроны) на катоде, а анионы окисляются (электроны удаляются) на аноде. Электроды не касаются друг друга, а электрически связаны электролитом. В некоторых элементах используются два полуэлемента с разными электролитами. Разделитель между полуячейками позволяет ионам течь, но предотвращает смешивание электролитов.
Каждая полуячейка обладает электродвижущей силой (или ЭДС), определяемой ее способностью проводить электрический ток изнутри клетки наружу. Суммарная ЭДС клетки представляет собой разность между ЭДС ее полуячеек или разность между восстановительными потенциалами полуреакций.
Электрическая движущая сила на клеммах ячейки известна как напряжение на клеммах (разность) и измеряется в вольтах. Когда батарея подключена к цепи, электроны от анода проходят через цепь к катоду по прямой цепи. Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за поток заряда через цепь, известную как электрический ток.
Аккумулятор накапливает электрический потенциал в результате химической реакции. Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи. Электрический потенциал определяется как потенциальная энергия на единицу заряда ( q ). Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q , перемещенного из точки 1 в точку 2, деленное на заряд. В перестановке это математическое соотношение может быть описано как:
В перестановке это математическое соотношение может быть описано как:
[латекс]\Delta \text{PE} =\text{q}\Delta \text{V}[/latex]
Напряжение — это не то же самое, что энергия. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один из них хранит гораздо больше энергии, чем другой. Автомобильный аккумулятор может передавать больше заряда, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами на 12 В.
Идеальные и настоящие батареи : Краткое введение в идеальные и реальные батареи для студентов, изучающих схемы.
Измерения тока и напряжения в цепях
Электрический ток прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению в цепи.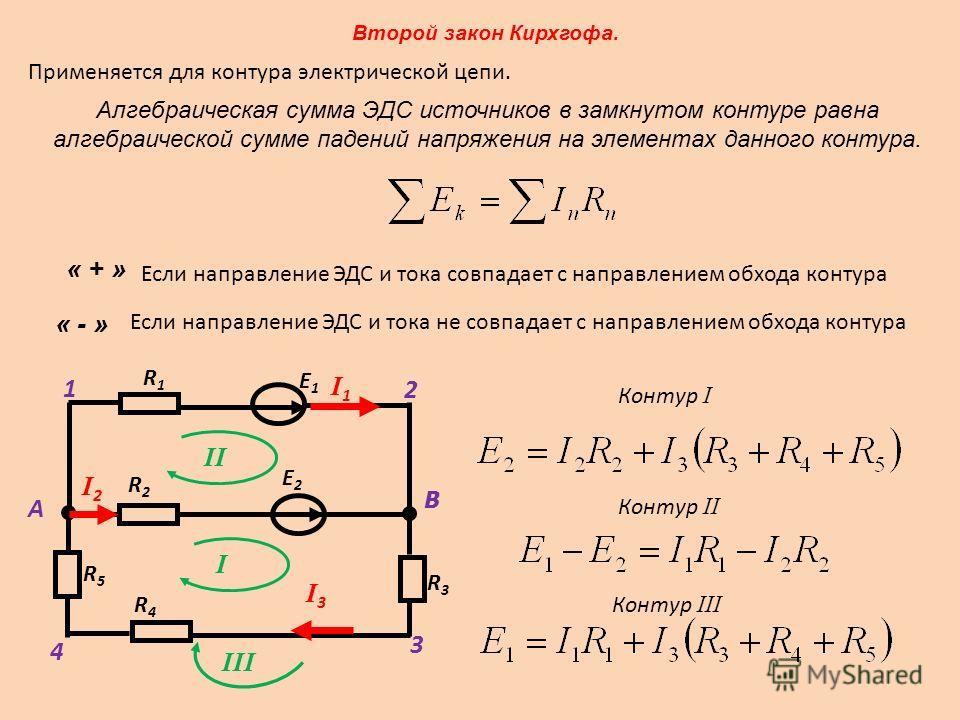
Цели обучения
Описать взаимосвязь между электрическим током, напряжением и сопротивлением в цепи
Ключевые выводы
Ключевые моменты
- Простая цепь состоит из источника напряжения и резистора.
- Закон Ома дает соотношение между током I , напряжением В и сопротивлением R в простой цепи: I = В / R .
- Единицей СИ для измерения скорости потока электрического заряда является ампер, который равен заряду, протекающему через некоторую поверхность со скоростью один кулон в секунду.
Ключевые термины
- электрический ток : движение заряда по цепи
- ом : в Международной системе единиц производная единица электрического сопротивления; электрическое сопротивление устройства, на котором разность потенциалов в один вольт вызывает ток в один ампер; символ: Ом
- ампер : Единица электрического тока; стандартная базовая единица в Международной системе единиц.
 Аббревиатура: амп. Символ: А.
Аббревиатура: амп. Символ: А.
Чтобы понять, как измерять ток и напряжение в цепи, вы также должны иметь общее представление о том, как работает цепь и как связаны ее электрические измерения.
Что такое напряжение? : Это видео помогает получить концептуальное представление о напряжении.
Электрическая цепь представляет собой тип сети с замкнутым контуром, который обеспечивает обратный путь для тока. Простая электрическая цепь состоит из источника напряжения и резистора и может быть схематически представлена следующим образом.
Простая электрическая цепь : Простая электрическая цепь, состоящая из источника напряжения и резистора I , или движение заряда, протекающего через большинство веществ, прямо пропорционально приложенному к нему напряжению V . Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току. Следовательно, закон Ома можно записать следующим образом:
Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току. Следовательно, закон Ома можно записать следующим образом:
[латекс]\текст{I} = \текст{V}/\текст{R}[/латекс]
, где I — ток через проводник в амперах, V — разность потенциалов, измеренная на проводнике в вольтах, а R — сопротивление проводника в омах (Ом). Точнее, закон Ома гласит, что R в этом отношении постоянна, не зависит от тока. Используя это уравнение, мы можем рассчитать ток, напряжение или сопротивление в данной цепи.
Например, если бы у нас была батарея на 1,5 В, которая была подключена по замкнутой цепи к лампочке с сопротивлением 5 Ом, какой ток протекает по цепи? Чтобы решить эту проблему, мы просто подставим данные значения в закон Ома: I = 1,5 В/5 Ом; I = 0,3 ампера. Если мы знаем силу тока и сопротивление, мы можем изменить уравнение закона Ома и решить для напряжения В :
Если мы знаем силу тока и сопротивление, мы можем изменить уравнение закона Ома и решить для напряжения В :
[латекс]\текст{В} = \текст{IR}[/латекс]
Микроскопический вид: скорость дрейфа
Скорость дрейфа — это средняя скорость, которую частица достигает благодаря электрическому полю.
Цели обучения
Связь скорости дрейфа со скоростью свободных зарядов в проводниках
Основные выводы
Ключевые моменты
- В проводниках существует электрическое поле, которое заставляет электроны дрейфовать в направлении, противоположном полю. Скорость дрейфа представляет собой среднюю скорость этих свободных зарядов.
- Выражение для связи между током и скоростью дрейфа можно получить, рассматривая количество свободных зарядов в отрезке проволоки.
- I = qnAv связывает скорость дрейфа с током, где I — ток через провод с площадью поперечного сечения A из материала с плотностью свободного заряда n .
 Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью v .
Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью v .
Ключевые термины
- скорость дрейфа : Средняя скорость свободных зарядов в проводнике.
Скорость дрейфа
Известно, что электрические сигналы распространяются очень быстро. Телефонные разговоры, переносимые токами по проводам, проходят большие расстояния без заметных задержек. Свет загорается, как только щелкаешь выключателем. Большинство электрических сигналов, переносимых током, распространяется со скоростью порядка 10 8 м/с, что составляет значительную часть скорости света. Интересно, что отдельные заряды, составляющие ток, движутся в среднем гораздо медленнее, обычно дрейфуя со скоростью порядка 10 −4 м/с.
Высокая скорость электрических сигналов обусловлена тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд попадает в проводник, входящий заряд отталкивает другие заряды впереди себя, которые, в свою очередь, отталкивают заряды дальше по линии. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Электроны, движущиеся по проводнику : Когда заряженные частицы попадают в этот объем проводника, такое же их количество быстро покидает его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.
Скорость дрейфа
Хорошие проводники содержат большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе. Однако в проводнике существует электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v d — средняя скорость свободных зарядов после приложения поля. Скорость дрейфа довольно мала, так как очень много свободных зарядов. Зная плотность свободных электронов в проводнике (количество электронов в единице объема), можно рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Скорость дрейфа v d — средняя скорость свободных зарядов после приложения поля. Скорость дрейфа довольно мала, так как очень много свободных зарядов. Зная плотность свободных электронов в проводнике (количество электронов в единице объема), можно рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Скорость дрейфа : Свободные электроны, движущиеся в проводнике, часто сталкиваются с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью и направлена в направлении, противоположном электрическому полю для электронов. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.
Можно получить выражение для зависимости между током и скоростью дрейфа, рассматривая количество свободных зарядов в отрезке проволоки. Количество свободных зарядов на единицу объема обозначается символом n и зависит от материала.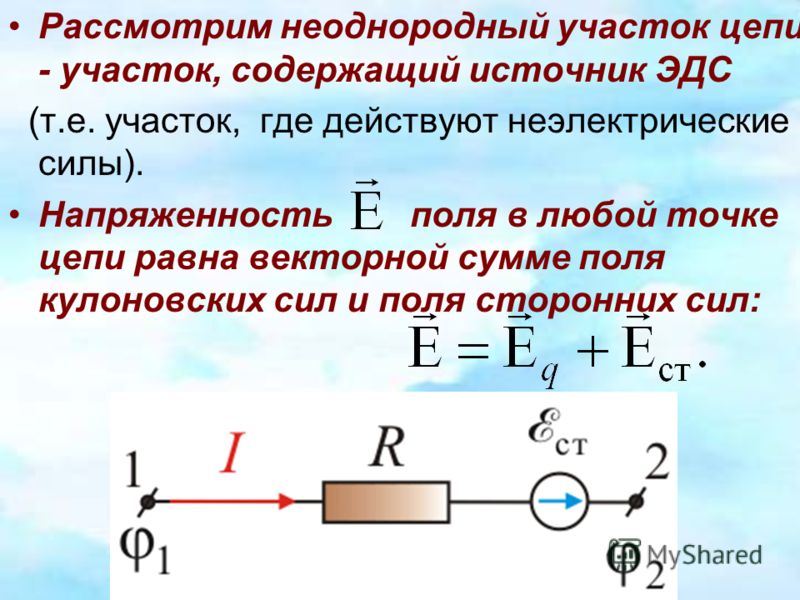 Ax — это объем сегмента, так что количество свободных зарядов в нем равно nAx . Таким образом, плата ΔQ в этом сегменте равна qnAx , где q — это сумма платы на каждом перевозчике. (Напомним, что для электронов q составляет 1,60×10-19°С. ) Ток — это заряд, перемещаемый в единицу времени. Таким образом, если все первоначальные заряды покидают этот отрезок за время t, ток равен:
Ax — это объем сегмента, так что количество свободных зарядов в нем равно nAx . Таким образом, плата ΔQ в этом сегменте равна qnAx , где q — это сумма платы на каждом перевозчике. (Напомним, что для электронов q составляет 1,60×10-19°С. ) Ток — это заряд, перемещаемый в единицу времени. Таким образом, если все первоначальные заряды покидают этот отрезок за время t, ток равен:
[латекс]\текст{I} = \Delta \text{Q}/\Delta \text{t} = \text{ qnAx}/\Delta \text{t}[/latex]
Примечательно, что x/Δt представляет собой величину скорости дрейфа v d , поскольку заряды проходят в среднем расстояние x за время t. Перестановка членов дает: I = qnAv d , где I – сила тока через провод сечением А , изготовленный из материала с плотностью свободного заряда n . Каждый из носителей тока имеет заряды q и движется с дрейфовой скоростью величины v d .
Плотность тока — это электрический ток на единицу площади поперечного сечения. Он измеряется в амперах на квадратный метр.
Электрическое сопротивление— Как протекает ток в цепи с конденсатором?
спросил
Изменено 1 год, 9 месяцев назад
Просмотрено 16 тысяч раз
$\begingroup$
Когда конденсатор подключен к батарее, в цепи начинает течь ток, который заряжает конденсатор до тех пор, пока напряжение между обкладками не станет равным напряжению батареи.
Так как между обкладками конденсатора находится изолятор/диэлектрик, как возможно, что в цепи с конденсатором протекает ток, ведь по закону Ома ток обратно пропорционален сопротивлению, а изолятор по определению имеет большое сопротивление, так что у нас в основном разомкнутая цепь?
- электрические цепи
- электрические сопротивления
- напряжения
- емкости
- диэлектрики
$\endgroup$
$\begingroup$
Так как это физика q и a, объяснение физики в порядке.
Есть два вида тока.
Ток проводимости представляет собой чистый поток зарядов. Это то, о чем люди обычно думают, когда используют слово «ток».
Ток смещения — еще одна форма тока, впервые обнаруженная Максвеллом. Ток смещения играет существенную роль в уравнениях Максвелла. Плотность тока смещения пропорциональна производной по времени от изменения плотности электрического потока.
Когда ток электронов течет в одну сторону конденсатора, электроны накапливаются, так как им некуда деваться. По мере накопления электронов плотность электрического потока изменяется. Это вызывает или, возможно, «является» током смещения.
На противоположной обкладке конденсатора происходит аналогичный процесс, но с противоположной электрической полярностью.
Ток смещения течет от одной пластины к другой через диэлектрик всякий раз, когда ток втекает или выходит из пластин конденсатора, и имеет точно такую же величину, что и ток, протекающий через клеммы конденсатора.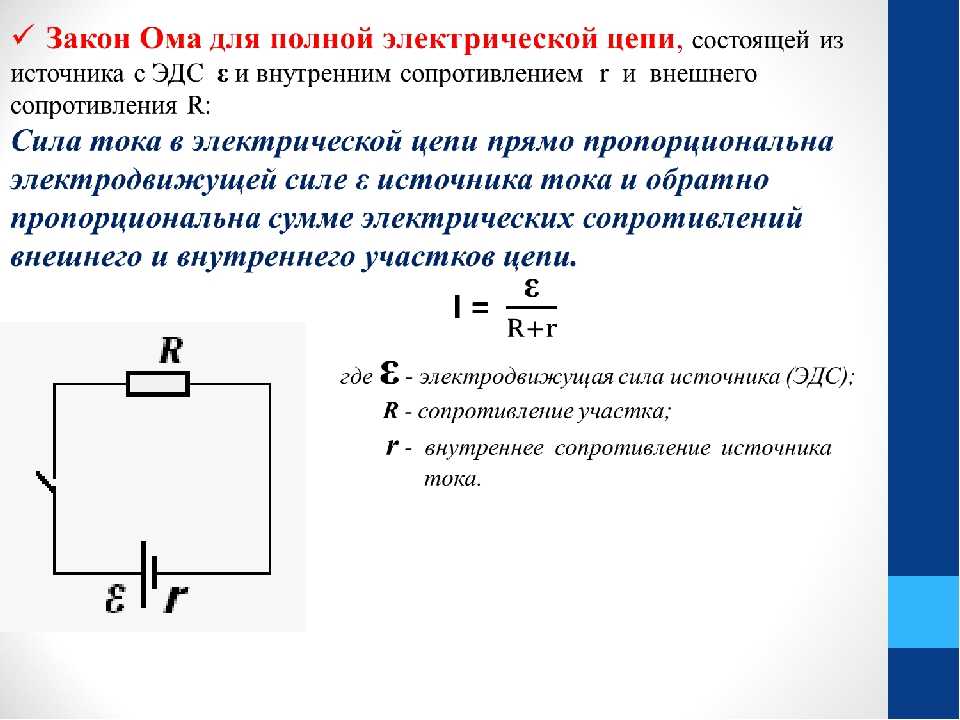
Можно предположить, что этот ток смещения не имеет никакого реального эффекта, кроме «сохранения» тока. Однако ток смещения создает магнитные поля так же, как и ток проводимости.
Этот ответ, возможно, больше, чем хотелось бы знать, но это часть истории электричества, которую стоит рассказать.
$\endgroup$
1
$\begingroup$
как возможно, что ток течет в цепи с конденсатором так как по закону Ома сила тока обратно пропорциональна сопротивление, а изолятор по определению имеет большое сопротивление, поэтому мы в основном есть разомкнутая цепь?
Короткий ответ заключается в том, что электроны могут течь к конденсатору и от него без необходимости прохождения электронов через изоляцию между пластинами. Предлагается следующее качественное объяснение:
Если предположить, что конденсатор изначально не заряжен, то перед его подключением к батарее каждая металлическая пластина имеет равное количество протонов (положительный заряд) и высокоподвижных электронов (отрицательный заряд), так что каждая пластина электрически нейтральна и между пластинами нет напряжения (разности потенциалов).
Когда конденсатор подключен к батарее, положительная клемма батареи притягивает электроны от пластины, соединенной с ним, перемещая их к положительной клемме батареи. Это оставляет дефицит электронов на этой пластине, что делает ее положительно заряженной.
В то же время отрицательный полюс батареи подает равное количество электронов на подсоединенную к нему пластину, создавая избыток электронов, делая пластину отрицательно заряженной.
Это перемещение электронов с одной пластины на положительную клемму батареи и с отрицательной клеммы батареи на другую пластину представляет собой ток конденсатора. Обратите внимание, что электроны не проходят через изоляционный материал (диэлектрик) между пластинами.
Вы можете представить себе это примерно как электроны, «выталкиваемые» с одной пластины и «выталкиваемые» на другую силой электрического поля, создаваемого батареей, но при этом заряды «застревают» на пластине. пластины, потому что они не могут пройти через изолирующий диэлектрик.
В конце концов, как вы, кажется, уже знаете, батарея перестает перемещать электроны между пластинами, когда разность потенциалов между пластинами становится равной разности потенциалов батареи.
Надеюсь, это поможет.
$\endgroup$
9
$\begingroup$
Удаление электронов с обкладки конденсатора, подключенной к клемме +, представляет собой ток. Поскольку эти электроны удаляются для этой пластины, происходит накопление электронов на другой пластине. Это движение электронов составляет ток.
Ток прекращается, когда потенциалы обкладок конденсатора становятся равными потенциалам соответствующих клемм аккумулятора. Это не происходит мгновенно, а скорее зависит от времени, потому что транспорт электронов из конденсатора и в него требует времени, а потенциалы зависят от дисбаланса заряда пластин.
$\endgroup$
$\begingroup$
Наличие плоского конденсатора означает, что в части
цепи (лишь малая часть; конденсаторы редко имеют такой большой зазор
как один миллиметр) нет движения электронов, только накопление
поля (в сопровождении электронов, если конденсатор не вакуумный
тип). Это проблематично, потому что есть простой способ обнаружения
ток, который заключается в наблюдении за магнитным полем, создаваемым током,
и ЧАСТЬ цепи больше не имеет тока.
Это проблематично, потому что есть простой способ обнаружения
ток, который заключается в наблюдении за магнитным полем, создаваемым током,
и ЧАСТЬ цепи больше не имеет тока.
Дело в том, что «поправка» на магнитное поле не существовать. Соответствующее уравнение Максвелла для тока, создающего магнетизм имеет член, добавленный к текущему току смещения, который представляет собой скорость изменения электрическое поле (например, поле внутри диэлектрика конденсатора). Это дополнение к уравнению необходимо не только для цепей, у него есть дополнительный побочный эффект, заключающийся в том, что изменяющееся электрическое поле создает магнитное поле даже при отсутствии движущихся заряженных частиц.
Этот член уравнения объясняет, почему электромагнитные волны (свет) путешествует в вакууме. И, почему зарядка конденсатора (по-нашему измерений) неотличимы от непрерывного течения тока в цепь.
Буквально мы можем видеть, как светит солнце, потому что конденсатор в цепи
не отличим от непрерывного тока в цепи.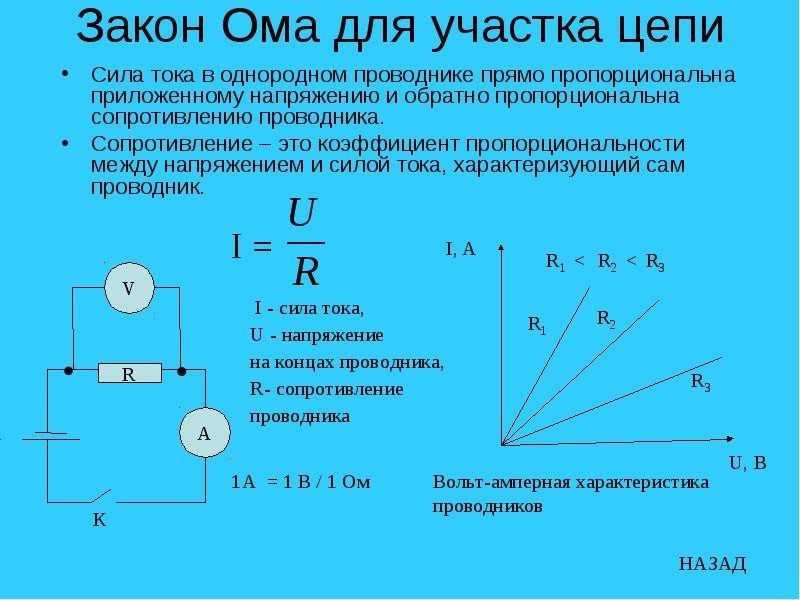
$\endgroup$
2
$\begingroup$
Конденсатор действительно блокирует постоянный ток. Однако значительный переменный ток (AC) может протекать, когда период колебаний меньше времени зарядки конденсатора.
$\endgroup$
3
$\begingroup$
Накачка электронов в одну пластину конденсатора приводит к тому, что свободные электроны на другой пластине отталкиваются, когда они «видят» входящие другие электроны. другая пластина. Для больших тарелок этот короткий импульс длинный, а для маленьких тарелок короткий импульс.
Это означает, что короткие импульсы переменного тока могут легко проходить через конденсатор, в то время как установившийся постоянный ток полностью блокируется.


 Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи.
Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию, когда электроны движутся по цепи. Аббревиатура: амп. Символ: А.
Аббревиатура: амп. Символ: А. Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью v .
Каждый из носителей тока имеет заряд q и движется с дрейфовой скоростью v .