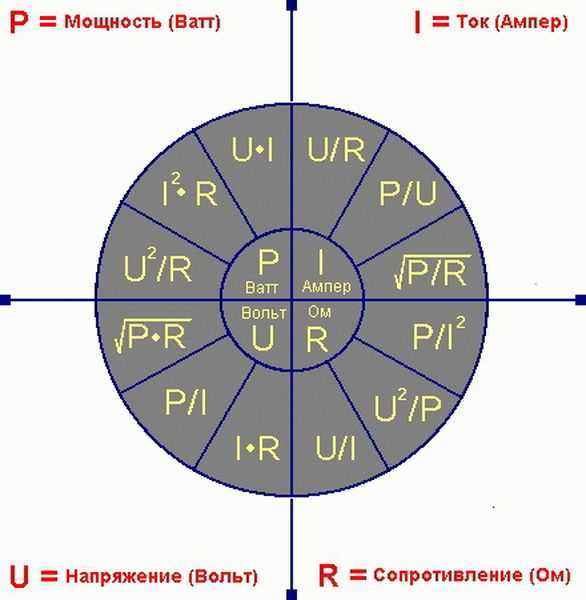
Полное руководство по извлечению квадратного корня из трех в расчетах мощности • Valence Electrical Training Services

Zach Stone, P.E. связался со мной после того, как я (Крис Верстюк пишет прямо сейчас) опубликовал свой недавний пост «Понимание великих дебатов о лидирующей и отстающей силе», потому что я неправильно определил кажущуюся силу. Благодаря его зоркому глазу и знанию предмета, никто из тех, кто приобрел Руководство по тестированию реле: Тестирование защиты реле генератора, никогда не видел моей ошибки, и я все еще могу выглядеть экспертом 😃

После того, как он позвонил мне, я зашел на его сайт и спросил себя: «Где был этот парень, когда я брал физкультуру? экзамен?» Он любезно предложил написать гостевой пост о квадратном корне из трех, который, вероятно, является наиболее распространенным числом, используемым в тестировании реле, которое мало кто действительно понимает.

Надеюсь, вам понравится этот гостевой пост от Зака.

Крис Верстюк

Вы когда-нибудь задумывались, почему квадратный корень из трех фигурирует во многих расчетах трехфазной мощности?

Откуда взялся этот номер и почему он такой особенный?

Хотя длинный ответ на эти вопросы исходит из тригонометрии, хорошая новость заключается в том, что мы можем использовать векторные диаграммы, чтобы сделать объяснение очень простым для понимания.

Понимание векторных диаграмм является важным навыком для тестирования реле, и работа с примерами в этой статье даст вам более глубокое понимание и понимание векторных величин в векторных диаграммах. Независимо от того, в какой отрасли вы работаете, это очень поможет вашей карьере в области электроэнергетики и тестирования реле.

Поскольку некоторые математические расчеты, приведенные ниже, могут быть вам незнакомы, мы рассмотрим их шаг за шагом с четкими схемами и пояснениями, чтобы вам было легко их понять.

Меня зовут Зак Стоун, физкультурник. Я ведущий инструктор популярной онлайн-программы обучения экзамену NCEES® по электроэнергетике на сайте www.electricalpereview.com, и в этой статье я собираюсь помочь вам понять, почему квадратный корень из трех так часто появляется в трехфазном питании.

Начнем со знакомого соединения звездой силового трансформатора.

1. Соединение звездой

Предположим, что у нас есть три отдельных вольтметра, подключенных поперек каждой линии к нейтрали на каждой фазе вторичных клемм трансформатора, соединенных звездой: 

Рисунок 1: Вторичные клеммы трансформатора, соединенного звездой

Если мы используем опорный угол в ноль градусов для напряжения линии A-фазы к нейтрали (VAN), результирующая векторная диаграмма напряжения для системы прямой последовательности (ABC) будет выглядеть следующим образом: 

Рис. 2: Векторная диаграмма напряжения фазы по схеме «звезда»

Взглянув на диаграмму трансформатора, мы можем использовать измерения напряжения между фазой и нейтралью, чтобы рассчитать линейное напряжение на фазе А трансформатора (VAB) путем суммирования векторных величин напряжения последовательно от клеммы фазы А до терминал B-фазы:

Рис. 3. Линейное напряжение фазы А трансформатора (VAB)  

Давайте сравним положительное опорное напряжение (+) на клемме фазы A и отрицательное опорное напряжение (-) на клемме фазы B для линейного напряжения фазы A (VAB) с фазой A и фазой B. напряжения линии к нейтрали (ВАН и ВБН):

• Полярность линии A-фазы к напряжению нейтрали (VAN) соответствует той же ориентации , что и полярность линейного напряжения A-фазы (VAB)
• Полярность линии B-фазы к напряжению нейтрали ( VBN) находится в  противоположной   ориентации  полярности линейного напряжения фазы A (VAB)

Вот почему напряжение линии B-фазы к нейтрали (VBN) является отрицательным, когда мы суммируем напряжение от Клемма фазы A к клемме фазы B, когда мы вычисляем линейное напряжение фазы A (VAB) по формуле:

ВАБ = ВАН – ВБН.

Помните, что это не обычные числа, это векторные величины с амплитудой и фазовым углом. Чтобы использовать сложение фазоров ниже, будет проще думать об этой формуле как о сложении двух фазоров. За исключением того, что один из них был умножен на минус вот так:

ВАБ = ВАН + (-ВБН).

2. Соединение звездой — умножение вектора на отрицательную единицу

Умножение векторной (или векторной) величины на отрицательное равносильно повороту векторной диаграммы на плюс-минус 180 градусов без изменения величины.

Мы можем использовать эту связь, чтобы найти -VBN из VBN:

Рис. 4. Поворот VBN на 180 градусов

Так как линия B-фазы к напряжению нейтрали (VBN) имеет фазовый угол отрицательных 120 градусов, фазовый угол для -VBN будет положительным 60 градусов и равным по величине.

Поскольку мы будем добавлять VAN и -VBN для расчета линейного напряжения фазы A (VAB), давайте покажем только эти два вектора на векторной диаграмме: 

Рисунок 5: Векторная диаграмма VAN и -VBN

Теперь мы готовы использовать сложение векторов, чтобы найти линейное напряжение фазы A (VAB).

3. Соединение звездой – Дополнение Phasor

Чтобы сложить два вектора (или вектора) вместе, сложите их друг над другом от начала до конца, затем нарисуйте новый вектор, начиная с начала координат и заканчивая головой последнего вектора.

Поскольку у нас есть два разных вектора, мы можем сделать это двумя разными способами и все равно получить одно и то же количество векторов для линейного напряжения фазы A (VAB):

F рисунок 6: VAN и -VBN Phasor Дополнение

Мы собираемся произвольно использовать первую диаграмму сложения векторов выше слева для расчета линейного напряжения фазы A (VAB), но любой из них даст одно и то же окончательное значение.

Мы также собираемся предположить, что система сбалансирована, что означает, что величины напряжения каждой линии относительно нейтрали в каждой фазе равны. Чтобы упростить предстоящую математику, мы также будем произвольно использовать значение в один вольт для этих значений (VAN = VBN = VCN = 1V).

Чтобы рассчитать линейное напряжение фазы A (VAB) с помощью сложения векторов, мы собираемся использовать немного тригонометрии, но я обещаю, что это будет просто, поэтому не пугайтесь, если вам не слишком удобно работать с синусоидой. функции косинуса и тангенса.

Во-первых, мы вычислим действительную (a) и мнимую составляющие (b) -VBN, что является еще одним способом сказать, что мы собираемся вычислить длину двух других сторон прямоугольного треугольника, который составляет -VBN. с горизонтальной осью:

Рисунок 7: Действительные (a) и мнимые (b) компоненты -VBN

Действительный компонент (a) -VBN равен 0,5, который находится с помощью функции косинуса:

Помните, что когда мы поворачивали VBN, чтобы найти -VBN, величина не менялась. Это означает, что величина -VBN по-прежнему равна одному вольту, поскольку ранее мы произвольно установили величины напряжения линии на нейтраль для каждой фазы равными 1 вольту для упрощения математики (VAN = VBN = VCN = 1 В).

Мнимая составляющая (b) -VBN приблизительно равна 0,866, что определяется с помощью функции синуса:

Мы можем использовать действительную (a) и мнимую составляющую (b) -VBN вместе с величиной VAN = 1 вольт при нуле градусов, чтобы заполнить недостающие значения векторной диаграммы линейного напряжения фазы A (VAB ): 

Рис. 8: Векторная диаграмма линейного напряжения фазы А (VAB)

Обратите внимание, что на рисунке выше мнимая составляющая линейного напряжения фазы А (VAB) равна мнимой составляющей -VBN (0,866).

Чтобы найти действительную составляющую линейного напряжения фазы А (VAB), мы просто добавим величину VAN (1 вольт) к действительной составляющей -VBN (0,5), поскольку они оба находятся под углом ноль градусов. .

Действительная составляющая линейного напряжения фазы A (VAB) равна 1 + 0,5 = 1,5: 

Рис. 9: Линейное напряжение фазы А (VAB), действительная и мнимая составляющие

Теперь мы готовы, наконец, рассчитать как амплитуду, так и фазовый угол линейного напряжения фазы А (VAB), откуда и берется квадратный корень из трех.

4. Соединение звездой – расчет величины линейного напряжения и фазового угла

Во-первых, мы рассчитаем величину линейного напряжения фазы A (VAB), используя Теорему Пифагора, где C – величина VAB, A – действительная составляющая VAB (1.5), а B – мнимая составляющая VAB. (0,866):

Величина линейного напряжения фазы A (VAB) составляет 1,732 В.

Далее мы рассчитаем фазовый угол линейного напряжения фазы A (VAB) с помощью тангенса:

Фазовый угол (ɸ) линейного напряжения фазы А (VAB) составляет 30 градусов.

Завершенная векторная диаграмма линейного напряжения фазы A (VAB) выглядит следующим образом: 

Рис. 10: Линейное напряжение фазы A (VAB), завершенная векторная диаграмма

Если вы знакомы с расчетами трехфазной мощности, то число 1,732 должно быть вам также знакомо.

Поскольку мы использовали значение 1 вольт для величины линейных напряжений фаз A, B и C к нейтрали (VAN = VBN = VCN = 1 В), линейное напряжение фазы A (VAB) ровно в 1,732 раза больше.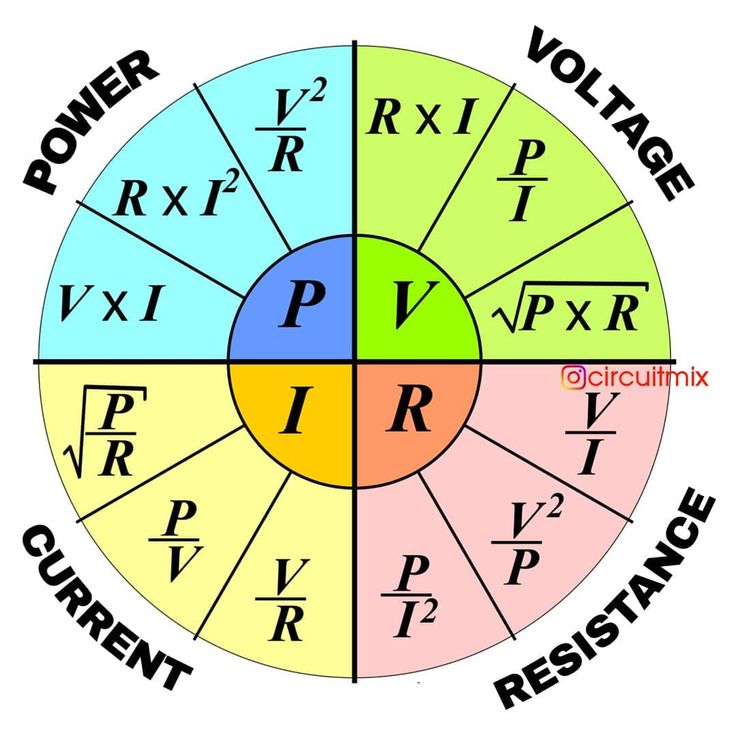 чем линия А-фазы к напряжению нейтрали (VAN).

1,732 на самом деле является квадратным корнем из трех:

5. Соединение звездой – линейные и фазовые отношения

Линейное напряжение сбалансированной трехфазной системы всегда будет больше, чем линейное напряжение к нейтрали, точно на квадратный корень из трех из-за сложения фазора.

В нашем случае мы добавили линию фазы A к напряжению нейтрали (VAN) с отрицательной линией фазы B к напряжению нейтрали (-VBN), чтобы найти линейное напряжение фазы A (VAB):

Рисунок 11: Линейное напряжение фазы А трансформатора (VAB)

Поскольку мы использовали опорный угол, равный нулю градусов, для напряжения линии фазы A к напряжению нейтрали (VAN), напряжение линии фазы A (VAB) опережает линию фазы A к напряжению нейтрали (VAN) ровно на 30 градусов.

Это же отношение сложения фазора также является причиной того, что линейное напряжение всегда опережает линейное напряжение на нейтраль на 30 градусов для сбалансированной системы с прямой последовательностью (ABC).

Если бы мы завершили весь этот процесс для двух других оставшихся фаз B и C и нарисовали результирующую векторную диаграмму, то увидели бы, что это применимо к каждой фазе: 

Рис. 12. Векторная диаграмма напряжения для всех трех фаз соединения звездой

Вы заметите, что приведенная выше векторная диаграмма представляет собой векторную диаграмму напряжения для сбалансированного и положительной последовательности (ABC) соединения звездой, с которым вы, скорее всего, уже знакомы.

6. Соединение звездой — использование калькулятора

Если у вас есть калькулятор, который может обрабатывать векторы как в полярной (величина и угол), так и в прямоугольной (действительная составляющая и мнимая составляющая), вы можете сделать все вышеперечисленное за один шаг в своем калькуляторе, хотя это действительно помогает знать что калькулятор делает в процессе, чтобы вы понимали, откуда берутся эти значения.

Здесь то же соединение трансформатора вторичной обмотки звездой, что и раньше, с линейным напряжением фазы A (VAB), показанным как разница между напряжением линии A-фазы и нейтрали (VAN) и напряжением фазы B-фазы-фазы-нейтрали (VBN). :

Рисунок 13: Линейное напряжение фазы А трансформатора (VAB)

Рассчитаем линейное напряжение фазы А (VAB) с помощью калькулятора.

Я использую Texas Instruments 36X Pro (TI 36X Pro), который является моим личным фаворитом для электрических расчетов, поскольку он может легко обрабатывать векторы как в полярной, так и в прямоугольной форме.

Мы будем использовать значение 1 В для величины напряжения между фазой A и нейтралью (VAN) и 1 В для величины напряжения между фазой B и нейтралью (VAB), как мы это делали вручную.

Мы также будем использовать 0 градусов для фазового угла между фазой A и напряжением нейтрали (VAN) и отрицательные 120 градусов для напряжения между фазой B и напряжением нейтрали (VAB):

Обратите внимание, что мы получаем одно и то же значение 1,732 для величины линейного напряжения фазы A (VAB) и 30 градусов для фазового угла линейного напряжения фазы A (VAB).

Обратите внимание, что это идентично величине квадратного корня из трех под углом 30 градусов: 

7.

Соединение Дельта

Теперь, когда мы понимаем, откуда берется квадратный корень из трех для соединения звездой, как насчет соединения треугольником?

Давайте посмотрим на клеммы вторичной обмотки трансформатора, соединенного треугольником, и покажем фазные токи внутри соединения треугольником: 

Рисунок 14: Клеммы вторичной обмотки трансформатора Delta Connected

При использовании амперметра в каждой фазе и опорного угла, равного нулю градусов, для фазного тока в фазе А соединения треугольником (IBA), результирующая векторная диаграмма фазных токов треугольника будет выглядеть следующим образом: 

Рис. 15: Диаграмма вектора тока фазы «треугольник»

Взглянув на схему трансформатора, мы можем рассчитать линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенной треугольником, используя закон Кирхгофа для тока: 

Рисунок 16: Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником

Текущий закон Кирхгофа гласит, что сумма токов, входящих в узел, должна равняться сумме токов, выходящих из того же узла.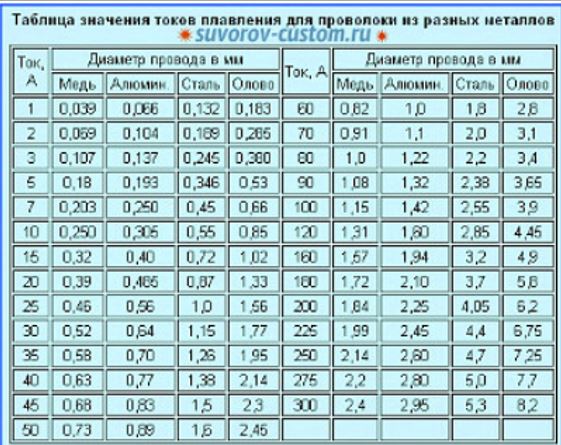

Глядя на клемму фазы A выше, обратите внимание, что единственный входящий ток — это ток фазы треугольника A (IBA), в то время как ток, выходящий из узла, представляет собой ток фазы треугольника C (IAC) и ток фазы A. линейный ток (IA).

Мы будем использовать закон тока Кирхгофа, чтобы установить их равными друг другу, а затем перестроить, чтобы найти линейный ток фазы A (IA):

Ток линии A (IA), выходящий из вторичной обмотки трансформатора, соединенного треугольником, равен разнице тока фазы треугольника A (IBA) и тока фазы треугольника C (IAC).

Или, если вместо этого мы хотим думать с точки зрения сложения, Ток линии A (IA), выходящий из вторичной обмотки трансформатора, соединенного треугольником, равен сумме тока фазы треугольника A (IBA) и отрицательной единицы, умноженной на C -фазный дельта-фазный ток (IAC).

Выглядит знакомо? Это очень похоже на соотношение, с которым мы работали в предыдущем примере напряжения линии А для соединения звездой.

8. Дельта-соединение — умножение вектора на отрицательную единицу

Как и раньше, сначала найдем -ICA, повернув ICA на плюс-минус 180 градусов: 

Рисунок 17: Поворот IAC на 180 градусов

Поскольку фазовый ток дельта-фазы (IAC) фазы C имеет фазовый угол 120 градусов, фазовый угол для отрицательного IAC будет отрицательным 60 градусов. Помните, что это не влияет на величину.

Поскольку IA = IBA – ICA, давайте покажем только IBA и -ICA на векторной диаграмме: 

Рисунок 18: Векторная диаграмма IBA и -IAC ​​

Как и раньше, мы готовы использовать сложение векторов, складывая каждый вектор поверх другого и рисуя полученный вектор из начала координат.

9. Соединение треугольником – дополнение Phasor

Поскольку мы добавляем два вектора, мы выполняем добавление векторов двумя разными способами и по-прежнему получаем одно и то же количество векторов для линейного тока фазы A (IA):

Рисунок 19: Дополнение IBA и -IAC ​​Phasor

Мы произвольно выберем диаграмму сложения первого вектора вверху слева для расчета линейного тока фазы A (IA).

Как и раньше, мы также будем считать, что система сбалансирована, что означает, что величина дельта-фазного тока в каждой фазе одинакова. Чтобы упростить дальнейшую математику, мы также будем произвольно использовать значение в один ампер для этих значений (IBA = ICB = IAC = 1A).

Для расчета IA мы будем использовать те же тригонометрические отношения, что и раньше.

Во-первых, мы вычислим действительную (a) и мнимую составляющие (b) -IAC, что является еще одним способом сказать, что мы собираемся вычислить длину двух других сторон треугольника, который -IAC ​​образует с горизонтальная ось:

Рисунок 20: Действительные (a) и мнимые (b) компоненты -IAC ​​

Действительный компонент (a) -IAC ​​равен 0,5, который находится с помощью косинуса:

Помните, что когда мы поворачивали IAC, чтобы найти -IAC, величина не менялась. Это означает, что величина -IAC ​​по-прежнему равна одному амперу, поскольку мы произвольно установили величины дельта-фазного тока в каждой фазе равными 1 амперу для упрощения математики (IBA = ICB = IAC = 1A).

Мнимая составляющая (b) -IAC ​​приблизительно равна -0,866, что определяется с помощью синуса:

Мы можем использовать действительную (a) и мнимую составляющие (b) -IAC ​​вместе с величиной IBA = 1 ампер при нуле градусов, чтобы заполнить значения для векторной диаграммы линейного тока фазы A (IA) :

Рис. 21. Векторная диаграмма линейного тока фазы А (IA)

Обратите внимание, что мнимая составляющая линейного тока фазы А (IA) равна мнимой составляющей -IAC ​​(0,866).

Чтобы найти действительную составляющую линейного тока фазы А (IA), мы просто добавим величину IBA (1 ампер) к действительной составляющей -IAC ​​(0,5), поскольку они оба находятся под одним и тем же углом нуля. градусов.

Действительная составляющая линейного тока фазы А (IA) равна 1 + 0,5 = 1,5:

Рис. 22: Действительная и мнимая составляющие линейного тока фазы A (IA)

Теперь мы готовы, наконец, рассчитать как величину, так и фазовый угол линейного тока фазы А (IA), откуда берется квадратный корень из трех.

10. Соединение треугольником – расчет величины линейного напряжения и фазового угла

Сначала мы рассчитаем величину линейного тока фазы A (IA), используя Теорему Пифагора, где C – величина IA, A – действительная составляющая IA (1.5), а B – мнимая составляющая IA. (-0,866):

Величина линейного тока фазы A (IA) составляет 1,732 А.

Далее мы рассчитаем фазовый угол линейного тока фазы A (IA) с помощью тангенса:

Фазовый угол (ɸ) линейного тока фазы А (IA) составляет минус 30 градусов.

Завершенная векторная диаграмма линейного тока фазы A (IA) выглядит следующим образом: 

Рис. 23. Линейный ток фазы А (IA), завершенная векторная диаграмма

Опять же, если вы знакомы с расчетами трехфазной мощности, то число 1,732 должно быть вам также знакомо.

Поскольку мы использовали значение 1 ампер для величины дельта-фазных токов фаз A, B и C (IBA = ICB = IAC = 1A), линейный ток фазы A (IA) точно в 1,732 раза больше, чем дельта-фазный ток фазы А (IBA).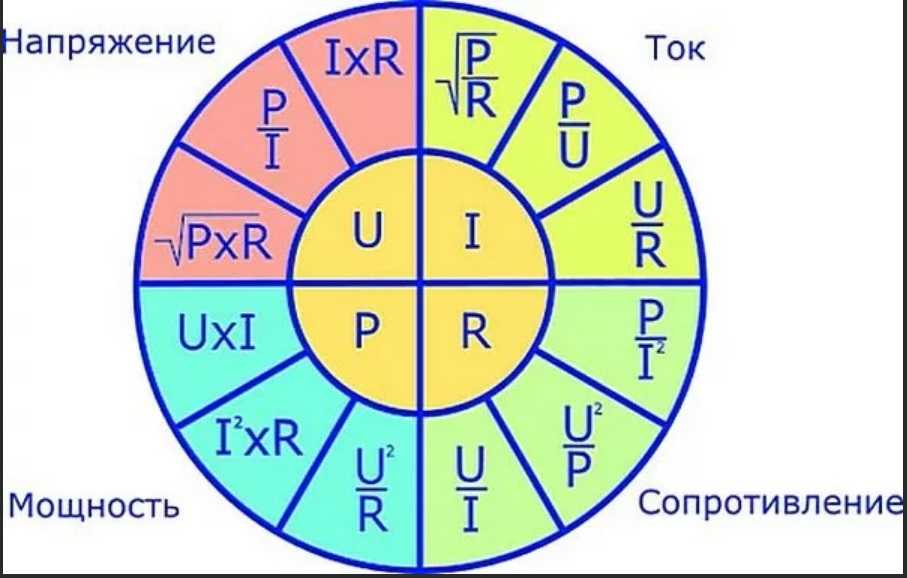

1,732 на самом деле является квадратным корнем из трех:

11. Соединение по схеме «треугольник» — соотношение между линией и фазой

Линейный ток сбалансированной трехфазной системы всегда будет больше дельта-фазного тока ровно на квадратный корень из трех из-за сложения векторов.

В нашем случае мы добавили дельта-фазный ток фазы A (IBA) с отрицательным дельта-фазным током фазы C (-IAC), чтобы найти линейный ток фазы A (IA): 

Рис. 24. Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником

Поскольку для дельта-фазного тока фазы A (IBA) мы использовали опорный угол, равный нулю, линейный ток фазы A (IA) отстает от дельта-фазного тока A-фазы (IBA) ровно на 30 градусов.

Это же отношение сложения векторов также является причиной того, что линейный ток системы всегда будет отставать от дельта-фазного тока на 30 градусов для сбалансированной системы с прямой последовательностью (ABC).

Если бы мы завершили весь этот процесс для двух других оставшихся фаз B и C и начертили результирующую векторную диаграмму, то увидели бы, что это применимо к каждой фазе: 

Рисунок 25: Текущая векторная диаграмма для всех трех фаз соединения треугольником

Вы заметите, что приведенная выше векторная диаграмма представляет собой текущую векторную диаграмму для треугольного соединения со сбалансированной прямой последовательностью (ABC), с которым вы, скорее всего, уже знакомы.

12. Соединение треугольником – Использование калькулятора

Как и раньше, давайте воспользуемся TI 36X Pro для расчета линейного тока фазы А (IA), выходящего из соединения треугольником, и сравним его со значением, полученным вручную.

Вот то же соединение вторичного трансформатора по схеме треугольника, где линейный ток фазы A (IA) показан как разница между током фазы треугольника A (IBA) и током фазы треугольником C (IAC):

Рис. 26. Линейный ток фазы А, выходящий из вторичной обмотки трансформатора, соединенного треугольником

Мы будем использовать значение 1 А для величины дельта-фазного тока фазы А (IBA) и 1 А для величины дельта-фазного тока фазы С (IAC), как мы это делали вручную.

Мы также будем использовать 0 градусов для фазового угла дельта-фазы (IBA) фазы A и положительные 120 градусов для дельта-фазы тока C (IAC):

Обратите внимание, что мы получаем то же значение 1,732 для величины линейного тока фазы A (IA) и отрицательные 30 градусов для фазового угла линейного тока фазы A (IA).

Обратите внимание, что это идентично величине квадратного корня из трех под углом минус 30 градусов: 

13. Трехфазная полная мощность и квадратный корень из трех

Мы выяснили, откуда берется квадратный корень из трех для соединения звездой и треугольником, но как насчет квадратного корня из трех в трехфазной формуле полной мощности?

Формула трехфазной полной мощности представляет собой произведение квадратного корня из трех, величины линейного напряжения (VL) и величины линейного тока (IL):

Эти значения представляют собой величин только , поэтому избегайте распространенной ошибки использования векторных величин в этой формуле для расчета как кажущейся мощности, так и угла мощности.

Эта формула чаще всего используется для расчета силы тока при полной нагрузке силового трансформатора путем подстановки номинальной трехфазной полной мощности трансформатора [вольт-ампер] и линейного напряжения первичного соединения для расчета полной первичной нагрузки. ток нагрузки, потребляемый трансформатором, или линейное напряжение вторичного соединения для расчета тока полной вторичной нагрузки, выдаваемого трансформатором:

Рис. 27. Первичный и вторичный номинальный ток

Чтобы понять, откуда в этой формуле берется квадратный корень из трех, давайте начнем с демонстрации того, как он получается из однофазной полной мощности (S1ø).

Для сбалансированной трехфазной системы величина полной мощности в каждой фазе всегда одинакова. Это означает, что трехфазная полная мощность (S3ø) на самом деле всего в три раза больше полной мощности в любой заданной фазе (S1ø) сбалансированной трехфазной системы:

Однофазная полная мощность (S1ø) в любой заданной фазе сбалансированной трехфазной системы является произведением величины фазного напряжения (VP) и величины фазного тока (IP):

Подставим это обратно в формулу трехфазной полной мощности (S3ø):

Давайте воспользуемся этой версией формулы трехфазной кажущейся мощности (S3ø) и посмотрим, как она применима к соединению звездой или треугольником, чтобы выяснить, откуда берется квадратный корень из трех в исходной формуле.

Сначала начнем с соединения звездой.

14. Соединение звездой, трехфазная полная мощность и квадратный корень из трех

Для соединения звездой величина линейного напряжения фазы нейтрали (VP) меньше величины линейного напряжения системы (VL) на коэффициент квадратный корень из трех, как мы обнаружили в первой половине этой статьи. .

Однако величина фазного тока (IP) соединения звездой равна величине линейного тока (IL) системы.

Когда мы подставляем соотношения напряжения и тока фазы по схеме «звезда» в формулу трехфазной полной мощности (S3ø), она выглядит следующим образом:

Мы можем начать упрощение, отделив коэффициенты (3 и 1/√3) от переменных (VL и IL):

Теперь самое сложное. Мы собираемся умножить на квадратный корень из трех на квадратный корень из трех (√3/√3). Поскольку это то же самое, что умножение на 1, значение формулы не меняется (любое число, умноженное на 1, остается тем же числом, что и раньше):

Теперь два квадратных корня из трех в нижней части каждой дроби при умножении вместе будут равны трем (√3 X √3 = 3):

Наконец, три в верхней части дроби и три в нижней части дроби будут отменены (3/3 = 1):

Результатом является знакомая нам формула трехфазной кажущейся мощности (S3ø), которая включает квадратный корень из трех.

Квадратный корень из трех в этой формуле получен путем подстановки соотношений напряжения и тока фазы по схеме «звезда» в формулу трехфазной полной мощности (S3ø).

Справедливо ли то же самое для соединения треугольником?

15. Соединение треугольником, трехфазная полная мощность и квадратный корень из трех

При соединении треугольником величина фазного тока (IP) меньше величины линейного тока системы (IL) на коэффициент квадратный корень из трех, как мы обнаружили в первой половине этой статьи.

Однако величина фазного напряжения (VP) соединения треугольником равна величине линейного напряжения (VL) системы.

Когда мы подставляем отношения дельта-фазы тока и фазного напряжения в формулу трехфазной полной мощности (S3ø), она выглядит следующим образом:

Опять же, мы можем начать упрощение, отделив коэффициенты (3 и 1/√3) от переменных (VL и IL):

Давайте снова умножим на квадратный корень из трех из квадратного корня из трех (√3/√3), так как это то же самое, что умножить на 1, а затем продолжим упрощать выражение, используя те же методы, что и раньше:

В результате снова получается та же знакомая нам трехфазная формула кажущейся мощности, которая включает квадратный корень из трех. Квадратный корень из трех в этой формуле получается из-за подстановки соотношения дельта-фазного напряжения и фазного тока в формулу трехфазной полной мощности (S3ø).

Обратите внимание, что квадратный корень из трех в формуле трехфазной полной мощности (S3ø) существует независимо от того, присутствует ли соединение треугольником или звездой, пока мы используем линейные значения системы. Аккуратный!

16. Кто я и где меня найти

Надеюсь, вам понравилось исследовать, откуда берется квадратный корень из трех в большинстве расчетов трехфазной электроэнергии.

Меня зовут Зак Стоун, ЧП. и я являюсь ведущим инструктором популярной онлайн-программы обучения для экзамена NCEES® по электроэнергетике на сайте www.electricalpereview.com. Я создаю все их учебные материалы и провожу их живые занятия каждый семестр.

Зак Стоун, ЧП
Обзор электрического оборудования PE, INC

Вот моя 10-секундная биография:

• Я инженер с профессиональной лицензией в штате Флорида.
• В 2010 году я получил диплом инженера-электрика, аккредитованный ABET.
• Я сдал экзамены FE и PE с первой попытки.
• У меня богатый опыт работы в области промышленной автоматизации, управления двигателями, производства электроэнергии и подстанций среднего напряжения.
• Мне нравится заниматься математикой в ​​области электротехники и учить других.

Если вы инженер-электрик и планируете когда-нибудь в будущем сдавать экзамен PE, или если вы хотите прочитать больше статей о нюансах математики, лежащих в основе электротехники, вы можете найти меня на www. www.electricpereview.com.

Если вы действительно хотите чему-то научиться, полезно посмотреть, как разные люди описывают тему. Я кратко освещаю эту тему в The Relay Testing Handbook: Principles and Practice/Глава 1, раздел D) Трехфазные соединения [страницы 14 и 15]. Вы можете просмотреть, если хотите сравнить два разных объяснения, чтобы копнуть глубже и по-настоящему понять, откуда берется квадратный корень из трех.