Катушка сопротивлением 100 Ом, состоящая из 1000 витков, площадью 5 см2 каждый

Условие задачи:

Катушка сопротивлением 100 Ом, состоящая из 1000 витков, площадью 5 см² каждый, внесена в однородное магнитное поле. Магнитная индукция уменьшилась на 5 Тл. Какой заряд протекает по катушке, если её концы замкнуты?

Задача №8.4.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=100\) Ом, \(N=1000\), \(S=5\) см², \(\Delta B=5\) Тл, \(q-?\)

Решение задачи:

В общем случае магнитный поток \(\Phi\) через некоторую плоскую поверхность, помещённую в однородном магнитном поле, можно определить по такой формуле:

\[\Phi = BS\cos \alpha \;\;\;\;(1)\]

В этой формуле \(B\) – индукция магнитного поля, \(S\) – площадь поверхности, через которую определяется магнитный поток, \(\alpha\) – угол между нормалью к площадке и вектором магнитной индукции.

Если учесть, что катушка имеет \(N\) витков, то формула (1) примет следующий вид:

\[\Phi = NBS\cos \alpha \]

Примем, что плоскость каждого витка катушки перпендикулярна вектору магнитной индукции, то есть угол \(\alpha\) равен 90°, поскольку иного не сказано в условии. Запишем формулы для определения начального \(\Phi_1\) и конечного \(\Phi_2\) значений магнитного потока:

\[\left\{ \begin{gathered}
{\Phi _1} = N{B_1}S \hfill \\
{\Phi _2} = N{B_2}S \hfill \\
\end{gathered} \right.\]

Тогда очевидно, что изменение магнитного потока \(\Delta \Phi\) равно:

\[\Delta \Phi = NS\left( {{B_1} – {B_2}} \right)\]

Или, если принять, что \(\Delta B = {B_1} – {B_2}\):

\[\Delta \Phi = NS\Delta B\;\;\;\;(2)\]

Понятно, что из-за изменения магнитного потока в рамке будет возникать ЭДС индукции. Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока. Поэтому:

\[{{\rm E}_i} = \frac{{\Delta \Phi }}{{\Delta t}}\]

Подставим в полученную формулу выражение (2):

\[{{\rm E}_i} = \frac{{NS\Delta B}}{{\Delta t}}\;\;\;\;(3)\]

С другой стороны, из закона Ома следует, что:

\[{{\rm E}_i} = IR\;\;\;\;(4)\]

В этой формуле \(I\) – сила тока в катушке, \(R\) – сопротивление катушки. { – 4}} \cdot 5}}{{100}} = 0,025\;Кл = 25\;мКл\]

Ответ: 25 мКл.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.4.39 Катушку с ничтожно малым сопротивлением и индуктивностью 3 Гн подключают
8.4.41 Проводник длиной 25 см движется в однородном магнитном поле с индукцией 4 Тл
8.4.42 Рамка площадью 300 см2 имеет 200 витков и находится в магнитном поле 0,1 Тл, силовые

Из архива С. Варламова

Из архива С. Варламова

Задачи ТЮФА

Среди стандартного оборудования школьных кабинетов физики есть разборный трансформатор, состоящий из катушек и железного сердечника, – он входит в комплект для демонстрации явления электромагнитной индукции. В этом же наборе есть два кольца – из алюминия и меди. Диаметр их такой, что они как раз надеваются на сердечник трансформатора. Для успешной демонстрации явления электромагнитной индукции достаточно поставить вертикально на стол только короткую часть железного сердечника, на нее надеть катушку с надписью «1200–2400», а обмотку катушки с выводами 0–1200 через ключ подключить к сети 220 В. Если кольца (поодиночке или вместе) расположить на верхнем торце катушки, то при замыкании ключа они подпрыгивают.

Думаю, что все учителя физики показывают этот эксперимент в 11-м классе, но позволю себе обратить внимание на то, что и в какой последовательности демонстрировать.

Для начала я показываю «прыжок» алюминиевого кольца – оно взлетает примерно на 30 см и обычно обратно на сердечник не попадает. Затем показываю опыт с медным кольцом – оно подпрыгивает совсем невысоко, на 5–7 см, и «зависает» на некотором расстоянии от своего начального положения – до тех пор, пока катушку не отключают от сети. Через несколько секунд даю подержать кольцо кому-нибудь из учеников. Оно разогрелось – это сразу чувствуется. Кстати, если прикоснуться к обмотке катушки, то никакого нагрева не обнаружится. Это говорит о том, что индуктивное сопротивление катушки много больше ее омического сопротивления.

После этой «затравки» задаю вопрос: а как поведут себя кольца, если надеть их на сердечник вместе? Что будем наблюдать, если положить медное кольцо сверху? а если алюминиевое? Предлагаю сначала предсказать результат эксперимента.

cos wt, так и горизонтальную В_ъЅ(t) = В_ъЅcoswt составляющие. Мы считаем направление «вверх» положительным. Амплитуда тока в катушке прямо пропорциональна амплитуде напряжения в сети U₀ и обратно пропорциональна частоте w и индуктивности катушки L_кат:

Если материал сердечника имеет большую магнитную восприимчивость m и при протекании тока не происходит его насыщения, то индукцию магнитного поля можно считать пропорциональной m и числу витков катушки N, приходящихся на единицу ее длины l:

Ток в катушке переменный, поэтому магнитный поток через площадку, ограниченную кольцом, изменяется. Следовательно, в кольце возникает ток самоиндукции. Все геометрические размеры и материал кольца нам известны. Ученики вспоминают, что кольцо при пропускании переменного тока через катушку разогревается, и быстро догадываются, что нужно учесть омическое сопротивление R кольца. Однако очень редко сразу вспоминают (в моей практике такого просто ни разу не было), что и кольцо имеет индуктивность.

coswt – составляющая индукции магнитного поля вдоль оси кольца. Теперь, зная ток, протекающий по кольцу, найдем силу Ампера, действующую на кольцо вдоль его оси:

Очевидно, что среднее значение силы Ампера за период равно нулю, – но кольцо-то прыгает! Что-то не в порядке с уравнением. Где же мы допустили ошибку? Вспоминаем, что магнитное поле самого кольца тоже создает магнитный поток через это самое кольцо, т.е. кольцо имеет индуктивность L. Исправленное уравнение для тока через кольцо будет теперь выглядеть так:

Это уравнение позволяет найти переменный ток в цепи, состоящей из последовательно включенных омического сопротивления R и индуктивности L, которая подключена к источнику переменного напряжения U (t) = SB

ъЅwsinwt. Решить это уравнение можно, например, методом векторных диаграмм. Фаза тока в цепи отличается от фазы напряжения источника:

Мгновенное значение силы, действующей на кольцо со стороны магнитного поля:

Вот теперь видно, что средняя за период сила, действующая на кольцо со стороны магнитного поля, не равна нулю:

Отметим, что средняя сила направлена в положительном направлении (вверх).

ЧB_ъЅ. Будем считать, что материал сердечника катушки имеет большую магнитную проницаемость m, но не достигает насыщения. Тогда это произведение компонент, в свою очередь, пропорционально величине:

Здесь U – напряжение сети, l – длина сердечника, N – число витков катушки, pr² – площадь сечения сердечника. Поскольку формула для средней силы запишется так:

В приведенных формулах омическое сопротивление кольца R и его индуктивность L сами зависят от радиуса кольца r и от других его геометрических размеров (высоты и толщины), а также от материала кольца. При заданных размерах сердечника и кольца, а также при фиксированной частоте колебаний тока средняя сила будет увеличиваться при увеличении напряжения на катушке и уменьшении числа витков катушки:

Предсказываемую зависимость от числа витков и напряжения можно проверить, взяв другую катушку из набора и подавая на нее напряжение от регулируемого источника – лабораторного автотрансформатора (ЛАТР).

Полученная формула для средней силы позволяет проанализировать результаты экспериментов, в которых кольца подпрыгивали вверх при включении катушки в сеть. И для алюминиевого кольца, и для медного существует определенная высота над катушкой, на которой средняя сила, действующая на кольцо со стороны магнитного поля, уравновешивается силой тяжести. Это связано с тем, что по мере перемещения кольца вверх уменьшаются и вертикальная, и горизонтальная составляющие индукции магнитного поля в месте расположения кольца. Экспериментально можно установить, что соответствующая высота для алюминиевого кольца больше высоты для медного кольца. Действительно, плотность меди (8960 кг/м

3) в 3,3 раза больше плотности алюминия (2690 кг/м³), а удельные сопротивления этих металлов отличаются всего в 1,6 раза.

Напомним, что выражения для средней силы, действующей на кольцо со стороны магнитного поля, были получены для покоящегося кольца. При механическом движении колец в магнитном поле магнитный поток изменяется.

Для точного описания движения кольца это изменение, конечно, необходимо учитывать.

Однако легко показать, что скорость изменения магнитного потока, связанная с механическим движением кольца, в данном эксперименте (при частоте переменного тока 50 Гц и высотах подпрыгивания кольца около 0,3 м) меньше скорости изменения потока, связанной с переменным характером тока в катушке. Например, алюминиевое кольцо разгоняется на участке длиной примерно 10 см, а взлетает вверх еще примерно на 20 см. Время движения с ускорением, направленным вверх, равно примерно 0,1 с. За это время магнитное поле успевает десять раз сменить направление. Это означает, что движение катушки можно рассматривать как медленное – квазистатическое. Участок пути, на котором алюминиевая катушка движется с ускорением вверх, длиннее соответствующего участка для медного кольца. Да и само ускорение больше. Вот почему алюминиевое кольцо прыгает выше, чем медное.

Теперь самый интересный вопрос: а почему же положенные на катушку вместе медное и алюминиевое кольца прыгают высоко? Кольцо находится в суммарном магнитном поле, созданным током в катушке и током, протекающим по второму кольцу.

Верхнее кольцо при протекании по нему тока уменьшает вертикальную компоненту индукции магнитного поля и одновременно увеличивает горизонтальную компоненту индукции для нижнего кольца. Произведение компонент индукции магнитного поля при этом увеличивается, а значит, увеличивается средняя сила, действующая на нижнее кольцо. Вот почему медное кольцо подскакивает выше, когда над ним находится алюминиевое кольцо. Это же рассуждение объясняет, откуда берется дополнительная сила, позволяющая находящемуся снизу алюминиевому кольцу не только взлететь, но и подтолкнуть лежащее сверху медное кольцо на большую высоту.

Эксперимент показывает, что после подключения катушки к сети оба кольца летят вместе. На начальном этапе полета они просто соприкасаются друг с другом. Это тоже легко объяснить. Индукционный ток в кольцах хоть и уменьшает внешнее магнитное поле, но не до нуля. Это означает, что индукционные токи в обоих кольцах имеют одинаковое направление. А как известно, провода с токами одного направления притягиваются друг к другу.

В заключение можно поставить перед собой задачу: подобрать такие условия, при которых кольцо взлетит как можно выше. Экспериментаторы! Дело за вами, найдите оптимальные размеры и форму катушки, сердечника и кольца, чтобы кольцо – на радость учителям и ученикам – взлетало в классе под самый потолок!

С. Варламов,

СУНЦ МГУ, МИОО, г. Москва

.

4 быстрых формулы для планирования производства

Обработка рулонной продукции — это простой и эффективный способ внедрения концепции бережливого производства при производстве листового металла: поточное производство, непрерывный процесс, сокращение незавершенного производства и минимальное количество отходов.

Четыре быстрые формулы помогают планировать производство и отвечают на следующие простые вопросы:

• Как рассчитать длину рулона по внутреннему диаметру, внешнему диаметру и толщине?
• Как рассчитать время работы металлической катушки?
• Как рассчитать длину рулона по весу, типу материала, ширине и толщине?
• Как рассчитать вес рулона по ширине, внешнему и внутреннему диаметру?

В этой статье я покажу, как получаются эти формулы, чтобы предоставить инструменты, которые можно легко адаптировать к новым материалам и условиям.

Перейдите по ссылкам и узнайте больше о линиях профилирования и системах пробивки рулонов и лазерной резки.

Определение металлической катушки

Прежде всего, давайте определим, какая основная информация определяет металлическую катушку.

Внутренний диаметр рулона ( ID измеряется в [мм]) зависит от типа моталки линии продольной резки. Наиболее распространенные размеры отверстия 508 мм, но также используются 406 и 610 мм.

Катушка наружный диаметр ( OD измеряется в [мм]) зависит от возможностей сервисного центра. Также необходимо сверить с геометрическими характеристиками разматывателя, на котором будет обрабатываться рулон металла.

В следующих расчетах толщина ( T , измеренная в [мм]) рулона металла означает общую толщину, включая краску, если она присутствует. В случае рулонов с покрытием толщина краски может составлять от 0,03 мм до 0,08 мм: обратите внимание, что некоторые производители рулонов с покрытием указывают на этикетках рулонов только толщину металла.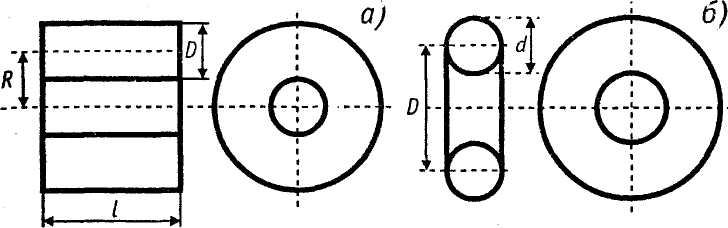 Толщина краски может незначительно влиять на результаты формул.

Катушка ширина ( Вт измеряется в [мм]) представляет собой поперечный размер катушки и вместе с предыдущей информацией позволяет рассчитать катушку 93

Определив геометрию рулона, легко рассчитать вес металлического рулона (измеряется в [кг]).

Давайте теперь посмотрим, как ответить на каждый из четырех вопросов.

Как рассчитать длину рулона по внутреннему диаметру, внешнему диаметру и толщине?

Довольно часто в мастерской нет информации о весе рулона или типе материала. В этой ситуации мы все еще можем рассчитать длину катушки по геометрии катушки. Все, что нам нужно, это измерить внешний диаметр катушки, внутренний диаметр и толщину. 92)/(T*1000)

Коэффициент 1000 используется для компенсации размеров в [мм] с длиной в [м].

Например, , рулон с наружным диаметром 1600 мм, внутренним диаметром 508 мм и толщиной 0,6 мм дает длину 3010 метров.

Эта формула чрезвычайно полезна, поскольку позволяет быстро рассчитать погонные метры на обрабатываемом рулоне (например, с помощью лазерного датчика, который считывает диаметр рулона) и, следовательно, по следующей формуле рассчитать время работы машины. .

Как рассчитать время работы металлической катушки?

Исходя из длины рулона, имея всего две информации, можно рассчитать автономную работу машины. Все, что нам нужно знать, это длина детали и время цикла.

(Количество деталей) = L/(Длина детали)

(Время работы катушки в минутах) = (Количество деталей)*(Секунд на деталь)/60

2 Например, 90 , где (Длина детали) = 1,4 м и (Время цикла на деталь) = 12 с, формула дает:

(Количество деталей) = 2150

(Время работы) = 430 минут = 7,2 часа

По моему мнению, эти две формулы остаются наиболее полезными в рулонном производстве.

В некоторых случаях детали могут иметь переменную длину и переменное время цикла: в этом случае мы можем использовать среднюю длину и время цикла или рассчитать время работы на основе количества метров в минуту, производимых линией (например, в профилегибочные линии).

Как рассчитать длину рулона по весу, типу материала, ширине и толщине?

При планировании производства иногда требуется принимать решения, не имея физической катушки для принятия мер. Например, у нас может быть только информация о весе рулона, ширине и толщине материала.

Для расчета длины рулона (L) мы исходим из веса рулона (W) и плотности материала (D)

(Вес в [кг]) = (Объем)*D 93).

Следующий график представляет собой интересный инструмент, показывающий вес на миллиметр ширины рулона стали с внутренним диаметром 508 мм.

Например, , тот же стальной рулон с наружным диаметром 1600 мм, внутренним диаметром 508 мм и шириной 250 мм имеет вес 3500 кг.

Важные примечания

• В определении катушки я определил единицу измерения, с которой размеры и плотность должны использоваться в формулах: в окончательные формулы введены коэффициенты для компенсации различных единиц измерения.
• На все размеры распространяются допуски (например, толщина листового металла). Эти допуски также повлияют на конечный результат.
• Мы исходили из катушек с плотной намоткой: если катушка будет свободной, это приведет к меньшему весу и меньшей длине, чем расчетные результаты.

Выводы

Обработка рулонов становится все более популярной из-за концепции бережливого производства, которая сразу же внедряется в мастерскую. Кроме того, рулоны металла облегчают планирование производства, обеспечивают длительное время безотказной работы технологических линий и зачастую имеют более низкую стоимость тонны, чем металлический лист.

При поиске в Интернете доступно множество калькуляторов катушек (просто введите в Google «калькулятор металлических катушек»).

Я считаю важным понять, как получаются эти формулы , так как это позволяет нам адаптировать их к различным практическим ситуациям, а также помогает нам принимать быстрые решения на семинаре благодаря более быстрому обучению .

Вопрос Видео: Расчет момента магнитного диполя круглой катушки

Стенограмма видео

Круглая катушка диаметром 12 мм см несет ток 𝐼, который создает магнитное поле в его центре. величина, умноженная на два раза по 10 в степени минус четыре тесла. Учитывая, что 𝜇 ноль равно четырем 𝜋 умножить на 10 в степени минус семь генри на метр, вычислить магнитное дипольный момент этой катушки. (A) 1,782 ампер-метра в квадрате, (B) 3,6 ампер-метра в квадрате, (C) 0,0624 ампер-метра в квадрате, (D) 0,216 ампер-метра метров в квадрате.

В этом вопросе мы попросили рассчитать магнитный дипольный момент этой катушки. Мы можем вспомнить, что если у нас есть петля из токоведущего провода, где ток имеет величину 𝐼 и площадь эта петля называется 𝐴, то магнитный дипольный момент петли 𝑚 sub 𝑑 равен равно 𝐼 раз 𝐴. Нам не присваивается значение текущий 𝐼, поэтому нам придется использовать замену уравнения, которая использует значения, которые мы дано в вопросе.

В вопросе нам говорят, что круглая катушка создает магнитное поле в своем центре. Теперь мы можем вспомнить, что задана напряженность магнитного поля 𝐵 в центре токопроводящего контура провода по уравнению 𝐵 равно 𝜇 нулю 𝐼 над двумя 𝑟, где 𝐼 — ток в петля, 𝑟 — радиус петли, а 𝜇 ноль — проницаемость свободной пространство.

Теперь мы можем изменить это уравнение чтобы сделать текущий 𝐼 предметом. Мы можем умножить обе части уравнения на два 𝑟, а затем разделите обе части на 𝜇 ноль, чтобы оставить нам уравнение 𝐼 равно двум 𝑟𝐵 над 𝜇 нулями. Подставляя это в наше уравнение для 𝑚 sub 𝑑 у нас есть 𝑚 sub 𝑑 равно двум 𝑟𝐵 над 𝜇 ноль, умноженному на 𝐴.

Теперь мы можем найти выражение для район 𝐴. Площадь круглой катушки равна площадь круга, равная 𝜋𝑟 в квадрате, где 𝑟 — радиус круг. Подставляя это в наше уравнение для 𝑚 sub 𝑑 у нас есть 𝑚 sub 𝑑 равно двум 𝑟𝐵 над 𝜇 ноль, умноженному на 𝜋𝑟 в квадрате. Хорошо, тогда у нас есть наш финал уравнение. Итак, давайте выпишем, какие значения мы есть для каждой переменной.

Те, которые нам явно даны — напряженность магнитного поля, 𝐵, умноженная на два, умноженная на 10 в степени минус четыре. тесла и проницаемость свободного пространства, 𝜇 равна нулю, как четыре 𝜋 умножить на 10 мощность минус семь генри на метр. Затем нам дан диаметр петля из проволоки 12 сантиметров, но нам нужен ее радиус, 𝑟. Прежде чем идти дальше, положим это значение диаметра в единицах СИ метров. Мы делаем это, разделив 12 сантиметров на 100, так как в одном метре 100 сантиметров.