Правила Кірхгофа — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Пра́вила Кірхгофа визначають метод розрахунку складних розгалужених електричних тіл. Методика розрахунку була вперше описана в 1845 році німецьким фізиком Густавом Кірхгофом.

Правила Кірхгофа є основоположними в електротехніці, а тому в рамках цієї дисципліни їх називають законами Кірхгофа.

Перше правило Кірхгофа[ред. | ред. код]

Перше правило Кірхгофа. В кожному вузлі електричного кола алгебраїчна сума значень сил струмів, що сходяться у даному вузлі, рівна нулю, або, алгебраїчна сума сил струмів, вхідних у вузол електричного кола, рівна алгебраїчній сумі вихідних з вузла значень сил струмів.

Перше правило встановлює зв’язок між сумою струмів, спрямованих до вузла електричного з’єднання (додатні струми), і сумою струмів, спрямованих від вузла (від’ємні струми). Згідно з цим законом алгебраїчна сума струмів, що збігаються в будь-якій точці розгалуження провідників, дорівнює нулю:

∑kIk=0. {\displaystyle \sum _{k}I_{k}=0.\ }

Перше правило Кірхгофа є наслідком закону збереження заряду. Для неперервно розподілених струмів у просторі воно відповідає рівнянню неперервності.

Друге правило Кірхгофа[ред. | ред. код]

Для будь-якого замкнутого контура проводів сума електрорушійних сил дорівнює сумі добутків сил струму на кожній ділянці контура на опір ділянки, враховуючи внутрішній опір джерел струму.

Математично друге правило Кірхгофа записується так:

∑iEi=∑kIkRk.{\displaystyle \sum _{i}{\mathcal {E}}_{i}=\sum _{k}I_{k}R_{k}.}

Послідовне застосування правил Кірхгофа до усіх вузлів й контурів у складній електротехнічній мережі дозволяє скласти повну систему лінійних рівнянь для визначення сил струму на кожній із ділянок.

Для розрахунку перш за все малюють електротехнічну схему й довільним чином позначають стрілками напрями струмів на кожній ділянці. Потім виділяються замкнуті контури й обходяться в одному довільно вибраному напрямку. Якщо стрілка, яка вказує напрям струму направлена проти обходу, то відповідний добуток струму на опір береться зі знаком мінус.

Якщо при обході переходять від від’ємного полюса джерела струму до додатного, то е.р.с. записується з додатним знаком, якщо навпаки, то з від’ємним.

В результаті отримують систему рівнянь, розв’язуючи яку визначають сили струму. Якщо сила струму вийшла від’ємною, то це значить, що напрям струму на даній ділянці вгадали неправильно , хоча це не впливає на правильність результату.

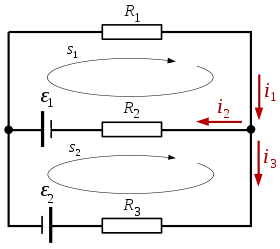
Припустимо, що електрична схема складається з двох джерел напруги і трьох резисторів.

Відповідно до першого правила маємо

i1−i2−i3=0{\displaystyle i_{1}-i_{2}-i_{3}=0\,}

Другий закон, застосований до замкненого кола s₁ дозволяє отримати

−R2i2+E1−R1i1=0{\displaystyle -R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}=0}

Другий закон, застосований до замкненого кола s₂ дозволяє отримати

−R3i3−E2−E1+R2i2=0{\displaystyle -R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}=0}

Таким чином, ми отримуємо лінійну систему рівнянь для i1,i2,i3{\displaystyle i_{1},i_{2},i_{3}}:

{i1−i2−i3=0−R2i2+E1−R1i1=0−R3i3−E2−E1+R2i2=0{\displaystyle {\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+{\mathcal {E}}_{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2}i_{2}&=0\end{cases}}}

Що еквівалентно наступному:

{i1+(−i2)+(−i3)=0R1i1+R2i2+0i3=E10i1+R2i2−R3i3=E1+E2{\displaystyle {\begin{cases}i_{1}+(-i_{2})+(-i_{3})&=0\\R_{1}i_{1}+R_{2}i_{2}+0i_{3}&={\mathcal {E}}_{1}\\0i_{1}+R_{2}i_{2}-R_{3}i_{3}&={\mathcal {E}}_{1}+{\mathcal {E}}_{2}\end{cases}}}

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М. : Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М. : Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М. : Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М. : Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Закони Кірхгофа

Закони Кірхгофа (або правила Кірхгофа) — співвідношення, які виконуються між струмами і напругами на ділянках будь електричного кола. Правила Кірхгофа дозволяють розраховувати будь-які електричні кола постійного та квазістаціонарного струму. ^[1] Мають особливе значення в електротехніці через свою універсальність, так як придатні для вирішення багатьох завдань теорії електричних ланцюгів. Застосування правил Кірхгофа до лінійного ланцюга дозволяє отримати систему лінійних рівнянь щодо струмів, і відповідно, знайти значення струмів на всіх гілках ланцюга. Сформульовано Густавом Кірхгофа в 1845.

1. Формулювання

Для формулювання законів Кірхгофа, в електричного кола виділяються вузли — точки з’єднання трьох і більше провідників і контури — замкнуті шляху з провідників. При цьому кожен провідник може входити в кілька контурів.

У цьому випадку закони формулюються таким чином.

1.1. Перший закон

Перший закон Кірхгофа (Закон струмів Кірхгофа, ЗТК) говорить, що алгебраїчна сума струмів в будь-якому вузлі будь ланцюга дорівнює нулю (значення випливають струмів беруться зі зворотним знаком):

Іншими словами, скільки струму втікає у вузол, стільки з нього і випливає. Даний закон випливає з закону збереження заряду. Якщо ланцюг містить p вузлів, то вона описується p — 1 рівняннями струмів. Цей закон може застосовуватися і для інших фізичних явищ (наприклад, водяні труби), де є закон збереження величини і потік цієї величини.

1.2. Другий закон

Другий закон Кірхгофа (Закон напруг Кірхгофа, ЗНК) говорить, що алгебраїчна сума падінь напружень по будь-якому замкнутому контуру кола дорівнює алгебраїчній сумі ЕРС, що діють уздовж цього ж контура. Якщо в контурі немає ЕРС, то сумарне падіння напруги дорівнює нулю:

для постійних напруг

для змінних напруг

Іншими словами, при обході ланцюга по контуру, потенціал, змінюючись, повертається до початкового значення. Якщо ланцюг містить гілок, з яких містять джерела струму гілки в кількості , То вона описується рівняннями напруг. Окремим випадком другого правила для ланцюга, що з одного контуру, є закон Ома для цього ланцюга.

Закони Кірхгофа справедливі для лінійних і нелінійних ланцюгів при будь-якому характері зміни в часі струмів і напруг.

Приклад

На цьому малюнку для кожного провідника позначений протікає по ньому струм (буквою «I») і напруга між сполучаються їм вузлами (буквою «U»)

Наприклад, для наведеної на малюнку ланцюга, відповідно до першого закону виконуються наступні співвідношення:

Зверніть увагу, що для кожного вузла має бути вибрано позитивний напрямок, наприклад тут, струми, що впадає у вузол, вважаються позитивними, а випливають — негативними.

Згідно з другим законом, справедливі співвідношення:

2. Особливості складання рівнянь для розрахунку струмів

• Закони Кірхгофа, записані для вузлів та контурів ланцюга, дають повну систему лінійних рівнянь, яка дозволяє знайти всі струми і напруги.
• Перед тим, як скласти рівняння, потрібно довільно вибрати:
  • позитивні напрямки струмів у гілках і позначити їх на схемі;
  • позитивні напрямки обходу контурів для складання рівнянь за другим законом.
• З метою однаковості рекомендується для всіх контурів позитивні напрямки обходу вибирати однаковими (напр.: за годинниковою стрілкою)
• Якщо напрямок струму збігається з напрямком обходу контуру (яке вибирається довільно), перепад напруги вважається позитивним, в іншому випадку — негативним.
• При запису лінійно незалежних рівнянь за другим законом, прагнуть, щоб у кожен новий контур, для якого складають рівняння, входила хоча б одна нова гілка, яка не увійшла в попередні контури, для яких вже записані рівняння за другим законом (достатнє, але не необхідна умова)

3. Про значення для електротехніки

Правила Кірхгофа мають прикладний характер і дозволяють поряд і в поєднанні з іншими прийомами і способами (метод еквівалентного генератора, метод контурних струмів, метод вузлових напруг, принцип суперпозиції, спосіб складання потенційної діаграми) вирішувати завдання електротехніки. Правила Кірхгофа знайшли широке застосування завдяки простій формулюванні рівнянь і можливості їх вирішення стандартними способами лінійної алгебри ( методом Крамера, методом Гаусса та ін.)

Існує думка, згідно з яким «Закони Кірхгофа» слід іменувати «Правилами Кірхгофа», бо вони не відображають фундаментальних сутностей природи (і не є узагальненням великої кількості досвідчених даних), а можуть бути виведені з інших положень і припущень.

4. Закон випромінювання

Закон випромінювання Кирхгофа — відношення випромінювальної здатності будь-якого тіла до його поглинальної здатності однакове для всіх тіл при даній температурі для даної частоти для рівноважного випромінювання і не залежить від їх форми, хімічного складу та ін.

Примітки

Література

• Матвєєв А. Н. Електрика і магнетизм — Навчальний посібник. — М .: Вища школа, 1983. — 463 с.
• Калашников С. Г. Електрика — Навчальний посібник. — М .: Физматлит, 2003. — 625 с.
• Безсонов Л. А. Теоретичні основи електротехніки. Електричні кола — 11-е видання. — М .: Гардарики, 2007.

1.7 Закони кірхгофа

Для розрахунку електричних ланцюгів|цепів| разом і|поряд з|з законом Ома застосовуються два закони Кірхгофа, що є |з’являються| слідством закону збереження|зберігання| енергії.

Методи розрахунку із застосуванням законів Кірхгофа дозволяють розрахувати електричний ланцюг|цеп| будь-якої конфігурації і складності, тобто є|з’являються| основними.

Перший закон Кірхгофа

Перший закон Кірхгофа застосовується до вузлів електричних ланцюгів і виражає баланс струмів в них: у вузлі електричного ланцюга алгебраічна сума струмів дорівнює нулю

:

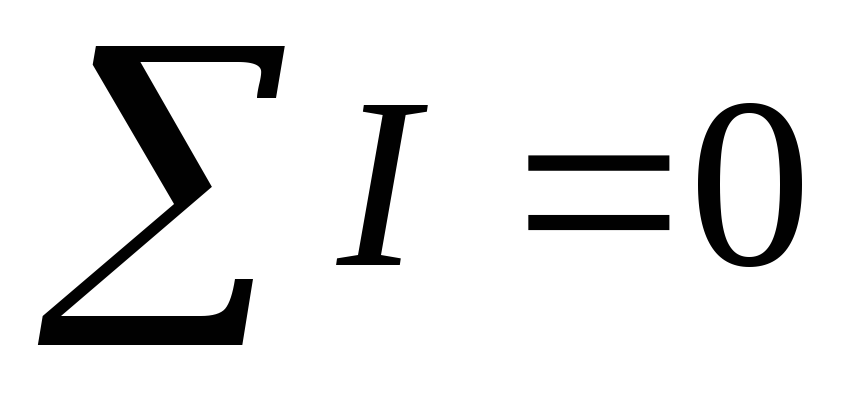. (1.17)

У цій сумі струми|токи| беруться з|із| різними знаками залежно від напряму|направлення| їх по відношенню до вузла. На підставі першого закону Кірхгофа для кожного вузла можна скласти рівняння струмів|токів|.

Наприклад, для точки|точки| 3 схеми, представленої|уявляти| на рис.3.2, таке рівняння має вигляд|вид|

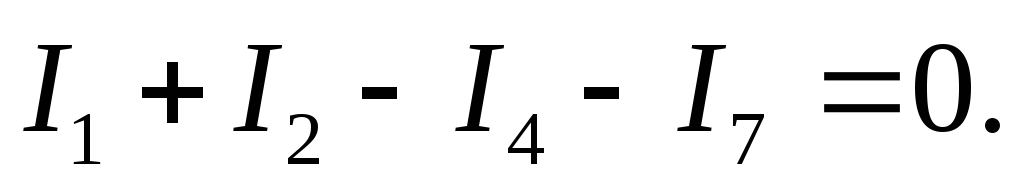
У цьому рівнянні струми|токи|, направлені|спрямовані| до вузла, умовно узяті позитивними, а струми|токи|, направлені|спрямовані| від вузла, — негативними|заперечними|:

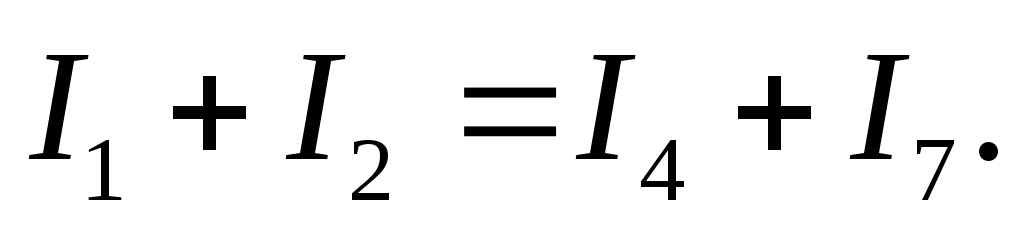
Останнє рівняння дозволяє дати інше формулювання першого| закону Кірхгофа : сума струмів|токів|, направлених|спрямованих| до вузла електричного ланцюга|цепу|, дорівнює сумі струмів|токів|, направлених|спрямованих| від цього вузла.

Цей закон виходить з принципу безперервності струму|току|. Якщо допустити|припуститися| переважання у вузлі струмів|токів| одного напряму|направлення|, то заряд одного знаку повинен накопичуватися і потенціал вузлової точки повинен безперервно змінюватися, що в реальних ланцюгах|цепах| не спостерігається.

Другий закон Кірхгофа

Другий закон Кірхгофа застосовується до контурів електричних ланцюгов і виражає баланс напруги в них: у контурі електричного ланцюга|цепу| алгебраічна| сума електрорушійних сил дорівнює алгебраічній| сумі падінь напруги|напруження| на опори, що входять в цей контур:

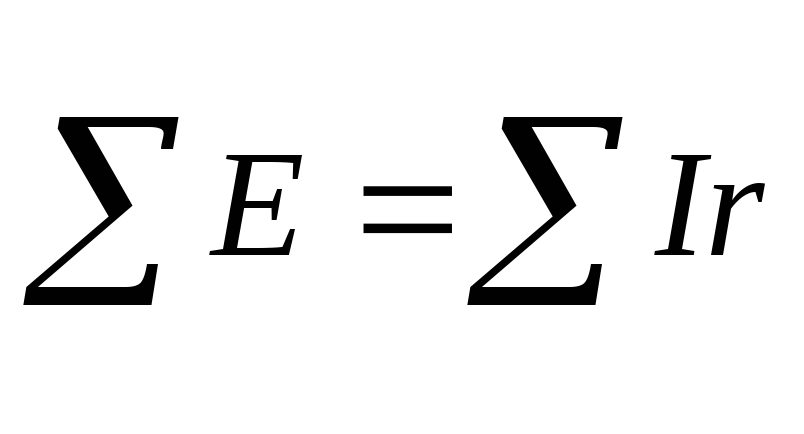. (1.18)

Для доведення іншого закону Кірхгофа визначимо потенціали окремих точок контура 1-2-3-4-5-6-1 в схемі, зображеній|змальовувати| на рис.1.17, обходячи|обминати| контур в довільному напрямі|направленні|, наприклад, за годинниковою стрілкою. Напрями|направлення| струмів|токів| в єлементах контура узяті також довільно.

Обхід контура почнемо від точки І, потенціал якої

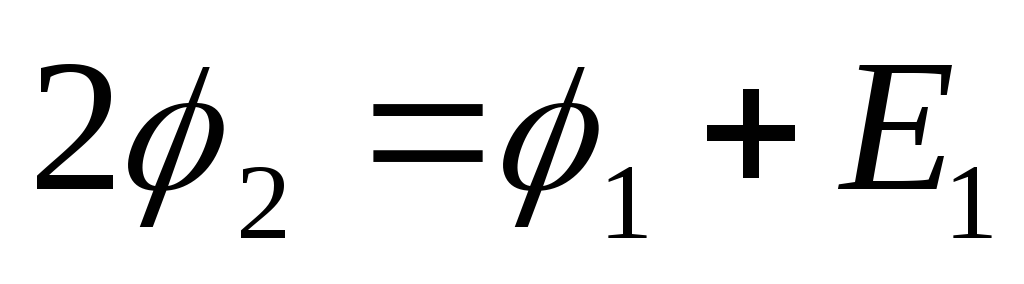. Потенціал точки і далі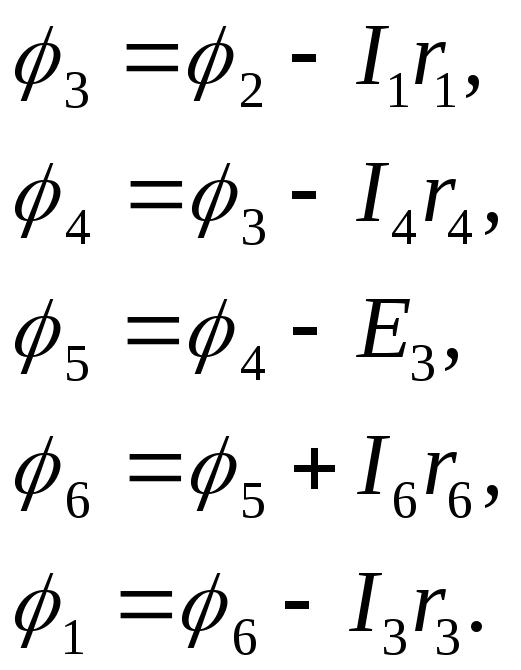

Зміна потенціалу по вибраному контуру має дорівнювати нулю|нуль-індикатору|, оскільки|тому що| воно виражає|виказує| роботу, витрачену на переміщення частинок|часток|, що володіють разом одиницею заряду, по замкнутому шляху|колії| в електричних полях джерел і приймачів енергії.

Таким чином, в замкнутому контурі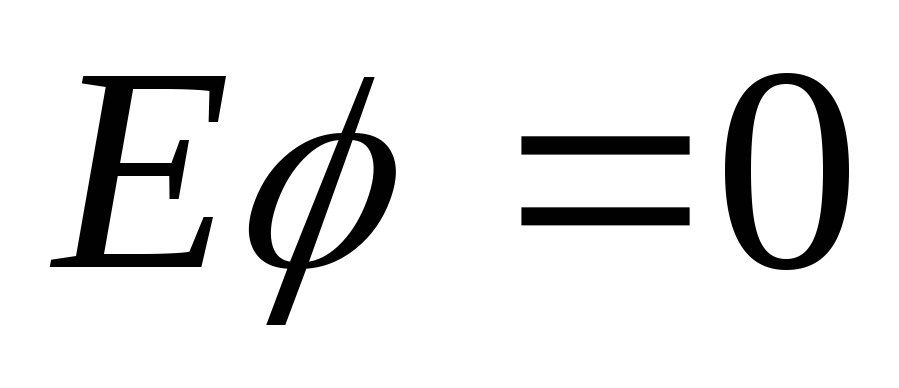

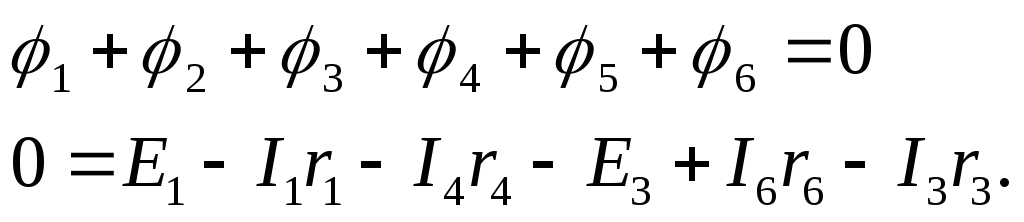
Перенісши в ліву частину|частку| рівняння значення і помінявши знаки, отримаємо|одержуватимемо| рівняння, відповідне другому закону Кірхгофа в застосуванні|вживанні| до вибраного контура:

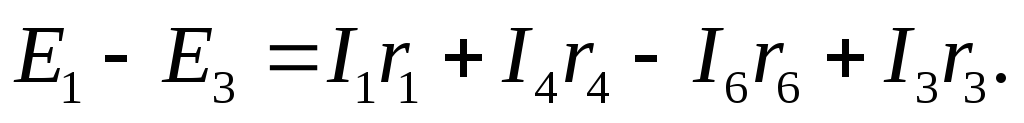
Для інших контурів виходять інші рівняння. Їх неважко написати, не удаючись до визначення потенціалів точок контура. Для цього можна користуватися наступним|таким| правилом.

У ліву частину|частку| рівняння слід записати алгебраічну| суму, що зустрічаються при обході контура, а в праву частину|частку| — алгебраічну| суму падінь напруги|напруження| в опорах контура.

При цьому за позитивну вважається така електрорушійна сила, напрям якої збігається з напрямом обходу; за позитивне вважається падіння напруги в такому опорі, в якому напрям струму збігається з напрямом обходу. Згідно|згідно з| цьому правилу, нижче записані рівняння два інших контурів схеми, представленої|уявляти| на рис.1.17:

контур 1-2-3-6-1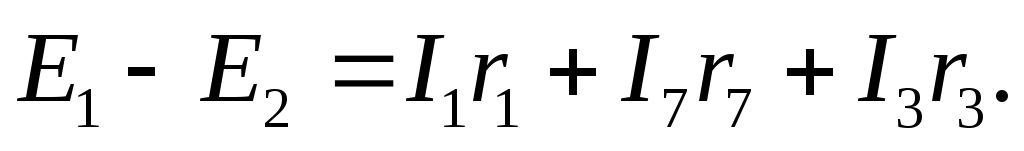

контур 3-4-6-3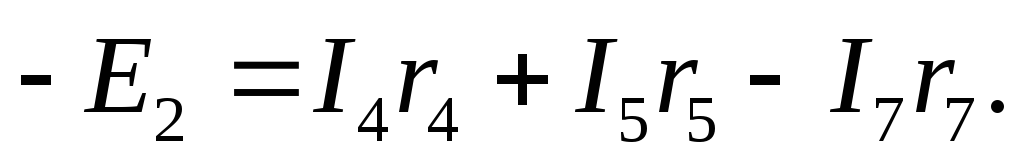

Закони Кірхгофа та їх застосування

Перший закон Кірхгофа

Закони Кірхгофа (коректніше – правила Кіргхгофа) застосовуються при розрахунку складних (розгалужених) електричних ланцюгів. Пропоную розглянути їх по черзі і почати, природно, з першого.

Визначення і формула першого закону Кірхгофа, який говорить: алгебраїчна сума струмів, що сходяться у вузлі дорівнює нулю, ілюструються малюнком 1.
тут:

I i – струм у вузлі,
n – число провідників, що сходяться у вузлі,
струми, що впадає до вузол (I1, In) вважаються позитивними,
випливають струми (I2, I3) – негативними.
У такому вигляді цей закон звучить і виглядає, напевно, дуже академічно, тому пропоную все дещо спростити.

Намалюємо розгалужену електричну ланцюг в більш звичному вигляді (рис.2) і дамо таке формулювання:

Сума струмів втікають у вузол дорівнює сумі струмів, що випливають з вузла.

Для цього випадку формула першого закону Кірхгофа набуде вигляду: I = I1 + I2 + … + In, що для повсякденних обчислень набагато зручніше.

Другий закон Кірхгофа

Другий закон Кірхгофа Другий закон Кірхгофа визначає залежність між падіннями напруг і ЕРС в замкнутих контурах і має такий вигляд (рис.3) і визначення:

алгебраїчна сума (з урахуванням знака) падінь напруг на всіх гілках будь-якого замкнутого контуру ланцюга, дорівнює алгебраїчній сумі ЕРС гілок цього контуру.
При відсутності в контурі ЕРС сума падінь напруг дорівнює 0.

Тепер кілька пояснень щодо практичного застосування цього правила Кірхгофа:

оскільки, алгебраїчна сума вимагає врахування знака слід вибрати напрямок обходу контура (на рис.3 – за годинниковою стреклке), струми і напруги, що збігаються з цим напрямком вважати позитивними, інші – негативними. При скруті у визначенні напрямку струму, візьміть довільне, якщо в результаті обчислень отримаєте результат зі знаком “-“, поміняйте обраний напрям на противоположенное.
для нашого прикладу можна записати:
U1 + U3-U2 = 0
U4 + U5-U3 = 0
крім того, керуючись першим правилом Кірхгофа:
Iвх – I1 – I2 = 0
I1 – I3 – I4 = 0
I4 – I5 = 0
I2 + I3 + I5 – Iвих = 0,

отримуємо систему з 6 рівнянь, повністю описує розглянуту електричний ланцюг.

« Закон ома для ділянки ланцюга Змінний і трифазний струм »

Перший і другий закони Кірхгофа

4.1 / 5 оцінка (116 голосів)

Приклад складної електричного кола ви можете подивитися на малюнку 1.

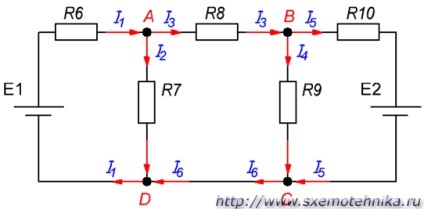
Малюнок 1. Складна електричний ланцюг.

Іноді закони Кирхгофа називають правилами Кірхгофа. особливо в старій літературі.

Перший закон Кірхгофа

Формулювання №1: Сума всіх струмів, що втікають у вузол, дорівнює сумі всіх струмів, що випливають з вузла.

Формулювання №2: Алгебраїчна сума всіх струмів в вузлі дорівнює нулю.

Поясню перший закон Кірхгофа на прикладі малюнка 2.

Малюнок 2. Вузол електричного кола.

Тут струм I1 — ток, впадає в вузол. а струми I2 і I3 — струми, що випливають з вузла. Тоді застосовуючи формулювання №1, можна записати:

Що б підтвердити справедливість формулювання №2, перенесемо струми I2 і I3 в ліву частину виразу (1). тим самим отримаємо:

Знаки «мінус» в вираженні (2) і означають, що струми випливають з вузла.

Знаки для втікають і випливають струмів можна брати довільно, проте в основному завжди втікає струми беруть зі знаком «+», а випливають зі знаком «-» (наприклад як вийшло в вираженні (2)).

Другий закон Кірхгофа.

Формулювання: Алгебраїчна сума ЕРС, що діють в замкнутому контурі, дорівнює алгебраїчній сумі падінь напруги на всіх резистивних елементах в цьому контурі.

Тут термін «алгебраїчна сума» означає, що як величина ЕРС так і величина падіння напруги на елементах може бути як зі знаком «+» так і зі знаком «-». При цьому визначити знак можна за наступним алгоритмом:

1. Вибираємо напрям обходу контуру (два варіанти або за годинниковою, або проти).

2. Довільно вибираємо напрямок струмів через елементи ланцюга.

3. Розставляємо знаки для ЕРС і напруг, що падають на елементах за правилами:

— ЕРС, що створюють струм в контурі, напрям якого збігається з напрям обходу контуру записуються зі знаком «+», в іншому випадку ЕРС записуються зі знаком «-».

— напруги, які падають на елементах ланцюга записуються зі знаком «+», якщо струм, що протікає через ці елементи збігається за напрямком з обходом контуру, в іншому випадку напруги записуються зі знаком «-».

Наприклад, розглянемо ланцюг, представлену на малюнку 3, і запишемо вираз згідно з другим законом Кірхгофа, обходячи контур за годинниковою стрілкою, і вибравши напрямок струмів через резистори, як показано на малюнку.

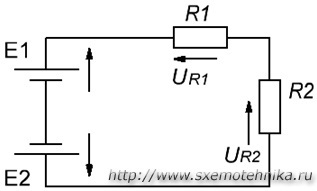
Малюнок 3. Електричне коло, для пояснення другого закону Кірхгофа.

Розрахунки електричних ланцюгів за допомогою законів Кірхгофа.

Тепер давайте розглянемо варіант складного ланцюга, і я вам розповім, як на практиці застосовувати закони Кірхгофа.

Отже, на малюнку 4 є складний ланцюг з двома джерелами ЕРС величиною E1 = 12 в і E2 = 5 ст. з внутрішнім опором джерел r1 = r2 = 0,1 Ом. працюючих на загальне навантаження R = 2 Ома. Як же будуть розподілені струми в цьому ланцюзі, і які вони мають значення, нам належить з’ясувати.

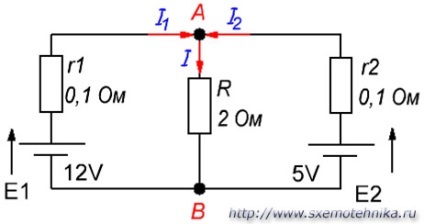
Малюнок 4. Приклад розрахунку складної електричного кола.

Тепер згідно з першим законом Кірхгофа для вузла А складаємо такий вислів:

Використовуючи другий закон Кірхгофа, запишемо ще два вирази для зовнішнього контуру і внутрішнього лівого контуру, вибравши напрямок обходу за годинниковою стрілкою.

Для зовнішнього контуру:

Для внутрішнього лівого контуру:

Отже, у нас вийшла система з трьох рівнянь з трьома невідомими:

Тепер підставимо в цю систему відомі нам величини напруг і опорів:

Далі з першого і другого рівняння висловимо струм I2

Наступним кроком прирівняємо перше і друге рівняння і отримаємо систему з двох рівнянь:

Висловлюємо з першого рівняння значення I

І підставляємо його значення в друге рівняння

Вирішуємо отримане рівняння

Тепер в вираз I = 2I1 — 70 підставимо значення

Ну, а згідно з першим закону Кирхгофа ток I2 = I — I1

Знак «мінус» для струму I2 означає, то що ми не правильно вибрали напрямок струму, тобто в нашому випадку струм I2 випливає з вузла А.

Тепер отримані дані можна перевірити на практиці або змоделювати цю схему наприклад в програмі Multisim.

Скріншот моделювання схеми для перевірки законів Кірхгофа ви можете подивитися на малюнку 5.

Малюнок 5. Порівняння результатів розрахунку і моделювання роботи ланцюга.

Ви можете абсолютно БЕЗКОШТОВНО отримати повноцінний курс з креслення схем і створення малюнків в програмі sPlan 7.0!

Якщо Ви хочете з новачка перетворитися в профессіноала, стати висококласним, конкурентним і грамотним фахівцем в області найперспективнішого напрямку мікроелектроніки, тоді вивчіть новий відокурс по мікроконтролерів!

Запевняю такого ще немає ніде!

В результаті ви навчитеся з нуля трохи Тольна розробляти власні пристрої, але і сполучати з ними різну переферію!

Схожі статті

Закони Кірхгофа

Академія ФСО Росії

Кафедра Фізики

Тема:

«Закони Кірхгофа та їх застосування для розрахунку електричних ланцюгів»

Зміст

Перший закон Кірхгофа
Другий закон Кірхгофа
Розрахунок складних кіл за допомогою рівнянь Кірхгофа

Перший закон Кірхгофа
Алгебраїчна сума струмів у гілках, що сходяться до будь-якого вузла електричного кола, тотожно дорівнює нулю. Згідно з цим законом, якщо до деякого вузла ланцюга приєднано n гілок зі струмами i _1, i _2, …, i _n, то в будь-який момент часу
,
де , Якщо напрямок струму позитивно і орієнтоване від вузла (струм виходить з вузла), або , Якщо струм входить у вузол. Таким чином, будь-якому вузлу ланцюга відповідає рівняння, що зв’язує струми в гілках ланцюга, з’єднаних з даним вузлом.
В якості прикладу наведемо схему на малюнку 1.

Рис.1.
Відповідно до першого закону Кірхгофа:
.
Загальне число рівнянь, яке можна скласти за першим законом Кірхгофа для ланцюга, дорівнює числу вузлів ланцюга .
Так, для чотирьох вузлів графа (малюнок 2) можна скласти наступні чотири рівняння:

Рис.2.
вузол 1: ,
вузол 2: ,
вузол 3: ,
вузол 4: .
Перший закон Кірхгофа часто називають законом Кірхгофа для струмів і скорочено у тексті позначають ЗКТ.
Число незалежних рівнянь дорівнює трьом, так як будь-яке з цих рівнянь відрізняється від суми трьох інших тільки знаком. Отже, якщо ланцюг містить вузлів, то для неї можна скласти за першим законом Кірхгофа незалежних рівнянь. Сукупність з N вузлів ланцюга, рівняння для яких утворюють систему лінійно незалежних рівнянь, називають сукупністю незалежних вузлів ланцюга.

Приклади на застосування першого закону Кірхгофа. Паралельне з’єднання елементів

Як приклад на застосування першого закону Кірхгофа розглянемо паралельне з’єднання декількох елементів активних опорів, конденсаторів, котушок індуктивності.
Особливістю паралельного з’єднання декількох елементів є рівність напруг, прикладених до затискачів кожного з елементів, що входять у з’єднання. Ланцюг при такому з’єднанні характеризується тільки одним незалежним вузлом.
Нехай паралельно з’єднані n елементів активного опору. Якщо вибрати напрями звітів струмів в елементах такими як це показано на малюнку 3, то згідно з першим законом Кірхгофа при паралельному з’єднанні елементів запишемо:

Рис.3.
;
враховуючи, що , Маємо ,
де .
Залежність не відрізняється від залежності між напругою на затискачах і струмом в елементі активного опору з провідністю G. Отже, ланцюг, складена з кількох опорі, включених паралельно, може бути замінена одним активним опором, при цьому провідність еквівалентного елемента дорівнює сумі провідностей елементів, що входять у з’єднання.
При паралельному з’єднанні конденсаторів (малюнок 4) струм гілці можна визначити за формулою: .

Рис.4.
Для обчислення загального струму необхідно підсумувати струми гілок:
,
де _..
Таким чином, при паралельному з’єднанні декількох конденсаторів еквівалентна ємність дорівнює сумі ємностей, що входять у з’єднання.
У разі паралельного з’єднання котушок індуктивностей (рисунок 5)
струм кожної з гілок дорівнює: .
Рис.5.
Рівняння для обчислення загального струму має вигляд:
.
Отже , Тобто .
Це означає, що значення еквівалентної індуктивності будить менше найменшого із значень з’єднаних паралельно індуктивностей.
Другий закон Кірхгофа
Другий закон Кірхгофа формулюється наступним чином: алгебраїчна сума напруг гілок в будь-якому контурі ланцюга тотожно дорівнює нулю. Для замкнутого контуру, зображеного на малюнку 6, можна записати співвідношення:
.

Рис.6.
Згідно з другим законом Кірхгофа при обході контура за годинниковою стрілкою справедливе співвідношення:
.
Зміна напрямку обходу еквівалентно зміни знаків напружень на протилежні (множенню на мінус одиницю).

Приклади на застосування другого закону Кірхгофа

Послідовне з’єднання елементів

Нехай n елементів активного опору з’єднані послідовно (рисунок 7).
Рис.7.
Відповідно до вибраного напрямом обходу за другим законом Кірхгофа отримаємо рівняння:
.
характерною особливістю послідовного з’єднання є рівність струмів в кожному з елементів, що входять у з’єднання.
При запишемо:
, Тобто .
Таким чином, при послідовному з’єднанні декількох резисторів еквівалентний опір дорівнює сумі опорів, що входять у з’єднання.
При послідовному з’єднанні котушок індуктивності (рисунок 8) можна записати:
.

Рис.8.
Якщо , То ,
отже .
Це означає, що еквівалентна індуктивність дорівнює сумі індуктивностей, що входять у послідовне з’єднання.
У разі послідовного з’єднання конденсаторів (малюнок 9) за другим законом Кірхгофа можна записати:

.
Рис.9.
Замінюючи отримаємо: .
Зворотній ємність всіх конденсаторів, з’єднаних послідовно, дорівнює сумі зворотних ємностей конденсаторів, які входять у з’єднання:
.
При цьому еквівалентна ємність з’єднання буде менше найменшою ємності конденсатора, який входить у послідовне з’єднання.

Розрахунок складних кіл за допомогою рівнянь Кірхгофа

Приклад 1
Далеко не у всіх випадках ланцюг представляє собою сукупність лише послідовно і паралельно з’єднаних гілок. В якості прикладу розглянемо варіант розрахунку за допомогою рівнянь Кірхгофа електричного кола (рисунок 10). Ланцюг містить = 4 вузлів і = 6 гілок, включаючи джерела напруги.

Рис.10.
Для визначення всіх струмів і напруг у схемі достатньо знайти значення струмів у всіх гілках ланцюга. Знаючи струм, що проходить через будь-яку з гілок ланцюга, можна знайти як напруга цієї гілки, так і напругу між будь-якою парою вузлів ланцюга.
Якщо ми поставимо собі довільно позитивними напрямками струмів в гілках ланцюги і пронумеруємо довільно ці струми, то за першим законом Кірхгофа можна скласти рівнянь відносно струмів в гілках ланцюга.
За другим законом Кірхгофа буде лінійно-незалежних рівнянь для напружень гілок схеми.
Сукупність з рівнянь за першим законом Кірхгофа, і рівнянь, складених за другим законом Кірхгофа, утворює систему лінійно — незалежних рівнянь. Ця система буде неоднорідною системою рівнянь, так як її вільними членами є задані напруги джерел.

Подібна система рівнянь має єдине рішення, що дозволяє знайти струми в гілках ланцюги, а за ним і значення напруг між будь-якою парою вузлів ланцюга.
Для прикладу складемо систему рівнянь за першим законом Кірхгофа (рисунок 10).
Число рівнянь: .
Вузол 1: ,
вузол 2: ,
вузол 3:   .
У теж час за другим законом Кірхгофа для контурів I, II, III можна скласти систему з рівнянь.
.
Контур I:   ,
контур II:   ,
контур III: .
Таким чином, вирішуючи систему з 6 рівнянь з шістьма невідомими струмами, наприклад за методом Крамера, визначимо невідомі. Якщо в ланцюзі буде джерело струму, то в системі рівнянь невідомим буде напруга на затискачах цього джерела, а струм через джерело буде дорівнює струму задає джерела. Загальне число невідомих збережеться колишнім.

Приклад 2

Для ланцюга (рисунок 11) визначити струми і , Якщо E = 20 В, I ₀= 2 A , R ₁= 15 Ом, R ₂ = 85 Ом.

Рис.11.

Рішення

Виберемо напрямки струмів ,   і обходу в контурі, складемо рівняння за законами Кірхгофа. Число рівнянь, що складаються за першим законом Кірхгофа:
.
Число рівнянь за другим законом Кірхгофа:
.
Рівняння струмів для вузла 1:
. (A)
Рівняння за другим законом Кірхгофа:
. (Б)
Підставимо в рівняння (а) і (б) числові значення отримаємо:
,
.
Вирішивши цю систему, визначимо струми і :
; .

Література
1. Білецький А.Ф. Теорія лінійних електричних ланцюгів. — М.: Радіо і зв’язок, 1986.
2. Бакалов В.П. та ін Теорія електричних ланцюгів. — М.: Радіо і зв’язок, 1998.
3. Качанов Н. С. та ін Лінійні радіотехнічні пристрої. М.: Воен. издат., 1974.
4. В.П. Попов Основи теорії ланцюгів — М.: Вища школа, 2000

Закони Кірхгофа | Електричні кола | Електротехніка, теорія

Перший і другий закони Кирхгофа в комплексній формі. Математичне формулювання законів Кирхгофа для ланцюгів синусоїдального струму залежать від обраного способу подання синусоїдальних величин. Перший закон Кирхгофа. По першому законі Кирхгофа алгебраїчна сума струмів у будь-якому вузлі електричного кола в кожний момент часу дорівнює нулю. 

Комплексний метод розрахунку ланцюгів синусоїдального струму. Визначити показання амперметра Аъ, якщо показання амперметрів Ах і А2 рівні . Рішення. Напруга по фазі збігається зі струмом у резистивном елементі IR і випереджає на кут л 2 струм в індуктивному елементі. Сума векторів комплексних значень струмів iR і iL по першому законі Кирхгофа для вузла а визначає вектор комплексного значення струму. Модуль вектора струму по теоремі Пифагора визначає показання амперметра. 

Комплексний метод розрахунку ланцюга синусоїдального струму полягає в наступному. Представляємо вихідні дані про параметри всіх елементів ланцюга в комплексній формі, тобто синусоїдальні ЭДС джерел напруги й струми джерел струму, заданих миттєвими значеннями (у тригонометричній формі), індуктивні і ємнісні елементи ланцюга відповідними їм комплексними значеннями й комплексними опорами або проводимостями.

Вибираємо позитивні напрямки комплексних струмів у всіх галузях і вказуємо їхніми стрілками на схемі ланцюга. За законами Ома й Кирхгофа в комплексній формі становимо систему рівнянь, що визначає режим роботи ланцюга. Вирішуємо отриману систему рівнянь і визначаємо комплексні значення струмів у галузях ланцюга й напруг на її елементах. 

По знайдених комплексних значеннях струмів і напруг визначаємо відповідні їм миттєві значення синусоїдальних струмів і напруг. Для спрощення обчислень при розрахунку лінійних ланцюгів синусоїдального струму, так само як і лінійних ланцюгів постійного струму, застосовні різні розрахункові методи: перетворення схем, вузлових потенціалів, контурних струмів, накладення. При цьому математичні формулювання методів розрахунку ланцюгів постійного струму залишаються справедливими й для розрахунку ланцюгів синусоїдального струму.

Потрібно тільки всі ЭДС, напруги й струми замінити комплексними значеннями відповідних синусоїдальних величин, а опору елементів — комплексними опорами. Надалі для понять комплексні значення ЭДС, напруги, струму й т.д., а також відповідних їм векторів комплексних значень будемо використовувати скорочені терміни, наприклад комплексний струм або струм

Електричне коло з послідовною сполукою елементів. Розглянемо загальний, а потім окремі випадки ланцюга з послідовною сполукою елементів, тобто нерозгалуженого ланцюга. 

Ланцюг з послідовною сполукою елементів R, L і С. У ланцюзі з послідовною сполукою елементів при дії джерела синусоїдальної струм також синусоїдальний напруги на резистивном, індуктивному і ємнісному елементах. Позначення комплексних опорів і провідності відрізняються від позначень комплексних значень струму й напруги тому, що другим відповідають фізичні величини, що змінюються в часі, а першим — немає. 

Кожному значенню комплексного опору Z як комплексному числу відповідає крапка на комплексній площині. Її положення визначається вектором на комплексній площині. Цей вектор є геометричною інтерпретацією комплексного опору й має таке ж позначення Z. Доданки комплексного опору у вигляді векторів для двох випадків. 

Геометрична інтерпретація комплексного опору дозволяє легко перейти від алгебраїчної форми запису комплексного опору до тригонометричної й показової форм модуль комплексного опору, або повний опір, одиниця виміру якого аргумент комплексного опору. Залежно від знака величини аргумент комплексного опору може бути або. Підставивши значення комплексного опору в показовій формі, одержимо вираження закону Ома для не-розгалуженого ланцюга. 

Якщо комплексний опір ланцюга має індуктивний характер, то струм у ланцюзі відстає по фазі від напруги. Якщо комплексний опір ланцюга має ємнісний характер, то струм у ланцюзі випереджає по фазі напруга. На векторній діаграмі позитивне (негативне) значення кута ф відлічується проти напрямку (по напрямку) руху годинникової стрілки від вектора комплексного значення струму. 

Ланцюг з послідовною сполукою елементів R і L. У ланцюзі з послідовною сполукою резистивного й індуктивного елементів вираження приймають вид яким відповідають на векторних діаграмах прямокутні трикутники напруг і опорів.