Перевод из шестнадцатеричной в десятичную систему счисления, калькулятор
Исходное число
Направление перевода
2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Сообщить об ошибке
В избранное
Виджет
Вы можете сохранять ваши расчеты и они будут отображаться здесь.
Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.
Преобразовать число из шестнадцатеричной системы счисления в десятичную можно следующим образом:
Каждый разряд числа необходимо умножить на 16n, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.
abc2 = (a×162 + b×161 + c×160)10
5A16 = (5*16
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в восьмеричную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в восьмеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
Перевод чисел из одной позиционной системы счисления в другую
Информатика.
10 класса. Босова Л.Л. Оглавление
§11. Перевод чисел из одной позиционной системы счисления в другую
11.1. Перевод целого десятичного числа в систему счисления с основанием q
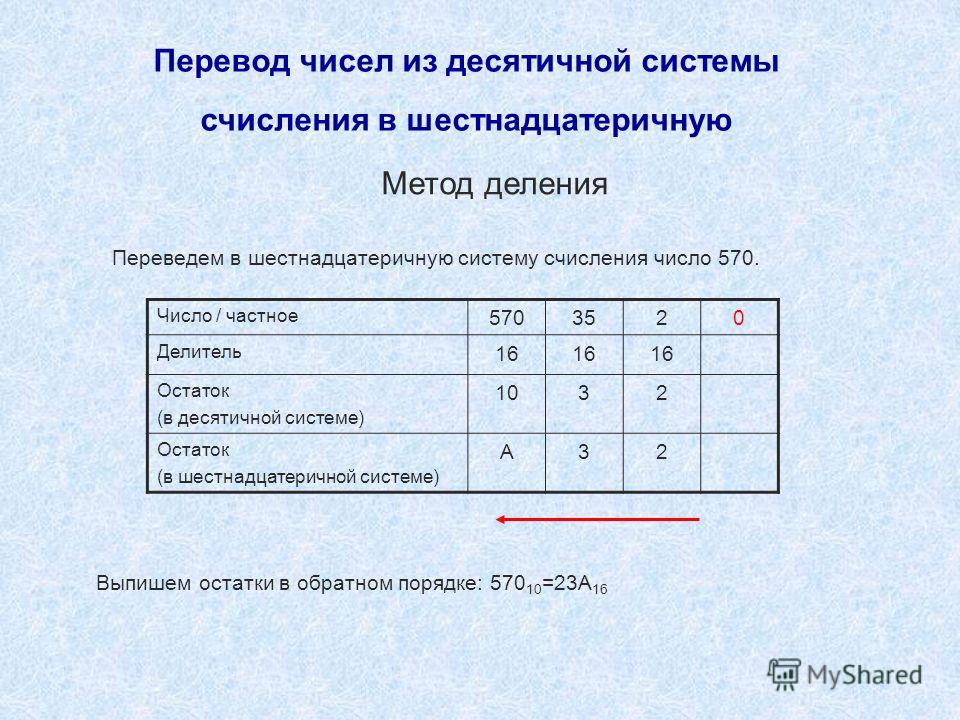
Для перевода целого десятичного числа в систему счисления с основанием q следует:
1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Рассмотрим примеры перевода целых десятичных чисел в 2-ичную, 8-ричную и 16-ричную системы счисления.
Пример 1.
Пример 2.
Пример 3.
Пример 4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 22 оканчивается на 4.
Поскольку запись числа в системе счисления с основанием q заканчивается на 4, остаток от деления числа 22 на q равен 4: 22 mod q = 41). Следовательно, 18 mod q = 0. Это верно для q ? {18, 9, 6, 3, 2, 1}.
1) Операция mod — вычисление остатка от целочисленного деления.
Так как в новой системе счисления запись числа оканчивается на 4, то q > 4. Следовательно, условию задачи удовлетворяют основания: 18, 9 и 6.
11.2. Перевод целого десятичного числа в двоичную систему счисления
Перевод целого десятичного числа, безусловно, может осуществляться по рассмотренному выше универсальному алгоритму. Но для чисел в пределах десяти тысяч (особенно если число немного больше некоторой степени двойки) бывает удобно снова воспользоваться таблицей степеней двойки.
Например: 109610 = 1024 + 72 = 1024 + 64 + 8 = 100010010002.
Здесь мы представили число в виде суммы степеней двойки: сначала взяли максимально возможное значение, не превышающее исходное число (1024 < 1096), и нашли разность между исходным числом и этим значением (72).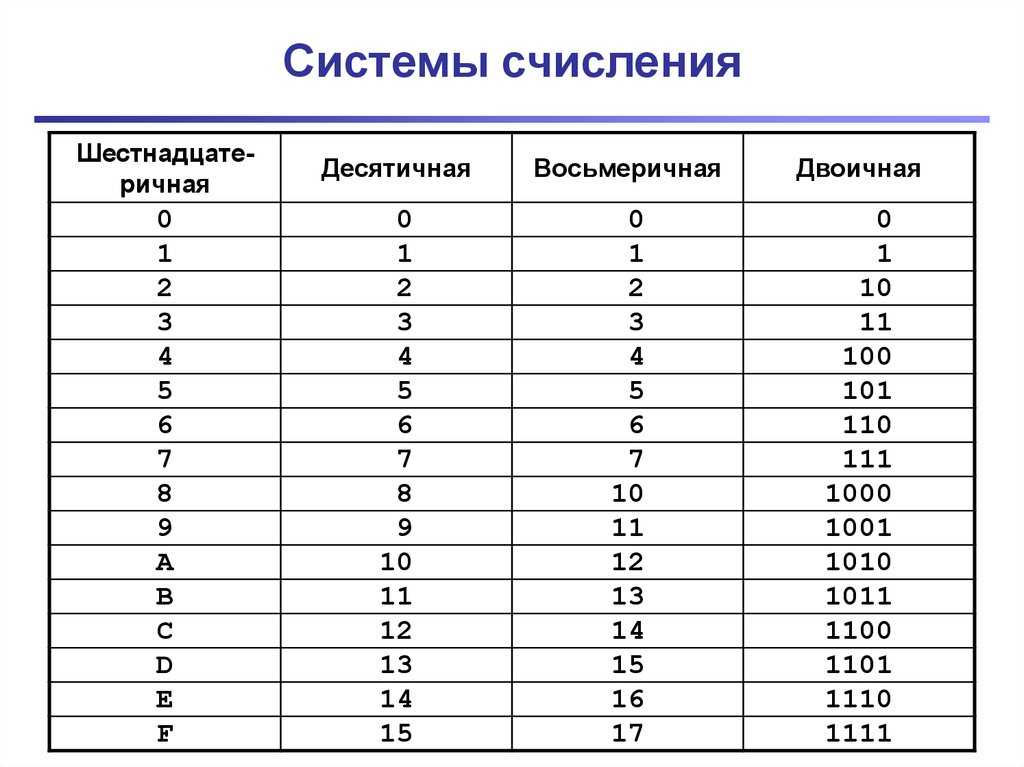
Затем выписали степень двойки, не превышающую эту разность, и т. д. Когда исходное число было представлено в виде суммы, мы построили его двоичное представление, записав 1 в разрядах, соответствующих слагаемым, вошедшим в сумму, и 0 — во всех остальных разрядах.
11.3. Перевод целого числа из системы счисления с основанием р в систему счисления с основанием q
Каждый из нас может выполнять арифметические операции в привычной десятичной системе счисления. Выполнять такие же операции в других системах счисления человеку непривычно, а поэтому и неудобно.
Для того чтобы перевести целое число из системы счисления с основанием р в систему счисления с основанием q, достаточно:
1) основание новой системы счисления выразить в исходной системе счисления и все последующие действия производить в исходной системе счисления;
2) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
3) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
4) составить число в новой системе счисления, записывая его, начиная с последнего остатка.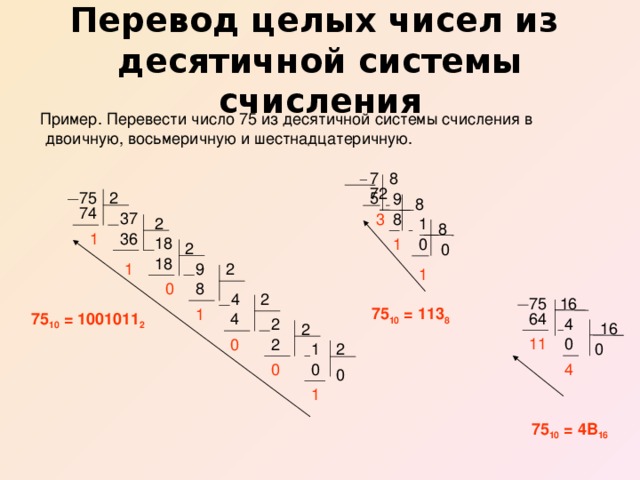
При необходимости перевести целое число из системы счисления с основанием р в систему счисления с основанием q можно попытаться воспользоваться описанным выше алгоритмом. Другой способ состоит в том, чтобы свести всё к хорошо знакомым действиям в десятичной системе счисления: перевести исходное число в десятичную систему счисления, после чего полученное десятичное число представить в требуемой системе счисления (рис. 3.3).
Рис. 3.3. Схема перевода целого числа из системы счисления с основанием р
в систему счисления с основанием q через десятичную систему счисления
Пример 5.
12345 = 1 • 53 + 2 • 52 + 3 • 51 + 4 • 50 = 19410 = 5226.
11.4. Перевод конечной десятичной дроби в систему счисления с основанием q
Для перевода конечной десятичной дроби в систему счисления с основанием q следует:
1) последовательно умножать данное число и получаемые дробные части произведения на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа;
2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.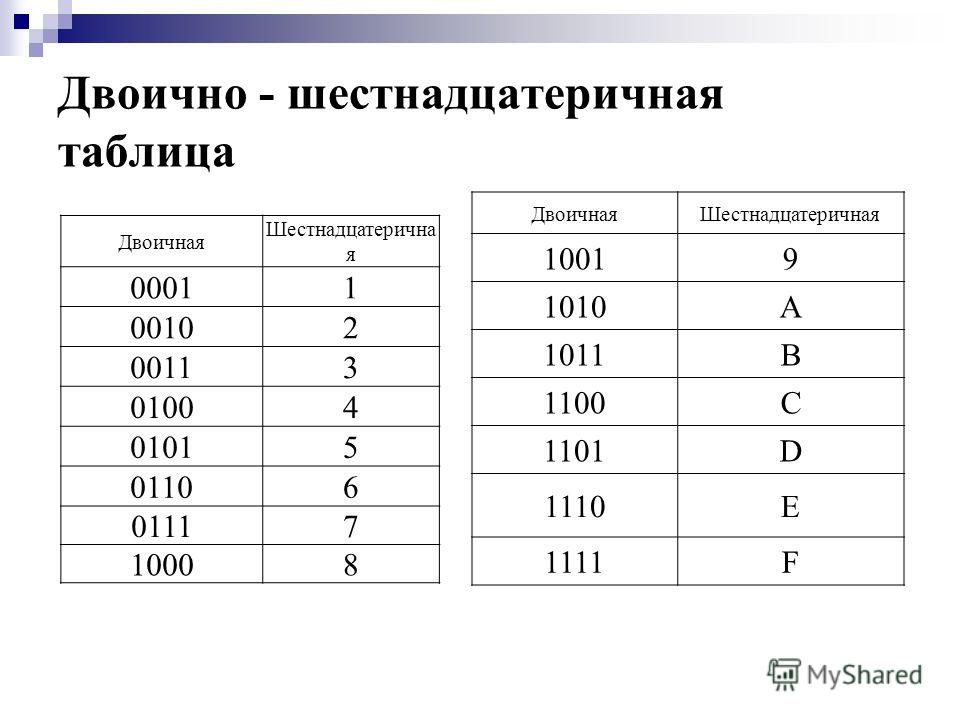
Пример 6. Переведём число 0,187510 в двоичную систему счисления.
Выполним умножение числа 0,187510 на 2:
Здесь жирным выделены цифры, участвующие в двоичном представлении дроби, а в скобках указан номер цифры в дроби.
0,187510 = 0,00112.
11.5. «Быстрый» перевод чисел в компьютерных системах счисления
Из курса информатики основной школы вы знаете, что в компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными».
Между основаниями этих систем существует очевидная связь: 16 = 24, 8 = 23.
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q = 2n) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
Для того чтобы целое двоичное число записать в системе счисления с основанием q = 2n, достаточно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.
Пример 7. Переведём число 110101001112 в восьмеричную систему счисления.
110101001112 — исходное число;
?11.010.100.111 — выделяем триады;
?011.010.100.111 — дополняем левую группу слева нулём;
?3.2.4.7 — выписываем восьмеричные цифры;
?32478 — результат.
Пример 8. Переведём число 16АС16 в двоичную систему счисления.
16АС16 — исходное число;
?0001.0110.1010.1100 — заменяем каждую цифру тетрадой;
?1.0110.1010.1100 — убираем слева незначащие нули;
?10110101011002 — результат.
Через двоичную систему счисления можно проводить быстрые переводы из восьмеричной системы счисления в шестнадцатеричную и обратно (рис. 3.4)
Рис. 3.4. Схема перевода целых чисел из восьмеричной системы счисления в шестнадцатеричную
и обратно через двоичную систему счисления
Пример 9. Выполним перевод восьмеричного 67 2528 числа в шестнадцатеричную систему счисления.
672528 — исходное число;
?110.111.010.101.010 — заменяем каждую цифру триадой;
?110.1110.1010.1010 — разбиваем двоичную строку справа налево на тетрады;
?0110.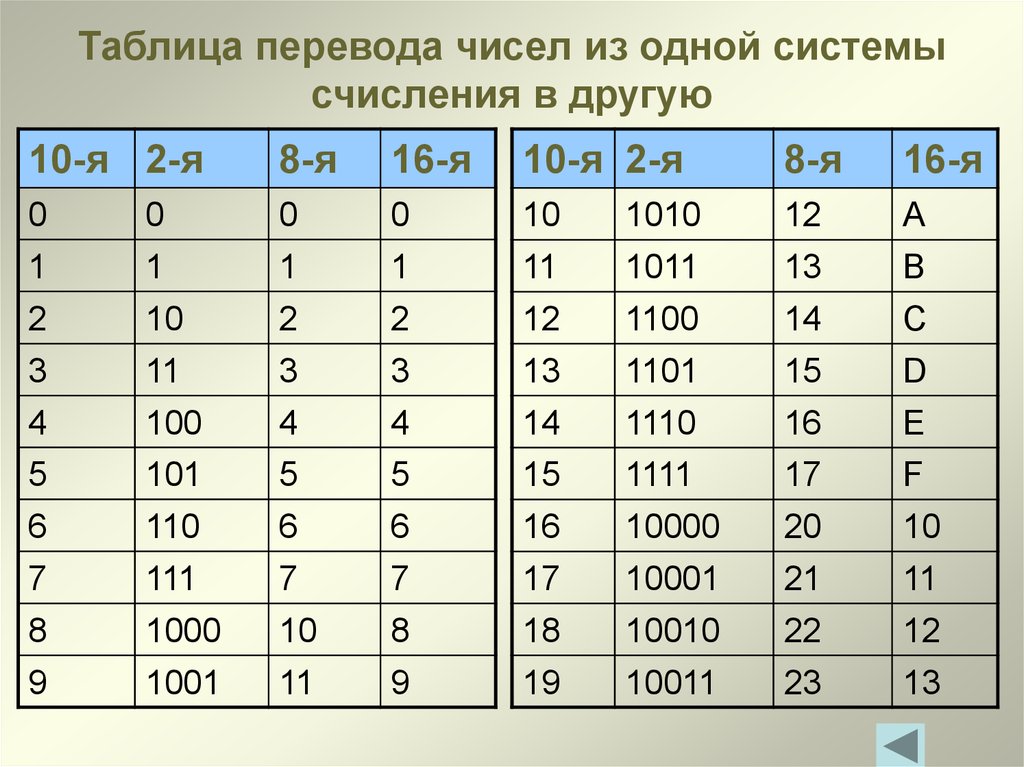
1110.1010.1010 — дополняем левую группу слева нулём;
?6.Е.А.А — выписываем шестнадцатеричные цифры;
?6ЕАА16 — результат.
Аналогичные алгоритмы быстрого перевода существуют и для дробных чисел. Для того чтобы записать правильную двоичную дробь в системе счисления с основанием q = 2n, достаточно:
1) двоичное число разбить слева направо на группы по n цифр в каждой;
2) если в последней правой группе окажется меньше n разрядов, то её надо дополнить справа нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2n.
Пример 10. Число 0,1011000112 заменим равным ему шестнадцатеричным числом.
0,1011000112 — исходное число;
?0,1011.0001.1 — разбиваем двоичную строку слева направо на тетрады;
?0,1011.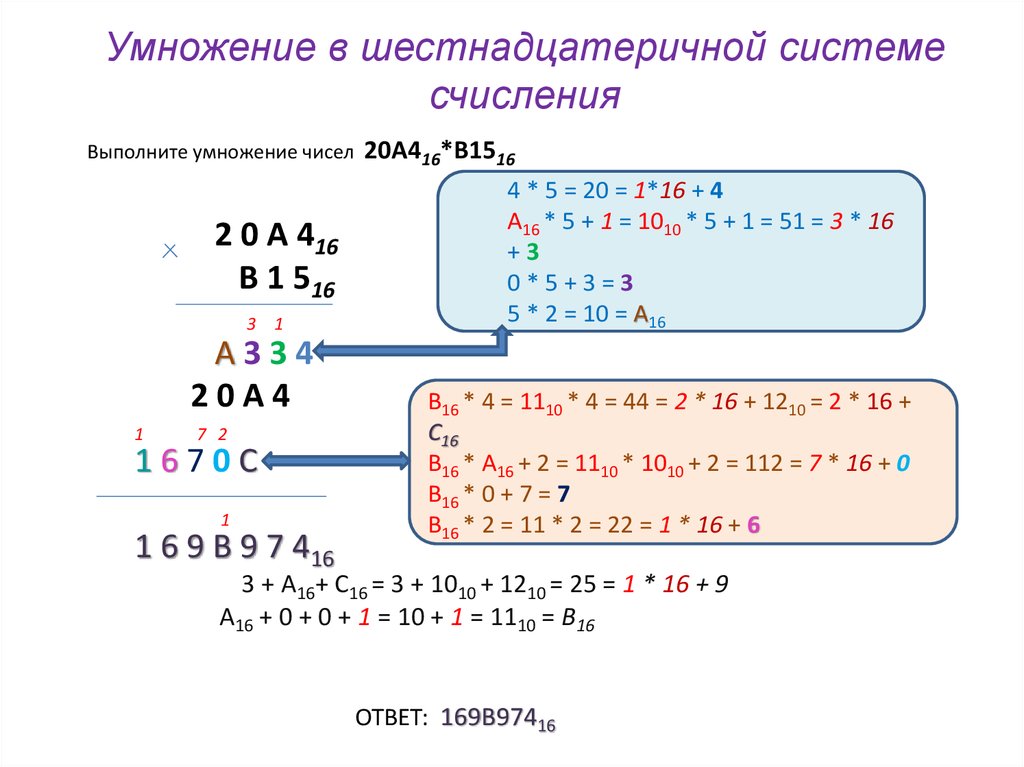
0001.1000 — дополняем правую группу справа нулями;
?0,В.1.8 — выписываем шестнадцатеричные цифры;
?0,В1816 — результат.
Попытайтесь самостоятельно сформулировать алгоритм быстрого перевода произвольного двоичного числа в восьмеричную систему счисления. Примените алгоритм к числу 11101001000,110100102.
Пример 11. Выясним, сколько значащих нулей в двоичной записи восьмеричного числа 16018.
Для ответа на этот вопрос достаточно знать двоичные триады, соответствующие восьмеричным цифрам от 0 до 7 и выполнить «быстрый» перевод числа 16018 в двоичную систему счисления:
16018 = 001 110 000 0012 = 11100000012.
В двоичной записи 6 значащих нулей, а первые два нуля являются незначащими и не учитываются.
Пример 12. Среди четырёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 единиц, найдём:
1) наименьшее число;
2) наибольшее число.
Наименьшее четырёхзначное шестнадцатеричное число — это 100016 = 0001 0000 0000 00002, и его двоичное представление содержит всего одну единицу. Чтобы получить наименьшее число, удовлетворяющее условию задачи, оставшиеся шесть единиц следует разместить в самых младших разрядах. Получим 1 0000 ОО11 11112 = 103F16. Чтобы получить наибольшее число, удовлетворяющее условию задачи, оставшиеся шесть единиц следует разместить в самых старших разрядах. Получим 1111 1110 0000 00002 = FE0016.
А сколько всего таких четырёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 единиц?
САМОЕ ГЛАВНОЕ
Для перевода целого десятичного числа в систему счисления с основанием q следует:
1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие алфавиту новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего остатка.
В компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными». Между основаниями этих систем существует очевидная связь: 16 = 24, 8 = 23.
Если основание системы счисления q кратно степени двойки (q = 2n), то любое число в этой системе счисления можно «быстро» перевести в двоичную систему счисления, выписав последовательно двоичные коды каждой из цифр, образующих исходное число. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
Вопросы и задания
1. Переведите целые числа из десятичной системы счисления в двоичную систему счисления:
1) 1025; 2) 512; 3) 600.
2. Переведите целое число 1147 из десятичной системы счисления в системы счисления:
1) пятеричную;
2) восьмеричную;
3) шестнадцатеричную.
3. Переведите двоичные числа в восьмеричную систему счисления:
1) 1010001001011;
2) 1010,00100101.
4. Переведите двоичные числа в шестнадцатеричную систему счисления:
1) 1010001001011;
2) 1010,00100101.
5. Переведите числа в двоичную систему счисления:
1) 2668; 2) 26616.
6. Переведите числа из восьмеричной системы счисления в шестнадцатеричную:
1) 12754; 2) 1515.
7. Переведите числа из шестнадцатеричной системы счисления в восьмеричную:
1) 1АЕ2; 2) 1С1С.
8. Сравните числа:
1) 12516 и 1111000101012;
2) 7578 и 11100101012;
3) А2316 и 12328.
9. Сколько из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству 2218<С<9516? Какие числа?
1) 100101002; 2) 100101102; 3) 100100112; 4) 100011002.
10. Сколько значащих нулей в двоичной записи:
1) восьмеричного числа 2501;
2) шестнадцатеричного числа 12А?
11.
Среди четырёхзначных восьмеричных чисел, двоичная запись которых содержит ровно 5 единиц, найдите:
1) наименьшее число;
2) наибольшее число.
12. Среди трёхзначных шестнадцатеричных чисел, двоичная запись которых содержит ровно 7 нулей, найдите:
1) наименьшее число;
2) наибольшее число.
13. Все 5-буквенные слова, составленные из букв О, П, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ООООО
2. ООООП
3. ООООР
4. ООООТ
5. ОООПО
…..
Какие слова находятся в этом списке на 531-м и 787-м местах?
14. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа 82 оканчивается на 5.
Оглавление
Представление чисел в позиционных системах счисленияПеревод чисел из одной позиционной системы счисления в другуюАрифметические операции в позиционных системах счисления
Конвертер системы счисления
— Blockchain Academy
Конвертер системы счисленияБинарный:
Десятичная дробь:
Шестнадцатеричный:
Вход Бинарный: к Восьмеричный: к Десятичная дробь: к Шестнадцатеричный:
Объяснение От двоичного до восьмеричного Так как в восьмеричной системе счисления всего 8 цифр (от 0 до 7), то мы можем представить любую цифру числа.
| Восьмеричный | Двоичный |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Итак, если вы сделаете каждую группу из 3-х битных двоичных входных чисел, то замените каждую группу двоичных чисел
из эквивалентных ему восьмеричных цифр.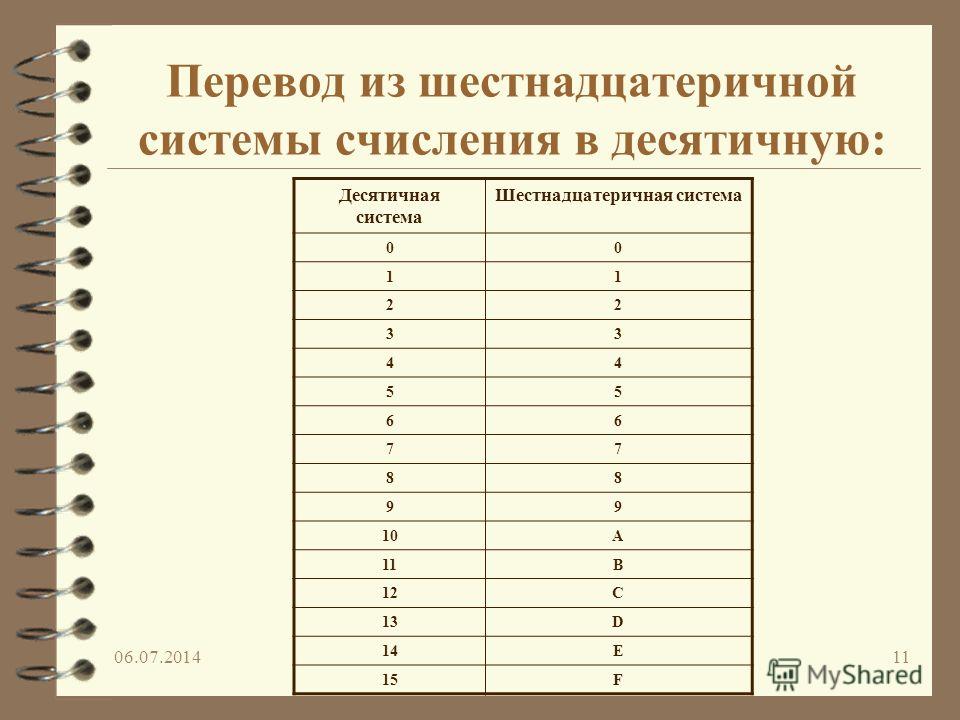
Это будет восьмеричное число заданного числа.
Обратите внимание, что вы можете добавить любое количество нулей в крайний левый бит (или в старший бит) для целочисленной части.
и добавьте любое количество нулей в самый правый бит (или в самый младший бит) для дробной части для
завершая группу из 3 бит, это не меняет значение входного двоичного числа.
Итак, это следующие шаги для преобразования двоичного числа в восьмеричное.
Взять двоичное число Разделить двоичные цифры на группы по три (начиная справа) для целой части
и начните слева для дробной части.
Преобразуйте каждую группу из трех двоичных цифр в одну восьмеричную цифру.
Это простой алгоритм, в котором вам нужно сгруппировать двоичные числа и заменить их эквивалентные восьмеричные числа
цифра.
.. Объяснение От двоичного к шестнадцатеричномуТак как в шестнадцатеричной системе счисления всего 16 цифр (от 0 до 9 и от A | a до F | f), то мы можем представлять любую цифру шестнадцатеричной системы счисления, используя только 4 бита, как показано ниже.
| Шестигранник | Двоичный | Шестигранник | Двоичный |
|---|---|---|---|
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | А | | 1010 |
| 3 | 0011 | Б | б | 1011 |
| 4 | 0100 | С | с | 1100 |
| 5 | 0101 | Д | д | 1101 |
| 6 | 0110 | Э | е | 1110 |
| 7 | 0111 | Ф | ф | 1111 |
Итак, если вы сделаете каждую группу из 4-х битных двоичных входных чисел, то замените каждую группу двоичных чисел
из его эквивалентных шестнадцатеричных цифр.
Это будет шестнадцатеричное число заданного числа. Обратите внимание, что вы можете добавить любое количество нулей в крайний левый бит.
или в старшем бите для целой части и добавьте любое количество нулей в самый правый бит или по крайней мере
значащий бит для дробной части для завершения группы из 4 битов, это не меняет значение ввода
двоичное число.
Вход Восьмеричный: к Бинарный: к Десятичная дробь: к Шестнадцатеричный:
Объяснение Восьмеричное в Двоичное Существует простой прямой метод преобразования восьмеричного числа в двоичное.
Поскольку в восьмеричной системе представления всего 8 символов (т. е. 0, 1, 2, 3, 4, 5, 6 и 7) и ее
основание (т.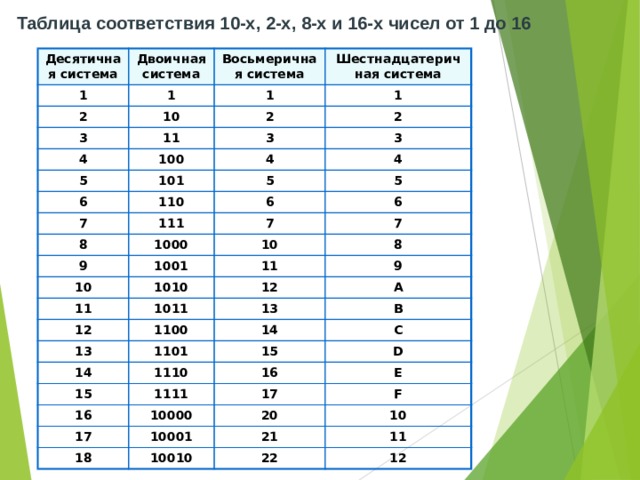
е. 8) эквивалентно 23=8.
Таким образом, вы можете представить каждую восьмеричную цифру в группе из 3 битов в двоичном числе.
| Восьмеричный | Двоичный |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Этот метод прост и также работает как обратный двоичному преобразованию в восьмеричное.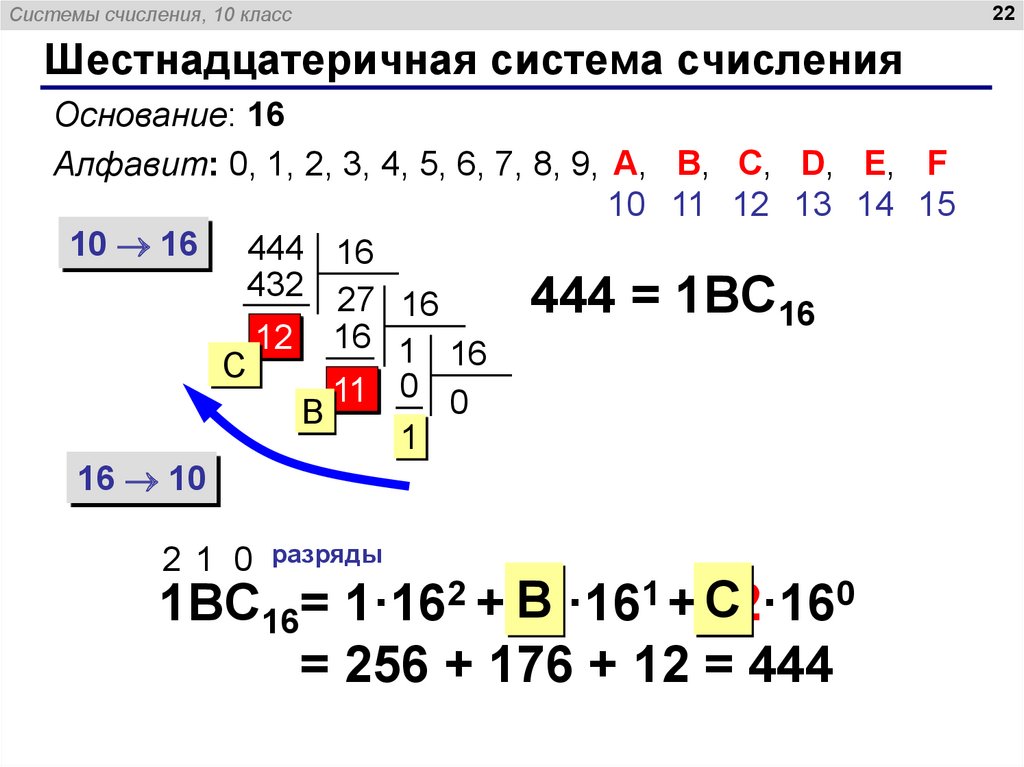
Алгоритм объясняется
как показано ниже.
- Принять восьмеричное число в качестве ввода
- Преобразование каждой восьмеричной цифры в двоичную.
- Будет выведено как двоичное число.
Десятичное число равно сумме двоичных цифр (dⁿ), умноженной на их степень 8 (8ⁿ): десятичный знак = d0×8⁰ + d1×8¹ + d2×8² + …
Объяснение Восьмеричное в ШестнадцатеричноеНет прямого преобразования. Один из способов — взять каждую восьмеричную цифру и преобразовать ее в двоичный эквивалент. Второй шаг — преобразовать двоичный эквивалент в шестнадцатеричное значение.
Вход Десятичная дробь: к Бинарный: к Восьмеричный: к Шестнадцатеричный:
Объяснение Десятичное в двоичноеШаги для двоичного преобразования:
- Разделите число на 2.
- Получить целое частное для следующей итерации.
- Получить остаток двоичной цифры.
- Повторяйте шаги, пока частное не станет равным 0.
Шаги для восьмеричного преобразования:
- Разделите десятичное число на 8. Считайте деление целочисленным делением.
- Запишите остаток (в шестнадцатеричном формате).
- Снова разделите результат на 8. Считайте деление целочисленным делением.
- Повторяйте шаги 2 и 3, пока результат не станет равным 0.
- Шестнадцатеричное значение представляет собой последовательность цифр остатков от последнего к первому.
Шаги для шестнадцатеричного преобразования:
- Разделите десятичное число на 16. Считайте деление целочисленным делением.
- Запишите остаток (в шестнадцатеричном формате).
- Снова разделите результат на 16. Считайте деление целочисленным делением.
- Повторяйте шаги 2 и 3, пока результат не станет равным 0.
- Шестнадцатеричное значение представляет собой последовательность цифр остатков от последнего к первому.
Считайте деление целочисленным делением.Вход Шестнадцатеричный: к Бинарный: к Восьмеричный: к Десятичная дробь:
Объяснение Hexal to BinaryПреобразуйте каждую шестнадцатеричную цифру в четыре двоичных цифры. Эта диаграмма — все, что вам нужно для преобразования одного в другое:
| Двоичный | Шестигранник | Двоичный | Шестигранник |
|---|---|---|---|
| 0000 | 0 | 1000 | 8 |
| 0001 | 1 | 1001 | 9 |
| 0010 | 2 | 1010 | А | |
| 0011 | 3 | 1011 | Б | б |
| 0100 | 4 | 1100 | С | с |
| 0101 | 5 | 1101 | Д | д |
| 0110 | 6 | 1110 | Э | е |
| 0111 | 7 | 1111 | Ф | ф |
Нет прямого преобразования.
Один из способов — взять каждую шестнадцатеричную цифру и преобразовать ее в двоичный эквивалент.
Второй шаг — преобразовать двоичный эквивалент в восьмеричное значение.
Десятичное число равно сумме двоичных цифр (dⁿ), умноженной на их степень 16 (16ⁿ): десятичный знак = d0×16⁰ + d1×16¹ + d2×16² + …
С помощью этого преобразователя число из одной системы счисления можно быстро и легко представить в других системах счисления. Для выбора доступны двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
При вводе символа, не принадлежащего соответствующему числовому формату, вы будете проинформированы об этом.
Преобразование происходит непосредственно с вводом. С помощью кнопки Очистить все поля очищаются.
Вероятно, большинство начинающих программистов сталкиваются с проблемой или путаницей при преобразовании различных типов систем счисления друг в друга при попытке изучить [. программирование системного уровня на языке ассемблера и при использовании […] двоичная а н д шестнадцатеричная система счисления и с м уст. datadoctor.biz datadoctor.biz | 大多数 可能 遇到 的 问题 开始 而 转换 或 多 个 不同 类型 的 系统 在 试图 试图 了解 制度 层面 的 编程 时 使 用 二 进制 数 和 十六 和 十六 和 十六 十六 十六 十六 十六 十六 和 用 必要的 . datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
T h e Шестнадцатеричная система счисления u s es основание 16 […] и включает только цифры от 0 до 9 и буквы A, B, C, D, E и F. […] номер для обозначения любого шестнадцатеричного числа. datadoctor.biz datadoctor.biz | 该 系统 采 用 十 六基地 16 多个,其中包括9只通过数字0和一个字母,二、三、四、五 、 六、 八 与 我们 使用 人数 以 标示 十六 号码. | |||||||||||||||||||||||||||||||||||||||||||
Таким образом, мы г е т шестнадцатеричное число 0 3 AB E H, эквивалент […] десятичное число 15038 и таким образом мы вернулись к исходному числу. datadoctor.biz datadoctor.biz | 因此 我们 得到 多 少 0 3ABE 十六 小 时 相当 于 十 进 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数 制数. datadoctor.biz datadoctor. | |||||||||||||||||||||||||||||||||||||||||||
Мы набрали 200 […] здесь, потому что команда DEBUG us e s шестнадцатеричная система a n | d десятеричный размер […]这 将 当前 语言 的 价值 与 Cx 登记, 让 你 作 改变 改变. 因为 这里 打印 200 用 进制 和 调试 指挥 反 射 面积 是 2 00 (八) 在 十 六 字 节 的 进制 是 512 是 512 是 512 是 512 是 512 是 512 是 512 是. datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Получить длину программы, вычитая конечный адрес из начального адреса, […]
натуральный y i n шестнадцатеричная система . datadoctor.biz datadoctor.biz | 在十六进制 自然 . datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
В этой таблице Square 16 строк, начиная с 0 до A, и 16 столбцов, также начинающихся с 0 […] до А. Из этой таблицы можно найти десятичное число […] значение a n y шестнадцатеричное число t h at находится между […] диапазон от 0H до FFH. datadoctor.biz datadoctor.biz | 这个 有 16 排方桌 、 从 0 到 16 个 栏目, 也 有 从 0 到 你 可以 找到 这个 小 数 有 十六 , 价 值 之 跳频 跳频 跳频 跳频 跳频 跳频 跳频 跳频 跳频 跳频 , 值 , 值 , . datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Кусочек специально входит в зону […] проценты когда мы […] talking about t h e number systems , B CD (Binary Coded Decimal) or /a n d hexadecimal ( b как e 16) номера. datadoctor.biz datadoctor.biz | 特别是 该 地区 蚕食 兴趣 当 我们 谈论 谈论 数 字 系 统 BCD 码 ( 进制 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 编码 | |||||||||||||||||||||||||||||||||||||||||||
Преобразовать би в R Y Номер I NT o HEXADECIMAL HEXADECIMAL . всех дополнить двоичным числом с ведущими нулями слева […] , чтобы убедиться, что двоичное число содержит числа, кратные четырем битам. datadoctor.biz datadoctor.biz | 一二进制数 转换 成 十六 格式 首 先垫 的 二进 制数 与 领先 的 左侧 的 使 二进制数 包含 个 位元 的 倍数 倍数. datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Я использовал t h e шестнадцатеричная система t o r e […] информацию, чтобы сделать ее легко понять. datadoctor.biz datadoctor.biz | 我使 用 十六进制为 代表 的信息使其易于理解. datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
В другом примере преобразование будет [. oapdf.com oapdf.com | 又如，将不同 进制转 换成 其 他 进制 的数 值的语法形式为：函 数 （ number ,pla ce s ） 其 中Number为待 转换 的数。 oapdf.com oapdf.com | |||||||||||||||||||||||||||||||||||||||||||
Нахождение шестнадцатеричного значения для десятичного числа из приведенной выше таблицы: В приведенной выше таблице количество строк представляет первые [. datadoctor.biz datadoctor.biz | 寻找 十六 值 十进 制数 从 上表: 本表 以上, 数 排 第一十六 代表 代表 (左 位 位) 和 一些 二十六 位 代表 代表 右 位 位) 的 人数 Datadoctor .biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Например, десятичное число отличается от […] шестнадцатеричные значения грамматической формы следующим образом: функция […] (число), из которых Число для преобразования в a шестнадцатеричное число . oapdf.com oapdf.com | 比如，将不同进制的数值转为十进制的语法形式为：函数 （ Номер) ， 其中 Номер 为 待转 换 的 某 种 进制数 。 进制数 。 进制数 。 . | |||||||||||||||||||||||||||||||||||||||||||
The m on t h number i s w ritte n i n hexadecimal , м и […] месяца октябрь, ноябрь и декабрь будут записываться как A, B и C соответственно. wavetronix.com wavetronix.com | 月 份 是 以 十 六 进 制 数 表 示 的 ，这 意 味 着 十 月 、十 一 月 和 圈 十 十 […] 别 以 A、B、C 表示。 wavetronix.com wavetronix.com | |||||||||||||||||||||||||||||||||||||||||||
Нахождение шестнадцатеричного значения для десятичного числа из приведенной выше таблицы: В приведенной выше таблице количество строк представляет первую шестнадцатеричную цифру (левая шестнадцатеричная цифра), а количество столбцов представляет вторую шестнадцатеричную цифру […] (правый шестнадцатеричный [. в таблице и […] найти эквивалентное шестнадцатеричное значение следующим образом datadoctor.biz datadoctor.biz | 寻找 十六 为 十进 制数 从 上表: 本表 以上, 数 排 第一十六 代表 代表 (左 十六 位) 和 栏目 二十六 位 代表 (右 十六 位 的 所以 如果 你 有 有多少给多少,可转换 成十进制数相当 于 十六 、 搜索数目在桌上找到价值 相当 于 十六 如 下 datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Для доступа к биту, […]
используйте следующий адрес, где b — a шестнадцатеричное число r e бит, представляющий указанное слово. maxthermo.com.tw maxthermo.com.tw | 欲存 取位 (бит) ， 使用 地址 地址 其中 其中 B 為 16 位 數 ， 代 表 指定 字 的 位 編號。。 Maxthermo.com.tw maxthermo.com.tw | |||||||||||||||||||||||||||||||||||||||||||
В пункте 63 своего доклада (A/64/380) […] Генеральный секретарь предоставляет […] информация по и Номер O F R Инициативы, внедренные одновременно с ERP в пределах секретариата Объединенных Наций | ||||||||||||||||||||||||||||||||||||||||||||
秘书长 在 其 报告 (a/64/380) 第 63 段中 提供 关于 在 联合国 秘书处 和 各 特派 团 内 与 资源 规划 执行 的 几 相关 举措 的 信息 ， 其中 ： ： ： 《公 部门 会计 的 信息准则》的实施，人才管 理系统 (征 聘和人员配置)， 精益六西格玛 (非 0419 系统 程序 改进). -ods.un.org daccess-ods.un.org | ||||||||||||||||||||||||||||||||||||||||||||
Этот экран позволяет пользователям […] для установки t h e система t y pe ) 9 (насос или счетчик0419 a n d номер o f g шт (1 или 2). gww.graco.com gww.graco.com | 本 屏幕 可 用户 用户 设置 系统 类 型 (泵 或 表） 和 喷枪 数量 (1 支 2 支）。 GWW.GRACO.com GWW. | |||||||||||||||||||||||||||||||||||||||||||
Этот экран позволяет пользователям […] настроить t h e system t y pe (pump or meter), the type of dosing (sequential or dynam ic ) , number o f g uns (1 or 2), and t h e system c o lo r configuration [ …] (1 или 3). gww.graco.com gww.graco.com | 本屏幕可使用 户 设置 系统 类型 （ 泵 或表）、配料类型 （顺序或动态）、喷枪数量 （1 支或 2 支） 以及 系统 颜 色配 置 （单色或三色）。 gww.graco.com gww.graco.com | |||||||||||||||||||||||||||||||||||||||||||
Шестнадцатеричный номер i s m [. используется для восстановления данных или любого другого типа устранения неполадок диска или программирования анализа диска. datadoctor.biz datadoctor.biz | 十 六 号 码 是 最 常 用 数据 恢复 或 任何 其他 类型 的 或 或 故障 分析 程式 程式 数据 恢复 任何 其他 类型 磁盘 或 磁盘 故障 分析 程式 . 多 少瓶 datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
Вы можете определить источник и […] пункт назначения, используя информацию, представленную в этом […] window ( di s c number , c ap acity, label, partition, and fi l e system и п для приказ). Seagate.com Seagate.com | 您可使用此窗口提供的信息（磁 盘 编号 、容 量、标签、分区 和文 件 系统 信 息 ）确 定源 盘和 目标 盘。 seagate. seagate.com | |||||||||||||||||||||||||||||||||||||||||||
Кат. или или г number d r iv en configuration makes mo ti o n system c o mm issioning […] быстро и просто, а также обширная библиотека движений […] Инструкции обеспечивают необходимую функциональность для любого приложения. emea.rockwellautomation.com emea.rockwellautomation.com | 采用 基于 产品 目 录号 的 组 态 方式 ， 得 运动 控制 系统 .控制指令库，能够为各种应用提供所需的功能。 литература.рок…lautomation.com литература.рок…lautomation.com | |||||||||||||||||||||||||||||||||||||||||||
При включении t h e шестнадцатеричное d u mp function, the printer prints all commands and dat a i n hexadecimal f o rm at along [. с направляющей секцией […] , чтобы помочь вам найти определенные команды. bixolon.com bixolon.com | Номер Номер 開 十六 進 位轉 儲功 能時，印表機 會 以 十 六進 位元 格式列印全部的命令及其它資 bixolon.com bixolon.com | |||||||||||||||||||||||||||||||||||||||||||
Обратите внимание на то, что параметр числового вывода может использоваться отдельно для ограничения […] шрифт для цифр, десятичных точек и других символов, используемых для отображения […] обычные, научные c o r шестнадцатеричные числа . redlion.net redlion.net | 请注意， […]
数字 输出 可 单独 用 于 将 字体 限制 为 数字 、 小数点 其它 用 于 呈现 常规 数字 、. | |||||||||||||||||||||||||||||||||||||||||||
Введите B для двоичного, D для десятичного и H f o r шестнадцатеричный . printronix.cn printronix.cn | 对于 二进制 ， 输入 B ； 对于 十进制 ， 输入 D ； 对于 十 六 进制 ， 输入 H。 Printronix.cn Printronix.cn | |||||||||||||||||||||||||||||||||||||||||||
Первый столбец […] содержит t h e шестнадцатеричный c o de s и […] Второй столбец содержит символы ASCII, соответствующие кодам. bixolon.com bixolon.com | 第一 栏 包 括 十六 进 制代 码 ， 第二 栏 为 代码 相 对应 的 ascii 字符。 Bixolon.com Bixolon.com | 66|||||||||||||||||||||||||||||||||||||||||||
Новые требования к маркировке расфасованных пищевых продуктов включали указание присутствия восьми наиболее распространенных веществ, вызывающих аллергию, маркировку функционального класса пищевой добавки и ее [. конкретное наименование или его […] identifica ti o n number u n de r the Internati on a l Numbering System f o r Пищевые добавки, […] и маркировка […] более гибкий формат даты. cfs.gov.hk cfs.gov.hk | 有關規定將於二零零七年七月十日生效，要求預先包裝食物須 […] 標示八種最常見致敏物質(如有的話)，以及所使用食物添加劑的作用類別和其 本身名稱或在食物添加劑國 際 編 碼 系 統中 的 識別 編號 並 在 標示 日期 的 格式 方面 容許 更 彈性。。 CFS.gov.hk CF.gov.hk | 66|||||||||||||||||||||||||||||||||||||||||||
Стол […] приведенный ниже может помочь получить быстрый поиск h o f Шестнадцатеричное число t o 9 преобразование [. ..]из […] Диапазон от 0 до 255 десятичных чисел. datadoctor.biz datadoctor.biz | 提交给明年能得到迅速查十进制数转换为十六人数反之亦然范围从0到255十进制数. datadoctor.biz datadoctor.biz | |||||||||||||||||||||||||||||||||||||||||||
После завершения Фазы 1 новой интегрированной информационной системы управления персоналом, STEPS (System To Enhance Personnel Services) в 2007 г., включая расчет заработной платы, управление персоналом, организационное управление, время […] управление, командировки и должность […] бюджетирование и контроль l, a number of system e n ha ncements have […] внедрено в 2008-2009 гг. по [. делает систему более удобной для пользователя и обеспечивает лучшую поддержку процессов HRM/расчета заработной платы. unesdoc.unesco.org unesdoc.unesco.org | 在 2007 年新的人力资源综合管理系统 […] ШАГИ（加强人事工作的系统），包括工资单、 […] 人事管理、组织管理、时间管理、旅行和职位的预算编制与控制第一阶段完成之后，2008-2009 年进行了多 次 系统 改造 ，使 该 系统 变 得更 加便 于用户使用，为人力资源管理/工资单程 […] 序提供更好的支持。 unesdoc.unesco.org unesdoc.unesco.org | |||||||||||||||||||||||||||||||||||||||||||
Рассмотрев отчет, […] Совет призвал Соединенные Штаты […]
Nations develop me n t system t o s tep up efforts in a number o f a реа, особенно [. реализация […] План действий по гармонизации деловой практики в системе Организации Объединенных Наций, принятый Координационным советом руководителей системы Организации Объединенных Наций (КСР) в 2007 году, политика возмещения затрат и внедрение согласованного подхода к денежным переводам ( см. резолюцию 2009/1). daccess-ods.un.org daccess-ods.un.org | 理事会在审议报告之后敦促联合 国发 展 系统 在 领 领 域 加紧 努力 特别是 要 实施 联合国 系统 行政 首长 协调 理事会 (行政 首长 会 会 特别是 要 联合国 系统 行政 首长 理事会 (行政 首长 会 会 特别是 要 实施 系统 行政 首长 理事会 理事会 (行政 协调 会 会) 2007 […] 年 的 《联合国 系统 统一 业务 做法 行动 计划》 、 回收 政策 ， 并 推出 现金 转账 统一 办法 办法 办法 见 第 费用 政策 ， 并 推出 现金 转账 办法 办法 (见 第 第 第 第 2009/1 号 决议)。 Daccess-ODS.UN.Org Daccess-ods. un.org | |||||||||||||||||||||||||||||||||||||||||||
HKMA сообщило, что признание [.  |
..]
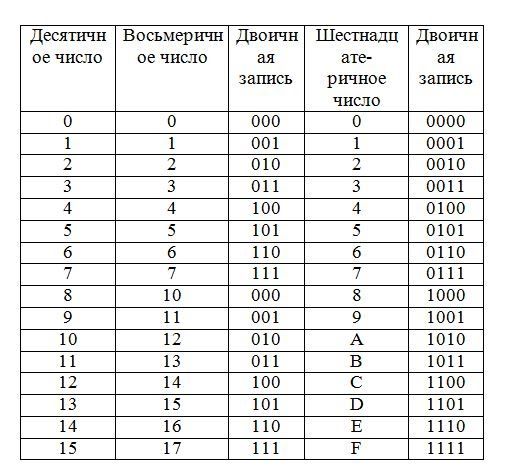Мы используем H с
biz
..]
разные для o th e r шестнадцатеричный n o t функция синтаксиса числовой формы 0419 io n ( number , p la ces) t o b e Number O n e в t h e номер o f c на версии 9s.
..]
[…]
hexadecimal digit (left Hexadecimal digit) and the number of columns represent the second hexadecimal digit (right hexadecimal digit) of t h e hexadecimal number 
..]
цифра) t h e шестнадцатеричное число t h можно преобразовать в любое десятичное число va, если у вас есть .0419 le n t шестнадцатеричное число , s каждый номер […]
..]
crac2.com266666666666666666666666666666666666666666666666666666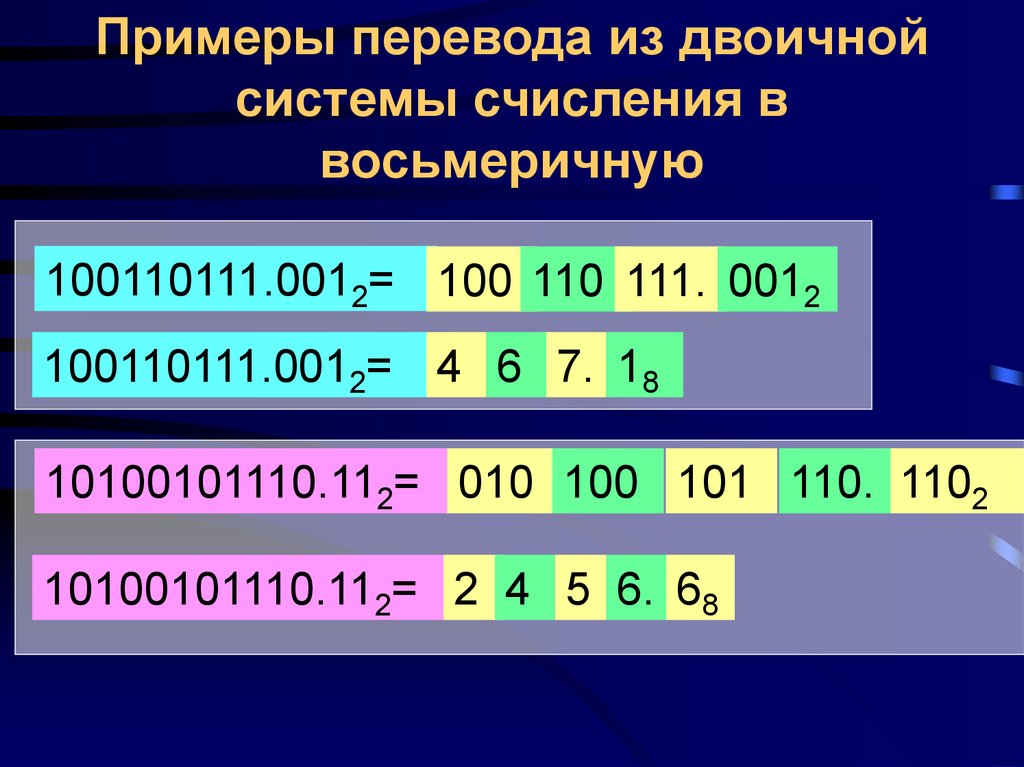
..]
com
..]
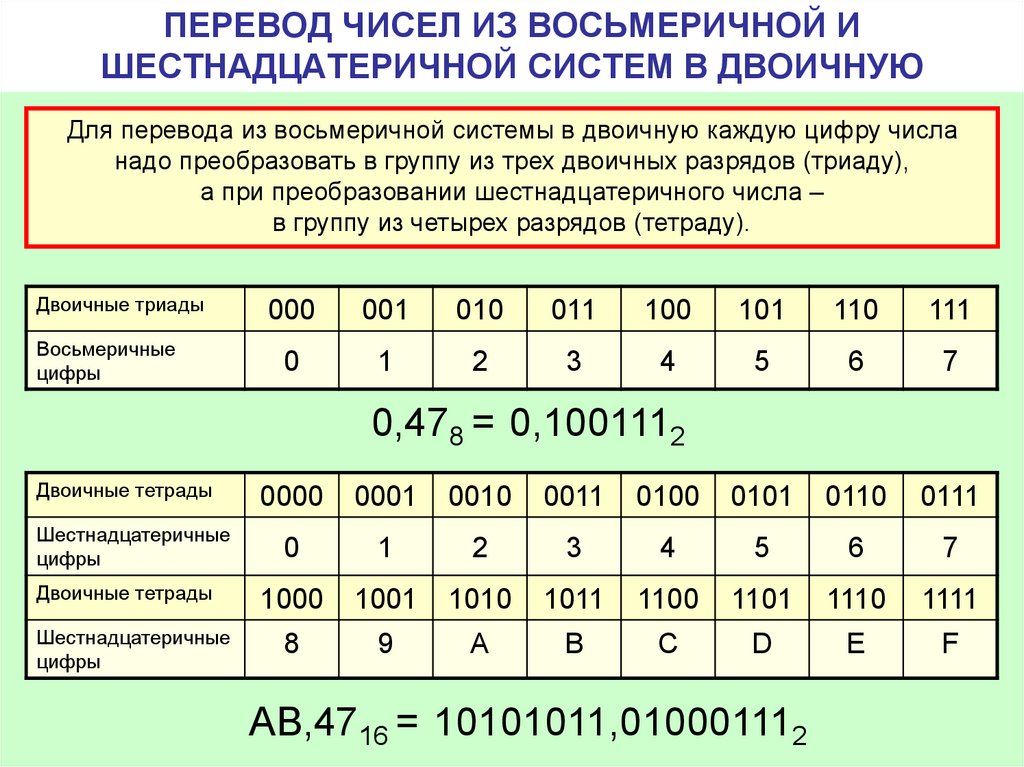.нет
..]
..]
..]