И хотя поначалу они могут казаться туманными, не особо нужными и востребованными только теми, кто пишет на низкоуровневых языках, на деле эти операторы имеют немалое значение. Причём некоторые из наиболее эффективных способов их применения совсем не требуют математики.
Побитовые операторы позволяют управлять двоичным представлением данных, что на деле оказывается очень полезной возможностью. Поэтому предлагаю познакомиться с этим инструментом и научиться грамотно его использовать.
▍ Дайте мне биты
Фундаментально компьютеры понимают только 1 и 0. На уровне же восприятия человеком смысл этим 1 и 0 придаёт контекст. Тут можно провести аналогию со словами в английском языке, смысл которых изменяется в зависимости от контекста. К примеру, слово «present» в зависимости от ситуации может означать «подарок» или «настоящее время».Одним из типичных примеров, в котором важен контекст двоичного представления, связан с кодированием текста. Если вам доводилось открывать файл с неверной кодировкой, то вы могли видеть в нём символы Null (�).
Отличный способ визуализировать общую группу бит – это открыть окно калькулятора Windows, кликнуть по иконке меню в верхнем левом углу и сменить режим со стандартного на режим программиста. Теперь вы будете видеть числа в их шестнадцатеричной (hex), десятичной, восьмеричной и двоичной формах. Над кнопкой битового сдвига
BIN-форматом значения, чтобы получить возможность самостоятельно инвертировать биты.
Это позволит вам выработать более интуитивное понимание представления 0 и 1, а также понять, как они переводятся в другие численные форматы.Целые числа являются знаковыми, то есть поддерживают как положительный, так и отрицательный диапазоныДля пользователей Linux отдельно скажу, что в этой системе аналогичную функциональность реализует приложение gnome-calculator.
В MacOS режим программиста в калькуляторе можно запустить путём ввода в стандартном режиме ⌘ и числа 3. Кодирование чисел в двоичную форму обеспечивает уникальное преимущество перед их десятичным представлением. Такая кодировка позволяет использовать само двоичное представление в качестве своеобразной команды, в которой сегменты двоичного числа соответствуют определённой функциональности. Инвертируя различные единицы и нули, можно управлять программой эффективным и компактным способом при относительно небольших размерах чисел.Разберём пример. Предположим, у нас есть байт данных (пробел здесь только для лучшей читаемости), 0010 0011, и мы хотим получить число, в котором установлены только 2 младших бита – 0000 0011.
Как это можно сделать? С помощью логической операции И (AND), которая реализуется через символ амперсанда &.
Но прежде, чем мы сможем получить итоговый результат, нам нужно создать ещё одно двоичное число, которое называется маской. Маска – это двоичное число, в котором определённые биты установлены как 1 или 0, чтобы при использовании с побитовым оператором нужным образом маскировать элементы исходного двоичного числа. Вот пример:
0010 0011 (исходное значение)
& -> 0000 0011 (итоговое значение)
0000 0011 (маска)
Каковы будут десятичные представления этих 3 двоичных чисел? Это не важно. Нам важно лишь, чтобы определённые биты в итоговом двоичном числе оказались 1 или 0. Реализуется это таким образом – операция & сравнивает биты в каждом индексе двух чисел, создавая в результате нуль или единицу. Вот правила, по которым работает это сравнение:- Если оба бита 0, то итоговый бит равен 0.
- Если оба бита 1, то итоговый равен 1.
- Если один бит 0, а второй 1, то итоговый будет равен 0.
0000 0011 с нужным нам битовым паттерном.Разберём ещё один пример. Предположим, у нас есть байт 1011 0011, и мы хотим получить другой байт – 1011 0000. Получается, нам нужно инвертировать два последних бита. На секунду обратитесь к перечисленным правилам, чтобы придумать подходящую маску самостоятельно. А теперь взгляните на пример ниже:
1011 0011
& -> 1011 0000
1011 0000
Если вы придумали правильную маску, то можете себя похвалить. Если же ошиблись, то ничего страшного, это новая тема, и на её усвоение может потребоваться некоторое время. Я хочу ещё раз подчеркнуть, что нам не нужно знать десятичные представления этих чисел, как и то, каким будет математический результат этих операций.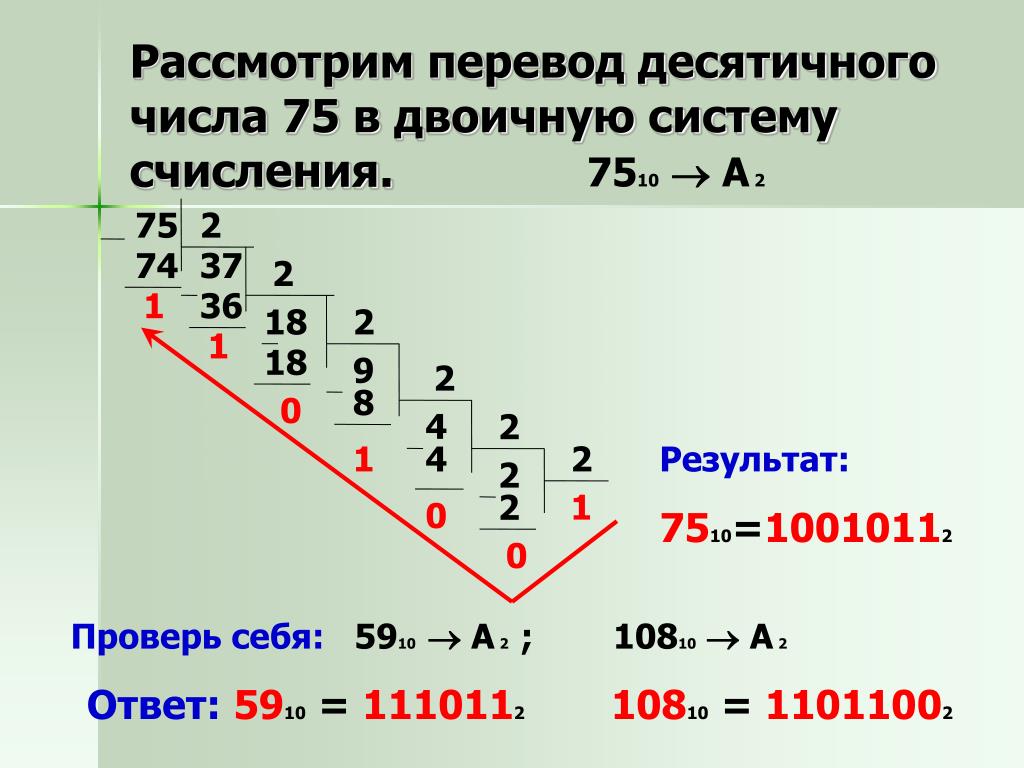
Здесь мы просто создаём маски, которые позволят получить желаемые битовые паттерны.▍ Побитовое ИЛИ (OR)
Мы разобрали использование побитового оператора &| для выполнения побитовой операции ИЛИ. Если, взяв предыдущий пример, мы захотим, чтобы результат был 1011 1111, то можем инвертировать два нуля в единицы с помощью ИЛИ. Для начала нужно создать маску с 1 в нужных нам позициях, после чего её применить.1011 0011
| -> 1011 1111
1011 1111
Обратившись к правилам побитовой операции И, мы видим, что они аналогичны правилам операции ИЛИ за исключением последнего:- Если оба бита 0, то итоговый бит равен 0.
- Если оба бита 1, то итоговый равен 1.
- Если один бит 0, а второй 1, то итоговый будет равен 1.
▍ Побитовое НЕ
Оператор НЕ обозначается тильдой~. Он используется для инвертирования всех битов в противоположное состояние. Его можно назвать особенным, поскольку он не требует маски для своего применения. Этот оператор относится к унарным, что отличает его от таких операторов, как – или +, которые являются бинарными. В этом случае бинарность означает не то, что они работают только для двоичных чисел, а то, что для их функционирования необходимо два числа. Как видите, тут снова всплывает значимость контекста.Принцип работы НЕ весьма прост. Если бит равен 1, то он становится 0, и наоборот. Обычно этот приём используется для создания маски, которая применяется совместно с оператором &.
-> 1001 0111
0001 0000
В этом случае XOR сравнивает каждый бит и в случае их отличия возвращает 1, а в случае совпадения – 0. В большинстве контекстов это означает, что нужно создать маску, которая будет содержать 1 в тех позициях, которые требуется инвертировать. Остальные биты маски нужно оставить равными 0.
▍ Сдвиг
Осталось разобрать последние два оператора: битовый сдвиг влево,<<, и битовый сдвиг вправо, >>. Они выражаются с помощью символов «больше»/«меньше» или левыми/правыми угловыми кавычками, « ». Оператор битового сдвига влево (<<) вставляет дополнительные нули в позицию наименее значимых бит двоичного числа. О наименее значимых битах мы не говорили, но вы можете представить их следующим образом.Возьмём, к примеру, десятичное число 123,456. Относительно него нам известно, что наименьшее число в нём – это 6, потому что оно находится в позиции исчисления единиц. При этом наибольшим числом является 1, поскольку занимает позицию исчисления сотен тысяч.
2, то есть его учетверению. И так далее.
Сдвиг вправо ведёт к противоположному результату. При использовании тех же приведённых выше чисел он половинит число или делит его на 4. Если вам нужно поделить или умножить число на степень 2, то операция сдвига окажется для этого очень быстрым решением. При этом она является типичной оптимизацией, выполняемой внутренне во время компиляции программ. Хотя для наших целей мы рассматриваем этот оператор просто как прибавляющий 0 в начало или конец двоичного числа или как смещающий это число влево/вправо на указанное количество нулей.
▍ Какая от этого польза?
Помимо нескольких грамотных приёмов оптимизации, как ещё можно использовать эти операторы на практике? Чтобы ответить на этот вопрос, нам нужно познакомиться с ещё одним принципом – шестнадцатеричными числами.Шестнадцатеричные числа представляют альтернативный способ выражения чисел в вычислительной технике. В отличие от двоичных, которые имеют основание 2, эти числа имеют основание 16.
Это означает, что в них используется уже не две цифры – 0 и 1 – а 16 символов, которые включают цифры от 0 до 9, а также буквы A, B, C, D, E и F, выражающие 10, 11, 12, 13, 14 и 15.
В вычислительной технике hex-числа важны тем, что позволяют более сжато выражать двоичные числа. Одно hex-значение может выразить четыре двоичных цифры (полубайт), то есть с помощью двух можно представить целый байт. Во многих языках программирования hex-числа обозначаются путём добавления приставки 0x, позволяющей отличать их от двоичных и десятичных значений. Получается, если вы захотите представить число 1234 в шестнадцатеричном виде, то его нужно будет записать как 0х1234.
Внимание. Не нужно путать десятичное число 1234 и шестнадцатеричное 0х1234. Первое – это десятичное значение 1,234, а второе – это десятичное значение 4,660.Чтобы преобразовать двоичное число в шестнадцатеричное, нужно разбить его на группы полубайтов, начиная с правой стороны, и затем заменить каждый полубайт соответствующей hex-цифрой.
Например, двоичное число 1101 1010 можно разбить на 1101 и 1010. Преобразование каждой группы в шестнадцатеричное значение даст DA. Следовательно, двоичное представление 1101 1010 равнозначно шестнадцатеричному 0хDA. Если же у вас под рукой всё ещё запущен калькулятор в режиме программиста, то эти вычисления можно поручить ему. Просто введите двоичную форму числа, и он сообщит вам его hex-эквивалент.
Шестнадцатеричные числа также используются в вычислительной технике для представления адресов памяти. Дело в том, что эти адреса обычно выражаются в виде 32- или 64-битных чисел, которые могут быть довольно длинными и сложными для чтения в двоичном виде. Представляя адреса памяти в hex-форме, мы делаем их более сжатыми и простыми для восприятия. Ниже показан пример
DA в виде 32-битного двоичного числа:0000 0000 0000 0000 0000 0000 1101 1010 vs 0000 00DA
▍ Побитовые операторы в эмуляторах
Теперь, обладая всей этой информацией, мы можем разобрать типичный практический случай – интерпретатор Chip-8.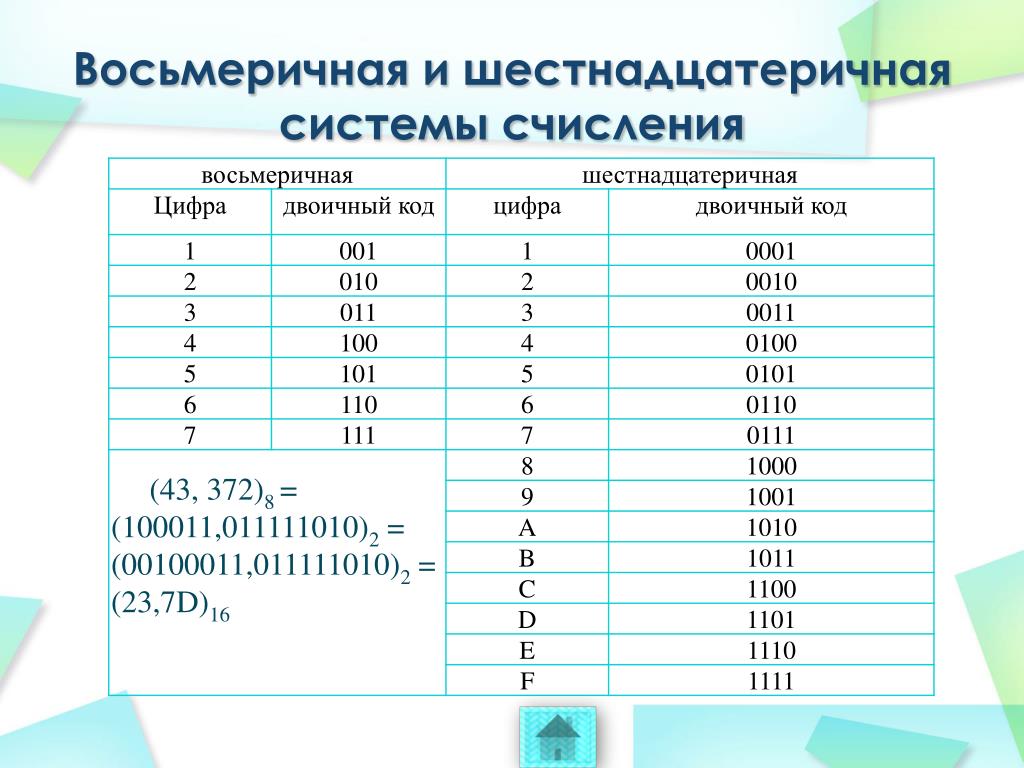
Этот интерпретатор станет хорошим стартовым проектом для людей, только начинающих знакомство с эмуляцией. В нём используется всего 36 инструкций, каждая длиной 2 байта, или 16 бит. Поскольку работать с 16 битами в двоичной форме сложно, мы будем представлять их в шестнадцатеричном виде. Напомню, что каждое шестнадцатеричное значение имеет размер 4 бита. И это удобно, потому что минимальный сегмент инструкции Chip-8, с которым нам придётся работать, составляет 4 бита.Игра Space Intercept, запущенная на Telmac 1800 через эмулятор Chip-8 (Джозеф Уэйсбекер, 1978 год)Также нужно иметь ввиду, что инструкции отличаются своими компонентами. Справка по Chip-8 от Cowdog прекрасно поясняет действия каждой из них. Разберём простой случай с инструкциями, которые относятся к диапазону 0х1000. В качестве примера мы будем использовать эмулятор Crystal Chip-8. Напомню, что эти числа представлены в hex-виде.
case op & 0xF000
#nnn или addr - A 12-битное значение, младшие 12 бит инструкции.
#n или nibble - A 4-битное значение, младшие 4 бита инструкции.
#x – 4-битное значение, младшие 4 бита старшего байта инструкции.
#y – 4-битное значение, старшие 4 бита младшего байта инструкции.
#kk или byte – 8-битное значение, младшие 8 бит инструкции.
when 0x1000
#1nnn
#установить счётчик команд на nnn, представляющее 3 младших байта.
@pc = op & 0x0FFF;
Предполагая, что нам представлена инструкция 
#n или nibble - A 4-битное значение, младшие 4 бита инструкции.
#x – 4-битное значение, младшие 4 бита старшего байта инструкции.
#y – 4-битное значение, старшие 4 бита младшего байта инструкции.
#kk или byte – 8-битное значение, младшие 8 бит инструкции.
when 0x1000
#1nnn
#установить счётчик команд на nnn, представляющее 3 младших байта.
@pc = op & 0x0FFF;0x1ABC, сначала нужно определить её наиболее значимый байт. Это позволит понять, как его интерпретировать. Обратившись к документации Cowdog, мы видим, что инструкции, содержащие в качестве наиболее значимого байта 1, устанавливают счётчик команд на последние 12 бит инструкции. При определении инструкции нам нужно сохранить наиболее значимый бит и очистить остальные 12, которые нас не интересуют. Этот процесс должен быть вам знаком.Можно написать оператор условия, который позволит нам создать несколько ветвлений на основе получаемой инструкции.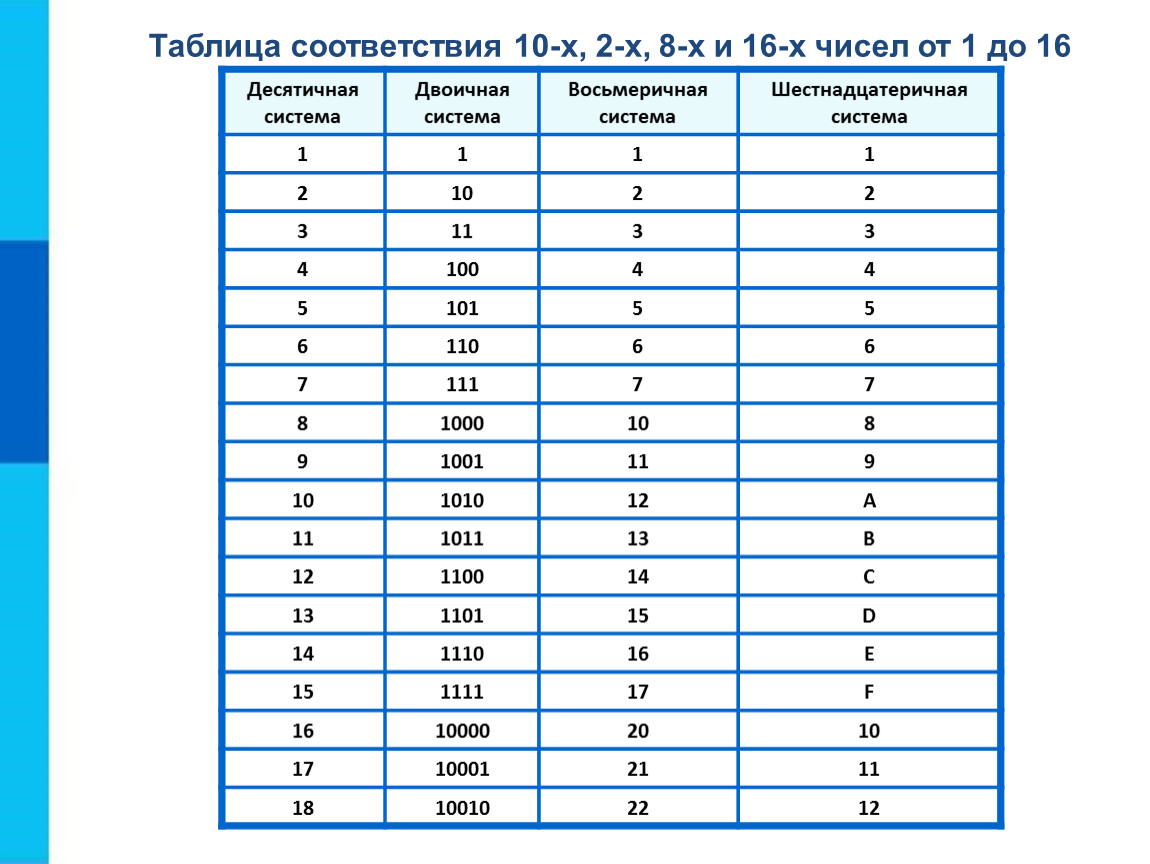
Мы возьмём код операции 0x1ABC и выполним побитовую операцию & с маской 0xF000, чтобы получить наиболее значимый бит нашей инструкции 0x1000. Это гарантирует, что любая входящая инструкция, которая начинается с 0x1, всегда будет отправлена по верной ветви, будь это 0x1DDD, 0x1012 и так далее.
Теперь, когда мы организовали правильное перенаправление инструкции, нужно получить её младшие 12 бит и установить наш счётчик команд на это значение. Опять же, для этого можно использовать &. Выполнив & для нашего кода операции и маски 0x0FFF, мы получим число 0x0ABC. Затем можно добавить это число в наш счётчик команд.
Вас может несколько запутать процесс перевода шестнадцатеричных значений обратно в двоичные, как мы делали в предыдущих примерах. Для большей ясности я покажу, как это происходит в текущем примере. Здесь 0x1ABC переводится в 0001 1010 1011 1100, а 0xF000 переводится в 1111 0000 0000 0000.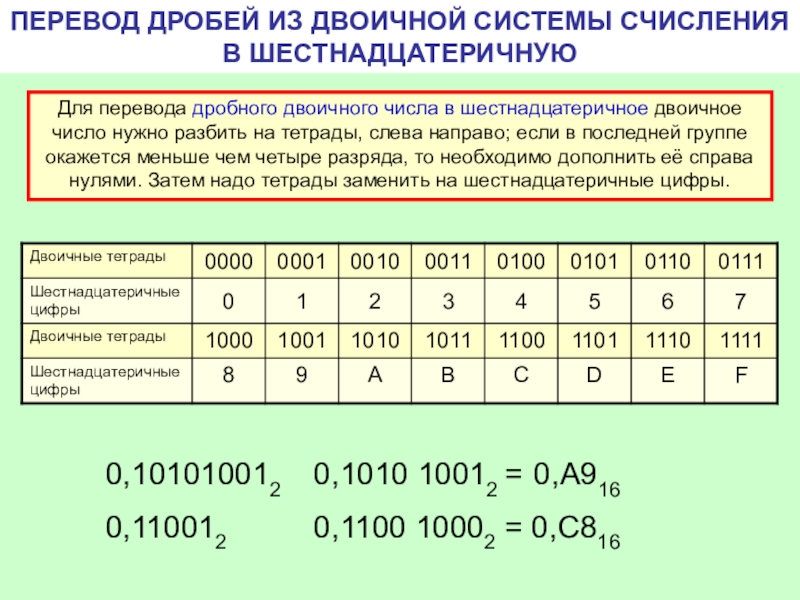
Выполнив для этих чисел операцию &, мы получим:
0001 1010 1011 1100
& -> 0001 0000 0000 0000
1111 0000 0000 0000
Результатом стало значение 0001 0000 0000 0000, которое просто является кодом операции с наиболее значимым битом. Как вы могли догадаться, 0001 0000 0000 0000 – это 0x1000 в двоичном виде, почему оно и отправляется по ветви 0x1000 нашего оператора ветвления.Та же логика касается и получения младших 12 бит нашей операции. В этом случае нас интересуют все числа, кроме первых 4 бит, поэтому их нужно убрать. На сей раз мы используем значение 0x0FFF, которое переводится в 0000 1111 1111 1111. Выполнив для него побитовое &, мы получим:
0001 1010 1011 1100
& -> 0000 1010 1011 1100
0000 1111 1111 1111
И это как раз то, что нам нужно. Последний вопрос, который у вас мог остаться: «Почему мы используем в hex-числе F, а не 1, как в двоичном?» Дело в том, что F в двоичном виде соответствует 1111.
Поэтому, если нам нужно сохранить этот битовый паттерн в данном индексе нашего исходного hex-значения, то можно просто использовать в нём F.Какой бы ни была комбинация 0 и 1 – при выполнении & она всегда будет сохранена. Поскольку мы хотели сохранить последние 12 бит нашего hex-значения, мы указали в нём три F. А так как для перехода по нужной ветви оператора ветвления нужно было сохранить только битовый паттерн наиболее значимых 4 бит, мы указали всего одну F в первой позиции hex-маски.
Закончим эту тему ещё одним примером, в котором используются операторы сдвига.
when 0x5000
#5xy0
#Пропустить следующую инструкцию, если Vx = Vy.
#Сравнивает регистр Vx с регистром Vy.
#Если они равны, инкрементирует счётчик команд на 2.
x = (op & 0x0F00) >> 8
y = (op & 0x00F0) >> 4
#индекс регистра
if @reg[x] == @reg[y]
@pc +=2
end
Предположим, что наша следующая инструкция – это 0x5120.
Нам нужно создать маску, которая будет направлять нашу операцию по ветви 0x5000 оператора ветвления. Для её создания нужно сохранить наиболее значимую цифру (первую hex-цифру), установив все остальные на 0. Попробуйте самостоятельно разобраться, как это сделать.Далее мы видим, что инструкции, относящиеся к диапазону 0x5000, дают нам значения x и y, которые можно использовать для обращения к регистрам в x и y. Следовательно, нам нужно каким-то образом получить из операции эти значения. Также, как в предыдущих примерах, можно поместить Fпо индексу интересующего нас hex-значения и 0 в остальных индексах. Для значения x это будет маска 0x0F00, а для значения y — – 0x00F0.
Мы узнали, что сдвиг вправо прибавляет 0 к наиболее значимой стороне двоичного числа. И хотя в большинстве случаев это верно, что должно происходить, когда ваше число имеет фиксированную длину? В Chip-8 минимальная двоичная инструкция соответствует 0000 0000 0000 0000, а максимальная – 1111 1111 1111 1111.
В обоих случаях они ограничены 16 битами. Здесь мы не можем просто прибавить нули к наиболее значимой стороне, например так: 0000 1111 1111 1111 1111, поскольку тогда мы получим уже 20-битную инструкцию при том, что Chip-8 поддерживает лишь 16-битные. Придётся чем-то пожертвовать.
Работает это в данном случае так. Числа с наименее значимой стороны вытесняются, освобождая место для нулей с наиболее значимой стороны. Это означает, что число 1111 1111 1111 1111 при сдвиге вправо на 4 станет:
(1111 1111 1111 1111 >> 4) 0000 1111 1111 1111Сегмент
1111 был вытеснен для освобождения места под 0000. Сколько раз нам нужно сдвинуть инструкцию вправо, чтобы получить x и y? Если взглянуть на шаблон инструкции для инструкций 0x5000 – 5xy0 – мы увидим, что x смещён от наименее значимой стороны на 8 бит. Поскольку один сдвиг перемещает целое число на 1 бит, то для перемещения x к наименее значимой стороне двоичного числа потребуется 8 таких сдвигов.
А поскольку y находится всего в 4 битах от наименее значимой стороны инструкции, то для него потребуется лишь 4 сдвига. Таким образом, чтобы получить значения x и y, мы выполняем сдвиг на 8 и на 4 соответственно.x = (op & 0x0F00) >> 8 y = (op & 0x00F0) >> 4После получения значений x и y следующим действием будет сравнение нашего регистра в x с регистром в y на предмет их равенства. Если они равны, то мы инкрементируем счётчик команд.
#индекс регистра
if @reg[x] == @reg[y]
@pc +=2
end
Здесь я не буду разбирать все инструкции, поскольку это получится очень долго, но если взглянуть на некоторые инструкции для Chip-8, например, на расположенные в диапазоне 0x8000:8xy1 - OR Vx, Vy Set Vx = Vx OR Vy. 8xy3 - XOR Vx, Vy Set Vx = Vx XOR Vy.То вы увидите, что в итоге мы используем все побитовые функции, с которыми познакомились в первой части статьи. Надеюсь, этот материал позволил вам понять важность побитовых операторов в программировании, а также послужил практическим примером их конкретного использования.
Эмуляторы – это не единственный случай применения, поэтому я рекомендую поискать и другие. Но в следующий раз, когда вы будете запускать свой эмулятор с легально полученными или собственными образами ROM, помните, что за его работой стоят побитовые операторы.
Если вы хотите получше разобраться в принципах работы эмуляторов, то советую создать собственный интерпретатор Chip-8, поскольку это будет очень ценным опытом. В качестве же справочного материала советую обращаться к документации от Cowdog, которая лично в моём опыте с Chip-8 оказала бесценную помощь.
Telegram-канал с розыгрышами призов, новостями IT и постами о ретроиграх 🕹️
| ||
| ||
Преобразователь шестнадцатеричных чисел в двоичные
Чтобы использовать этот инструмент для преобразования шестнадцатеричных данных в двоичные , просто введите шестнадцатеричное значение, например 1E, в левое поле ниже, а затем нажмите кнопку «Преобразовать».
Таким образом, вы можете преобразовать до 16 шестнадцатеричных символов (макс. значение 7ffffffffffffffff).
Шестнадцатеричное значение (макс. 7ffffffffffffffff) Прокладка
Двоичное значение Преобразование подкачки: Преобразователь двоичного кода в шестнадцатеричный
Hex в двоичный результат преобразования в основные числаШестнадцатеричная система (шестнадцатеричная система)
Шестнадцатеричная система (коротко шестнадцатеричная) использует число 16 в качестве основания (основания). В системе счисления с основанием 16 используется 16 символов. Это 10 десятичных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и первые шесть букв английского алфавита (A, B, C, D, E, F). Буквы используются из-за необходимости представлять значения 10, 11, 12, 13, 14 и 15 каждое в одном единственном символе.
Hex используется в математике и информационных технологиях как более удобный способ представления двоичных чисел.
Каждая шестнадцатеричная цифра представляет четыре двоичных цифры; следовательно, hex — это язык для записи двоичного кода в сокращенной форме.
Четыре двоичных разряда (также называемые полубайтами) составляют половину байта. Это означает, что один байт может содержать двоичные значения от 0000 0000 до 1111 1111. В шестнадцатеричном формате они могут быть представлены более удобным образом, в диапазоне от 00 до FF.
В HTML-программировании цвета могут быть представлены 6-значным шестнадцатеричным числом: FFFFFF представляет белый цвет, а 000000 — черный.
Двоичная система счисления
В двоичной системе счисления в качестве основания (основания) используется число 2. Система счисления с основанием 2 состоит только из двух чисел: 0 и 1.
В то время как двоичная система применялась в Древнем Египте, Китае и Индии для различных целей, в современном мире двоичная система стала языком электроники и компьютеров. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала.
Это также основа для двоичного кода, который используется для составления данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.
Чтение двоичного числа проще, чем кажется: это позиционная система; следовательно, каждая цифра двоичного числа возводится в степень 2, начиная с самой правой с 2 0 . В двоичной системе каждая двоичная цифра соответствует 1 биту.
Как преобразовать шестнадцатеричные числа в двоичные
Преобразование шестнадцатеричных чисел в двоичные несложно, поскольку шестнадцатеричные числа представляют собой упрощенные версии двоичных строк. Вам просто нужно помнить, что каждое шестнадцатеричное значение будет производить четыре двоичных цифры.
- Шаг 1 : Запишите шестнадцатеричное число. Если они есть, измените шестнадцатеричные значения, представленные буквами, на их десятичные эквиваленты.
- Шаг 2 : Каждая шестнадцатеричная цифра представляет четыре двоичных цифры и, следовательно, равна степени 2. Крайняя правая цифра равна 2 0 (1), следующая равна 2 1 (2), следующая один равен 2 2 (4), а крайний левый равен 2 3 (8). Запишите эти числа (8, 4, 2 и 1) под шестнадцатеричными значениями.
- Шаг 3 : Определите, какие степени двойки (8, 4, 2 или 1) дают в сумме ваши шестнадцатеричные цифры. Например, если одно из ваших шестнадцатеричных значений равно 10, это означает, что 8 и 2 в сумме дают 10 (4 и 1 не используются). Если ваше шестнадцатеричное число равно 2, используется только 2; 8, 4 и 1 нет.
- Шаг 4 : Запишите 1 под используемыми цифрами 8, 4, 2 и 1. Запишите 0 ниже тех, которые не используются.
- Шаг 5 : Прочитайте 1 и 0 слева направо, чтобы получить двоичный эквивалент данного шестнадцатеричного числа.
Крайняя правая цифра равна 2 0 (1), следующая равна 2 1 (2), следующая один равен 2 2 (4), а крайний левый равен 2 3 (8). Запишите эти числа (8, 4, 2 и 1) под шестнадцатеричными значениями.Применим эти шаги к шестнадцатеричному номеру (4FA) 16
Шаг 1: 4 Ф А 4 15 10 Шаг 2: 4 Ф А 4 15 10 8421 8421 8421 Шаг 3: 4 Ф А 4 5 10 8421 8421 8421 (Обратите внимание, что сумма выделенных жирным шрифтом цифр равна шестнадцатеричному значению выше.
Таким образом, выделенные жирным шрифтом цифры равны 1, а остальные — 0.)
Шаг 4:
4 Ф А
4 15 10
8421 8421 8421
0100 1111 1010
Шаг 5: (4FA) 16 = (10011111010) 2 Примеры преобразования шестнадцатеричного кода в двоичный
Пример 1: (2C1) 16 = (1011000001) 2 2 С 1 2 12 1 8421 8421 8421 0010 1100 0001 Пример 2: (9DB2) 16 = (1001110110110010) 2 9 ДБ 2 9 13 11 2 8421 8421 8421 8421 1001 1101 1011 0010
Связанные конвертеры: Преобразователь двоичного кода в шестнадцатеричный
Таблица преобразования шестнадцатеричного кода в двоичный
| Шестнадцатеричный | Двоичный |
|---|---|
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 9 0105 00000011|
| 4 | 00000100 |
| 5 | 00000101 | 6 | 00000110 |
| 7 | 00000111 |
| 8 | 00001000 |
| 9 | 0000100 1 |
| А | 00001010 |
| Б | 00001011 |
| С | 00001100 | 901 03
| D | 00001101 |
| E | 00001110 |
| F | 000 01111 |
| 10 | 00010000 |
| 11 | 00010001 |
| 12 | 00010010 | 13 | 00010011 |
| 14 | 00010100 |
| 15 | 00010101 |
| 16 | 00 010110 |
| 17 | 00010111 |
| 18 | 00011000 |
| 00011001 | |
| 1A | 00011010 |
| 1B | 00011011 |
| 1C | 00011100 9 0106 |
| 1Д | 00011101 |
| 1E | 00011110 |
| 1F | 00011111 |
| 20 | 00100000 |
| 21 | 00100001 |
| 22 | 00100010 |
| 23 | 00100011 |
| 24 | 00100100 |
| 25 | 00100101 |
| 26 | 9010 5 00100110|
| 27 | 00100111 |
| 28 | 00101000 |
| 29 | 00101001 |
| 2A | 00101010 |
| 2B | 00101011 |
| 2C | 00101100 |
| 2D | 00101101 |
| 2Е | 00101110 |
| 2Ф 0 | 00110000 |
| 31 | 00110001 |
| 32 | 00110010 |
| 33 | 00110 011 |
| 34 | 00110100 |
| 35 | 00110101 |
| 36 | 00110110 |
| 37 | 00110111 |
| 38 | 00111000 |
| 39 | 00111001 9010 6 |
| 3А | 00111010 |
| 3B | 00111011 |
| 3C | 00111100 |
| 3D | 00111101 |
| 3E | 00111110 |
| 3F | 00111111 |
| 40 | 01000000 |
| Шестнадцатеричный | Двоичный |
|---|---|
| 41 | 01000001 |
| 42 | 01000010 |
| 43 | 01000011 |
| 44 | 01000100 |
| 45 | 01000101 |
| 46 | 01000110 |
| 47 | 01000111 |
| 48 | 01001000 |
| 49 | 01001001 |
| 4A | 01001010 |
| 4B | 0100 1011 |
| 4С | 01001100 |
| 4D | 01001101 |
| 4E | 01001110 |
| 4F | 01001111 |
| 50 | 01010000 |
| 51 | 01010001 |
| 52 | 01010010 |
| 53 | 01010011 |
| 54 | 01010100 |
| 55 | 9010 5 01010101|
| 56 | 01010110 |
| 57 | 01010111 |
| 58 | 01011000 |
| 59 | 01011001 |
| 5A | 01011010 |
| 5B | 01011011 |
| 5С | 01011100 |
| 5D | 01011101 |
| 5E | 01011110 |
| 5 Ф | 01011111 |
| 60 | 01100000 |
| 61 | 01100001 |
| 62 | 01100 010 |
| 63 | 01100011 |
| 64 | 01100100 |
| 65 | 01100101 |
| 66 | 01100110 |
| 67 | 01100111 |
| 68 | 01101000 9010 6 |
| 69 | 01101001 |
| 6A | 01101010 |
| 6B | 01101011 |
| 6C | 01101100 |
| 6D | 01101101 |
| 6E | 01101110 |
| 6F | 01101111 |
| 70 | 01110000 |
| 71 | 01110001 |
| 72 | 0111 0010 |
| 73 | 01110011 |
| 74 | 01110100 |
| 75 | 01110101 |
| 76 | 01110110 |
| 77 | 01110111 |
| 78 | 01111000 |
| 79 | 01111001 |
| 7A | 01111010 |
| 7B | 01111011 |
| 7C | 9010 5 01111100|
| 7Д | 01111101 |
| 7E | 01111110 |
| 7F | 01111111 |
| 80 | 10000000 |
| Шестнадцатеричный | Двоичный |
|---|---|
| 81 | 10000001 |
| 82 | 10000010 |
| 83 9010 6 | 10000011 |
| 84 | 10000100 |
| 85 | 10000101 |
| 86 | 10000110 |
| 87 | 10000111 |
| 88 | 10001000 |
| 89 | 10001001 |
| 8A | 10001010 |
| 8Б | 10001011 |
| 8C | 10001100 |
| 8D | 10001101 |
| 8 Е | 10001110 |
| 8F | 10001111 |
| 90 | 10010000 |
| 91 | 10010 001 |
| 92 | 10010010 |
| 93 | 10010011 |
| 94 | 10010100 |
| 95 | 10010101 |
| 96 | 10010110 |
| 97 | 10010111 9010 6 |
| 98 | 10011000 |
| 99 | 10011001 |
| 9А | 10011010 |
| 9В | 10011011 |
| 9C | 10011100 |
| 9D | 10011101 |
| 9Е | 10011110 |
| 9F | 10011111 |
| A0 | 10100000 |
| A1 | 101000 01 |
| А2 | 10100010 |
| А3 | 10100011 |
| А4 | 10100100 |
| А5 90 106 | 10100101 |
| А6 | 10100110 |
| А7 | 10100111 | 9010 3
| А8 | 10101000 |
| АС | 10101100 |
| AD | 10101101 |
| AE | 10101110 | AF | 10101111 |
| B0 | 10110000 |
| B1 | 10110 001 |
| В2 | 10110010 |
| B3 | 10110011 |
| B4 | 10110100 |
| B5 9 0106 | 10110101 |
| B6 | 10110110 |
| B7 | 10110111 |
| B8 | 10111000 |
| B9 | 10111001 |
| BA | 10111010 |
| BB 90 106 | 10111011 |
| БК | 10111100 |
| БД | 10111101 |
| БЭ | 10111110 |
| БФ | 10111111 |
| C0 | 11000000 |
| Шестнадцатеричный | Двоичный |
|---|---|
| С1 | 11000001 |
| С2 | 11000010 |
| С3 | 9 0105 11000011|
| C4 | 11000100 |
| C5 | 11000101 | С6 | 11000110 |
| С7 | 11000111 |
| C8 | 11001000 |
| C9 | 11001001 |
| CA | 901 05 11001010|
| CB | 11001011 |
| CC | 11001100 |
| КД | 11001101 |
| CE | 11001110 |
| CF | 11001111 |
| D0 | 1101000 0 |
| D1 | 11010001 |
| D2 | 11010010 |
| D3 | 11010011 |
| D4 90 106 | 11010100 |
| D5 | 11010101 |
| D6 | 11010110 | 9010 3
| D7 | 11010111 |
| ДБ | 11011011 |
| DC | 11011100 |
| ДД | 11011101 | DE | 11011110 |
| DF | 11011111 |
| E0 | 11100 000 |
| E1 | 11100001 |
| E2 | 11100010 |
| E3 | 11100011 |
| E4 9 0106 | 11100100 |
| E5 | 11100101 |
| E6 | 11100110 |
| E7 | 11100111 |
| E8 | 11101000 |
| E9 | 11101001 |
| EA 90 106 | 11101010 |
| ЭБ | 11101011 |
| ЕС | 11101100 |
| ЭД | 11101101 |
| ЕЕ | 11101110 |
| EF | 11101111 |
| F0 | 11110000 |
| F1 | 90 105 11110001|
| F2 | 11110010 |
| F3 | 11110011 | F4 | 11110100 |
| F5 | 11110101 |
| F6 | 11110110 |
| F7 | 1111011 1 |
| F8 | 11111000 |
| F9 | 11111001 |
| FA | 11111010 |
| FB 90 106 | 11111011 |
| ФК | 11111100 |
| ФД | 11111101 | 9010 3
| ФЭ | 11111110 |
| FF | 11111111 |
Binary Converter Calculator on the App Store
Описание
Binary Converter Calculator — отличное приложение для преобразования текста, двоичных, шестнадцатеричных чисел или чисел в текст, двоичные, шестнадцатеричные числа или числа.
Вы также можете конвертировать пользовательские базы.
Минималистичный дизайн
Хороший способ кодирования сообщений в двоичном формате
Узнайте, как работают различные базовые системы
Получайте удовольствие!
Версия 1.5
В этой версии исправлено множество ошибок и добавлены новые функции.
Особенности:
1. Добавлена клавиатура Custom Base, так что теперь она отображает правильные символы для базы.
2. Добавлена кнопка подкачки, позволяющая легко менять базы.
1. Исправлена ошибка, из-за которой версия для iPad вылетала при нажатии кнопки «Поделиться».
2. Исправлены ошибки, из-за которых вычисления не происходили там, где должны были бы.
3. Исправлены некоторые ошибки интерфейса для улучшения опыта.
4. Исправлены ошибки, вызывающие замедление и зависание.
5. Исправлена ошибка, из-за которой длительное нажатие для автоматического удаления на клавиатуре не работало.
6. Исправлена ошибка, из-за которой iPad не мог установить собственный значок.
Рейтинги и обзоры
29 оценок
Отличная работа
Возвращает меня в 2004 год, когда мы использовали двоичный код для передачи заметок в производственном классе.
Так было бы проще.
Хороший.
Это просто, удобно и не сложно! Мне нравится, нет подписки и прочего. Просто переведи одно из другого и готово! Очень хороший.
Довольно хорошо
Я не могу заставить его работать правильно.
Какие у вас проблемы?
Разработчик Стейси Горовиц указала, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, не связанные с вами
Могут быть собраны следующие данные, но они не связаны с вашей личностью:
- Расположение
- Данные об использовании
- Диагностика
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста.
