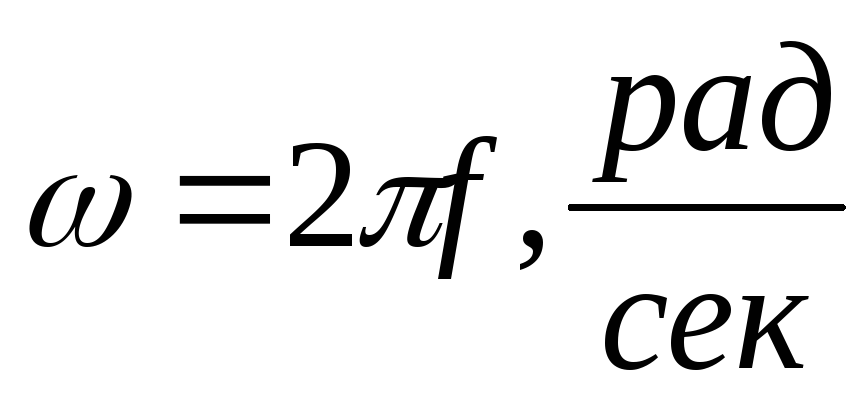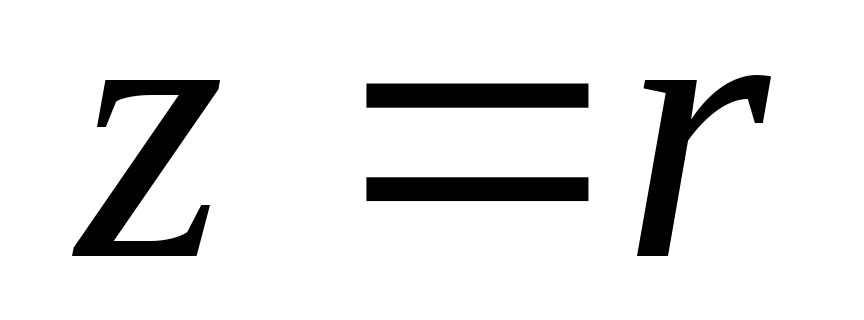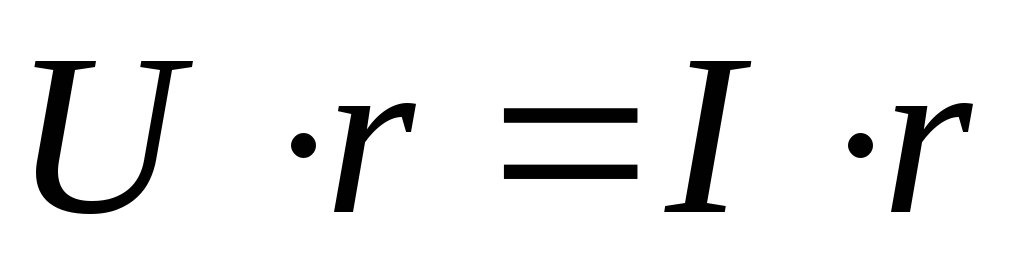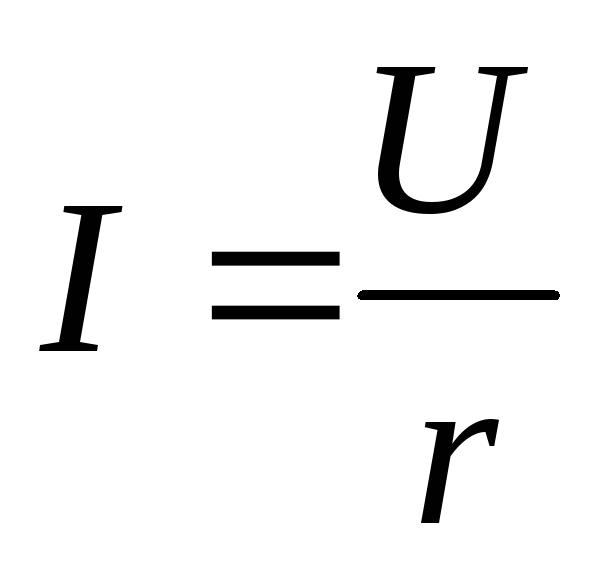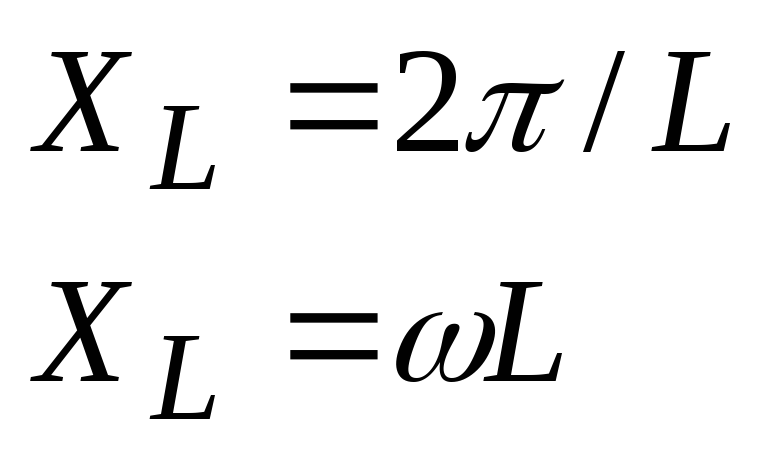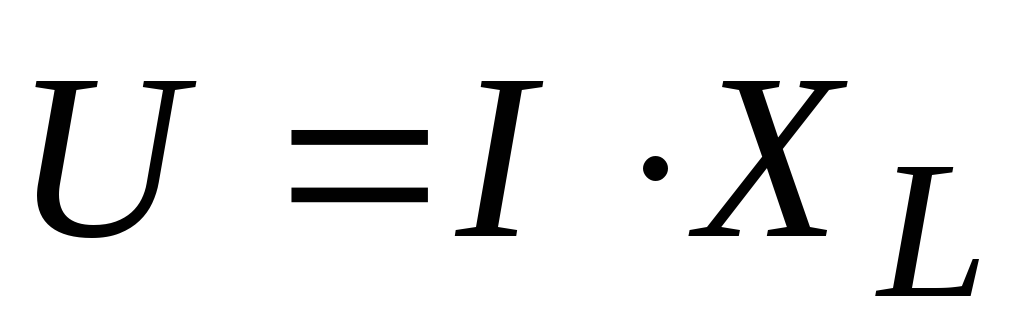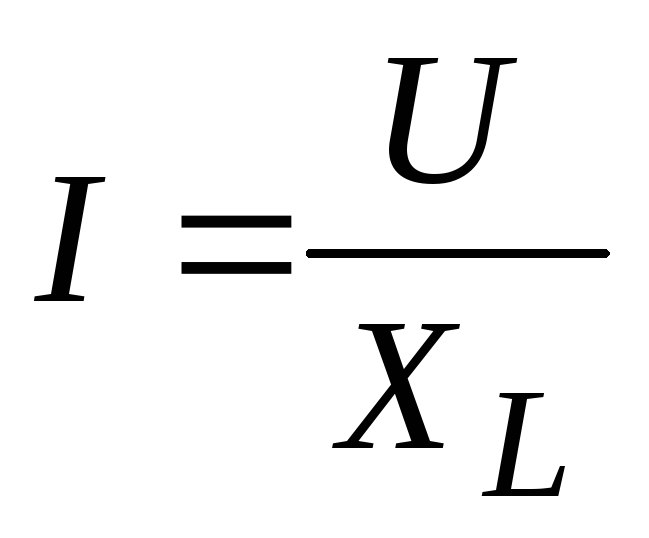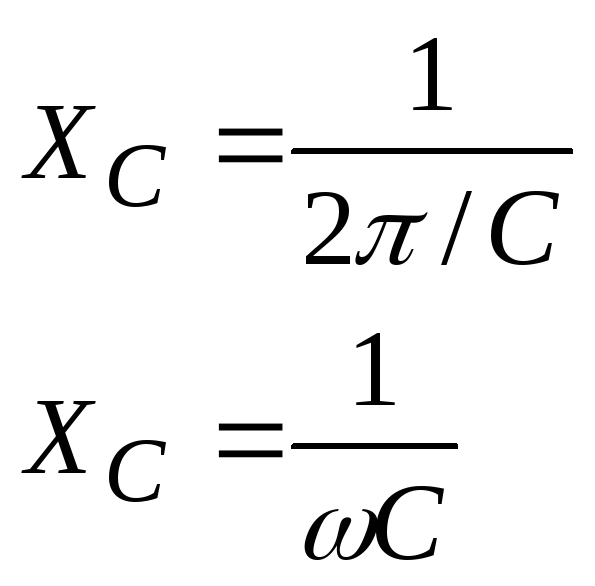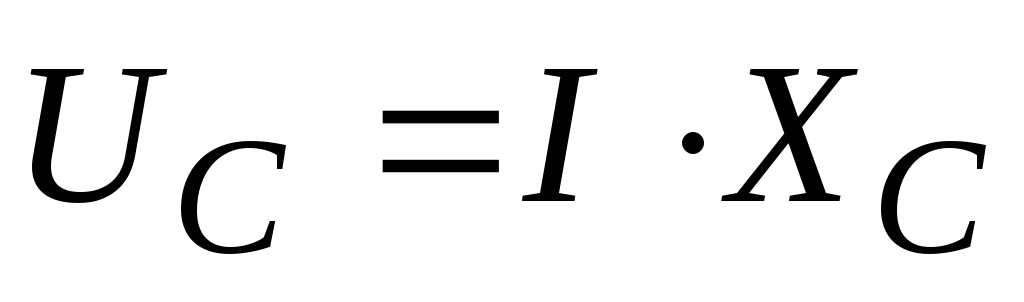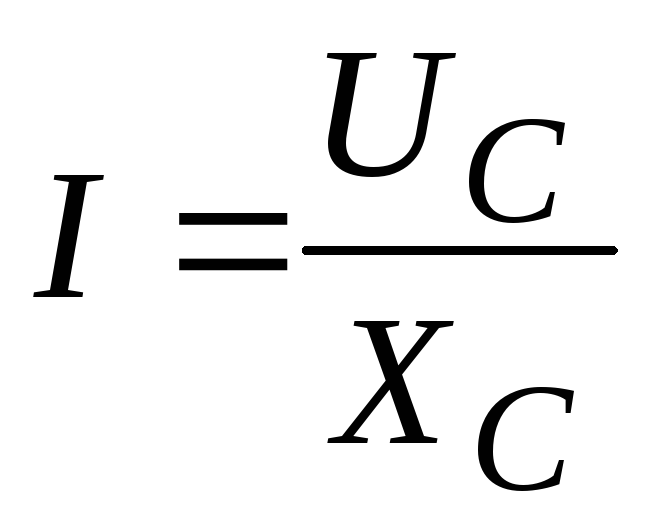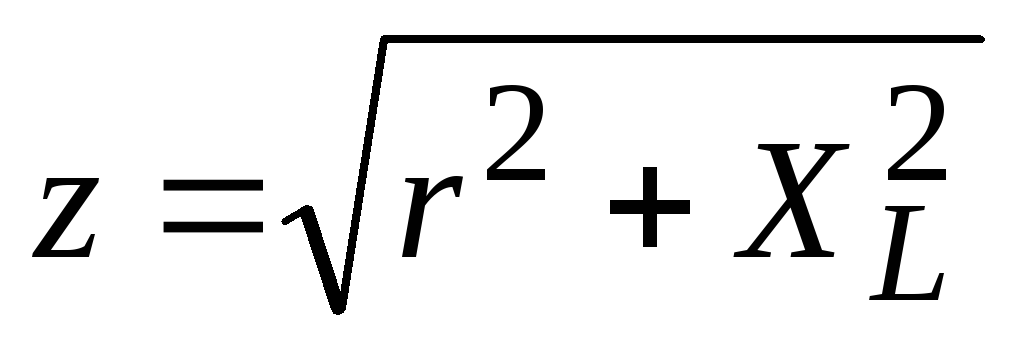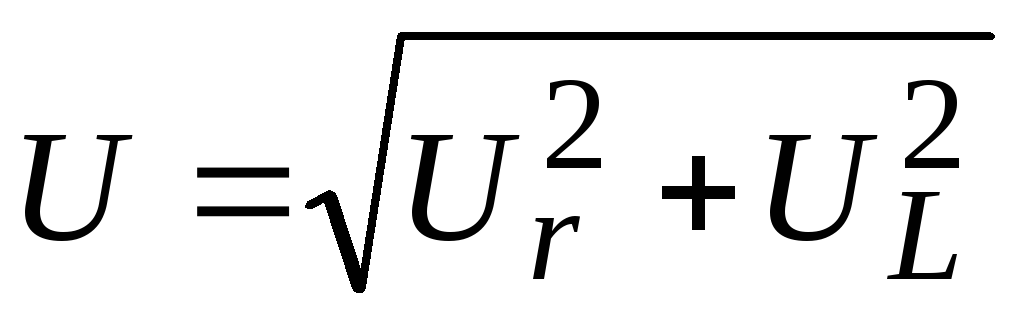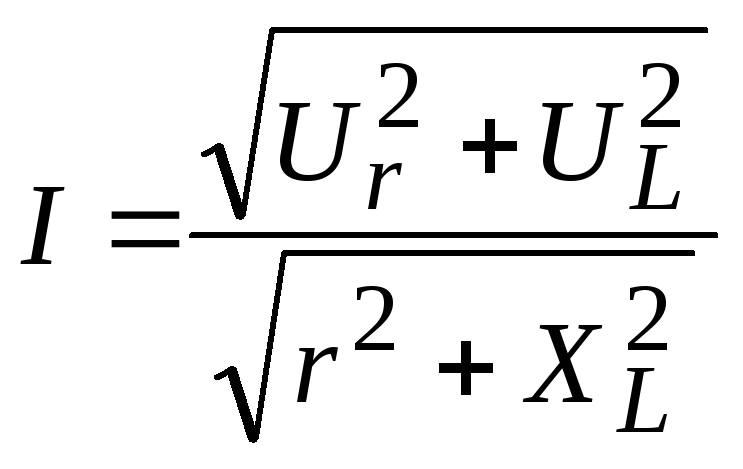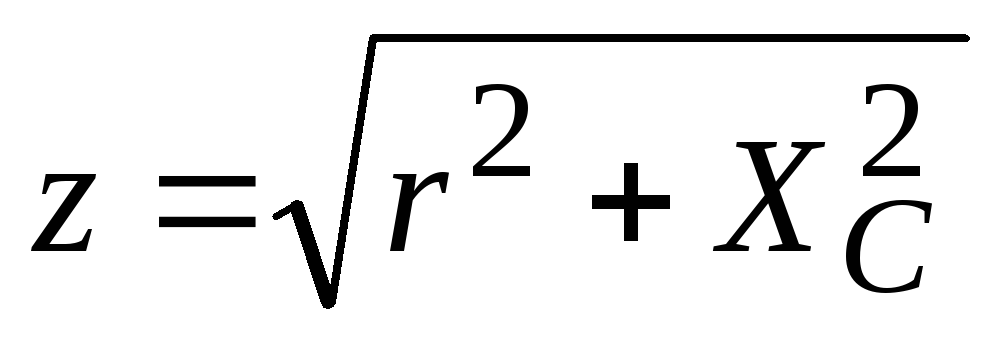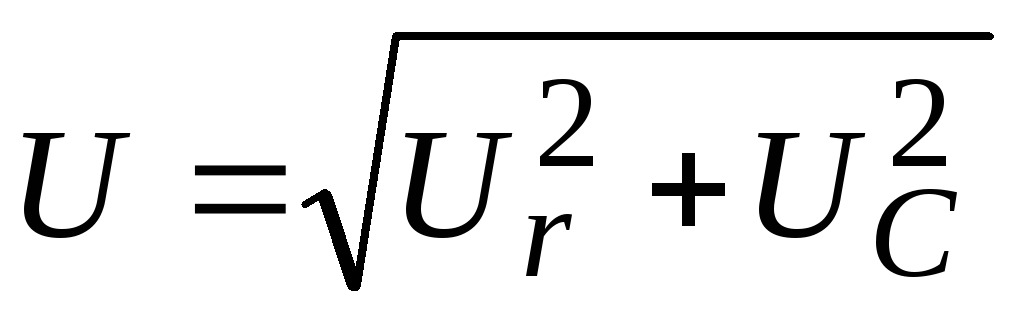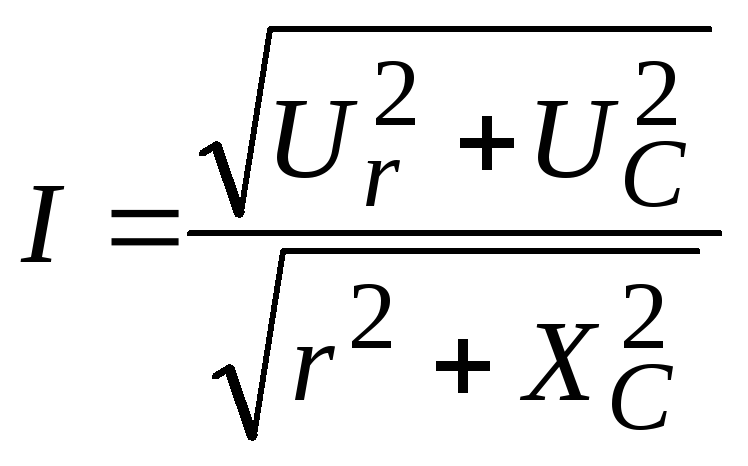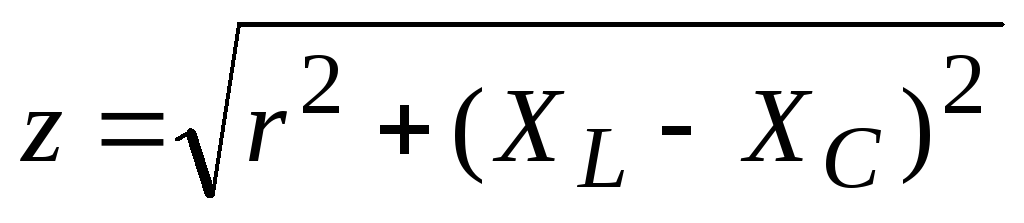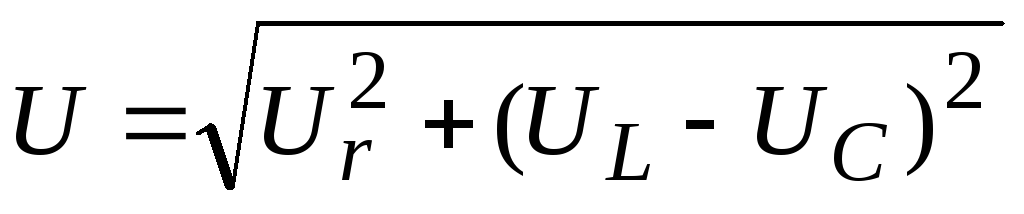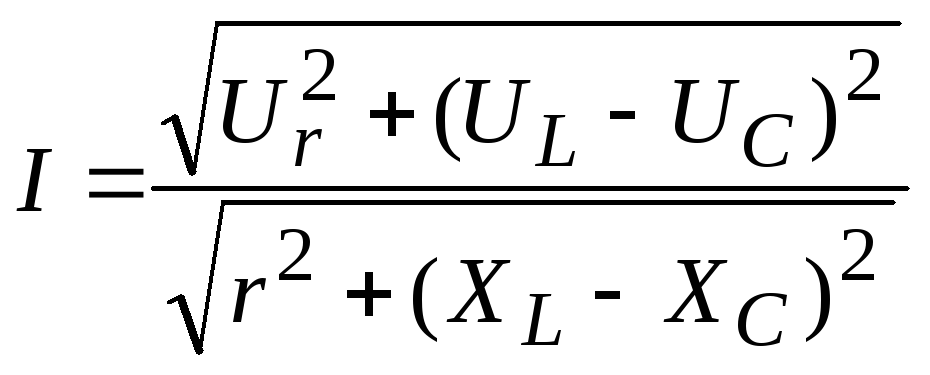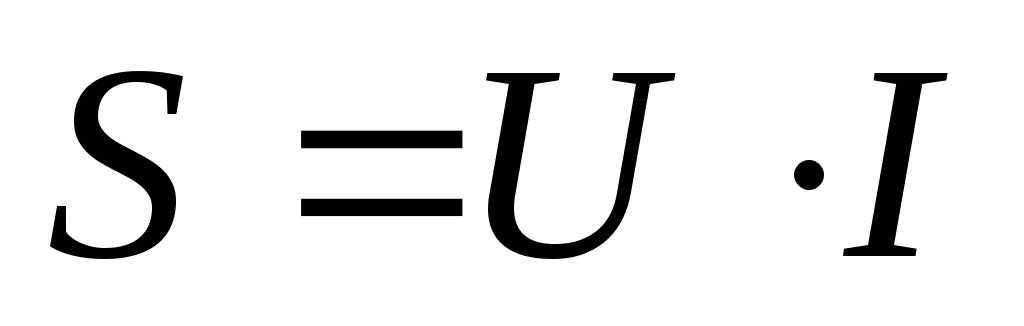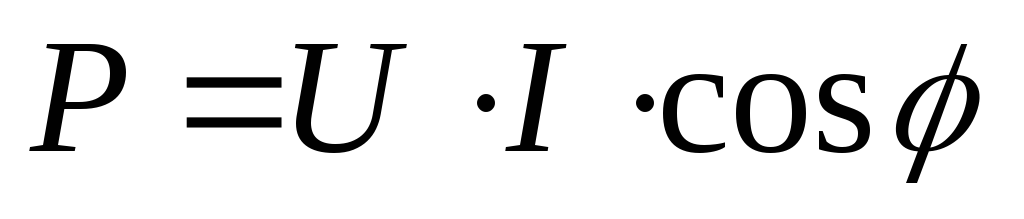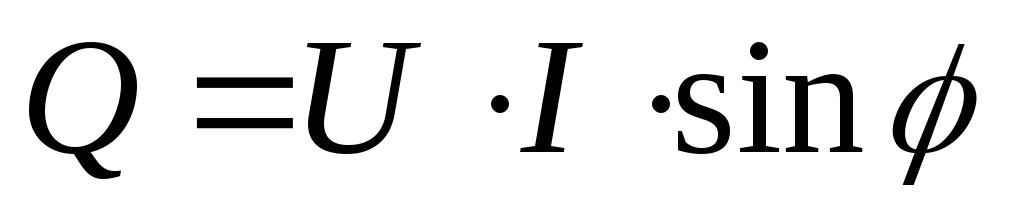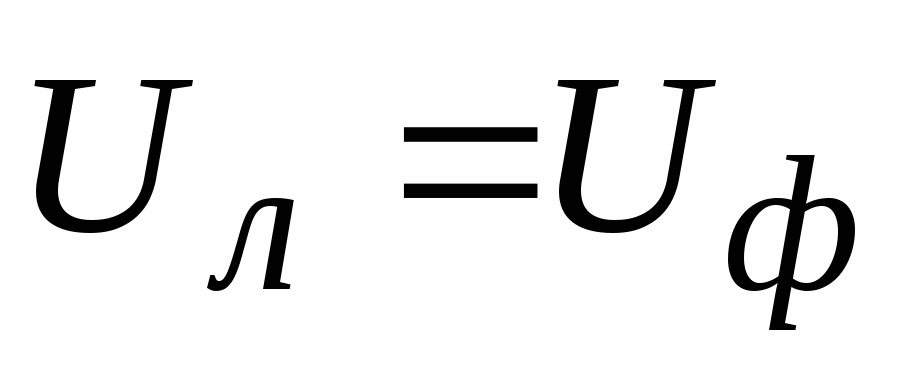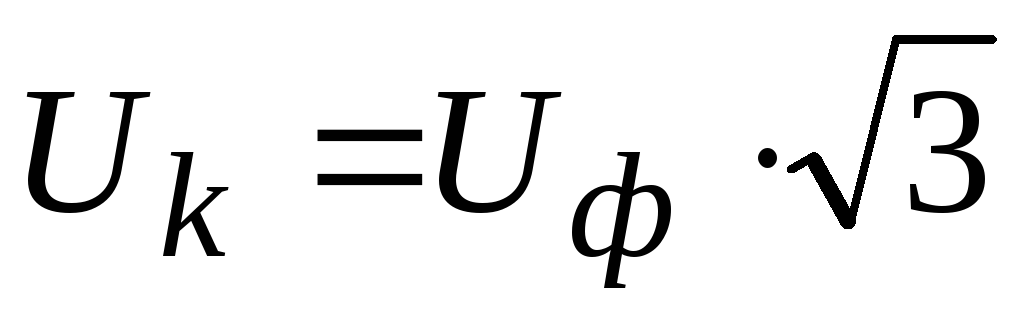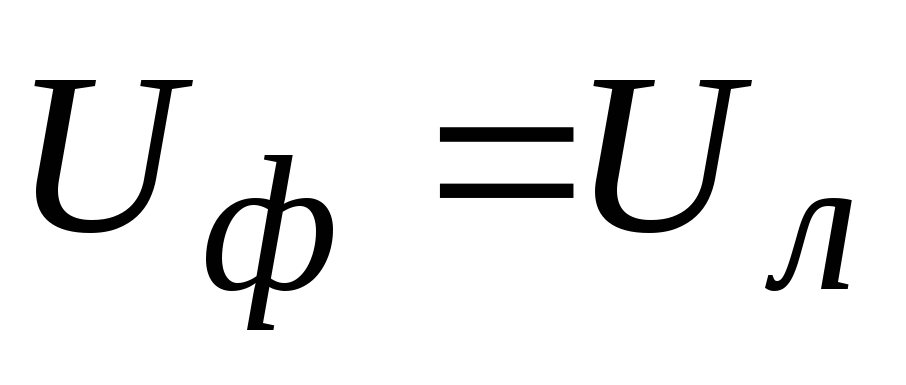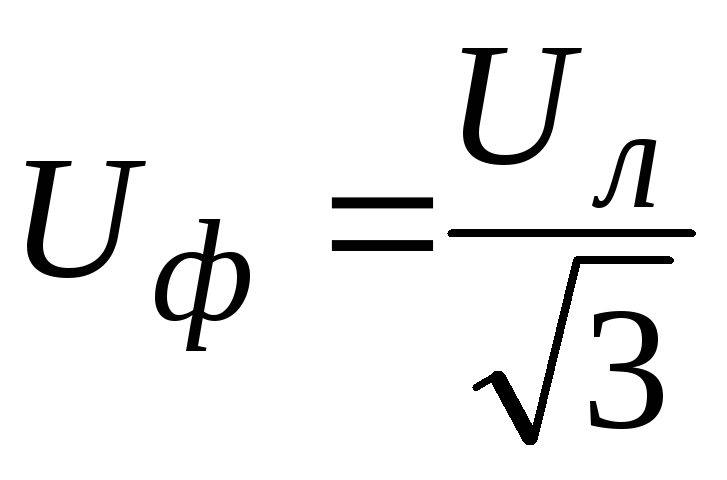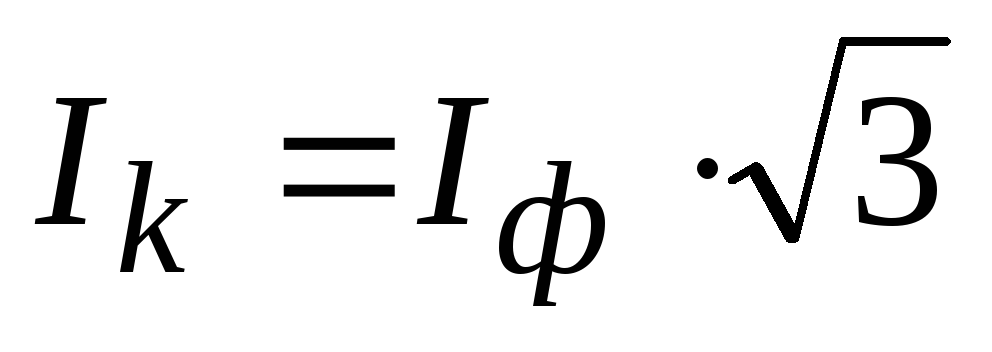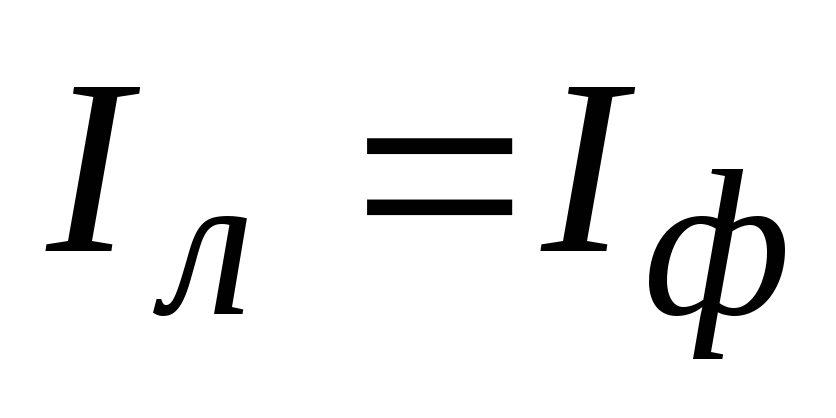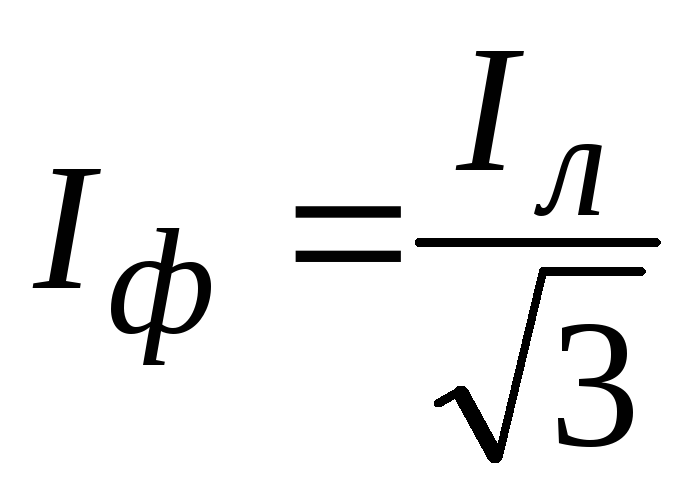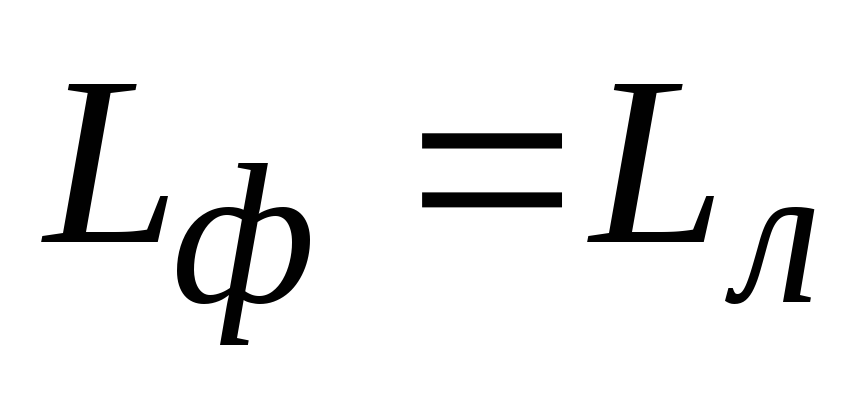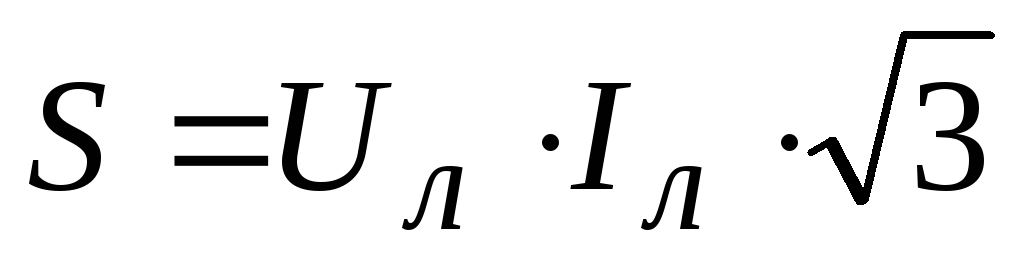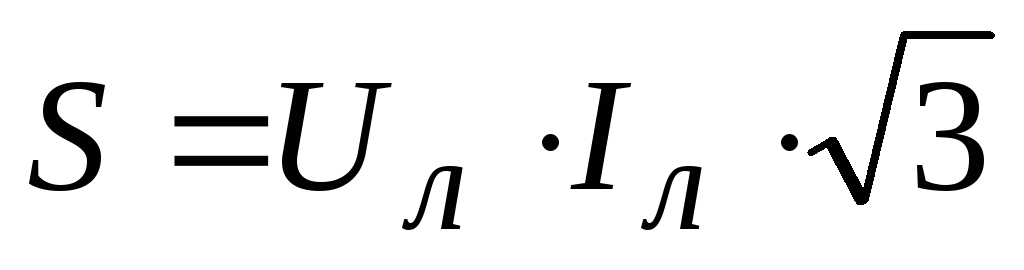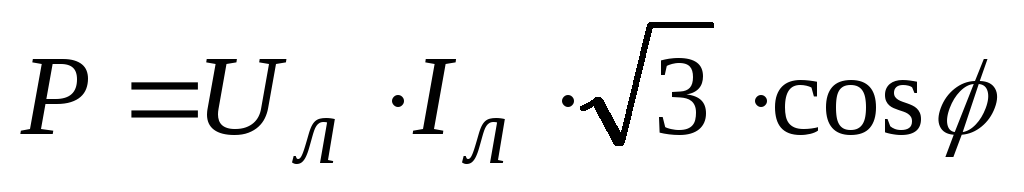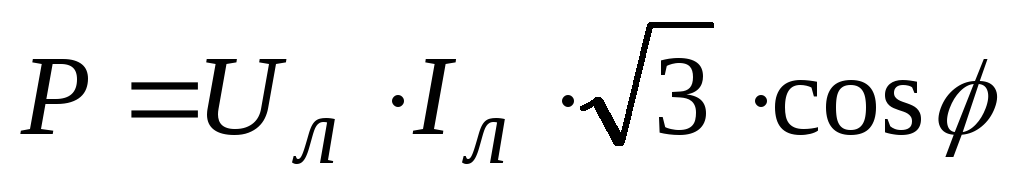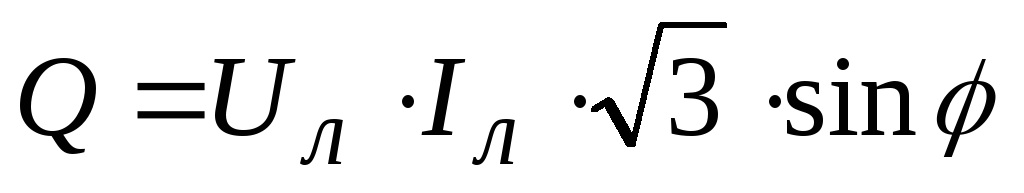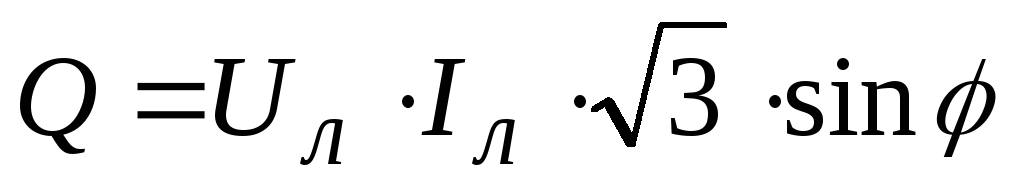Переменный ток. ЭДС, напряжение, сила тока, заряд. Амплитудные значения. Формулы
Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.
Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:
Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.
Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (
), напряжение на элементе (), сила тока (), заряд конденсатора (). Рассмотрим ЭДС источника гармонический колебаний: (1)Аналогичным образом можно ввести колебания напряжения
на элементе: (2)Таким же образом вводится и колебание силы тока:
(3)И, аналогично, заряд на конденсаторе:
(4)Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:
(5)- где
- — новая начальная фаза колебания.
Вывод: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
формулы, составляющие и особенности применения
 В быту, как правило, применяются такие словосочетания, как потребляемая мощность или просто электрическая мощность. Всегда актуален вопрос о том, как много электроэнергии потребляет тот или другой прибор. Но в физике понятие мощности переменного тока трактуется несколько шире.
В быту, как правило, применяются такие словосочетания, как потребляемая мощность или просто электрическая мощность. Всегда актуален вопрос о том, как много электроэнергии потребляет тот или другой прибор. Но в физике понятие мощности переменного тока трактуется несколько шире.
Особенности переменного тока
 Формула мощности для тока, который меняется во времени по силе, напряжению и направлению, не совпадает с простой формулой для постоянного электротока. Она может примяться исключительно для вычисления мгновенного значения этой физической величины, но на практике для нахождения мощности меняющегося тока бесполезна. Рассчитывая её усреднённую величину напрямую, применяют интегрирование по такому параметру, как время. То есть интегрируется мгновенное значение на протяжении определённого периода.
Формула мощности для тока, который меняется во времени по силе, напряжению и направлению, не совпадает с простой формулой для постоянного электротока. Она может примяться исключительно для вычисления мгновенного значения этой физической величины, но на практике для нахождения мощности меняющегося тока бесполезна. Рассчитывая её усреднённую величину напрямую, применяют интегрирование по такому параметру, как время. То есть интегрируется мгновенное значение на протяжении определённого периода.
Такой подход применяется для тех электрических цепей, в которых напряжение и сила электротока меняются циклически. В основном рассчитывается мощность в цепях с изменениями электрического напряжения и силы электротока по синусоиде.
В электродинамике различают связанные друг с другом понятия реактивной, активной и полной мощности.
Активная величина Real Power
Активная мощность Р измеряется в ваттах. Сокращённые варианты единицы измерения: Вт (русское обозначение) или W (международное). Само понятие этой мощностной величины означает среднее значение мгновенных показателей этой характеристики за промежуток времени Т (период).
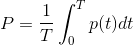
Для электрических цепей с одной фазой изменяющегося по синусоиде тока формула выглядит так:
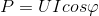 .
.
В этом выражении Ι и U являются значениями силы электротока и напряжения в среднеквадратичном представлении. А угол φ показывает, на сколько сдвинуты фазы между этими физическими величинами.
Активная мощность указывает, как быстро превращается электрическая энергия в другие типы: тепловую или электромагнитную.
Она может выражаться как через силу тока и активное сопротивление цепи r, так и через напряжение и проводимость g по формуле:
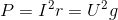 .
.
В любых электрических цепях этот вид мощности равняется сумме значений на отдельных элементах. В трёхфазном варианте суммируются показатели для каждой отдельной фазы.
Реактивная характеристика
Реактивная мощность Q охарактеризовывает нагрузки, создаваемые в электроустройствах периодическими изменениями энергии электромагнитного поля в цепи с переменным током, который меняется во времени по синусоидальному принципу.
Численно она равняется умножению среднеквадратичных U (напряжения), I (силы) и синуса φ (угла сдвига фаз):
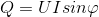 .
.
Измеряется в вольт-амперах реактивных (русское сокращение: вар, а международное — var).
Реактивная Q даёт характеристику энергии, передающейся от источника питания к реактивным элементам и возвращающуюся обратно за временной промежуток, численно равный одному периоду колебаний. К элементам реактивного типа относят катушки индуктивности, конденсаторы, обмотки. Этот вид мощностной характеристики тока принимает:
- отрицательное значение, если нагрузка активно-ёмкостная;
- положительное — в случае активно-индуктивного характера нагрузочных элементов.
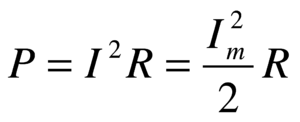 Принято считать, что устройства с положительной Q потребляют энергию, а с отрицательной, наоборот, производят. Но это условные обозначения. Реактивная мощность по факту не принимает участия в работе электротока. Синхронные генераторы, которые функционируют на электростанциях, в зависимости от численного значения тока возбуждения в обмотке могут и вырабатывать, и потреблять эту реактивную характеристику тока.
Принято считать, что устройства с положительной Q потребляют энергию, а с отрицательной, наоборот, производят. Но это условные обозначения. Реактивная мощность по факту не принимает участия в работе электротока. Синхронные генераторы, которые функционируют на электростанциях, в зависимости от численного значения тока возбуждения в обмотке могут и вырабатывать, и потреблять эту реактивную характеристику тока.
Такую особенность синхронных электрических машин используют для регулирования определённого значения напряжения сети. Чтобы устранять перегрузки либо увеличение мощностного коэффициента, осуществляют компенсацию реактивной составляющей.
Полная мощность
Полная мощность S представляется в единицах измерения с названием вольт-амперы и вычисляется через умножение действующих значений I в цепи и напряжения U на её окончаниях:
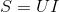
 Этот вид электрической характеристики на практике описывает нагрузки, которые по факту налагаются потребителем на части электросети, обеспечивающей подвод электроэнергии (кабели разных видов, трансформирующие устройства и линии для передачи электрической энергии на большие расстояния).
Этот вид электрической характеристики на практике описывает нагрузки, которые по факту налагаются потребителем на части электросети, обеспечивающей подвод электроэнергии (кабели разных видов, трансформирующие устройства и линии для передачи электрической энергии на большие расстояния).
Данные нагрузки находятся в зависимости исключительно от потребляемого тока, а не от энергии, которую по факту использует потребитель. Этот момент является причиной того, что полная мощность устройств, обеспечивающих трансформацию электрической энергии, а также распределительных щитов, измеряют в вольт-амперах, а не в ваттах.
Все виды мощностных характеристик переменного тока связываются между собой следующими математическими выражениями:
Эти формулы позволяют производить расчёты для цепей переменного тока любой конфигурации:
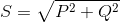
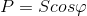
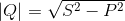
- Полная, выраженная через активную и реактивную.
- Активная — через полную и угол сдвига фаз.
- Реактивная — через полную и активную.
Знания этих нюансов важны при подборе оборудования и построения систем энергообеспечения различных объектов. Учёт электрических параметров устройств даёт возможность сделать правильный выбор электрических устройств и построить экономически оптимальную схему энергетического обеспечения.
Часть 3. Переменный ток (краткая теория)
Получение, передача и распределение электрической энергии осуществляются в основном с помощью устройств и сооружений переменного тока. Для этого применяют генераторы, трансформаторы, линии передачи и распределительные сети переменного тока. Широко используют приемники электрической энергии, работающие на переменном токе.
Переменным током называют любой изменяющийся с течением времени электрический ток.
Переменным синусоидальным током называют изменяющийся по закону синуса (косинуса) с течением времени электрический ток.
В электротехнике чаще всего приходится иметь дело с переменным током, величина которого изменяется по периодическому синусоидальному закону. В некоторых случаях ток изменяется по периодическому несинусоидальному закону
В линейных электрических цепях переменный синусоидальныйток возникает под действием ЭДС такой же формы. Дляизучения электрических устройств и цепейпеременного тока необходимо прежде рассмотреть способы получения синусоидальной ЭДС и основные понятия, относящиеся к величинам, которые изменяются по синусоидальному закону.
3.1. Получение синусоидальной эдс
Переменным током (ЭДС) в электрических цепях называется такой ток (ЭДС), который изменяет свое значение и направление во времени.
В электротехнике в основном приходится иметь дело с током, величина которого изменяется по синусоидальному закону. Для получения ЭДС синусоидальной формы генератор переменного тока промышленного типа имеет определенные конструктивные особенности.
Рис. 3.1 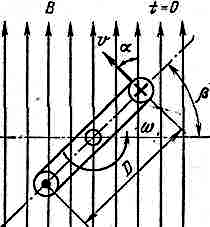
Синусоидально изменяющуюся величину ЭДС со временем можно получить, вращая с постоянной скоростью в однородном магнитном поле проводник в виде прямоугольной рамки. При движении проводника в магнитном поле в нем возбуждается ЭДС индукции
e=Bυlsina (3.1)
При вращении витка в магнитном поле с постоянной скоростью изменяется угол между направлением индукции магнитного поля и нормалью к плоскости рамки
ЕМ =Bυl. (3.2)
Синусоидальное изменение ЭДС достигается путем равномерного изменения угла, под которым виток пересекает линии магнитной индукции. Таким образом,
е = ЕМ sinα = ЕМ sin ωt (3.3)
Аналогично запишутся формулы переменного напряжения и тока: и = UМ sin ωt, i = IМ sin ωt
3.2. Характеристики синусоидальных величин
Синусоидально изменяющиеся ЭДС, напряжение и ток характеризуются следующими величинами: мгновенным значением, амплитудой, периодом, частотой, фазой (сдвигом фаз) (рис. 3.2). Мгновенное значение ЭДС, напряжения и силы тока – значение этих величин в любой момент времени. Мгновенные значения обозначаются строчными буквами е, и, i.
Амплитуда — это наибольшие значения, которые принимает ЭДС, напряжение и сила тока. Амплитудные значения обозначаются прописными буквами Еm , Um , Im .
Период Т — промежуток времени, в течение которого ЭДС, напряжение и ток совершают полное колебание и принимают прежнее по величине и знаку значение.
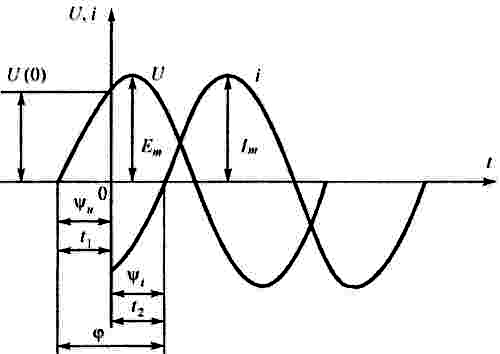
Рис.3.2 Графики изменения переменного тока и ЭДС.
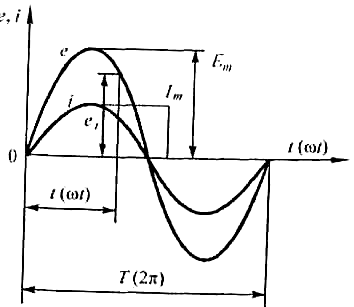
Частота f (число периодов в
секунду) — величина, обратная периоду:f = 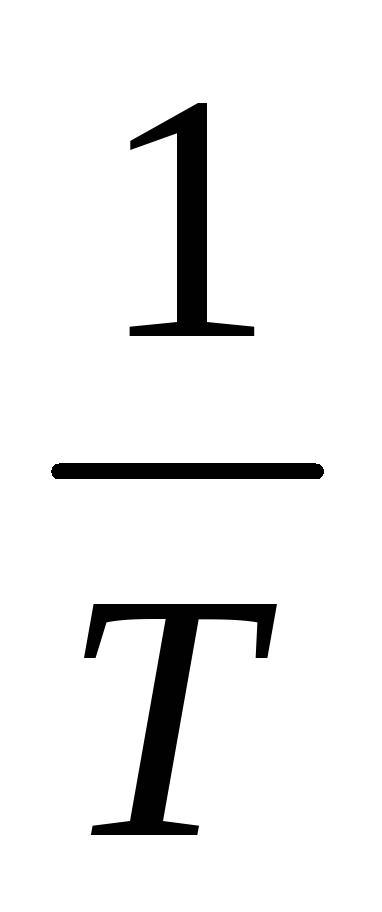 (3.4)
(3.4)
Единица частоты — герц (Гц). Стандартная промышленная частота 50 Гц. В США и Японии-60 Гц. В некоторых областях промышленности находят применение другие частоты.
Угловая частота ω есть величина, равная числу периодов
за 2п секунд.
Так как в течение периода α = 2π, то ω = 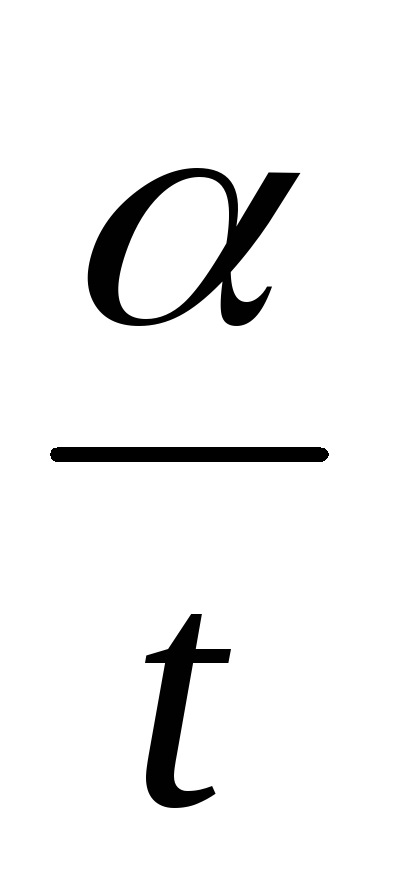 , т. е. ω =
, т. е. ω = 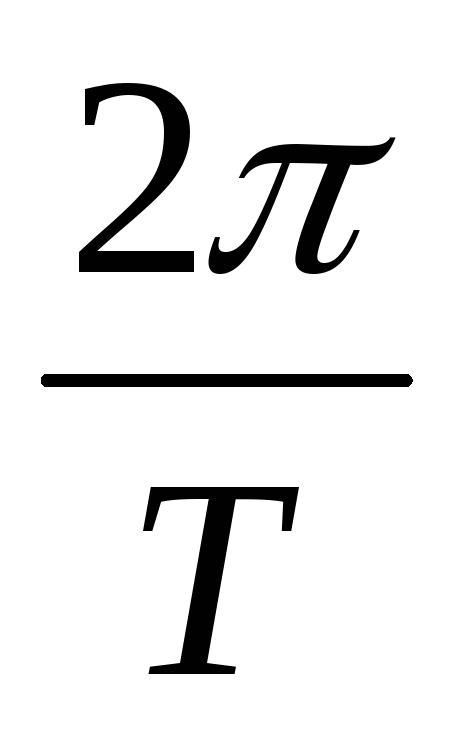 (3.5)
(3.5)
Размерность угловой частоты
— град/с или рад/с.ω = 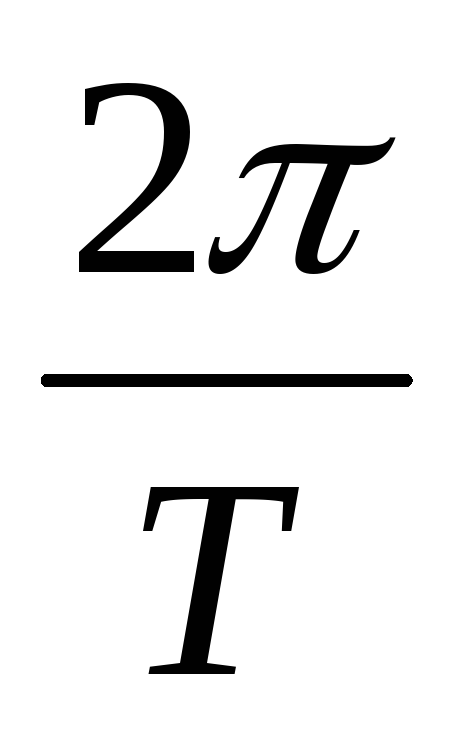 или ω = 2π f
или ω = 2π f
Фаза — угловое значение аргумента синусоидальной ЭДС, напряжения, тока, определяющее мгновенное значение этих величин. При α = ωt = 0 мгновенные значения е, и и i будут равны нулю. Если фаза имеет выражение (ωt + ψ), то при t = 0 фаза не равна нулю и мгновенное значение е будет равнo е = Еm sin(ωt + ψ),а фаза ψ называется начальной фазой.
Таким образом, в общем виде уравнение ЭДС может быть записано так:
е = Еm sin(ωt + ψ) (3.6)
где α = (ωt + ψ) — угол, называемый фазой. Аналогично запишутся выражения для переменного напряжения и тока.
Две синусоидальные величины, имеющие разные начальные фазы, называются сдвинутыми по фазе (рис. 3.3). Угол сдвига фаз φ = ψu + ψi
Та величина, в которой начало периода, или положительная амплитуда достигается раньше, чем у другой, считается опережающей по фазе, а та, у которой те же значения достигаются позже — отстающей по фазе.
Изображенные на рис. 3.2 синусоидальные величины называют совпадающими по фазе. Если угол сдвига составляет π, то говорят, что они находятся в противофазе. Сдвиг по фазе можно установить и на графике. Для этого достаточно выбрать две ближайшие точки, соответствующие положительным амплитудам величин, и установить разность фазовых углов.
Действующая и средняя
величины переменного тока. Переменный
ток, как и постоянный, оказывает тепловое,
механическое, магнитное и химическое
действие. В формулы расчета теплового,
механического, магнитного и химического
действия переменного тока подставляют
действующее значение переменного тока.
Действующим значением переменного
тока называется постоянный ток,
который за время одного периода оказывает
такое тепловое (механическое и др.)
действие, как и данный переменный ток.
Действующее значение для данного
переменного тока есть величина постоянная
и равна амплитудному значению,
деленному на 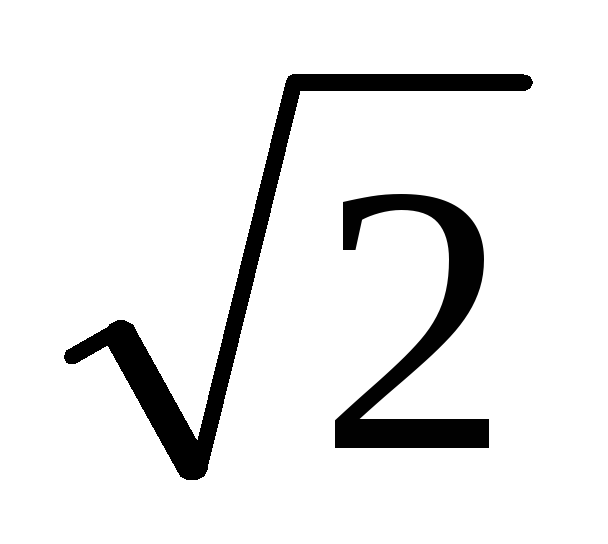 ,
т. е.IД =
,
т. е.IД =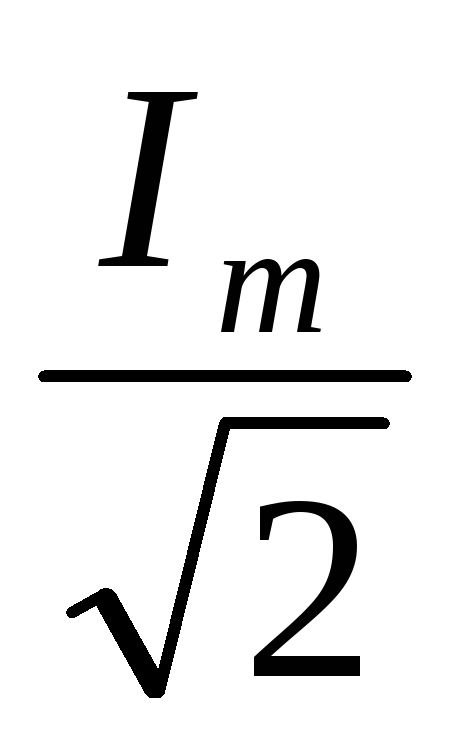
Для доказательства этого рассмотрим тепловое действие тока. Тепловое действие постоянного тока определяется по закону Джоуля -Ленца: Q = I2 RT (3.7)
где Т- время, равное одному периоду.Такое же количество теплоты в данном проводнике за это время выделится и при переменном токе i = 1тsinωt. Тогда формула (3.7) для переменного тока примет вид:Q = IД2RT, (3.8)
где IД — действующее значение переменного тока. Из формулы (3.8) можно записать
I Д2 R=Р (5.9)
где Р — средняя мощность
переменного тока за период. Мгновенная
мощность синусоидального тока равнаp = i2R =Iт2 sin2 ωt ·R =Iт2·R 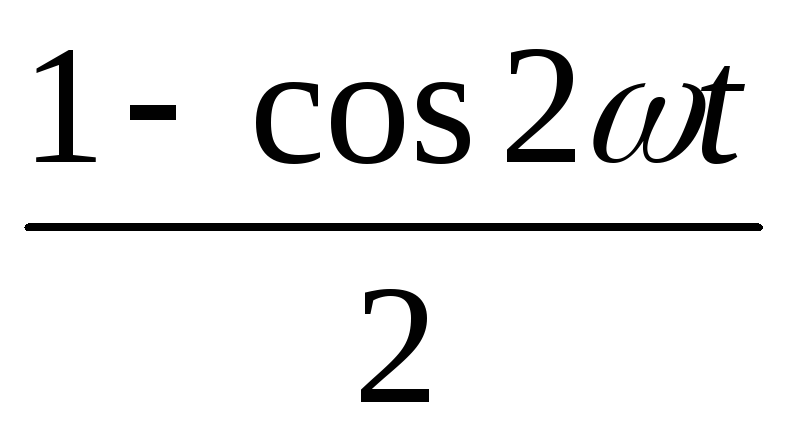 = Iт2·
= Iт2·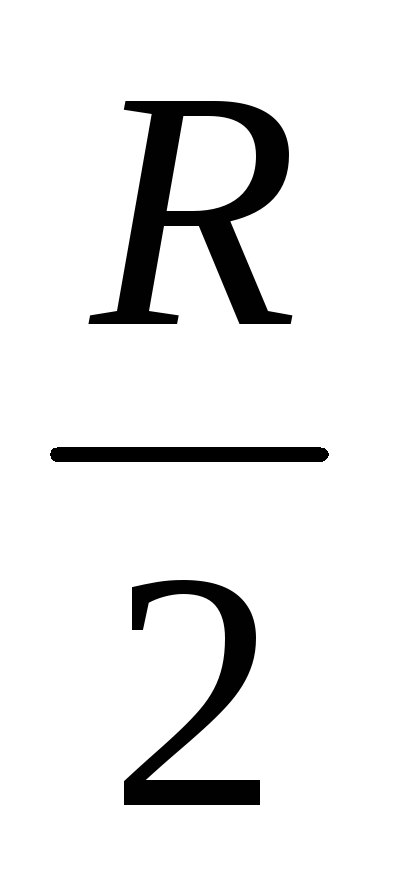 −Iт2
−Iт2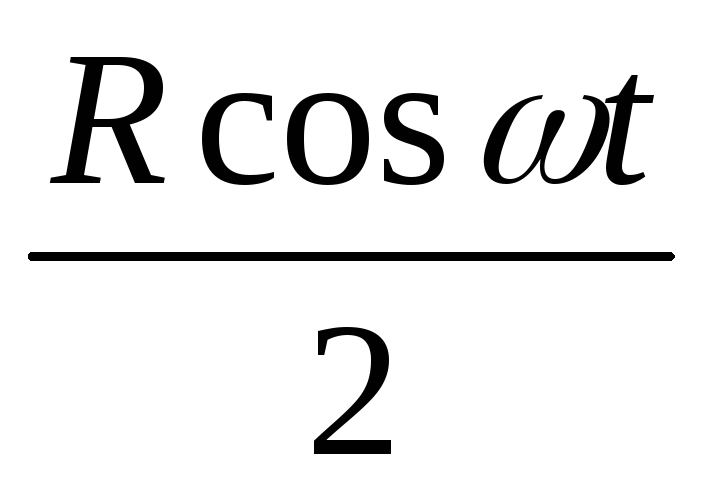 (3.10)
(3.10)
Как видно из формулы (3.10), мгновенная мощность переменного тока выражается двумя слагаемыми. Первое слагаемое является величиной постоянной и от времени не зависит, а второе − изменяется по синусоидальному закону и в сумме за период равно нулю. Следовательно, средняя мощность переменного тока за период может быть выражена формулой
р = Iт2·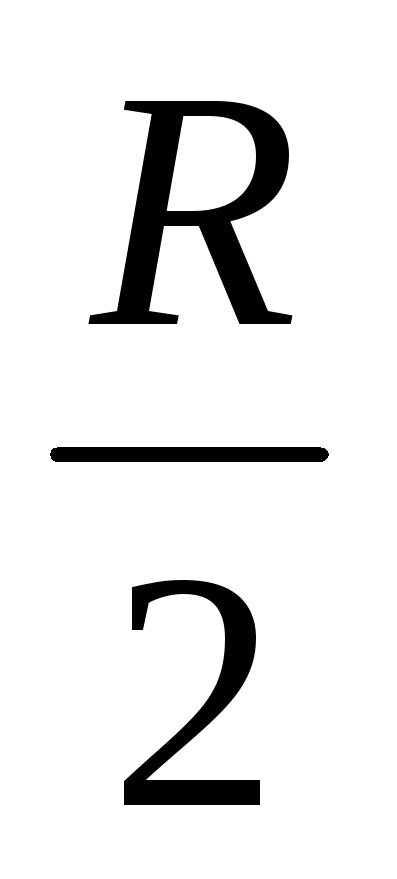 (3.11)
(3.11)
Из равенств (3.9) и (3.11) можно записать:
I Д2 R
= Iт2·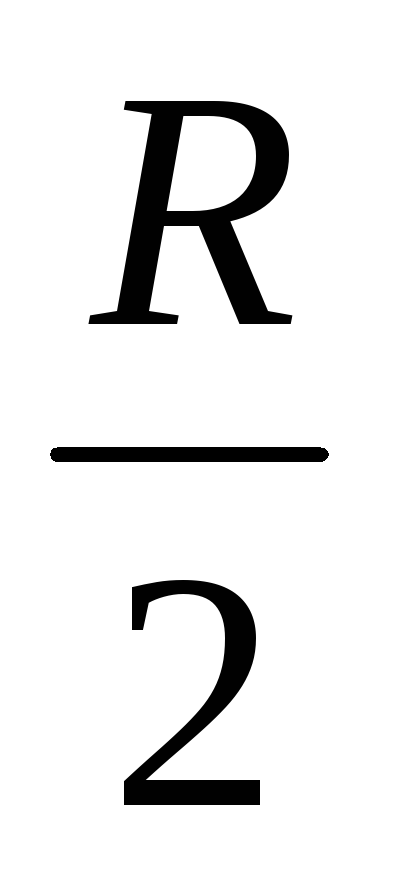 ,
т. е. IД =
,
т. е. IД =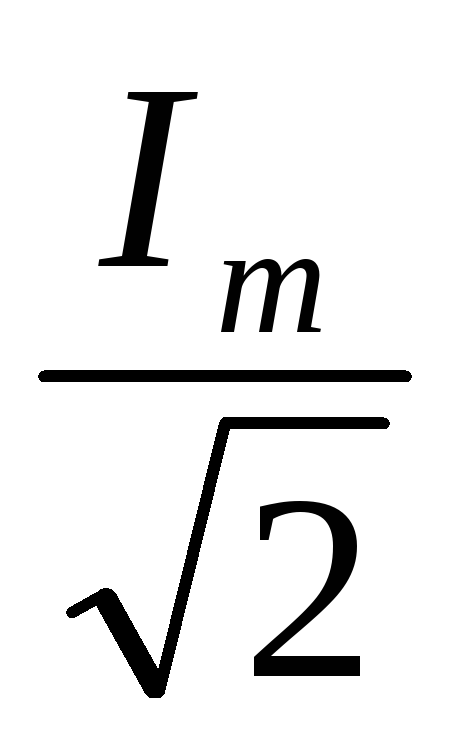 илиIД = 0,707 · Iт,
т. к.
илиIД = 0,707 · Iт,
т. к. 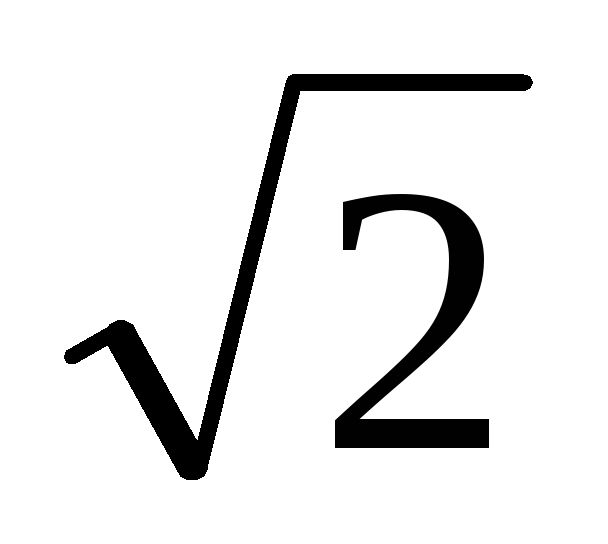 ≈1,41
≈1,41
Все определения и соотношения действующего значения переменного тока справедливы и для переменного напряжения, и для ЭДС.
Все амперметры и вольтметры при измерении переменного тока и напряжения показывают их действующие значения, так как принцип работы их основан на механическом или тепловом действии тока.Пусть при включении в сеть сопротивления R = 40 Ом амперметр показал ток 5,5 А. Действующее напряжение в сети U = R · I = 40 Ом • 5,5А = 220 В,
а амплитудное Um = 220В • 1,41 =310,2 В.
При изучении электрических машин, выпрямительных устройств пользуются средним значением ЭДС, силы тока и напряжения. Средним значением переменного тока, напряжения и ЭДС называется среднее арифметическое из всех мгновенных значений за полупериод.
Для
синусоидального тока IСР=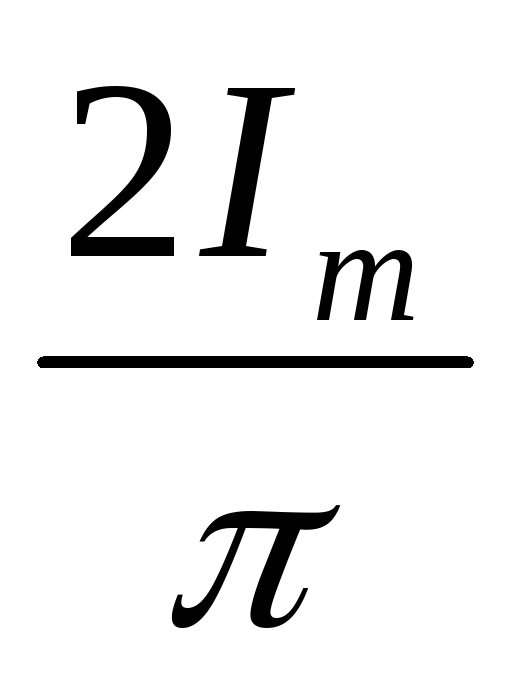 = 0,637 ·Iт
= 0,637 ·Iт
Изображение синусоидальных величин вращающимся вектором.
Прирасчете электрических цепей переменного тока пользуются простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.Пусть напряжение задано уравнением и = Um sin(ωt + ψ)
Проведем две перпендикулярные оси, затем из точки пересечения осей вектор длиной U в выбранном масштабе (рис/3.4). Направление вектора выбирается таким, чтобы с горизонтальной осью он составлял угол ψ, т. е. равный начальной фазе. Проекция этого вектора на ось ординат определяет мгновенные значения напряжения u(0) = Um sin ψt
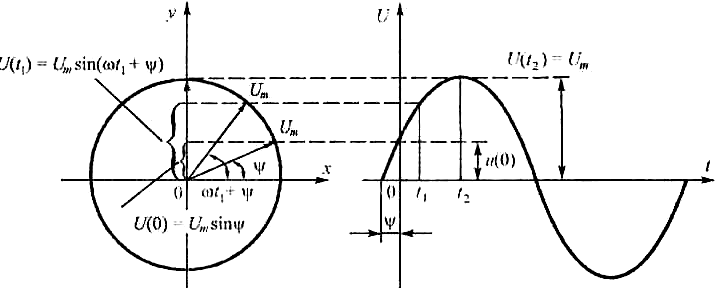
Вращаем вектор U против часовой стрелки с угловой скоростью ω. Положение радиуса-вектора в любой момент времени определяется углом (ωt + ψ). Для произвольного значения времени t мгновенное значение напряжения определяется проекцией вектора U на вертикальную ось в этот момент времени. Например, для t = t1, u(t1) = Um sin(ωt1 + ψ), т. е. мы имеем уравнение такого вида, как и заданное. Это дает нам возможность изобразить напряжение вращающимся вектором, нанесенном на чертеж в начальном положении.Вращая вектор Um против часовой стрелки, построим в прямоугольной системе координат график изменения проекции его на вертикальную ось за один период. Соединив полученные точки, получим график синусоидальной функции, соответствующий заданному уравнению.Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты, называется векторной диаграммой.
Достоинством векторных диаграмм является простота и наглядность. Сложение и вычитание синусоидальных величин осуществляется по правилам сложения и вычитания векторов.
Генераторы переменного тока | Формулы и расчеты онлайн
Если для получения электрического напряжения используется прополочная рамка, вращающаяся в магнитном поле, то напряжение индукции не постоянно, а зависит от мгновенного положения рамки в магнитном поле.
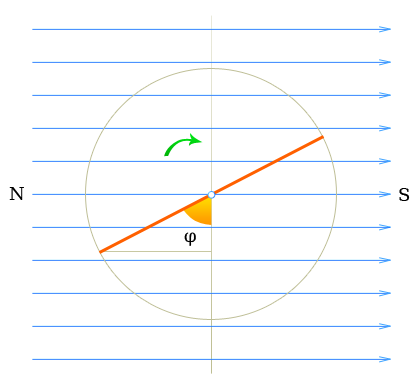
Генераторы переменного тока
В соответствии с формулой №1 напряжение индукции пропорционально скорости изменения магнитного потока. Согласно выражению
\[ Φ = BS \]
, магнитный поток пропорционален площади сечении магнитного поля, пересекающего рамку, т.е.
\[ Φ = B · S · \cos(φ) \]
Аналогичное выражение справедливо для вращающейся катушки.
Если
| u | мгновенное значение напряжения индукции, | Вольт |
|---|---|---|
| Um | амплитуда напряжения, т.е. максимальное напряжение, возникающее дважды за оборот катушки, | Вольт |
| φ = ωt | угол поворота катушки, отсчитываемый, от начального положения, перпендикулярного направлению магнитного поля, | радиан |
| S | площадь витка, | метр2 |
| N | число витков катушки, | штук |
| T | период вращения катушки, | секунд |
| f | частота вращения, | Герц |
| t | время, | секунд |
то
\[ u= — N \frac{dФ}{dt} \]
\[ u= — \frac{d(NBS \cos(φ))}{dt} \]
\[ u= — \frac{d(NBS \cos(ωt))}{dt} \]
откуда
Переменное напряжение
\[ u = NBS ω \sin(ωt) \]
Переменное напряжение Напряжение индукции меняется во времени по синусоидальному закону. В течение периода оно дважды меняет знак. Поэтому его называют переменным напряжением.
Амплитуда, или максимальное значение напряжения индукции, определяется формулой
\[ U_{m}= NBSω \]
Тогда для мгновенного напряжения имеем
\[ u = U_{m} \sin(ωt) \]
\[ u = U_{m} \sin(2πft) \]
\[ u = U_{m} \sin(2π\frac{t}{T}) \]
Величина ω=2πf называется угловой частотой.
Частота переменного тока промышленной сети f = 50 Гц, и соответственно ω = 100π 1/с.
Переменный ток
Если к клеммам вращающейся катушки присоединить внешнюю электрическую цепь, то в ней возникает электрический ток, сила которого изменяется по синусоидальному закону во времени и меняет свой знак (направление) дважды за период. Такой ток называется переменным током.
Если
| i | мгновенное значение силы тока, | Ампер |
|---|---|---|
| Im | амплитуда тока, | Ампер |
| ω=2πf | угловая частота, | радиан/секунда |
то
то по аналогии получаем
\[ i = I_{m} \sin(ωt) \]
\[ i = I_{m} \sin(2πft) \]
\[ i = I_{m} \sin(2π \frac{t}{T}) \]
График зависимости напряжения u от времени t (или от φ = ωt) представляет собой синусоиду.
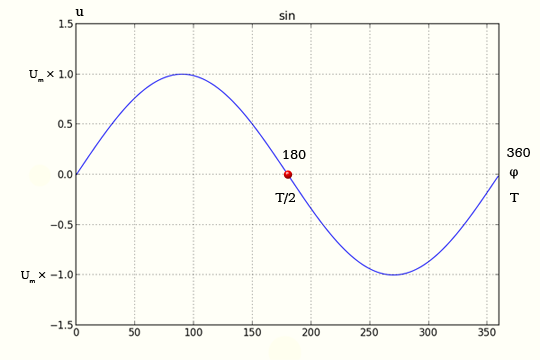
Переменное напряжение
В любом генераторе переменного тока имеются магнит, создающий требуемое магнитное поле (чаще всего электромагнит; в генераторах малой мощности используются постоянные магниты), вращающиеся обмотки и контактные кольца. Для получения достаточно высокого напряжения применяют обмотки с большим числом витков и железные сердечники.
Вращающаяся часть генератора называется ротором, неподвижная часть — статором.
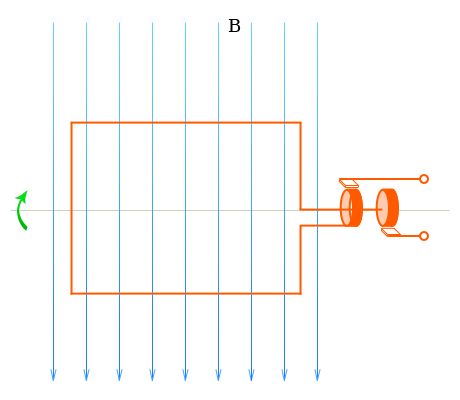
генератор переменного тока
В генераторах большой мощности обмотки, в которых индуцируется напряжение, располагаются на статоре, а магниты — на роторе (машина с внутренними полюсами). При этом контактные кольца служат лишь для подвода небольшой мощности к электромагнитам.
В помощь студенту
Генераторы переменного тока |
стр. 672 |
|---|
Переменный синусоидальный ток
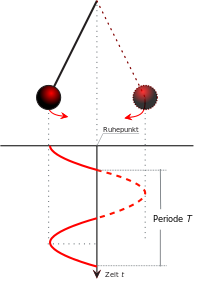
Колебания маятника также подчиняются закону синуса. Если записать проекцию траектории движения математического маятника на движущуюся бумажную ленту — получится синусоида.
Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по закону синуса.
Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи.
Переменный синусоидальный ток выражается формулой:
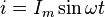 ,
где
,
где
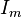 —
амплитуда
синусоидального тока;
—
амплитуда
синусоидального тока;
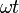 —
некоторый угол,
называемый фазой
синусоидального тока.
—
некоторый угол,
называемый фазой
синусоидального тока.
Фаза синусоидального
тока 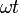 изменяется
пропорционально времени
изменяется
пропорционально времени  .
.
Множитель 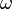 ,
входящий в выражение фазы
,
входящий в выражение фазы 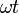 —
величина постоянная, называемая угловой
частотой переменного
тока.
—
величина постоянная, называемая угловой
частотой переменного
тока.
Угловая
частота 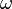 синусоидального
тока зависит от частоты
синусоидального
тока зависит от частоты 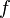 этого
тока и определяется формулой:
этого
тока и определяется формулой:
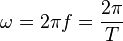 ,
где
,
где
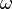 —
угловая частота
синусоидального тока;
—
угловая частота
синусоидального тока;
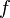 —
частота синусоидального
тока;
—
частота синусоидального
тока;
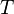 — период синусоидального
тока;
— период синусоидального
тока;
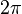 —
центральный
угол окружности,
выраженный в радианах.
—
центральный
угол окружности,
выраженный в радианах.
Зависимость синусоидального тока от времени
Зависимость синусоидального тока от угла ωt
Периоду 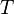 соответствует
угол
соответствует
угол 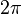 ,
половине периода
,
половине периода  угол
угол 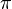 и
так далее…
и
так далее…
Исходя
из формулы 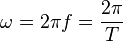 ,
можно определить размерность угловой
частоты:
,
можно определить размерность угловой
частоты:
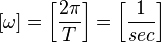 ,
где
,
где
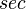 — время в секундах,
— время в секундах,
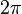 —
угол в радианах,
является безразмерной величиной.
—
угол в радианах,
является безразмерной величиной.
Фаза 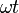 синусоидального
тока измеряется радианами.
синусоидального
тока измеряется радианами.
1
радиан = 57°17′, угол 90° = 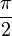 радиан,
угол 180° =
радиан,
угол 180° = 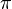 радиан,
угол 270° =
радиан,
угол 270° = 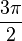 радиан,
угол 360° =
радиан,
угол 360° = 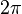 радиан,
где
радиан,
где 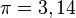 радиан;
радиан; 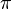 — число
«Пи», ° — угловой
градус и ′ — угловая
минута.
— число
«Пи», ° — угловой
градус и ′ — угловая
минута.
Формула 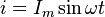 описывает
случай, когда наблюдение за изменением
переменного синусоидального тока
начинается с момента времени
описывает
случай, когда наблюдение за изменением
переменного синусоидального тока
начинается с момента времени 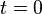 при
при 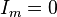 .
Если
.
Если  не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид:
не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид:
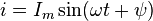 ,
где
,
где
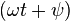 — фаза переменного
синусоидального тока;
— фаза переменного
синусоидального тока;
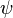 — угол,
называемый начальной
фазой переменного синусоидального
тока.
— угол,
называемый начальной
фазой переменного синусоидального
тока.
Начальная
фаза переменного тока 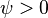
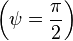
Начальная
фаза переменного тока 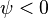
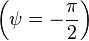
Если
в формуле 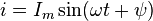 принять
принять 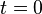 ,
то будем иметь
,
то будем иметь
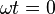 ,
, 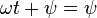 и
и 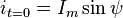 .
.
Начальная
фаза — это фаза синусоидального тока
в момент времени 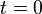 .
.
Начальная
фаза переменного синусоидального тока
может быть положительной 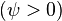 или
отрицательной
или
отрицательной 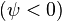 величиной.
При
величиной.
При 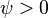 мгновенное
значение синусоидального тока в момент
времени
мгновенное
значение синусоидального тока в момент
времени 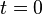 положительно,
при
положительно,
при 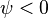 —
отрицательно.
—
отрицательно.
Если
начальная фаза 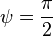 ,
то ток определяется по формуле
,
то ток определяется по формуле 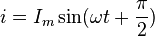 .
Мгновенное значение его в момент
времени
.
Мгновенное значение его в момент
времени 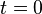 равно
равно
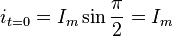 ,
то есть равно положительной амплитуде
тока.
,
то есть равно положительной амплитуде
тока.
Если
начальная фаза 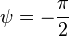 ,
то ток определяется по формуле
,
то ток определяется по формуле 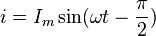 .
Мгновенное значение его в момент
времени
.
Мгновенное значение его в момент
времени 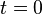 равно
равно
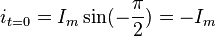 ,
то есть равно отрицательной амплитуде
тока.
,
то есть равно отрицательной амплитуде
тока.
9. Идеальные элементы электрической цепи синусоидального тока
11. Неразветвленная цепь синусоидального тока. Резонанс напряжений
Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Описание явления
Пусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f.
В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.
Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.
Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.
Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.
Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.
Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.
Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.
В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.
Однофазный и трехфазный переменный ток
Переменным электрическим током называется такой ток, который с течением времени периодически изменяется по величине и направлению.
Основными величинами, которыми характеризуется переменный ток, являются: период, частота, максимальное (амплитудное) значение, действующее (эффективное) значение, мгновенное значение и угловая частота (табл.
Формулы для расчета цепей переменного тока приведены в табл. 9 и 10.
Таблица 8
Основные величины, характеризующие синусоидальный переменный ток
Параметр | Определение | Формула для вычисления |
Период | Время, в течение которого переменный ток (или напряжение) совершает одно полное изменение по величине и направлению |
|
Частота | Число полных изменений переменного тока (или напряжения), совершаемых за одну секунду |
|
Максимальное (амплитудное) значение | Наибольшая величина, которую достигает переменный ток (или напряжение) за один период |
|
Действующее (эффективное) значение | Значение силы переменного тока (или напряжения), который проходя через равное сопротивление, что и постоянный ток, за одно и то же -время выделяет одинаковое количество тепла |
|
Мгновенное значение | Величина переменного тока (или напряжения) в любой рассматриваемый момент времени |
|
Удельная частота | Величина,
выраженная в |
|
Таблица 9
Основные формулы для расчета цепей переменного тока
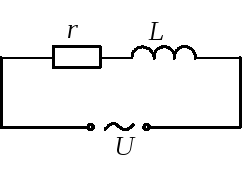
Схема цепи | Сопротивление цепи | Напряжение в зажимах цепи | Закон Ома |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
Таблица 10
Формулы для расчета мощности однофазного переменного тока
Мощность | Формула | Единица измерения |
Полная |
| в·а |
Активная |
| вт |
Реактивная |
| вар |
Коэффициент мощности 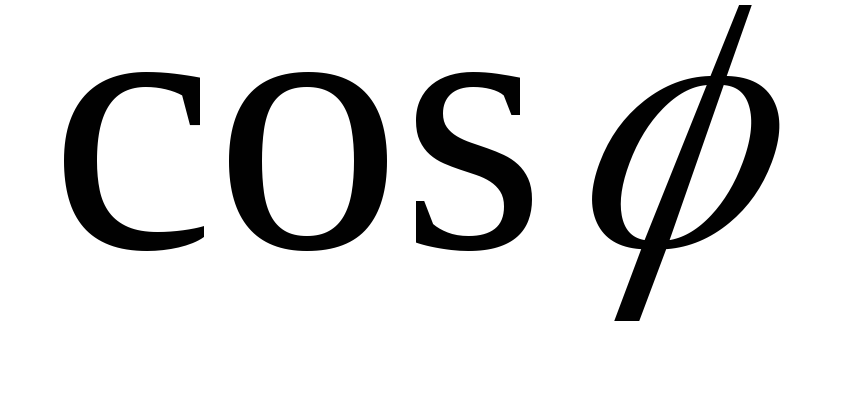 показывает, какая часть полной мощности
генератора используется в виде активной
мощности. Коэффициент мощности вычисляют
по формулам:
показывает, какая часть полной мощности
генератора используется в виде активной
мощности. Коэффициент мощности вычисляют
по формулам:
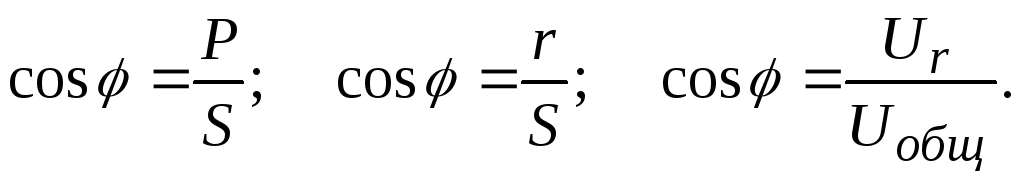
Трехфазной системой переменного тока называется такая электрическая цепь, в которой действуют три электродвижущие силы одинаковой частоты и амплитуды, взаимно смещенные по фазе на 120○( (табл. 11).
Таблица 11
Основные величины трехфазной системы переменного тока
Наименование величины | Схемы соединения фаз | |
|
| |
Линейное напряжение |
|
|
Фазное напряжение |
|
|
Линейный ток |
|
|
Фазный ток |
|
|
Полная мощность |
|
|
Активная мощность |
|
|
Реактивная мощность |
|
|
Переменный ток
“Стартовые” задачи по теме “переменный ток”. Познакомимся с понятиями индуктивного и емкостного сопротивлений, полного сопротивления, узнаем, что такое амплитудное и действующее значение тока и напряжения.
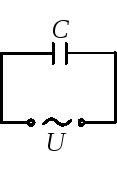
Задача 1. В цепь переменного тока последовательно включены конденсатор, резистор и катушка индуктивности. Как соотносятся по фазе колебания напряжения на этих элементах от фазы колебаний силы тока в цепи?
А) на обкладках конденсатора;
Б) на зажимах резистора;
В) на зажимах катушки.
1) отстают-по фазе от силы тока на ;
2) опережают по фазе силу тока на ;
3) совпадают по фазе с колебаниями силы тока;
4) опережают по фазе силу тока на катушки на некоторый угол .
Ток и напряжение в резисторе совпадают по фазе, всегда.
Чтобы хорошо запомнить, как соотносятся фазы напряжения и тока в реактивных элементах (катушке и конденсаторе), я даже для студентов своих стишок придумала:
«Каждый студент – запомни твердо!
От этого твой зависит зачет!
В емкости ток – опережает,
А в индуктивности – отстает!»
Ответ: 132
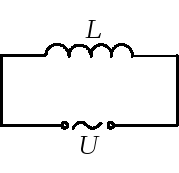
Задача 2. Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 3 А. Какова индуктивность катушки?
Определим угловую частоту:
Индуктивное сопротивление катушки:
По закону Ома:
Ответ: Гн.
Задача 3. Амплитудные значения напряжения и тока на резисторе соответственно равны В, А. Какая средняя мощность выделится резисторе этой цепи?
Средняя мощность вычисляется по формуле:
Где и – действующие значения тока и напряжения (они в раз меньше амплитудных), а – угол сдвига фаз напряжения и тока. Для резистора . Тогда
Ответ: 100 Вт.
Задача 4. Напряжение на резисторе в цепи переменного тока изменяется по закону , В. Чему равно действующее значение напряжения?
Действующие значения тока и напряжения в раз меньше амплитудных:
Ответ: 100 В.
Задача 5. Найдите активное сопротивление электрической лампы, включенной в цепь переменного тока с действующим напряжением 220 В, если при этом на ней выделяется средняя мощность 200 Вт.
Ответ: 242 Ом.
Задача 6. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?
По закону Ома
Ответ: 82 мА
Задача 7. Какое количество теплоты выделится на активном сопротивлении Ом за 2 периода колебаний, если мгновенное значение переменного напряжения на сопротивлении описывается уравнением ‚ В?
Из записи напряжения видим: – амплитуда напряжения, – действующее значение, .
Так как , то c.
Количество теплоты равно:
Ответ: 0,45 Дж.
Задача 8. В последовательной цепи переменного тока из резистора сопротивлением Ом, конденсатора электроемкостью С = 4,8 мкФ и катушки индуктивностью Гн наблюдается электрический резонанс. Во сколько раз амплитуда напряжения на катушке больше амплитуды приложенного напряжения?
Добротность определяет то, во сколько раз напряжение на катушке или конденсаторе больше входного (напряжения питания).
Добротность:
Где – волновое сопротивление контура.
Ответ: в 10 раз.


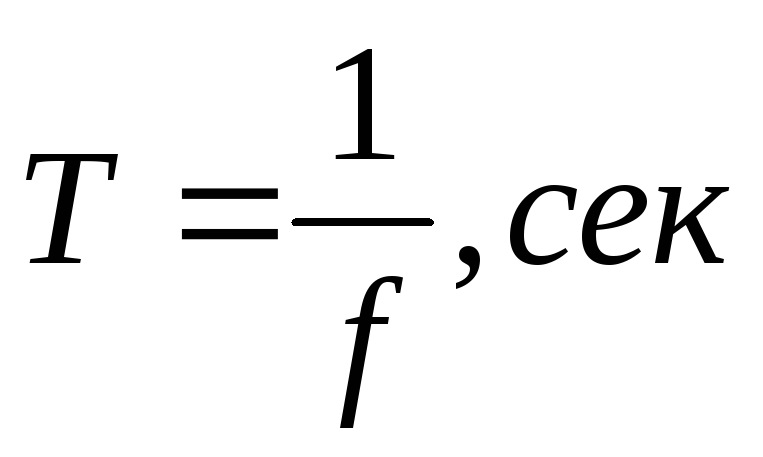
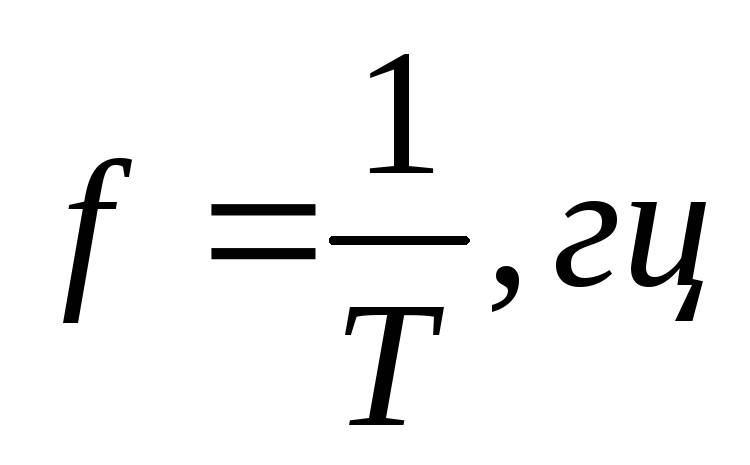
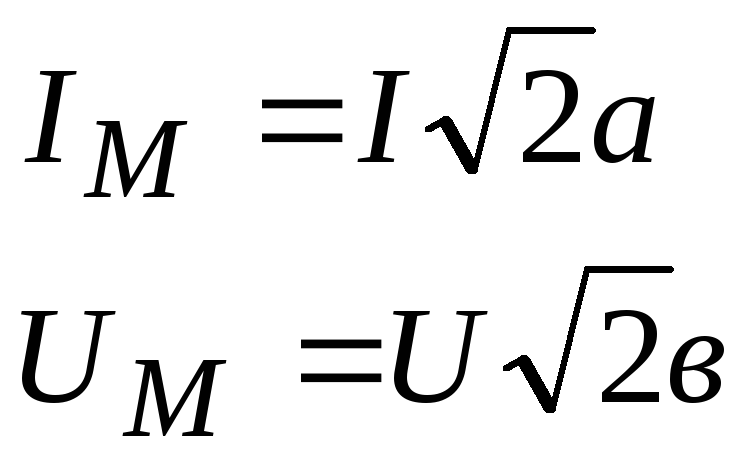
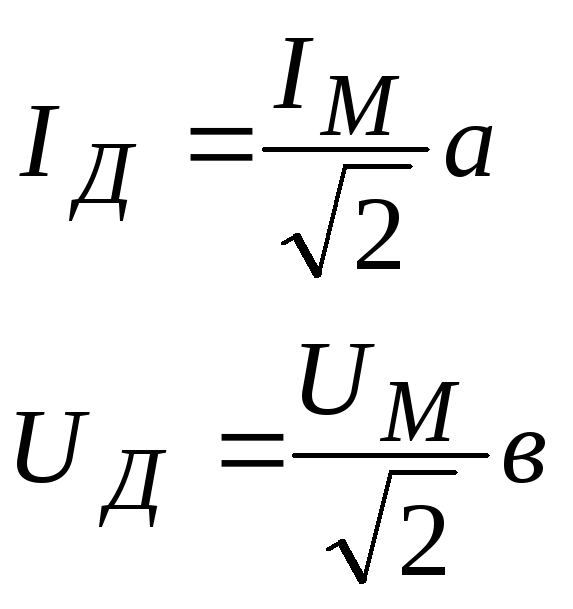
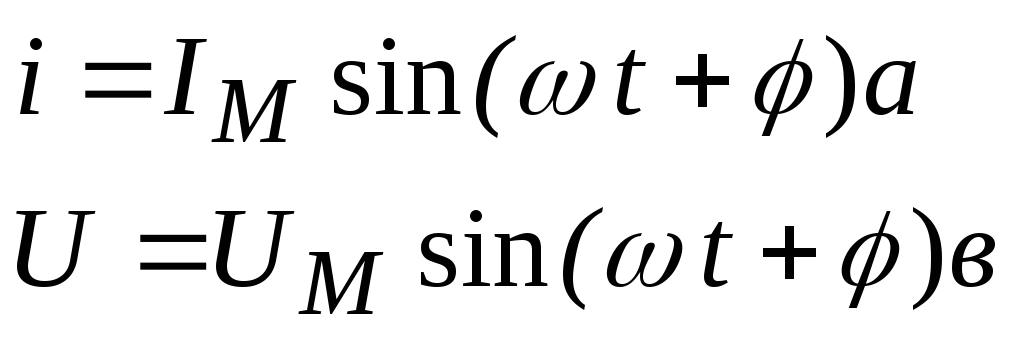
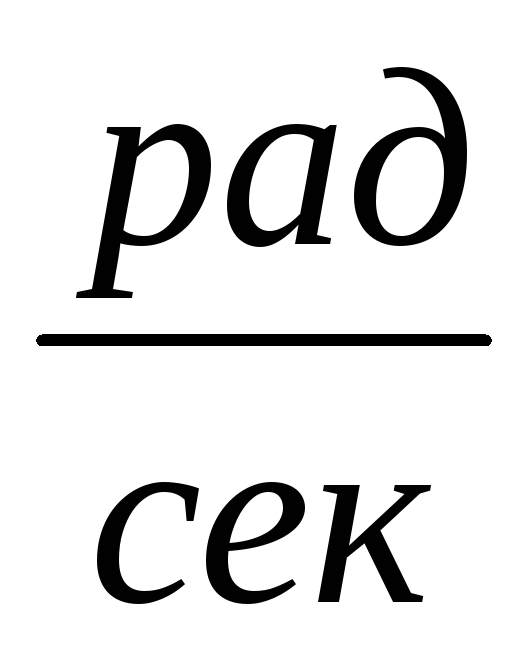 , которая больше частоты, выраженной
в гц, в
2π раз
, которая больше частоты, выраженной
в гц, в
2π раз