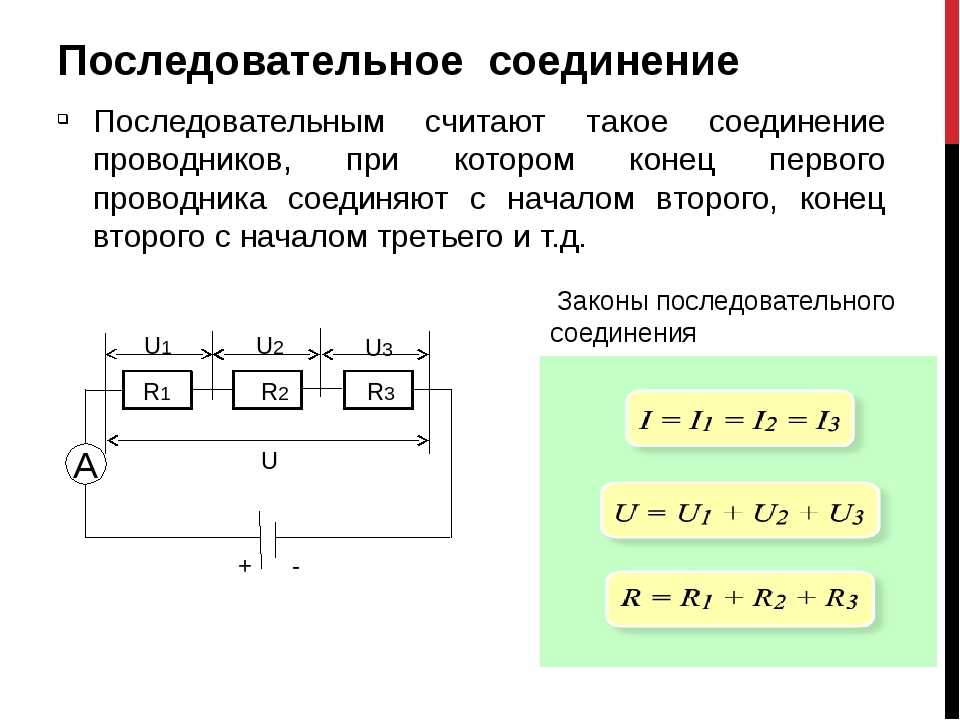
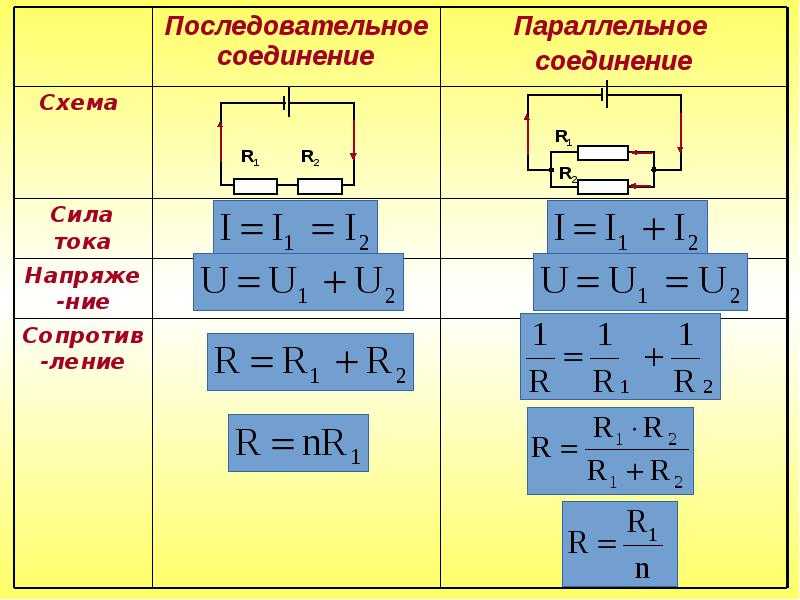
Параллельное соединение резисторов
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.
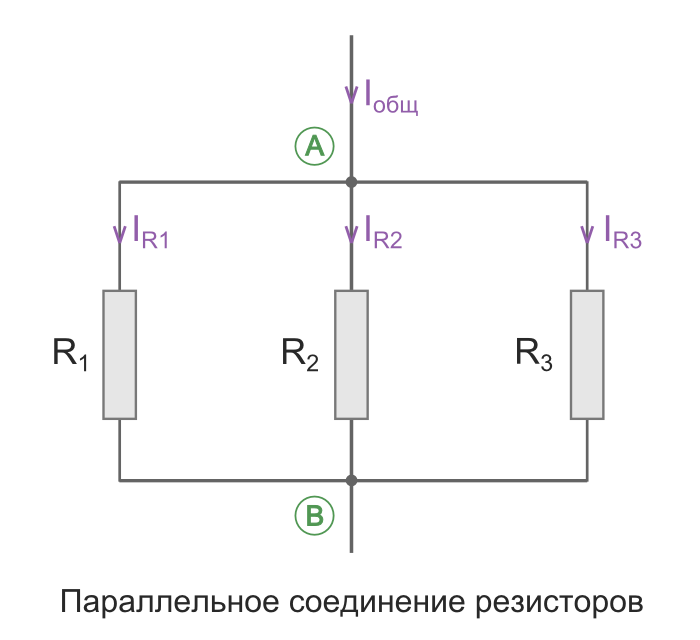
Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .
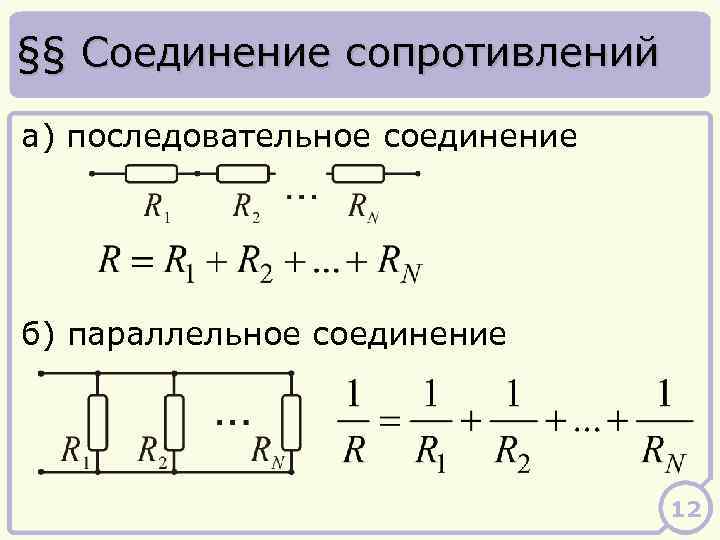
А) – Последовательное соединение
В) – Параллельное соединение
Рисунок 1 – Последовательное и параллельное соединение
Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения.
Рисунок 2 – Параллельное соединения
Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.
Как следует из статьи про потенциалы, это означает,
С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I.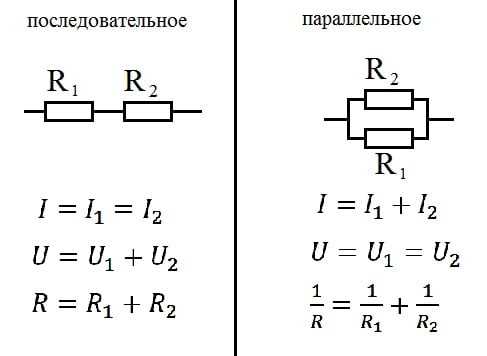 Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.
Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.
То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так
Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома.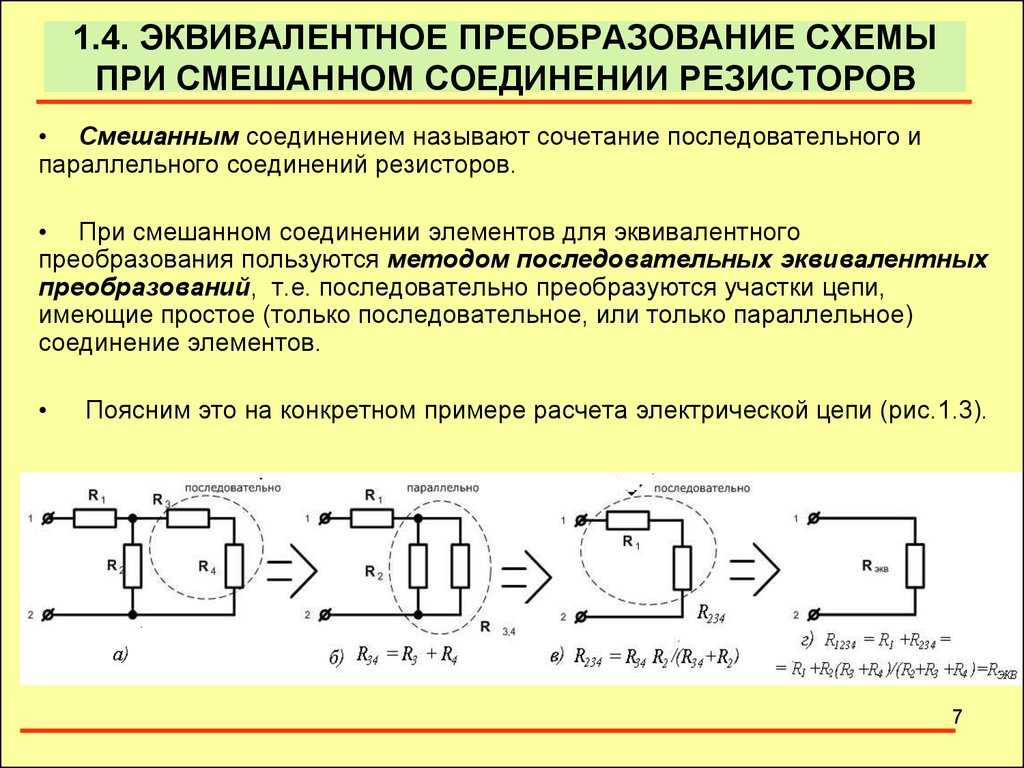 Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом
Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
Рисунок 3 – Преобразование параллельного соединение
Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:
То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?
Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.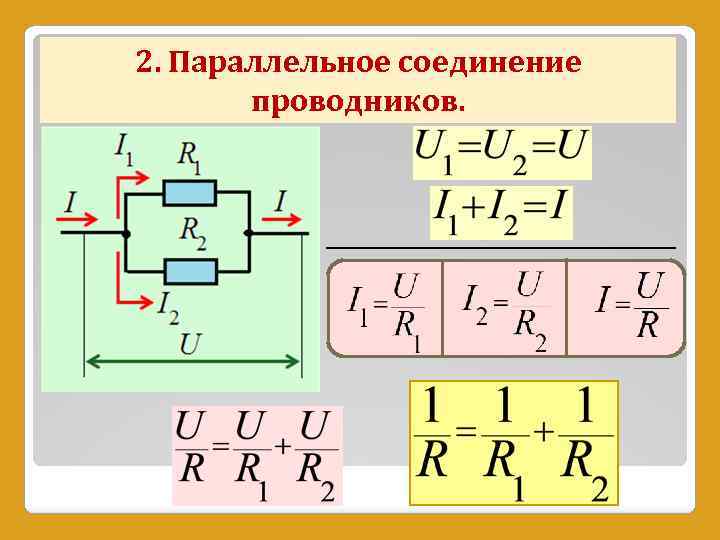
Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления
То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
Умножим левую и правую части на напряжение U.
Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
где Р – мощность, выдаваемая источником;
P1 – мощность, рассеиваемая на резисторе R1;
P2 – мощность, рассеиваемая на резисторе R2;
P3 – мощность, рассеиваемая на резисторе R3.
Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.
Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить,
1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.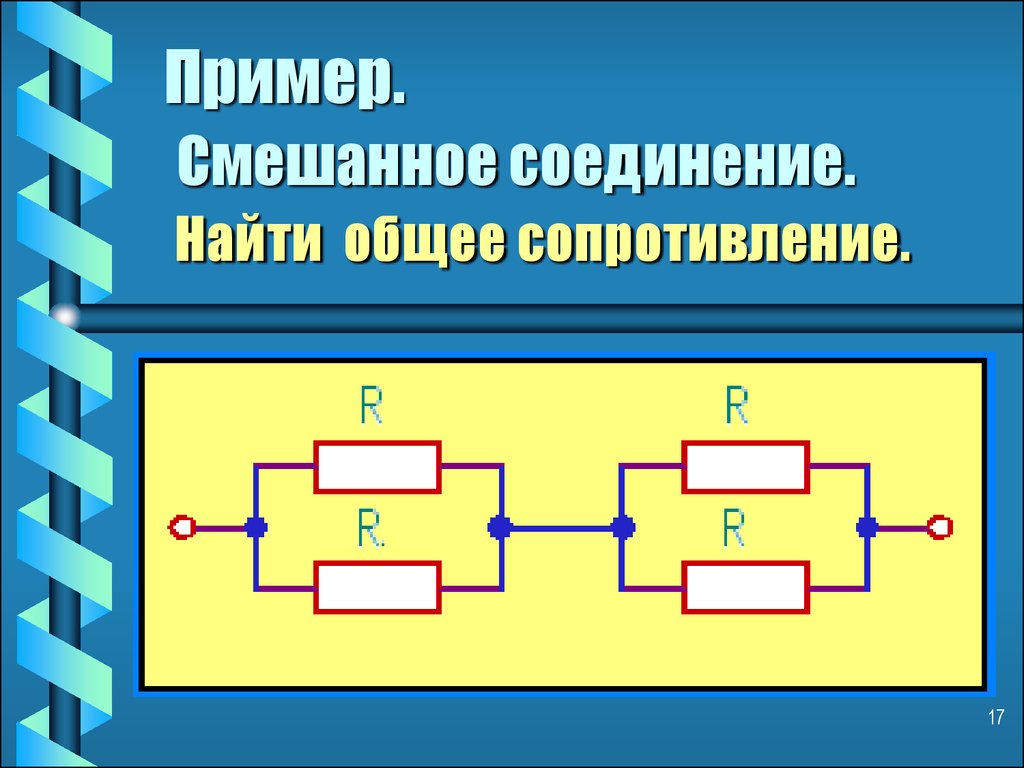
2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.
3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу
Мы же помним нашу формулу
Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.
Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.
Рисунок 4 – Плата нагревателя
На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов.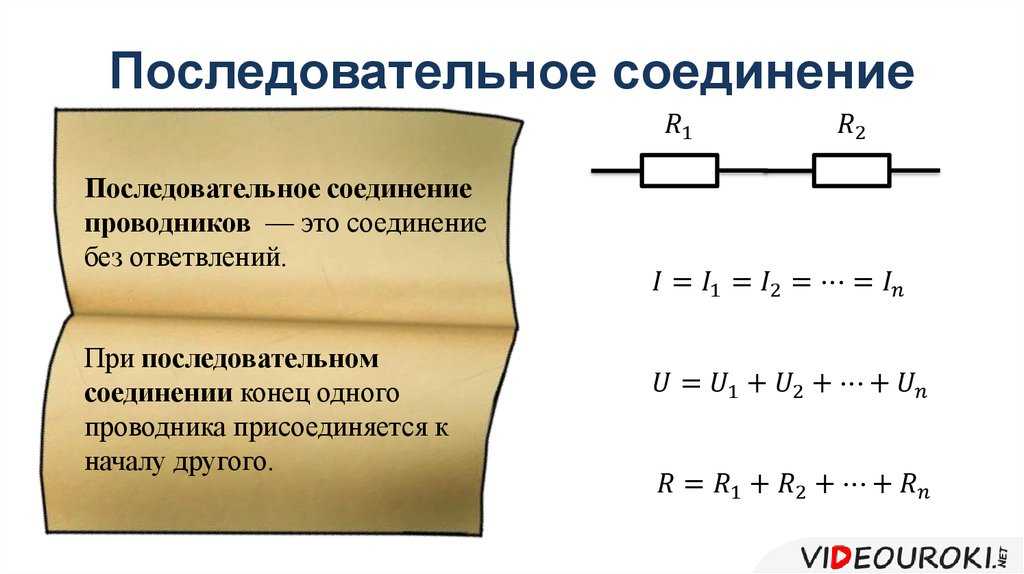 Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
и теоретически может рассеивать мощность
Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться
Это значит, что на каждом резисторе будет выделяться
что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно
Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти. Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось
а на всей плате
Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
На сегодня все, господа. Удачи вам и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Лабораторная работа по исследованию свойств параллельного и последовательного соединения резисторов беспаечным способом
В работе исследованы свойства и физические законы соединения резисторов без пайки.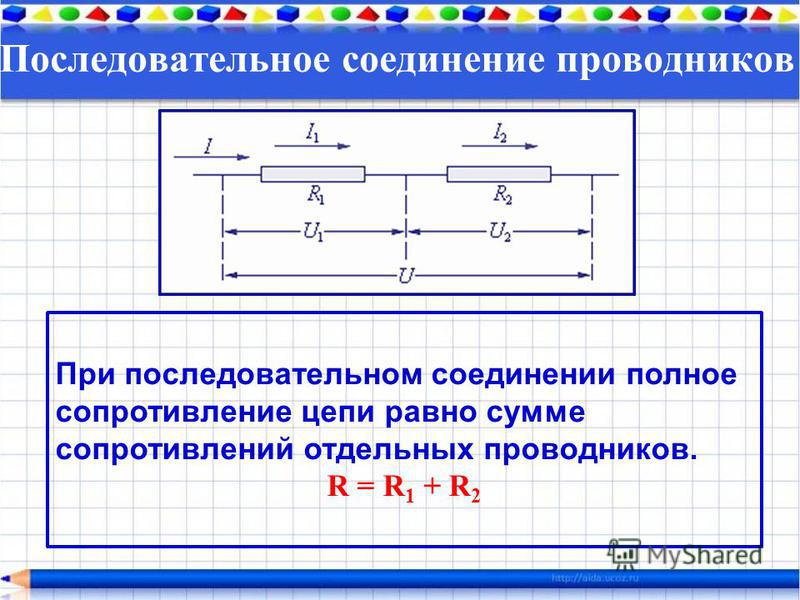 При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Ключевые слова: резисторы, макетная плата, соединение без пайки, параллельное и последовательное соединение, токи, напряжение и сопротивления при соединения резисторов.
The paper studies the properties and physical laws of connecting resistors without soldering. When building layouts, soldering installation can be completely, abandoned or reduced to a minimum. As experience has shown, the practical use of layout boards can significantly save time and material costs.
Keyword: resistors, layout Board, connection without soldering, parallel and serial connection, currents, voltage and resistance when connecting resistors.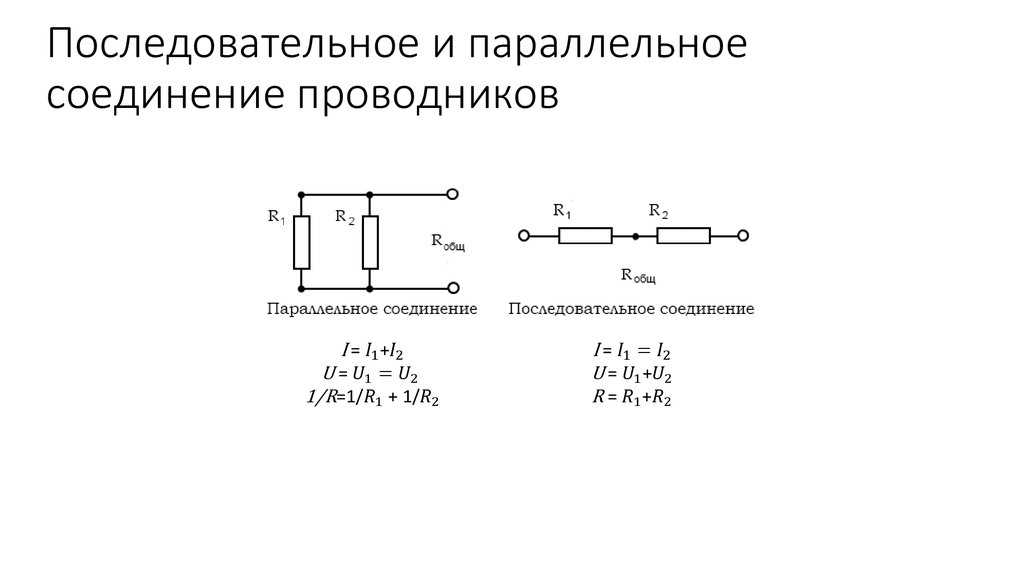
В современном высшем учебном заведении перед каждым преподавателем стоит цель по развитию научно-исследовательских навыков студентов. Один из задач являетсямотивации студента и совершенствование научно-исследовательских навыков в формулировке исследовательского вопроса во время лабораторной работы на уроках физики. В данной работе исследованы свойства и физические законы соединения резисторов без пайки. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты. [1,2].
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединение резисторовспомощью беспаечное соединение и определить формулы сопротивлений таких участков. Резисторы примениется в электронных приборах и робототехнике. [3].
Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т.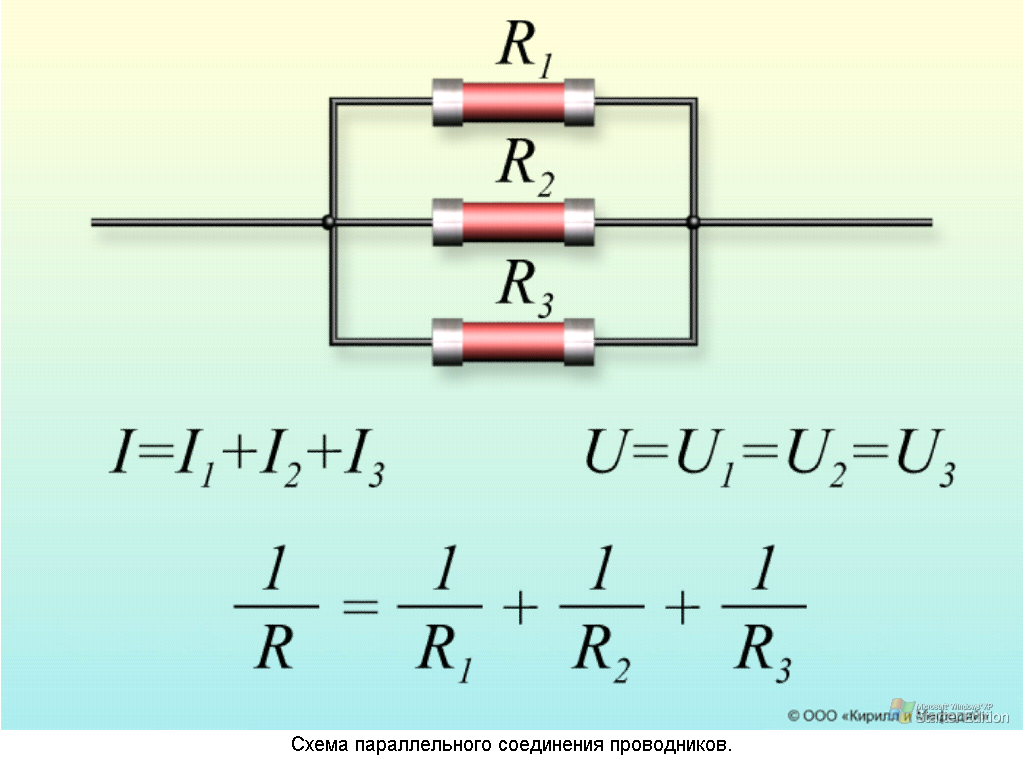 д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.
д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.
Перечень оборудования
Рис. 1. Резистор и провода
Рис. 2. Мультиметр
Рис. 3. Макетная плата
Последовательно соединенных резисторов
Сопротивление впоследовательной цепи. Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.
Rобщ = R1+R2+R2+ •••+Rn(1)
Если последовательно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, умножив сопротивление одного резистора на количество резисторов.
Rобщ = nR1 (2)
Пример последовательного соединения двух резисторов показан на рис.4.
Общее сопротивление для двух резисторов.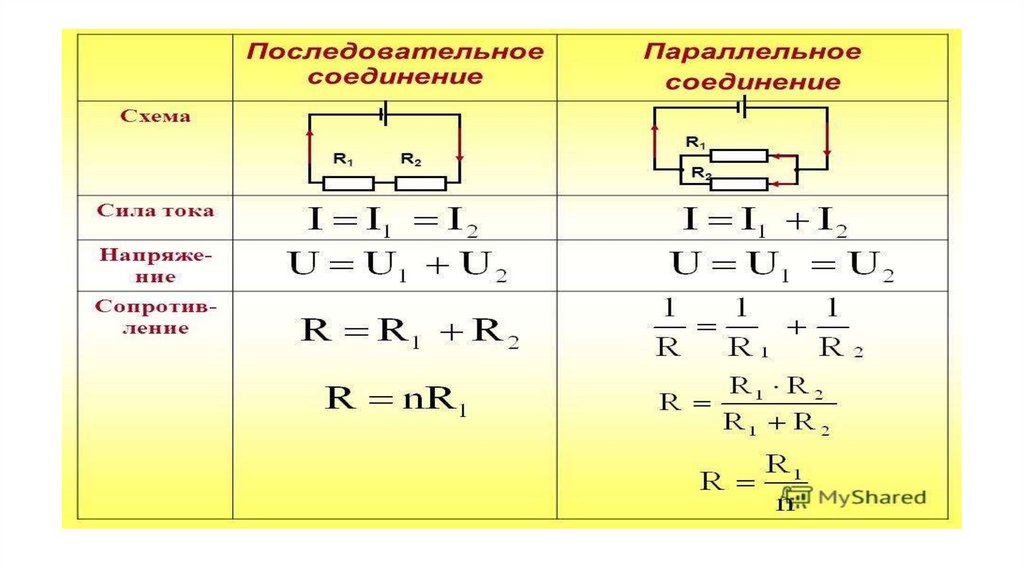
Rобщ=R1+R2 (3)
Rобщ = 25 Ом+35 Ом=60 Ом (4)
Рис. 4. Последовательное соединение двух резисторов
Величина тока впоследовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени в любой точке цепи, будет одинаковым. Следовательно, во всех точках последовательной цепи величина тока одинакова.
Поэтому при последовательном соединении, для измерения тока достаточно включать один амперметр на любом участке цепи.
В качестве примера, можно привести цепь последовательного соединения двух резисторов, который показан на рис.5.
I=I1=I2=0,2A
Рис. 5. Величина тока в последовательнойцепи
Распределение напряжения впоследовательной цепи
Напряжение источника тока, приложенное, к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков.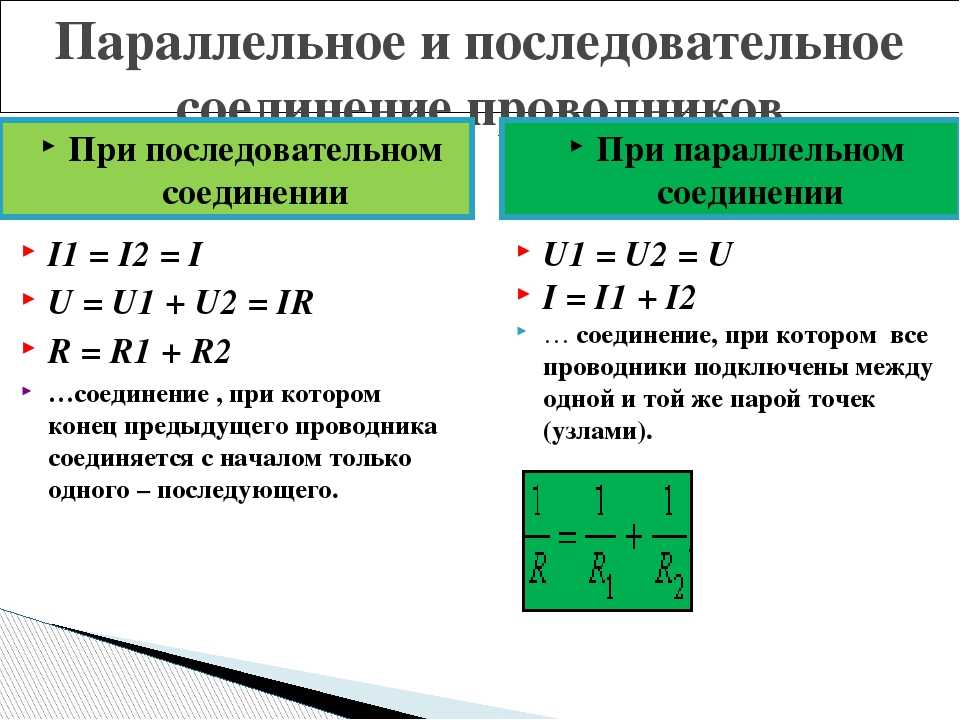 Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:
Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:
U=IR (5)
Так как ток в последовательной цепи везде одинаков, значит, действительно напряжение на ее участках зависит от сопротивления, чем больше сопротивление, тем большее напряжение приложено к данному участку. Сумма напряжений на участках последовательной цепи равна напряжению источника тока.
Uобщ=U1+ U2+ U3+ ••• +Un(6)
Пример, распределение напряжения в последовательной цепи соединения двух резисторов показан на рис.6.
Uобщ=U1+ U2(7)
12В=5В+7В
Параллельное соединение сопротивлений
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.
Рис. 6. Распределение напряжения в последовательной цепи
Сопротивлениев параллельной цепи
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
(8)
Если параллельно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, если сопротивление одного резистора разделить на количество резисторов.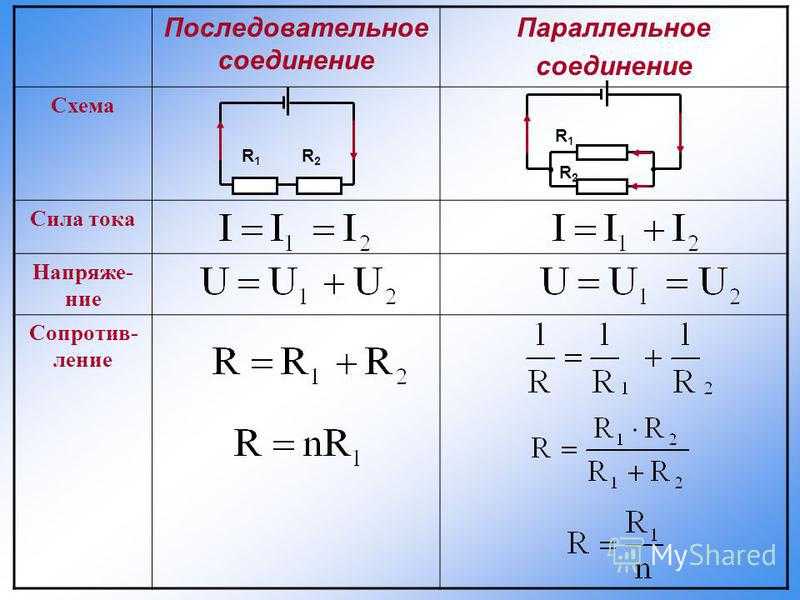
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. Пример, если параллельно включено только два резистора (рис.7), то их общее сопротивление можно определить по формуле:
(10)
Рис. 7. Параллельное соединение двух резисторов
Распределение тока впараллельной цепи
В цепи с параллельным соединением, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит, что чем больше сопротивление, тем меньше по нему пойдет ток.
(11)
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее:
I=I1+ I2+ I3 +••• +In(12)
Следовательно, величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
Пример, распределение тока в параллельной цепи соединения двух резисторов показан на рис. 8.
I=I1+ I2
Рис. 8. Распределение тока в параллельной цепи
Величина напряжения впараллельных цепях
Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
U=U1=U2=U3=•••=Un (13)
Содержание хода работы ипоследовательность действий
Техническое задание
1) Собрать электрическую цепь в макетную плату (рис.9.)
2) Снять показания приборов и записать их в таблицу.
3) Произвести расчеты.
4) Ответить на контрольные вопросы.
5) Сделать вывод.
Порядок выполнения работы
1) Собрать схему в макетную плату (Рис. 9.).
2) Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм+ N, где N — номер студента по журналу (мощность резисторов более 1 Вт).
3) Включить источник и установить напряжение U=5В, 9В, 12В, 15В.
4) Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А иВ; Ви С; Аи С; Dи Е.
Запишите эти показания в таблицу 1, 2.
Рис. 9. Схема исследования: а) последовательное соединение, б) параллельное соединение
5) Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.
6) Измерьте с помощью мультиметра (в режиме измерения постоянного тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 1.
Запишите показания прибора в таблицу 1.
7) Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.
8) Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2.
9) Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.
10) Отключить схему.
Таблица 1
Рассчитанные иизмеренные параметры для последовательного соединения резисторов: Аи В; Ви С; Аи С.
№вар. | Установлено | Рассчитано | Измёренные параметры | ||||||
R1 | R2 | А— В | В— С | А— С | I | U | U1 | U2 | |
кОм | кОм | кОм | кОм | кОм | А | В | В | В | |
Таблица 2
Рассчитанные иизмеренные параметры для параллельного соединения резисторов: Dи Е.
№вар. | Установлено | Рассчитано | Измерённые параметры | ||||||
R3 | R4 | D иЕ | U | I | I1 | I2 | |||
кОм | кОм | кОм | В | А | А | А | |||
Содержание отчета
а) название и цель работы;
б) схемы экспериментов и таблицы полученных экспериментальных данных;
в) результаты расчётов:
г) выводы по работе.
Контрольные вопросы
1) Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
2) Как по вольтамперной характеристике определить величину сопротивления цепи?
3) Как по показаниям мультиметра можно определить величину сопротивления участка электрической цепи и потребляемая мощность?
4) Нарисуйте схемы последовательное и параллельное соединение двух резисторов.
5) Объясните физические законы соединения резисторов.
Выводы
В работе исследованы свойства и физические законы параллельного и последовательного соединения резисторов бес применения пайки.
При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Литература:
- А.
 Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С. - Л. Г. Белиовская, Белиовский Н. А. Роботизированные лабораторныее работы по физики, Пропедевтетический курс физика. -М.:ДМК Пресс.2016.-164С.
- Википедия [Электронный ресурс]. http://ru.wikipedia.org/wiki/Processing.
Основные термины (генерируются автоматически): общее сопротивление, резистор, сопротивление, последовательная цепь, последовательное соединение, соединение резисторов, величина тока, ком, макетная плата, параллельная цепь, параллельное соединение.
Параллельное включение резисторов — схема и расчет. Как отличается параллельное и последовательное соединение резисторов?
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).

- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.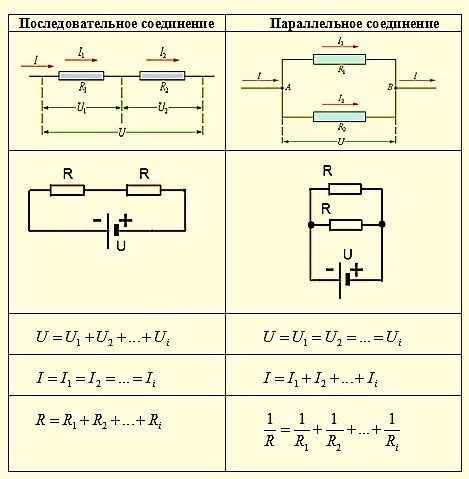
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.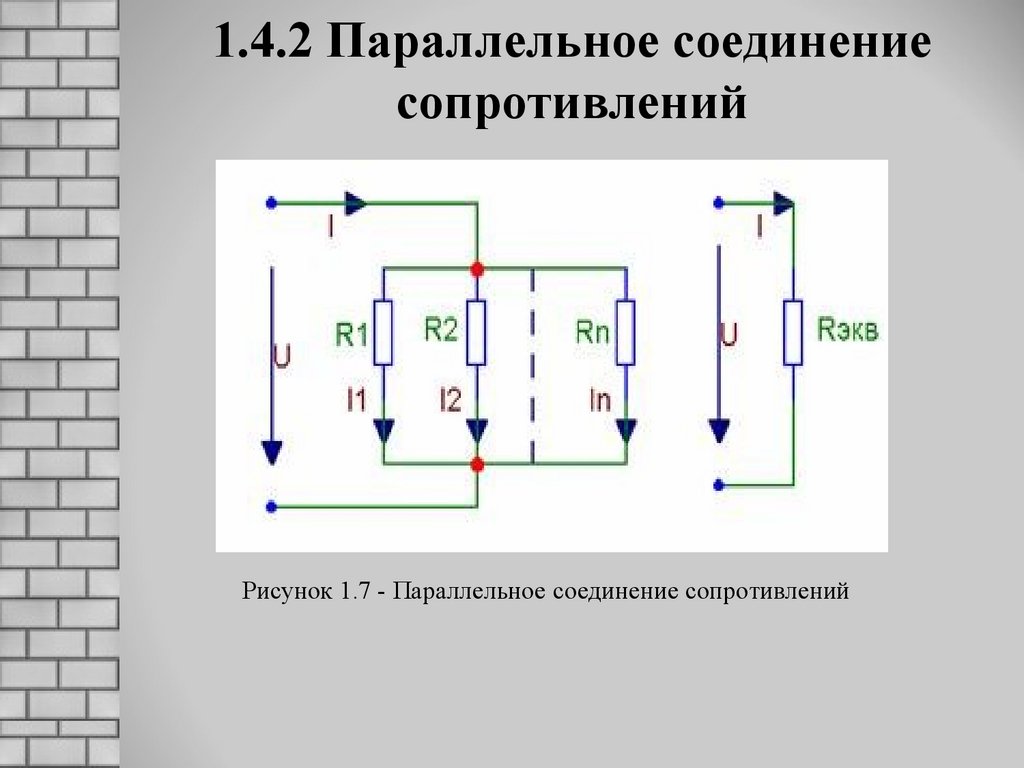
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Общее сопротивление
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Схема
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Будет интересно➡ Переменный резистор
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Как выглядит формула Георга Ома
Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.
Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:
U1 = U2 = U.
Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:
I = I1 + I2.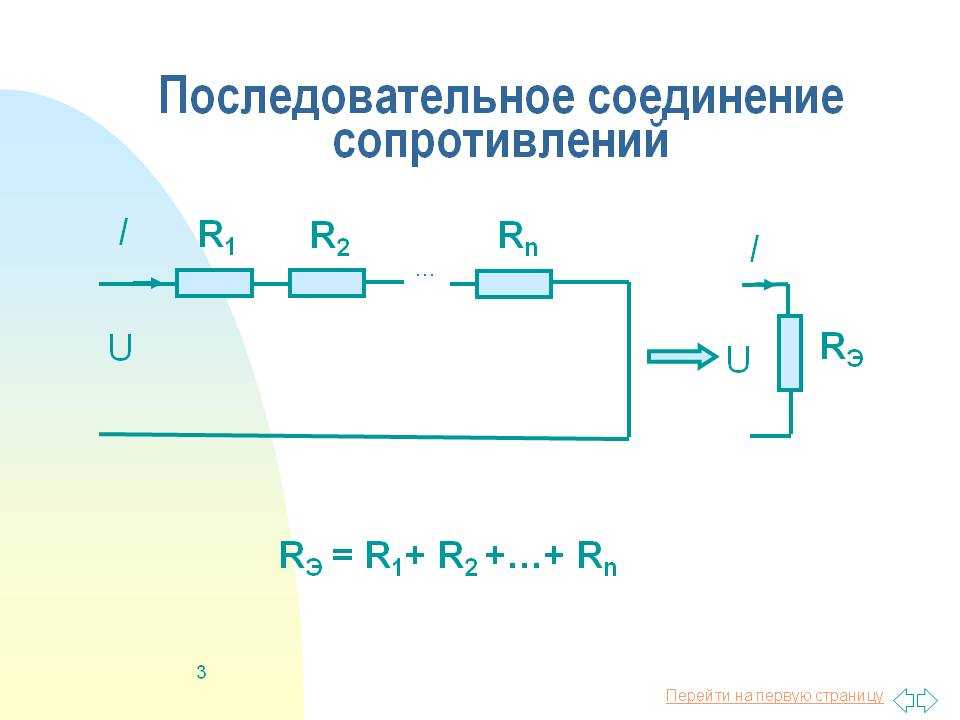
Расчет силы тока при помощи закона Ома записывается как:
I = U/R;
I1 = U1/R1;
I2 = U2/R2.
Из формулы следует:
U/R = U1/R1 + U2/R2;
U = U1 = U2;
1/R = 1/R1 + 1/R2.
Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.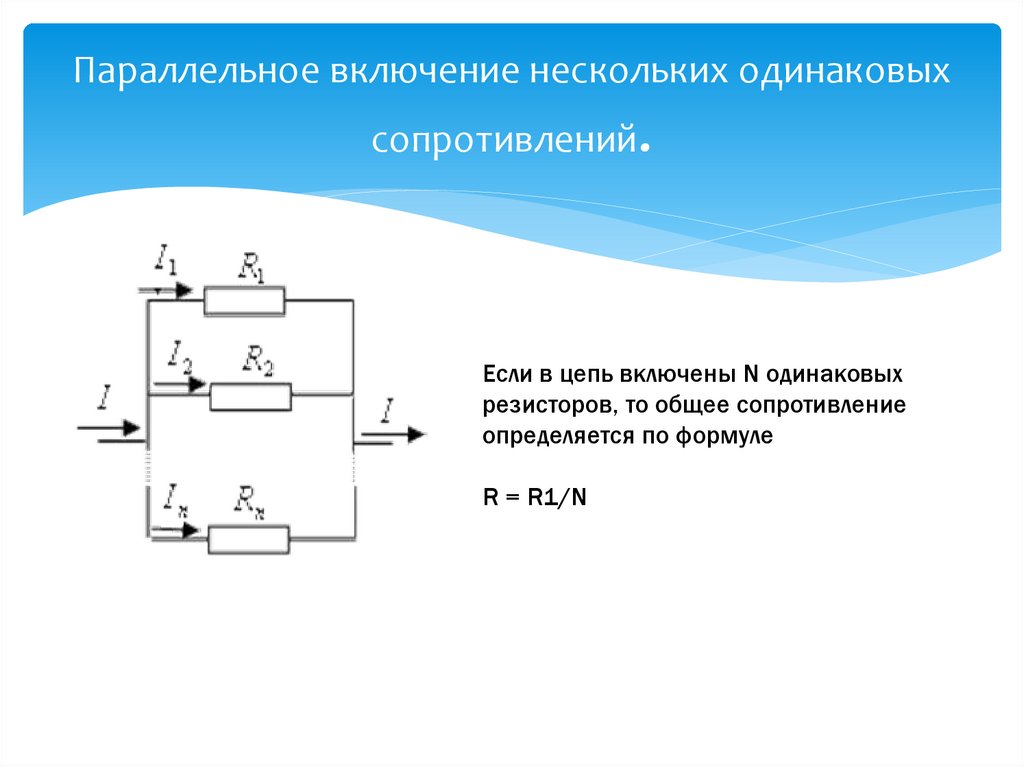
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе.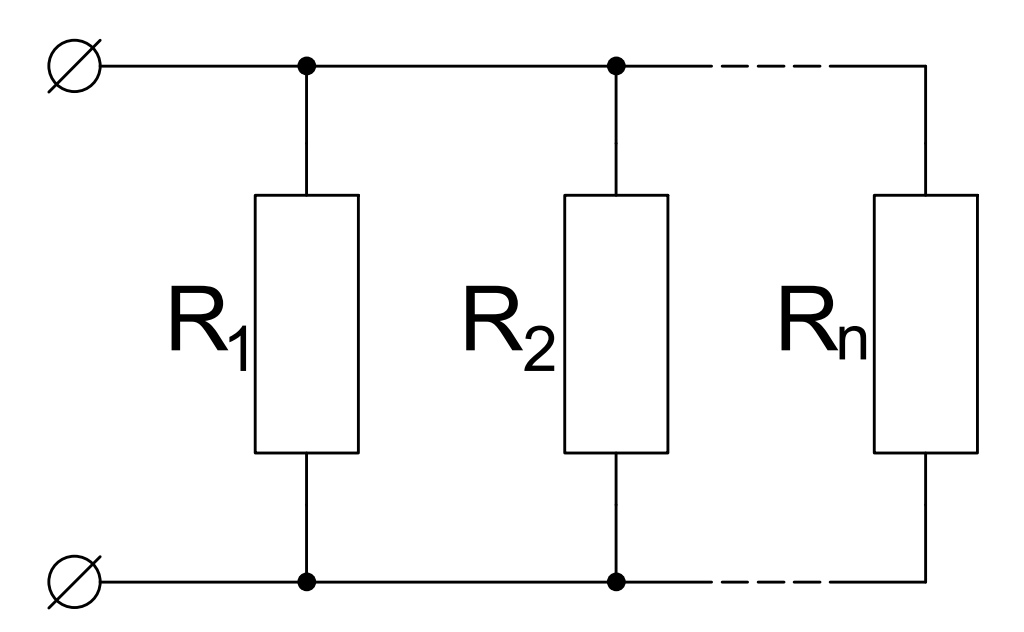 Давайте так и сделаем.
Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.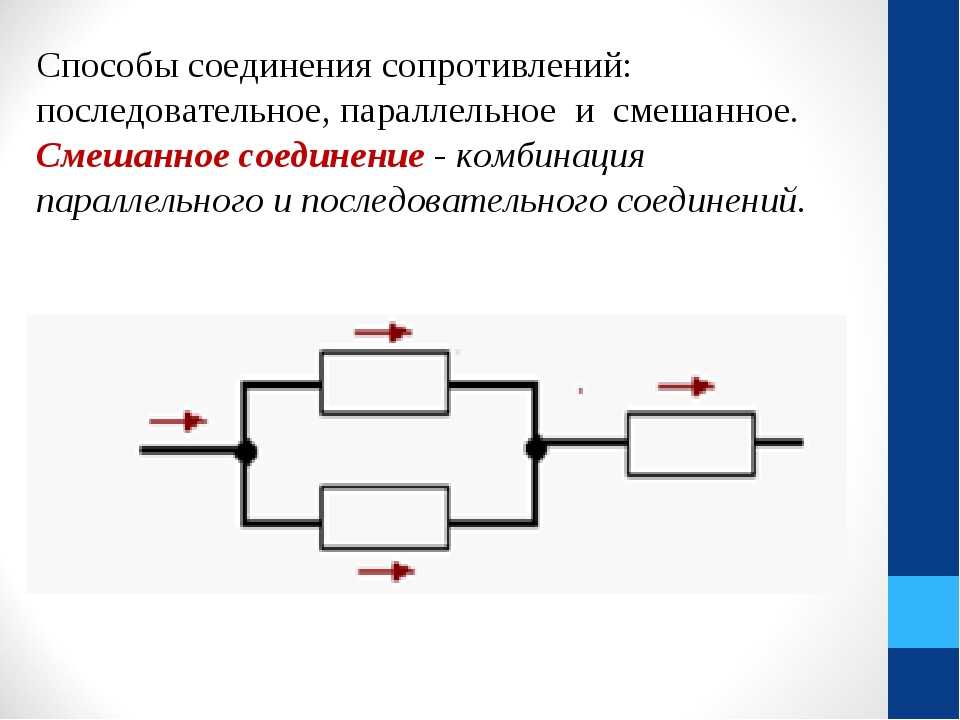
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Отличия от последовательного и смешанного подключений
Параллельное соединение проводников
Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.
Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:
Rобщ = R1 + R2 + … + Rn.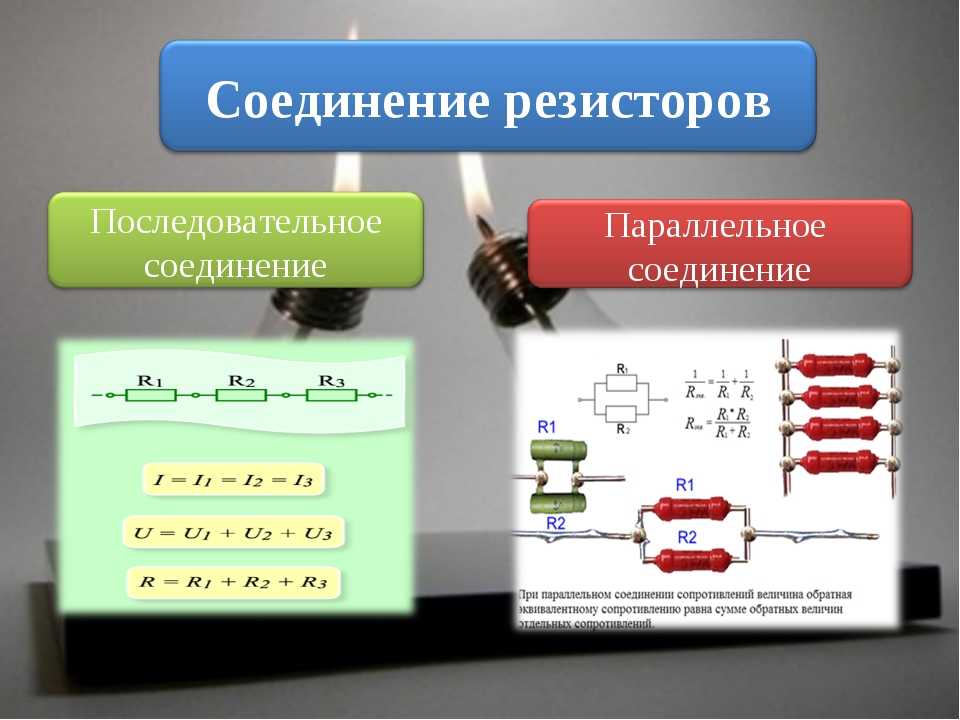
Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками.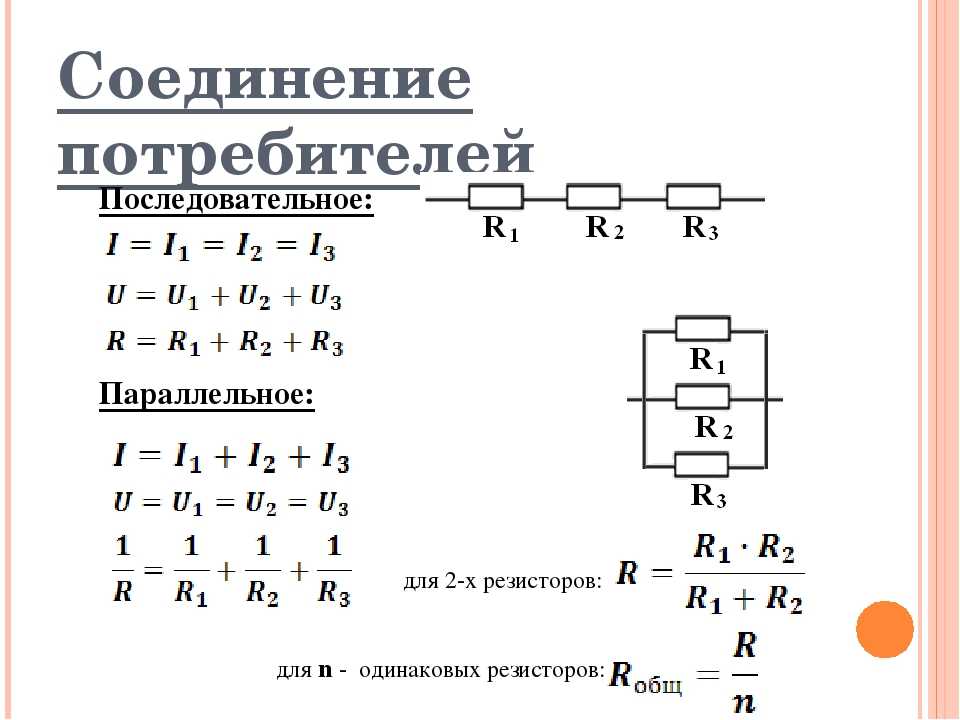 Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения.
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм.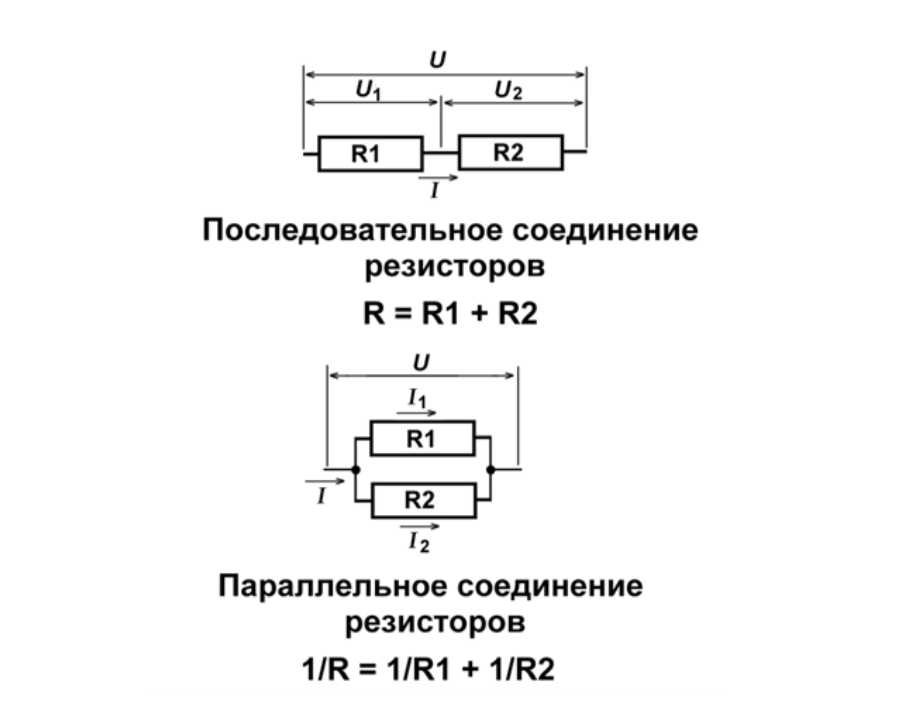 Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Источники
- https://rusenergetics.
 ru/praktika/raschet-soprotivleniya-rezistorov
ru/praktika/raschet-soprotivleniya-rezistorov - https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
- https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
- https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
- https://www.RusElectronic.com/serial-and-parallel/
- https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html
- https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallel-resistance/
- http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
4.1 Резисторы последовательно и параллельно
Цели обученияПоследовательное соединение резисторовПараллельное соединение резисторовСочетания последовательного и параллельного соединенияПрактические выводыПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Нарисуйте цепь с параллельными и последовательными резисторами
- Используйте закон Ома для расчета падения напряжения на резисторе, когда через него проходит ток
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи
- Рассчитать общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 4.
 E.5.1 Учащийся может сделать и обосновать количественный прогноз влияния изменения значений или расположения одного или двух элементов цепи на токи и разности потенциалов в цепи, содержащей небольшое количество источники ЭДС, резисторы, конденсаторы и переключатели, включенные последовательно и/или параллельно. (СП 2.2, 6.4)
E.5.1 Учащийся может сделать и обосновать количественный прогноз влияния изменения значений или расположения одного или двух элементов цепи на токи и разности потенциалов в цепи, содержащей небольшое количество источники ЭДС, резисторы, конденсаторы и переключатели, включенные последовательно и/или параллельно. (СП 2.2, 6.4) - 4.E.5.2 Учащийся способен сделать и обосновать качественный прогноз влияния изменения значений или расположения одного или двух элементов цепи на токи и разности потенциалов в цепи, содержащей небольшое количество источников ЭДС, резисторы, конденсаторы и переключатели последовательно и/или параллельно. (СП 6.1, 6.4)
- 4.E.5.3 Учащийся может планировать стратегии сбора данных и выполнять анализ данных для изучения значений токов и разностей потенциалов в электрической цепи, которая модифицируется путем изменения или перестановки элементов цепи, включая источники ЭДС, резисторы , и конденсаторы.
 (Ст.2.2, 4.2, 5.1)
(Ст.2.2, 4.2, 5.1) - 5.B.9.3 Учащийся может применять закон сохранения энергии (правило петли Кирхгофа) в расчетах, включающих полную разность электрических потенциалов для полных цепей только с одной батареей и резисторами, соединенными последовательно и/или не более , одна параллельная ветвь. (СП 2.2, 6.4, 7.2)
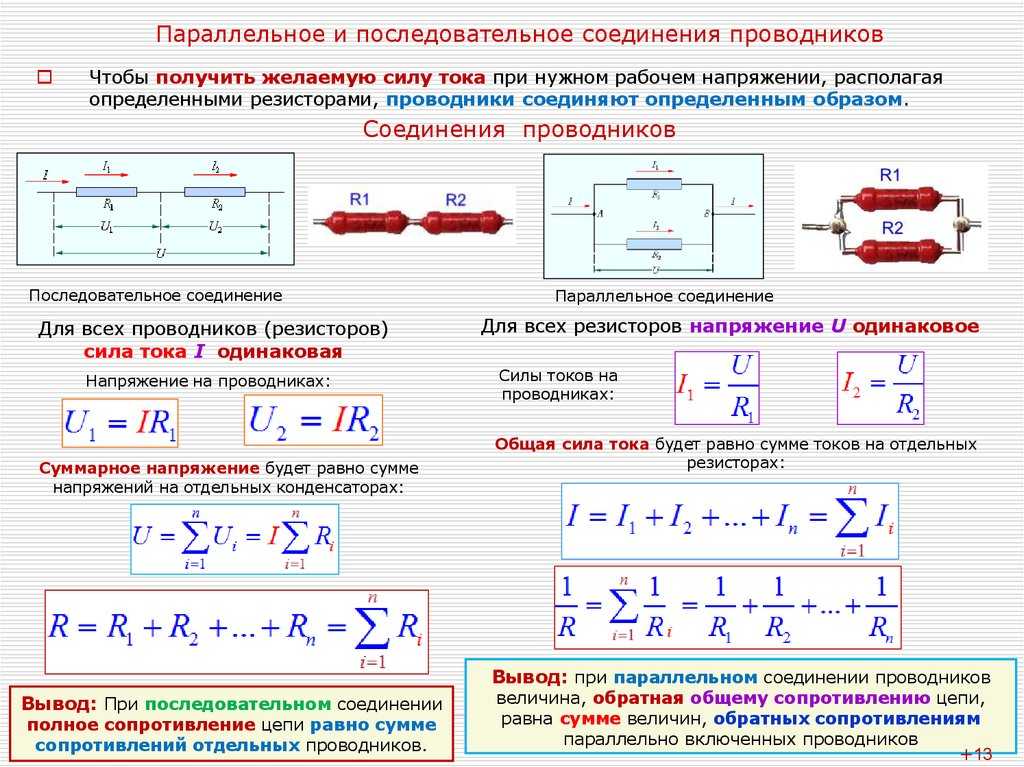
Большинство цепей имеют более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением. Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рис. 4.2. Общее сопротивление комбинации резисторов зависит как от их отдельных значений, так и от того, как они соединены.
Рисунок 4.2 (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.
Резисторы серии
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно.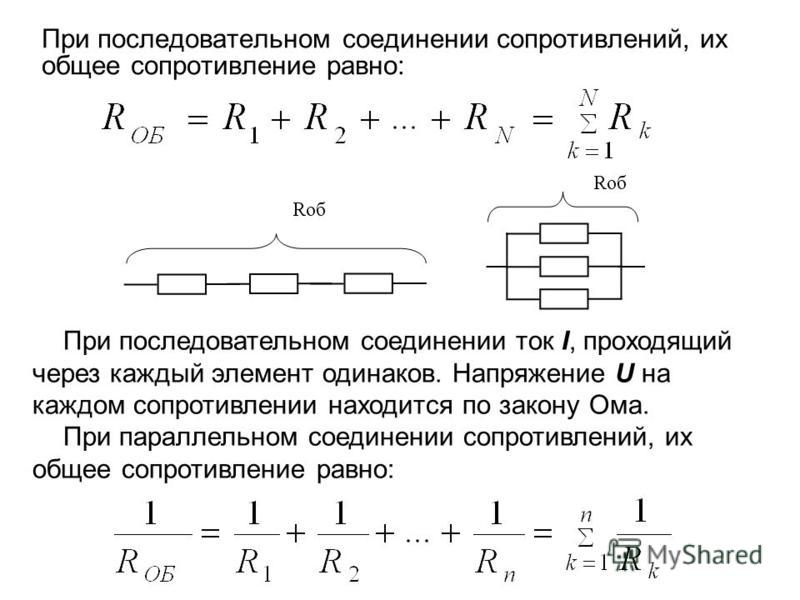 Например, если ток течет через человека, держащего отвертку, в землю, то R1.R1.на рис. 4.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, и R4R4 сопротивление ее обуви.
Например, если ток течет через человека, держащего отвертку, в землю, то R1.R1.на рис. 4.2(а) может быть сопротивлением стержня отвертки, R2R2 — сопротивлением ее рукоятки, R3R3 — сопротивлением тела человека, и R4R4 сопротивление ее обуви.
На рис. 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить силу тока, надев обувь на резиновой подошве с высоким сопротивлением. Это могло бы быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением для устройства, которое уменьшило бы рабочий ток.
Рис. 4.3. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).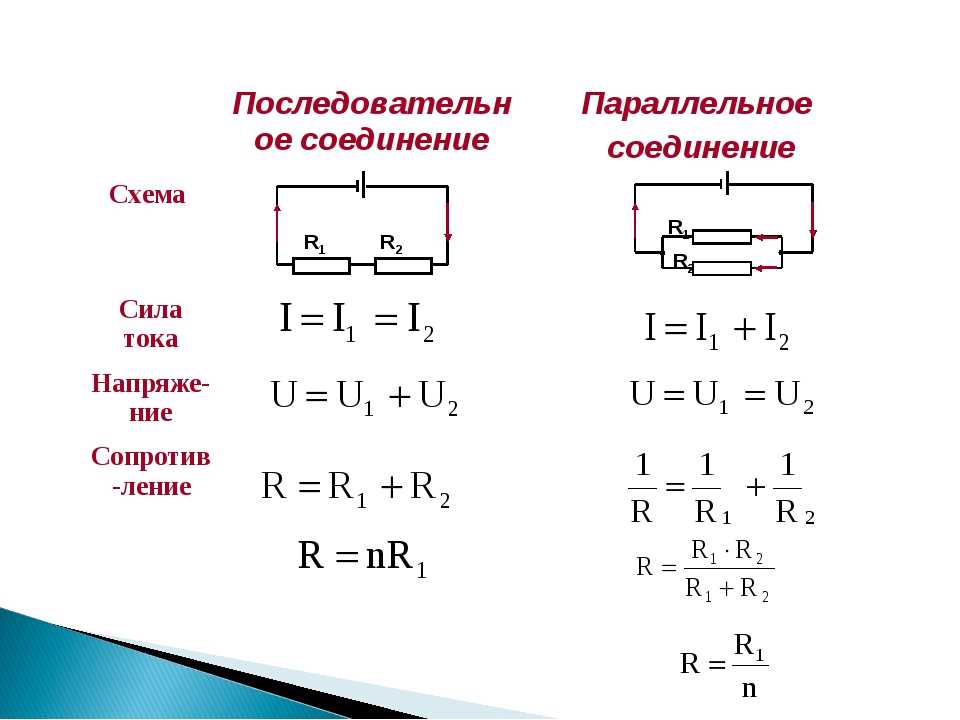
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения, в каждом резисторе на рис. 4.3.
В соответствии с законом Ома падение напряжения V,V на резисторе при протекании через него тока рассчитывается по уравнению V=IR,V=IR, где II равно току в амперах (А), а RR равно сопротивление в омах Ω.Ω. Другой способ представить это так: VV — это напряжение, необходимое для того, чтобы ток II протекал через сопротивление R. R.
Таким образом, падение напряжения на R1R1 равно V1=IR1,V1=IR1, на R2R2 — V2=IR2, V2=IR2, а на R3R3 — V3=IR3.V3=IR3. Сумма этих напряжений равна выходному напряжению источника; то есть
4.1 В=В1+В2+В3.В=В1+В2+В3.
Это уравнение основано на законе сохранения энергии и законе сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением PE=qV, PE=qV, где qq — электрический заряд, а VV — напряжение. Таким образом, энергия, подводимая источником, равна qV,qV, а рассеиваемая резисторами —
4.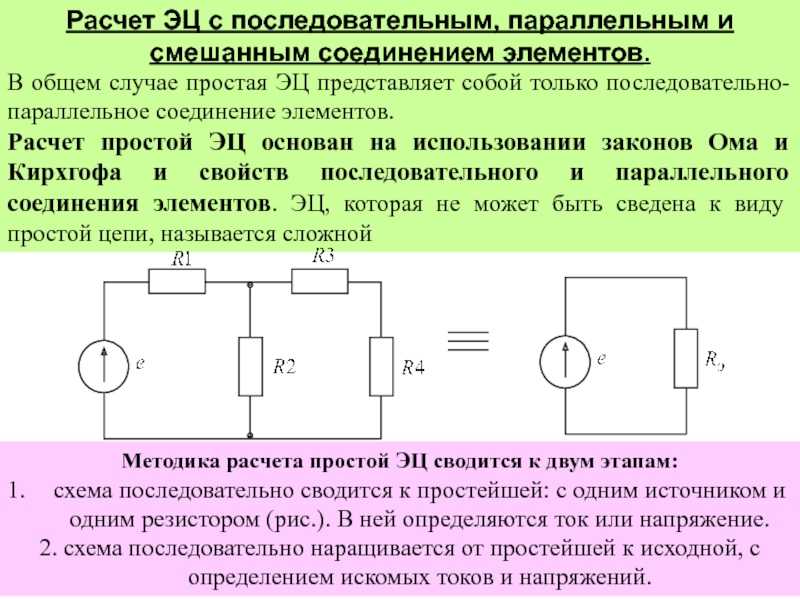 2 qV1+qV2+qV3.qV1+qV2+qV3.
2 qV1+qV2+qV3.qV1+qV2+qV3.
Соединения: законы сохранения
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и назначения энергии. Таким образом, qV=qV1+qV2+qV3.qV=qV1+qV2+qV3. Заряд qq компенсируется, что дает V=V1+V2+V3, V=V1+V2+V3, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
4,3 В=IR1+IR2+IR3=I(R1+R2+R3).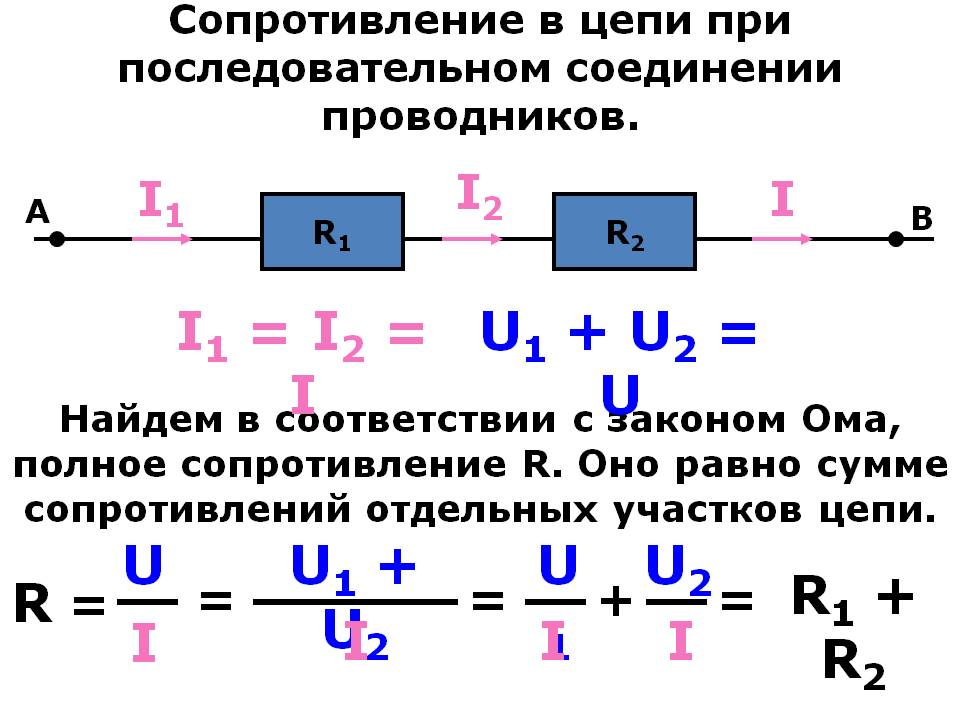 V=IR1+IR2+IR3=I(R1+R2+R3).
V=IR1+IR2+IR3=I(R1+R2+R3).
Обратите внимание, что для эквивалентного последовательного сопротивления Rs,Rs мы имеем
4,4 В=IRs.V=IRs.
Это означает, что общее или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs=R1+R2+R3.Rs=R1+R2+R3.
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, общее сопротивление RsRs последовательного соединения равно
.4,5 Rs=R1+R2+R3+…,Rs=R1+R2+R3+…,
как предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис. , R2 = 6,00 Ом, R2 = 6,00 Ом и R3 = 13,0 Ом. R3 = 13,0 Ом. а) Чему равно полное сопротивление? б) Найдите силу тока.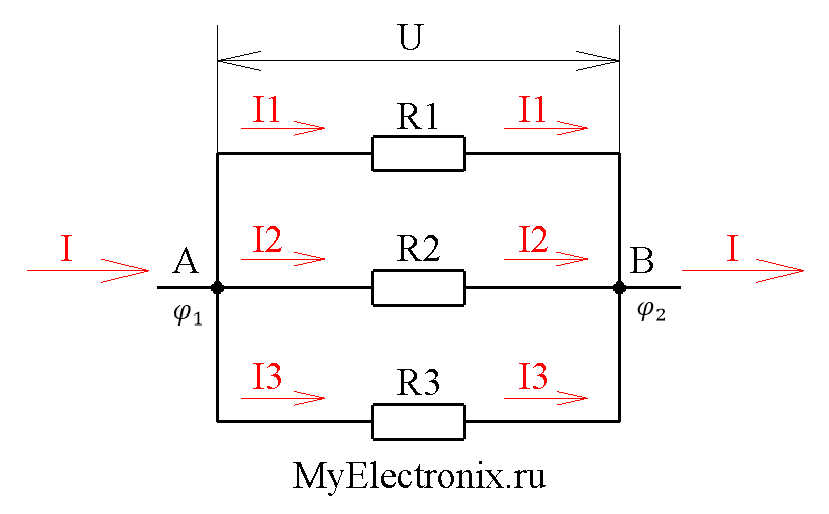 (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление представляет собой просто сумму отдельных сопротивлений, определяемую уравнением
4,6 Rs=R1+R2+R3=1,00 Ом+6,00 Ом+13,0 Ом= 20,0 Ом. Rs=R1+R2+R3=1,00 Ом+6,00 Ом+13,0 Ом=20,0 Ом.
Стратегия и решение для (b)
Ток определяется по закону Ома, V=IR.V=IR. Ввод значений приложенного напряжения и общего сопротивления дает ток в цепи.
4,7 I=VRs=12,0 В20,0 Ом=0,600 AI=VRs=12,0 В20,0 Ом=0,600 А
Стратегия и решение для (c)
Падение напряжения или IRIR падения на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
4,8 V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.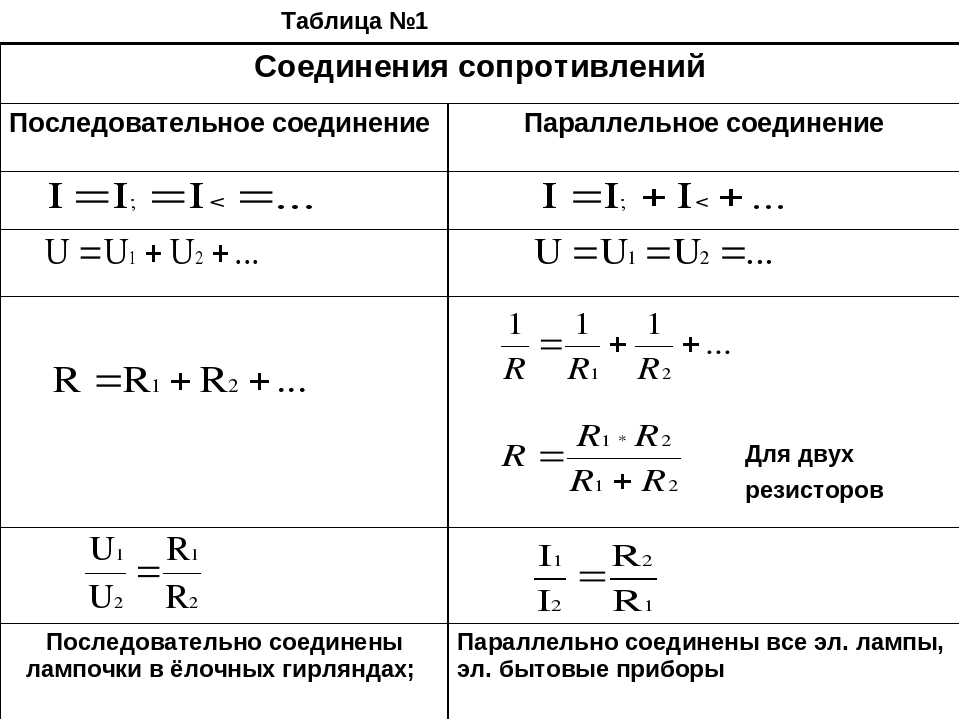 V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.
V1=IR1=(0,600 А)(1,0 Ом)=0,600 В.
Аналогично,
4,9 V2=IR2=(0,600 А)(6,0 Ом)=3,60 VV2=IR2=(0,600 А)(6,0 Ом)=3,60 В
и
4,10 V3=IR3=(0,600 А)(13,0 Ом) =7,80 В.V3=IR3=(0,600 А)(13,0 Ом)=7,80 В.
Обсуждение для (c)
Три капли IRIR добавляются к 12,0 В, 12,0 В, как и предполагалось.
4.11 V1+V2+V3=(0,600+3,60+7,80)V=12,0 VV1+V2+V3=(0,600+3,60+7,80)V=12,0 В
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, где PP — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток. Подставив закон Ома V=IRV=IR в закон Джоуля, мы получим мощность, рассеиваемую первым резистором, как
4.12 P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт.P1=I2R1=(0,600 А)2(1,00 Ом)=0,360 Вт. A)2(6,00 Ом)=2,16 WP2=I2R2=(0,600 А)2(6,00 Ом)=2,16 Вт
и
4,14 P3=I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.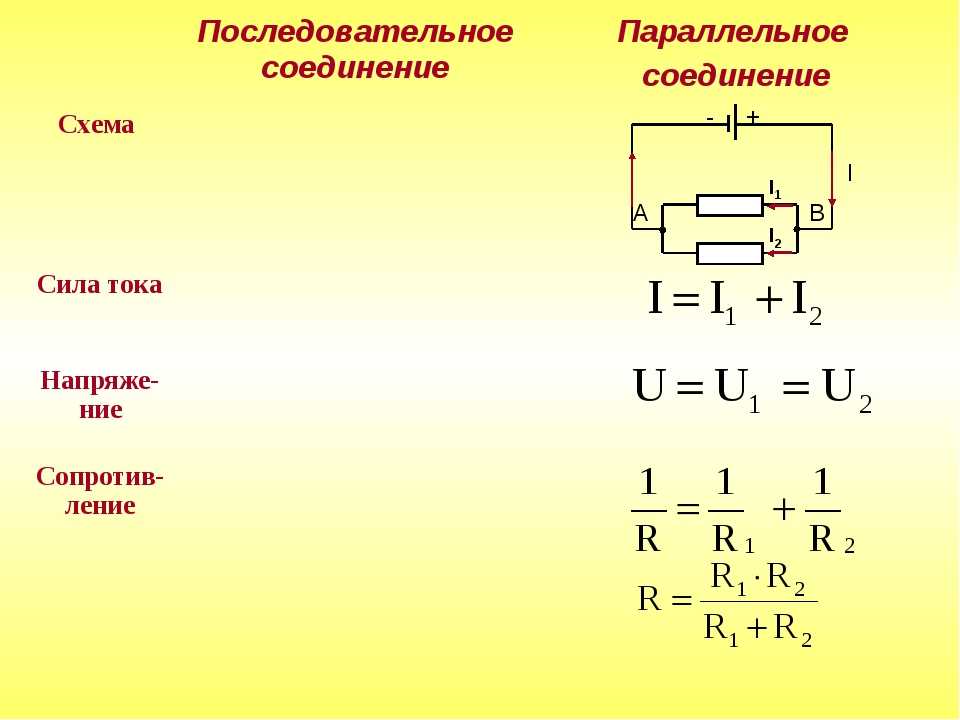 P3= I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.
P3= I2R3=(0,600 А)2(13,0 Ом)=4,68 Вт.
Обсуждение для (d)
Мощность также можно рассчитать, используя либо P=IVP=IV, либо P=V2R,P=V2R, где VV равно падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P=IV,P=IV, где VV — напряжение источника. Это дает
4,15 P = (0,600 А) (12,0 В) = 7,20 Вт. P = (0,600 А) (12,0 В) = 7,20 Вт. рассеиваемая резисторами также составляет 7,20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
4,16 P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт.P1+P2+P3=(0,360+2,16+4,68)W=7,20 Вт.
Мощность — это энергия в единицу времени (ватты), поэтому для сохранения энергии необходимо, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Добавление последовательного сопротивления Rs=R1+R2+R3+.
 …Rs=R1+R2+R3+….
…Rs=R1+R2+R3+…. - Один и тот же ток протекает через каждый последовательно соединенный резистор.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
Резисторы параллельно
На рис. 4.4 показаны резисторы, подключенные параллельно к источнику напряжения. Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения, при условии, что источник напряжения не перегружен. Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое можно сказать и о вашем доме или любом другом здании (см.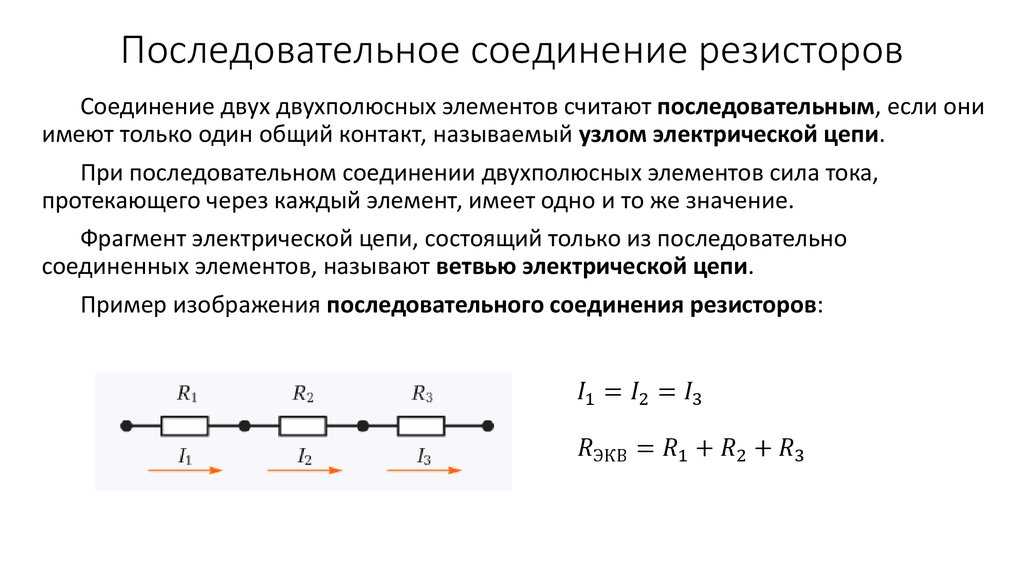 рис. 4.4(b)).
рис. 4.4(b)).
Рисунок 4.4 (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (Дмитрий Г., Wikimedia Commons)
Чтобы найти выражение для эквивалентного параллельного сопротивления Rp,Rp, рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны I1=VR1, I1=VR1, I2=VR2, I2=VR2 и I3=VR3.I3=VR3. Сохранение заряда подразумевает, что полный ток II, производимый источником, представляет собой сумму этих токов.
4.17 I=I1+I2+I3I=I1+I2+I3
Подстановка выражений для отдельных токов дает
4.18 I=VR1+VR2+VR3=V1R1+1R2+1R3.I=VR1+VR2+VR3=V1R1+1R2+1R3.
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
4.19 I=VRp=V1Rp.I=VRp=V1Rp.
Члены в скобках в последних двух уравнениях должны быть равны.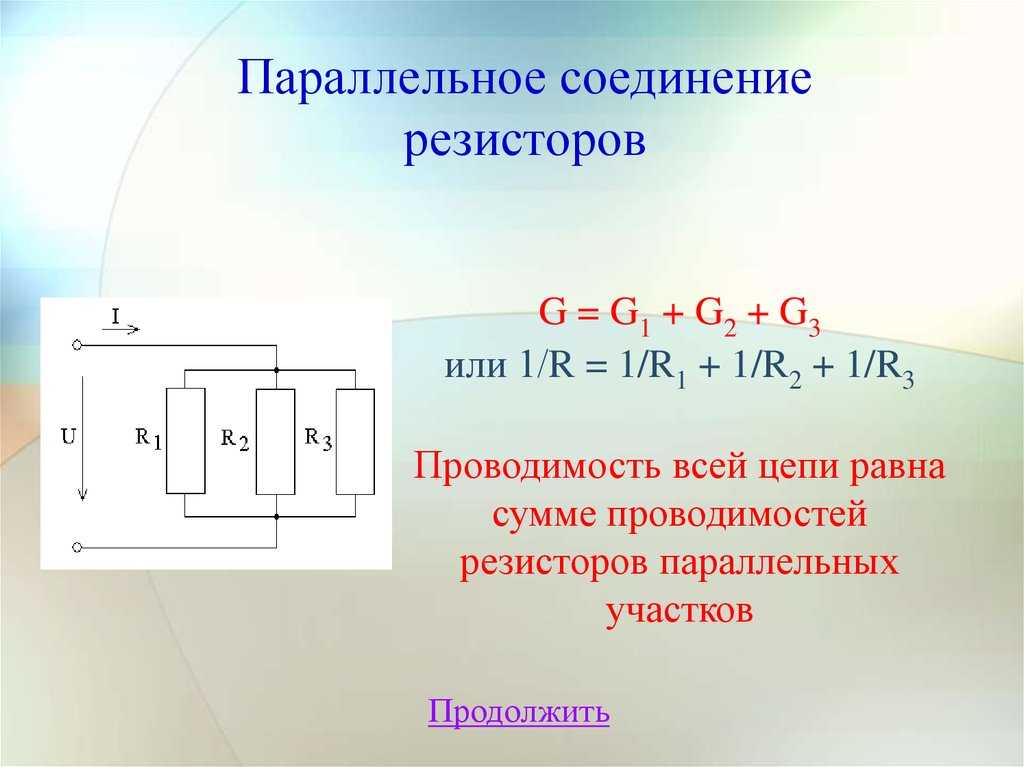 Обобщая на любое количество резисторов, общее сопротивление RpRp параллельного соединения связано с отдельными сопротивлениями как 9.0003
Обобщая на любое количество резисторов, общее сопротивление RpRp параллельного соединения связано с отдельными сопротивлениями как 9.0003
4.20 1Rp=1R1+1R2+1R.3+….1Rp=1R1+1R2+1R.3+….
Это соотношение приводит к тому, что общее сопротивление RpRp меньше наименьшего из индивидуальных сопротивлений. Это видно на следующем примере. Когда резисторы соединены параллельно, от источника протекает больший ток, чем по каждому из них по отдельности, поэтому общее сопротивление меньше.
Пример 4.2 Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис. 4.4 будут такими же, как и при последовательном соединении, рассмотренном ранее: V=12,0 В, V=12,0 В, R1=1,00 Ом, R1=1,00 Ом, R2= 6,00 Ом, R2 = 6,00 Ом и R3 = 13,0 Ом. R3 = 13,0 Ом. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника.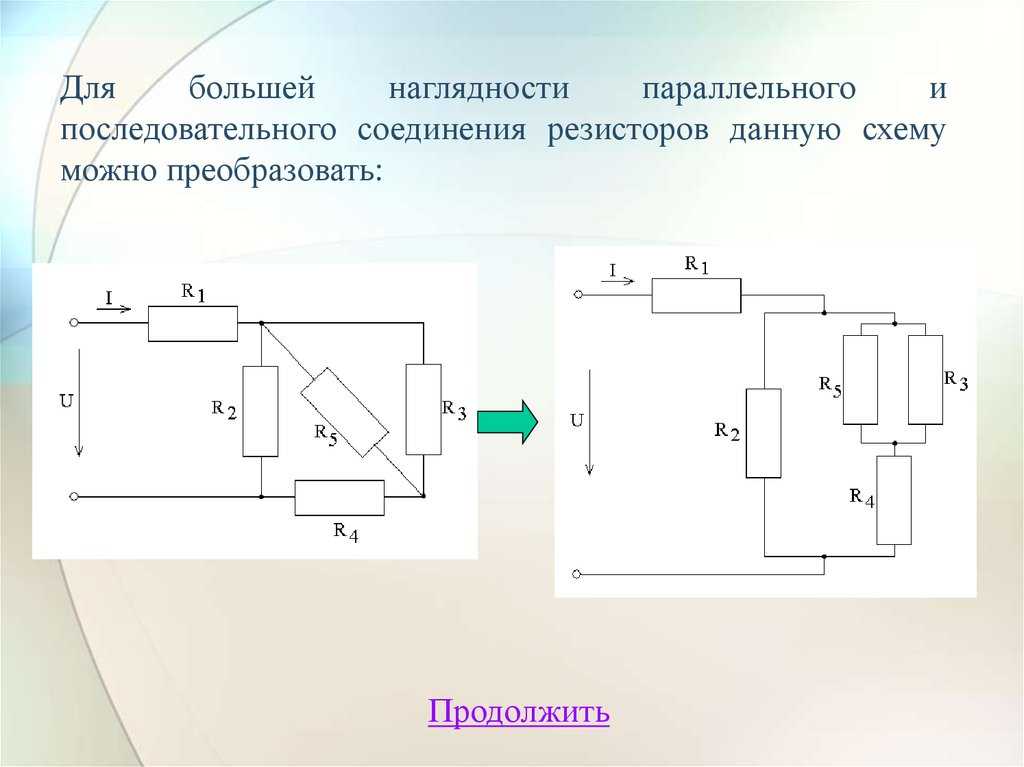 г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает
4,21 1Rp=1R1+1R2+1R3=11,00 Ом+16,00 Ом+113,0 Ом.1Rp=1R1+1R2+1R3=11,00 Ом+16,00 Ом+113,0 Ом.
Таким образом,
4,22 1Rp=1,00 Ом+0,1667 Ом+0,07692 Ом=1,2436 Ом.1Rp=1,00 Ом+0,1667 Ом+0,07692 Ом=1,2436 Ом.
Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.
Мы должны инвертировать это, чтобы найти полное сопротивление Rp.Rp. Это дает
4,23 Rp=11,2436 Ом=0,8041 Ом. Rp=11,2436 Ом=0,8041 Ом.
Общее сопротивление с правильным количеством значащих цифр Rp=0,804 Ом. Rp=0,804 Ом.
Обсуждение для (a)
RpRp, как и предполагалось, меньше наименьшего индивидуального сопротивления.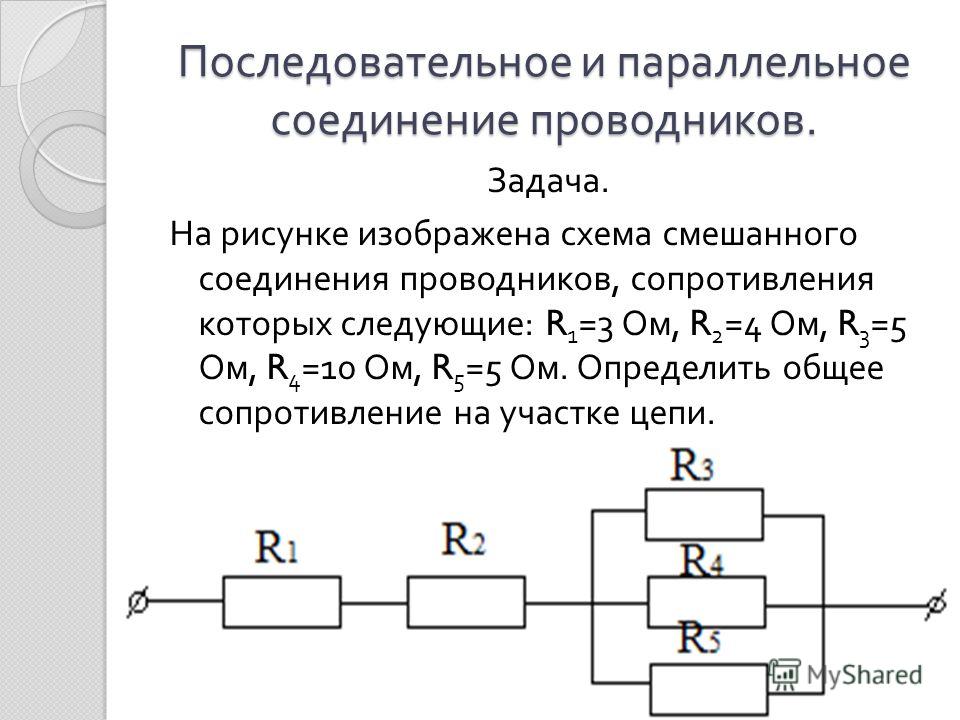
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив RpRp вместо полного сопротивления. Это дает
4,24 I=VRp=12,0 В0,8041 Ом=14,92 A.I=VRp=12,0 В0,8041 Ом=14,92 А. устройства, соединенные последовательно (см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
4,25 I1=VR1=12,0 В1,00 Ом=12,0 A.I1=VR1=12,0 В1,00 Ом=12,0 А. =12,0 В6,00 Ом=2,00 А
и
4,27 I3=VR3=12,0 В13,0 Ом=0,92 A.I3=VR3=12,0 В13,0 Ом=0,92 А.
Обсуждение для (c)
Общий ток представляет собой сумму отдельных токов.
4,28 I1+I2+I3=14,92 AI1+I2+I3=14,92 A
Это соответствует закону сохранения заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать P=V2RP=V2R, так как каждый резистор получает полное напряжение. Таким образом,
Давайте использовать P=V2RP=V2R, так как каждый резистор получает полное напряжение. Таким образом,
4,29 P1=V2R1=(12,0 В)21,00 Ом=144 Вт. P1=V2R1=(12,0 В)21,00 Ом=144 Вт. =24,0 WP2=V2R2=(12,0 В)26,00 Ом=24,0 Вт
и
4,31 P3=V2R3=(12,0 В)213,0 Ом=11,1 Вт.P3=V2R3=(12,0 В)213,0 Ом=11,1 Вт.
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбрав P=IVP=IV и введя суммарные выходы по току
4,32 P=IV=(14,92 А)(12,0 В)=179 W.P=IV=(14,92 А)(12,0 В)=179 Вт.
Обсуждение для (д)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт. закон сохранения энергии.
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.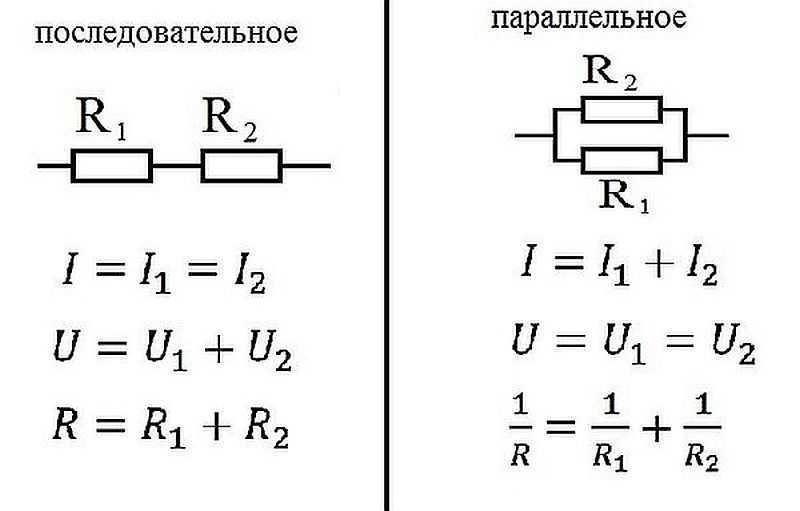
Основные характеристики резисторов, включенных параллельно
- Параллельное сопротивление определяется из 1Rp=1R1+1R2+1R3+…,1Rp=1R1+1R2+1R3+…, и оно меньше любого отдельного сопротивления в комбинации.
- К каждому резистору, подключенному параллельно, приложено одинаковое полное напряжение источника. Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.
- Параллельные резисторы не каждый получают общий ток, а скорее делят его.
Комбинации серий и параллелей
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.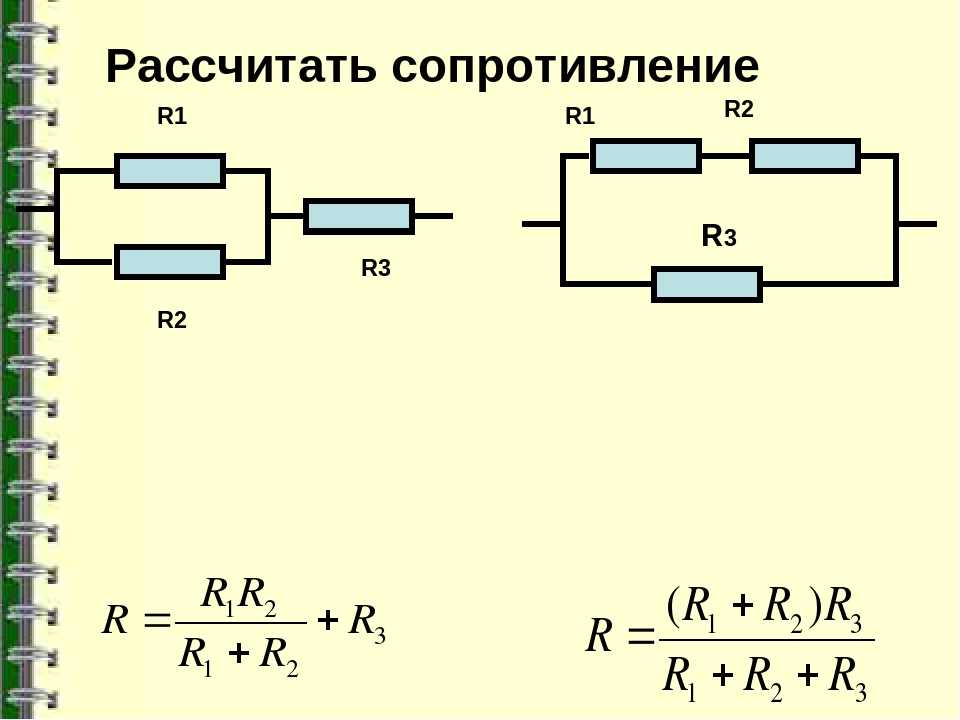
Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рис. 4.5. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс более трудоемкий, чем сложный.
Рисунок 4.5 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.
Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 4.6, также является наиболее информативной, поскольку она используется во многих приложениях. Например, R1R1 может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, включенным параллельно. R2R2 и R3R3 могут быть стартером и освещением салона.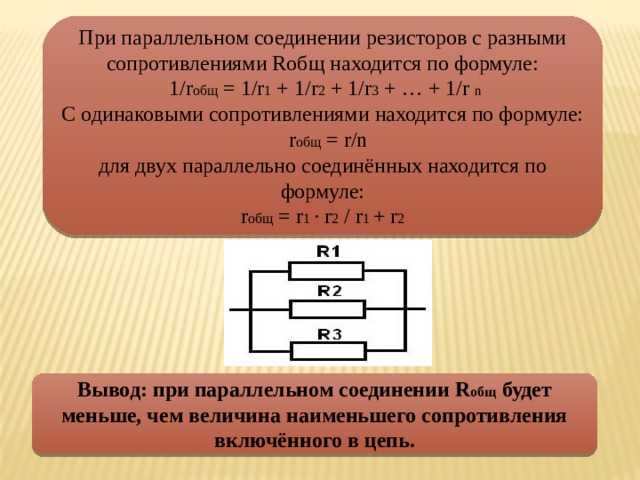 Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 4.3 Расчет сопротивления, падения IRIR, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рис. 4.6 показаны резисторы из двух предыдущих примеров, соединенные по-другому — комбинация последовательного и параллельного соединения. Можно считать R1R1 сопротивлением проводов, ведущих к R2R2 и R3.R3. а) Найдите полное сопротивление. (b) Каково падение IRIR в R1R1? (c) Найдите ток I2I2 через R2.R2. г) Какая мощность рассеивается на R2?R2?
Рисунок 4.6 Эти три резистора подключены к источнику напряжения таким образом, что R2R2 и R3R3 параллельны друг другу, а эта комбинация последовательно с R1.R1.
Стратегия и решение для (a)
Чтобы найти общее сопротивление, заметим, что R2R2 и R3R3 включены параллельно, а их комбинация RpRp последовательно с R1.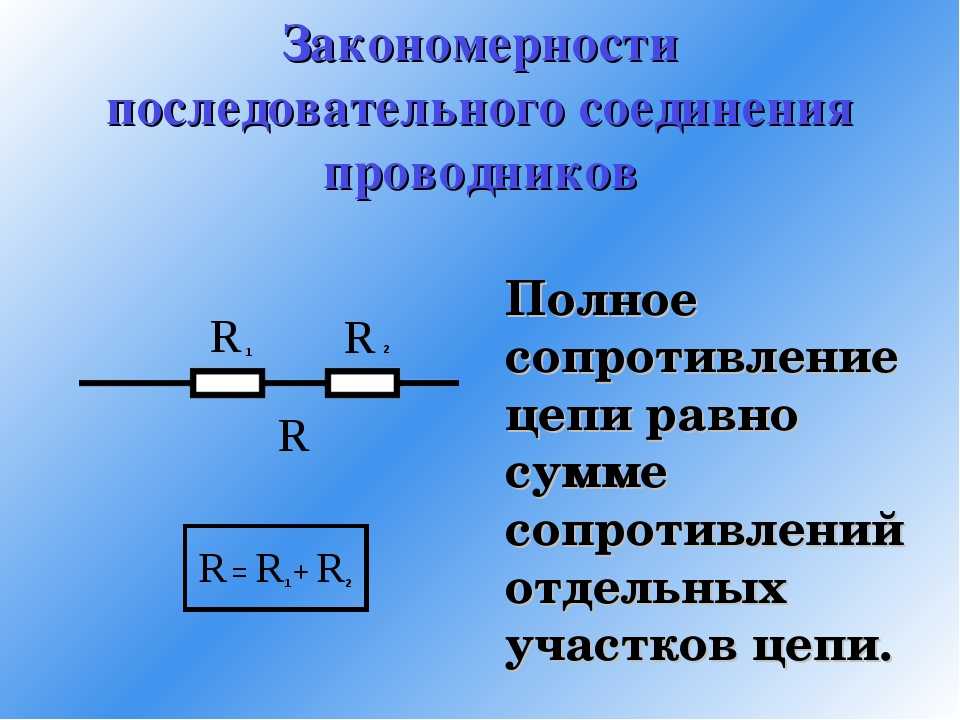 R1. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
R1. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
4,34 Rtot=R1+Rp.Rtot=R1+Rp.
Сначала находим RpRp, используя уравнение для параллельных резисторов и вводя известные значения
4,35 1Rp=1R2+1R3=16,00 Ом+113,0 Ом=0,2436 Ом1Rp=1R2+1R3=16,00 Ом+113,0 Ом=0,2436 Ом 4,11 Ом.
Таким образом, общее сопротивление равно
4,37 Rtot=R1+Rp=1,00Ω+4,11 Ω=5,11 ΩRtot=R1+Rp=1,00Ω+4,11 Ω=5,11 Ω
Обсуждение для (a) Стратегия и решение для (b) Чтобы найти падение IRIR в R1, R1, заметим, что полный ток II протекает через R1.R1. Таким образом, его падение IRIR равно 4,38 V1=IR1.V1=IR1. Мы должны найти II, прежде чем мы сможем вычислить V1. 4,39 I=VRtot=12,0 В5,11 Ом=2,35A.I=VRtot=12,0 В5,11 Ом=2,35A. Подставив это в приведенное выше выражение, мы получим 4,40 V1=IR1=(2,35 А)(1,00 Ом)=2,35 В. V1=IR1=(2,35 А)(1,00 Ом)=2,35 В. Обсуждение для (b) Напряжение, подаваемое на R2R2 и R3R3, меньше общего напряжения на величину V1.V1. При большом сопротивлении провода это может существенно повлиять на работу устройств, представленных R2R2 и R3.R3. Стратегия и решение для (c) Чтобы найти ток через R2, R2, мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение VpVp, потому что оно приложено к параллельной комбинации резисторов. Напряжение, подаваемое как на R2R2, так и на R3R3, уменьшается на величину V1,V1, поэтому оно равно 4,41 Vp=V-V1=12,0 В-2,35 В=9,65 В.Vp=V-V1=12,0 В-2,35 В=9,65 В. Теперь по закону Ома находим ток I2I2 через сопротивление R2R2. 4,42 I2=VpR2=9,65 V6,00 Ом=1,61 AI2=VpR2=9,65 V6,00 Ом=1,61 A Обсуждение для (c) он был подключен параллельно батарее в предыдущем примере с параллельной схемой. Стратегия и решение для (d) Мощность, рассеиваемая резистором R2R2, определяется как 4,43 P2=(I2)2R2=(1,61 А)2(6,00 Ом)=15,5 Вт.P2=(I2)2R2=(1,61 А)2(6,00 Ом)= 15,5 Вт. Обсуждение для (d) Мощность меньше 24,0 Вт, которые рассеивает этот резистор при параллельном подключении к источнику 12,0 В. Спланируйте эксперимент, чтобы проанализировать влияние на токи и разность потенциалов перестановки резисторов и изменений в источниках напряжения. Ваше экспериментальное исследование должно включать сбор данных по крайней мере для пяти различных сценариев перестановки резисторов (т. е. нескольких комбинаций последовательного и параллельного соединения) и трех сценариев с различными источниками напряжения. Одним из следствий этого последнего примера является то, что сопротивление в проводах уменьшает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IRIR в проводах также может быть значительным. Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи). То, что происходит в таких сильноточных ситуациях, показано на рис. 4.7. Устройство, представленное R3R3, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IRIR в проводах, представленных R1, R1, уменьшая напряжение на лампочке (которой является R2R2), которая затем заметно тускнеет. Рисунок 4.7 Почему при включении крупного электроприбора гаснет свет? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IRIR в проводах и снижает напряжение на светильнике. Можно ли любую произвольную комбинацию резисторов разбить на последовательные и параллельные комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательных и параллельных соединений. Нет, существует множество способов соединения резисторов, которые не являются комбинацией последовательного и параллельного соединения, включая контуры и соединения. В таких случаях правила Кирхгофа, которые будут введены в Правилах Кирхгофа, позволят вам проанализировать схему. Существует множество методов поиска параллельного сопротивления, которые мы рассмотрим в этой статье. В отличие от последовательных резисторов, резисторы, соединенные параллельно, имеют разные методы расчета эквивалентного сопротивления. Предположим, у нас есть два резистора R 1 и R 2 , как показано на рисунке 1. Мы знаем, что общий ток в параллельной цепи = сумма токов ветвей. Следовательно, [Latex] i = \frac{V} {R_{1}}+ \frac{V} {R_{2}} [/Latex] (потенциалы A и B одинаковы) Или, [Latex] i = V\left ( \frac{1} {R_{1}}+ \frac{1} {R_{2}} \right ) [/Latex] Теперь общий ток i = напряжение / эквивалентное сопротивление = V/R 9{-1} [/Latex] Метод расчета эквивалентного сопротивления для более чем двух резисторов аналогичен. На рисунке 2 изображена цепь, состоящая из n параллельно расположенных резисторов. Найдем эквивалентное сопротивление в этом случае. Мы знаем из закона Ома, 6 Итого сопротивление этой комбинации является промежуточным между чисто последовательным и чисто параллельным значениями (20,0 Ом (20,0 Ом и 0,804 Ом, 0,804 Ом соответственно), полученными для тех же резисторов в двух предыдущих примерах).0003
 V1. Полный ток II находится по закону Ома для цепи. То есть
V1. Полный ток II находится по закону Ома для цепи. То есть
Применение научных методов: набор для построения схемы (только для постоянного тока)
Практические выводы
Решение
Стратегии решения проблем с последовательными и параллельными резисторами
 Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.
Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее. Подробная информация — Lambda Geeks
Мы можем заменить значения в соответствии с требованиями схемы и получить желаемое эквивалентное сопротивление.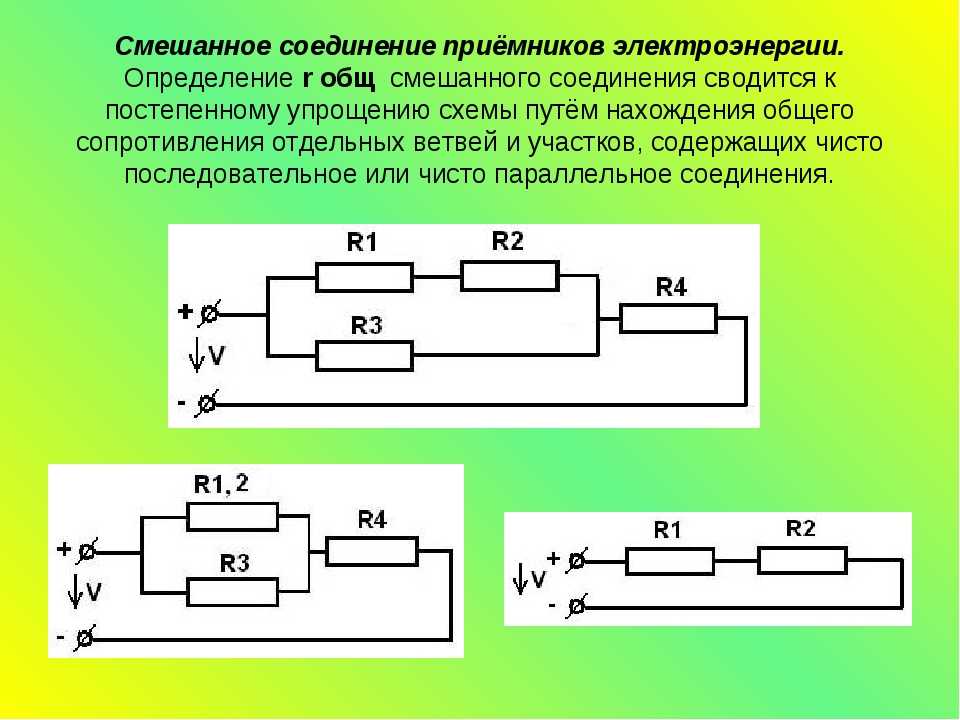
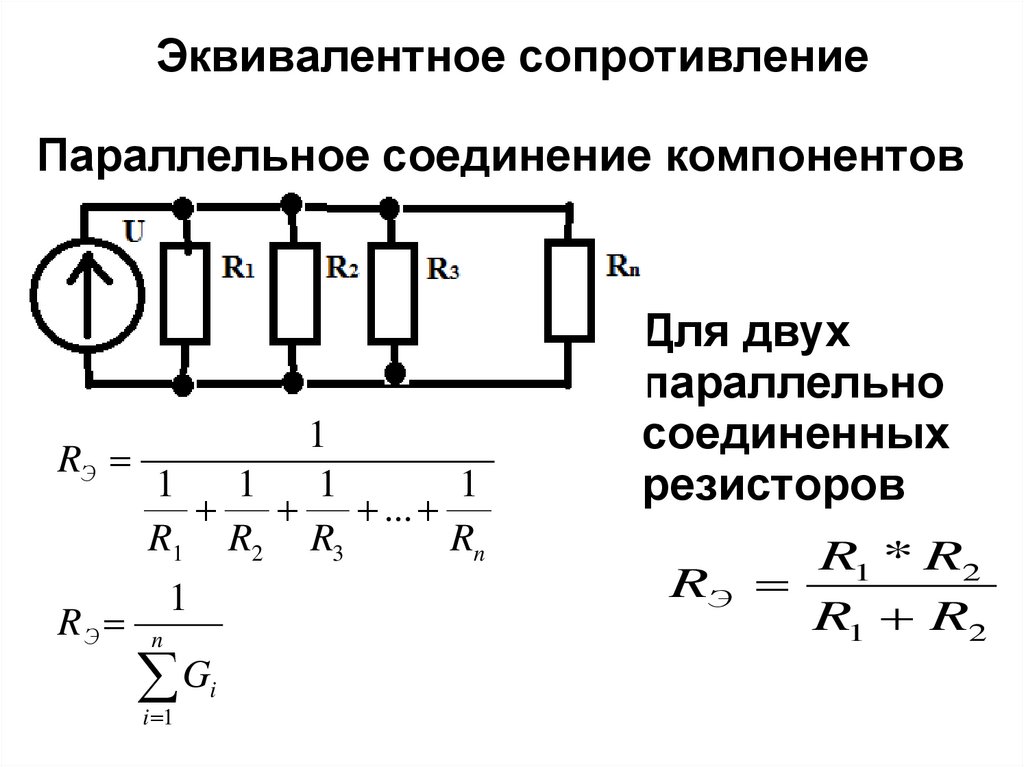
Параллельные сопротивления имеют несколько свойств в цепи. Наиболее важной особенностью параллельного сопротивления является то, что обратное эквивалентное сопротивление представляет собой сумму всех отдельных обратных сопротивлений.
Другие особенности параллельного сопротивления:
- Все резисторы имеют одинаковое напряжение, и оно равно напряжению узла
- Токи через резисторы суммируют чистый ток вне всего параллельного соединения.
- Значение эквивалентного сопротивления меньше любого резистора, присутствующего в цепи.
Подробнее….Одинаков ли ток при параллельном подключении: полная информация и ответы на часто задаваемые вопросы
Как параллельное сопротивление влияет на напряжение и ток? Нам известен тот факт, что эквивалентное сопротивление в параллельной схеме получается путем суммирования всех сопротивлений, обратных величине, и их обратного действия.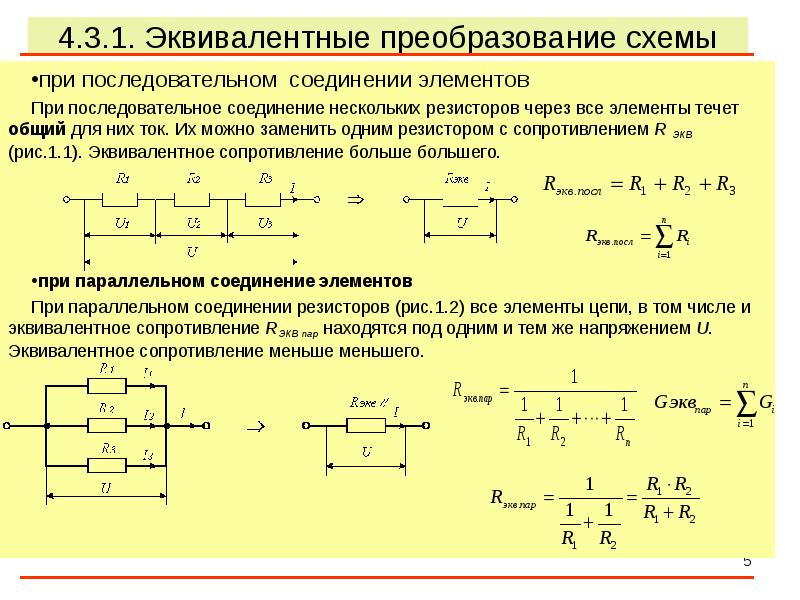 Это сопротивление определяет ток в цепи.
Это сопротивление определяет ток в цепи.
Предположим, мы строим электрическую цепь с параллельным соединением резисторов R A и R B с источником напряжения V. Напряжение источника будет общим для обоих резисторов и падение напряжения на обоих из них будет V. Ток на пути R A будет V/R A , а ток на пути R A будет V/R B .
Подробнее….Одинаково ли напряжение при параллельном подключении: полная информация и ответы на часто задаваемые вопросы
Почему эквивалентное сопротивление при параллельном подключении меньше, чем отдельные сопротивления?Параллельно заряд, вытекающий из источника, когда он достигает узла, имеет возможность двигаться в любую ветвь. Так что от источника течет большое количество зарядов. Поэтому ток увеличивается.
Из закона Ома мы знаем, что V = IR
Напряжение будет одинаковым для всех параллельных ветвей.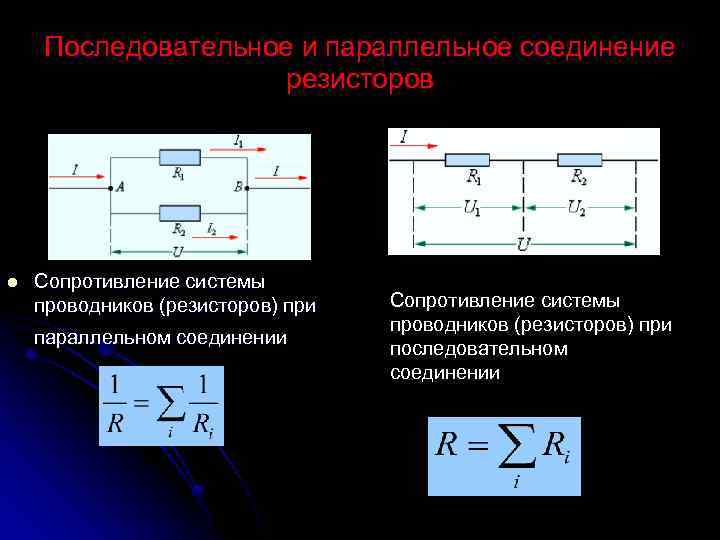 Таким образом, ток растет с ростом ветвей (т.е. при подключении большего сопротивления). Единственный способ, при котором напряжение может оставаться неизменным при уменьшении сопротивления. Поэтому сопротивление снижается.
Таким образом, ток растет с ростом ветвей (т.е. при подключении большего сопротивления). Единственный способ, при котором напряжение может оставаться неизменным при уменьшении сопротивления. Поэтому сопротивление снижается.
Читайте также… Что такое падение напряжения в параллельной цепи: как найти, примеры проблем и подробные факты
Численные задачи Рассчитайте эквивалентное параллельное сопротивление для этой бесконечной лестницы, показанной на рисунке 3Для этой бесконечной лестницы сопротивлений мы можем сказать, что эквивалентное сопротивление Req между точками P и Q равно сопротивлению остальной цепи. . Поэтому [Latex]R_{eq} = 2+ 1|| R_{eq}[/Latex]
Итак, [Latex] R_{eq} = 2+ \frac {1\times R_{eq}}{1 + R_{eq}} = \frac{ 2 + 3R_{ экв} }{1 + R_{экв} } [/латекс]
9009{2} – 2R_{eq} -2 = 0 [/Latex]
Решая приведенное выше уравнение, мы получаем [Latex] R_{eq} = 1 \pm \sqrt{3}\; ом [/Latex]
Пренебрегая отрицательной величиной, мы можем сказать [Latex] R_{eq} = 1 + \sqrt{3}\; Ом [/Latex]
Это требуемое эквивалентное сопротивление .
Теперь [латекс] R_{eq} = 4 + 4 + \frac{ 15R }{ 15 + R} = 8 + \frac{ 15R } { 15 + R} = \frac{ 120 + 23 R} { 15+R}[/Latex]. Далее у нас снова параллельная сетка. Таким образом, R eq теперь равен [Latex] 14\; ||\; \frac{ 120 + 23 R}{ 15 + R} = \frac{ 14 \times \frac{ 120 + 23 R}{ 15 + R} }{ 14 + \frac{ 120 + 23 R}{ 15 + R} } = \frac{ 14 \left (120 + 23 R \right )}{ 330 + 37R} [/Latex]. Окончательная сетка представляет собой еще одно последовательное соединение, которое дает R eq как [Latex] 5 + 3 + \frac{ 14 \left (120 + 23 R \right )}{ 330 + 37R} = 15 [/Latex] Ом. Решив это, мы получим R = 10 Ом.
Каково будет эквивалентное сопротивление Req для цепи, изображенной на рисунке 5.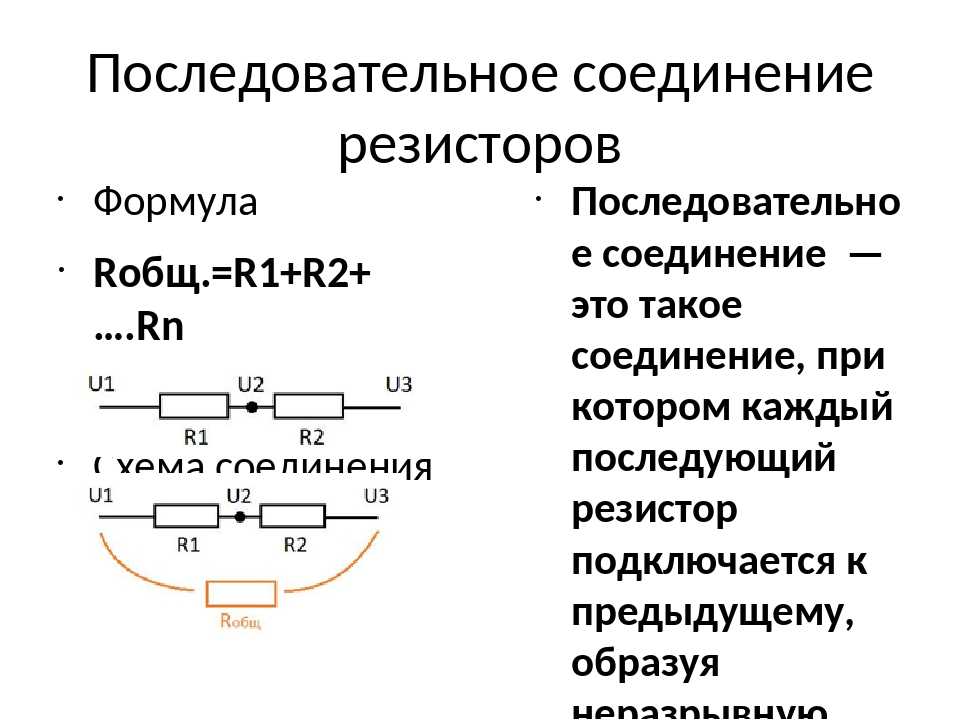
Мы можем перерисовать приведенную выше схему как изображение 5. Таким образом, для крайне правой сетки R eq = 4+6 = 10 Ом. Теперь у нас есть 3 параллельных резистора для правой сетки и 2 параллельных резистора для верхней сетки, как показано на 5.1.
Эквивалентное сопротивление для правой сетки [Latex] = \frac{10 \times 15\times 30}{ 10\times 15 +15\times 30 + 10\times 30} = 6\; ом[/латекс].
Эквивалентное сопротивление для верхней сетки [Latex] = \frac{ 20\times 5}{ 20 + 5} = 4\; ом[/латекс]. Теперь мы сократили систему до простой последовательной цепи с тремя резисторами 1 Ом, 4 Ом и 6 Ом, как показано в 5.2. Таким образом, окончательный R eq равен [Latex] 1 + 4 + 6 = 11 \; ом[/латекс].
Найдите эквивалентное сопротивление в приведенной ниже цепи: V S = 12 В, R 1 = 2,5 Ом, R 2 = 2 Ом, R 3 = 1,5 Ом, R 4 = 3 Ом, R 5 = 5 Ом и R 6 = 3,25 Ом.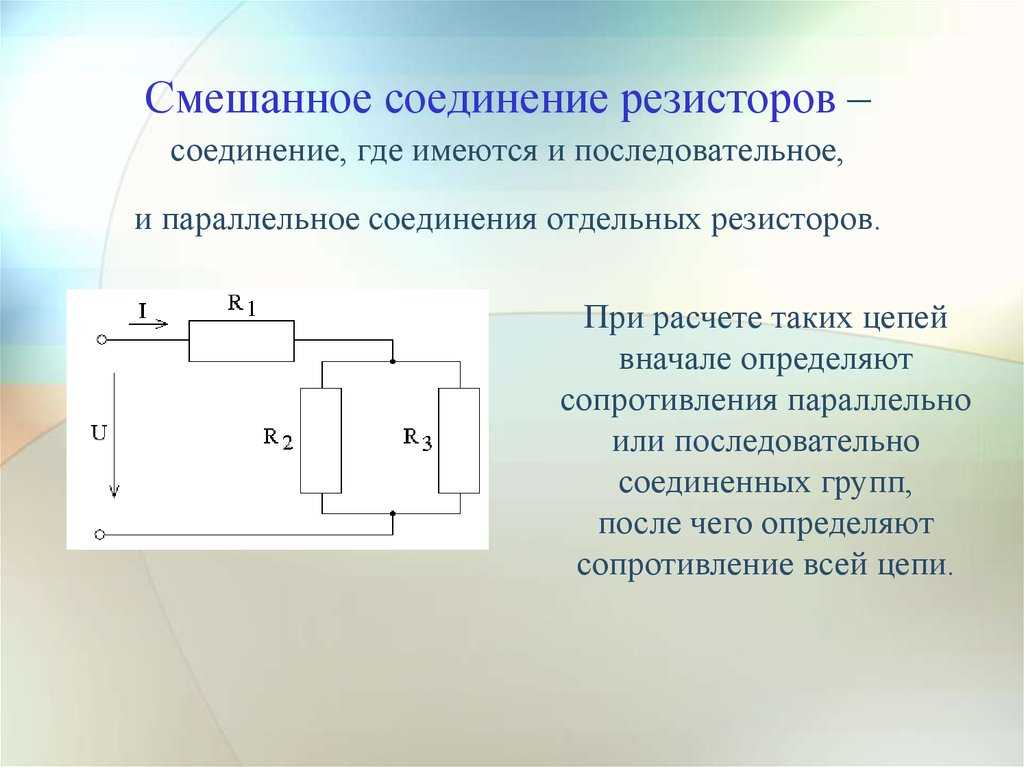
Упрощенная схема для изображения 6 показана на 6.1. Найдем эквивалентное сопротивление самой внутренней сетки. Таким образом, R eq для сетки с R 4 и R 5 равно [Latex] \frac{ R_{4} \times R_{5} }{ R_{4} + R_{5} } = \ frac{5 \times 3}{5 + 3} = 1,875\; ом[/латекс].
Теперь у нас есть R 3 и 1,875 Ом последовательно. Итак, [латекс] R_{экв} = 1,5+ 1,875 = 3,375\; ом[/латекс]. Это сопротивление параллельно R 2 . Итак, теперь [Latex] R_{eq} = \frac{2\times 3,375}{2 + 3,375} = 1,25\; ом[/латекс]. Наконец, у нас есть это сопротивление последовательно с R 1 и R 6 . Следовательно, [Latex] R_{eq} = \left ( 2,5 + 3,25 + 1,25 \right ) = 7\; ом[/латекс]. Это эквивалентное сопротивление цепи.
17,5 Параллельные резисторы | Электрические цепи
17.5 Параллельные резисторы (ESAFK)
Когда мы добавляем резисторы параллельно цепи:
Существует больше путей для протекания тока, что обеспечивает разделение тока по разным пути .

Напряжение то же на резисторах. Напряжение на аккумуляторе в цепи равно напряжению на каждом из параллельных резисторов:
\[{V}_{\text{батарея}} = {V}_{1} = {V}_{2} = {V}_{3} \ldots\]Сопротивление протеканию тока уменьшается . Общее сопротивление, \({R}_{P}\), дано автор:
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
При параллельном соединении резисторов начальная и конечная точки для всех резисторов одинаковы. Эти
точки имеют одинаковую потенциальную энергию, поэтому разность потенциалов между ними одинакова независимо от того, что
поставить между ними. Вы можете иметь один, два или несколько резисторов между двумя точками, разность потенциалов будет
не изменить. Вы можете игнорировать любые компоненты, находящиеся между двумя точками в цепи, при вычислении разницы
между двумя точками.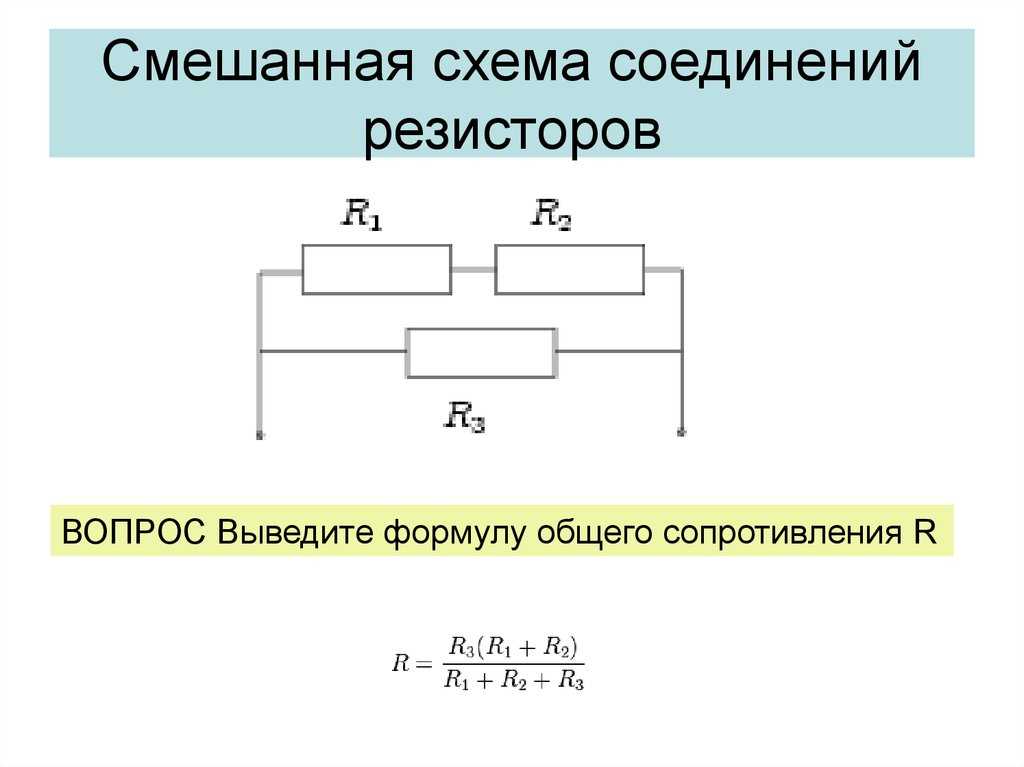
Посмотрите на следующие электрические схемы. Аккумулятор во всех случаях одинаков, меняется только количество резисторов. добавляются между точками, отмеченными черными точками. Если бы мы измерили разность потенциалов между две точки в этих схемах, мы получили бы один и тот же ответ для всех трех случаев.
Давайте посмотрим на два резистора, включенных параллельно. Когда вы строите цепь, вы используете провода, и вы можете думаю, что измерение напряжения в разных местах проводов будет иметь значение. Это неправда. разность потенциалов или измерение напряжения будут отличаться только в том случае, если вы измеряете другой набор компонентов. Все точки на проводах, между которыми нет компонентов схемы, дадут вам одинаковые измерения.
Все три измерения, показанные на рисунке ниже (т. е. A–B, C–D и E–F), дадут вам
одинаковое напряжение. Между различными точками измерения слева нет компонентов, поэтому
изменение потенциальной энергии. Точно то же самое относится к различным точкам справа. Когда вы измеряете
разность потенциалов между точками слева и справа вы получите тот же ответ.
Точно то же самое относится к различным точкам справа. Когда вы измеряете
разность потенциалов между точками слева и справа вы получите тот же ответ.
Рабочий пример 7: Напряжение I
Рассмотрим следующую электрическую схему:
Какое напряжение на резисторе в показанной цепи?
Проверьте, что у вас есть и единицы
У нас есть схема с батареей и одним резистором. Мы знаем напряжение на аккумуляторе. Мы хотим найти это напряжение на резисторе.
\[{V}_{\text{батарея}} = \text{2}\text{V}\]
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях составные части.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
В цепи есть только один компонент — резистор.
\[{V}_{\text{всего}}={V}_{1}\]
Это означает, что напряжение на батарее равно напряжению на резисторе.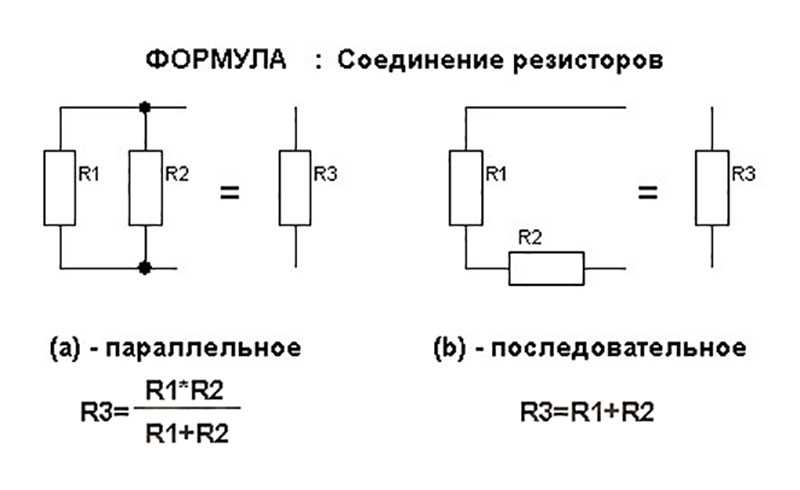
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} = {V} _ {1} \\ {V}_{1} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 8: Напряжение II
Рассмотрим эту цепь:
Каково напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы измерения
У нас есть схема с батареей и двумя резисторами. Мы знаем напряжение на аккумуляторе и одном из резисторы. Мы хотим найти это напряжение на резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {2} \ text {V} \\ {V}_{B} & = \text{1}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
компоненты, которые находятся в последовательном соединении.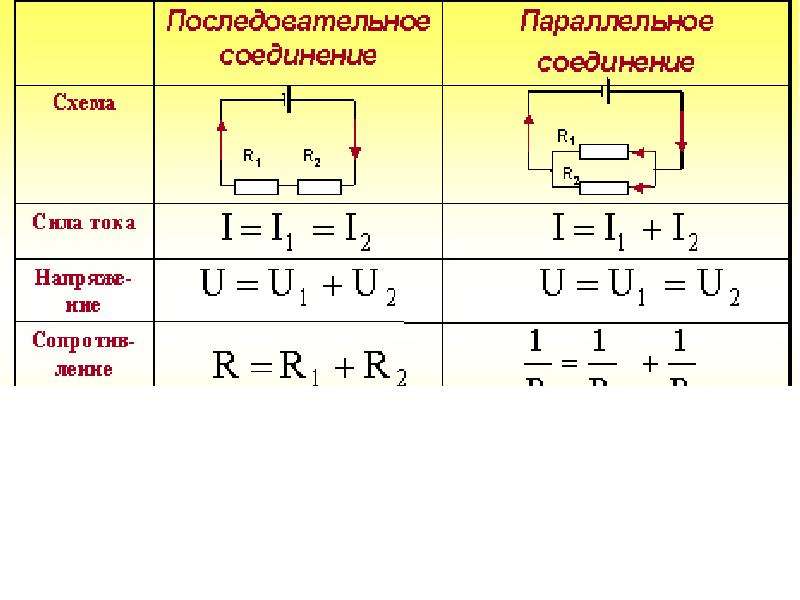
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V}_{\text{всего}} = {V}_{A} + {V}_{B}\]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\\\ {V} _ {\ text {батарея}} & = {V} _ {1} + {V} _ {\ text {резистор}} \\ \text{2}\text{V} & = {V}_{1} + \text{1}\text{V} \\ {V}_{1} & = \text{1}\text{V} \конец{выравнивание*}
Рабочий пример 9: Напряжение III
Рассмотрим принципиальную схему:
Каково напряжение на неизвестном резисторе в показанной цепи?
Проверьте, что у вас есть и единицы измерения
У нас есть схема с батареей и тремя резисторами.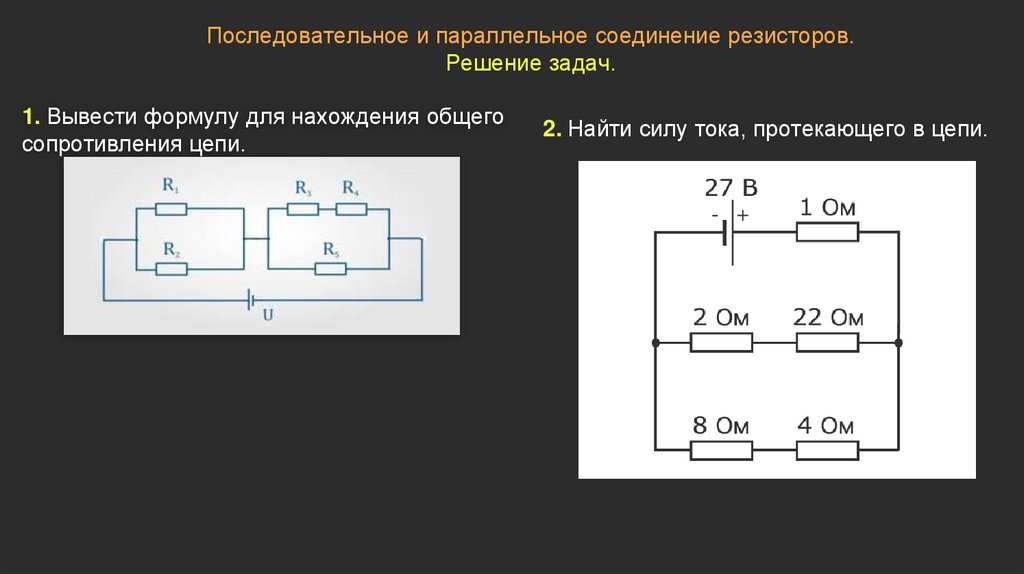 Мы знаем напряжение на аккумуляторе и двух
резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
Мы знаем напряжение на аккумуляторе и двух
резисторы. Мы хотим найти это напряжение на неизвестном резисторе.
\начать{выравнивать*} {V} _ {\ text {батарея}} & = \ text {7} \ text {V} \\ {V} _ {\ text {известно}} & = {V} _ {A} + {V} _ {C} \\ & = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на аккумуляторе должно быть равно общему напряжению на всех остальных цепях. компоненты, которые находятся в последовательном соединении.
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Общее напряжение в цепи равно сумме напряжений на отдельных резисторах
\[{V} _ {\ text {всего}} = {V} _ {B} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {B} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{B} + \text{5}\text{V} \\ {V}_{B} & = \text{2}\text{V} \конец{выравнивание*}
Рабочий пример 10: Напряжение IV
Рассмотрим принципиальную схему:
Каково напряжение на параллельной комбинации резисторов в показанной цепи? Подсказка: остальное
схема такая же, как и в предыдущей задаче.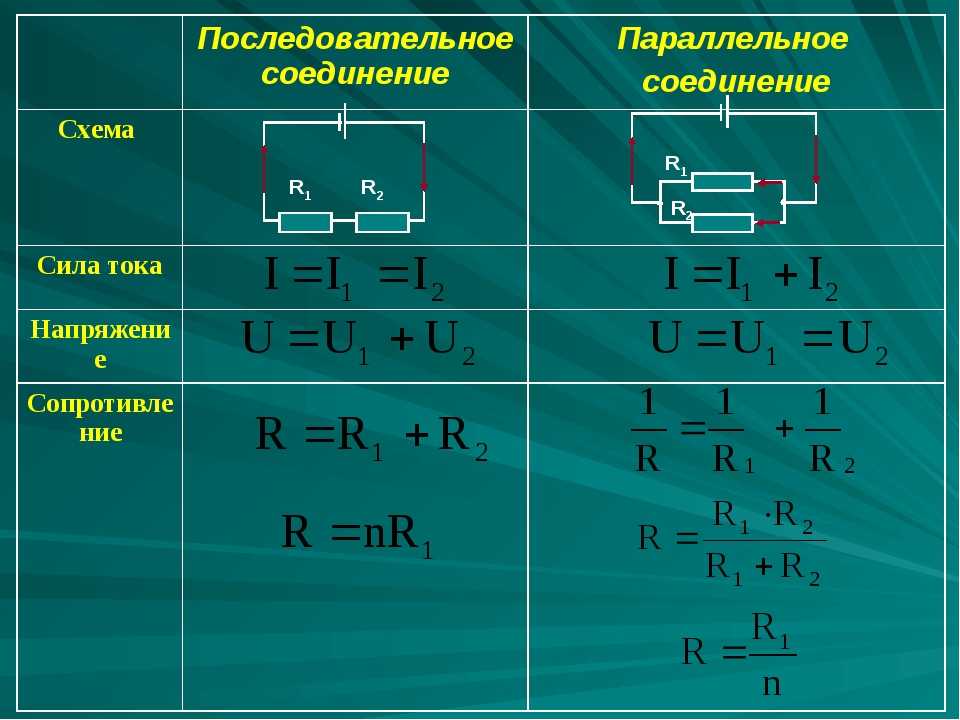
Быстрый ответ
Схема такая же, как в предыдущем примере, и мы знаем, что разница напряжений между двумя точками в схема не зависит от того, что находится между ними, поэтому ответ такой же, как и выше \({V}_{\text{parallel}} = \text{2}\text{V}\).
Проверьте, что у вас есть и единицы измерения — подробный ответ
У нас есть схема с батареей и пятью резисторами (два последовательно и три параллельно). Мы знаем напряжение на аккумуляторе и двух резисторах. Мы хотим найти это напряжение на параллельном резисторы, \({V}_{\text{параллельные}}\).
\начать{выравнивать*} {V} _ {\ text {батарея}} = \ text {7} \ text {V} \\ {V}_{\text{известно}} = \text{1}\text{V} + \text{4}\text{V} \конец{выравнивание*}
Применимые принципы
Мы знаем, что напряжение на батарее должно быть равно общему напряжению во всех других цепях
составные части.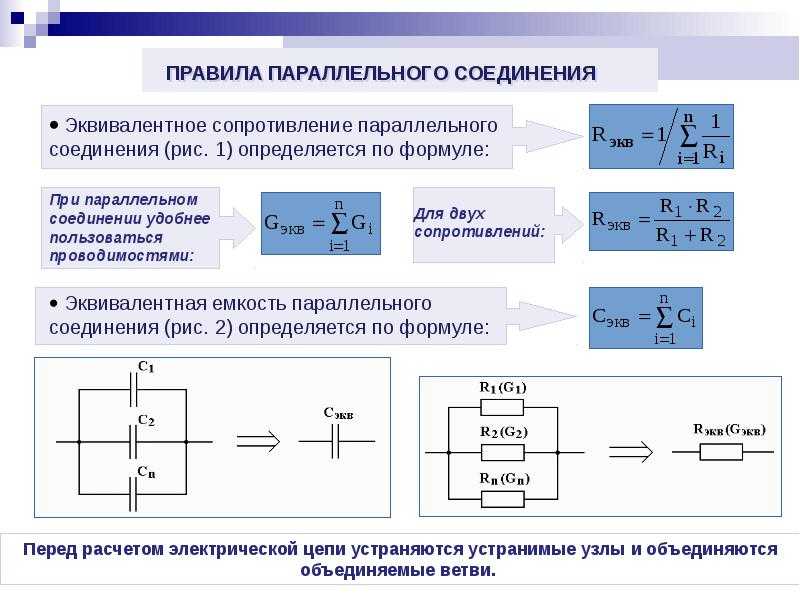
\[{V} _ {\ text {батарея}} = {V} _ {\ text {всего}} \]
Напряжения складываются только алгебраически для компонентов, соединенных последовательно. Параллельные резисторы можно рассматривать как один компонент, который последовательно с другими компонентами, а затем напряжения могут быть добавлены.
\[{V} _ {\ text {всего}} = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \]
Использование соотношения между напряжением на батарее и полным напряжением на резисторах
\начать{выравнивать*} {V} _ {\ text {батарея}} & = {V} _ {\ text {всего}} \\ {V} _ {\ text {батарея}} & = {V} _ {\ text {параллельно}} + {V} _ {\ text {известно}} \\ \text{7}\text{V} & = {V}_{\text{параллельно}} + \text{5}\text{V} \\ {V} _ {\ text {параллельно}} & = \ text {2} \ text {V} \конец{выравнивание*}
temp text В отличие от последовательного случая, когда мы добавляем резисторы параллельно, мы создаем еще путей вдоль
какой ток может течь.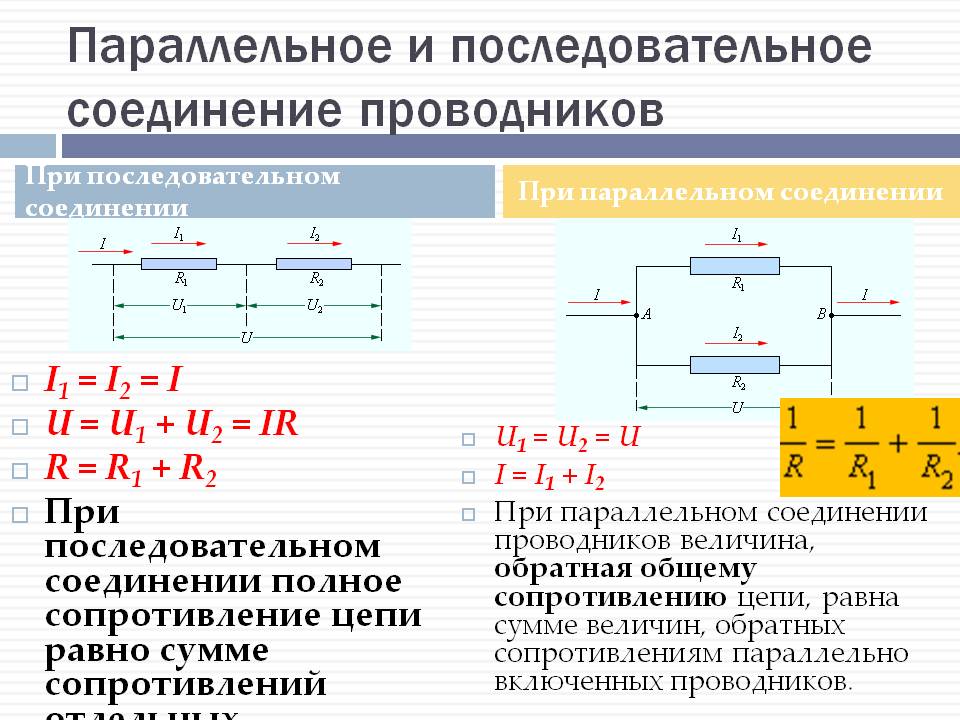 Делая это, мы уменьшаем общее сопротивление цепи!
Делая это, мы уменьшаем общее сопротивление цепи!
Взгляните на диаграмму ниже. Слева у нас такая же схема, как и в предыдущем разделе с аккумулятором и резистор. Амперметр показывает силу тока \(\text{1}\) \(\text{A}\). Справа мы добавили второй резистор параллельно первому резистору. Это увеличило количество путей (ответвлений), по которым может пройти заряд. по цепи — общее сопротивление уменьшилось. Вы видите, что ток в цепи вырос. Также обратите внимание, что ток в разных ветвях может быть разным.
Общее сопротивление ряда параллельно соединенных резисторов НЕ является суммой отдельных сопротивлений, поскольку общее сопротивление уменьшается с увеличением количества путей для тока. Общее сопротивление для параллельных резисторов дано автор:
\[\frac{1}{{R}_{P}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\ldots\ ] Давайте рассмотрим случай, когда у нас есть два резистора, включенных параллельно, и выясним, каким будет конечное сопротивление. Эта ситуация показана на диаграмме ниже:
Эта ситуация показана на диаграмме ниже:
Применяя формулу для полного сопротивления имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{Там всего два резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} \\ & \text{Сложите дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}}{{R}_{2 }} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}}{{R}_{1}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}}{{R}_{1}{R}_{2}} + \frac{{R} _{1}}{{R}_{1}{R}_{2}} \\ & \text{Переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2} + {R}_{1}}{{R}_{1}{R}_{2} } \\ \frac{1}{{R}_{P}} & = \frac{{R}_{1} + {R}_{2}}{{R}_{1}{R}_{2} } \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}}{{R}_{1} + {R}_{2}} \конец{выравнивание*}Теперь для любых двух резисторов, включенных параллельно, мы знаем, что
\[{R}_{P} = \frac{\text{произведение сопротивлений}}{\text{сумма сопротивлений}} = \frac{{R}_{1}{R}_{2}}{ {Р}_{1} + {Р}_{2}}\]Делители тока
Цель
Проверьте, что происходит с током и напряжением в последовательных цепях при добавлении дополнительных резисторов.
Аппарат
Аккумулятор
Вольтметр
Амперметр
Провода
Резисторы
Метод
Подключите каждую цепь, показанную ниже
Измерьте напряжение на каждом резисторе в цепи.
Измерьте ток до и после каждого резистора в цепи, а также до и после параллельного резистора. ветви.
Результаты и выводы
Сравните токи через отдельные резисторы друг с другом.
Сравните сумму токов через отдельные резисторы с током перед параллельным ветви.

Сравните различные измерения напряжения на параллельных резисторах.
Рабочий пример 11: Параллельные резисторы I
Цепь содержит два резистора, включенных параллельно. Резисторы имеют значения сопротивления \(\text{15}\) \(\text{Ω}\) и \(\text{7}\) \(\text{Ω}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно вычислить общую сопротивление. Значения двух резисторов указаны в правильных единицах, Ом.
Применять соответствующие принципы
Было показано, что общее сопротивление резисторов, включенных параллельно, представляет собой произведение сопротивлений, деленное на сумма. Мы можем использовать
\[{R}_{P} = \frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}\]
9{2}}{\текст{22}\текст{Ом}} \\ & = \text{4,77}\text{ Ом} \конец{выравнивание*}Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{4,77}\) \(\text{Ом}\)
Рабочий пример 12: Параллельные резисторы II
Мы добавляем третий параллельный резистор к конфигурации (настройке) в предыдущем примере.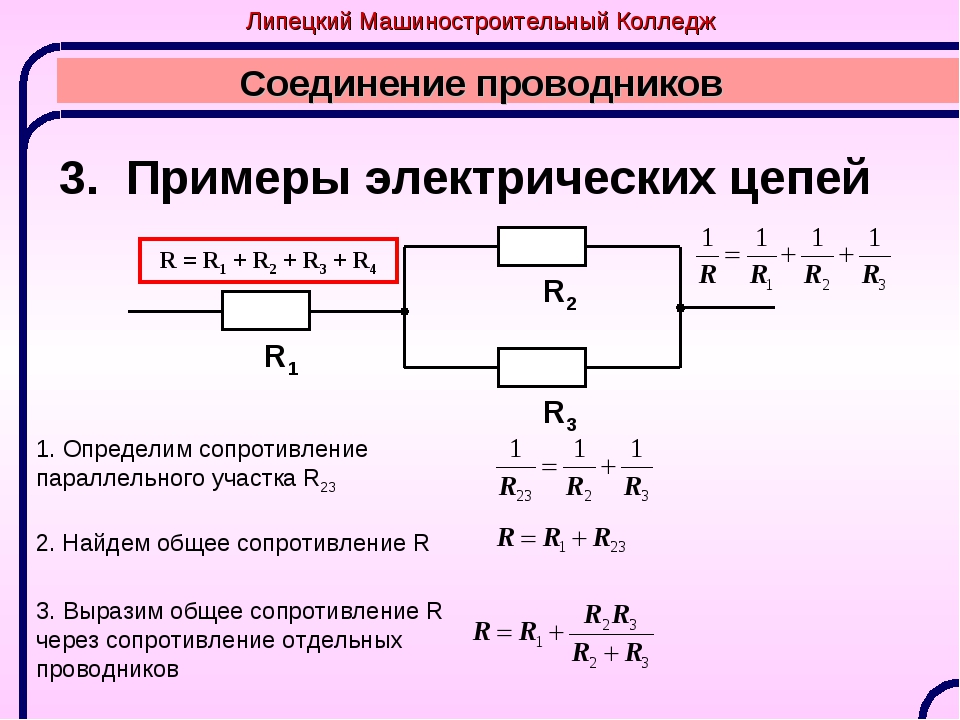 Дополнительный
резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Дополнительный
резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\).
Какое общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Применить соответствующие принципы
Общее сопротивление для параллельных резисторов указано как
\[\frac{1}{{R}_{P}} = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots\ ]
У нас есть три резистора, и мы теперь сопротивления. В данном случае имеем:
\начать{выравнивать*} \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \ldots \\ & \text{три резистора} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} + \frac{1}{{R}_{2}} + \frac{1 }{{R}_{3}} \\ & \text{сложить дроби} \\ \frac{1}{{R}_{P}} & = \frac{1}{{R}_{1}} \times \frac{{R}_{2}{R}_{3}} {{R}_{2}{R}_{3}} + \frac{1}{{R}_{2}} \times \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{3}} + \frac{1}{{R}_{3} } \times \frac{{R}_{1}{R}_{2}}{{R}_{1}{R}_{2}} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3}}{{R}_{1}{R}_{2}{ Р}_{3}} + \frac{{R}_{1}{R}_{3}}{{R}_{1}{R}_{2}{R}_{3}} + \frac{{R}_{ 1}{R}_{2}}{{R}_{1}{R}_{2}{R}_{3}} \\ & \текст {переставить} \\ \frac{1}{{R}_{P}} & = \frac{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + { Р}_{2}{Р}_{3}}{{Р}_{1}{Р}_{2}{Р}_{3}} \\ {R}_{P} & = \frac{{R}_{1}{R}_{2}{R}_{3}}{{R}_{2}{R}_{3} + {R}_{1}{R}_{3} + {R}_{2}{R}_{3}} \\ {R}_{P} & = \frac{\left(\text{15}\text{Ω} \right)\left(\text{7}\text{Ω} \right)\left(\text{3}\text{ Ω} \right)}{\left(\text{7}\text{ Ω} \right)\left(\text{3}\text{ Ω} \right) + \left(\text{15}\text{ Ω} \right)\left(\text{3}\text{ Ω}\right) + \left(\text{7}\text{ Ω} \right)\left(\text{15}\text{ Ω}\right)} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {21 {\ Omega} ^ {2} + 45 {\ Omega} ^ {2} + 105 {\ Omega} ^ { 2}} \\ {R} _ {P} & = \ frac {315 {\ Omega} ^ {3}} {171 {\ Omega} ^ {2}} \\ {R}_{P} & = \text{1,84}\text{ Ом} \конец{выравнивание*}
Укажите окончательный результат
Суммарное сопротивление резисторов, включенных параллельно, равно \(\text{1,84}\) \(\text{Ом}\)
При расчете сопротивления для сложных конфигураций резисторов можно начать с любой комбинации двух
резисторы (последовательно или параллельно) и рассчитайте их общее сопротивление.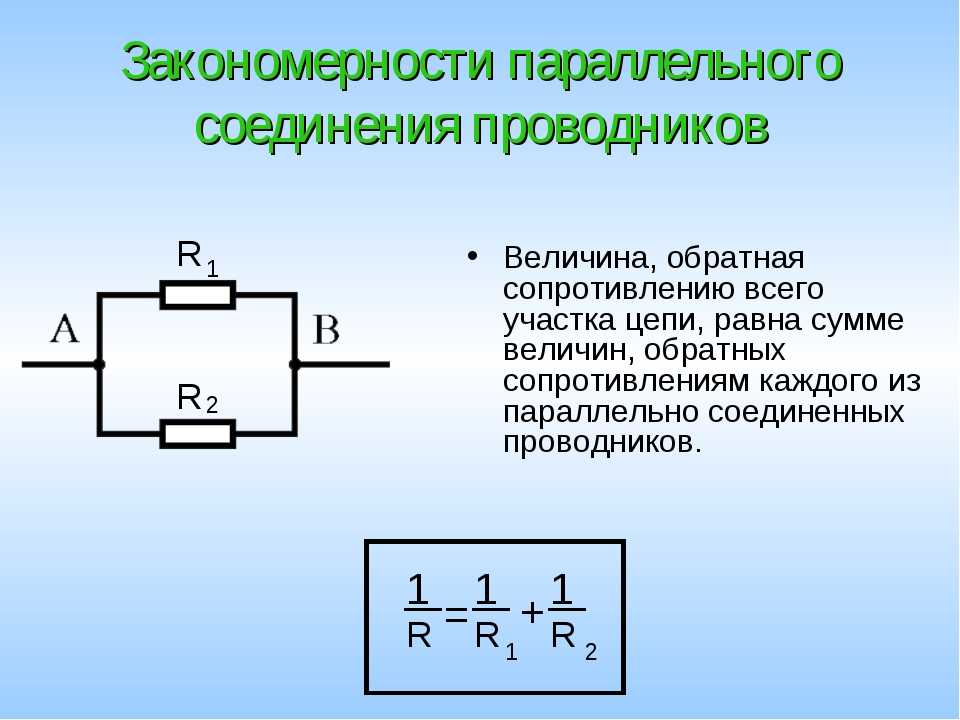 Затем вы можете заменить их одним
резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим
резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь
использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Затем вы можете заменить их одним
резистор, который имеет общее сопротивление, которое вы рассчитали. Теперь используйте этот новый резистор в сочетании с любым другим
резистор и повторяйте процесс, пока не останется только один резистор. В приведенном выше примере мы могли бы просто иметь
использовали ответ из первого примера параллельно с новым резистором, и мы получили бы тот же ответ.
Рабочий пример 13: Параллельные резисторы III
Мы добавляем третий параллельный резистор к первой параллельной рабочей конфигурации (настройка). Дополнительный резистор имеет сопротивление \(\text{3}\) \(\text{Ом}\)
Каково общее сопротивление в цепи?
Проанализируйте вопрос
Нам говорят, что резисторы в цепи находятся в параллельной цепи и что нам нужно рассчитать общую сопротивление. Значение дополнительного резистора указано в правильных единицах, Ом.
Примените соответствующие принципы
Мы можем поменять местами резисторы без изменения схемы:
Мы уже рассчитали общее сопротивление двух резисторов в пунктирной рамке, равное \(\text{4,77}\)
\(\текст{Ω}\).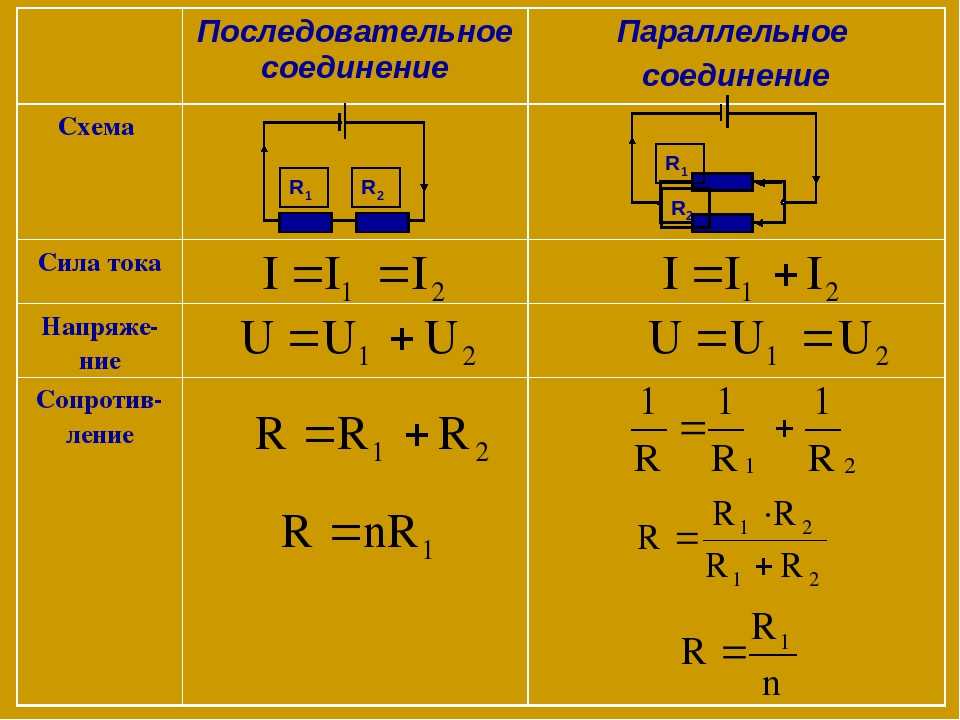


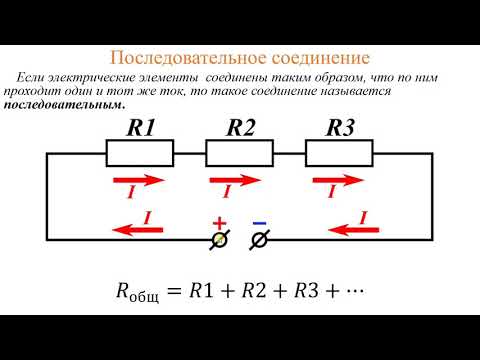
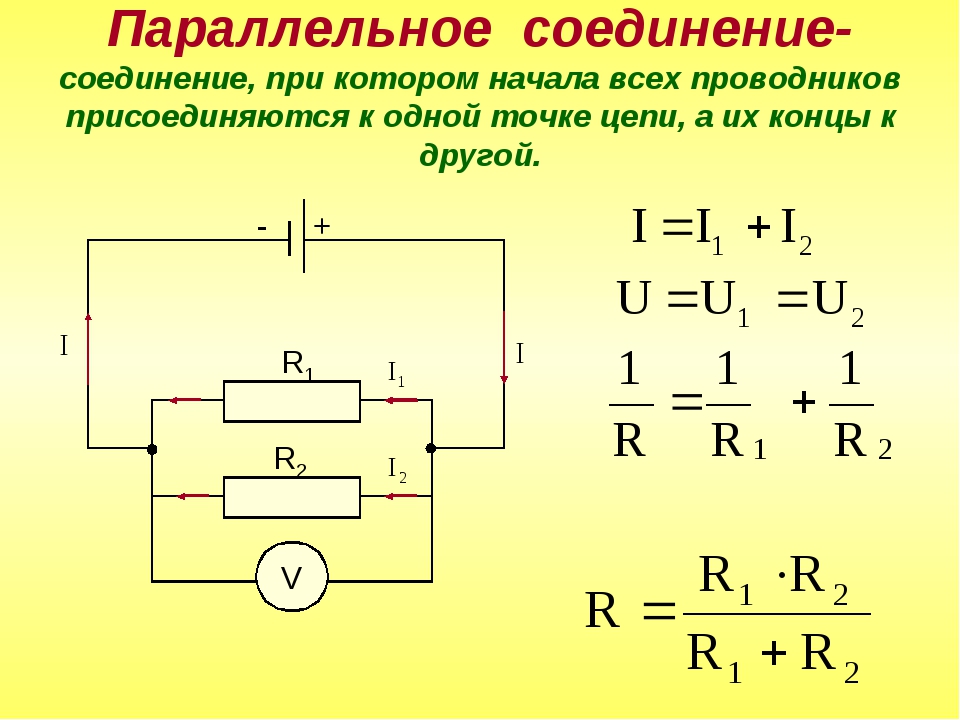 Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.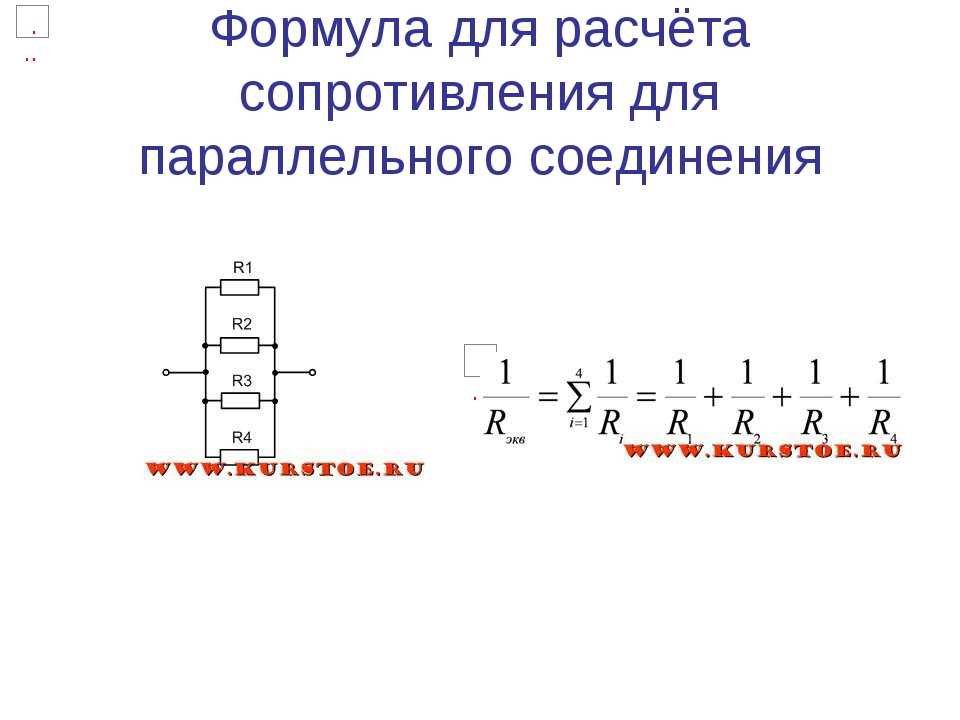
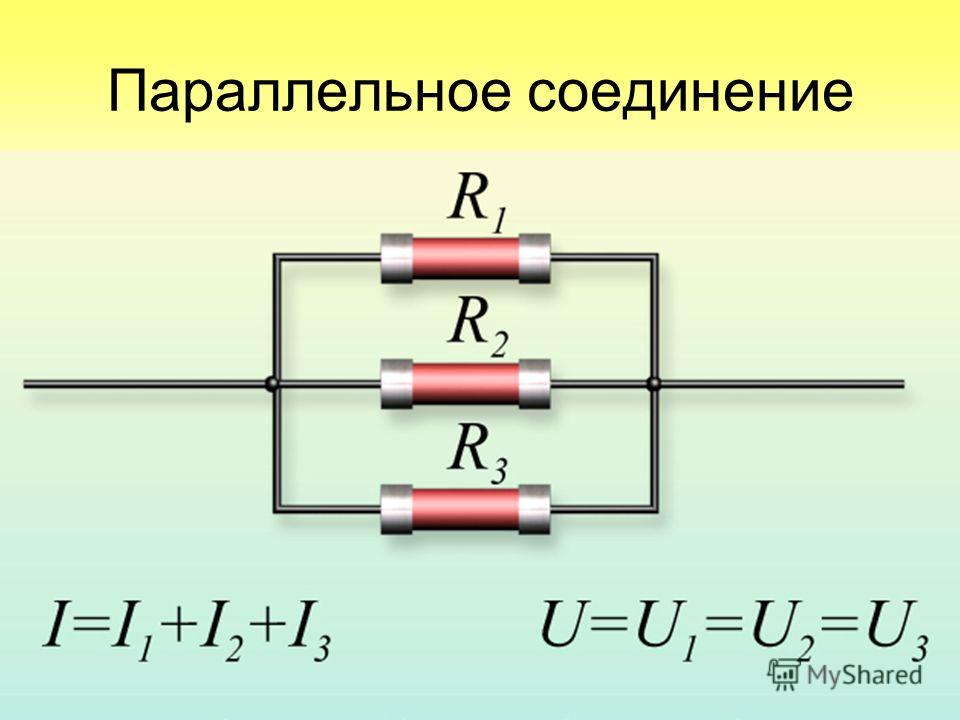
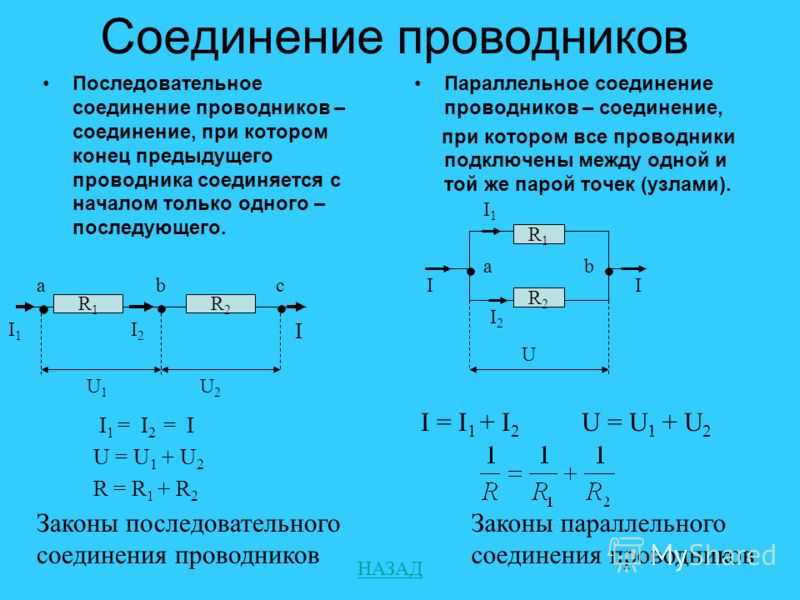 ru/praktika/raschet-soprotivleniya-rezistorov
ru/praktika/raschet-soprotivleniya-rezistorov E.5.1 Учащийся может сделать и обосновать количественный прогноз влияния изменения значений или расположения одного или двух элементов цепи на токи и разности потенциалов в цепи, содержащей небольшое количество источники ЭДС, резисторы, конденсаторы и переключатели, включенные последовательно и/или параллельно. (СП 2.2, 6.4)
E.5.1 Учащийся может сделать и обосновать количественный прогноз влияния изменения значений или расположения одного или двух элементов цепи на токи и разности потенциалов в цепи, содержащей небольшое количество источники ЭДС, резисторы, конденсаторы и переключатели, включенные последовательно и/или параллельно. (СП 2.2, 6.4) 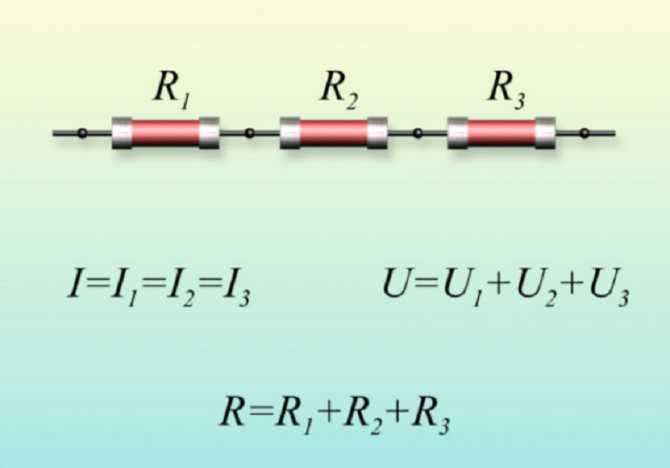 (Ст.2.2, 4.2, 5.1)
(Ст.2.2, 4.2, 5.1) 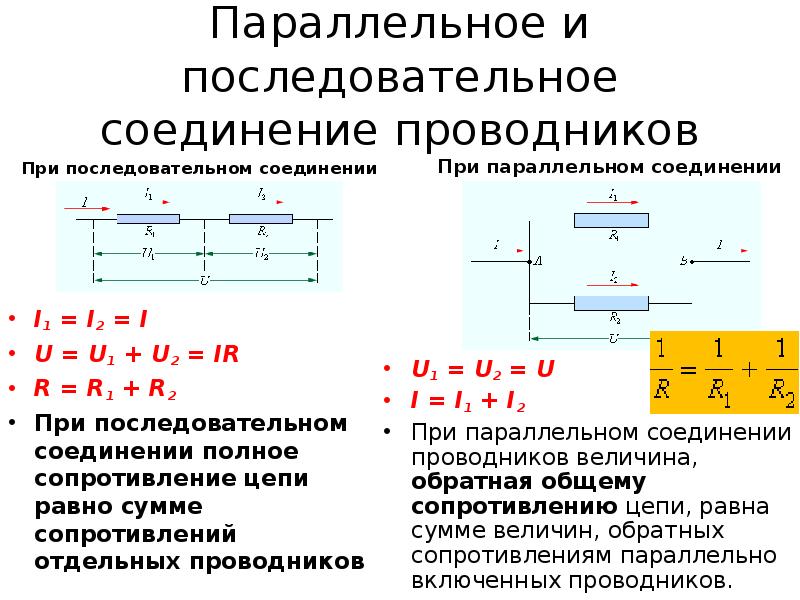 …Rs=R1+R2+R3+….
…Rs=R1+R2+R3+….