Параллельное соединение резисторов

Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.

Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье.  Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .

А) – Последовательное соединение

В) – Параллельное соединение

Рисунок 1 – Последовательное и параллельное соединение

Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения.

Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.

 

Рисунок 2 – Параллельное соединения

Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ₁, а узел В – потенциал φ₂. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.

Как следует из статьи про потенциалы, это означает,

что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.

С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I₁, I₂, I₃. При этом будет выполняться равенство

То есть через резистор R1 будет протекать ток I₁, через резистор R2 – ток I₂, а через резистор R3 – ток I₃.

Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I₁, I₂, I₃ вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.

То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так

Как же найти эти самые токи I₁, I₂, I₃? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи

Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом

Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I₁, I₂, I₃

Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем

Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.

То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.

Рисунок 3 – Преобразование параллельного соединение

Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:

То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?

Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих. Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет). Этот факт полезно запомнить.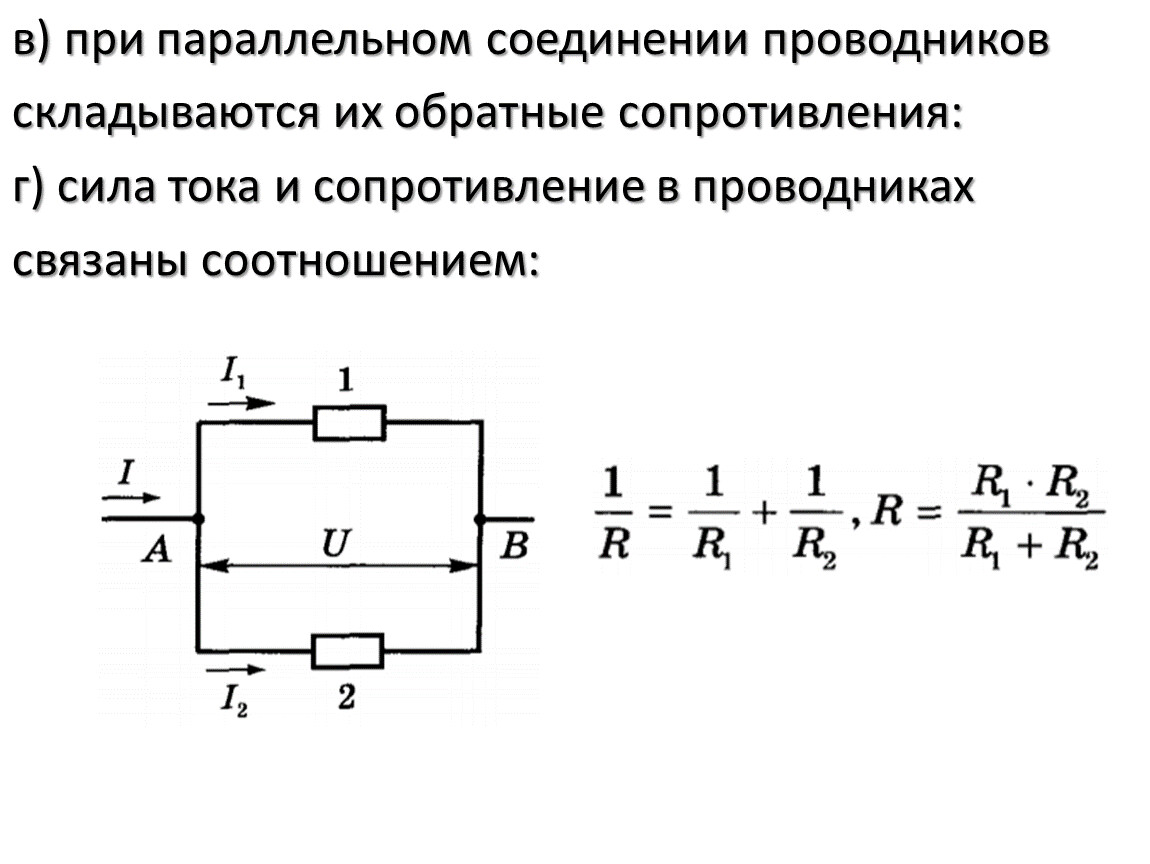

Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления

То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.

Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье

Умножим левую и правую части на напряжение U.

Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать

где Р – мощность, выдаваемая источником;

P₁ – мощность, рассеиваемая на резисторе R1;

P₂ – мощность, рассеиваемая на резисторе R2;

P₃ – мощность, рассеиваемая на резисторе R3.

Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.

Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить,

где это параллельное соединение можно использовать и для чего.

1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково. То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В. Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.

2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм. Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления. Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.

3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт.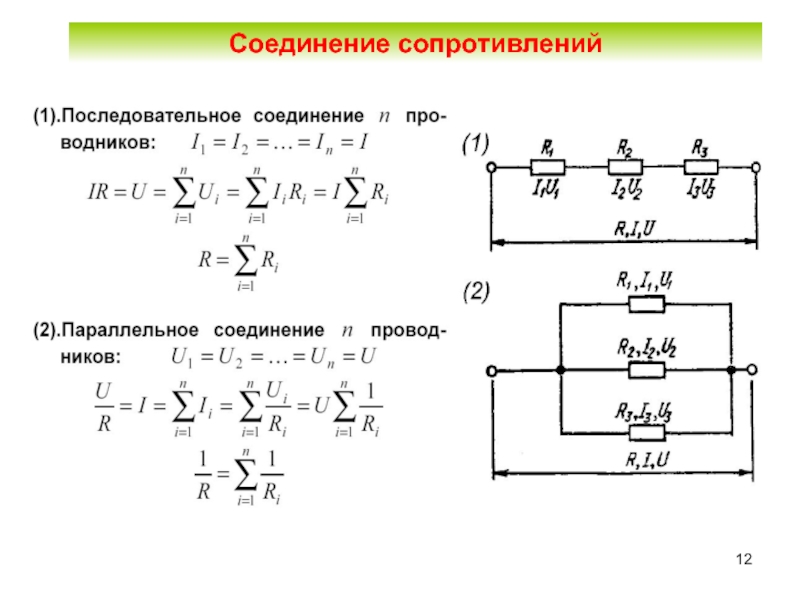 Мы же помним нашу формулу

Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.

Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.

Рисунок 4 – Плата нагревателя

На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях. Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов. И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов. Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением

и теоретически может рассеивать мощность

Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо. Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению. Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт.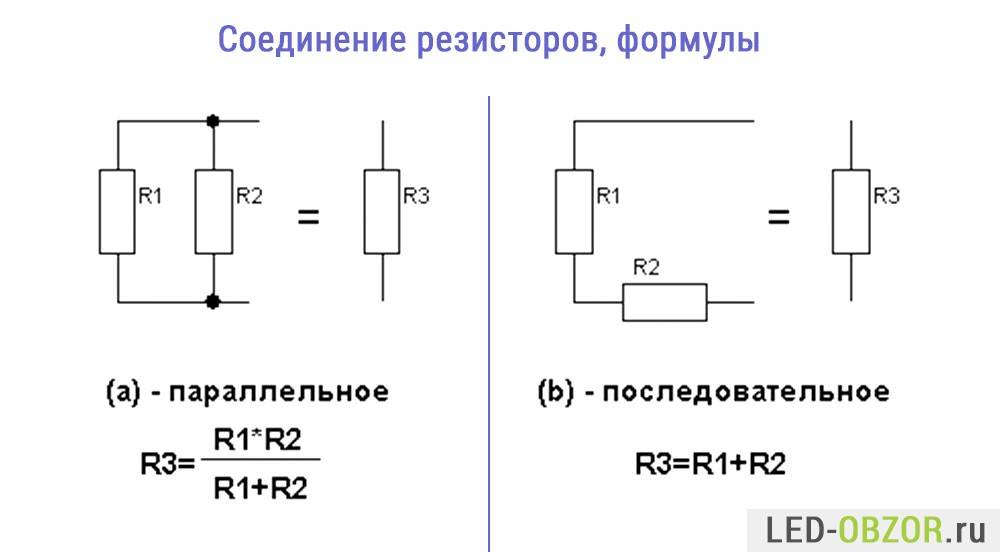 Это значит, что на каждом резисторе будет выделяться

что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно

Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти. Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя. Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось

а на всей плате

Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя. Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность. А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .

На сегодня все, господа. Удачи вам и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Как найти параллельное сопротивление: подробная информация —

By Кошики Банерджи

Существует множество методов «Как найти параллельное сопротивление», которые мы объясним в этой статье. В отличие от последовательных резисторов, резисторы, соединенные параллельно, имеют разные методы расчета эквивалентного сопротивления.

Предположим, у нас есть два резистора R₁ и R₂ как показано на рисунке 1. Мы знаем, что общий ток в параллельной цепи = сумма токов ветвей. 

Следовательно, i = V/R₁+ В/Р₂ (потенциалы А и В одинаковы)

Или, я = V (1 / R₁+ 1 / R₂)

Теперь общий ток i = напряжение / эквивалентное сопротивление = V/R_eq

Итак, В/Р_eq = В(1/Р₁+ 1 / R₂) и R_eq =(1/р₁+ 1 / R₂)^-1

Как найти параллельное сопротивление — часто задаваемые вопросы

Как найти параллельное сопротивление для n резисторов?

Метод расчета эквивалентного сопротивления для более чем двух резисторов аналогичен. На рисунке 2 изображена цепь, состоящая из n параллельно расположенных резисторов. Найдем эквивалентное сопротивление в этом случае.

Мы знаем из закона Ома, 

1. Каждая ветвь имеет одинаковое напряжение = V
2. Чистый ток я = я₁ + я₂ + я₃ + ……..+ я_n

Чистый ток = V/R, где R — эквивалентное сопротивление

Следовательно,

Or

Мы можем заменить значения в соответствии с требованиями схемы и получить желаемое эквивалентное сопротивление.

Каковы особенности параллельного сопротивления?

Параллельные сопротивления имеют несколько свойств в цепи. Наиболее важной особенностью параллельного сопротивления является то, что обратное эквивалентное сопротивление представляет собой сумму всех отдельных обратных сопротивлений.

Другие особенности параллельного сопротивления:

1. Все резисторы имеют одинаковое напряжение, и оно равно напряжению узла.
2. Токи через резисторы суммируют чистый ток вне всего параллельного соединения.
3. Эквивалентное значение сопротивления меньше любого резистора, присутствующего в цепи.

Подробнее….В настоящее время одинаково параллельно: полная информация и часто задаваемые вопросы

Как параллельное сопротивление влияет на напряжение и ток?

Мы знаем, что эквивалентное сопротивление в параллельной схеме получается путем суммирования обратной величины всех сопротивлений и их обратного действия. Это сопротивление определяет ток в цепи.

Предположим, мы строим электрическую цепь с параллельным соединением резисторов R_A и R_B с источником напряжения V. Напряжение источника будет общим для обоих резисторов, и падение напряжения на обоих из них будет V. Ток на пути R_A будет В/Р_A и ток на пути R_A будет В/Р_B. 

Подробнее….Напряжение одинаково параллельно: полная информация и часто задаваемые вопросы

Почему эквивалентное сопротивление при параллельном соединении меньше, чем отдельные сопротивления?

Параллельно с этим заряд, вытекающий из источника, когда он достигает узел есть возможность перехода в любую ветку. Так что от источника течет большое количество зарядов. Поэтому ток увеличивается.

Из закона Ома мы знаем, что V = IR.

Напряжение будет одинаковым для всех параллельных ветвей. Таким образом, ток растет с ростом ветвей (т.е. подключением большего сопротивления). Единственный способ, при котором напряжение может оставаться неизменным при уменьшении сопротивления. Поэтому сопротивление снижается.

Также читайте дальше…Что такое падение напряжения в параллельной цепи: как найти, примеры проблем и подробные факты

Численные задачи

Рассчитайте эквивалентное параллельное сопротивление для этой бесконечной лестницы, показанной на рисунке 3.

Для этого бесконечное сопротивление лестнице, можно сказать, что эквивалентное сопротивление Req между точками P и Q равно сопротивлению остальной цепи. Поэтому R_eq = 2+ 1|| р_eq

Итак,

Или,

Или,

Решая приведенное выше уравнение, мы получаем,

Пренебрегая отрицательной величиной, мы можем сказать

Это необходимое эквивалентное сопротивление.

Если эквивалентное сопротивление для цепи на рисунке 4 равно 15 Ом, найдите недостающее значение R.

На первом этапе мы рассчитаем эквивалентное сопротивление крайней правой сетки. Так,

Итак, схема теперь уменьшена до изображения 4.1. Теперь рассчитаем следующую сетку из трех последовательных резисторов.

Теперь,

Далее у нас снова параллельная сетка. Итак, Р_eq сейчас

Окончательная сетка представляет собой еще одно последовательное соединение, которое дает R_eq as

Решив это, мы получим R = 10 Ом.

Каким будет эквивалентное сопротивление Req для цепи, изображенной на рисунке 5.

Мы можем перерисовать приведенную выше схему как изображение 5. Итак, для крайнего правого меша R_eq = 4+6 = 10 Ом. Теперь у нас есть 3 параллельных резистора для правой сетки и 2 параллельных резистора для верхней сетки, как показано на 5. 1.

Эквивалентное сопротивление для правильной сетки

Эквивалентное сопротивление верхней сетки = {20*5}/{20+5} = 4 Ом. Теперь мы сократили систему до простой последовательной цепи с тремя резисторами 1 Ом, 4 Ом и 6 Ом, как показано в 5.2. Итак, окончательная Р._eq 1 + 4 + 6 = 11 Ом.

Найдите эквивалентное сопротивление в цепи, приведенной ниже: V_S = 12 В, R₁ = 2.5 Ом, R₂ = 2 Ом, R₃ = 1.5 Ом, R₄ = 3 Ом, R₅ = 5 Ом, а R₆ = 3.25 Ом.

Упрощенная схема для изображения 6 показана на 6.1. Найдем эквивалентное сопротивление самой внутренней сетки. Итак, Р_eq для сетки с R₄ и R₅ is

Теперь у нас есть Р₃ и 1.875 Ом последовательно. Итак, Р_eq = 1.5+ 1.875 = 3.375 Ом. Это сопротивление параллельно R.₂. А сейчас R_eq = { 2 * 3.375}/{ 2 + 3. 375} = 1.25 Ом. Наконец, у нас есть это сопротивление последовательно с R₁ и R₆. Таким образом, R_eq = (2.5 + 3.25 + 1.25) = 7 Ом. Это эквивалентное сопротивление цепи.

Анализ цепи

— Доказательство формулы для параллельных резисторов

спросил 2 года 11 месяцев назад

Изменено 2 года, 11 месяцев назад

Просмотрено 2к раз

\$\начало группы\$

В настоящее время я изучаю Искусство электроники , третье издание, Горовиц и Хилл. В упражнении 1.3 предлагается доказать формулы для последовательных и параллельных резисторов. Я получил следующую соответствующую информацию ранее в этой главе:

1. Сумма токов в точке цепи равна сумме выходных токов (сохранение заряда). Иногда его называют текущим законом Кирхгофа (KCL). Инженеры любят называть такую ​​точку узлом . Отсюда следует, что для последовательной цепи (куча двухполюсников, соединенных встык) ток везде одинаков.
   
2. Вещи, соединенные параллельно (рис. 1.1), имеют одинаковое напряжение на них. Другими словами, сумма «падений напряжения» от A до B по одному пути в цепи равна сумме по любому другому пути и представляет собой просто напряжение между A и B . Другими словами, сумма падений напряжения на любой замкнутой цепи равна нулю. Это закон напряжения Кирхгофа (KVL).

Я пытаюсь использовать эту информацию (и закон Ома \$V = IR\$, конечно) для доказательства параллельного случая \$R = \dfrac{R_1 R_2}{R_1 + R_2} \$. Однако я не понимаю, как предоставленной информации достаточно, чтобы сделать такой вывод.

Мне сказали, что это хороший учебник, так что, возможно, я просто новичок в электронике и поэтому чего-то не понимаю. Или, возможно, дело в том, что авторы не смогли предоставить достаточно информации для решения этой проблемы без внешних знаний. Я был бы очень признателен, если бы люди нашли время, чтобы объяснить, как это можно сделать с помощью данной информации.

• анализ цепей
• резисторы
• сопротивление
• закон Ома

\$\конечная группа\$

4

\$\начало группы\$

AoE — это не особо теоретическая книга, это скорее практическое руководство с минимальным количеством математики, которое требуется для проведения анализа. «Хорошо» это или нет, зависит от ваших целей в изучении электроники.

В любом случае, если мы хотим заменить два резистора одним эквивалентным, мы можем рассчитать эквивалентный резистор по протекающему току. Принято считать, что напряжение на каждом резисторе одинаково.

Для R1 ток равен I1 = V/R1, для R2 ток I2 = V/R2, поэтому общий ток равен:

I1 + I2 = V(1/R1+1/R2) и наш «эквивалентный» резистор Rp = 1/(1/R1+1/R2) = R1R2/(R1+R2).

Добавление токов в узел: Ip — I1 — I2 = 0 (KCL), поэтому Ip = I1 + I2

\$\конечная группа\$

4

\$\начало группы\$

Возможно, будет легче понять, как это работает, если использовать обратное сопротивление — проводимость.

В параллельной цепи каждый компонент имеет одинаковое напряжение, поэтому ток, протекающий через него, не зависит от других. Общий ток — это сумма отдельных токов, поэтому общая проводимость — это просто сумма отдельных проводимостей.

Возьмем приведенный ниже пример:

^{смоделируйте эту схему — схема создана с помощью CircuitLab}

R1 имеет проводимость 1/1 Ом = 1 А/В, R2 составляет 1/2 Ом = 0,5 А/В. , а R3 составляет 1/4 Ом = 0,25 А/В. Сложите их все вместе, чтобы получить общую проводимость 1,75 А/В, затем инвертируйте результат, чтобы получить общее сопротивление 1/1,75 = 0,571 Ом.

Это дает общую формулу для параллельных сопротивлений:-

\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1}{R2} + . ..\frac{1 }{Rn}\$

В частном случае только двух резисторов, подключенных параллельно, вы можете изменить формулу из

\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1 }{R2}\$

до

\$Rt = \frac{R_1 R_2}{R_1 + R_2}\$

\$\конечная группа\$

3

\$\начало группы\$

^{смоделируйте эту цепь — схема создана с помощью CircuitLab}

Полный ток в цепи будет It = V/Rt

Согласно KCL It = I1+I2, где I1 — ток, протекающий через резистор R1 и I2 — ток, протекающий через резистор R2.

Если подставить (закон Ома):

V/Rt = V1/R1+V2/R2. Но поскольку резисторы включены параллельно V1 = V2.

Но так как между источником напряжения и резисторами нет резистора V = V1 = V2.

V/Rt = V1/R1+V2/R2 -> V/Rt = V/R1+V/R2 и если мы разделим на V, мы получим 1/Rt = 1/R1 + 1/R2.

\$\конечная группа\$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Расчет параллельного сопротивления — Pi My Life Up

от Emmet

Обновлено 9 июля 2021 г.

Электроника

В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления.

Параллельное сопротивление является полезной частью электроники, но его может быть трудно рассчитать, когда вы начинаете иметь дело с более чем двумя резисторами.

Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Такое поведение удобно, когда вам нужно определенное сопротивление, но у вас нет резистора, соответствующего требуемому значению.

Уменьшение сопротивления вызвано тем, что ток имеет больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больший ток через цепь и, следовательно, уменьшает общее сопротивление, с которым сталкивается ваша цепь.

Например, в цепи с двумя параллельными резисторами одинакового номинала сопротивление уменьшится ровно вдвое. Математика немного отличается для разных сопротивлений и если у вас больше резисторов. Мы углубимся в это позже в руководстве.

Если вы хотите увеличить сопротивление цепи, а не уменьшить его, то вместо этого вы можете использовать последовательно соединенные резисторы.

Чтобы рассчитать общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает этот процесс.

Если вас смущают цвета на резисторе, обязательно ознакомьтесь с руководством по цветовой маркировке резистора, поскольку оно научит вас всему, что вам нужно знать.

Калькулятор параллельного сопротивления

Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление. Затем введите значение для каждого резистора.

Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.

Количество резисторов:

Резистор 1:

Резистор 2:

Расчет общего сопротивления при параллельном подключении

Если вы хотите научиться, вы можете рассчитать сопротивление параллельно подключенных резисторов вручную. Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами, включенными параллельно.

Существует три различных уравнения, которые можно использовать для параллельного расчета общего сопротивления.

Суммарное сопротивление двух одинаковых резисторов

Первое уравнение следует использовать только в том случае, если у вас есть два параллельных резистора с одинаковым сопротивлением.

Если у вас есть два резистора с одинаковым сопротивлением параллельно, то общее сопротивление равно половине одного резистора.

Пример использования уравнения

Для этого примера предположим, что у нас есть два резистора по 200 Ом, включенных параллельно, как показано на схеме ниже.

Зная, что параллельно подключены только два резистора и что они одного номинала, мы можем использовать наше уравнение.

Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).

Чтобы получить общее сопротивление, все, что нам нужно сделать сейчас, это разделить наше значение 200 Ом на 2 .

Ответ очень прост: 100 .

Теперь у вас должно быть представление о том, как справиться с простейшим сценарием с двумя параллельными резисторами одинакового номинала.

Суммарное сопротивление двух разных резисторов

Второе уравнение представляет собой упрощенную версию основного уравнения, которое мы будем использовать позже. Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.

Есть несколько других процессов, которые необходимо выполнить для расчета сопротивления двух параллельных резисторов, но это не намного сложнее.

Пример использования уравнения

В этом примере мы будем предполагать, что у нас есть цепь с двумя параллельными резисторами разных номиналов.

В этой схеме у нас есть резистор 600 Ом и резистор 250 Ом параллельно. Теперь мы хотим определить общее сопротивление, обеспечиваемое этими резисторами.

Для начала нам нужно заполнить наше уравнение, где R1 — это резистор 600  Ом, а значение R2 — 9.0204 250 Резистор.

Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение, прежде чем продолжить.

Умножение 600 (R1) на 250 (R2) должно дать результат 150,000 . Добавление 600 (R1) к 250 (R2) должно дать вам ответ 850 .

Выработав оба значения, все, что нам нужно сделать, это разделить верхнее число на нижнее число.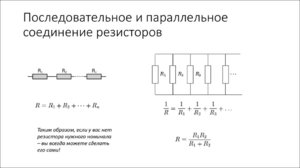 Сделав это, мы можем определить общее сопротивление двух резисторов, включенных параллельно.

Математика, которую вы должны выполнить в этом примере, равна 150 000 , деленная на 850 . Отсюда вы должны получить результат 176,47 . Будут лишние десятичные знаки, но мы округлим до ближайших двух.

Теперь у вас должно быть представление о том, как рассчитать общее сопротивление двух параллельно соединенных резисторов.

Далее мы покажем вам, как обращаться с тремя или более резисторами. Это уравнение представляет собой немного более сложный процесс, так как оно включает в себя много делений, что приводит к большим десятичным числам.

Общее сопротивление нескольких резисторов

Третье и последнее уравнение, с которым мы будем иметь дело, это то, которое вы будете использовать для трех или более резисторов, включенных параллельно.

Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.

Единственным недостатком этого уравнения является то, что оно занимает больше времени, чем больше резисторов вы добавляете.

Простым решением является использование параллельного калькулятора резисторов, который мы включили выше.

Пример использования уравнения

В этом примере мы покажем, как использовать более сложное уравнение параллельного резистора.

Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1K OHMS (R4) .

Для начала нам нужно заполнить уравнение всеми нашими значениями.

Каждое из наших значений резисторов будет делителем 1 , и вы можете добавить в это уравнение столько резисторов, сколько вам нужно. В этом примере мы обрабатываем только четыре.

Наш следующий шаг — разделить 1 на каждое из значений резистора . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.