применение, формулы расчёта ёмкости и напряжения
Содержание
Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным). Если провести аналогию между соединением конденсаторов и соединением резисторов, то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений: Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
- Cобщ — общая емкость.
- Rобщ — общее сопротивление.
При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q. Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.
Соединения конденсаторов.
Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3. Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов. Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.
Материал в тему: все о переменном конденсаторе.
Примеры расчетов
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 330нанофарада и 390нанофарада
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 4,3нанофарада и 5,1нанофарада
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 100нанофарад и 120нанофарад
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 470нанофарад и 560нанофарад
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 22нанофарад и 27нанофарад
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 680нФ и 820нФ
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 51нФ и 62нФ
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 30нФ и 36нФ
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 62нанофарад и 75нанофарад
Пример: Общая емкость соединенных последовательно конденсаторов емкостью 120нанофарада и 150нанофарада
Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:
Калькулятор резистивно-емкостной цепи
Калькулятор параллельных сопротивлений
Калькулятор параллельных индуктивностей
Калькулятор импеданса конденсатора
Калькулятор импеданса катушки индуктивности
Калькулятор взаимной индукции
Калькулятор взаимоиндукции параллельных индуктивностей
Калькулятор взаимной индукции — последовательное соединение индуктивностей
Калькулятор импеданса параллельной RC-цепи
Калькулятор импеданса параллельной LC-цепи
Калькулятор импеданса параллельной RL-цепи
Калькулятор импеданса параллельной RLC-цепи
Калькулятор импеданса последовательной RC-цепи
Калькулятор импеданса последовательной LC-цепи
Калькулятор импеданса последовательной RL-цепи
Калькулятор импеданса последовательной RLC-цепи
Калькулятор аккумуляторных батарей
Калькулятор литий-полимерных аккумуляторов для дронов
Калькулятор индуктивности однослойной катушки
Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC)
Калькулятор расчета параметров коаксиальных кабелей
Калькулятор светодиодов. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Калькулятор цветовой маркировки резисторов
Калькулятор максимальной дальности действия РЛС
Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов
Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС
Калькулятор радиогоризонта
Калькулятор эффективной площади антенны
Симметричный вибратор
Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации
Калькулятор мощности постоянного тока
Калькулятор мощности переменного тока
Калькулятор пересчета ВА в ватты
Калькулятор мощности трехфазного переменного тока
Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую
Калькулятор коэффициента гармонических искажений
Калькулятор законов Ома и Джоуля — Ленца
Калькулятор времени передачи данных
Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора
Калькуляторы Электротехнические и радиотехнические калькуляторы
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение
Принципиальная схема параллельного соединения
Последовательное соединение
Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!
Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C1, C2 в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!
Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.
Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:
Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .
Или то же самое, но более понятно:
Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.
В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:
Здесь, вместо буквы M ставиться количество конденсаторов, а C1 – его ёмкость.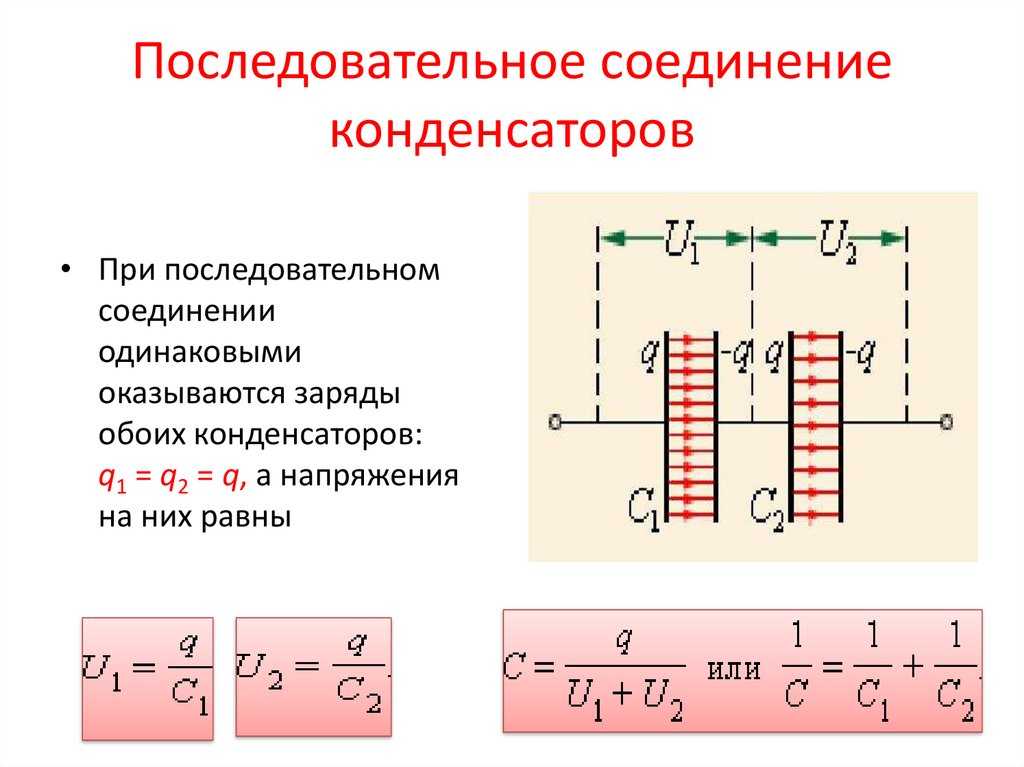
Стоит также запомнить простое правило:
При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.
Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.
Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.
Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).
Замер ёмкости при последовательном соединении
Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)
А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).
фото).
Измерение ёмкости при параллельном соединении
Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.
Параллельное соединение электролитов
Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.
Последовательное соединение электролитов
Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Источник: go-radio.ru
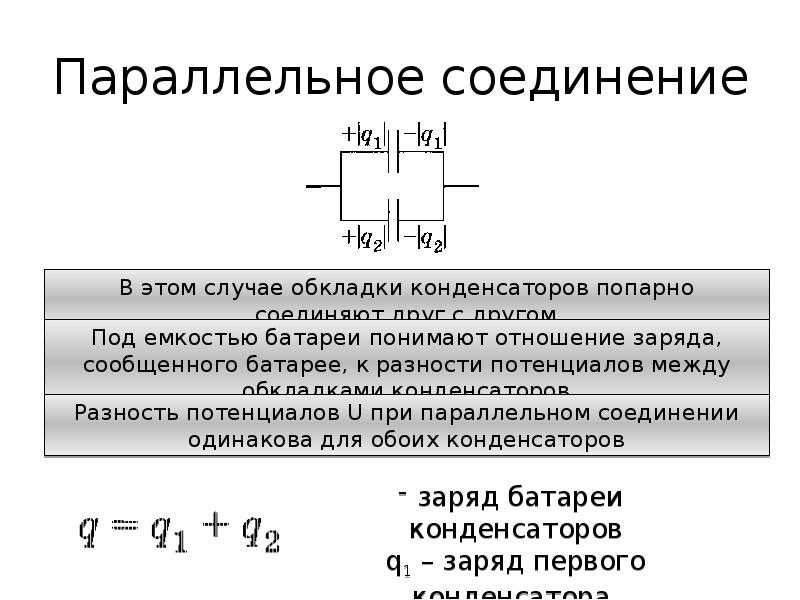
Параллельное соединение конденсаторов
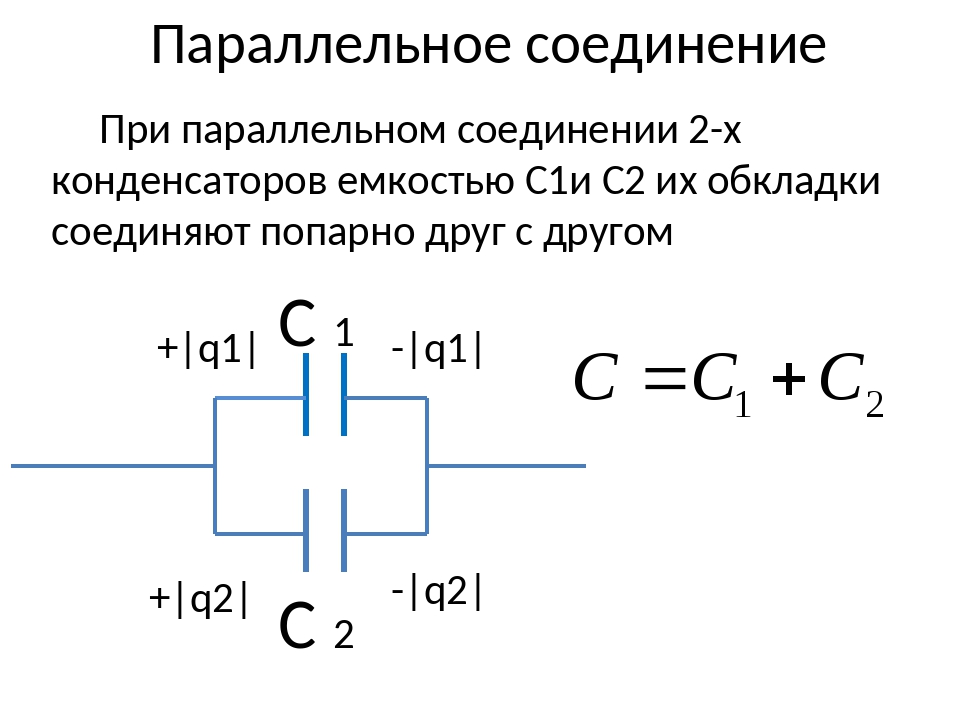
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов. При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения. Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
Будет интересно➡ Чем отличается пусковой конденсатор от рабочего?
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
Читайте также: Как соединить розетки между собой
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным. При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заряжаются через влияние. При этом заряд пластины будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
Типы соединений конденсаторов.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Последовательное и параллельное соединение конденсаторов
Последовательное соединение более двух конденсаторов редко встречается в реальных схемах. Хотя для увеличения общего напряжения такую комбинацию можно найти в высоковольтных источниках питания. Однако для низковольтных приложений довольно часто используется несколько параллельно включенных конденсаторов для сглаживания эффектов пульсаций после выпрямления при больших токах.
Содержание
Последовательное и параллельное соединение конденсаторов
При параллельном соединении суммарная емкость конденсатора складывается, и допустимое напряжение всего комплекта будет равно напряжению конденсатора с наименьшим допустимым напряжением из всего комплекта.
C = C1 + C2 + C3 + C4 + .
Например: у нас есть три конденсатора 30 мкФ x 100 В, соединенных параллельно. Параметры всего набора конденсаторов в этом случае составят 90 мкФ x 100 В.
Последовательное соединение более двух конденсаторов редко встречается в реальных схемах. Хотя для увеличения общего напряжения такую комбинацию можно найти в высоковольтных источниках питания. Однако в низковольтных источниках питания довольно распространено параллельное подключение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах.
Обратите внимание, что формулы для расчета емкости последовательных и параллельных конденсаторов точно такие же, как и формулы для расчета сопротивления последовательных и параллельных резисторов.
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-параллельным (смешанным). Если провести аналогию между подключением конденсаторов и подключением резисторов, то стоит отметить, что формулы для расчета общей емкости и общего сопротивления идентичны, просто между разными типами соединений: Формула Cвсего При параллельном соединении конденсаторов = Rобщий При последовательном соединении резисторов.
Последовательное и параллельное соединение конденсаторов
Конденсаторы в электрической цепи могут быть соединены последовательно, параллельно и последовательно-параллельно (смешанно). Чтобы провести аналогию между подключением конденсатора и подключением резистора, стоит отметить, что формулы для расчета общей емкости и общего сопротивления идентичны, просто между разными типами соединений: Формула Cвсего при параллельном соединении конденсаторов = Rвсего при последовательном соединении резисторов.
- Cобщий – общая емкость.
- Rвсего – общее сопротивление.
Когда конденсаторы соединены последовательно (рис. 3), электрические заряды на выводах отдельных конденсаторов равны по величине: Q1 = Q2 = Q3 = Q. Действительно, от сети заряды достигают только внешних обкладок цепи конденсаторов, а на соединенные между собой внутренние обкладки соседних конденсаторов передается только заряд одинаковой величины от одной обкладки к другой (электростатическая индукция), поэтому на них имеются одинаковые и разные электрические заряды.
Напряжение между стенками отдельных конденсаторов в последовательном соединении зависит от емкости отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3. Общая емкость эквивалентного конденсатора C = Q / U = Q / (U1 + U2 + U3), т.е. если конденсаторы соединены последовательно, то обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Формулы для эквивалентных емкостей аналогичны формулам для эквивалентных проводимостей.
_________________
| Страница 5 Со страницы 6 | [Новости: 104 ] | На предыдущую страницу. 1 , 2 , 3 , 4 , 5 |
Объяснить, почему емкость уменьшается, когда конденсаторы одного номинала соединены последовательно, очень просто На этом сказка заканчивается, и хорошо тому огурцу, который слушал. _________________ JLCPCB, всего $2 за прототип платы! Любой цвет по вашему желанию! Подпишитесь и получите два купона на $5 каждый: https://jlcpcb. Сегнетокерамика и имеет проницаемость около 10000. Керамические конденсаторы имеют низкую емкость, потому что между диэлектриком и пластиной есть микроскопический слой воздуха, а воздух имеет проницаемость = 1. У нас конденсаторы соединены последовательно, или субж. В электролите удалили один из слоев и емкость увеличилась, а в суперконденсаторе удалили и другой слой и получили гигант (на пальцах). Если электролиты соединены последовательно, то нет необходимости в диодах, внутреннее сопротивление таких электролитов в обратном режиме в любом случае довольно низкое. Поэтому первоначально один конденсатор действительно будет заряжаться в обратной полярности, но затем напряжение на нем упадет, а на другом вырастет. Такие цепи не используются при больших токах – в основном они применяются для развязки цепей по постоянной составляющей. В тех же схемах можно нагрузить средний отвод конденсаторов резистором на землю (если подключен к минусу) или на питание (если подключен к плюсу), тогда оба конденсатора будут иметь положительную полярность и срок их службы немного увеличится. _________________ Сборка печатной платы от $30 + БЕСПЛАТНАЯ доставка по всему миру + шаблон Согласно закону сохранения заряда, если центральная точка никуда не подключена, то ни один из конденсаторов не поляризован, они оба вращаются вокруг нулевой точки и каждый получает полупериод обратного заряда. либо диоды, либо резистор, оба дадут центральную точку, поляризованную в нужном направлении – диоды, как и резистор, не работают непрерывно, ток через них течет только в начале, при включении нельзя, но необходимо – обратное смещение будет постепенно разрушать оксидный слой даже при малых токах Модули Navigator позволяют значительно сократить время разработки программного обеспечения. Во время вебинара 17 ноября вы сможете узнать о новых семействах Teseo-LIV3x, Teseo-VIC3x и Teseo-LIV4F. Вы узнаете, как легко добавить функцию позиционирования с повышенной точностью, используя двухдиапазонный приемник и навигационную функцию MEMS-датчика. _________________ Компания Infineon представила семейство 40-вольтовых МОП-транзисторов OptiMOS 5. Эти транзисторы относятся к МОП-транзисторам нормального уровня с более высоким пороговым напряжением (по сравнению с другими низковольтными МОП-транзисторами) для защиты от ложных срабатываний в шумной обстановке. Это уже обсуждалось в другом месте, при подключении привода переменного тока. _________________ _________________ _________________ _________________ _________________ _________________ _________________ Конденсатор имеет паразитную проводимость, она же ток утечки, она же саморазряд. Если два одинаковых конденсатора соединены последовательно, и общее напряжение на них одинаково, ток утечки будет вдвое меньше (потому что напряжение на каждом конденсаторе будет вдвое меньше; а сопротивление последовательно соединенных конденсаторов суммируется). _________________ _________________ _________________ Часовой пояс: UTC + 3 часа Кто в настоящее время находится на форумеСейчас этот форум просматривают: нет зарегистрированных пользователей или гостей: 17 Рисунок 5: Пример расчета последовательно-параллельного соединения конденсаторов. Последовательно-параллельное (смешанное) соединение конденсаторовПараллельно-последовательное соединение конденсаторов представляет собой цепь с последовательно и параллельно соединенными секциями конденсаторов. На рисунке 4 показан пример схемы со смешанным соединением конденсаторов. Рисунок 4: Последовательно-параллельное соединение конденсаторов. При расчете общей емкости такого участка цепи с последовательно-параллельными конденсаторами участок разбивается на простые секции, состоящие только из групп последовательных или параллельных конденсаторов. Алгоритм расчета следующий: 1. определить эквивалентную емкость секций с последовательно-параллельными конденсаторами. 2. если в этих секциях есть последовательно соединенные конденсаторы, сначала рассчитайте их емкости. 3. рассчитав эквивалентные емкости конденсаторов, перерисуйте схему. Обычно получается схема последовательно соединенных эквивалентных конденсаторов. 4 Вычислите емкость полученной цепи. Один из примеров расчета емкости в смешанном конденсаторном соединении показан на рисунке 5. Рисунок 5: Пример расчета последовательно-параллельного соединения конденсаторов. Подробнее о расчете соединений конденсаторов вы можете узнать в мультимедийном учебнике по основам электротехники и электроники: ПОНРАВИЛАСЬ ЛИ ВАМ СТАТЬЯ? ПОДЕЛИТЕСЬ ИМ СО СВОИМИ ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Пример 2. 100 конденсаторов по 2 мкФ каждый соединены параллельно. Определите общую емкость. Общая емкость C = 100 кф = 200 мкф. Параллельное и последовательное соединение конденсаторовОтдельные конденсаторы могут быть соединены вместе различными способами. Во всех случаях для замены серии конденсаторов, соединенных вместе, можно найти емкость некоторого эквивалентного конденсатора. Для эквивалентного конденсатора выполняется условие: если напряжение, приложенное к выводам эквивалентного конденсатора, равно напряжению, приложенному к крайним выводам группы конденсаторов, то эквивалентный конденсатор будет накапливать такой же заряд, как и группа конденсаторов. Параллельное соединение конденсаторов На рисунке 1 показано параллельное соединение нескольких конденсаторов. В этом случае напряжения, приложенные к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на выводах отдельных конденсаторов равны Q1 = C1U , Q 2 = C 2 U , Q 3 = C 3 U , а заряд, поступающий от источника Q = Q1 + Q2 + Q3. Рисунок 1: Схема параллельного соединения конденсаторов Общая емкость эквивалентного конденсатора: C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3 , т.е. При параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. Последовательное подключение конденсаторов При последовательном соединении конденсаторов (рис. 3) электрические заряды на выводах отдельных конденсаторов равны по величине: Q1 = Q2 = Q3 = Q Действительно, источник электрических зарядов приложен только к внешним катушкам цепи конденсаторов, а на внутренних катушках соединенных конденсаторов происходит только перенос электрических зарядов одинаковой величины с одной катушки на другую (электростатическая индукция), поэтому на них имеются одинаковые и разные электрические заряды. Рис. 3 Схема последовательного соединения конденсаторов Напряжение между выводами отдельных конденсаторов в последовательном соединении зависит от емкости отдельных конденсаторов: U1 = Q/C1 , U1 = Q/C 2, U1 = Q/C 3, а общее напряжение U = U1 + U2 + U3 Общая емкость эквивалентного конденсатора C = Q / U = Q / ( U1 + U2 + U3 ), т.е. если конденсаторы соединены последовательно, то обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Формулы для эквивалентных емкостей аналогичны формулам для эквивалентных проводимостей. Пример 1. Три конденсатора емкостью C1 = 20 мкФ, C2 = 25 мкФ и C3 = 30 мкФ соединены последовательно, определите их общую емкость. Общая емкость определяется из выражения 1/C = 1/C1 + 1/C2 + 1/C3 = 1/20 + 1/25 + 1/30 = 37/300, где C = 8,11 мкф. Пример 2: 100 конденсаторов по 2 мкФ каждый соединены параллельно. Определите общую емкость. Общая емкость C = 100 Ck = 200 мкф. Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. 25.04.2016 Lega95 0 комментариев Привет всем. Этот небольшой пост посвящен теме подключения конденсаторов. На практике часто случается, что у нас нет конденсатора с нужным номиналом для установки, а технику требуется срочный ремонт. Именно для таких случаев нам необходимо знать правила подключения конденсаторов. Существует только два способа подключения конденсаторов. Это последовательное соединение и параллельное соединение. Теперь мы рассмотрим оба метода более подробно. Параллельное соединение конденсаторов. Это наиболее распространенный способ подключения конденсаторов. При параллельном соединении емкость конденсатора увеличивается, а напряжение остается прежним. Формула для параллельного соединения конденсаторов: C= C1+C2+C3… Давайте рассмотрим пример. Предположим, вам нужен конденсатор 100 мкФ 50 Ви у тебя есть только 47 мкФ при 50 В. Параллельное подключение конденсаторов Конденсаторы соединены последовательно. При таком подключении общая емкость уменьшается, а рабочее напряжение конденсатора увеличивается. Конденсаторы соединяются последовательно в соответствии со следующей формулой: Формула расчета для последовательного соединения конденсаторов Например, подключим 3 конденсатора со следующими номиналами 100 мкф при 100 В в серии. Согласно формуле, разделите единицу на емкость конденсаторов. Итак, подведем итоги. Затем разделите единицу на результат. (1:100)+(1:100)+(1:100) = 0,01 + 0,01 + 0,01 = 0,03 далее 1 : 0,03 = 33 мкф для 300 В (напряжение добавить 100 + 100 + 100 = 300в). В общей сложности 33 мкФ для 300 В. |
Читайте далее:
- Принцип работы транзисторов Мосфета.
- Урок 28 Электрическая емкость. Конденсатор – Физика – 10 класс – Российская электронная школа.
- Расчет цепи постоянного тока с конденсаторами.
- Биполярные транзисторы.
- Как работает транзистор.
- Конденсаторы.
- Расчет понижающего конденсатора.
Понимание конденсаторов в параллельных соединениях
В предыдущем разделе мы подробно рассмотрели введение конденсаторов, сегодня мы обсудим параллельные конденсаторы. Вы поймете пример, формулу, расчет и применение параллельных конденсаторов. Помните, мы говорили, что конденсаторы — это компоненты, которые хранят электрическую энергию в электрическом поле. Мы также узнали, что разные конденсаторы имеют свое номинальное напряжение, то есть способность накапливать заряд. так что давайте углубимся в то, что привело нас сюда.
Электрические устройства могут быть спроектированы с максимально возможным количеством конденсаторов.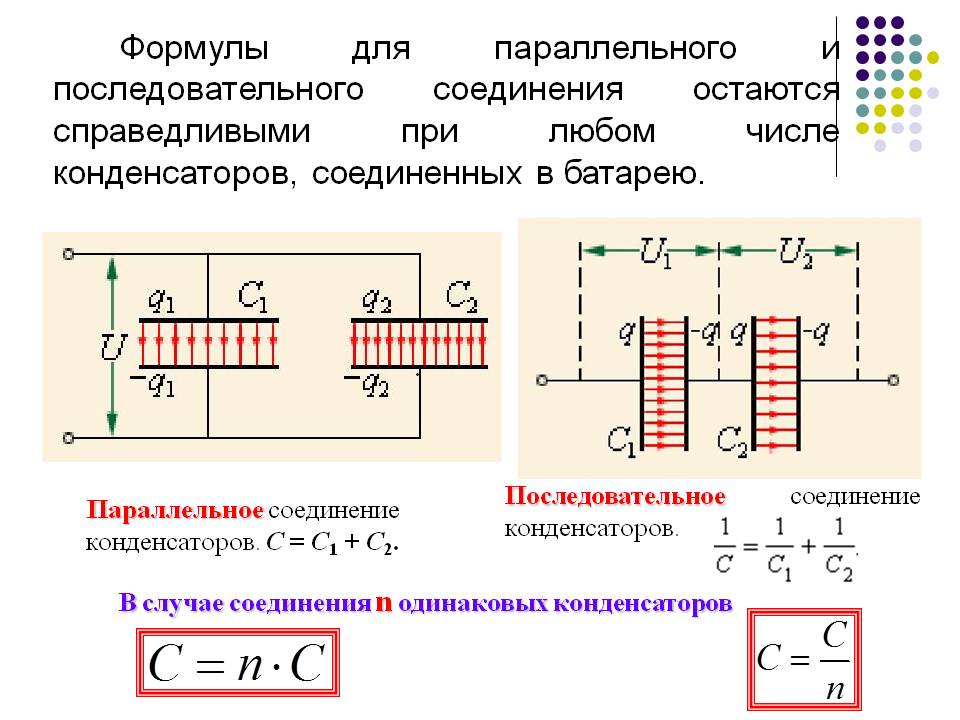 Несколько соединений конденсаторов действуют как один эквивалентный конденсатор с общей емкостью. Что ж, величина требуемой емкости будет определять количество конденсаторов и способ их подключения. Два простых и распространенных типа соединений называются последовательными и параллельными соединениями. С помощью этих соединений мы можем легко рассчитать общую емкость. Хотя более сложные соединения могут включать комбинации последовательного и параллельного.
Несколько соединений конденсаторов действуют как один эквивалентный конденсатор с общей емкостью. Что ж, величина требуемой емкости будет определять количество конденсаторов и способ их подключения. Два простых и распространенных типа соединений называются последовательными и параллельными соединениями. С помощью этих соединений мы можем легко рассчитать общую емкость. Хотя более сложные соединения могут включать комбинации последовательного и параллельного.
Читать Подробнее: понимание рейтинга напряжения конденсатора
Содержание
- 1 Конденсаторы в параллельном соединении
- 2 Расчет параллельного конденсатора
- 2.1 СОВЕРИТЕСЬ НА НАШЕГО НАЙНА параллельно
- 2.3.1 Посмотрите видео ниже, чтобы увидеть работу конденсаторов при параллельном соединении:
- 2.1 СОВЕРИТЕСЬ НА НАШЕГО НАЙНА параллельно
- 3 Применение
- 3.1 Источники питания постоянного тока:
- 3.2 Более высокие значения емкости:
- 3.3 Импульсная нагрузка:
- 3.
 4 Конструктивные ограничения:
4 Конструктивные ограничения: - 3.5 Безопасность:
- 3.6 Пожалуйста, поделитесь!
Конденсаторы в параллельном соединении
Конденсаторы называются параллельными, когда оба их вывода подключены к каждому выводу другого конденсатора. Напряжение Vc, подключенное ко всем параллельно соединенным конденсаторам, одинаково. Таким образом, конденсаторы, включенные параллельно, имеют общую подачу напряжения на них. например,
V C1 = V C2 = V C3 = V AB = 12 В
Все конденсаторы с параллельными соединениями имеют одинаковое напряжение на них, такие как V 1 = V 2 = В п . где от V 1 до V n представляют собой напряжение на каждом соответствующем конденсаторе. Это напряжение равно напряжению, приложенному к параллельному соединению конденсатора через входные провода. Хотя количество заряда, хранящегося в каждом конденсаторе, неодинаково. Кроме того, это зависит от емкости каждого конденсатора в соответствии с приведенной ниже формулой:
Кроме того, это зависит от емкости каждого конденсатора в соответствии с приведенной ниже формулой:
Q n = C n . V n
Где Q n — количество заряда, накопленного на конденсаторе, C n — емкость конденсатора, а V n — напряжение, подаваемое на весь блок параллельного соединения. Блок конденсатора хранит общий заряд конденсатора, который представлен Q и делится между всеми конденсаторами в цепи. Это можно представить как:
Q = Q 1 + Q 2 + … + Q n
Подробнее: Типы конденсаторов
Приведенное выше уравнение параллельного конденсатора используется для определения эквивалентной емкости при параллельном соединении нескольких конденсаторов:
C eq = = = + + … +
Где C eq — эквивалентная емкость при параллельном соединении конденсаторов, V — напряжение, подаваемое на конденсаторы по входным проводам, а Q 1 9От 0050 до Q n — заряды, хранящиеся в каждом соответствующем конденсаторе. Вот почему у нас есть следующее уравнение:
Вот почему у нас есть следующее уравнение:
C eq = C 1 + C 2 + …. + C n
Приведенное выше уравнение означает, что эквивалентная емкость параллельного соединения конденсаторов равна сумме емкостей отдельных конденсаторов. Что ж, конденсаторы, включенные параллельно, можно рассматривать как один конденсатор, а его пластины равны сумме площадей пластин отдельных конденсаторов.
Подробнее: Понимание заряда в конденсаторе
Расчет параллельного конденсатора
С объяснением приведенного выше уравнения параллельного соединения конденсатора. В этом разделе вы узнаете, как рассчитать емкость конденсаторов при параллельном соединении. Имейте в виду, что значения отличаются от значений уравнения. Следующая схема показывает, что конденсаторы C1, C2 и C3 подключены в параллельную ветвь между точками A и B, как показано на рисунке ниже:
Помните, что общая или эквивалентная емкость C eq в цепи равна сумме всех отдельных конденсаторов, сложенных вместе, когда конденсаторы соединены параллельно.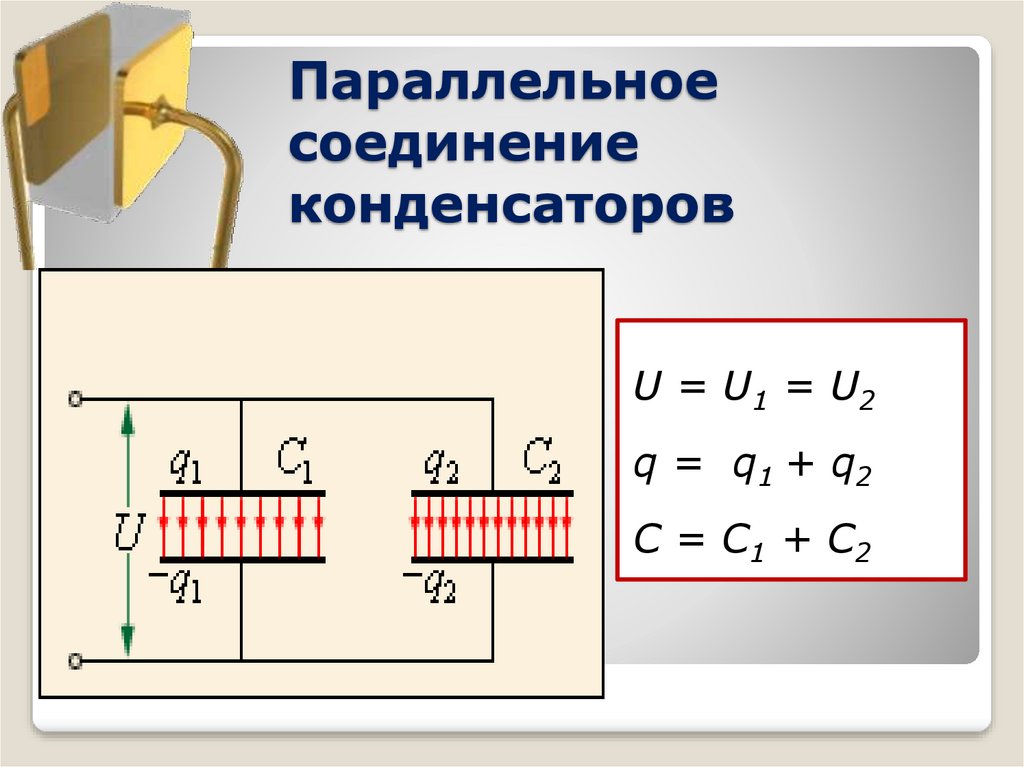 Это связано с тем, что верхняя пластина конденсатора C 1 подключена к верхней пластине C 2 , которая подключена к пластине C 3, и так далее.
Это связано с тем, что верхняя пластина конденсатора C 1 подключена к верхней пластине C 2 , которая подключена к пластине C 3, и так далее.
Это также относится к нижним пластинам конденсаторов, в результате чего три набора пластин соприкасаются друг с другом. Они равны одной большой одиночной пластине, что увеличивает эффективную площадь пластины в м 2 .
Поскольку емкость C связана с площадью пластины (C = E(A/d), значение емкости комбинации также будет увеличиваться. Затем общая емкость конденсатора, подключенного параллельно, рассчитывается путем суммирования площади пластины. . Другими словами, общая емкость равна сумме всех отдельных емкостей, соединенных параллельно. Таким же образом мы получаем общее сопротивление последовательных резисторов.0003
Подпишитесь на нашу рассылку новостей
Примеры параллельного подключения конденсаторов
Возьмем значения трех конденсаторов, чтобы мы могли рассчитать общую эквивалентную емкость цепи C T . Тогда мы можем сказать:
Тогда мы можем сказать:
C1 = C1 + C2 + C3 = 0,1 мкФ + 0,2 мкФ + 0,3 мкФ = 0,6 мкФ
Вы должны знать общую емкость (C T ) любых двух или более конденсаторов, соединенных в параллельное будет БОЛЬШЕ, чем значение самого большого конденсатора в цепи. Это потому, что все значения суммируются. Итак, в приведенном выше примере C T = 0,6 мкФ, тогда как конденсатор большей емкости в цепи равен 0,3 мкФ.
Пример 2 конденсаторов, включенных параллельно
Рассчитайте емкость в микрофарадах (мкФ) следующих конденсаторов при параллельном соединении:
- Два конденсатора емкостью 47 нФ каждый
- параллельно конденсатору 1 мкФ
Подробнее: Понимание емкости в цепях переменного тока
Решение
- Общая емкость,
C T = C 1 + C 2 = 47NF + 47NF = 94NF или 0,094 мкл
- . + C 2 = 470 нФ + 1 мкФ
Итак, C T = 470 нФ + 1000 нФ = 1470 нФ или 1,47 мкФ
Следовательно, общая или эквивалентная емкость CT электрической цепи, содержащей два или более конденсаторов, включенных параллельно, равна сумма всех отдельных емкостей, сложенных вместе по мере увеличения эффективной площади пластин.

Посмотрите видео ниже, чтобы увидеть работу конденсаторов при параллельном соединении:
Применение
При параллельном подключении нескольких конденсаторов цепь может накапливать больше энергии, поскольку общая или эквивалентная емкость представляет собой сумму индивидуальных емкостей всех конденсаторов. Ниже приведены области применения этого эффекта емкости:
Подробнее: Цветовой код конденсатора
Источники питания постоянного тока:
Источники питания постоянного тока часто используются для правильной фильтрации выходного сигнала и устранения пульсаций переменного тока. В этом методе есть возможность использовать конденсаторы меньшего размера, которые имеют лучшие характеристики пульсаций, получая при этом более высокие значения емкости.
Более высокие значения емкости:
В некоторых приложениях требуются значения емкости, которые намного выше, чем у имеющихся в продаже конденсаторов, в таких ситуациях используются конденсаторные батареи.
 Одним из хороших примеров является использование батареи конденсаторов для коррекции коэффициента мощности с индуктивными нагрузками. Кроме того, эти банки могут использоваться в приложениях для хранения энергии, таких как автомобильная промышленность, KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи и гибридные автомобили.
Одним из хороших примеров является использование батареи конденсаторов для коррекции коэффициента мощности с индуктивными нагрузками. Кроме того, эти банки могут использоваться в приложениях для хранения энергии, таких как автомобильная промышленность, KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи и гибридные автомобили.Импульсная нагрузка:
Батареи конденсаторов предназначены для достижения очень высоких значений емкости. Так, соединив параллельно несколько суперконденсаторов, можно получить емкости в несколько десятков килофарад. Между тем, ультраконденсаторы способны достигать значений емкости более 2000 фарад.
Конструктивные ограничения:
При параллельном соединении конденсаторов следует знать, что максимальное номинальное напряжение при параллельном соединении конденсаторов равно наименьшему номинальному напряжению всех конденсаторов, используемых в системе.
 Таким образом, если несколько конденсаторов на 500 В подключены параллельно к конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.
Таким образом, если несколько конденсаторов на 500 В подключены параллельно к конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.Подробнее: Понимание заряда конденсатора
Безопасность:
Конденсаторные батареи могут быть опасны из-за большого запаса энергии. И тот факт, что конденсаторы могут высвобождать накопленную энергию за очень короткое время. Эта накопленная энергия может привести к серьезным травмам или повреждению электропроводки и устройств в случае случайного короткого замыкания.
Это все для этой статьи, где обсуждаются пример, формула, расчеты, работа и применение конденсаторов при параллельном соединении. Я надеюсь, что вы получили много от чтения, если это так, пожалуйста, поделитесь с другими студентами. Спасибо за чтение, увидимся в следующий раз!
3.6 Конденсаторы, соединенные последовательно и параллельно – Колледж Дугласа, физика 1207
Глава 3 Электрический потенциал и электрическое поле
Резюме
- Выведите выражения для полной емкости при последовательном и параллельном подключении.

- Определите последовательное и параллельное соединение конденсаторов.
- Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.
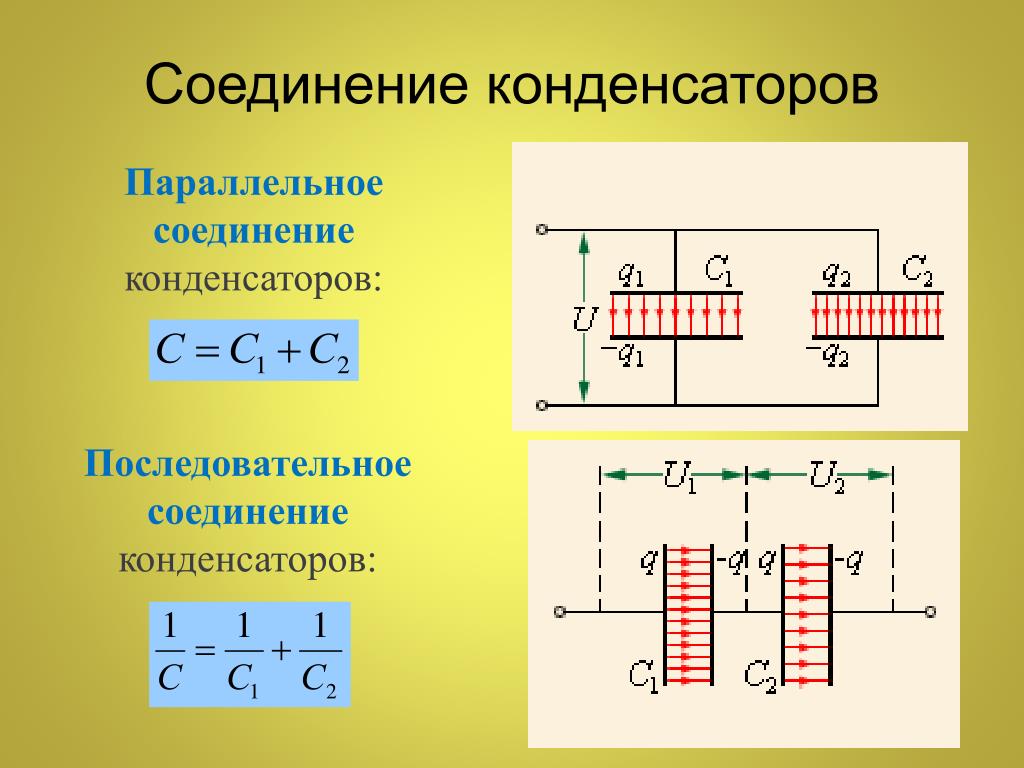
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0259 серии
На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением как 90 269 C = Q/V.

Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обеим сторонам первоначально незаряженной комбинации конденсаторов, когда приложено напряжение
 Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение C = Q/V для V дает V = C / Q . Таким образом, напряжения на отдельных конденсаторах равны . Общее напряжение представляет собой сумму отдельных напряжений:
В = В 1 + В
Теперь, назвав общую емкость C ряд = C с для последовательной емкости, учтем, что
Ввод выражений для V 1 , V 2 , и V 3 получаем
Отменив Q s , мы получим уравнение для полной емкости в ряду C равной
, где «…» указывает, что выражение справедливо для любого количества последовательно соединенных конденсаторов.
 Выражение этой формы всегда приводит к тому, что общая емкость
Выражение этой формы всегда приводит к тому, что общая емкость Общая емкость последовательно,
C сСуммарная емкость последовательно:
Пример 1: Что такое последовательная емкость?
Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 мкФ.
Стратегия
При наличии данной информации общую емкость можно найти, используя уравнение для последовательной емкости.
Решение
Ввод данных емкостей в выражение для дает .
Инвертирование для нахождения C серии или C s дает .
Обсуждение
Суммарная последовательная емкость C с меньше наименьшей отдельной емкости, как и было обещано.
 При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,так что
На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C параллельно или C
p, сначала отметим, что напряжение на каждом конденсаторе равно В , такое же, как и у источника, так как они подключены непосредственно к нему через дирижер. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд Q — это сумма отдельных сборов:
Общий заряд Q — это сумма отдельных сборов:Q = Q 1 + Q 2 + Q 3
Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.Использование отношения Q = CV , we see that the total charge is Q total = C p V , and the individual charges are Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V . Ввод их в предыдущее уравнение дает
Q всего = Q 1 + Q 2 + Q 3
C p V = C 1 V+ C 2 V+ C 3 V
C p = C 1 + C 2 + C 3
Вычеркивая из уравнения В , получаем уравнение для полной емкости параллельно C p :
C p = C 1 + C 2 + C 3 + ….

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … » указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы
C p = C 1 + C 2 + C 3 = 1,000 мкФ + 5,000 мкФ + 8,000 мкФ = 14,000 7 мкФ 9000
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рис. 2(b).
Суммарная емкость при параллельном включении,
C pСуммарная емкость при параллельном включении C p = C 1 + C 2 + 4, + 9 C 900
Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения.
Рис. 3. (a) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C 1 и C 2 последовательно; их эквивалентная емкость C S меньше любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме C S и C 3 . (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.
(См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.A Смесь последовательных и параллельных емкостей
Найдите общую емкость комбинации конденсаторов, показанной на рисунке выше. Рисунок 3. Предположим, что емкости известны с точностью до трех знаков после запятой + C 2 + C 3 = 1,000 мкФ + 5,000 мкФ + 8,000 мкФ = 14,000 мкФ
C p = C 1 + C 2 + C 3 = 1.
 000 μF + 5.000 μF + 8.000 μF = 14.000 μF
000 μF + 5.000 μF + 8.000 μF = 14.000 μF C 1 = 1.000 μF, C 2 = 5.000 μF and C 3 = 8 000 мкФ. Округлите ответ до трех знаков после запятой.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы C 1 и C 2 включены последовательно. Их комбинация, Cs на рисунке параллельно C 3 .
Решение
Поскольку C 1 и C 2 соединены последовательно, их общая емкость определяется как . Ввод их значений в уравнение дает
Инвертирование дает
Cs = 0,833 мкФ
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общая сумма равна сумме
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к более крупным комбинациям конденсаторов.

- Выведите выражения для полной емкости при последовательном и параллельном подключении.


 Но что происходит с емкостью? Подключаем источник питания. Электроны бегут к положительной стороне конденсатора. И что они там видят? Они увидели, что есть одна диэлектрическая стена и другая, которую они действительно хотят преодолеть. Но какова толщина этих стен? Бедные электроны не знают. Они могут ощущать противоположный заряд (минус) только через эти стенки. Минус кричит на них: “Эй, собирайтесь вместе! У меня есть потенциал, и мне нужно так много вас!”.
Но что происходит с емкостью? Подключаем источник питания. Электроны бегут к положительной стороне конденсатора. И что они там видят? Они увидели, что есть одна диэлектрическая стена и другая, которую они действительно хотят преодолеть. Но какова толщина этих стен? Бедные электроны не знают. Они могут ощущать противоположный заряд (минус) только через эти стенки. Минус кричит на них: “Эй, собирайтесь вместе! У меня есть потенциал, и мне нужно так много вас!”. 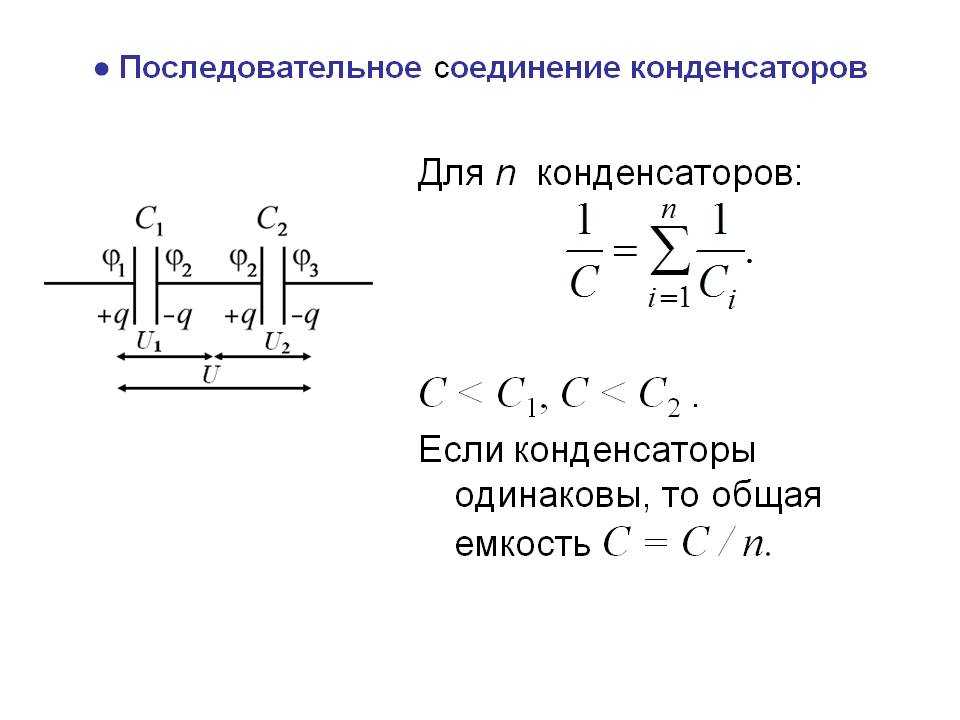 com/cwc
com/cwc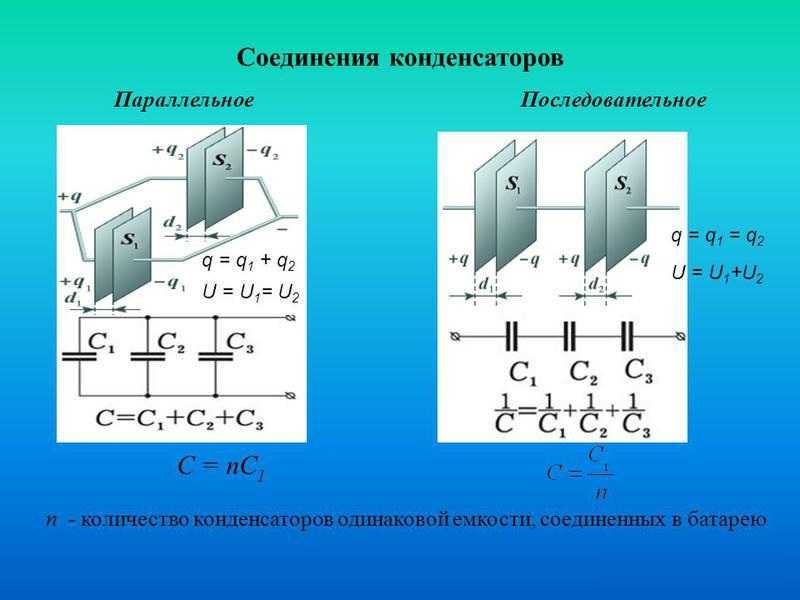 Но обычно так не поступают.
Но обычно так не поступают. Давайте поработаем с Teseo Suite и посмотрим на результаты полевых испытаний.
Давайте поработаем с Teseo Suite и посмотрим на результаты полевых испытаний.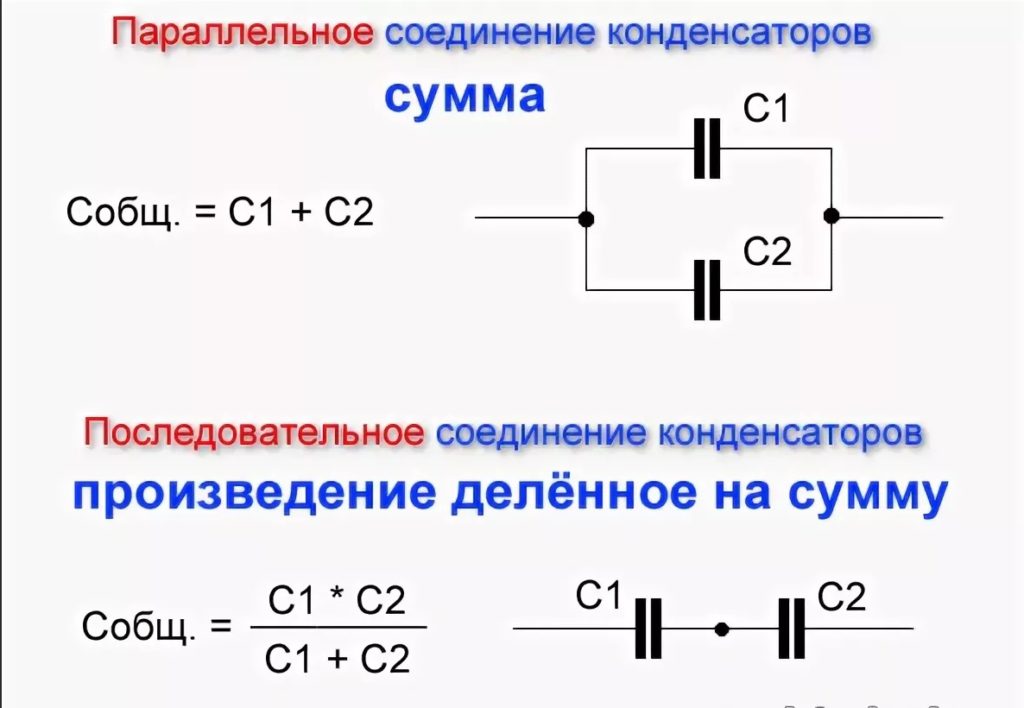




 Это очень поможет в развитии нашего сайта!
Это очень поможет в развитии нашего сайта! Если мы соединим эти конденсаторы параллельно (плюс к плюсу и минус к минусу), общая емкость составит ок. 94 мкФ при 50 В. Это приемлемый допуск, чтобы его можно было свободно установить в технике.
Если мы соединим эти конденсаторы параллельно (плюс к плюсу и минус к минусу), общая емкость составит ок. 94 мкФ при 50 В. Это приемлемый допуск, чтобы его можно было свободно установить в технике.
 4 Конструктивные ограничения:
4 Конструктивные ограничения:
 Одним из хороших примеров является использование батареи конденсаторов для коррекции коэффициента мощности с индуктивными нагрузками. Кроме того, эти банки могут использоваться в приложениях для хранения энергии, таких как автомобильная промышленность, KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи и гибридные автомобили.
Одним из хороших примеров является использование батареи конденсаторов для коррекции коэффициента мощности с индуктивными нагрузками. Кроме того, эти банки могут использоваться в приложениях для хранения энергии, таких как автомобильная промышленность, KERS (система рекуперации кинетической энергии), используемая для рекуперативного торможения в больших транспортных средствах, таких как трамваи и гибридные автомобили. Таким образом, если несколько конденсаторов на 500 В подключены параллельно к конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.
Таким образом, если несколько конденсаторов на 500 В подключены параллельно к конденсатору на 100 В, максимальное номинальное напряжение всей системы составляет всего 100 В, поскольку на все конденсаторы в параллельной цепи подается одинаковое напряжение.

 Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов. Выражение этой формы всегда приводит к тому, что общая емкость
Выражение этой формы всегда приводит к тому, что общая емкость  При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом, Общий заряд Q — это сумма отдельных сборов:
Общий заряд Q — это сумма отдельных сборов:
 (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.
(См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.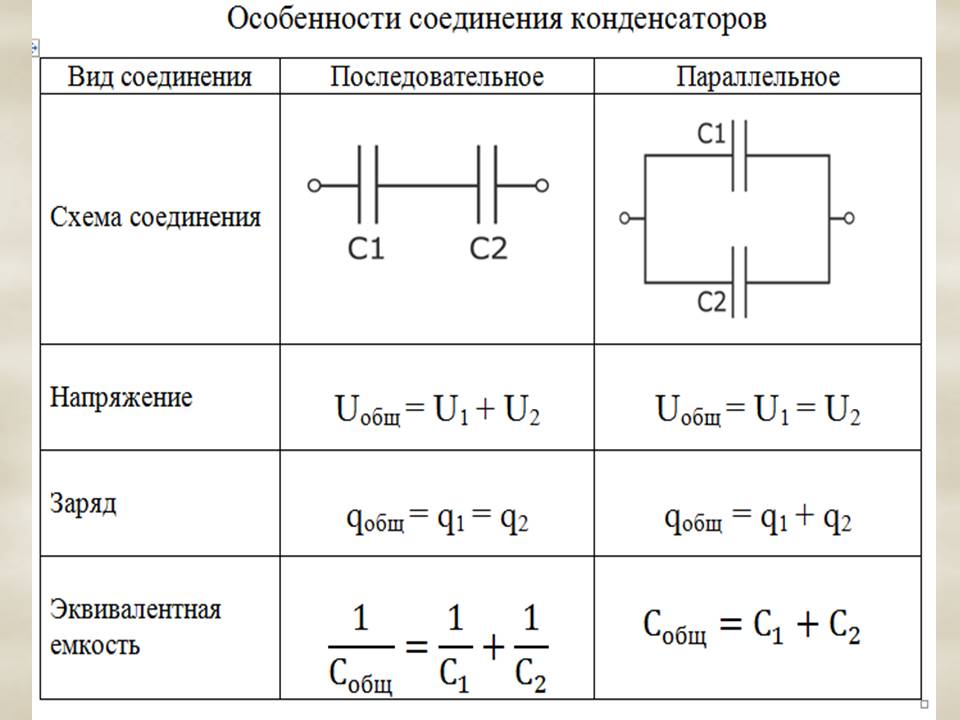 000 μF + 5.000 μF + 8.000 μF = 14.000 μF
000 μF + 5.000 μF + 8.000 μF = 14.000 μF 