Site Loader
Posted on 27.09.2023

Пара сил. Момент пары сил. Свойства пар сил. Момент силы относительно точки

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

Пара сил и момент
силы относительно
точки
Пара сил, момент пары сил
• Парой сил называется система двух сил, равных по модулю,
параллельных и направленных в разные стороны, приложенных к телу в
двух разных точках.
• Плечом пары h называется кратчайшее расстояние между линиями
действия сил, составляющих пару.
• Моментом пары сил называется взятое со знаком «плюсом» или
«минусом» произведение модуля одной из сил на плечо пары.


Пара сил вызывает вращение тела и ее действие на тело оценивается
моментом. Силы, действующие на пару, не уравновешиваются, т.к. они
приложены к двум точкам. Их действие на тело не может быть заменено одной
силой (равнодействующей)
Момент пары сил численно равен произведению модуля силы на расстояние
между линиями действия сил (плечо пары).
Момент считается положительным, если пара вращает тело по часовой стрелке
и наоборот.
М<0
М>0
Свойства пар
• Пару можно перемещать в плоскости ее действия
• Эквивалентность пар. Две пары моменты которых равны, эквивалентны
(действие их на тело аналогично).
• Сложение пар сил. Систему пар сил можно заменить равнодействующей
парой. Момент равнодействующей пары равен алгебраической сумме
моментов пар, составляющих систему
• Равновесие пар.
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма
моментов пар системы равнялась нулю:
Момент пары
В результате силы тяжести все конструкции имеют опору. Если к
конструкции приложить активные силы, то на опоре возникает такая же, но
реактивная противоположно направленная. Если две силы || то они
обозначают пару.
При подсчёте момента пары достаточно видеть одну силу и расстояние
до второй. Поэтому решая задачи подсчитывают момент силы
относительно точки, вокруг которой эта сила стремится повернуть тело.
Момент силы относительно точки
Решение задач
Пример 1
Контрольные вопросы
и задания
Тема: «Пара сил и момент силы
относительно точки»
Контрольные вопросы и задания
5. Ответьте на вопросы тестового задания.
Вопросы
1. Какие силы из заданной системы сил,
действующих на тело, образуют пару сил?
Ответы
а) 7 Н; 7 Н
б) 7 Н; 10 Н
в) 10 Н; 10 Н
г) 15 Н; 15 Н;
2. Определить момент заданной пары сил.
а) 0,35 Н·м
б) -35,35 Н·м
в) 50 Н·м
г) -70,7 Н·м
Вопросы
3. Укажите пару сил, эквивалентную заданной.
Ответы
а)
б)
в)
г)
Вопросы
Ответы
4. Найдите момент уравновешивающей пары сил.
а) -0,4 Н·м
б) 0,4 Н·м
в) -0,8 Н·м
г) 0,8 Н·м
5. Определить сумму моментов сил относительно
точки С.
а) 7 Н·м
б) 47 Н·м
в) 19 Н·м
г) 77 Н·м

English     Русский Правила

Пара сил. Момент пары сил. Теоремы о парах — Студопедия

Поделись с друзьями: 

Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной – момент пары.

Он определяется:

Его модулем = F*d. d – расстояние между линиями действия сил пары, называется плечом пары.

Положением в пространстве плоскости действия пары.

Направлением поворота пары в этой плоскости.

Момент пары сил – вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.

Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Для абсолютно твердого тела пара – свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.

Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.

Теоремы о парах.

1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. .

2) Две пары, имеющие геометрически равные моменты, эквиваленты.

3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором.

4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Т.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Условие равновесия пар сил: – геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, если алгебраическая сумма их моментов åМi=0.

Момент силы относительно точки

– вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо «h»– кратчайшее расстояние от точки до линии действия силы. – момент силы равен векторному произведению вектора на вектор . Модуль векторного произведения: R×F×sina = F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль: ± F×h, >0 – против час.стр.; x, Fy, Fz – проекции силы на оси координат и точка 0 – начало координат, то

= (yFz – zFy) + (zFx – xFz) + (xFy – yF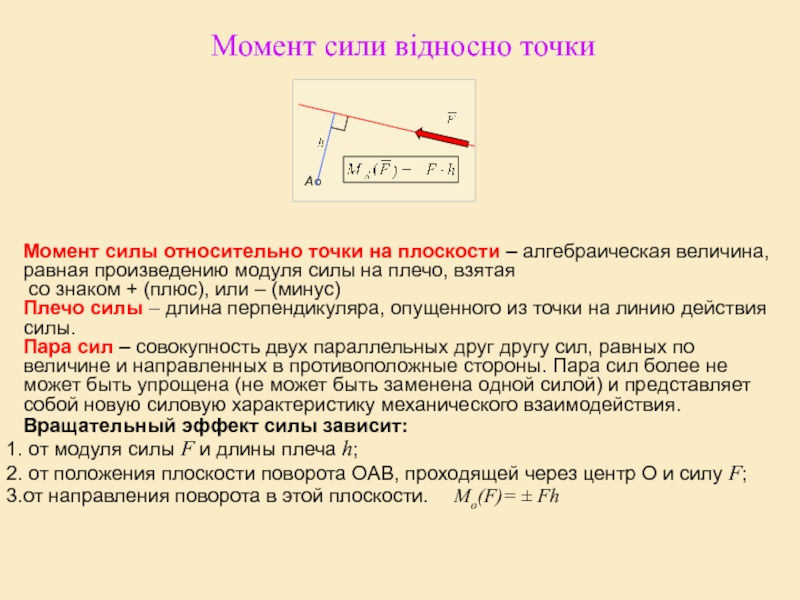

x) , откуда проекции момента силы на оси коорд. : М0x() = yFz – zFy; М0y () = zFx – xFz; М0z () = xFy – yFx.

Главный вектор – векторная сумма всех сил, приложенных к телу. Главный момент относительно центра – векторная сумма моментов всех сил, приложенных к телу относительно того же центра.

Теорема (лемма) о параллельном переносе силы: сила приложенная в какой-либо точке тверд. тела, эквивалента такой же силе, приложенной в любой др. точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  



Единица СИ, формула, характеристики, применение

Серия испытаний

Автор Deepak Yadav|Обновлено: 4 октября 2022 г. и рука пары. Прежде чем вдаваться в подробности момента пары, давайте сначала поймем пару. Пара – это частный случай момента. Пара состоит из двух параллельных сил, равных по величине, противоположных по смыслу и не имеющих общей линии действия. Он просто производит вращение, а не перемещение. Результирующая сила пары равна нулю. Однако результирующая пары не равна нулю; это чистый момент.

В механике пара определяется как пара равных параллельных сил, направленных в противоположные стороны. Единственный эффект, который может иметь пара, — это то, как поворачивается тело. Величина любой силы умножается на угол между их линиями действия, чтобы получить поворотный эффект или момент пары. Давайте теперь рассмотрим концепции момента пары.

Скачать формулы для машиностроения GATE — Сопротивление материалов

Содержание

  • 1. Что такое момент пары?
  • 2. Характеристики пар
  • 3. Математическое представление момента пары
  • 4. Практическое применение момента пары
Прочитать статью полностью

Что такое момент пары?

Момент пары равен любой силе, умноженной на перпендикулярное расстояние между двумя силами. Когда две равные и противоположно направленные силы приложены одновременно к разным точкам тела, их результирующая сила равна нулю. Тем не менее, эти равные и противоположные силы пытаются повернуть тело в одном направлении. Эти силы называются парами.

Момент пары Пример

Такая пара сил имеет тенденцию вращать это тело. Рассмотрим A и B как две точки на теле, к которым приложены две силы F одинакового результата в противоположных направлениях, параллельных друг другу. Под действием этой силы это тело начинает вращаться против часовой стрелки или пытается повернуться вокруг оси, проходящей через 0. Имейте в виду, что если линии действия этих двух равных сил совпадают или они действуют в то же самое, они будут аннулировать друг друга.

Момент пары PDF

Момент пары действует на тело в результате действия пары, заставляя тело вращаться вокруг фиксированной точки.

СИ Единица момента пары

Пара – это пара сил с одинаковой величиной, но разными линиями действия сил. Произведение любой силы и расстояния между перпендикулярными осями сил дает момент пары. Единицей момента пары в СИ является Нм.

Загрузить формулы для машиностроения GATE — Технология производства и материалы

Характеристики пар

Пара – это пара сил, равных по величине, противоположно направленных и разделенных перпендикулярным расстоянием или моментом. Самый простой тип пары состоит из двух равных и противоположных сил с противоположными линиями действия. Ниже приведены характеристики пары:

  • Пара не производит поступательного движения, потому что две силы, составляющие пару, равны и противоположны.
  • При воздействии на тело чистая результирующая сила, действующая на тело, равна нулю.
  • Чистое вращательное движение тела возникает из-за того, что алгебраическая сумма моментов двух сил вокруг любой точки их плоскости не равна нулю.
  • Момент пары вокруг любой точки своей плоскости фиксирован по размеру и ориентации.

 Математическое представление момента пары

Момент пары математически описывается как произведение силы и перпендикулярного расстояния между линиями действия двух сил. Рукав Пары — это другое название расстояния, которое в данном контексте разделяет направления действия двух сил перпендикулярно друг другу.

Формула момента пары

Приложенная сила, умноженная на сумму плеч любых двух сил, дает момент силы. Следовательно, момент пары сил определяется выражением

Τ = F×d

Формула для момента пары сил ясно говорит, что момент пары сил будет более необыкновенным, если:

  • Сила более значительна по величине.
  • Расстояние между линиями действия двух сил больше, потому что плечо пары сил длиннее.

Скачать формулы для машиностроения ВОРОТ — ТОМ и вибрации

Практическое применение момента пары

Результирующая сила двух равных и противоположно направленных сил, действующих одновременно на различные места тела, равна нулю. Тем не менее, эти силы пытаются вращать тело в том же направлении. Эти силы называются Пара. Пара сил этого типа имеет тенденцию вращать это тело. Ниже приведены практические приложения для пар.

  • Мы нажимаем руками на ручку при повороте движущегося велосипеда.
  • всякий раз, когда мы открываем и закрываем носик крана.
  • Пара усилий выполняется пальцами для открытия и закрытия крышки устройства.
  • Когда ладони обеих рук движутся в противоположном направлении, удерживая карандаш между ними, карандаш начинает вращаться.
  • Другой пример пары, когда маслобойка начинает вращаться, удерживая одной рукой концы веревки, а другую двигая в противоположном направлении.

Часто задаваемые вопросы о моменте пары

  • Почему крутящий момент называется моментом пары?

    Поскольку обе силы действуют на расстоянии, они образуют момент. Это называется моментом пары. Мы также можем обозначить пару как крутящий момент. Это происходит в ответ на формирование вращательного движения тела. Силы, связанные с парой, равны по силе, но по-разному направлены.

  • Что отличает пару от момента пары?

    Пара состоит из двух равных и противоположных сил, которые действуют в двух разных, но параллельных направлениях. Момент силы зависит от размера силы и расстояния от точки опоры, но момент пары является результатом совместного действия двух моментов сил.

  • Что такое формула «Момент пары»?

    Момент сцепления рассчитывается по данной формуле 069 Т есть момент, который измеряется в ньютон-метрах (Нм)

  • Что такое пара силы?

    Пара — это пара сил равной силы, действующих в противоположных направлениях и разделенных перпендикулярным пространством или моментом. Две равные и противоположные силы с расходящимися путями действия составляют простейший тип пары, известный как «простая пара» 9.0003

  • Что такое пара и пример?

    Пара состоит из двух параллельных сил, равных по величине, противоположных по направлению и не имеющих общей линии действия. Он просто производит вращение, а не перемещение. Результирующая сила пары равна нулю. Например, открытие двери.

ESE & GATE ME

Mechanical Engg. GATEGATE MEHPCLBARC SOESEIES MEBARC ExamISRO ExamOther Exams

Избранные статьи

Следите за нашими новостями

Наши приложения

  • BYJU’S Exam Prep: приложение для подготовки к экзаменам
GradeStack Learning Pvt. Ltd.Windsor IT Park, Tower — A, 2nd Floor,

Sector 125, Noida,

Uttar Pradesh 201303

[email protected]

3.3: Пары — Engineering LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    50581
    • Джейкоб Мур и участники
    • Университет штата Пенсильвания Мон-Альто via Mechanics Map 9 0018

    Пара представляет собой набор равных и противоположных сил, которые действуют на объект как результирующий момент, но не результирующая сила. Поскольку пара проявляет чистый момент без приложения чистой силы, пары также иногда называют 9.0069 чистых мгновений .

    Рисунок \(\PageIndex{1}\): Две равные и противоположные силы, действующие на этот гаечный ключ, представляют собой пару. Они воздействуют на зажимную гайку на этом колесе, не оказывая никакого чистого усилия на колесо. Адаптировано из изображения Steffen Heinz Caronna CC-BY-SA 3.0.

    Момент, создаваемый парой, также отличается от момента, создаваемого одиночной силой, тем, что он не зависит от места, в котором вы берете момент. В приведенном ниже примере у нас есть пара, действующая на балку. Каждая сила имеет величину \(F\), а расстояние между двумя силами равно \(d\).

    Рисунок \(\PageIndex{2}\): Момент, создаваемый этой парой, не зависит от расстояния \(x\).

    Теперь у нас есть некоторая точка A, которая находится на расстоянии \(x\) от первой из двух сил. Если мы возьмем момент каждой силы относительно точки А, а затем сложим эти моменты вместе для чистого момента относительно точки А, мы получим следующую формулу.

    \[ M \, = \, -(F*x) + (F*(x+d)) \] Если мы переформулируем и упростим приведенную выше формулу, мы увидим, что переменная \(x\) фактически исчезает из уравнение, оставляя чистый момент равным величине сил (\ (F \)) умноженной на расстояние между двумя силами (\ (d \)).

    \[ М \, = \, -(F*x) + (F*x) + (F*d) \]

    \[ М \, = \, (F*d) \]

    Это означает, что независимо от того, какое значение \(х\) мы имеем, величина момента, создаваемого парой, будет одинаковой. Величина момента, связанного с парой, не зависит от места, в котором мы фиксируем момент. Это будет работать в двух или трех измерениях. Величина момента из-за пары всегда будет равна величине сил, умноженной на перпендикулярное расстояние между двумя силами.

    Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник YouTube: https://youtu.be/2U4APUz__Gk.

    Пример \(\PageIndex{1}\)

    Какой момент действует на пару ниже относительно точки A?

    Рисунок \(\PageIndex{3}\): схема проблемы для примера \(\PageIndex{1}\). К стержню приложена пара, причем каждая сила равноудалена от точки А на стержне.
    Раствор
    Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/rfD-b6V5qNY.

    Пример \(\PageIndex{2}\)

    Какой момент действует на пару ниже относительно точки A?

    Рисунок \(\PageIndex{4}\): схема проблемы для примера \(\PageIndex{2}\). Пара приложена к стержню, причем одна сила приложена непосредственно к точке А, а другая приложена на 1,5 метра вправо от точки А.
    Решение
    Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром.

    alexxlab

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *