Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика
Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Момент силы относительно точки Алгебраический момент силы Основные типы связей и их реакции Упражнения ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ Сходящиеся силы. Приведение сходящихся сил к простейшему виду Вычисление и построение равнодействующей Условия равновесия сходящихся сил Теорема о трех силах Теорема Вариньона Пара сил и ее момент Приведение системы пар сил к простейшему виду или сложение пар сил Упражнения ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ Аналитический способ вычисления момента Геометрический способ вычисления момента Преобразование пространственной произвольной системы сил Приведение пространственной произвольной системы сил к данному центру.  Главный вектор и главный момент. Основная теорема статикиВычисление и построение главного вектора и главного момента Перемена центра приведения ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ Случаи приведения к простейшему виду Частные случаи системы сил Плоская система сил Система параллельных сил Равновесие системы тел Вопросы для самопроверки ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ Центр параллельных сил Распределенные силы Центр тяжести Интегральные формулы для координат центра тяжести Метод разбиения Вопросы для самопроверки ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ Трение покоя и трение скольжения Трение качения Решение задач статики при учете сил трения Заклинивание Упражнения КИНЕМАТИКА ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ Способы задания движения точки Определение траектории, скорости и ускорения точки при координатном способе задания движения Определение скорости и ускорения точки при естественном способе задания движения Естественные координатные оси и их орты Определение скорости Определение ускорения Вопросы для самопроверки ЛЕКЦИЯ 8. 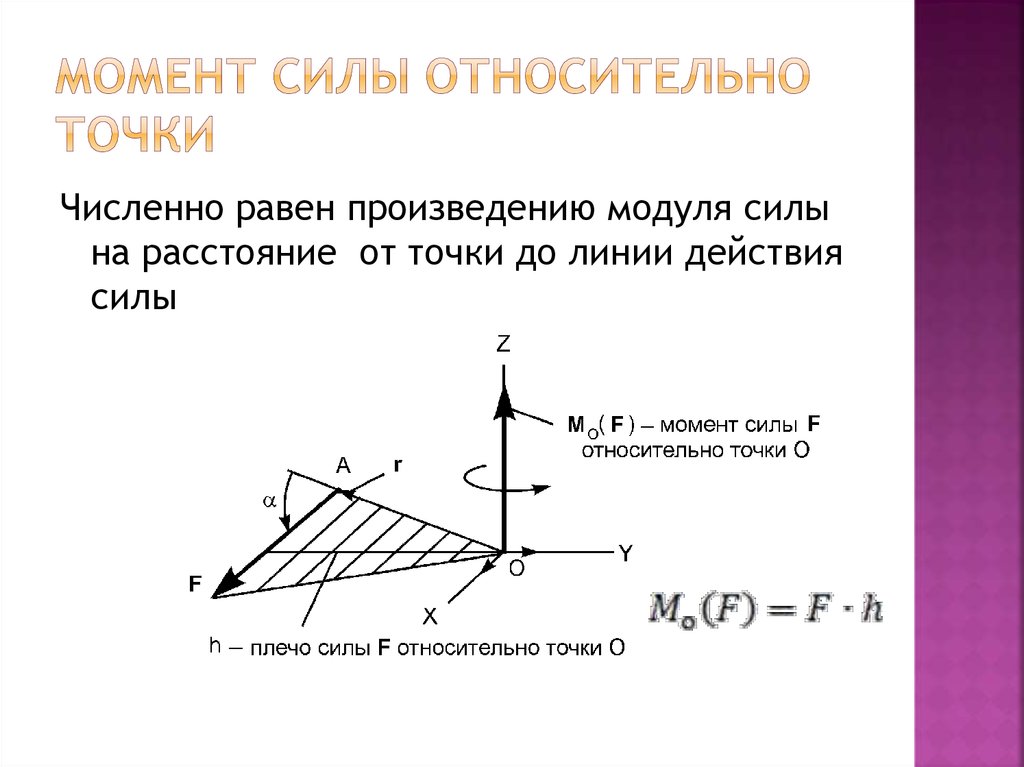 ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛАПоступательное движение Вращательное движение Уравнение вращательного движения. Угловая скорость и угловое ускорение тела Векторы угловой скорости и углового ускорения тела Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела Вопросы для самопроверки ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Уравнения движения Угловая скорость и угловое ускорение тела при плоскопараллельном движении Определение скоростей точек тела. Метод полюса Мгновенный центр скоростей Определение скоростей точек плоской фигуры через мгновенный центр скоростей Различные случаи определения положения мгновенного центра скоростей Определение ускорений точек тела Вопросы для самопроверки ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Теорема сложения ускорений Причины появления ускорения Кориолиса Вычисление и построение ускорения Кориолиса Вопросы для самопроверки ДОБАВЛЕНИЕ. 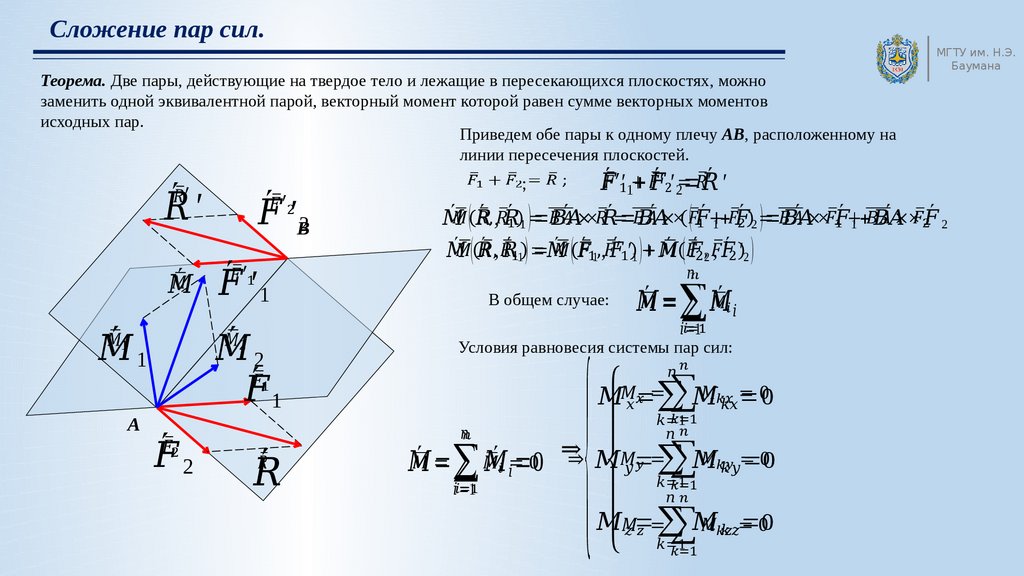 КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫСхема и расчетная модель процесса фугования Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке Геометрические характеристики поверхности в случае многоножевой головки РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА |
Пара сил и момент силы относительно точки
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. ПАРА СИЛ И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
2.
СОДЕРЖАНИЕ1. Пара сил.2. Свойство пар.
3. Сложение пар сил.
Условие равновесия пар.
4. Момент силы относительно точки.
3. ПАРА СИЛ
Парой силы – называется системадвух сил, равных по модулю, параллельных и направленных в
разные стороны.
Пара сил вызывает вращение тела и её действие на тело оценивается моментом М .
Силы входящие в пару не уравновешиваются, т.к. они приложены
к двум точкам. Их действие на
тело не может быть заменено одной
силой (равнодействующей).
Момент пары силы численно равен произведению
модуля силы на расстояние между линиями действия
сил (плечо пары).
Момент считают положительным, если пара вращает тело по часовой стрелке М > 0.
Плечо пары сил – это кратчайшее расстояние между
линиями действия сил F, F’.
Плоскость, проходящая через линии действия сил
пары, называется плоскостью действия пары.
Вращательное действие пары сил на тело зависит не
только от численного значения её момента, но и от положения плоскости действия пары.
Поэтому моментпары можно рассматривать как векторную величину
Вектор момента пары перпендикулярен плоскости
пары, причем если пара стремится повернуть плоскость против хода часовой стрелки, то вектор момента
направлен к нам и наоборот, если пара поворачивает
по часовой стрелке, то вектор момента пары направлен от нас ( правило винта с правой нарезкой ).
6. СВОЙСТВО ПАР
1). ТЕОРЕМА 1. Пару сил можно перемещать в плоскости её действия в любое новое положение, действие пары на тело приэтом не изменится.
2). ТЕОРЕМА 2. Две пары, расположенные
в одной плоскости, момент которых равны
– эквивалентны (действие их на тело
аналогично).
7. СЛОЖЕНИЕ ПАР СИЛ
Систему пар сил можно заменить равнодействующей парой.Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему.
Если в результате сложения
пар
, то действующие
на тело пары сил образуют
уравновешенную систему.
Условие равновесия системы пар:
Для равновесия системы пар сил, действующих на
тело в одной плоскости, необходимо и достаточно,
чтобы алгебраическая сумма их моментов была
равна нулю.
9. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
Моментом силы относительно точки называетсявзятое со знаком + или – произведение модуля силы
на кратчайшее расстояние от точки до линии действия
силы.
Точка О, относительно которой берется момент, называется центром момента.
Плечом силы относительно точки называется кратчайшее расстояние от точки до линии действия силы.
Знак + ставится в случае, если сила стремится повернуть тело вокруг данной точки по ходу часовой
стрелки.
11. ДОМАШНЕЕ ЗАДАНИЕ
А.И. Аркуша ,,Теническая механика”Стр. 35 – 44
В.П. Олофинская ,,Теническая механика”
Стр. 28 – 32
Лекции
English Русский Правила
Карта механики — Разложение силы на силу и пару
Как обсуждалось на странице моментов, сила может иметь тенденцию вызывать как линейное, так и угловое ускорение. Например, ниже приведена схема силы, действующей на протяженное тело. Если бы мы думали обо всем относительно центра масс этого тела, то на центр масс действовала бы некоторая сила, вызывающая такое же линейное ускорение, и некий чистый момент (пара), вызывающий такое же угловое ускорение.
Это будет сила и пара, которая равна статически эквивалентен исходной силе , хотя точка приложения силы меняется.
Процесс преобразования одной силы, приложенной в одной точке, в силу и пару в какой-то другой точке известен как разложение силы на силу и пару . Есть несколько причин, по которым мы можем захотеть это сделать, но одна из основных причин заключается в том, чтобы найти эквивалентную систему пары сил для сложного набора сил и моментов. Система эквивалентной пары сил используется для упрощения более сложного анализа и состоит из одной силы и одного чистого момента (пары), которые статически эквивалентны некоторой более сложной комбинации сил и моментов. Важным первым шагом в поиске эквивалентной системы пары сил является определение всех сил так, чтобы все они действовали в одной и той же точке.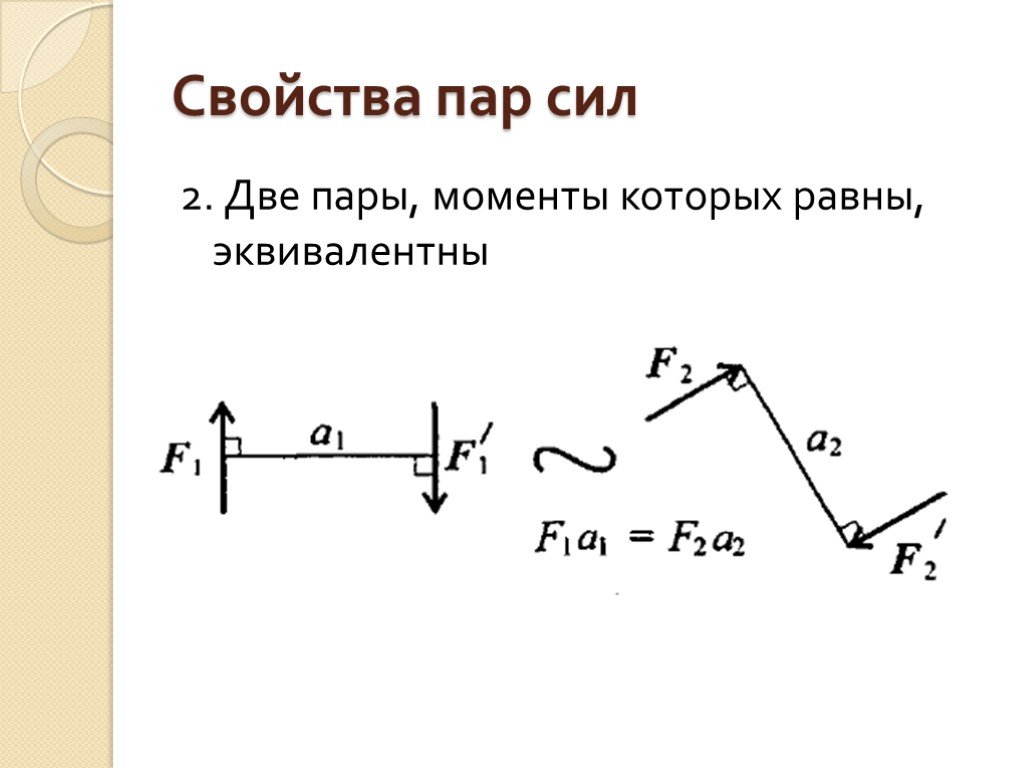
Чтобы визуализировать процесс разложения силы на силу и пару, вы можете использовать процесс, показанный на диаграмме ниже. Представьте, что у нас есть тело с силой, действующей в некоторой точке A. Мы хотим разложить эту силу на силу и пару относительно некоторой другой точки B. Для этого мы сначала добавим на диаграмму две силы в точке B. Одна будет имеют ту же величину и направление, что и первоначальная сила, а другая будет равна и противоположна первоначальной силе. Поскольку эти две силы равны, противоположны и коллинеарны, это не изменит ситуацию (это эквивалентно добавлению нуля к уравнению). Теперь, когда эти три силы действуют на диаграмму, мы можем разбить ее на две части. Первая — это сила, действующая в точке В с той же величиной и направлением, что и первоначальная сила. Две другие силы действуют как пара, прилагая чистый момент к точке B. Наконец, мы можем перерисовать систему как силу, действующую в точке B, и чистый момент, действующий вокруг точки B.
Процесс разложения силы относительно некоторой точки A на силу и пару относительно некоторой точки B.
и направление равно исходной силе, а пара будет равна моменту, действующему исходной силе на новую точку приложения.механик —
механик — Этот момент может быть представлен вектором M o перпендикулярно плоскости и
направлена в направлении +z, если сила F направлена в направлении +x
декартова система координат с началом в точке O. Расстояние d известно
как плечо момента силы и перпендикулярно направлению
сила. Если
в плоскости действуют несколько сил на разных расстояниях d Два
параллельные, но противоположно направленные силы равной величины, F, составляют
пара.» Если эти силы находятся на расстоянии d от связанного момента
с парой М
= Фд.  | ||||||||||||||
