Момент силы. Пара сил и ее свойства контрольная 2010 по физике | Экзамены Физика
Скачай Момент силы. Пара сил и ее свойства контрольная 2010 по физике и еще Экзамены в формате PDF Физика только на Docsity! 1. Плоская система сходящихся сил Система сходящихся сил находится в равновесии, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю. Проекция силы на ось. Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной. Проекция вектора считается положительной (+), если направление от начала к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (-), если направление от начала проекции к ее концу противоположно положительному направлению оси. Если сила совпадает с положительным направлением оси, но угол будет тупой – тогда проекция силы на ось будет отрицательною. Итак, проекция силы на ось координат равна произведению модуля силы на косинус или синус угла между вектором силы и положительным направлением оси. Силу, расположенную на плоскости хОу, можно спроецировать на две координатные оси Ох и Оу: ; ; . Проекция векторной суммы на ось. Геометрическая сумма, или равнодействующая, этих сил определяется замыкающей стороной силового многоугольника: , где п – число слагаемых векторов. Итак, проекция векторной суммы или равнодействующей на какую- либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. 2. Пара сил Сумма проекций пары сил на ось х и на ось у равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил находится в равновесии. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента: Кратчайшее расстояние между линиями действия сил называется – плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.
Силу, расположенную на плоскости хОу, можно спроецировать на две координатные оси Ох и Оу: ; ; . Проекция векторной суммы на ось. Геометрическая сумма, или равнодействующая, этих сил определяется замыкающей стороной силового многоугольника: , где п – число слагаемых векторов. Итак, проекция векторной суммы или равнодействующей на какую- либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. 2. Пара сил Сумма проекций пары сил на ось х и на ось у равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил находится в равновесии. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента: Кратчайшее расстояние между линиями действия сил называется – плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо. Момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения. Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки, и отрицательным, если – против часовой стрелки. Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой механическое состояние тела не изменяется, т.е. не изменяется движение тела или не нарушается его равновесие. Следовательно, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью. 3. Метод кинетостатики Представим себе материальную точку массой т, движущуюся с ускорением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F. Воспользуемся одной из известных нам формул (основным уравнением динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики): F = ma.
Момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения. Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки, и отрицательным, если – против часовой стрелки. Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой механическое состояние тела не изменяется, т.е. не изменяется движение тела или не нарушается его равновесие. Следовательно, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью. 3. Метод кинетостатики Представим себе материальную точку массой т, движущуюся с ускорением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F. Воспользуемся одной из известных нам формул (основным уравнением динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики): F = ma. Перепишем это уравнение в следующем виде: F + (-/ma) = 0. Выражение обозначается Кин и называется силой инерции: Kин= -mа. Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению. Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717—1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, в действительности является видоизмененным уравнением движения материальной точки. Принцип Даламбера формулируется гак: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, в результате чего оно будет действовать на связь, вызывающую ускорение, с силой, равной силе инерции.
Перепишем это уравнение в следующем виде: F + (-/ma) = 0. Выражение обозначается Кин и называется силой инерции: Kин= -mа. Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению. Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717—1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, в действительности является видоизмененным уравнением движения материальной точки. Принцип Даламбера формулируется гак: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, в результате чего оно будет действовать на связь, вызывающую ускорение, с силой, равной силе инерции. В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями. Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести. 4. Момент силы относительно точки Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы. Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519).
В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями. Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести. 4. Момент силы относительно точки Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы. Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519). Моментом силы относительно точки называется произведение модуля силы на ее плечо: М0(¥) = РИ. Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину. Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю Зная две проекции Рх и Ру, из треугольника ЛВС определяем модуль и направление вектора силы Р по следующим формулам: Р = у/Р* + Р*, направляющий тангенс угла между вектором силы Р и осью х 1ёа = Ру/Рх. Отметим, что силу Р можно представить как равнодействующую двух составляющих сил Рх и Р, параллельных осям координат (рис. 2.3). Составляющие Рх и Ру и проекции Рх и Ру принципиально отличны друг от друга, так как составляющая есть величина векторная, а проекция — величина алгебраическая; но проекции силы на две взаимно перпендикулярные оси х и у и модули составляющих той же силы соответственно численно равны, когда сила разлагается по двум взаимно перпендикулярным направлениям, параллельным осям х и у. Очевидно, что, согласно третьему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению.
Моментом силы относительно точки называется произведение модуля силы на ее плечо: М0(¥) = РИ. Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину. Если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю Зная две проекции Рх и Ру, из треугольника ЛВС определяем модуль и направление вектора силы Р по следующим формулам: Р = у/Р* + Р*, направляющий тангенс угла между вектором силы Р и осью х 1ёа = Ру/Рх. Отметим, что силу Р можно представить как равнодействующую двух составляющих сил Рх и Р, параллельных осям координат (рис. 2.3). Составляющие Рх и Ру и проекции Рх и Ру принципиально отличны друг от друга, так как составляющая есть величина векторная, а проекция — величина алгебраическая; но проекции силы на две взаимно перпендикулярные оси х и у и модули составляющих той же силы соответственно численно равны, когда сила разлагается по двум взаимно перпендикулярным направлениям, параллельным осям х и у. Очевидно, что, согласно третьему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению.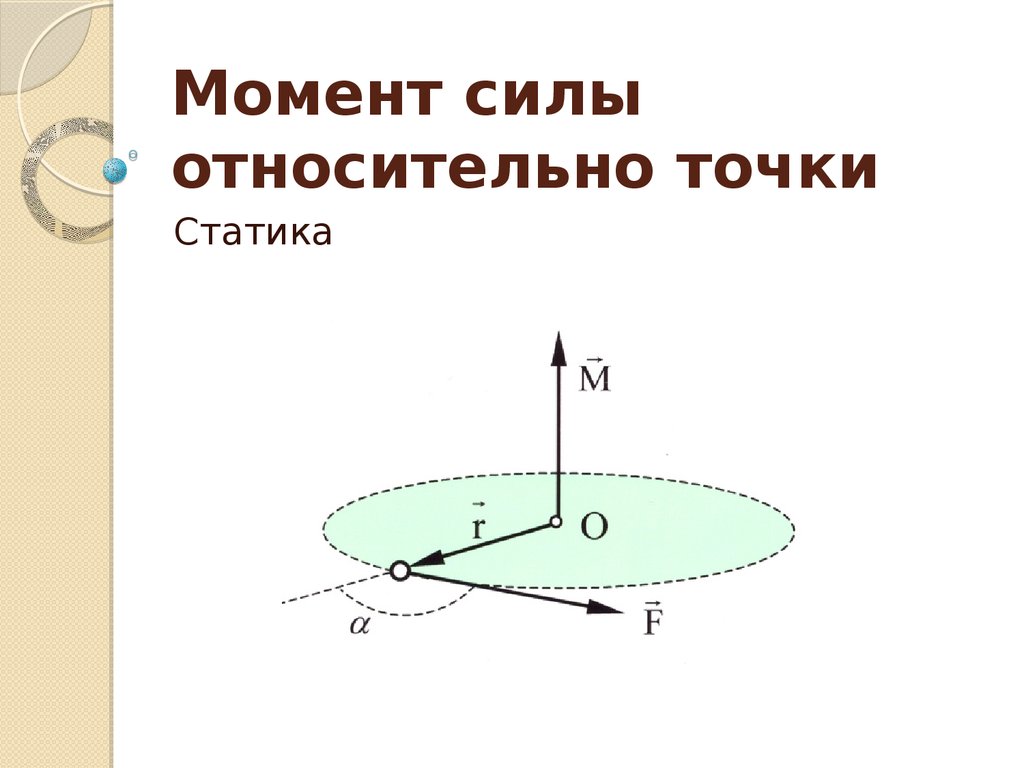 Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще. Далее перейдем к рассмотрению основных деформаций. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации: 1. растяжение; эту деформацию испытывают, например, канаты, тросы, цепи, шток протяжного станка; 2. сжатие; на сжатие работают, например, колонны, кирпичная кладка, пуансоны штампов; 3. сдвиг; деформацию сдвига испытывают заклепки, болты, шпонки, швы сварных соединений. Деформацию сдвига, до- веденную до разрушения материала, называют срезом. Срез возникает, например, при резке ножницами или штамповке деталей из листового материала; 4. кручение; на кручение работают валы, передающие мощность при вращательном движении. Обычно деформация кручения сопровождается другими деформациями, например изгибом; 5. изгиб; на изгиб работают балки, оси, зубья зубчатых колес и другие элементы конструкций.
Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще. Далее перейдем к рассмотрению основных деформаций. Из практики известно, что в процессе эксплуатации элементы конструкций испытывают следующие основные деформации: 1. растяжение; эту деформацию испытывают, например, канаты, тросы, цепи, шток протяжного станка; 2. сжатие; на сжатие работают, например, колонны, кирпичная кладка, пуансоны штампов; 3. сдвиг; деформацию сдвига испытывают заклепки, болты, шпонки, швы сварных соединений. Деформацию сдвига, до- веденную до разрушения материала, называют срезом. Срез возникает, например, при резке ножницами или штамповке деталей из листового материала; 4. кручение; на кручение работают валы, передающие мощность при вращательном движении. Обычно деформация кручения сопровождается другими деформациями, например изгибом; 5. изгиб; на изгиб работают балки, оси, зубья зубчатых колес и другие элементы конструкций.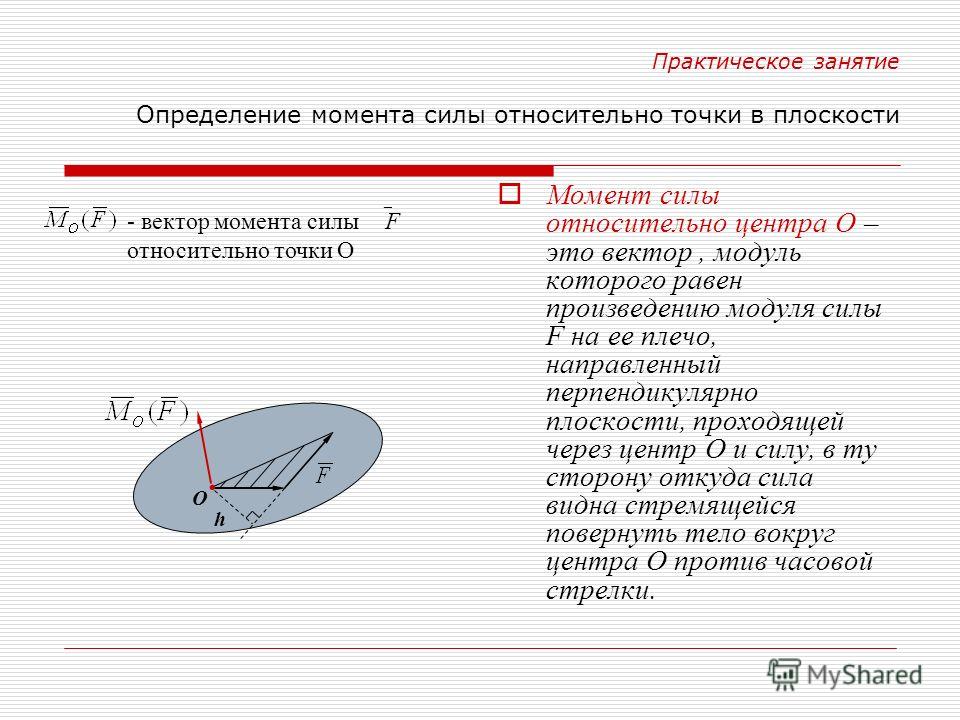 Очень часто элементы конструкций подвергаются действию нагрузок, вызывающих одновременно несколько основных деформаций. Так, например, в теоретической механике мы рассмотрели усилия, действующие на колесо червячной передачи. Очевидно, что в этом случае возникают следующие деформации вала червячного колеса: Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635 — 1703). Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Коэффициент пропорциональности Е характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода. Модуль упругости и напряжение выражаются в одинаковых единицах: [£] = [а]/[8] = Па.
Очень часто элементы конструкций подвергаются действию нагрузок, вызывающих одновременно несколько основных деформаций. Так, например, в теоретической механике мы рассмотрели усилия, действующие на колесо червячной передачи. Очевидно, что в этом случае возникают следующие деформации вала червячного колеса: Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635 — 1703). Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Коэффициент пропорциональности Е характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода. Модуль упругости и напряжение выражаются в одинаковых единицах: [£] = [а]/[8] = Па. Значения Е, МПа, для некоторых материалов: Чугун (1,5…1,6) 105 Сталь (1,96…2,16) 105 Диаграмма растяжения низкоуглеродистой стали представлена на рис. 19.6. Эта диаграмма имеет следующие характерные точки. Точка А практически соответствует и другому пределу, который называется пределом упругости. Пределом упругости ауп называется то наибольшее напряжение, до которого деформации практически остаются упругими. Точка С соответствует пределу текучести. Пределом текучести ат называется такое напряжение, при котором в образце появляется заметное удлинение без увеличения нагрузки. При достижении предела текучести поверхность образца становится матовой, так как на ней появляется сетка линий Людерса-Чернова, наклоненных к оси под углом 45°. Эти линии впервые были описаны в 1859 г. немецким металлургом Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839—1921), предложившим использовать их при экспериментальном изучении напряжений в сложных деталях. Предел текучести является основной механической характеристикой при оценке прочности пластичных материалов.
Значения Е, МПа, для некоторых материалов: Чугун (1,5…1,6) 105 Сталь (1,96…2,16) 105 Диаграмма растяжения низкоуглеродистой стали представлена на рис. 19.6. Эта диаграмма имеет следующие характерные точки. Точка А практически соответствует и другому пределу, который называется пределом упругости. Пределом упругости ауп называется то наибольшее напряжение, до которого деформации практически остаются упругими. Точка С соответствует пределу текучести. Пределом текучести ат называется такое напряжение, при котором в образце появляется заметное удлинение без увеличения нагрузки. При достижении предела текучести поверхность образца становится матовой, так как на ней появляется сетка линий Людерса-Чернова, наклоненных к оси под углом 45°. Эти линии впервые были описаны в 1859 г. немецким металлургом Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839—1921), предложившим использовать их при экспериментальном изучении напряжений в сложных деталях. Предел текучести является основной механической характеристикой при оценке прочности пластичных материалов. Точка В соответствует временному сопротивлению или пределу прочности. Временным сопротивлением ав называется условное напряжение, равное отношению максимальной силы, которую выдерживает образец, к первоначальной площади его поперечного сечения (для стали СтЗ ав400 МПа). При достижении временного сопротивления на растягиваемом образце образуется местное сужение — шейка, т. е. начинается разрушение образца. В определении временного сопротивления говорится об условном напряжении, так как в сечениях шейки напряжения будут больше. Пределом прочности апч называется временное сопротивление образца, разрушающегося без образования шейки. Предел прочности является основной механической характеристикой при оценке прочности хрупких материалов. Точка И соответствует напряжению, возникающему в образце в момент разрыва во всех поперечных сечениях, кроме сечений шейки. Точка М соответствует напряжению, возникающему в наименьшем поперечном сечении шейки в момент разрыва. Это напряжение можно назвать напряжением разрыва.
Точка В соответствует временному сопротивлению или пределу прочности. Временным сопротивлением ав называется условное напряжение, равное отношению максимальной силы, которую выдерживает образец, к первоначальной площади его поперечного сечения (для стали СтЗ ав400 МПа). При достижении временного сопротивления на растягиваемом образце образуется местное сужение — шейка, т. е. начинается разрушение образца. В определении временного сопротивления говорится об условном напряжении, так как в сечениях шейки напряжения будут больше. Пределом прочности апч называется временное сопротивление образца, разрушающегося без образования шейки. Предел прочности является основной механической характеристикой при оценке прочности хрупких материалов. Точка И соответствует напряжению, возникающему в образце в момент разрыва во всех поперечных сечениях, кроме сечений шейки. Точка М соответствует напряжению, возникающему в наименьшем поперечном сечении шейки в момент разрыва. Это напряжение можно назвать напряжением разрыва. 6. Расчетная формула при растяжении и сжатии Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных. Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой я: Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным. Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [д]. Допускаемый коэффициент запаса прочности зависит от свойств, качества и однородности материала, точности представления о нагрузках, действующих на конструкцию, ответственности
6. Расчетная формула при растяжении и сжатии Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных. Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой я: Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным. Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [д]. Допускаемый коэффициент запаса прочности зависит от свойств, качества и однородности материала, точности представления о нагрузках, действующих на конструкцию, ответственности
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 11Следующая ⇒ Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Рассмотрим силу , приложенную в точке А твердого тела (рис. 20). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы , называется плечом силы относительно центра О. Так как точку приложения силы можно произвольно перемещать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть: 1) от модуля силы F и длины плеча h; 2) от положения плоскости поворота ОАВ, проходящей через центр О и силуF; 3) от направления поворота к этой плоскости. Рис.20
Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается. Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча. Момент силы относительно центра О будем обозначать символом В дальнейшем условимся считать, что момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки, и знак минус, — если по ходу часовой стрелки. Так, для силы , изображенной на рис.20,а, момент относительно центра О имеет знак плюс, а для силы, показанной на рис.20,б, — знак минус. Отметим следующие свойства момента силы: 1) Момент силы не изменяется при переносе точки приложения силы вдольее линии действия. 2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю). 3) Момент силы численно выражается удвоенной площадью треугольника Этот результат следует из того, что Теорема Вариньона о моменте равнодействующей. Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра. Рис.21
Рассмотрим систему сил , , …, , сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох Для доказательства теоремы найдем соответствующие выражения моментов m0( ), m0( ), … . По формуле . Но, как видно из рисунка, , где F1x — проекция силы на ось Ох; следовательно . Аналогично вычисляются моменты всех других сил. Обозначим равнодействующую сил , , …, , через, где . Тогда, по теореме о проекции суммы сил на ось, получим . или, .
Пара сил. Момент пары. Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис.22). Очевидно, , и . Рис.22
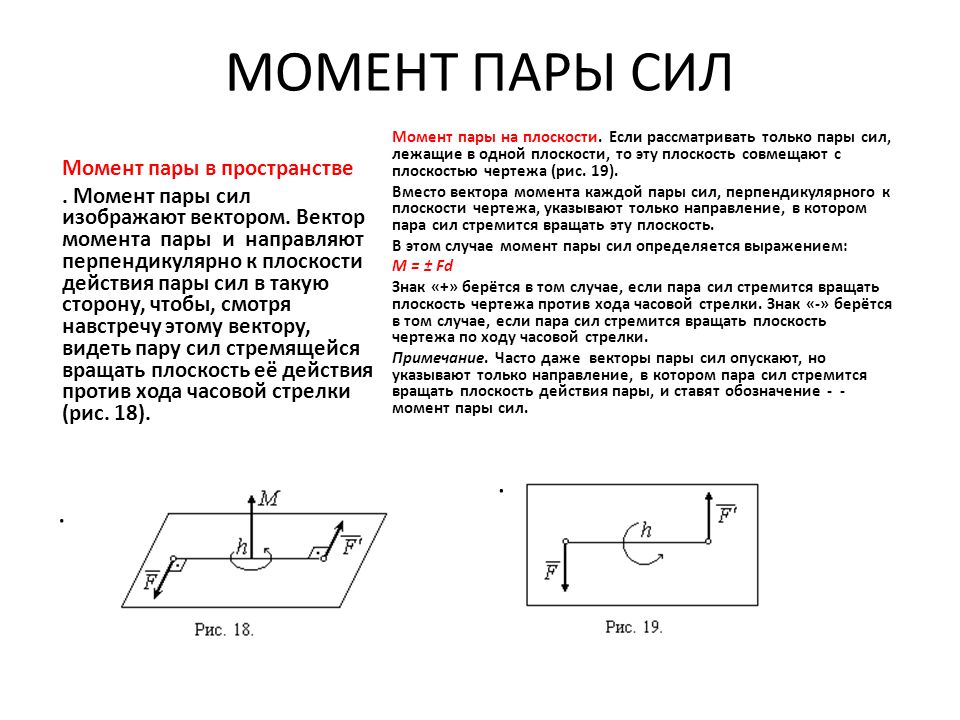
Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары: . Расстояние a между линиями действия сил называется плечом пары. Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором. Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. Нетрудно доказать, что вектор момента пары – есть вектор этого векторного произведения (рис. 23). И заметим, что он равен вектору момента силы относительно точки . О точке приложения вектора будет сказано ниже. Пока приложим его к точке А. Рис.23 Свойства пар 1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил. 2) Найдём сумму моментов сил и составляющих пару, относительно какой-либо точки О (рис.24). Рис.24
Покажем радиусы-векторы точек А1 и А2 и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О . Но . Поэтому . Но , а . Значит . Момент пары сил относительно любой точки равен моменту этой пары. Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Поэтому можно сформулировать ещё два свойства. 3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость. 4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны. Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента 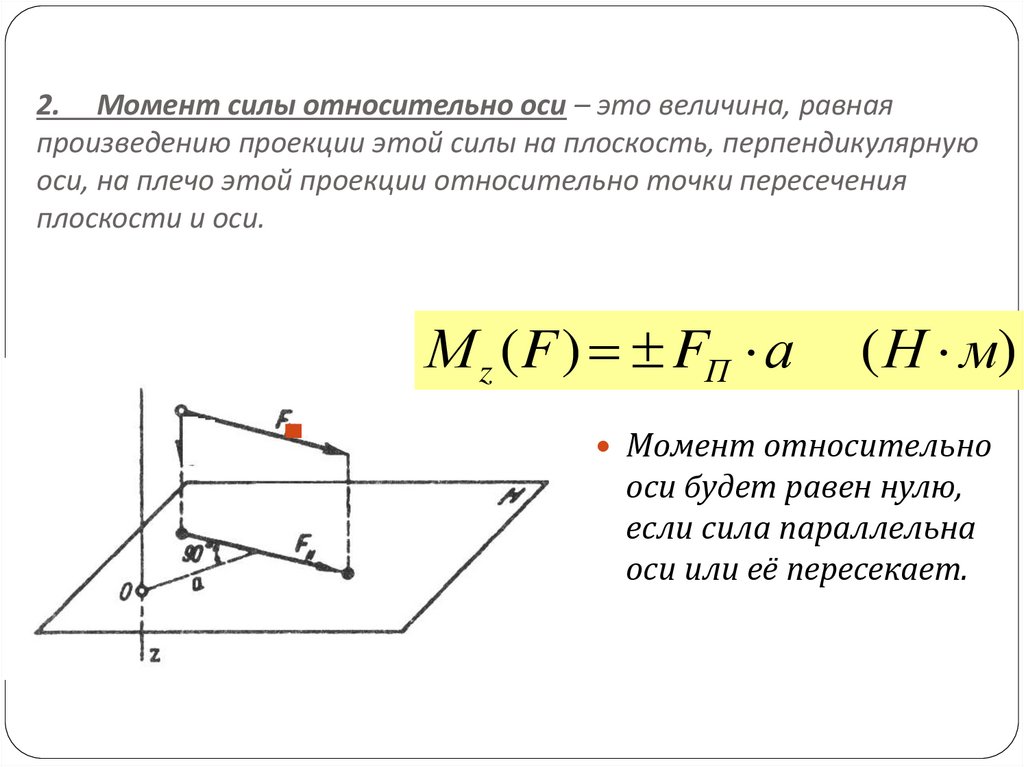 Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары – свободный вектор. Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары – свободный вектор.И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары на эту ось: , где – угол между вектором и осью z. Сложение пар Пусть даны две пары с моментами m1и m2, расположенные в пересекающихся плоскостях (рис.25). Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а образующих вторую пару: . Эти пары показаны на рис.25, где , . И расположены они в своих плоскостях так, что плечи пар совпадают с прямойАВ на линии пересечения плоскостей. Рис.25
Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие и . Так как , то эти силы и будут образовывать пару, момент которой , где – радиус-вектор точкиВ, совпадающий с АВ. Так как , то момент полученной пары . Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар. При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом . Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору . Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар . Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар. Рис.26
Например, пары, показанные на рис.26, расположены в одной плоскости и моменты их: m1=2 Hсм , m2=5 Hсм, m3=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю: . ⇐ Предыдущая12345678910Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
Карта механики — Разложение силы на силу и пару
Как обсуждалось на странице моментов, сила может иметь тенденцию вызывать как линейное, так и угловое ускорение. Например, ниже приведена схема силы, действующей на протяженное тело. Если бы мы думали обо всем относительно центра масс этого тела, то на центр масс действовала бы некоторая сила, вызывающая такое же линейное ускорение, и некий чистый момент (пара), вызывающий такое же угловое ускорение. Это будет сила и пара, которая равна статически эквивалентен исходной силе , хотя точка приложения силы меняется.
Первоначальная сила, действующая на A, вызвала бы как линейное, так и угловое ускорение. Сила в точке B вызовет такое же линейное ускорение, а момент в точке B вызовет такое же угловое ускорение. Сила и момент в B статически эквивалентны первоначальной силе в A. Процесс преобразования одной силы, приложенной в одной точке, в силу и пару в какой-то другой точке известен как разложение силы на силу и пару . Есть несколько причин, по которым мы можем захотеть это сделать, но одна из основных причин заключается в том, чтобы найти эквивалентную систему пары сил для сложного набора сил и моментов. Система эквивалентной пары сил используется для упрощения более сложного анализа и состоит из одной силы и одного чистого момента (пары), которые статически эквивалентны некоторой более сложной комбинации сил и моментов. Важным первым шагом в поиске эквивалентной системы пары сил является определение всех сил так, чтобы все они действовали в одной и той же точке.
Есть несколько причин, по которым мы можем захотеть это сделать, но одна из основных причин заключается в том, чтобы найти эквивалентную систему пары сил для сложного набора сил и моментов. Система эквивалентной пары сил используется для упрощения более сложного анализа и состоит из одной силы и одного чистого момента (пары), которые статически эквивалентны некоторой более сложной комбинации сил и моментов. Важным первым шагом в поиске эквивалентной системы пары сил является определение всех сил так, чтобы все они действовали в одной и той же точке.
Чтобы визуализировать процесс разложения силы на силу и пару, вы можете использовать процесс, показанный на диаграмме ниже. Представьте, что у нас есть тело с силой, действующей в некоторой точке A. Мы хотим разложить эту силу на силу и пару относительно некоторой другой точки B. Для этого мы сначала добавим на диаграмму две силы в точке B. Одна будет имеют ту же величину и направление, что и первоначальная сила, а другая будет равна и противоположна первоначальной силе. Поскольку эти две силы равны, противоположны и коллинеарны, это не изменит ситуацию (это эквивалентно добавлению нуля к уравнению). Теперь, когда эти три силы действуют на диаграмму, мы можем разбить ее на две части. Первая — это сила, действующая в точке В с той же величиной и направлением, что и первоначальная сила. Две другие силы действуют как пара, прилагая чистый момент к точке B. Наконец, мы можем перерисовать систему как силу, действующую в точке B, и чистый момент, действующий вокруг точки B.
Поскольку эти две силы равны, противоположны и коллинеарны, это не изменит ситуацию (это эквивалентно добавлению нуля к уравнению). Теперь, когда эти три силы действуют на диаграмму, мы можем разбить ее на две части. Первая — это сила, действующая в точке В с той же величиной и направлением, что и первоначальная сила. Две другие силы действуют как пара, прилагая чистый момент к точке B. Наконец, мы можем перерисовать систему как силу, действующую в точке B, и чистый момент, действующий вокруг точки B.
Сила, момент и крутящий момент — изучите динамику многотельных систем
Примечание
Вы можете скачать этот пример в виде скрипта Python: load.py или блокнот Jupyter: загружает.ipynb .
импортировать sympy как sm импортируйте sympy.physics.mechanics как я me.init_vprinting(use_latex='mathjax')
класс ReferenceFrame(me.ReferenceFrame):
def __init__(я, *args, **kwargs):
kwargs.pop('латексы', нет)
лаборатория = аргументы [0].нижний()
tex = r'\шляпа{{{}}}_{}'
super(ReferenceFrame, self).__init__(*args,
латекс = (tex.format (лаборатория, 'x'),
tex.format (лаборатория, 'у'),
tex.format (лаборатория, 'z')),
**кваргс)
me.ReferenceFrame = Эталонный кадр
Сила
Сила — это абстракция, которую мы используем для описания того, что заставляет массу
двигаться (т.е. ускоряться из стационарного состояния). Есть четыре основных
сил природы, из которых могут быть получены все остальные силы. Моменты и
крутящие моменты возникают из-за сил и являются абстракциями, полезными для описания того, что вызывает
распределенное вращение массы. Силы, моменты и крутящие моменты имеют величину и
направление, и поэтому мы используем векторы для их математического описания.
Силы, моменты и крутящие моменты имеют величину и
направление, и поэтому мы используем векторы для их математического описания.
Связанные и бесплатные векторы
Векторы могут иметь линию действия . Линия действия параллельна вектору и проходит через определенную точку. Если у вектора есть линия действия, то говорят, что связан с его направлением действия. Если вектор не привязан к линии действие, как говорят, бесплатно .
Угловая скорость является примером свободного вектора. имеет направление и величина, но не связанная с какой-либо линией действия. Вектор силы, на другая рука связана. Если к твердому телу приложена сила, мы должны знать где на теле он применяется для устранения эффекта силы. Вектор силы действует на твердое тело \(B\) в точке \(P\), имеет линию действия, проходящую через \(P\) и параллельно вектору силы. 9{L/P}\) — вектор положения из \(P\) в любую точку \(L\) на линии действия \(\bar{v}\).
Рис. 31 \(\bar{v}\) привязан к линии, проходящей через точку \(L\). момент можно рассчитать на основе вектора положения от \(P\) до любого
точку на линии, например \(L_1,L_2\) или \(L_3\), как показано на рисунке.
момент можно рассчитать на основе вектора положения от \(P\) до любого
точку на линии, например \(L_1,L_2\) или \(L_3\), как показано на рисунке.
Момент может быть результатом набора векторов. результирующих набора \(S\) векторов \(\bar{v}_1,\ldots,\bar{v}_\nu\) определяется как:
(129{S}=0\). Пара, состоящая из двоих векторов называется простой парой . Рис. 32 показывает несколько примеры пар.
Рис. 32 Три пары: а) простая пара, б) и в) пары, состоящие из нескольких сил
Крутящий момент пары, \(\bar{T}\), это момент пары относительно a точка. Поскольку равнодействующая пары равна нулю, крутящий момент пары равен так по всем пунктам. Крутящий момент, будучи моментом, также является вектором.
Эквивалентность и замена
Два набора связанных векторов эквивалентны , если они обладают следующими двумя свойствами:
равные результаты
равные моменты около любые точки
Если 1. и 2. верны, говорят, что наборы являются заменами друг друга.
Пары с равными крутящими моментами эквивалентны, потому что равнодействующие равны нулю.
а моменты относительно любой точки равны крутящему моменту.
и 2. верны, говорят, что наборы являются заменами друг друга.
Пары с равными крутящими моментами эквивалентны, потому что равнодействующие равны нулю.
а моменты относительно любой точки равны крутящему моменту.
Дан набор связанных векторов \(S\) и набор связанных векторов, состоящих из момента пары \(\bar{T}\) и вектора \(\bar{v}\), связанных с произвольной точки \(P\) является необходимым и достаточным условием того, что второй сет является заменой первого if([Kane19{S/P}\end{split}\]
Это означает, что каждый набор связанных векторов может быть заменен эквивалентным крутящий момент пары и одиночный связанный вектор, который является результирующей заменил комплект. Эта замена упрощает описание сил, действующих на тела.
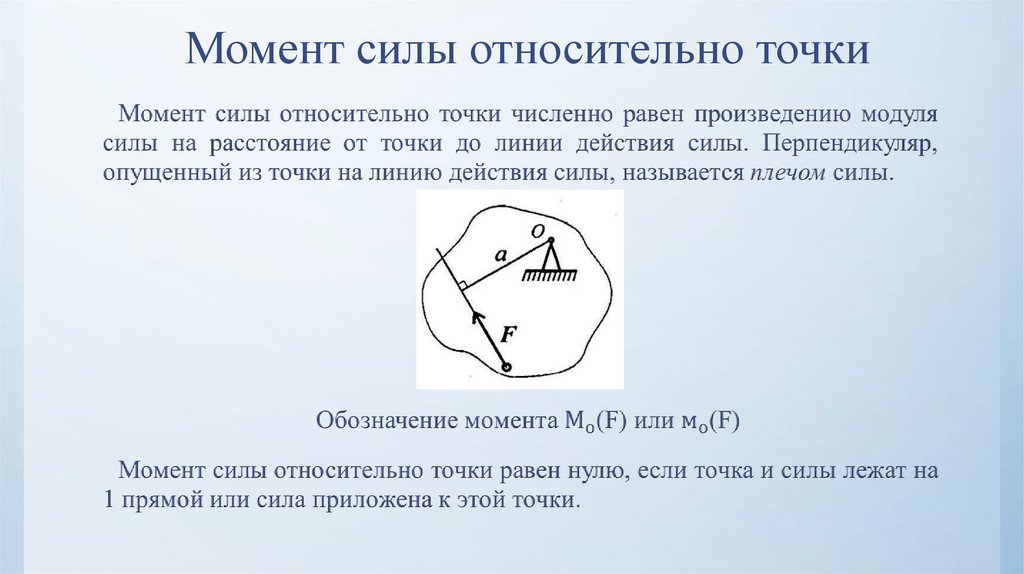
Возьмем, к примеру, вид с высоты птичьего полета четырехколесного автомобиля с передней
рулевое управление и двигатели на каждом колесе, что позволяет точно контролировать
движущие силы на каждом колесе. График сил, действующих на каждое колесо
показан на рис. 33.
33.
Рис. 33 Множество сил, действующих на каждую шину, можно заменить равнодействующей и крутящий момент в указанной точке, в данном случае \(B_o\).
В SymPy Mechanics сначала определите символы:
l, w = sm.symbols('l, w')
Ffl, Ffr, Frl, Frr = me.dynamicsymbols('F_{fl}, F_{fr}, F_{rl}, F_{rr}')
alphafl, alphafr = me.dynamicsymbols(r'\alpha_{fl}, \alpha_{fr}')
alpharl, alpharr = me.dynamicsymbols(r'\alpha_{rl}, \alpha_{rr}')
дельта = я.динамическиесимволы('дельта')
После определения символов я использую некоторые вспомогательные системы отсчета, чтобы установить ориентации с \(B\) позади кузова автомобиля, \(W\) является управляемые передние колеса, а остальные — для установления направления силы на каждое колесо.
B = я.ReferenceFrame('B')
W = я.ReferenceFrame('W')
FR = я.ReferenceFrame('F_R')
FL = я.ReferenceFrame('F_L')
RR = я.ReferenceFrame('R_R')
RL = me.ReferenceFrame('R_L')
W.ориент_ось (B, дельта, B.z)
FR.orient_axis(W, alphafr, W. z)
FL.orient_axis(W, alphafl, W.z)
RR.orient_axis(B, alpharr, B.z)
RL.orient_axis(B, alpharl, B.z)
z)
FL.orient_axis(W, alphafl, W.z)
RR.orient_axis(B, alpharr, B.z)
RL.orient_axis(B, alpharl, B.z)
Тогда равнодействующая сил, выраженных в системе \(B\), равна:
R = Ffl*FL.x + Ffr*FR.x + Frl*RL.x + Frr*RR.x R.express(B).упростить()
\[\displaystyle (F_{fl} \cos{\left(\alpha_{fl} + \delta \right)} + F_{fr} \cos{\left(\alpha_{fr} + \delta \right )} + F_{rl} \cos{\left(\alpha_{rl} \right)} + F_{rr} \cos{\left(\alpha_{rr} \right)})\hat{b}_x + (F_{fl} \sin{\left(\alpha_{fl} + \delta \right)} + F_{fr} \sin{\left(\alpha_{fr} + \delta \right)} + F_{rl } \sin{\left(\alpha_{rl} \right)} + F_{rr} \sin{\left(\alpha_{rr} \right)})\hat{b}_y\]
Этот результат привязан к линии действия через \(B_o\). Ассоциированный пара затем рассчитывается как общий момент около \(B_o\):
T = (me.cross(l/2*B.x - w/2*B.y, Ffl*FL.x) +
me.cross(l/2*B.x + w/2*B.y, Ffr*FR.x) +
me.cross(-l/2*B.x - w/2*B.y, Frl*RL.x) +
me.cross(-l/2*B.x + w/2*B.y, Frr*RR. x))
T = T.express(B).simplify()
Т
x))
T = T.express(B).simplify()
Т
\[\displaystyle (\frac{\left(l \sin{\left(\alpha_{fl} + \delta \right)} + w \cos{\left(\alpha_{fl} + \delta \right )}\right) F_{fl}}{2} + \frac{\left(l \sin{\left(\alpha_{fr} + \delta \right)} — w \cos{\left(\alpha_{ fr} + \delta \right)}\right) F_{fr}}{2} — \frac{\left(l \sin{\left(\alpha_{rl} \right)} — w \cos{\left (\alpha_{rl} \right)}\right) F_{rl}}{2} — \frac{\left(l \sin{\left(\alpha_{rr} \right)} + w \cos{\ влево(\alpha_{rr} \right)}\right) F_{rr}}{2})\шляпа{b}_z\]
Так как мы всегда можем описать силы, действующие на твердое тело как равнодействующую сила и связанный крутящий момент пары, мы часто будем использовать это в своих интересах. упрощенная форма построения моделей.
Задание сил и крутящих моментов
Силы — это связанные векторы, которые можно считать действующими в определенных точках, поэтому нам всегда будет нужен вектор и точка, чтобы полностью описать силу. Методы и функции в SymPy Mechanics, которые используют силы, обычно требуют кортеж, содержащий точку и вектор, например результирующую силу \(R^{S/B_o}\), действующий на центр масс автомобиля, будет указан как так:
Бо = я.Точка('Бо') сила = (Во, R) сила
(Bo, F_{fr}(t)*F_R.x + F_{fl}(t)*F_L.x + F_{rr}(t)*R_R.x + F_{rl}(t)*R_L .Икс)
Крутящие моменты пары являются свободными векторами (не привязанными к линии действия), но представляют пару, действующую на твердое тело, таким образом, система отсчета, связанная с твердым телом, и вектор, представляющий крутящий момент, будет использоваться для опишите крутящий момент в SymPy Mechanics. Например:
крутящий момент = (В, Т) крутящий момент
(Б,
((l*sin(\alpha_{fl}(t) + delta(t)) + w*cos(\alpha_{fl}(t) + delta(t))*F_{fl}(t)/2 + (l*sin(\alpha_{fr}(t) + delta(t)) - w*cos(\alpha_{fr}(t) + delta(t))*F_{fr}(t)/2 - (l*sin(\alpha_{rl}(t)) - w*cos(\alpha_{rl}(t)))*F_{rl}(t)/2 - (l*sin(\alpha_{rr }(t)) + w*cos(\alpha_{rr}(t)))*F_{rr}(t)/2)*B.z)
Мы часто будем называть силы и крутящие моменты вместе нагрузками .
Равные и противоположные
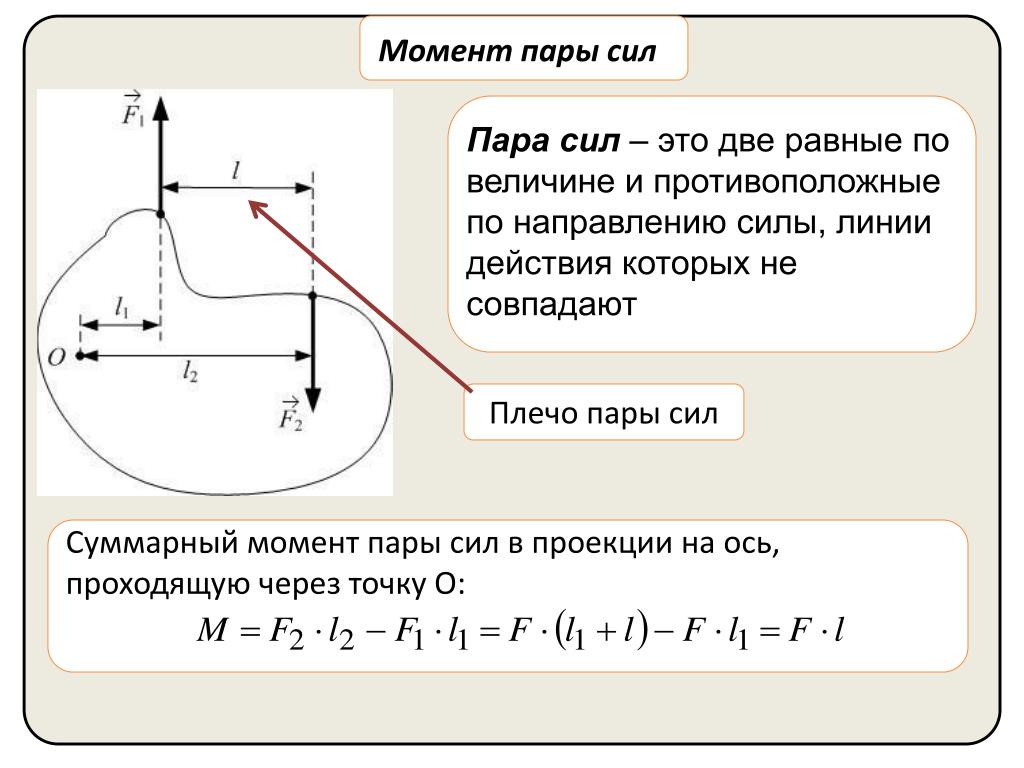
И силы, и крутящие моменты, приложенные к системе из нескольких тел, должны подчиняться третьему закону Ньютона. Закон, т. е. что силы и моменты действуют равны и противоположны. Возьмем, к примеру,
крутящий момент от двигателя, который заставляет шарнирный рычаг \(B\) вращаться относительно
заземление \(N\) показано на рис. 34. Двигатель
можно смоделировать крутящий момент между статором и ротором. У нас есть
произвольно выбрал показанное соглашение о знаках, т. Е. Положительное значение крутящего момента
применяет положительный крутящий момент к \(B\) и отрицательный крутящий момент к \(N\), если
крутящий момент параллелен \(\шляпа{n}_z=\шляпа{b}_z\).
Закон, т. е. что силы и моменты действуют равны и противоположны. Возьмем, к примеру,
крутящий момент от двигателя, который заставляет шарнирный рычаг \(B\) вращаться относительно
заземление \(N\) показано на рис. 34. Двигатель
можно смоделировать крутящий момент между статором и ротором. У нас есть
произвольно выбрал показанное соглашение о знаках, т. Е. Положительное значение крутящего момента
применяет положительный крутящий момент к \(B\) и отрицательный крутящий момент к \(N\), если
крутящий момент параллелен \(\шляпа{n}_z=\шляпа{b}_z\).
Рис. 34 Статор двигателя \(N\), закрепленный на земле, с плечом, прикрепленным к двигателю ротор \(B\) показан как единое целое на а) и как отдельные тела на б) с равные и противоположные векторы крутящего момента, приложенные к паре тел, представляющих крутящий момент пары, создаваемый двигателем.
Момент двигателя может быть задан как изменяющийся во времени вектор:
T, q = me.dynamicsymbols('T, q')
N = я.ReferenceFrame('N')
B = я. ReferenceFrame('B')
Тм = Т*Н.з
ReferenceFrame('B')
Тм = Т*Н.з
Затем равные и противоположные моменты захватываются этими двумя кортежами:
(Б, Тм), (Н, -Тм)
((B, T(t)*N.z), (N, - T(t)*N.z))
с равными и противоположными крутящими моментами, приложенными к каждому телу.
Предупреждение
Условные обозначения на самом деле просто условности. Это также справедливо для выбрать (B, -Tm), (N, Tm) или даже (B, Tm), (N, Tm) и (B, -Tm), (B, -Тм) . Но полезно выбрать соглашение о знаках таким образом, чтобы, когда знаки угловой скорости и крутящего момента одинаковы, это соответствует мощности в система. Так, например, B.orient_axis(N, q, N.z) соответствует (T*N.z, B) и включите питание. Главное, чтобы вы знали, каково ваше соглашение, поэтому что вы можете правильно интерпретировать числовые результаты и знаки.
Предоставляющие и не предоставляющие войска
Содействующие силы — это силы, которые совершают работу в системе с несколькими телами. Работа
сила \(\bar{F}\), действующая на путь \(S\), определяется как:
Работа
сила \(\bar{F}\), действующая на путь \(S\), определяется как:
(133)\[W = \int_S \bar{F} \cdot d\bar{s}\]
, где \(d\bar{s}\) — дифференциальный вектор, касательный к пути в точку приложения силы.
Например, гравитационная сила, действующая на частицу, движущуюся через однонаправленное постоянное гравитационное поле (т.е. где гравитационная сила равно по величине, не меняется и всегда в одном и том же направлении) работает в системе.
Внешние силы не работают с системой. Например, когда сила действует между двумя точками, которые не имеют относительного движения, работа не совершается. Примеры невзаимодействующих сил:
контактные силы на частицы через гладкие (без трения) поверхности твердых тела
любые внутренние контактные и массовые (расстоятельные) силы между любыми двумя точками в жесткий корпус
контактные силы между телами, катящимися без проскальзывания друг относительно друга, которые является частным случаем 1.

В следующей главе мы увидим, как использование обобщенных координат облегчает нам от необходимости указывать какие-либо не содействующие силы.
Гравитация
Нас часто будет интересовать движение системы из нескольких тел, когда оно подвергается к гравитационным силам. Простейший случай – постоянная однонаправленная гравитационное поле, которое является подходящей моделью для объектов, движущихся и вблизи поверхности Земли. Силы гравитации могут быть приложены только к центры масс каждого твердого тела как результирующая сила. Гравитационный крутящий момент на телах равна нулю, так как сила одинакова по модулю для каждой частицы в теле. См. [Kane1985] с. 110 для более общей модели Ньютона. Закон всемирного тяготения, где это не так. Исследования динамика космического корабля часто требует учета как гравитационных сил, так и моменты.
В SymPy Mechanics гравитационная сила, действующая на частицу массы \(m\) с ускорением свободного падения, равным \(g\) в Направление \(-\hat{n}_y\) будет иметь следующий вид:
м, г = sm.symbols('м, г') Fg = -m*g*N.y фг
\[\displaystyle — g m\hat{n}_y\]
Пружины и амортизаторы
Идеализированные пружины и амортизаторы являются полезными моделями элементов, которые имеют расстояние силы и моменты, зависящие от скорости. Пружина свободной длины \(q_0\) и где \(q_1,q_2\) расположите концы пружины вдоль линия, параллельная \(\hat{n}_x\), показана на рис. 35.
Если мы сместим \(P\) в положительном \(\hat{n}_x\) направлении, пружина приложит силу в отрицательном направлении \(\hat{n}_x\) к точке \(П\). Итак, мы выбрали соглашение о знаках, согласно которому сила, действующая на \(P\) со стороны пружина противоположна направлению смещения.
Рис. 35 Схема пружины с условным знаком положительного натяжения. \(P\) показан отдельно от конца пружины, чтобы показать равные и противоположные силы.
Если пружина является линейной с жесткостью \(k\), вектор силы пружины равен тогда:
q0, k = sm.symbols('q0, k')
q1, q2 = me. dynamicsymbols('q1, q2')
водоизмещение = q2 - q1 - q0
смещение
dynamicsymbols('q1, q2')
водоизмещение = q2 - q1 - q0
смещение
\[\displaystyle — q_{0} — q_{1} + q_{2}\]
Здесь положительное смещение представляет растянутую пружину, а отрицательное смещение — это сжатие.
Fs = -k*перемещение*N.x Фс
\[\displaystyle — k \left(- q_{0} — q_{1} + q_{2}\right)\шляпа{n}_x\]
Трение
Демпферы часто используются параллельно или последовательно с пружинами для обеспечения диссипация через вязкоподобное трение. Пружины в сочетании с амортизаторами позволяют классическое движение второго порядка с недо-, пере- и критически затухающим движением. линейный вязкий демпфер с коэффициентом демпфирования \(c\) можно определить так:
c = sm.symbols('c')
t = me.dynamicsymbols._t
Fc = -c*displacement.diff(t)*N.x
ФК
\[\displaystyle — c \left(- \dot{q}_{1} + \dot{q}_{2}\right)\hat{n}_x\]
Закон Кулона обеспечивает простую модель сухого трения между двумя телами. Это принимает скалярную форму:
(134)\[\begin{split}F_f = \begin{случаи} \mu F_N & v < 0 \\ 0 и v = 0 \\ -\mu F_N & v > 0 \end{case}\end{split}\]
, где \(F_N\) — нормальная сила между двумя объектами, \(v\) —
относительная скорость между двумя объектами, а \(\mu\) — коэффициент
трение.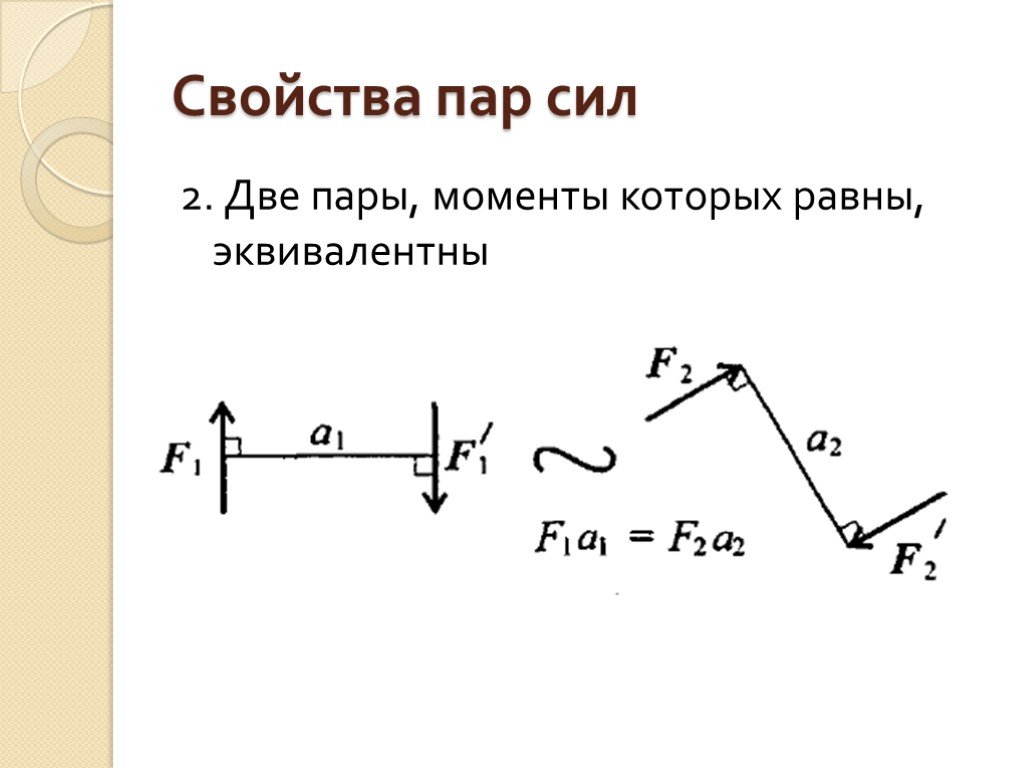
SymPy’s Кусочный один из способов создать символическое представление этой функции:
мю, м, г = sm.symbols('мю, м, г')
Fn = м*г
водоизмещение = q2 - q1
Ff = sm.Piecewise((mu*Fn, offset.diff(t) < 0),
(-mu*Fn, смещение.diff(t) > 0),
(0, Истинно))*Nx
Фф
\[\begin{split}\displaystyle \begin{case} g m \mu & \text{for}\: \dot{q}_{1} — \dot{q}_{2} > 0 \\ — g m \mu & \text{for}\: \dot{q}_{1} — \dot{q}_{2} < 0 \\0 & \text{иначе} \end{case}\hat{ n}_x\end{split}\]
Сигнум-функция
( знак ) также может быть
используется в аналогичной и более простой форме:
Ff = -mu*Fn*sm.sign(displacement.diff(t))*N.x Фф
\[\displaystyle — g m \mu \operatorname{sign}{\left(- \dot{q}_{1} + \dot{q}_{2} \right)}\hat{n}_x\ ]
Аэродинамическое сопротивление
В аэродинамическом сопротивлении тупого тела преобладает сопротивление лобовой области и величина этой силы сопротивления может быть смоделирована с помощью следующего уравнения:
(135)\[\frac{1}{2}\rho C_dAv^2\]
где \(\rho\) плотность воздуха, \(C_d\) сопротивление
коэффициент, \(A\) — площадь фронта, а \(v\) — скорость воздуха
относительно тела.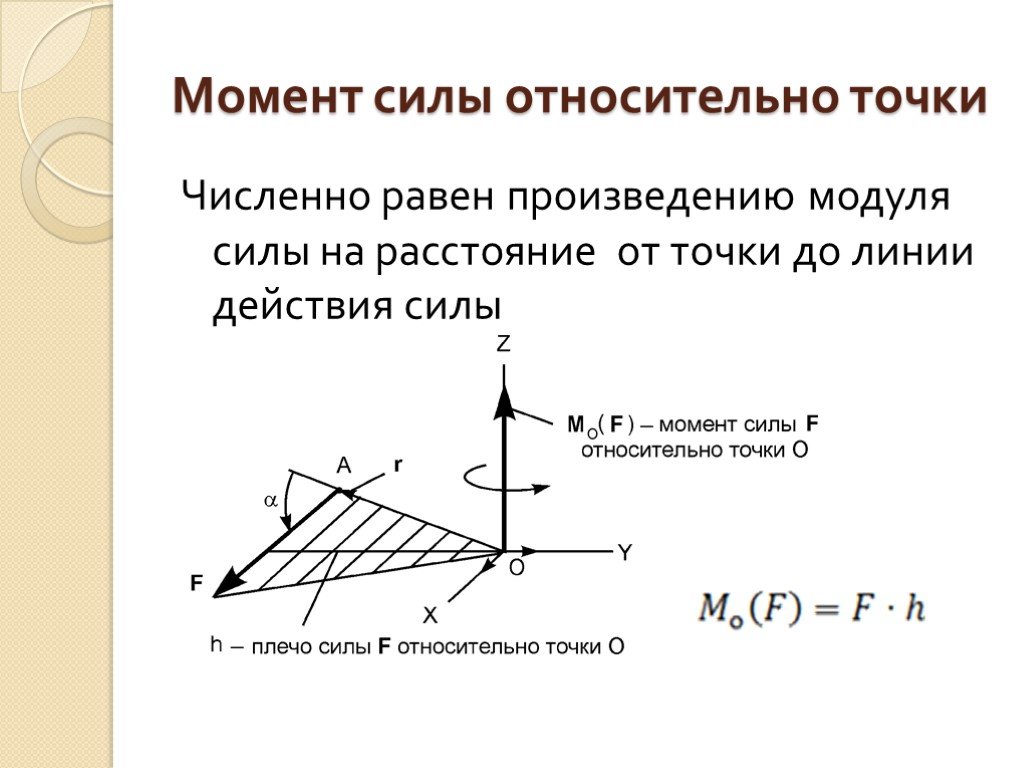
Если тело движется в неподвижном воздухе с произвольной скоростью и точкой \(P\) — аэродинамический центр тела, то вектор силы аэродинамического сопротивления противодействующее движению можно найти с помощью такого уравнения:
A, Cd, rho = sm.symbols('A, C_d, rho')
ux, uy, uz = me.dynamicsymbols('u_x, u_y, u_z', real=True)
N_v_P = ux*N.x + uy*N.y + uz*N.z
Fd = -N_v_P.normalize()*Cd*A*rho/2*N_v_P.dot(N_v_P)
Фд
9{2}} u_{z}}{2}\шляпа{n}_z\]
Если движение происходит только в направлении \(\hat{n}_x\), например,
уравнение для вектора силы сопротивления сводится к:
Fd.xreplace({uy: 0, uz:0})
\[\displaystyle - \frac{A C_{d} \rho u_{x} \left|{u_{x}}\right|}{2}\hat{n}_x\]
Столкновение
Если две точки, точка и поверхность или две поверхности сталкиваются при ударе
поведение зависит от свойств материала и массы сталкивающихся тел.
В общем, упругий и неупругий импульсы уравновешиваются непосредственно до и после
удар может быть решен для системы многих тел. Для более простого, но, как мы будем
учиться, часто менее благоприятный для численного подхода оценки, влияние может быть
захватывается путем создания жесткой пружины, которая срабатывает только в том случае, если одно тело проникает
другое тело. Можно включить некоторое вязкое демпфирование, чтобы уловить неупругий
аспекты. 9{3}\right) \left|{\dot{y}}\right|}{\dot{y}}\hat{n}_y\end{split}\]
Для более простого, но, как мы будем
учиться, часто менее благоприятный для численного подхода оценки, влияние может быть
захватывается путем создания жесткой пружины, которая срабатывает только в том случае, если одно тело проникает
другое тело. Можно включить некоторое вязкое демпфирование, чтобы уловить неупругий
аспекты. 9{3}\right) \left|{\dot{y}}\right|}{\dot{y}}\hat{n}_y\end{split}\]
Эти значения меры для вектора силы затем оцениваются как нуль, когда есть
нет проникновения \(z_p\) и оценивается как пружина и демпфер и Кулон
трения, когда есть. Например, используя такие числовые значения для установки
проникновение:
vz = me.dynamicsymbols('v_z', отрицательный=Истина)
repl = {z.diff(): vz, z: 0}
Fx.xreplace(repl), Fy.xreplace(repl), Fz.xreplace(repl)
\[\displaystyle \left( 0, \ 0, \ 0\right)\]
repl = {z.diff(): vz, z: 2}
Fx.xreplace(repl), Fy.xreplace(repl), Fz.xreplace(repl)
\[\displaystyle \left( 0, \ 0, \ 0\right)\]
repl = {z.


 — КиберПедия
— КиберПедия



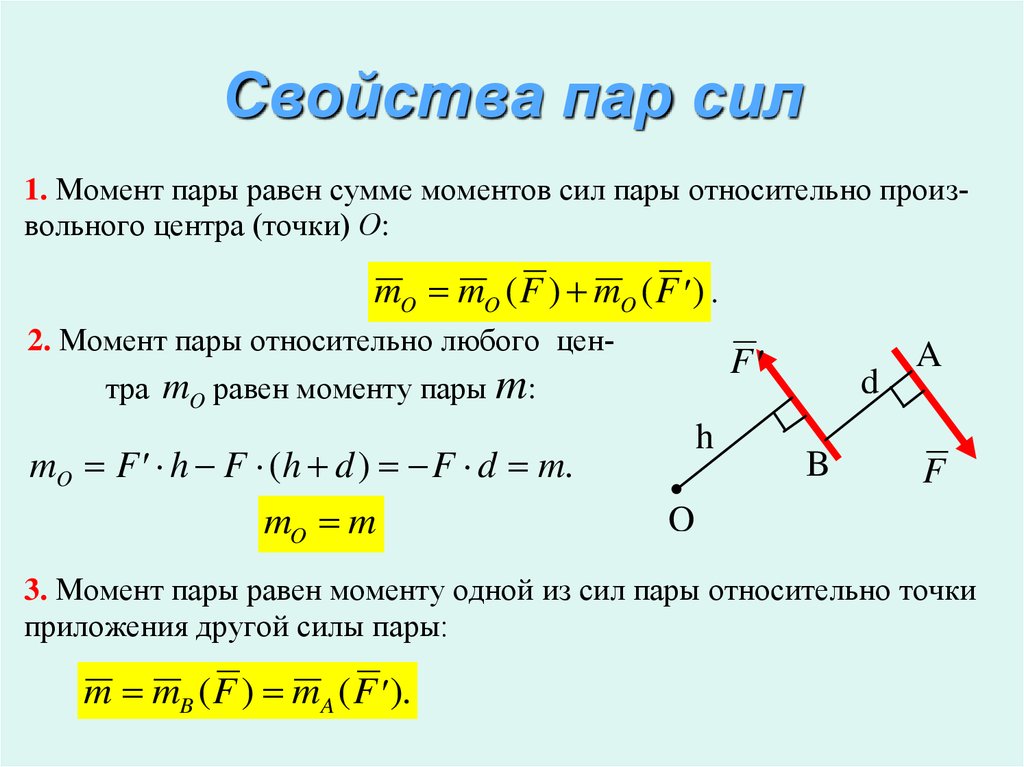
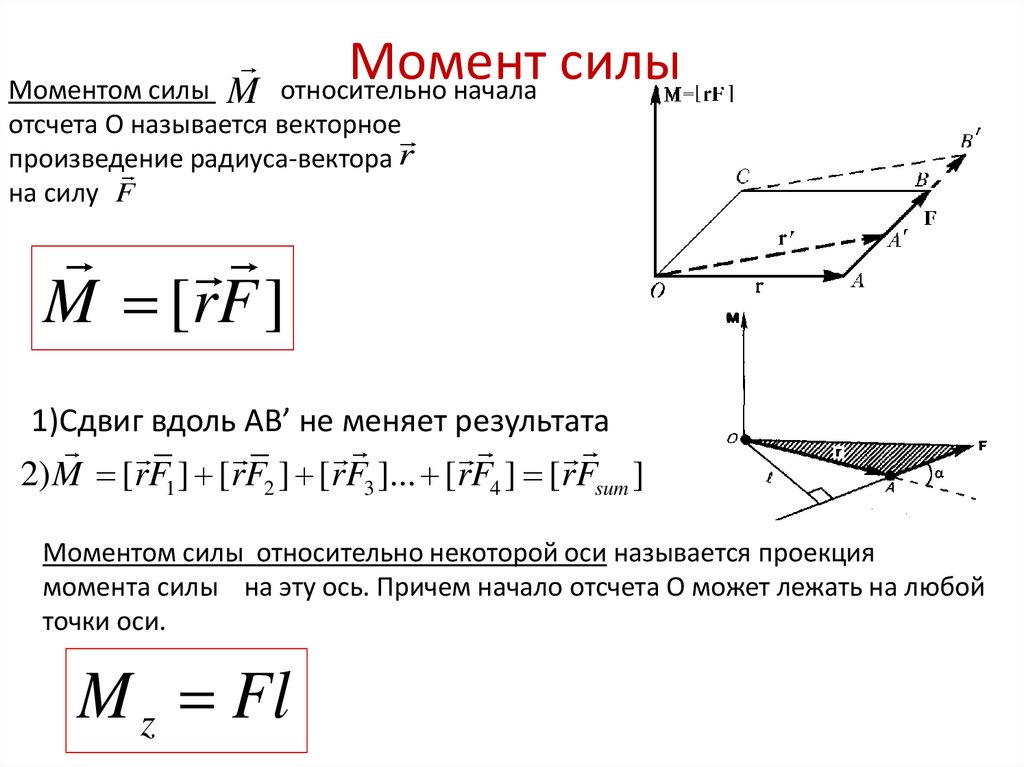 23).
23).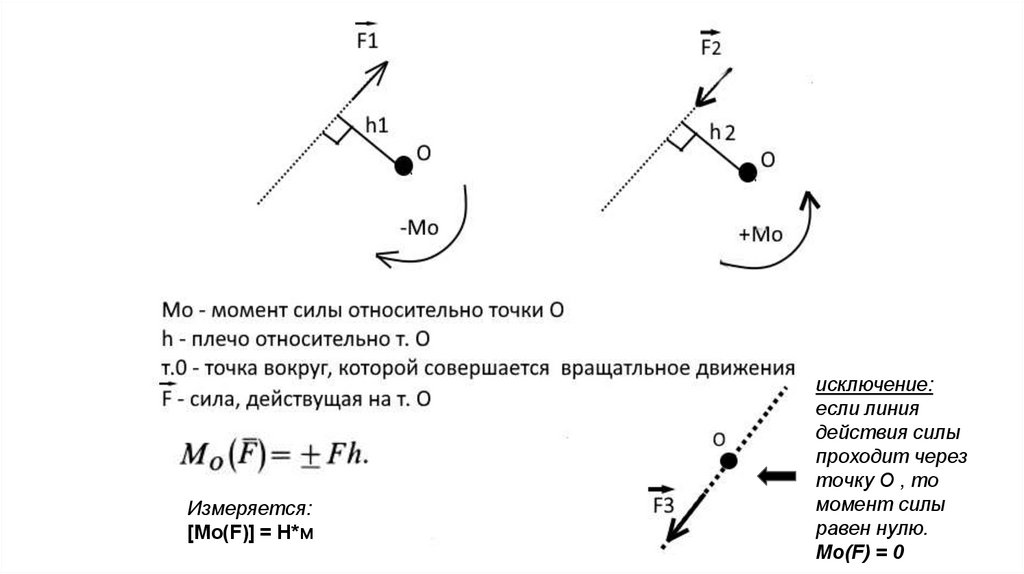 Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары .
Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары .
 ..
.. physics.mechanics как я
me.init_vprinting(use_latex='mathjax')
physics.mechanics как я
me.init_vprinting(use_latex='mathjax')
 z)
FL.orient_axis(W, alphafl, W.z)
RR.orient_axis(B, alpharr, B.z)
RL.orient_axis(B, alpharl, B.z)
z)
FL.orient_axis(W, alphafl, W.z)
RR.orient_axis(B, alpharr, B.z)
RL.orient_axis(B, alpharl, B.z)
 x))
T = T.express(B).simplify()
Т
x))
T = T.express(B).simplify()
Т
 Точка('Бо')
сила = (Во, R)
сила
Точка('Бо')
сила = (Во, R)
сила
 ReferenceFrame('B')
Тм = Т*Н.з
ReferenceFrame('B')
Тм = Т*Н.з

 symbols('м, г')
Fg = -m*g*N.y
фг
symbols('м, г')
Fg = -m*g*N.y
фг
 dynamicsymbols('q1, q2')
водоизмещение = q2 - q1 - q0
смещение
dynamicsymbols('q1, q2')
водоизмещение = q2 - q1 - q0
смещение
 Для более простого, но, как мы будем
учиться, часто менее благоприятный для численного подхода оценки, влияние может быть
захватывается путем создания жесткой пружины, которая срабатывает только в том случае, если одно тело проникает
другое тело. Можно включить некоторое вязкое демпфирование, чтобы уловить неупругий
аспекты. 9{3}\right) \left|{\dot{y}}\right|}{\dot{y}}\hat{n}_y\end{split}\]
Для более простого, но, как мы будем
учиться, часто менее благоприятный для численного подхода оценки, влияние может быть
захватывается путем создания жесткой пружины, которая срабатывает только в том случае, если одно тело проникает
другое тело. Можно включить некоторое вязкое демпфирование, чтобы уловить неупругий
аспекты. 9{3}\right) \left|{\dot{y}}\right|}{\dot{y}}\hat{n}_y\end{split}\]