Как найти падение напряжения 🚩 формула падения напряжения 🚩 Естественные науки

Независимо от того, какие именно параметры даны в условии задачи, переведите их в систему СИ.

Если в условии даны сопротивление нагрузки и выделяемая на ней мощность, руководствуйтесь следующими соображениями:R=U/I, где R — сопротивление, Ом, U — напряжение, В, I — сила тока, А.P=UI, где P — мощность, Вт, U — падение напряжения, В, I — сила тока, А.Отсюда следует, что P=I^2*R, то есть, I^2=P/R, или I=sqrt(P/R). Следовательно, U=R(sqrt(P/R)) или, после упрощения выражения, U=sqrt(P)*sqrt(R), где U — искомое падение напряжения на нагрузке, В, R — сопротивление, Ом, P — мощность, Вт.

Значительно более простой случай возникает, если найти падение напряжение необходимо, зная мощность и силу тока. Преобразовывать выражение не потребуется, поэтому сразу воспользуйтесь следующей формулой: U=P/I,где U — искомое падение напряжения, В, P — мощность, выделяемая на нагрузке, Вт, I — сила тока, проходящего через нагрузку, А. Если известны сопротивление нагрузки и проходящий через нее ток, падение напряжения на ней также вычислите в одно действие:U=IR,где U — искомое падение напряжения, В, I — ток, проходящий через нагрузку, А, R — сопротивление нагрузки, Ом. Помимо приведенных выше наиболее часто встречающихся задач, в учебниках попадаются и другие, в которых необходимо узнать падение напряжения на отрезке длинного однородного стержня, выполненного из материала, обладающего высоким сопротивлением. Для этого вначале вычислите падение напряжения на всей длине стержня (если оно не дано в условии задачи изначально). После этого вычтите друг из друга горизонтальные координаты точек, падение напряжения между которыми необходимо определить.

Напряжение на всей длине стержня поделите на его длину, после чего умножьте на рассчитанную вами длину отрезка, и вы получите падение напряжения между точками. Подобные делители встречаются в аппаратуре с бестрансформаторным питанием и используются в качестве переключателей сетевого напряжения — в данном случае простоте конструкции приносится в жертву коэффициент полезного действия и безопасность.

Завершив вычисления, при необходимости переведите результат в удобные для его представления единицы: вольты, милливольты, киловольты и т.п.

Источники энергии. Потенциал и падение напряжения

Еще один пост из серии основы основ. Заметил я, что многие совершенно не въезжают в концепцию падения напряжения, разности потенциалов и типов источников питания. Поэтому запилю ка я ликбез по этой теме. С самого начала. Потом заброшу его в начало рубрики «Начинающим». Пойдет как замена цикла статей канализационной электроники. Т.к. тот цикл писался для «Хакера» и особой подробностью не отличался ввиду ограничений на размер полосы.

Начало начал. Ноль.
Итак, начну с самого начала. Со дна. То есть с земли. Точки нулевого потенциала. Эта точка совершенно произвольная. Просто нам так удобно, что мы приняли ее за ноль. Надо же с чего то начинать. В однополярном питании это, обычно, минус питания. В двуполярном — нечто посредине, впрочем от конструкции зависит.

Источник энергии
Что такое вообще источник электрической энергии? Это всего лишь «зарядовый насос» который перекачивает электроны (или ионы) посредством химической, электростатической, сегнетоэлектрической, электромагнитной, термической, да любой энергии. Это не важно. Суть лишь в том, что он искажает нейтрально-равномерное распределение зарядов, стаскивая положительные в одну сторону, отрицательные в другую.

Как насос, поднимая воду на высоту, за счет энергии толпы грязных нигр, в поте лица вращающих его маховик, увеличивает потенциальную энергию воды, поднятую на высоту.

И вот если мы примем один конец нашей трубы-проводника за ноль, то на другой будет какой то потенциал. Какой?
А это зависит от силы источника энергии, ведь заряды сопротивляются, хотят обратно, к нулевому состоянию. Системе с минимальной энергией. А еще от характеристик самой силы. Например, химическая, что в солевых батарейках, не дает напряжения больше 1.5 вольт. Это свойства электролита и электродов (я химию уже подзабыл, но что то там связано с электрохимическим рядом).

Причем мы можем источники энергии составлять цепочкой. И тогда выходит, что выход первого, станет точкой нулевого потенциала для второго, такого же, и он сможет накачать еще столько же сверху. А относительно общего нуля будет вдвое больше.

Как если бы мы соединили два насоса последовательно, один набивает нам давление в 1 атмосферу, и второй относительно него набивает 1 атмосферу, а вместе они выдают аж два очка.

У меня на прошлой работе делали стендовые мультиметры. Делали их из обычных DT-838 прикручивая их на панели. Делали массово, сотнями. А все они с завода комплектуются батарейкой типа КРОНА которая тут оказывалась не нужна. Батарейка была голимая, но свои 9вольт давала. И таких батареек была целая коробка от телевизора, россыпью. А Крона прикольна тем, что она может соединяться своим разьемом с другой Кроной. Ну я от нефиг делать давай их соединять последовательно, раскладывая на полу. Сколько я их соединил я уже не помню. Потом мне тупо стало страшно, т.к. в длину у меня пространство кончилось, а в два слоя их соединять сцыкотно — так как концы близко получались. А у меня в результате получился источник напряжением чуть ли не под киловольт и способный дать в течении нескольких минут ток в пару ампер. Коротни я его на себя и от меня бы одни ботинки остались. Пришлось разобрать адскую машину.

Замкнутая цепь
Ну вот есть у нас источники энергии, каждый наращивает потенциал согласно своей дури. На вершине же этой цепи у нас будет их суммарный потенциал. Дикое количество нескомпенсированных зарядов, рвущихся к нулю. Их можно сравнить с сжатым воздухом.

Обратно они прорваться не могут — источник энергии не дает. Вперед — некуда. Для пробоя воздуха энергии не хватает. Вот и висят в таком состоянии. Как батарейка, никуда не подключенная — на выходе голый потенциал и никакой движухи. Напряжение есть, а тока нет. Осталось только дать им путь. Замкнем цепь. Накоротко, без полезной нагрузки.

И ток рванет по короткому пути, а потом обратно за счет источника энергии наверх и так далее. Напряжение наверху сразу же упадет в ноль. Но раз сопротивления нет, то с какой скростью он это будет делать? Идеальный насос, с бесконечной мощностью, разгонит нам ток до бесконечности.

Но в реальности выходит на сцену производительность насоса. Т.е. насос физически, ввиду своей конструкции, не может нам прокачать больше определенного объема (скажем, ограниченный размер цилиндра), а у батареи есть ограниченная площадь электродов, у генератора есть сопротивление обмоток. Получается в цепи все же есть сопротивление, это сопротивление источника. И выше него не прыгнешь. Также и с реальным источником напряжения. У него тоже всегда есть внутреннее сопротивление. И чем оно ниже, тем мощней источник, тем больший ток он сможет отдать.

Впрочем, никто не мешает взять и соединить два насоса-источника параллельно. И у нас получится, что они с одинаковым давлением (напряжением) родят вдвое больший ток. Правда тут надо учитывать, что ставить в параллель два источника с разным напряжением нельзя — тогда более слабый будет продавливаться более сильным и служить потребителем. Разумеется если внешней нагрузки, которая бы просадила напряжение до уровня слабого, нет.

Тоже самое касается и последовательного включения. Если мы воткнем в последовательное включение источник с большим внутренним сопротивлением чем у всех остальных, то он забьет всю цепь и будет обузой, не давая развивать максимальный ток.

Теперь вспомним о батарейках. Когда батарейка новая, то у ней малое внутреннее сопротивление, но чем больше электролита вступает в реакцию тем внутреннее сопротивление становится больше. И получается, что напряжение то она выдает и мультиметр показывает вроде бы четкие полтора вольта, но стоит затребовать с нее большой ток, как она мгновенно сдувается — возросшее сопротивление не позволяет выдать его и напряжение падает.

А теперь немног больше конкретики. Закон Ома для полной цепи.

Есть просто закон Ома: напряжение = ток * сопротивление

U = I * R

Это частный случай закона Ома для отдельного элемента цепи. Но есть еще закон Ома для полной цепи, с учетом источника.

Итак, у нас в цепи есть:

Наш идеальный насос — источник электродвижущей силы (ЭДС) — Е. У него бесконечная мощность и нулевое внутреннее сопротивление.
Но, чтобы жизнь не казалась медом, добавим еще и внутреннее сопротивление. Чтобы получить реальный источник. Re
А также есть нагрузки R1 и R2, включенные последовательно.

Ток (I) в последовательной неразветвленной цепи одинаков везде. И равен он величине ЭДС поделенной на сумму ВСЕХ сопротивлений, в том числе и внутреннего. И из этого получается вот что:

E = I*R_e+I*R₁+I*R₂

Т.к. I*R=U перепишем все по иному:

E = I*R_e + U₁ + U₂

Получается, что электродвижущая сила нашего источника, раскладывается, в зависимости от величины нагрузки, по всей цепи. Чем больше нагрузка, тем больше там надо приложить энергии для ее преодоления. Т.е. в нашей батарейке, если у нас E константа и не меняется (напомню, что она зависит только от химии процесса и подбора материалов батареи — т.е. это конструктивная особенность батареи), то при увеличении Re у нас, чтобы сохранить равенство, приходится снижать ток. А раз так, то падает U1 и U2 т.е. напряжение на потребителе. Еще, можно заметить, что у последовательных потребителей напряжение на каждом из них зависит от его R. И там где сопротивление больше — будет большее напряжение.

А что происходит когда мы тыкаем вольтметром в нашу дохлую батарею? А у вольтметра ОГРОМНОЕ сопротивление. И по сравнению с ним внутреннее сопротивление источника даже не отсвечивает.

Re <<<< Rвольтметра

А ток одинаково мал (доли милиампера) для всех потребителей. Таким образом в уравнении:

Е = I*R_e + I*R_{вольтметра}

На цифрах:

Е=1.5
R_e=10 Ом
Rвольтметра = 10 000 000 Ом
I = 1.5/10 000 010 = 1,499Е-7
I*R_e = 0.00000015 * 10 = 1.499Е-6
I*R_{вольтметра} = 1,499Е-7 * 10 000 000 = 1.499

1.5 = 1.499Е-6 + 1.499

Львиная доля напряжения высадится там, где сопротивление больше — на вольтметре. И вольтметр покажет практически величину Е, но это будет работать лишь на малых токах. При снижении сопротивления нагрузки и увеличении тока, часть I*Re будет все весомей и весомей, пока не перетащит на себя все напряжение. Тогда на нагрузке напряжение упадет почти до нуля — батеря просто не способна дать ток, такой, чтобы удержать напряжение. Либо, если это не батарейка, а какой либо другой источник — источник не тянет нагрузку. А если у батареи от долгой работы на нагрузку увеличилось внутреннее сопротивление, то в этом случае батарейка села.

Источник напряжения. Стабилизация
Но бывают такие хитрые схемы, где у источника внутреннее сопротивление можно менять в широких пределах. И есть следящая система, которая регулирует его таким образом, чтобы на нагрузке было строго определенное напряжение. Разумеется до тех пор пока токи не выходят за оговоренные рамки, а дальше неизбежный провал. Причем если сопротивление нагрузки, например, уменьшится, то и сопротивление источника уменьшится, чтобы иметь возможность пустить через нагрузку больший ток и выровнять напряжение на нагрузке.

Если брать идеальный источник напряжения — фактически голый источник ЭДС с нулевым сопротивлением, то он при снижении нагрузки в ноль даст бесконечный ток. Простейшим примером источника напряжения является конденсатор в момент разрядки. У идеального конденсатора внутреннее сопротивление равно нулю, поэтому когда он разряжается, то на бесконечно малом промежутке времени дает бесконечно большой ток.

Потенциал
Исходя из названия величины — это потенциальная энергия электрического поля в конкретной точке. Но для того, чтобы ее замерить надо задать отправную точку, систему отсчета — точку нулевого потенциала. Она может быть где угодно. Зависит лишь от наших целей в текущий момент. Но обычно за ноль принимают корпус или минус питания. Это и будет нашей точкой нулевого потенциала — Землей.

Возьмем и пририсуем к нашей цепи эту точку, вот так.

Итак, у нас есть цепь. Параметры такие:

Е = 5В
R = 1 Ом — все резисторы, для простоты.
I = 1 A

Теперь найдем потенциал во всех точках. Он, традиционно, обозначется буквой фи. Правило тут простое:

• 0. Выбираем точку нуля.
• 1. Выбираем направление обхода.
• 2. Выбираем направление тока в контуре. Совершенно произвольно, если ошибешься с направлением, то ряд величин будет с отрицательным знаком, но уравнение все равно сойдется. Однако лучше все же выбирать ток исходя из логического предположения того, как он должен течь при данном направлении источника — минусов будет меньше.
• 2. Если источник нам по пути, то он увеличивает потенциал, на величину своей ЭДС.
• 3. Если по пути нагрузка. То если ток совпадает с выбранным направление обхода, то потенциал уменьшаем на I*Rн Если же ток через нагрузку идет против нашего обхода, то увеличиваем потенциал на I*Rн.

И вернемся к нашему контуру:

• 0. Точка нуля задана.
• 1. Пусть обход контура по часовой.
• 2. Ток по часовой.
• 3. Проходим источник ЭДС. Потенциал в точке Б сразу же подскакивает на его величину. Вот оно максимальное напряжение. Но это где то в глубине батареи, мы его не замерим кроме как математически. Поэтому проходим внутреннее сопротивление. Идем по току, поэтому у нас потенциал снижается на I*R_е. В Точке В мы получили реальный потенциал на клемме нашей батареи. Идем дальше, дальше у нас резистор. Там ток течет по обходу, а значит потенциал уменьшается еще на I*R₁. Дальше аналогично. В итоге, когда мы сделаем круг, на каждом резисторе потенциал будет падать до тех пор, пока не выйдет в ноль, по возвращении в точку начала обхода.

Если сделать обход в обратную сторону, то получится все то же самое, только потенциал будет рости до тех пор пока мы не дойдем до Е и, пройдя его против направления, не вычтем ЭДС выйдя опять на ноль.

Но это мы получали потенциал относительно нуля. А если взять разность потенциалов между точкой Г и Е ? А мы получим напряжение между двумя этими точками. Если ткнуть туда вольтметром, то он покажет именно это напряжение. Т.е. напряжение это разность потенциалов. А падение напряжения между точками — это та величина на которую меняется потенциал при переходе из одной точки схемы в другую.

И главное надо очень четко понять тот факт, что главное в цепи это разность потенциалов. Есть разность потенциалов — есть ток, заряды текут и стремятся эту разность свести на ноль. Нет — тока не будет, т.к. зарядам в этом случае совершенно не захочется куда то бежать и где то там что то выравнивать, т.к. энергия системы в этом случае минимальная.

Тока может и не быть, если цепь не замкнута, а вот потенциала хоть отбавляй. Например, лежит кусок провода, никуда не подключен. На концах разность ноль — все заряды равномерно распределены.
Пошла мимо провода электромагнитная волна, извне откуда то прилетела, послужила тем самым источником энергии и раскидала заряды по разным концам провода. Появилась разность потенциалов на концах.

Таким образом, даже в никуда не подключенной ноге микроконтроллера, если она висит в режиме высокого входного сопротивления (HiZ — т.е. практически никуда не подключена и цепь разомкнута), из воздуха, от случайных помех, могут наводится большие потенциалы, достаточные для хаотичного переключения входа из 0 в 1 и обратно. А если к ноге приделать длинный провод, то на нем может навестись такой потенциал, что контроллер пожгет нафиг. Поэтому то длинные линии обычно делают в виде токовой петли, с низким сопротивлением, чтобы не наводилось на них перенапряжений. А наличие-отсутствие сигнала ловят по наличию-отсутствию тока нужной величины.

Эту концепцию потенциала и зависимости тока от него надо понять досконально, на уровне спинного мозга. Потому что потом дальше оперирование будет в основном потенциалами относительно общей точки.

Понятие падения напряжения активно юзается при обсчете нелинейных элементов, вроде диодов.

Расчет резистора для светодиода
Итак, есть у нас светодиод. Некий абстрактный. И у него по даташиту падение напряжения 2.5 вольта. А допустимый ток 10мА. А еще есть батарея, дающая 5 вольт и имеющая внутреннее сопротивление в 1Ом.

Что означает падение напряжения светодиода? А то, что между его выводами напряжение может быть не выше 2.5 вольта. Т.е. воткнешь ты его на батарею хоть в 100 вольт, а там все равно должно быть 2.5 вольта. Достигается это за счет того, что сопротивление диода тем меньше, чем большее к нему приложено напряжение. Куда же деть остальные 97.5 вольт? А их придется высадить на внутреннем сопротивлении источника. А если оно мало? А не волнует! Придется вкачать большой ток, настолько болшой, чтобы на внутреннем сопротивлении источника высадило это злосчастные 97.5 вольт. Вот только ток там уйдет в сотни ампер. А светодиод от таких токов пыхнет плазменной вспышкой и устроит тебе КЗ со взрывом.

Конечно, у реального светодиода все не так страшно и сопротивление его бесконечно падать не может, а падение напряжения не константное и меняется, но когда эти отклонения будут значительными ток будет уже за гранью допустимого. Так что можно смело принять падение напряжения на светодиоде за константу.

Итак, вернемся к нашим баранам.

Есть источник, есть диод. Вот такая схема.

Е=I*R_e+V_led
5=I*1 + 2.5

Воткнув наш пятивольтовый источник на наш 2.5 вольтовый диод мы получим падение напряжения на диоде 2.5 вольта. И столько же должно высадиться на внутреннем сопротивлении источника. Ток будет 2.5А это очень много, на два порядка выше чем разрешено. Значит надо добавить еще один резистор, дабы он сбросил на себя часть напряжения и обеспечил ток в 10мА.

Е=I*R_e + I*R + 2.5

Понятно, т.к. I = 0.01 то вычислить R не сложно. R = 249 Ом. Ближайший из ряда E24 — 240 Ом.

Параметры диода из его даташита, токоограничительное сопротивление мы выбираем, а откуда взять внутреннее сопротивление источника? А обычно им пренебрегают, считая его равным нулю. Один фиг его сопротивление в порядки меньше чем сопротивление ограничивающего резистора.

Источник тока
Антипод источника напряжения. Если источник напряжения выдает напругу и может развить бесконечный ток, лишь бы эту напругу удержать.

То источник тока выдает ток и может выдать бесконечное напряжение, лишь бы этот ток продавить. Имеет бесконечное внутреннее сопротивление, поэтому его выдаваемое напряжение (I*R_вн) и стремится к бесконечности. У реального же источника тока есть внутреннее сопротивление и расположено оно параллельно. Т.е. если ток через нагрузку не продавливается, то он уходит по внутреннему сопротивлению, не давая броска напряжения до победного конца. И чем выше внутреннее сопротивление источника тока, тем большее падение напряжения будет на нем, а значит и большее напряжение на нагрузке. Тем самым, по закону Ома, через нагрузку продавит больший ток.

Источниками тока в природе является катушка индуктивности, в момент разрыва цепи. Поэтому то она так и искрит, т.к. накачивает дикое напряжение, стремясь пробить дорогу току и удержать его на прежнем уровне.

Расчет простых цепей постоянного тока

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R₁ = 20 и R₂ = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

  Общий ток цепи, содержащей два соединенных параллельно резистора R₁=70 Ом и R₂=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах 

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи 

А затем напряжение 

Зная напряжения, найдем токи, протекающие через резисторы 

Как видите, токи получились теми же.

Пример 3

  В электрической цепи, изображенной на схеме R₁=50 Ом, R₂=180 Ом, R₃=220 Ом. Найти мощность, выделяемую на резисторе R₁, ток через резистор R₂, напряжение на резисторе R₃, если известно, что напряжение на зажимах цепи 100 В.

 

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R₁, необходимо определить ток I₁, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи 

Отсюда мощность, выделяемая на R₁ 

Ток I₂ определим с помощью формулы делителя тока, учитывая, что ток I₁ для этого делителя является общим 

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U₃, как напряжение на резисторе R₂ 

Таким образом производится расчет простых цепей постоянного тока.

Просмотров: 42430

Расчет токоограничивающего резистора для светодиода

В данной статье речь пойдет о расчете токоограничивающего резистора для светодиода.

Расчет резистора для одного светодиода

Для питания одного светодиода нам понадобится источник питания, например две пальчиковые батарейки по 1,5В каждая. Светодиод возьмем красного цвета, где прямое падение напряжения при рабочем токе 0,02 А (20мА) равно -2 В. Для обычных светодиодов максимально допустимый ток равен 0,02 А. Схема подключения светодиода представлена на рис.1.

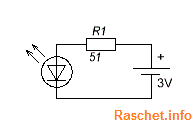
Рис.1 – Схема подключения одного светодиода

Почему я использую термин «прямое падение напряжение», а не напряжение питания. А дело в том, что параметра напряжения питания как такового у светодиодов нет. Вместо этого используется характеристика падения напряжения на светодиоде, что означает величину напряжения на выходе светодиода при прохождении через него номинального тока. Значение напряжения, указанное на упаковке, отражает как раз падение напряжения. Зная эту величину, можно определить оставшееся на светодиоде напряжение. Именно это значение нам нужно применять в расчетах.

Прямое падение напряжение для различных светодиодов в зависимости от длины волны представлено в таблице 1.

Таблица 1 — Характеристики светодиодов

Цветовая характеристика	Длина волны, нМ	Напряжение, В
Инфракрасные	от 760	до 1,9
Красные	610 — 760	от 1,6 до 2,03
Оранжевые	590 — 610	от 2,03 до 2,1
Желтые	570 — 590	от 2,1 до 2,2
Зеленые	500 — 570	от 2,2 до 3,5
Синие	450 — 500	от 2,5 до 3,7
Фиолетовые	400 — 450	2,8 до 4
Ультрафиолетовые	до 400	от 3,1 до 4,4
Белые	широкий спектр	от 3 до 3,7

Точное значение падения напряжения светодиода, можно узнать на упаковке к данному светодиоду или в справочной литературе.

Сопротивление резистора определяется по формуле:

R = (Uн.п – Uд)/Iд = (3В-2В)/0,02А = 50 Ом.

где:

• Uн.п – напряжение питания, В;
• Uд — прямое падение напряжения на светодиоде, В;
• Iд – рабочий ток светодиода, А.

Поскольку такого сопротивления в стандартном ряду нет, выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 51 Ом.

Чтобы гарантировать долгую работу светодиода и исключить ошибку в расчетах, рекомендую при расчетах использовать не максимально допустимый ток – 20 мА, а немного меньше – 15 мА.

Данное уменьшение тока никак не скажется на яркости свечения светодиода для человеческого глаза. Чтобы мы заметили изменение яркости свечения светодиода например в 2 раза, нужно уменьшить ток в 5 раза (согласно закона Вебера — Фехнера).

В результате мы получим, расчетное сопротивление токоограничивающего резистора: R = 50 Ом и мощность рассеивания Р = 0,02 Вт (20мВт).

Расчет резистора при последовательном соединении светодиодов

В случае расчета резистора при последовательном соединении, все светодиоды должны быть одного типа. Схема подключения светодиодов при последовательном соединении представлена на рис.2.

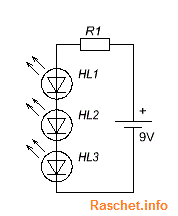
Рис.2 – Схема подключения светодиодов при последовательном соединении

Например мы хотим подключить к блоку питания 9 В, три зеленых светодиода, каждый по 2,4 В, рабочий ток – 20 мА.

Сопротивление резистора определяется по формуле:

R = (Uн.п – Uд1 + Uд2 + Uд3)/Iд = (9В — 2,4В +2,4В +2,4В)/0,02А = 90 Ом.

где:

• Uн.п – напряжение питания, В;
• Uд1…Uд3 — прямое падение напряжения на светодиодах, В;
• Iд – рабочий ток светодиода, А.

Выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 91 Ом.

Расчет резисторов при параллельно – последовательном соединении светодиодов

Часто на практике нам нужно подключить к источнику питания большое количество светодиодов, несколько десятков. Если все светодиоды подключить последовательно через один резистор, то в таком случае напряжения на источнике питания нам не хватит. Решением данной проблемы является параллельно-последовательное соединение светодиодов, как это показано на рис.3.

Исходя из напряжения источника питания, определяется максимальное количество светодиодов, которые можно соединить последовательно.

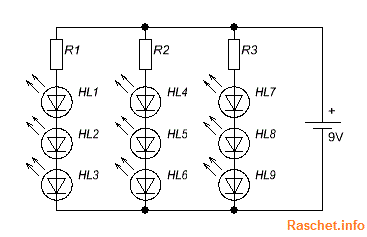
Рис.3 – Схема подключения светодиодов при параллельно — последовательном соединении

Например у нас имеется источник питания 12 В, исходя из напряжения источника питания максимальное количество светодиодов для одной цепи будет равно: 10В/2В = 5 шт, учитывая что на светодиоде (красного цвета) падение напряжения — 2 В.

Почему 10 В, а не 12 В мы взяли, связано это с тем, что на резисторе также будет падение напряжения и мы должны оставить, где то 2 В.

Сопротивление резистора для одной цепи, исходя из рабочего тока светодиодов определяется по формуле:

R = (Uн.п – Uд1 + Uд2 + Uд3+ Uд4+ Uд5)/Iд = (12В — 2В + 2В + 2В + 2В + 2В)/0,02А = 100 Ом.

Выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 110 Ом.

Количество таких цепочек из пяти светодиодов параллельно соединенных практически не ограничено!

Расчет резистора при параллельном соединении светодиодов

Данное подключение является не желательным и я его не рекомендую применять на практике. Связано это с тем что, у каждого светодиода присутствует технологическое падение напряжения и даже если все светодиоды из одной упаковке – это не является гарантией, что у них падение напряжение будет одинаково из-за технологии производства.

В результате у одного светодиода, ток будет больше чем у других и если он превысить максимально допустимый ток, он выйдет из строя. Следующий светодиод перегорит быстрее, так как через него уже будет проходить оставшийся ток, распределенный между другими светодиодами и так до тех пор, пока все светодиода не выйдут из строя.

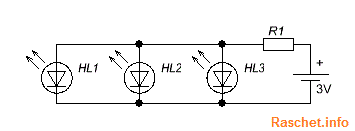
Рис.4 – Схема подключения светодиодов при параллельном соединении

Решить данную проблему можно подключив к каждому светодиоду свой резистор, как это показано на рис.5.

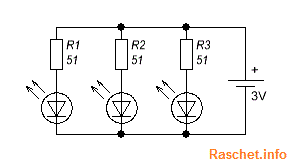
Рис.5 – Схема подключения светодиодов и резисторов при параллельном соединении

Что такое падение напряжения

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в электрической цепи (имеется в виду глобальная классификация). Их всего два вида. Первый – это напряжение источника питания, который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид – это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную лампу накаливания, вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания – проводники – нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на электрическом сопротивлении, которым обладает лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:

I = U / R,

где R – активное сопротивление цепи или ее элемента, измеряется в Омах; U – электрическое напряжение, в Вольтах; и, наконец, I – ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа – вышеуказанная формула.

Электрическая энергия – это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны. Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения. Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.

Падение напряжения на резисторе зависит от его внутреннего сопротивления и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На переменном токе приходится дополнительно учитывать реактивную составляющую.

Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС – E.

Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:

R = (R1*R2) / (R1+R2)

Определяем сопротивление всей цепи через сумму R4 = R+R3.

Рассчитываем ток:

I = E / (R4+r)

Остается узнать значение падение напряжения на выбраном элементе:

U = I * R5

Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.