Как рассчитать падение напряжения в последовательной цепи: подробные факты —

В этой статье объясняется, что такое падение напряжения и как рассчитать падение напряжения в последовательной цепи. Когда напряжение встречается с резистивным элементом в цепи, значение уменьшается или «падает».

В последовательной цепи имеется несколько сопротивлений или импедансов. Каждый раз, когда через них проходит ток, напряжение падает. Итак, нам нужно знать значение конкретного сопротивления и ток, проходящий через него, чтобы вычислить падение напряжения на нем. Падение напряжения — это ток, умноженный на сопротивление.

Что такое падение напряжения?

Допустим, мы соединяем батарею с резистором через провод. Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительной клеммы к отрицательной. 

Когда одна единица заряда встречает резистор, она на время останавливается. Когда он проходит мимо резистора, появляется другая единица заряда и останавливается. В любой момент количество заряда на конце резистора меньше заряда в начале резистора. Это явление создает «падение потенциала или напряжения».

Подробнее… ..Постоянно ли напряжение в серии: полная информация и ответы на часто задаваемые вопросы

Как рассчитать полное падение напряжения в последовательной цепи?

Общее падение напряжения в последовательной цепи — это сложение всех отдельных падений напряжения, вызванных параметрами импеданса. Кроме того, сумма равна общему напряжению, подаваемому в цепь, или напряжению до любого «падения».

Разберем явления с помощью схемы. В схеме ниже два резистора R₁ 100 Ом и R₂ 200 Ом, подключенный к источнику питания V 30 вольт. Ток i = В/(R₁ + R₂) = 30/(100+200) = 0.1 А. Следовательно, падение напряжения на резисторе R₁ = икс р₁ = 0. 1 x 100 = 10 В и через R₂ = икс р₂ = 0.1 х 200 = 20 В. 

Как рассчитать падение напряжения в последовательной цепи переменного тока?

переменного тока или переменный ток цепи – это электрические цепи с переменным напряжением питания. AC последовательная схема состоит из любой комбинации резистора, катушки индуктивности и конденсатора, соединенных последовательно.

Как и в случае с постоянным током, мы можем вычислить чистый импеданс последовательной цепи переменного тока, сложив их. Аналогичным образом можно найти и падения напряжения. Падение напряжения на любом элементе в последовательной цепи переменного тока равно V = iZ, где Z — полное сопротивление цепи, а i — полный ток, протекающий через нее.«Файл: AC Source-RC.svg» by Pierre5018 под лицензией CC BY-SA 4.0

Подробнее… ..Как рассчитать напряжение в последовательной цепи: подробные факты

Падение напряжения в последовательной цепи RLC:

Цепь RLC является частным случаем цепей переменного тока. Цепь RLC состоит из резисторов, конденсаторов и катушек индуктивности, соединенных последовательно. Давайте поймем падение напряжения в последовательной цепи RLC на примере.

Схема состоит из трех компонентов, показанных ниже: резистора R Ом, индуктивности L Генри и конденсатора C Фарад. Ранее мы знали, что падение напряжения на любом из них = импеданс × ток. Так,

Падение напряжения на резисторе = iR, катушка индуктивности = iXL и конденсатор = iXC, где XL = 2πfL и XC = 1/2πfC

Как рассчитать падение напряжения в последовательной цепи — численные примеры

Q1. Три резистора подключены последовательно со значениями R₁= 4 Ом, R₂= 5 Ом, а R₃ = 6 Ом. Схема подключена к источнику питания 15 В. Узнайте падение напряжения на резисторах.

Для расчета капель потенциала на R₁, R₂и R₃, нам сначала нужно получить ток в цепи. Мы знаем, ток = чистое напряжение/эквивалентное сопротивление

Эквивалентное сопротивление R_eq = R₁ + R₂ + R₃ = 4 + 5 + 6 = 15 Ом

Следовательно, общий ток = 15 В / 15 Ом = 1 А.

Теперь мы можем использовать закон Ома (V = IR) для каждого резистора и найти падение напряжения на них.

Итак, V₁ = я х р₁ = 1 х 4 = 4 В

V₂ = я х р₂ = 1 х 5 = 5 В

V₃ = я х р₃ = 1 х 6 = 6 В

Q2. Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Определите другие падения напряжения и вычислите общее падение напряжения или напряжение питания.

Мы знаем, что падение напряжения на любом резисторе в последовательная цепь = сопротивление × общий ток

Если в цепи протекает ток i, падение напряжения на резисторе 6 Ом составляет 6i.

6i = 12 или i = 2 ампер

Следовательно, падение напряжения на резисторе 2 Ом = 2 x 2 = 4 В. {-6} }= 159.15 Ом

Следовательно, полное сопротивление,

Теперь для цепей переменного тока существует объект, называемый фазовым углом. Он дает меру угла, на который ток отстает или опережает напряжение. Фазовый угол φ = arctan (X_C — ИКС_L/Р)

φ = арктангенс (27.2/100) = 15.22°

Итак, текущий

Следовательно,

Здесь ток опережает напряжение как X_C > X_L.

Подробнее….Что такое напряжение в последовательной цепи: подробные факты

Напряжение и падение напряжения: сравнительный анализ —

By Кошики Банерджи

В этой статье показаны ключевые различия между напряжением и падением напряжения. Мы часто называем напряжение и падение напряжения одними и теми же объектами. Но дело в том, что они разные и обладают уникальными атрибутами.

Вот основные различия между напряжением и падением напряжения.

параметры	напряжение	Падение напряжения
Определение	Напряжение — это электрическое давление, которое заставляет заряженные электроны течь из одного места в другое через проводящий материал. Мы также можем сказать, что напряжение — это разность электрических потенциалов между двумя точками цепи.	Падение напряжения также является величиной, связанной с напряжением, но это не совсем то же самое, что и напряжение. Падение напряжения — это разность потенциалов, возникающая при наличии какого-либо препятствия в цепи, такого как резистор, катушка индуктивности или конденсатор. Это потерянное напряжение.
Значение в DC	В однонаправленном постоянном токе, согласно закону Ома, напряжение является простым произведением силы тока и сопротивления. Постоянное напряжение постоянно.	Падение постоянного напряжения — это разность потенциалов от одной точки к другой, когда постоянный ток проходит через какой-либо резистивный компонент между точками.
Значение в переменном токе	Переменный ток течет в двух направлениях или меняет свою полярность в течение определенного периода времени. Из-за этого изменения периодически менялось и напряжение. Это произведение тока и импеданса.	Концепция падения напряжения переменного тока аналогична падению напряжения постоянного тока. Точно так же, как напряжение переменного тока, падение напряжения переменного тока учитывает импеданс в цепи, а не только сопротивление.
Расчет	Напряжение рассчитывается по закону Ома путем умножения силы тока и сопротивления. В емкостных и индуктивных цепях наряду с сопротивлением учитываются также емкость и индуктивность.	Расчет падения напряжения аналогичен расчету напряжения, поскольку он является частью самого напряжения. Просто в цепи падение напряжения относится только к падениям, происходящим из-за реактивных сопротивлений, но не к напряжению питания или источника.
Анализ эффективности	Напряжение измеряется аналоговым или цифровым вольтметром или мультиметром.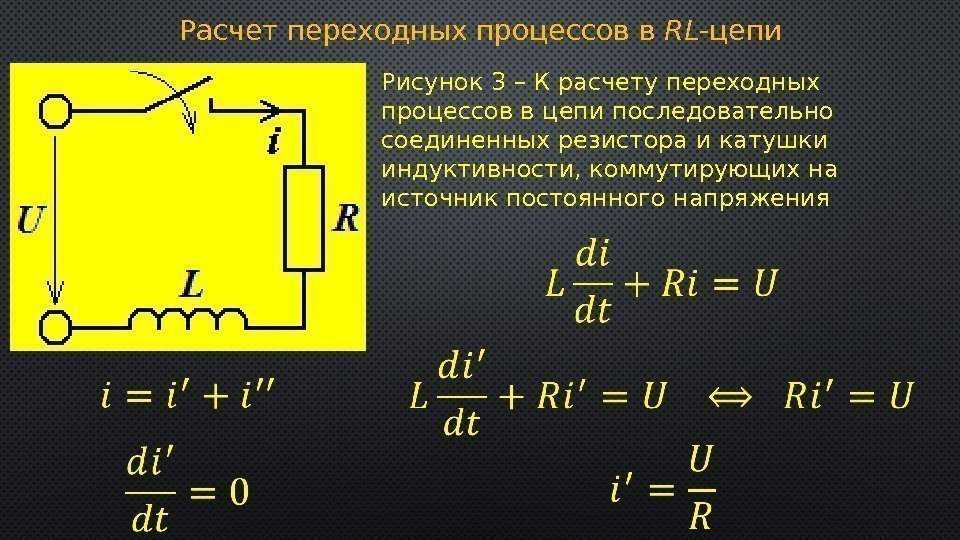	Поскольку падение напряжения представляет собой часть чистого напряжения, оно измеряется тем же прибором, который используется для измерения напряжения.

Мультиметр для измерения напряжения и падения напряжения; Кредиты изображений: Википедия

Когда напряжение и падение напряжения могут совпадать?

Напряжение и падение напряжения немного отличаются друг от друга. Когда мы говорим о зависимости напряжения от падения напряжения на любом компоненте, таком как резистор, конденсатор или катушка индуктивности в цепи, это то же самое, что и напряжение на нем. 

Предположим, есть два резистора в последовательной конфигурации. В цепь подается напряжение источника. Напряжение — это напряжение питания, а также напряжения через отдельные резисторы. Но отдельные напряжения будут единственными падениями напряжения в цепи. Это относится как к цепям постоянного тока, так и к цепям переменного тока, таким как цепи RC, LR или RLC.

Напряжение и падение напряжения: часто задаваемые вопросы

Электрический потенциал против напряжения

Электрический потенциал известен как энергия на единицу заряда, полученная или потерянная, когда любой заряд течет из определенной точки с нулевым электрическим потенциалом. Напряжение – это разность потенциалов между любыми двумя точками.

Возьмем пример. Предположим, что потенциал произвольной точки P относительно фиксированной точки B равен 100 вольт, а потенциал точки Q называется 120 вольт. Тогда напряжение или разность потенциалов между точками P и Q составляет (120-100) = 20 вольт. Здесь 100 вольт и 120 вольт — это электрические потенциалы, а 20 вольт — это напряжение. 

Напряжение в зависимости от падения напряжения в цепи

Каковы причины падения напряжения в цепи?

Напряжение — очень важное свойство заряда. Это движущая сила, которая перемещает электроны из одной точки в другую и меняет величину. Напряжение генерируется за счет электрохимической реакции или магнитной индукции.

Падение напряжения обычно вызвано влиянием резисторов, конденсаторов и катушек индуктивности в цепи. Когда ток протекает через замкнутую цепь, в которой есть эти реактивные элементы, напряжение питания уменьшается, когда ток встречается с любым элементом. Чем больше реактивное сопротивление, тем больше падение напряжения.

Замыкание индукторов на постоянном токе или падение напряжения?

спросил 3 года, 6 месяцев назад

Изменено 3 года, 6 месяцев назад

Просмотрено 2к раз

\$\начало группы\$

В предыдущих курсах, я помню, нам говорили, что конденсаторы действуют как разомкнутая цепь на постоянном токе, а катушки индуктивности действуют как короткое замыкание.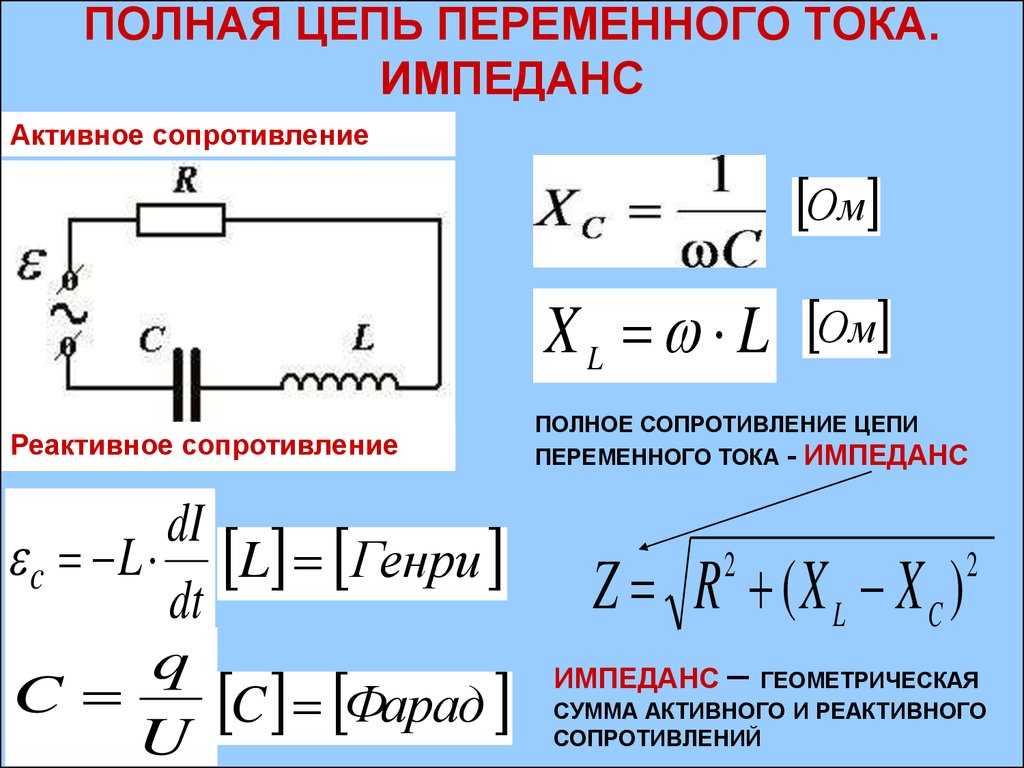

Наткнулся на это видео: и в этом у него есть источник постоянного тока.

Теперь, с моим предыдущим пониманием, означает ли это, что все напряжение на самом деле падает из-за неидеального последовательного сопротивления катушки индуктивности?

Я просто пытаюсь найти связь между разными курсами, которые я проходил/прохожу.

• индуктор

\$\конечная группа\$

\$\начало группы\$

Да, идеальный индуктор имеет нулевое сопротивление постоянному току. Чтобы смоделировать реальную катушку индуктивности, мы часто добавляем последовательное сопротивление, которое может выдерживать падение постоянного напряжения. Однако невозможно измерить это падение напряжения независимо от катушки индуктивности.

\$\конечная группа\$

2

\$\начало группы\$

Напряжение на катушке индуктивности возникает при изменении тока в катушке индуктивности. Как только ток достигнет своего установившегося значения, падение напряжения будет нулевым, потому что ток не будет меняться. Когда переключатель сначала замыкается, ток будет нулевым, и на резисторе не будет падения напряжения, поэтому полное падение напряжения будет от индуктора.

Я обнаружил, что мое понимание цепей индуктивности значительно улучшилось, когда я узнал о балансе вольт-секунд и смог решить простой понижающий преобразователь.

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Есть ли напряжение на идеальной катушке индуктивности?

\$\начало группы\$

Я изучал схемы LC и LCR.

Мой вопрос касается самих катушек индуктивности, точнее идеальных катушек индуктивности с нулевым сопротивлением.

Если я отключу идеальную катушку индуктивности от источника постоянного тока, на катушке должен появиться очень высокий скачок напряжения в соответствии с \$V=L\frac{dI}{dt}\$.

Как это может быть? Два конца индуктора соединены через нулевое сопротивление через катушку самого индуктора, и поэтому не будет ли напряжение на двух концах индуктора всегда равным нулю?

• индуктор

\$\конечная группа\$

3

\$\начало группы\$

Два конца индуктора соединены через нулевое сопротивление через катушку самого индуктора, и поэтому не будет ли напряжение на двух концах индуктора всегда равным нулю?

Вы предполагаете, что катушка индуктивности подчиняется закону Ома. Это не так. Закон Ома — это закон для резисторов. [Идеальная] катушка индуктивности не является резистором, поэтому она не подчиняется закону Ома (как и источник напряжения, конденсатор, диод, трансформатор или любое другое устройство, не являющееся резистором).

«Закон», управляющий работой катушки индуктивности:

$$V = L\frac{dI}{dt}.$$

Вам необходимо проанализировать работу катушки индуктивности, используя этот закон, а не закон Ома. . И этот закон говорит вам, что для мгновенного размыкания переключателя на катушке индуктивности должен быть бесконечный (дельта-функция) импульс напряжения.

Иногда два «идеальных» компонента в цепи создают логическое противоречие, например два идеальных источника напряжения, включенных параллельно, или переключатель, соединяющий два идеальных конденсатора.

В этом случае нельзя считать, что и катушка индуктивности, и переключатель идеальны, и получить физически значимый результат анализа. Вы должны учитывать либо поведение дуги переключателя, либо межобмоточную емкость катушки индуктивности (или и то, и другое), чтобы правильно смоделировать цепь без сингулярностей.

\$\конечная группа\$

6

\$\начало группы\$

Как это может быть? Два конца индуктора соединены через нулевое сопротивление через катушку самого индуктора, и поэтому не будет ли напряжение на двух концах индуктора всегда равным нулю?

Идеальная катушка индуктивности имеет нулевое сопротивление , но индуктивность

.

должен быть очень высокий скачок напряжения на катушке индуктивности в соответствии с \$V=L\frac{dI}{dt}\$.

В математической модели цепи индуктивность определяется этим уравнением. Если вы анализируете схему, содержащую катушку индуктивности, вы просто соглашаетесь с тем, как ведет себя катушка индуктивности.

Конечно, существует физическое объяснение того, почему катушка с проводом обладает индуктивностью — почему поведение катушки приблизительно описывается этим уравнением — но понимание этого уведет вас глубоко в физику и математику.

(см. статьи Википедии о законах Фарадея и законе Ленца, а также о катушках индуктивности в целом). магнитное поле. (Витки проводящего провода и ферромагнитный сердечник в практичном индукторе служат для концентрации этого поля.)

В любом случае, это магнитное поле накапливает энергию. Для создания поля (то есть для увеличения тока) требуется энергия, и индуктор возвращает эту энергию в цепь, когда поле разрушается (ток снова снижается). Эти изменения энергии проявляются в виде напряжения, которое противодействует изменению тока. , как описано уравнением, которое вы привели.

\$\конечная группа\$

\$\начало группы\$

Пока есть колебания тока, на идеальном индукторе будет напряжение \$V=L\frac{dI}{dt}\$.

Я думаю, что ваше неправильное представление заключается в том, «где» находится «резистор» в неидеальной катушке индуктивности: он должен быть смоделирован ПОСЛЕДОВАТЕЛЬНО с идеальной катушкой индуктивности:

^{смоделируйте эту схему — схема создана с помощью CircuitLab}

Таким образом, если внутренний резистор (r) стремится к 0 (т. е. идеальная катушка индуктивности), то он НЕ закорачивает клеммы идеальной катушки индуктивности.

Теперь, почему мы можем смоделировать катушку индуктивности как идеальную катушку индуктивности с одним концом и резистором на другом конце?

Предположим, что мы разрезаем катушку индуктивности на N маленьких (одинаковых) катушек с сопротивлением r/N и индуктивностью L/N, мы получаем:

^{смоделируем эту схему}

^{имитировать эту схему}

Теперь, когда резисторы добавляются последовательно, общее сопротивление равно Rtot=N*(r/N)=r. Точно так же катушки индуктивности добавляются последовательно, так что Ltot=N*(L/N)=L.

РЕДАКТИРОВАТЬ: с вашим новым комментарием о конкретном случае цепи постоянного тока только с идеальным индуктором и переключателем.

^{смоделируйте эту схему}

Если нет внутреннего резистора ни в дросселе, ни в проводах, ни в питании, ни в выключателе (т.е. все компоненты идеальны), то получится короткое замыкание когда переключатель замкнут. Это означает, что ваш источник напряжения обеспечивает бесконечный ток (и, следовательно, мощность).

Теперь предположим, что источник напряжения каким-то образом ограничивает ток (например, с помощью внутреннего сопротивления). Мы получаем некоторый ток через индуктор. Когда мы размыкаем переключатель:

• , если он не идеален, мы, вероятно, получим электрическую дугу, рассеивающую энергию, запасенную в индукторе.
• , если он идеален и не создает дуги, то может быть какой-то другой неидеальный элемент, способный замедлить изменение напряжения (например, какая-то паразитная емкость).
• если вы отрицаете и эти неидеальности, то вы получаете бесконечное напряжение на вашем дросселе (и тогда нет смысла продолжать считать, что все идеально, потому что с бесконечным напряжением вы создаете электрические дуги или что-то разрушаете).

\$\конечная группа\$

5

\$\начало группы\$

Часто в практических целях мы не проводим различия между падением напряжения на компоненте и электродвижущей силой, создаваемой этим компонентом. Оба измеряются в 9b \vec{E}_{rot} \cdot d\vec{s}$$

Согласно закону Кирхгофа о напряжении вокруг любой петли сумма ЭДС через компоненты в петле равна сумме падений напряжения через компоненты цикла.

$$\sum_i \mathscr{E}_i = \sum_i U_i$$

Или в оригинальном представлении Кирхгофа

$$\sum_i \mathscr{E}_i = \sum_i I_iR_i$$

где \$I_i\ $ — это ток, протекающий через компонент, а \$R_i\$ — это сопротивление, оказываемое этому току этим компонентом.

Вы правы в том, что падение напряжения, как определено выше, на катушке индуктивности зависит от сопротивления провода и тока через него.

Два конца индуктора соединены через нулевое сопротивление через катушку самого индуктора, и поэтому не будет ли напряжение на двух концах индуктора всегда равным нулю?

Для идеальной катушки индуктивности, сопротивление которой равно 0, падение напряжения на ней будет равно 0. Однако ЭДС, создаваемая катушкой индуктивности, приведет к падению напряжения на сопротивлениях, подключенных к катушке индуктивности в контуре цепи. Таким образом, если вы подсоедините вольтметр к выводам катушки индуктивности (испытывая изменяющийся ток), на вольтметре будет присутствовать падение напряжения, и, следовательно, показания вольтметра пропорциональны ЭДС, создаваемой катушкой. индуктор, а не падение напряжения на индукторе. В некотором смысле ЭДС вызывает падение напряжения в другом месте в цепи.

\$\конечная группа\$

\$\начало группы\$

Два конца идеального индуктора соединены проводом с нулевым сопротивлением. Однако, чтобы сделать это катушкой индуктивности, этот провод заключает в себе петлю некоторой площади.

Когда по этой петле провода протекает ток, в области, определяемой петлей, создается магнитное поле.

При изменении магнитного поля в области контура вокруг контура генерируется напряжение. Это напряжение появляется на концах провода.

Мы наблюдаем это экспериментально. Почему это происходит, зависит от вашего определения «почему». Вы могли бы объяснить это с точки зрения других более глубоких теорий, например, квантовая электродинамика (КЭД), вероятно, самая глубокая, или немного выше, используя уравнения Максвелла. Однако, в конечном счете, вы можете сказать «почему» и этим теориям. Не забывайте, что обе эти теории были разработаны для обобщения экспериментальных результатов, которые мы наблюдаем.

Чтобы ответить на ваш вопрос «Как может быть так, что два конца провода с нулевым сопротивлением генерируют между собой напряжение при изменении тока?» Бывает. Это наблюдаемая реальность. Иметь дело с этим.

\$\конечная группа\$

\$\начало группы\$

Есть два взгляда на это: катушка индуктивности с сопротивлением подчиняется уравнению \$U = R\cdot I + L\cdot\frac{\mathrm d\,I}{\mathrm d\,t}\$. При нулевом сопротивлении левый член равен нулю, но правый член все еще существует.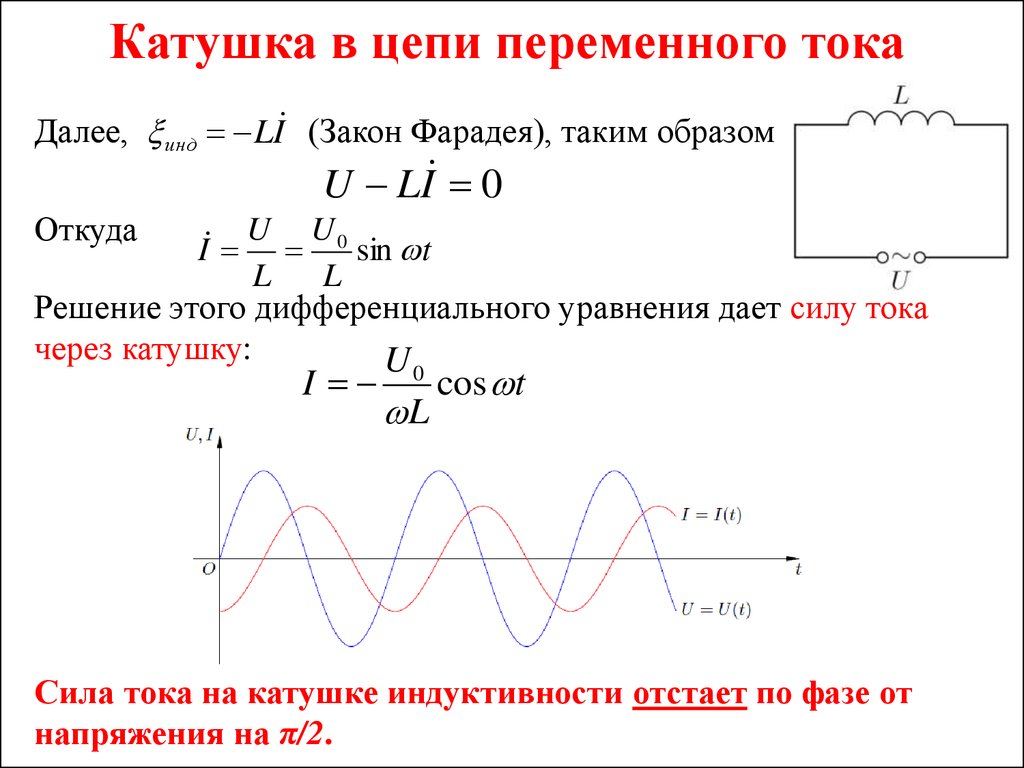

Другой способ взглянуть на это — рассмотреть уравнения Кирхгофа, которые утверждают, что полное напряжение в каждом контуре цепи равно нулю: измененная версия состоит в том, что общее напряжение не равно нулю, а складывается с (отрицательной) производной по времени от изменение потока через петлю. Индуктор имеет множество петель вокруг соответствующего потока, и он также отвечает за создание потока в первую очередь за счет намагничивания своего сердечника (или воздуха/вакуума) в соответствии с его проницаемостью.

С любой из этих точек зрения вам необходимо принять во внимание то, что делает индуктор индуктором (а именно привязку его тока к значительной намагниченности и его напряжения к временному изменению соответствующего значительного магнитного потока). При задании идеального индуктора без сопротивления напряжение не возникает из-за электропроводности материала, но это не учитывает связанные магнитные поля и напряжения, индуцированные их изменением.

\$\конечная группа\$

\$\начало группы\$

Неважно, идеален индуктор или нет. И идеальный индуктор просто имеет индуктивность, у него нет последовательного сопротивления. Изменяющееся магнитное поле индуцирует напряжение в любом индукторе. Если ток в катушке индуктивности внезапно отключается, скорость изменения тока di/dt становится бесконечной, поэтому индуцированное напряжение также бесконечно.

\$\конечная группа\$

\$\начало группы\$

(Источник изображения: Electronics Tutorials — Transient Curves for the LR Series Circuit)

Ссылка на рисунок:
По мере того, как R стремится к 0, а время стремится к бесконечности, экспоненциальный член приближается к 0.
I = V/0 > бесконечность
VL = V x 0 = 0

Нет R
DC V, бесконечная шина
Ваша система неопределима.
Эта мысленная модель не поможет вам понять L в цепи.

Постоянная времени L/R = бесконечность означает, что время должно быть равно 0 или мгновенно.