5.Силы трения.

Опыт показывает, что всякое тело, движущееся по горизонтальной поверхности другого тела и предоставленное самому себе, с течением времени замедляет свое движение и наконец останавливается. Это значит, что на него со стороны другого тела, по поверхности которого оно движется, действует сила, направленная противоположно его скорости и наз. силой трения. О наличии сил трения свидетельствует и тот факт, что для приведения в движение тела, лежащего на поверхности другого тела, к нему необходимо приложить конечную силу, направленную в сторону движения и превышающую некоторую определенную минимальную величину. Эта сила необходима для преодоления силы трения покоя, препятствующей движению.

Рис.1

Силу F, действующую со стороны тела А на соприкасающееся с ним тело В, можно разложить на составляющие F_n и F_ (рис.1):

F = F_ + F_n (1).

Составляющая F_ лежит в плоскости соприкасающихся тел и зависит от состояния и свойств соприкасающихся поверхностей. Эта составляющая и вызывает силу трения.

Т.о., силы трения – это силы, действующие между телами вдоль их соприкасающихся поверхностей как при покое, так и при относительном движении тел и зависящие от состояния и свойств поверхностей соприкосновения, а также от их относительной V.При этом сила трения, действующая на тело, всегда направлена противоположно его скорости по отношению к другому телу, соприкасающемуся с ним. Силы трения возникают при действии на соприкасающиеся тела внешних сил, имеющих составляющие, направленные вдоль поверхности соприкосновения, а также при движении этих тел относительно друг друга.

Силы трения действуют на оба соприкасающихся тела, будучи равными по величине и противоположно направленными, причем их направления противоположны относительным скоростям тел. Так, пусть тело А (Рис.2) движется со скоростью V_A по

Рис.2.

поверхности другого тела В, скорость которого V_B, направлена в ту же сторону, но |V_B| < |V_A|. Относительная скорость тела А (по отношению к условно неподвижному телу В) равна 

V_A— V_В и направлена, как и V_A. Поэтому сила трения _А, действующая на него со стороны тела В, будет направлена противоположно его относительной скорости (влево). Относительная же скорость тела В равна V_B — V_A и направлена в сторону противоположную V_A (т.к. V_B < V_A). Поэтому сила трения _В будет действовать на тело В в направлении его скорости V_B (вправо).

Силы трения, действуя на тело, как и всякие другие силы, влияют на характер движения, поэтому их тоже необходтмо учитывать.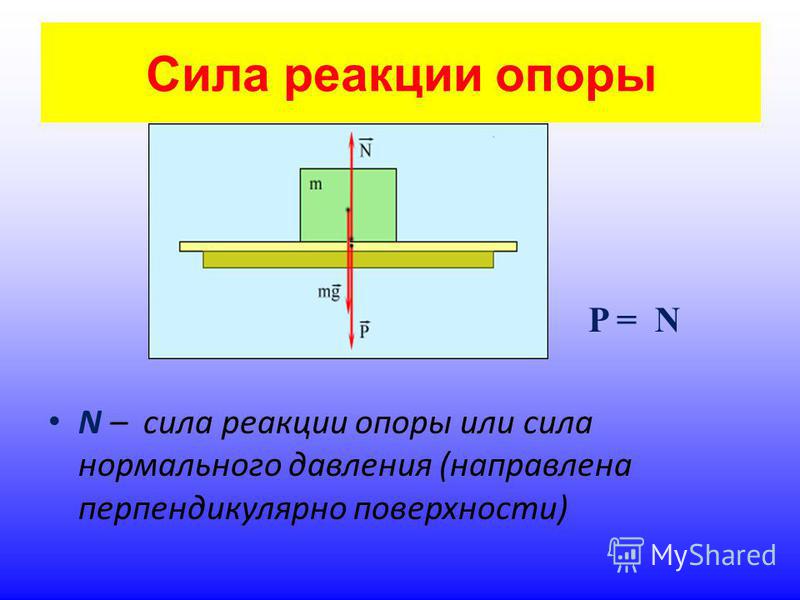

В частности, чтобы поддерживать скорость движущегося тела V неизменной, на него необходимо все время действовать с силой F, направленной в сторону движения и по величине равной силе трения , препятствующей движению. Тогда эти две силы уравновесят др. др. и ускорение тела

dV/dt = (F + )/m = 0 , т.к. F +  = 0.

В действительности тела движутся равномерно и прямолинейно не тогда, когда на них никакие силы не действуют (это невозможно осуществить в земных условиях), а когда силы трения уравновешиваются другими, противоположно направленными силами, приложенными к телу извне.

Чтобы измерить силу трения , действующую на некоторое тело массы m , к нему прилагают известную (измеримую непосредственно) движущую силу F, подобрав ее величину такой, чтобы тело двигалось без ускорения. Тогда по 2-му закю Ньтона:

F + =mdV/dt = 0   =F.

В частности, для измерения силы трения  применяется такой метод, рис. 3.

Рис.3.

Груз M подбирают таким, чтобы тело двигалось без ускорения. В этом случае  = Т = Mg.

Прибор для измерения сил трения называется трибометром.

Силы трения, действуют между соприкасающимися твердыми телами, наз. силами сухого трения. Они действуют и при движении соприкасающихся тел и при их относительном покое. Характерной особенностью, отличающей их от трения в жидкостях и газах, является то, что по мере уменьшения относительной скорости соприкасающихся тел вплоть до нуля силы сухого трения, действующие между ними, не обращаются в нуль, а стремятся к определенной величине, наз. трением покоя. Рассказать о силе трения покоя по рис.3.

При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения покоя, величина которой может меняться от 0 до _пред, называется предельной силой трения. Сила трения покоя – неоднозначная величина: с изменением внешней силы соотв. изменяется и сила трения покоя так, чтобы уравновесить внешнюю силу. Когда внешняя сила окажется по величине больше _пред, то возникнет скольжение данного тела по поверхности соприкасающегося с ним другого тела.

Опыт показывает, что

силы трения зависят от относительной скорости скольжения. Вначале с возрастанием относительной скорости величина  несколько уменьшается, а затем при дальнейшем увеличении скорости, величина  медленно начинает возрастать. Но эти изменения слабые, так что часто считают, что  не зависит от скорости.  зависит от материала, от состояния соприкасающихся поверхностей (от их шероховатости), а также от величины силы нормального давления одного из данных тел на другое. Кулон исследовал силы трения и установил закон Кулона :

Величина сил трения , действующих между двумя данными телами, не зависит от площади их соприкасающихся поверхностей и пропорциональна силе нормального давления

N:

 = kN , где к – коэф.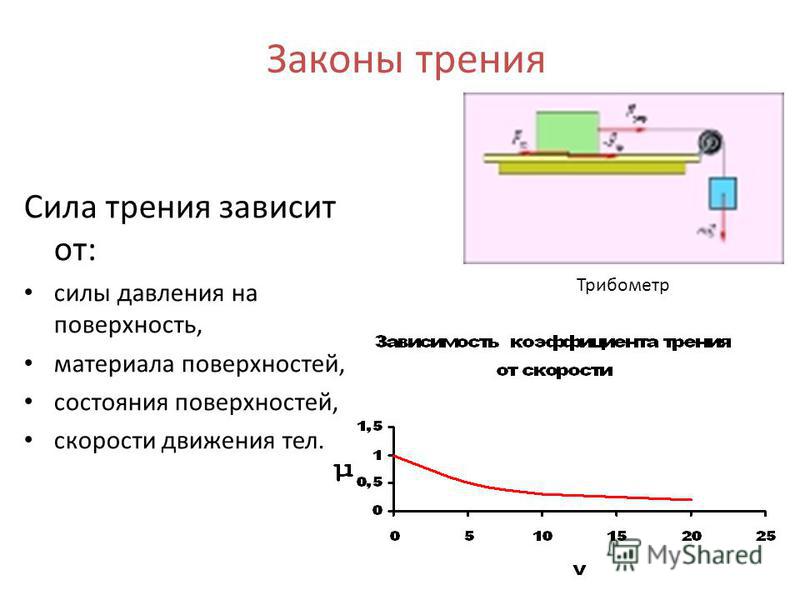 трения скольжения, N – сила нормального давления.

_пред = к₀ N, где

к₀ – коэф. трения покоя. k > k₀. Коэф. трения в таблицах.

Силы трения действуют и при качении тела по поверхности другого тела. В этом случае

 = SN/R, где

R – радиус катящегося тела, S – коэффициент трения качения.

Обычно S/R <<k !  замена скольжения тела его качением. Для уменьшения трения между трущимися поверхностями твердых тел помещают смазку, т.к. внутренее трение жидкости меньше трения скольжения.

6.СИЛЫ УПРУГОСТИ. ЗАКОН ГУКА.

Силы упругости – это силы, возникающие только при деформации тел. Действующая на тело сила может деформировать тело, составляющие его частицы смещаются друг относительно друга.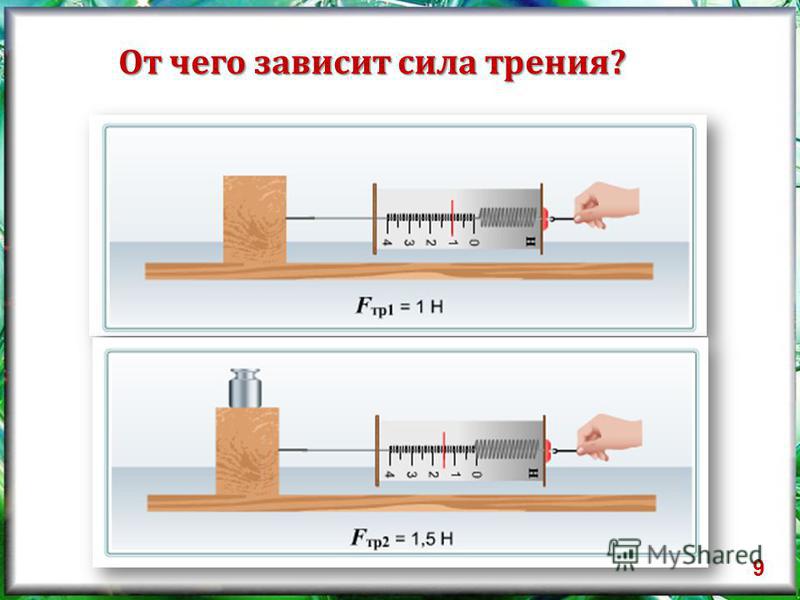 При этом в соответствии с 3-м законом Ньютона внутри деформированного тела возникает противодействующая сила, равная по модулю деформирующей силе и называемая силой упругости

. При прекращении деформации силы упругости исчезают.

Пример: растяжение пружины или резинки.

Заметим, что хотя силы упругости появляются только при деформациях, но не всегда деформация приводит к появлению сил упругости. Силы упругости возникают в телах, которые восстанавливают свою форму или объем после прекращения действия сил, вызывающих деформацию. Именно такие силы называются упругими.

Деформация называется упругой, если после прекращения внешнего воздействия тело полностью восстанавливает свою форму и размеры. При пластической деформации изменения размеров и формы тела полностью не исчезают после прекращения действия силы. Мы будем рассматривать только упругую деформацию.

Существует несколько видов деформации тел: одностороннее растяжение или сжатие, всестороннее растяжение или сжатие, кручение, сдвиг, изгиб.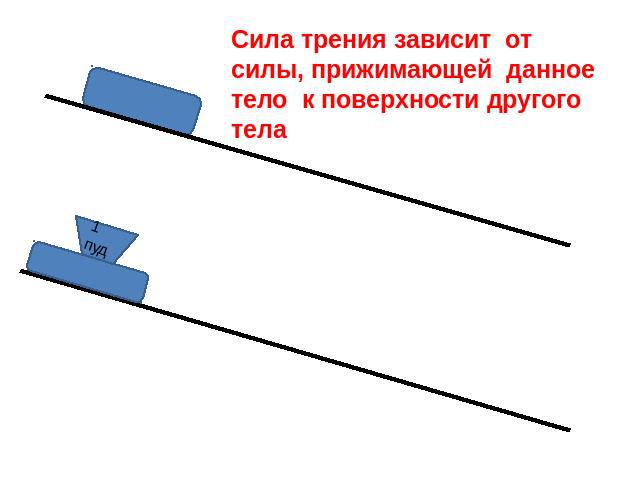 Каждый вид деформации вызывает появление соответствующие силы упругости.

Английский физик Роберт Гук установил экспериментальную зависимость между силой упругости и величиной деформации: сила упругости F, возникающая при малых деформациях любого вида, пропорциональна деформации X (закон Гука)

F = — k X.

При больших смещениях X возникает остаточная деформация –тело не восстанавливает полностью свои форму и размер. При значительных деформациях может даже произойти разрушение тела (рис.) Этот закон легко установить, наблюдая растяжение пружины под действием силы F, приложенной к ее концу.

Рис.1.

Легко установить, что |F_упр| = k |X|. Коэф. k –наз. коэф. упругости или жесткостью пружины. Коэффициент k различных тел зависит от формы и материала вещества, в котором возникают силы упругости.

При растяжении и сжатии стержней из стали, чугуна и т.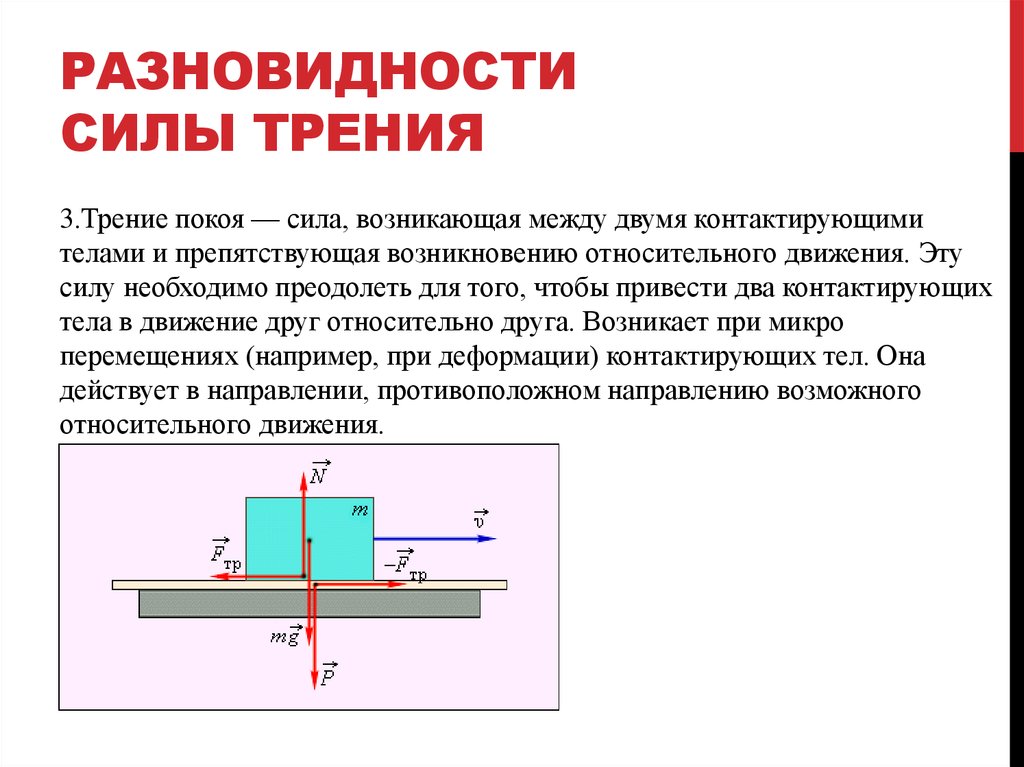 д. уменьшение или увеличение их длины также пропорционально приложенной силе. Величина k для стержней зависит не только от материала стержня, но и от его начальной длины l₀ и площади поперечного сечения S. Эта зависимость отражается следующей формулой:

K = SE/l₀,

где Е – называется модулем упругости материала или модулем Юнга, он характеризует упругие свойства вещества стержня и не зависит от размеров тела. Сила же упругости для стержня будет F_упр = SEl /l₀ , откуда при l = l₀ и S = 1 получим Е = F_упр, т.е модуль упругости вещества равен отношению силы, растягивающей вдвое стержень из этого вещества, к площади поперечного сечения стержня.

Не останавливаясь на других видах деформации, отметим только, что все они в конечном счете могут быть сведены к соотвующим комбинациям деформаций одностороннего растяжения и сжатия.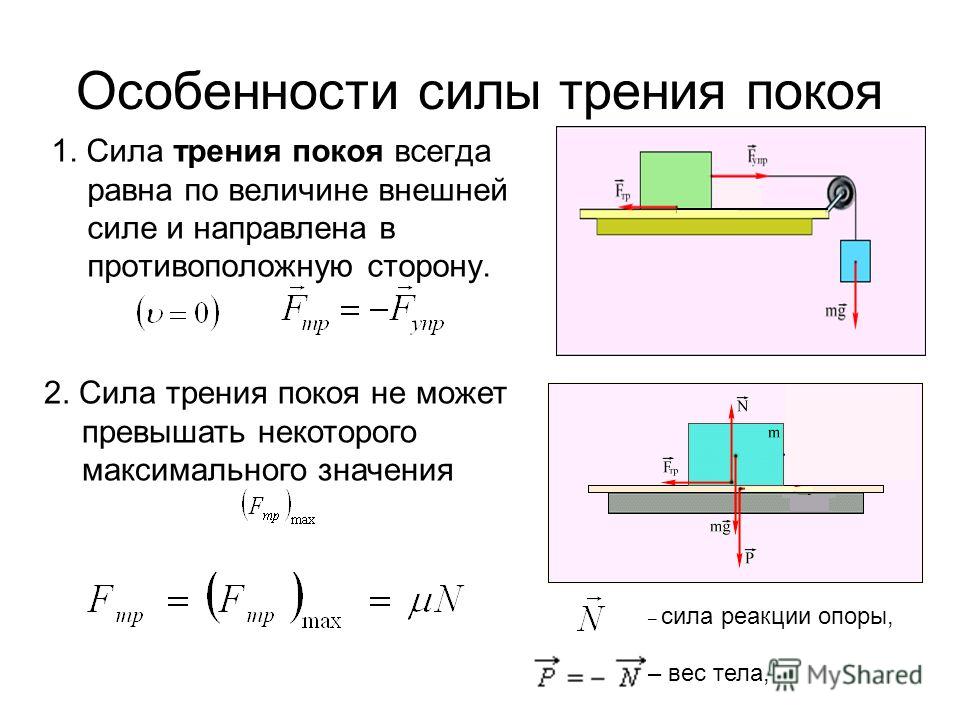

Величиной, указывающей в какой мере деформировано тело независимо от его длины, является относительная деформация

 = (l – l₀)/l₀.

Отношение деформирующей силы к площади S, на которую она действует F/S = P_н, численно равно силе, действующей на единицу площади в перпендикулярном ей направлении, наз. нормальным напряжением.

При описании деформации сдвига подобно модулю Юнга используют модуль сдвига N.

Трение. Сила трения | Физика

Кто из вас не катался с горы на санках? Приобретя большую скорость, санки, выехав на горизонтальный участок, останавливаются. Почему? Вспомните, что действующая на тело сила может изменить скорость его движения. Этой силой является сила трения скольжения. А что нужно сделать, чтобы санки продолжали движение с той же скоростью? Необходимо скомпенсировать силу трения. Для этого следует тянуть санки горизонтально с силой, равной по модулю силе трения. От чего зависит сила трения?

Проведем опыт. Будем с помощью динамометра равномерно перемещать брусок по горизонтальной поверхности стола. Динамометр показывает, что на брусок действует сила тяги, но скорость движения бруска не изменяется. Значит, на брусок действует еще одна сила — компенсирующая сила. Этой силой является сила трения F_тр. Равнодействующая сил F_тяги и F_тр равна нулю. Обратите внимание, что модуль силы трения равен модулю силы тяги только в случае равномерного прямолинейного движения. Если же модуль силы тяги больше модуля силы трения, скорость движения тела будет возрастать. А если F_тяги меньше F_тр — убывать.

Итак, сила трения скольжения возникает при движении одного тела по поверхности другого и направлена в сторону, противоположную движению.

Почему возникает сила трения? Продолжим опыт. Будем равномерно перемещать брусок сначала по шероховатой, затем по обработанной поверхности доски. Сила тяги будет больше при движении по шероховатой поверхности. Значит, и модуль равной ей силы трения будет тем больше, чем более шероховатой, неровной окажется поверхность. При движении неровности цепляются друг за друга, деформируются, разрушаются. Это создает препятствия движению. А если бы поверхности были идеально гладкие, то возникла ли бы сила трения при движении одного тела по поверхности другого? Не спешите ответить «нет». При хорошо отполированных поверхностях расстояние между поверхностями тел или их участками при движении тел так мало, что станут существенными силы притяжения молекул поверхности одного тела к молекулам поверхности другого. Эти силы будут тормозить движение тел.

Значит, шероховатость поверхностей и силы притяжения между молекулами соприкасающихся поверхностей — причины возникновения сил трения.

Если при движении соприкасаются твердые поверхности тел, трение называют сухим.

От чего еще зависит сила сухого трения? Дадим ответ, исходя из опыта. Будем равномерно двигать брусок по различным поверхностям: по металлической, деревянной, резиновой — с примерно одинаковым качеством обработки. Динамометр показывает различную силу тяги. Следовательно, силы трения дерева по металлу, дерева по дереву, дерева по резине будут различны. Наибольшая сила трения возникнет при движении по поверхности резины. Не случайно подошвы в спортивной обуви делают резиновыми и рельефными.

Поставим теперь на брусок гирю и сравним силы трения при равномерном движении ненагруженного бруска и бруска с гирей. Видно, что во втором случае сила тяги, а значит, и сила трения увеличились. Но брусок с гирей с большей силой давит на поверхность, с которой соприкасается. Следовательно, сила трения тем больше, чем больше сила, прижимающая тело (брусок) к поверхности.

Как уменьшить трение? Здесь есть два пути. Первый — заменить трение скольжения трением качения. Проделаем такой опыт. Будем равномерно передвигать металлическую тележку по столу скольжением и качением. Сила трения во втором случае значительно меньше, хотя материал поверхностей и прижимающая сила не изменяются. Значит, трение качения меньше трения скольжения. С тяжелым чемоданом справиться легко, если прикрепить к нему колеса.

Второй путь уменьшения трения скольжения — это смазывание трущихся поверхностей. Смазка (например, масло) заполняет все неровности трущихся поверхностей и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга. При этом сухое трение заменяется трением слоев жидкости (масла), а оно в 8-10 раз меньше.

Опытный водитель никогда не отправится в далекий путь, не проверив, достаточно ли масла в двигателе машины. Объясните, зачем он это делает.

А знаете ли вы, что с помощью катков перемещают дома? Например, в городе Москве во время реконструкции улицы Тверской некоторые дома были передвинуты на другое место именно таким способом.

В машинах для замены трения скольжения трением качения используют шариковые и роликовые подшипники. Подшипники диаметром 1,5-2 мм применяют в точных измерительных приборах. Вращающийся вал машины или другого механизма не скользит по неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах. Это снижает трение в 20-30 раз.

Главные выводы:

1. Сила трения скольжения возникает при движении одного тела по поверхности другого.
2. Сила трения скольжения направлена против движения.
3. Сила трения зависит от свойств соприкасающихся поверхностей и силы, прижимающей тело к поверхности.

Читать далее

← Сложение сил. Равнодействующая сила

Давление. Единицы давления →

Объяснение урока: Движение тела на шероховатой плоскости

В этом толкователе мы научимся изучать движение частицы на горизонтальной и наклонной шероховатой плоскостях против силы трения.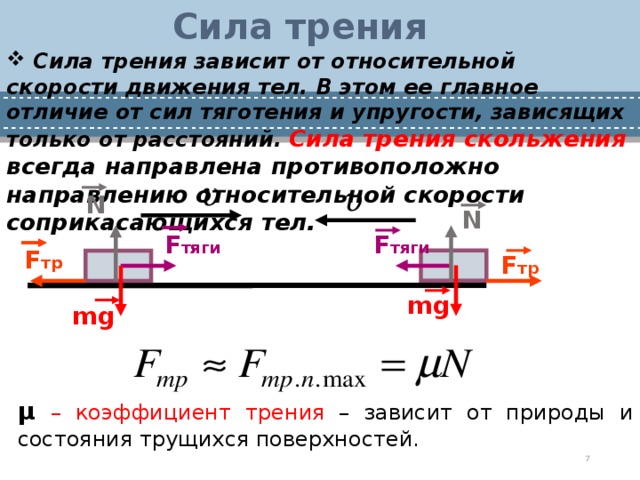

Тело, находящееся в равновесии на горизонтальной поверхности, имеет нулевую результирующую силу, действующую на него. На тело действуют две силы: его вес, 𝑊, и нормальная сила реакции поверхности, ⃑𝑅, как показано на следующем рисунке.

Величина 𝑊 определяется выражением𝑊=𝑚𝑔, где 𝑚 — масса тела, а 𝑔 — ускорение свободного падения.

Сила 𝑊 действует вертикально вниз. Сила ⃑𝑅 действует нормально к поверхности. Для тела на горизонтальной поверхности ⃑𝑅 действует вертикально вверх. Для неподвешенного тела, находящегося в равновесии на горизонтальной поверхности, величины 𝑊 и ⃑𝑅 равны.

На тело может действовать горизонтальная сила ⃑𝐻. Если величина ⃑𝐻 ниже или равна определенному значению, известному как предельное трение, тело останется в покое. Это происходит из-за статической силы трения ⃑𝐹, которая действует в направлении, противоположном ⃑𝐻. Однако, когда величина ⃑𝐻 больше, чем величина предельного трения, тело будет ускоряться в направлении ⃑𝐻.

Величина силы трения, 𝐹трения, между телом, движущимся по поверхности, и поверхностью, по которой оно движется, определяется выражением 𝐹=𝜇𝑅,трение, где 𝜇 называется коэффициентом кинетического трения между телом и поверхностью.

Очень похож на коэффициент статического трения, но относится к движущимся телам.

Для горизонтальной поверхности 𝑅=𝑚𝑔, поэтому 𝐹=𝑚𝑔𝜇.friction

Рассмотрим пример определения коэффициента кинетического трения между телом и горизонтальной поверхностью.

Пример 1. Расчет коэффициента трения для тела, движущегося по шероховатой горизонтальной плоскости

Тело массой 28 кг движется по горизонтальной плоскости с ускорением, равным величине 2,2 м/с ² . На него действует приложенная сила 155 N, направление которого указано на рисунке. Рассчитать коэффициент кинетики трение округляет результат до ближайших двух знаков после запятой. Возьмем ускорение свободного падения 𝑔=90,8/мс.

Ответ

На следующем рисунке показаны силы, действующие на тело.

Сила трения, действующая на тело, зависит от силы нормальной реакции тела, ⃑𝑅. Нормальная сила реакции, действующая на тело, зависит от силы, с которой тело действует на поверхность.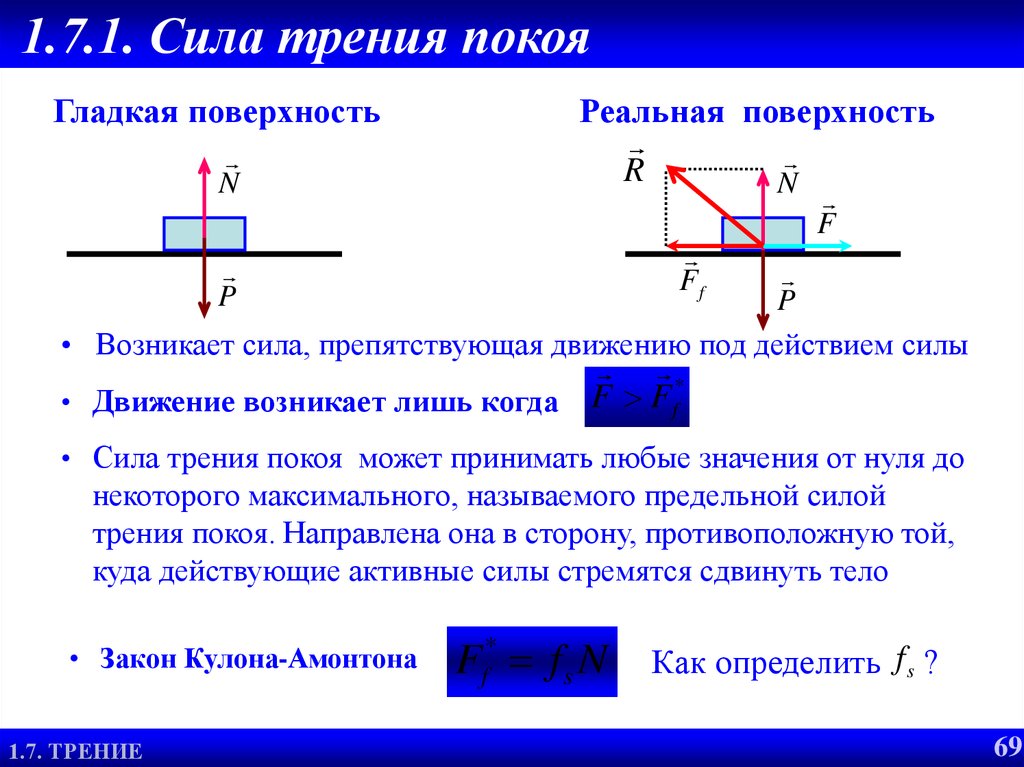 Сила, с которой тело действует на поверхность, обусловлена ​​его весом. Однако некоторая составляющая силы 155 Н, действующей на тело, действует в противоположном направлении. веса тела вертикально вверх.

Приняв силу, направленную вертикально вниз, за ​​положительную, сумма веса тела и вертикально направленной составляющей приложенной силы имеет заданную величину по 𝐹=𝑚𝑔−155(45)=28(9,8)−155√2=𝑅.surfacesin

Таким образом, величина ⃑𝑅 равна 𝑅=274,4−155√2=164,8.N

Используя формулу 𝐹=𝜇𝑅, трения, мы видим, что сила трения имеет величину 𝐹=𝜇×164,8.frictionN

Величина силы трения может быть определена по величине горизонтальной составляющей силы, приложенной к телу, и результирующей силы, действующей на тело.

Величина результирующей силы, действующей на тело, равна произведению массы тела на величину ускорения тела; следовательно, 𝐹=28×2.2=61.6.netN

Принимая направление движения за положительное, результирующая сила, действующая на тело, определяется выражением 155(45)−𝐹=𝐹. cosfrictionnet

Следовательно,𝐹=155√2−61,6=48.frictionN

Зная силу трения, находим коэффициент трения 𝜇: 48=𝜇×164,8.

Значение 𝜇 можно определить, сделав его предметом уравнения: 𝜇=48164,8.

С точностью до двух знаков после запятой это 0,29.

Сила трения также действует на тело, движущееся по шероховатой поверхности. На тело, покоящееся на шероховатой поверхности, действует сила трения. Коэффициент кинетического трения 𝜇k и коэффициент трения покоя 𝜇s связаны следующим неравенством: 𝜇>𝜇.sk

Сила трения, действующая на тело на шероховатой поверхности, определяется выражением 𝐹=𝜇𝑅.friction

Если бы у нас было 𝜇>𝜇,ks, то для горизонтальной силы с величиной 𝐹, приложенной к телу так, что 𝐹 немного превышает 𝜇𝑅s и, следовательно, тело начинает двигаться, было бы так, что 𝐹−𝜇𝑅0,k означает что тело будет ускоряться из состояния покоя в направлении, противоположном направлению приложенной силы. Это никогда не наблюдается. Коэффициент кинетического трения всегда меньше коэффициента статического трения.

Взаимосвязь между коэффициентами статического и кинетического трения может быть интуитивно оценена по воспринимаемой трудности толкания объекта, находящегося в состоянии покоя, до точки, в которой он начинает двигаться, по сравнению с воспринимаемой трудностью толкания объекта для поддержания его движения.

Давайте теперь рассмотрим пример, включающий статический и кинетический коэффициенты трения.

Пример 2. Расчет статического и кинетического трения на шероховатой горизонтальной плоскости

Тело массой 11√3 кг помещено на шероховатой горизонтальной плоскости. Коэффициент статического трения между телом и самолетом равен √33, а коэффициент кинетического трения равен √37. На тело действует сила, линия ее действия образует с горизонтом угол 60∘. Сила заставляет тело двигаться. Если модуль силы увеличить с 𝐹 до 𝐹, тело начнет двигаться и ускорится со скоростью 5√33 м/с ² . Найдите 𝐹 и 𝐹. Возьми 𝑔=90,8/мс.

Ответ

Силы, действующие на тело, показаны на следующем рисунке.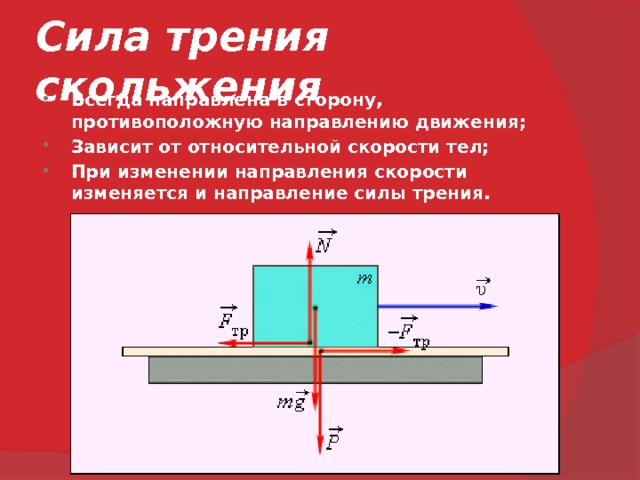

Когда тело находится в равновесии с действующей на него силой 𝐹, модуль силы трения на теле равен горизонтальной составляющей 𝐹. Таким образом, мы имеем, что нормальная сила реакции на тело.

Выражение для 𝑅 можно найти, переформулировав выражение для силы трения, выраженное через 𝐹, следующим образом: 𝐹2=√33𝑅𝑅=𝐹32√3.𝑅 не равно весу тела в в этом случае, поскольку 𝐹 имеет восходящую вертикальную составляющую, которая уменьшает силу, действующую на поверхность, поддерживающую тело, уменьшая нормальную силу реакции на тело.

Вертикальные силы, действующие на тело, представляют собой вес тела, направленный вниз, реакцию на тело, направленную вверх, и вертикальную составляющую 𝐹, направленную вверх. Приравнивая вертикальные силы, направленные вниз, к вертикальным силам, направленным вверх, мы получаем 11√3×9,8=𝑅+𝐹60=𝑅+√32𝐹.sin

Подставляя выражение для 𝑅 через 𝐹, находим, что 107,8 √3=32√3𝐹+√32𝐹107,8√3=√32𝐹+√32𝐹107,8√3=𝐹√3𝐹=107,8.003N

Когда 𝐹 увеличивается по величине до 𝐹, нормальная сила реакции изменяет величину по мере увеличения направленной вверх силы, действующей на тело, как показано на следующем рисунке.

Приравнивая вертикальные направленные вниз силы вертикальным направленным вверх силам, действующим на тело, получаем, что 107,8√3=𝑅+√32𝐹.𝑅 можно выразить через 𝐹, переставив следующим образом:𝑅= 107.8√3−√32𝐹.

Когда 𝐹 увеличивается по модулю до 𝐹, тело ускоряется горизонтально со скоростью 5√33 м/с ² .

Согласно второму закону движения Ньютона 𝐹=𝑚𝑎; величина горизонтальной (чистой) силы, действующей на тело, теперь определяется как 11√3×5√33.N

Кроме того, сила трения определяется как √37𝑅.

Величина чистой горизонтальной силы равна величине горизонтальной составляющей 𝐹 минус величина силы трения, действующей на тело; следовательно, 11√3×5√33=𝐹2−√37𝑅.

Это выражение можно преобразовать, чтобы определить горизонтальную составляющую 𝐹, которая определяется как 𝐹2=55+√37𝑅.

Подставляя полученное значение 𝑅, находим 𝐹2=55+√37107,8×√3−√32𝐹𝐹2=55+17107,8×3−32𝐹𝐹2=55 +17323.4 — 32𝐹𝐹2 = 55+323,47 — 314𝐹𝐹2+314𝐹 = 55+323,47𝐹714+314 = 55+46,2 = 101,2𝐹 = 1410101,2 = 141,68 .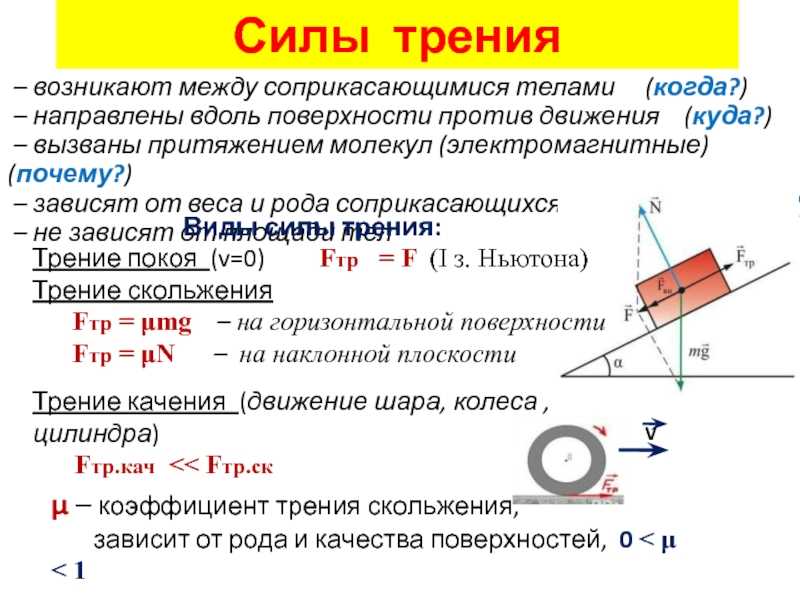 N

Если тело находится на наклонной плоскости, то нормальная сила реакции ⃑𝑅 на тело показана на следующем рисунке.

Если нет движения в направлении, перпендикулярном плоскости, то величина силы реакции ⃑𝑅 равна составляющей веса, перпендикулярной плоскости, 𝑚𝑔𝜃cos:𝑅=𝑚𝑔𝜃,cos где 𝜃 угол от горизонтали при которой наклонена поверхность.

Результат ⃑𝑅 и веса тела показан на следующем рисунке как сила ⃑𝐹.

Направление ⃑𝐹 вниз вдоль поверхности. На следующем рисунке показано, как можно определить величину ⃑𝐹.

Мы видим, что 𝐹=𝑚𝑔𝜙=𝑚𝑔𝜃.cossin

Если наклонная поверхность шероховатая, то на тело действует сила трения, параллельная поверхности, в направлении, противоположном результирующей силе на тело.

Теперь рассмотрим пример, когда тело движется по шероховатой наклонной поверхности.

Пример 3. Расчет тела на шероховатой наклонной плоскости

Тело массой 𝑚 кг было помещено на плоскость, наклоненную под углом 45∘ к горизонту. На тело по линии наибольшего наклона вверх по плоскости действовала сила величиной 392√2 Н. В результате тело равномерно ускорилось со скоростью 𝑎 м/с ² вверх по плоскости. Если модуль силы, действующей на тело, уменьшить вдвое при сохранении его первоначального направления, тело будет двигаться вниз по плоскости со скоростью 𝑎 м/с ² . Учитывая, что сопротивление самолета движению тела в обоих случаях равно 38√2 Н, определить значения 𝑚 и 𝑎, округлив результаты до двух знаков после запятой. Возьми 𝑔=90,8/мс.

Ответ

На следующем рисунке показаны силы, действующие на тело до изменения величины приложенной к телу силы. Ускорение тела показано красным цветом.

Когда тело движется вверх параллельно плоскости, величина результирующей силы, параллельной плоскости, определяется выражением 𝐹=392√2−38√2−𝑚𝑔(45)𝐹=392√2− 38√2−𝑚𝑔√2.upupsin

На следующем рисунке показаны силы, действующие на тело после изменения величины приложенной к телу силы.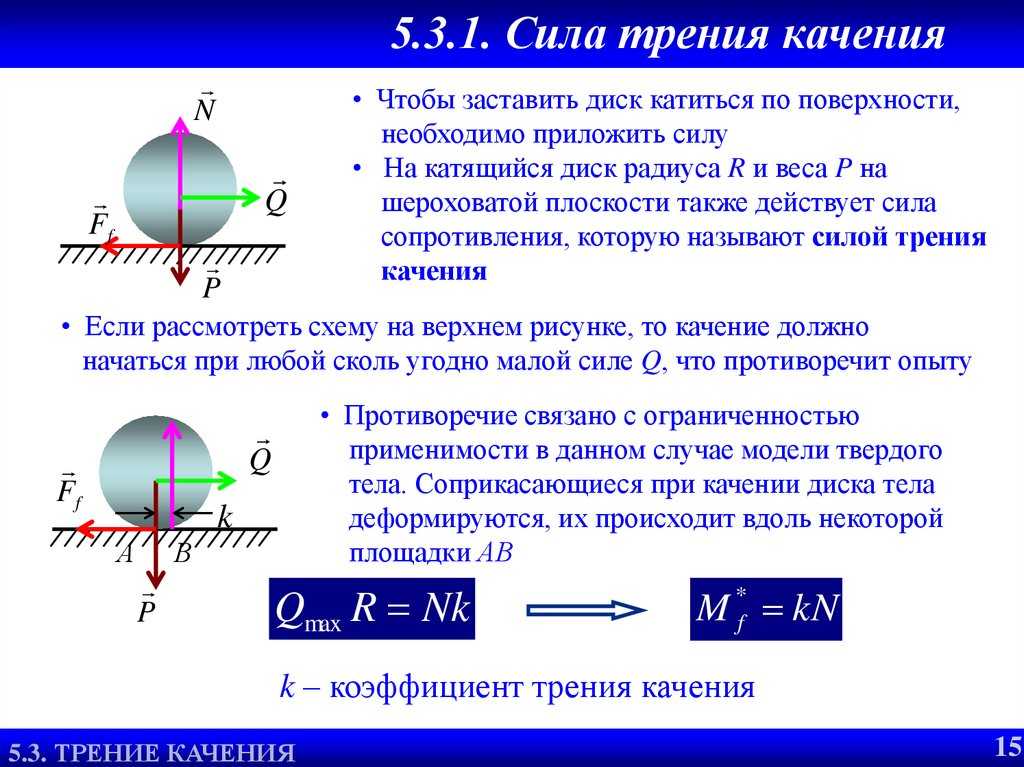 Ускорение тела показано красным цветом.

Когда тело движется вниз параллельно плоскости, сила трения действует вверх параллельно плоскости, поскольку сила трения действует в направлении, противоположном движению объекта. Величина чистой силы, действующей вниз параллельно плоскости, определяется как Поскольку 𝐹=𝑚𝑎, это означает, что восходящая и нисходящая силы имеют одинаковую величину, но действуют в противоположных направлениях; поэтому имеем 𝐹=𝐹,392√2−38√2−𝑚𝑔√2=𝑚𝑔√2−196√2−38√2.updown

К обеим частям уравнения добавляется следующее: 196√2+38√2+𝑚𝑔√2, откуда мы получаем up

Подставляя полученное значение 𝑚, получаем 𝐹=354√2−588√2=60√2.up

Значение 𝑎 определяется как С точностью до двух знаков после запятой это 1,41 м/с ² .

Подведем итог тому, что мы узнали из этих примеров.

Ключевые моменты

• Величина силы трения, 𝐹friction, между телом, движущимся по поверхности, и поверхностью, по которой оно движется, определяется выражением 𝐹=𝜇𝑅,трение, где 𝜇 — коэффициент кинетического трения между телом и поверхностью.
• Сила кинетического трения на движущееся тело действует в направлении, противоположном движению тела.
• Сила трения покоя на покоящееся тело действует в направлении, противоположном результирующей силе, действующей на тело.
• Коэффициент кинетического трения 𝜇k и коэффициент трения покоя 𝜇s связаны следующим неравенством: 𝜇>𝜇.sk
• Тело на наклонной плоскости действует на сила реакции на нее определяется выражением 𝐹=𝑚𝑔𝜃,sin, где 𝑚 — масса тела, 𝑔 — ускорение свободного падения, а 𝜃 — угол, который плоскость образует с горизонтом.
• Когда к телу, движущемуся по наклонной плоскости, приложена сила, не параллельная плоскости, сумма составляющей приложенной силы, перпендикулярной плоскости, веса тела и нормальной силы реакции равна нуль. Следовательно, сила реакции имеет другую величину, чем если бы приложенная сила действовала параллельно плоскости.

Трение, Коэффициент трения и силы, действующие на тело Экзаменационные уроки

Основная концепция : Когда два тела соприкасаются, каждое из них оказывает силу на другое. Следовательно, трение можно определить как силу, которая стремится противодействовать относительному скользящему движению двух соприкасающихся поверхностей. Сила трения – это противодействующая сила между двумя контактирующими силами.

Направление трения противоположно направлению, в котором будет происходить движение. Сила трения для любых двух соприкасающихся поверхностей имеет значение, определяемое формулой 9.0003

            F = UR

Где R – нормальная реакция между телами, полученная как; R = m x g

            U  = коэффициент трения, и его значение зависит только от характера контактирующих поверхностей.

Примеры

1: Груз массой 4 кг лежит на грубом горизонтальном столе с U = 0,4. Найдите наименьшую силу, достаточную для перемещения массы: (примите g = 10 мс ^-2 )

Решение

Достаточная сила; Ф = УР.

r = m x g = 4 x 10 = 40

f = 0,4 x 40

f = 16n

2. Если сила 10N достаточно для перемещения массы 2 кг, покоясь на грубой горизонтальной таблице, найдите коэффициент трения (g = 10 мс ^-2 )

Раствор

            F = 10 Н, m = 2 кг.

            F = UR

            10 = U x 2 x 10

            10 = 20U0003

            U = 0,5

ОЦЕНКА

Тело массой 8 кг лежит на горизонтальной поверхности. Если коэффициент трения между телом и горизонтальной поверхностью равен 0,65, рассчитайте минимальную горизонтальную силу, достаточную для того, чтобы просто сдвинуть тело.

Грубая наклонная плоскость: две основные силы действуют на объект, расположенный на наклонной плоскости; приложенные силы P и сила трения F         P= Mg SinӨ

            F = Mg SinӨ

            R = Mg Cos Ө

            Recal F = U R

            :. F = U MgCos Ө      где F – предельное

           Трение:

Наименьшая сила, необходимая в P, чтобы заставить тело двигаться вверх по наклонной плоскости r, равна P = UR + Mg Sin Ө

:. P = F + MgSinӨ

  P = UR + MgSinӨ

Таким образом, наименьшая сила, необходимая для того, чтобы заставить тело скользить по плоскости, составляет

            P + f = mgSin Ө

            P = мг Sin Ө- U r.

Где m = масса и Ө= угол трения.

Значение коэффициента Фритона из F = U R и

MgSinө = U MGCOS ө определяется

U = Mg SIN ө / MG COS ө

:. U = tan Ө

Примеры

1. Брусок лежит на наклонной плоскости под углом 30 ^o к горизонту и просто остается в покое. Найдите коэффициент трения.

Решение

ө = 30 ^O , U = TAN ө

U = TAN 30 ^O

U = 1/√3 или 0,5774.

2. Тело массой 4,5 кг лежит на гладкой плоскости, наклоненной под углом 47 ^o к горизонту. Рассчитайте величину силы P, параллельной плоскости, достаточной для предотвращения скольжения тела по плоскости

(g = 9,8 мс ^-2 ).

Решение

            P = мг Sin Ө

            P = 4,5 x 9,8 x sin 47 ^o   = 44,1 x 0,7314.

            P = 32,25 Н.

ОЦЕНКА

Частица массой 25 кг скользит по шероховатой плоскости, наклоненной под углом 30 ^o к горизонту. Если коэффициент трения равен 0,2, найдите в мс ^-2 ускорение частицы с точностью до 3 значащих цифр (примите g = 10 мс ^-2 )

ОБЩАЯ ОЦЕНКА

Однородная лестница длиной 6 м и массой 30 кг опирается одним концом на неровную вертикальную стену, а другим концом на неровную горизонтальную поверхность. Коэффициент трения в каждой точке контакта равен 0,3. Если лестница находится в точке скольжения, рассчитайте (i) нормальную реакцию земли, (ii) силу трения о стену, (iii) угол наклона лестницы к земле. (Возьмите g = 10 мс ^-2 )

НАЗНАЧЕНИЕ ЧТЕНИЯ

Чтение трения стр. 191 -195

ЗАДАНИЕ НА ВЫХОДНЫЕ

1.          Тело находится в предельном равновесии на плоскости, наклоненной под углом к ​​горизонту. если Cos   = 0,8, рассчитайте коэффициент трения.

2.         Масса большого камня 13 кг. На камне сидит мальчик весом 59 Н. Найдите минимальную горизонтальную силу P, необходимую для перемещения камня по земле. Если коэффициент трения равен 0,25 (g = 9,8 мс ^-2 ).

3.         Испытания массы 8 кг на шероховатой поверхности стола с U = 0,6. Найдите наименьшую силу, которая заставит массу двигаться (g = 10 мс ^-2 ).

4.         Тело массой 10 кг скользит по шероховатой плоскости с наклоном Ө к горизонту, где sin Ө = 0,6. если U = 0,3, найти ускорение ящика.

5.         Тело может просто находиться в равновесии на склоне, наклоненном под углом Ө к горизонту, где sinӨ = ⁵ / _13, найти U

Зарегистрируйтесь на форуме и выполните задание : Найдите вопросы в конце каждого урока.