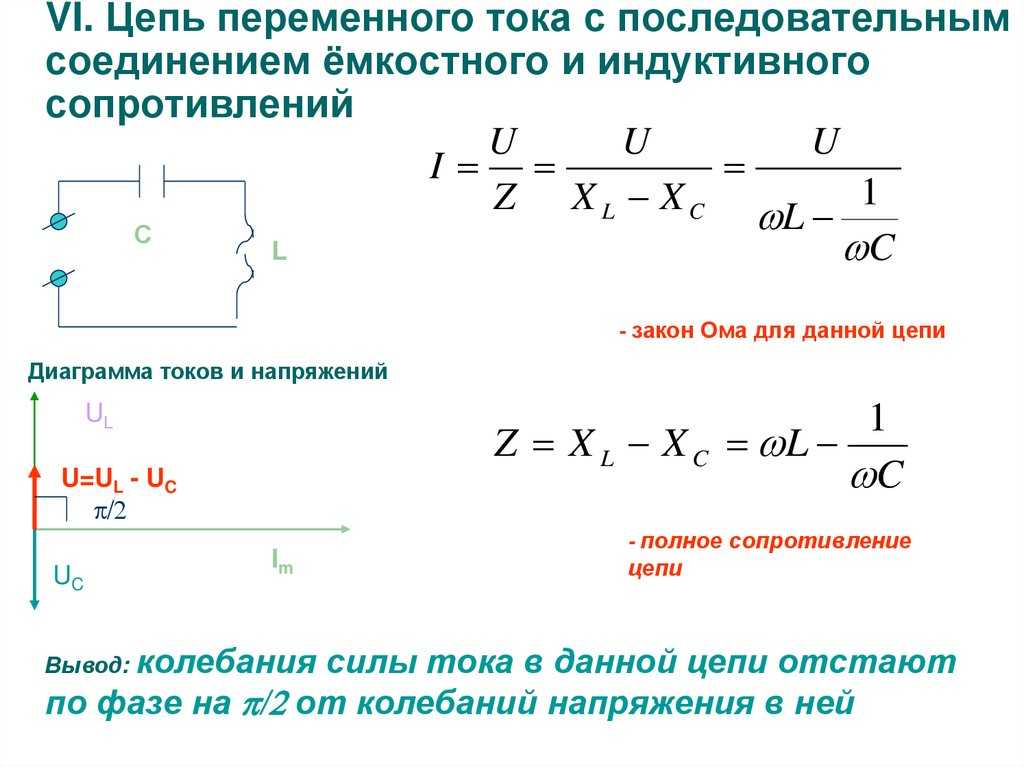
Переменный электрический ток. Активное, индуктивное, ёмкостное сопротивления.
Переменный электрический ток Электромагнитные колебания, как и механические, бывают двух типов: свободные и вынужденные. Свободные электромагнитные колебания, всегда колебания затухающие. Поэтому на практике они почти не используются. В то время, как вынужденные колебания используются везде и повсеместно. Ежедневно мы с вами можем наблюдать эти колебания. Все наши квартиры освещены с помощью переменного тока. Переменный ток есть не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение будут меняться с течением времени согласно гармоническому закону. Колебания, например, напряжения можно обнаружить, если подать напряжение из розетки, на осциллограф. На экране
осциллографа появится синусоида. Можно вычислить частоту переменного тока. Она
будет равняться частоте электромагнитных колебаний. Изменение напряжения на концах цепи будет вызывать за собой изменение силы тока в цепи колебательного контура. Следует всё же понимать, что изменение электрического поля во всей цепи не происходит мгновенно. Но так как это время, значительно меньше, чем период колебания напряжения на концах цепи, то обычно считают, что электрическое поле в цепи сразу же меняется, как меняется напряжение на концах цепи. Переменное напряжение создается генераторами на электростанциях. Простейшим генератором можно рассматривать проволочную рамку, которая вращается в однородном магнитном поле.  Следовательно, магнитный поток будет изменяться по гармоническому закону: Ф = BScos(ωt) Скорость изменения магнитного потока, взятая с обратным знаком, согласно закону ЭМИ, будет равняться ЭДС индукции. Ei = -Ф’ = Emsin(ωt). Если к рамке подключить колебательный контур, то угловая скорость вращения рамки определит частот колебаний напряжения на различных участках цепи и силы тока. В дальнейшем мы будем рассматривать только вынужденные электромагнитные колебания. Они описываются следующими формулами: u = Umsin(ωt), u = Umcos(ωt) Здесь Um – амплитуда колебаний напряжения. Напряжение и сила тока меняются с одинаковой частой ω. Но колебания напряжения не всегда будут совпадать с колебаниями силы тока, поэтому лучше использовать более общую формулу: I = Imsin(ωt
+φ), где Im — амплитуда колебаний силы тока, а φ – сдвиг фаз между
колебаниями силы тока и напряжения. Активное сопротивление Рассмотрим
следующую цепь. Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением. Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону: U = Umcos(ωt). I = u/R = Umcos(ωt)/R = Imcos(ωt). Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. Действующее значение силы тока Амплитуда силы тока определяется по следующей формуле: Im = Um/R. Среднее значение квадрата силы тока за период вычисляется по следующей формуле: i2 = (Im)2 Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока. Для обозначения действующего значения силы тока используется буква I. То есть в виде формулы это будет выглядеть следующим образом: I = √(i2) = Im/√2. Действующее значение силы переменного тока будет равно силе такого постоянного тока, при котором за одинаковый промежуток времени в рассматриваемом проводнике будет выделяться столько же теплоты, сколько и при переменном токе. Для определения действующего значения напряжения используется следующая формула. U = √(u2) = Um/√2. Теперь подставим
действующие значения силы тока и напряжения, в выражение Im = Um/R. I = U/R. Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения. Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока. Для вычисления средней мощности используется следующая формула: P = I2R = UI. Отметим, что измерительные приборы (амперметры и вольтметры переменного
тока) регистрируют именно действующие значения. При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор — это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен. В отличии от
постоянного переменный ток может идти и через цепь, в которой присутствует
конденсатор. Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора. рисунок Напряжение на
конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем
приравнять эти две величины. u = φ1-φ2 = q/C, u = Umcos(ωt). Имеем: q/C = Umcos(ωt). Выражаем заряд: q = CUmcos(ωt). Видим, что заряд будет изменяться по гармоническому закону. Сила тока — это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока. I = q’ = UmCωcos(ωt+π/2). Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной π/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на π/2. Это представлено на рисунке. Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока: Im = UmCω. Введем следующее обозначение: Xc = 1/(Cω). Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения: I = U/Xc. Xc — величина,
называемая емкостным сопротивлением. Индуктивность в
цепи переменного тока будет влиять на силу переменного тока. Рассмотрим цепь, в которой есть только катушка индуктивности. При этом значение сопротивления катушки и соединительных проводов пренебрежимо мало. рисунок Выясним, как будут связаны напряжение на катушке с ЭДС самоиндукции в ней. При сопротивлении катушки равном нулю, напряженность электрического поля внутри проводника тоже будет равна нулю. Равенство нулю напряженности возможно. Напряженности электрического поля создаваемого зарядами Eк будет соответствовать такая же по модулю и противоположно направленная напряженность вихревого электрического поля, которое появится вследствие изменения магнитного поля. Следовательно, ЭДС самоиндукции ei будет равна по модулю и противоположна по знаку удельной работе кулоновского поля. Следовательно: ei = -u. Сила тока будет
изменяться по гармоническому закону: I = Im sin(ωt). ЭДС самоиндукции будет равна: Ei = -Li’ = -Lω Im cos(ωt). Следовательно, напряжение будет равно: U = Lω Im cos(ωt) = Lω Im sin(ωt+ π/2). Отсюда значение действующего напряжения будет равняться Um = Lω Im. Видим, что между колебаниями тока и напряжения получилась разность фаз равная π/2. Следовательно, колебания силы тока отстают от колебания напряжения на π/2. Это наглядно представлено на следующем рисунке. рисунок Im = Um/(ωL). Введем обозначение XL = ωL. Эта величина называется индуктивное сопротивление. |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа. Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Интересное: Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 6 из 58Следующая ⇒
Л. Н. – Нужно некоторое время, чтобы я привык к этому понятию, так как все‑таки, по моему мнению, какой бы эластичной мембрана ни была, она является препятствием. Л. – Конечно! Емкостным сопротивлением и назвали то сопротивление, которое конденсатор оказывает переменному току. Н. – Ну вот еще один термин, да к тому же опять страшно сложный. Л. – Наоборот, все это в сущности очень просто. Ты легко догадаешься сам, от чего зависит емкостное сопротивление. Н. – Я полагаю, что оно зависит от емкости. Чем эластичнее мембрана, тем она больше изгибается и тем самым дает возможность большему количеству электронов входить с одной стороны и выходить с другой. Л. – Итак, чем больше емкость, тем переменный ток легче проходит через конденсатор, и тогда мы говорим, что емкостное сопротивление меньше. Н. – Как раз противоположно тому, что, происходит при индуктивном сопротивлении, которое возрастает с увеличением индуктивности катушек. Ну, а в действительности разве емкостное сопротивление, так же как и индуктивное, не зависит от частоты тока? Л. – Конечно, чем больше частота, тем больше зарядов и разрядов конденсатора происходит в секунду и, следовательно, больше электронов проходит через поперечное сечение цепи в секунду. Н. – Значит, ток возрастает с увеличением частоты; имение это и доказывает, что емкостное сопротивление увеличивается. Но, дорогой Любознайкин, много ли еще у тебя в запасе всяких сопротивлений? Я чувствую, что мое сильно уменьшается. Л. – Успокойся, теперь ты уже знаешь три вида сопротивлений, имеющихся в электрорадиотехнике.
Н. – Со свойствами различных видов сопротивлений, положим, я разберусь, но мне бы хотелось увидеть их в том наборе деталей, которые ты уже начал приобретать для приемника. Л. – Желание законное, хотя оно свидетельствует о том, что ты еще не все понял. В отличие от активного сопротивления, присущего тому или иному конкретному материалу проводника, индуктивное и емкостное сопротивления называют реактивными . Эти как бы кажущиеся сопротивления катушек или конденсаторов появляются только тогда, когда через них проходит переменный ток. Активное же сопротивление существует в виде детали. Посмотри на эти цилиндрики с выводами для припайки. Это – активные сопротивления. Они называются резисторами . Н. – А можно ли комбинировать различные виды сопротивлений? Л. – Конечно. Впрочем, по правде говоря, мы довольно редко имеем дело с сопротивлением только одного вида.
⇐ Предыдущая12345678910Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Индуктивное и емкостное сопротивление | Определение и формула
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
В основном, в цепях переменного тока можно найти три типа элементов. Их можно разделить на резистивные, индуктивные и емкостные. Значение сопротивления не зависит от частоты, но значение как индуктивной цепи, так и емкостной цепи зависит от частоты напряжения.
Если цепь содержит только резистивных элементов , значение тока в цепи переменного тока можно рассчитать по соотношению
\[I=\frac{V}{R}\]
где R — сопротивление (Ом). В чисто резистивной цепи ток совпадает по фазе с приложенным напряжением.
Рисунок 1: Векторная диаграмма для чисто резистивной цепи
Если цепь содержит только индуктивных элементов , значение тока можно определить по соотношению Л}\]
Где
В — вольт (переменный ток)
ω = 2πf (рад/с)
L — индуктивность (Гн)
В чисто индуктивной цепи ток отстает от приложенного напряжения на 90° в В –Векторная диаграмма.
Рис. 2: Векторная диаграмма чисто индуктивной цепи
Если в цепи всего емкостных элементов , значение тока можно определить по соотношению Где C – емкость (Ф). На векторной диаграмме V – I для чисто емкостной цепи ток опережает приложенное напряжение на 90°.
На векторной диаграмме V – I для чисто емкостной цепи ток опережает приложенное напряжение на 90°.
Рис. 3: Векторная диаграмма для чисто емкостной цепи
Вышеупомянутые отношения напряжения и тока интересны и ценны. Будет обнаружено, что при вычислении напряжений и токов, состоящих из смеси этих элементов, понятие импеданса будет иметь очень практическое применение.
Сопротивление переменному току представляет собой комплексное (не скалярное) отношение вольт к амперу в цепи переменного тока. Импеданс представляет собой способность цепи переменного тока сопротивляться протеканию тока. Импеданс также является отношением двух векторов, но это не вектор. Это комплексное число, которое соединяет один вектор с другим вектором. Импеданс, выраженный буквой «Z», может быть выражен математически как
\[\underline{Z}=\frac{\underline{V}}{\underline{I}}\]
ПРИМЕЧАНИЕ : Подчеркнутая переменная, как «$\underline{Z}$ » обозначает, что переменная является векторной величиной, а не скалярной величиной. Однако практика подчеркивания переменных для обозначения векторной величины строго не соблюдается. В большинстве случаев подразумевается, что указанная переменная является векторной величиной и не обязательно подчеркнута.
Однако практика подчеркивания переменных для обозначения векторной величины строго не соблюдается. В большинстве случаев подразумевается, что указанная переменная является векторной величиной и не обязательно подчеркнута.
В основном подчеркивание служит напоминанием о том, что переменная является векторной величиной. Переменная, обозначенная как абсолютное значение, как |Z|, специально указывает, что переменная является скалярной величиной, и ее не следует путать с векторной величиной. 9{1}/{}_{j\omega C}\]
Формула индуктивного реактивного сопротивленияПредположим, что синусоидальный ток течет в чистой индуктивности, как показано на следующем рисунке, то есть
$i= {{I}_{m}}\sin \left( wt \right)$
Поскольку синусоида тока постоянно меняется, катушка создает противоЭДС, определяемую выражением
${{V}_{ L}}=L\frac{di}{dt}$
Напряжение на дросселе пропорционально наклону синусоиды тока и, следовательно, является косинусоидальной волной, как показано на рис.
Таким образом, в чисто индуктивной цепи ток отстает от напряжения на фазовый угол 90°. Подставляя теперь уравнение для тока в уравнение для напряжения на дросселе, находим, что
\[{{V}_{L}}=L\frac{di}{dt}=L\frac{d\left( {{ I}_{m}}sinwt \right)}{dt}={{I}_{m}}wL\cos \left( wt \right)\]
Величина I m ωL максимальное значение напряжения на катушке индуктивности (это происходит при t=0)
\[\begin{matrix} {{V}_{m}}={{\operatorname{I}}_{m}}\omega L & {} & \left( 1 \right) \\\end{matrix}\]
Величина ωL называется индуктивным сопротивлением и является мерой сопротивления переменному току. Индуктивное сопротивление измеряется в Омах. Символ X L используется для обозначения индуктивного реактивного сопротивления.
${{X}_{L}}=wL=2\pi fL$
Поскольку максимальные значения уравнения (1) связаны с эффективными значениями, мы можем написать
${{V}_{ L}}={{I}_{L}}{{X}_{L}}$
Чистая индуктивность не может рассеивать мощность. Скорее, индуктивность хранит и высвобождает энергию в виде магнитного поля. Индуктивная реактивная мощность равна произведению В 9{2}{{X}_{L}}$
Скорее, индуктивность хранит и высвобождает энергию в виде магнитного поля. Индуктивная реактивная мощность равна произведению В 9{2}{{X}_{L}}$
Напряжение на катушке индуктивности 1 Гн составляет e=10sin200t. каково выражение мгновенного тока?
Решение
${{X}_{L}}=\omega L=200*1=200~\Omega $
${{I}_{m}}=\frac{{{V }_{m}}}{{{X}_{L}}}=\frac{10}{200}=0,05~A$
В индуктивности I отстает от e на 90 градусов, поэтому мы можем написать выражение для мгновенного тока как:
$i={{I}_{m}}\sin \left( wt-{{9\circ }} \right)$
- Вы также можете прочитать: Индуктивное реактивное сопротивление в деталях
Рассмотрим чистый конденсатор, подключенный к синусоидальному переменному напряжению, как показано на следующем рисунке.
Напряжение на конденсаторе равно
$v={{V}_{m}}\sin \left( wt \right)$
В то время как мгновенный ток, протекающий через конденсатор, равен
\[i= C\frac{dV}{dt}\]
Это выражение показывает, что ток пропорционален наклону кривой напряжения.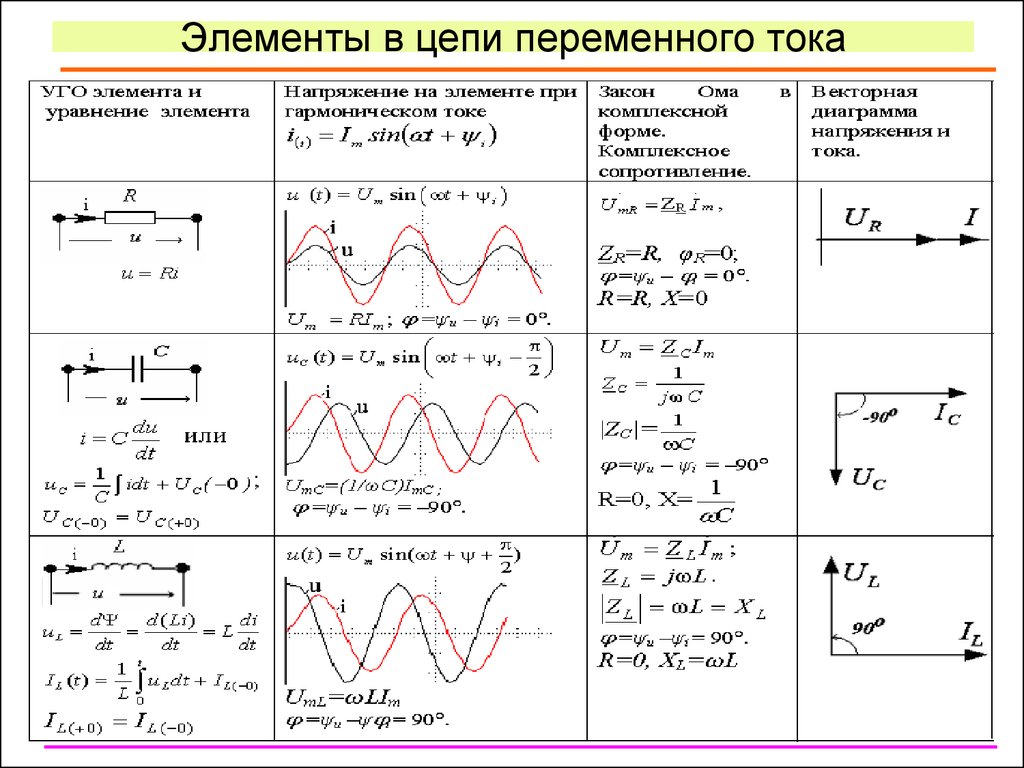 В этом случае ток пропорционален наклону синусоиды. На самом деле наклон синусоиды представляет собой косинусоидальную волну, как показано на рис. Следовательно, в чисто емкостной цепи ток опережает напряжение на угол 90°.
В этом случае ток пропорционален наклону синусоиды. На самом деле наклон синусоиды представляет собой косинусоидальную волну, как показано на рис. Следовательно, в чисто емкостной цепи ток опережает напряжение на угол 90°.
Теперь подставим синусоидальное выражение для напряжения в уравнение тока. Получаем
\[i=C\frac{d\left( {{V}_{m}}\sin \left( wt \right) \right)}{dt}=wC{{V}_{m }}\cos \left( wt \right)\]
$i=wC{{V}_{m}}\cos \left( wt \right)~~~~~\text{ }\cdots \text { }~~\left( 2 \right)$
Из уравнения (2) находим максимальный ток равным;
\[\begin{matrix} {{\operatorname{I}}_{m}}=\omega C{{V}_{m}} & {} & at\text{ }t=0 \\\ end{matrix}\]
Или
\[\frac{{{V}_{m}}}{{{I}_{m}}}=\frac{1}{wC}\]
Величина 1/ωC равна называется емкостным реактивным сопротивлением, измеряется в омах и обозначается Xc.
\[{{X}_{C}}=\frac{1}{wC}=\frac{1}{2\pi fC}\]
Помня, что эффективные значения связаны с максимальными значениями соотношением такое же соотношение, поэтому мы можем написать
${{V}_{C}}={{I}_{C}}{{X}_{C}}$
Чистая емкость не может рассеивать мощность.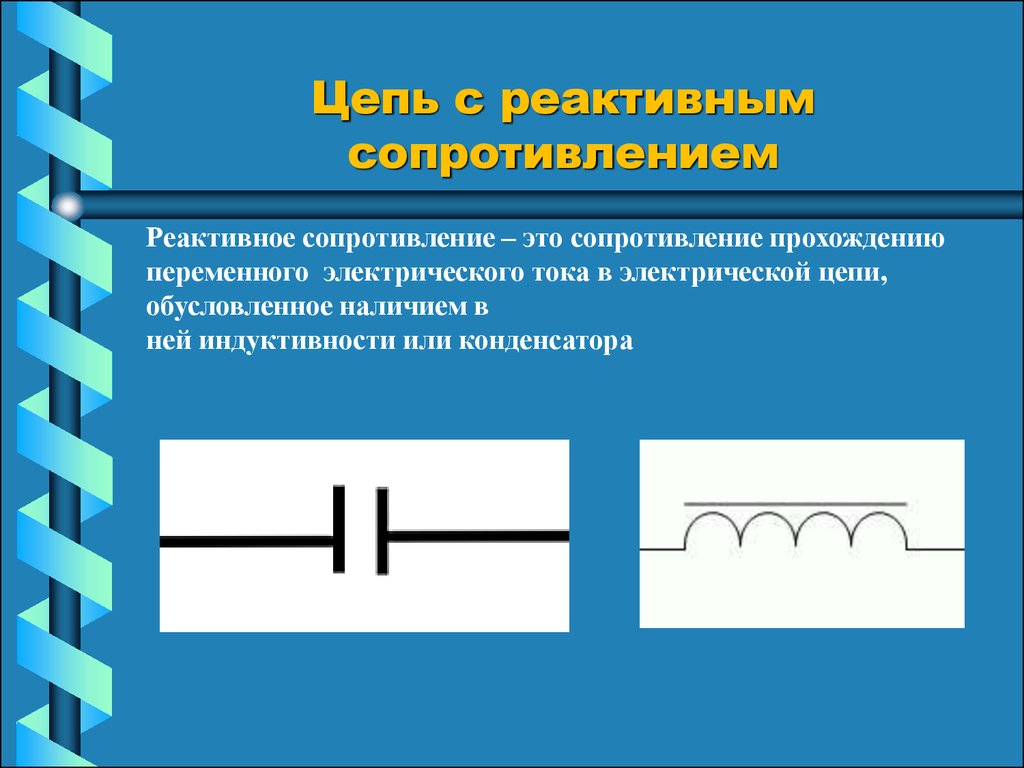 Скорее, емкость хранит или высвобождает энергию в виде электрического поля. Емкостная реактивная мощность равна произведению V 9{-6}}}=79,5~\Omega \]
Скорее, емкость хранит или высвобождает энергию в виде электрического поля. Емкостная реактивная мощность равна произведению V 9{-6}}}=79,5~\Omega \]
${{I}_{C}}=\frac{{{V}_{C}}}{{{X}_{C}}} =\frac{10}{79,5}=0,126~A$
(b):
${{Q}_{C}}={{V}_{C}}{{I}_{C} }=10*0,126=1,26~vars$
Суммарное сопротивление и реактивность
На практике большинство цепей содержат смесь резистивных компонентов наряду с реактивными компонентами, которые могут быть индуктивными или емкостными. Для анализа этих типов цепей использование импеданса оказывается особенно полезным инструментом. Как указывалось ранее, импеданс цепи, независимо от природы компонентов, может быть описан соотношением
\[Z=\frac{V}{I}\]
Рис. 8: Диаграмма импеданса
отношение, изображенное на рис. 8 , где в прямоугольной форме
\[Z=R+jX\]
R — резистивная составляющая импеданса (Ом)
X — реактивная составляющая импеданса (Ом)
- Вы также можете прочитать: Подробно о емкостном реактивном сопротивлении
Вы нашли apk для Android? Вы можете найти новые бесплатные игры и приложения для Android.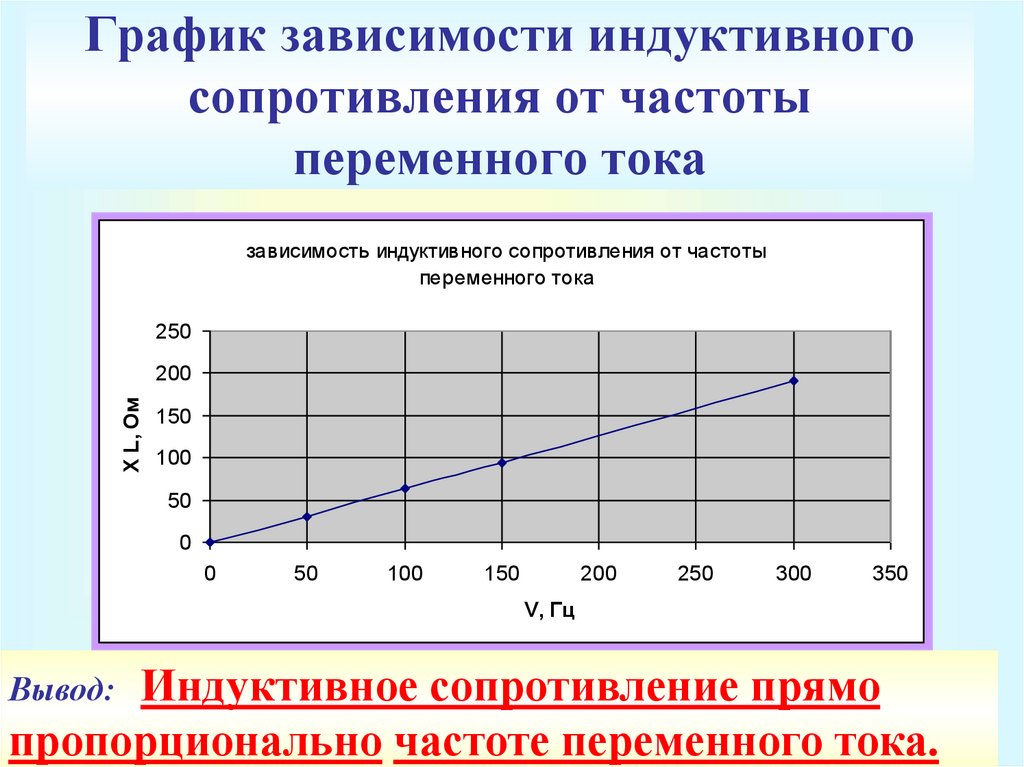
Индуктивное и емкостное реактивное сопротивление
[smartslider3 slider=»2″]
Введение
Емкостное реактивное сопротивление определяется как реактивное сопротивление, создаваемое емкостными компонентами (конденсаторами). Это может быть выражено как. Емкостное реактивное сопротивление представляет собой сопротивление напряжения на емкостном устройстве, которое используется для временного накопления электрической энергии в виде электрического поля. Емкостное сопротивление вызывает противофазу тока и напряжения.
Ток опережает напряжение в емкостной цепи. Напряжение управляется током в идеальной емкостной цепи. Из-за емкостного реактивного сопротивления коэффициент мощности системы или цепи улучшается.
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебные материалы
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
В чем разница между реакцией и сопротивлением?
1. Реактивное сопротивление — это составляющая импеданса, тогда как сопротивление — это постоянная составляющая сопротивления.
Реактивное сопротивление — это составляющая импеданса, тогда как сопротивление — это постоянная составляющая сопротивления.
2. Значение реактивного сопротивления всегда является комплексным числом, но сопротивление всегда должно быть действительным числом.
3. Сопротивление в полностью индуктивной или емкостной цепи равно нулю, а реактивное сопротивление в полностью резистивной цепи равно нулю.
4. Из-за реактивного сопротивления будут изменяться амплитуда и фаза тока. Ток и напряжение всегда будут в фазе из-за сопротивления.
5. На значение реактивного сопротивления влияет частота питания, но на значение сопротивления частота питания не влияет.
6. Индуктивное сопротивление для источника постоянного тока должно быть равно 0, а емкостное сопротивление должно быть неограниченным. Сопротивление для питания постоянным током останется прежним.
7. Реакции обозначаются буквами и. Термин «сопротивление» используется для описания способности человека сопротивляться чему-либо
8. Из-за аспекта реактивного сопротивления коэффициент мощности в реактивном сопротивлении либо опережает, либо отстает. Когда реактивное сопротивление равно нулю, мощность в сопротивлении равна единице.
Из-за аспекта реактивного сопротивления коэффициент мощности в реактивном сопротивлении либо опережает, либо отстает. Когда реактивное сопротивление равно нулю, мощность в сопротивлении равна единице.
Электрическое реактивное сопротивление
Определяется как поток в электрической цепи, который течет в направлении, противоположном течению тока. Чем меньше ток для этого подаваемого напряжения, тем сильнее реактивное сопротивление. В магнитных и электрических полях реактивное сопротивление ведет себя по-разному. В магнитном поле реактивное сопротивление противостоит изменениям тока, а в электрическом поле сопротивляется изменениям напряжения.
Индуктивное реактивное сопротивление Обозначается символом XL и образуется при наличии индуктивного элемента, такого как индуктор. Индуктивный элемент может использоваться для хранения электрической энергии в виде магнитного поля, что является одним из его применений. Направление тока, создаваемого индуктивным сопротивлением, явно противоположно направлению основного тока в соответствии с законом Ленца. Это может привести к задержке мощности между кривыми напряжения и тока.
Это может привести к задержке мощности между кривыми напряжения и тока.
Обозначаемое символом XC, оно образуется при наличии емкостного элемента, такого как конденсаторы. В отличие от индуктивного элемента, емкостной элемент способствует накоплению электрической энергии в виде электрического поля. Противоположность напряжения на конденсаторах вызывает емкостное реактивное сопротивление. В результате этого также возникает отставание между током и напряжением. В индуктивной цепи оптимальное отставание составляет 90 градусов, а в емкостной цепи идеальное опережение напряжения по току равно 90 градусов.
Читайте также: HC Verma Solutions Class 11 Chapter 5 Закон движения Ньютона
Часто задаваемые вопросыЧто такое электрическое реактивное сопротивление и что оно означает?
Из-за своей индуктивности и емкости электрическое реактивное сопротивление описывается как поток в элементе цепи, который течет в направлении, противоположном току. При том же приложенном напряжении, если реактивное сопротивление выше, ток будет ниже. Хотя реактивное сопротивление очень похоже на электрическое сопротивление, оно различается в нескольких областях. При прохождении переменного тока через электрическую цепь или элемент изменяются как фаза, так и амплитуда тока. Кроме того, энергия запасается в элементе, содержащем реактивное сопротивление.
При том же приложенном напряжении, если реактивное сопротивление выше, ток будет ниже. Хотя реактивное сопротивление очень похоже на электрическое сопротивление, оно различается в нескольких областях. При прохождении переменного тока через электрическую цепь или элемент изменяются как фаза, так и амплитуда тока. Кроме того, энергия запасается в элементе, содержащем реактивное сопротивление.
У индуктивного и емкостного реактивного сопротивления разные формулы?
Это последствие известно как РЕАКТИВНОСТЬ, обозначается буквой X и формулируется как X = XL XC или X = XC X L. В цепи с последовательным индуктивным сопротивлением 50 Ом и емкостным сопротивлением 25 Ом полное реактивное сопротивление , или X, 50 Ом, 25 Ом или 25 Ом, индуктивное сопротивление.
Сопутствующий контент
| Программа JEE Main 2024 |
| Лучшие книги для JEE Main 2024 |
| JEE Advanced 2024: Дата экзамена, Syllabus, Критерии приемлемости |
| JEE Main 2024: Date Date, Syllabus, критерия для значения |
| JEE 2024: Syrighabure |
| JEE 2024: Syrigle Datilliabus |


 Стандартная частота для
промышленного переменного тока принята равной 50 Гц. То есть за 1 секунду
направление тока в розетке меняется 50 раз.
Стандартная частота для
промышленного переменного тока принята равной 50 Гц. То есть за 1 секунду
направление тока в розетке меняется 50 раз.

 Получим:
Получим: Кроме того, номинальные
значения напряжений и токов бытовых приборов также указываются как
действующие значения. Так стандартное напряжение в цепи −
Кроме того, номинальные
значения напряжений и токов бытовых приборов также указываются как
действующие значения. Так стандартное напряжение в цепи − 


 ..
.. – Электрики даже говорят, что переменный ток проходит через конденсатор. Это вовсе не значит, что электроны проходят через диэлектрик (мембрану, см. рис. 12). Наличие конденсатора лишь не препятствует движению взад и вперед электронов, т.е. прохождению переменного тока в цепи.
– Электрики даже говорят, что переменный ток проходит через конденсатор. Это вовсе не значит, что электроны проходят через диэлектрик (мембрану, см. рис. 12). Наличие конденсатора лишь не препятствует движению взад и вперед электронов, т.е. прохождению переменного тока в цепи.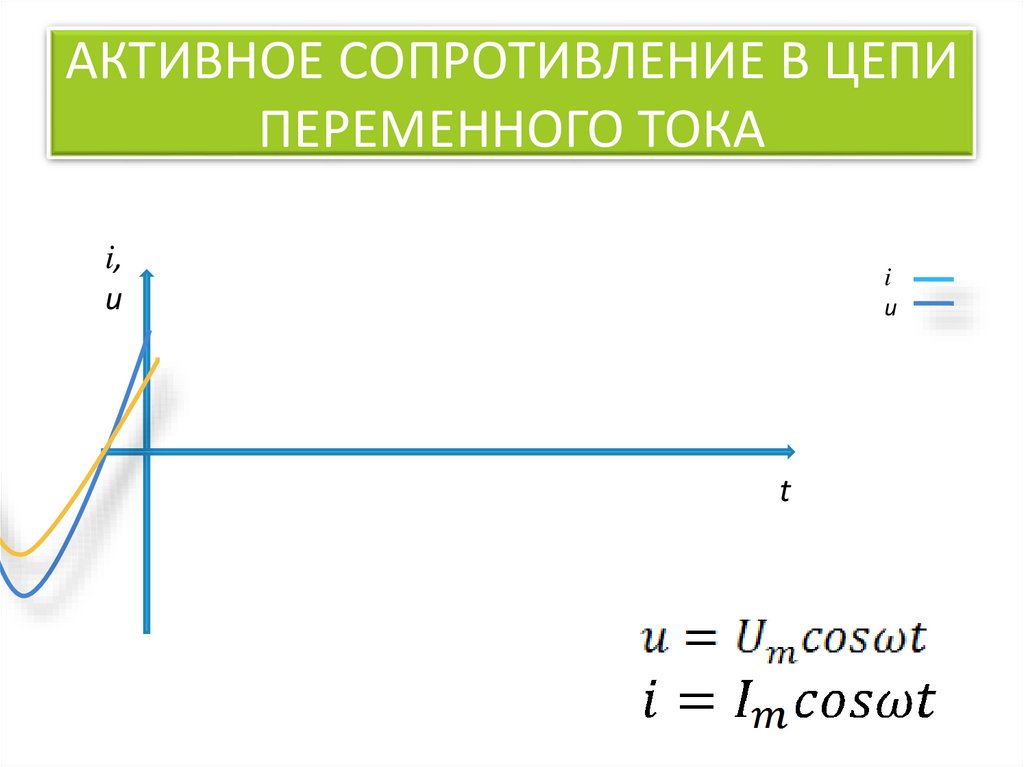
 Чтобы лучше понять их свойства, позволь привести тебе маленькую табличку.
Чтобы лучше понять их свойства, позволь привести тебе маленькую табличку. Так, например, катушка, кроме индуктивного, обладает также некоторым активным сопротивлением, которое зависит от длины, диаметра и материала проволоки. Катушка имеет также «распределенную емкость», образующуюся между соседними витками, которые как бы образуют пластины конденсатора.
Так, например, катушка, кроме индуктивного, обладает также некоторым активным сопротивлением, которое зависит от длины, диаметра и материала проволоки. Катушка имеет также «распределенную емкость», образующуюся между соседними витками, которые как бы образуют пластины конденсатора.