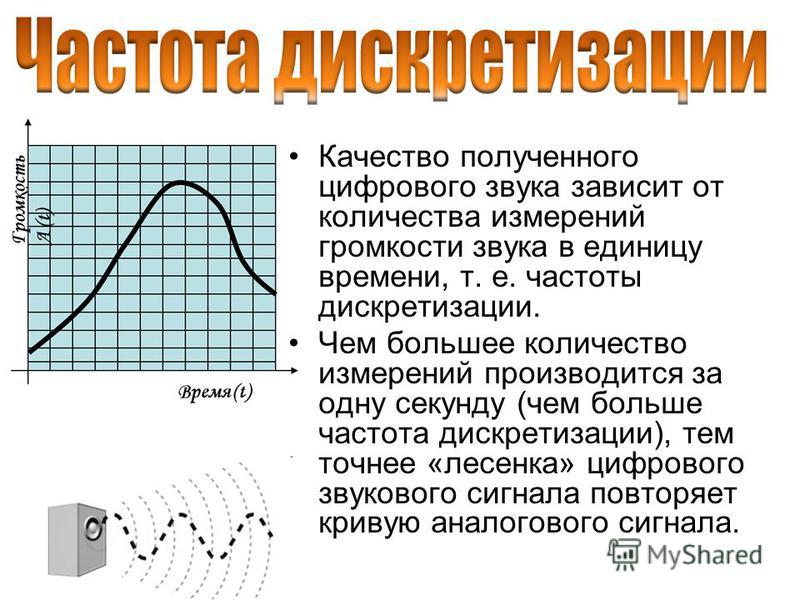
Выбор частоты дискретизации для анализа сигналов последовательных шин

Выбор частоты дискретизации для анализа сигналов последовательных шин

Осциллографы компании Teledyne LeCroy имеют уникальный тип программных опций — TDME, которые объединяют измерения, синхронизацию, декодирование, графический анализ и построения глазковых диаграмм для более чем 20 стандартов последовательных шин, и этот список постоянно пополняется. В данной статье будут рассмотрены практические советы по успешному использованию программной опции TDME и продемонстрированы некоторые примеры применения возможностей TDME для решения реальных проблем.

Учитывая широкий спектр поддерживаемых протоколов, пользователю будет полезно знать, как выбрать оптимальную частоту дискретизации осциллографа для данного конкретного стандарта при получении сигналов последовательных данных. Оптимальное значение частоты дискретизации определяется тремя основными факторами:

1. Ширина полосы сигнала, оцифровываемого аналого-цифровым преобразователем (АЦП) осциллографа.
2. Желаемое время захвата.
3. Дальнейшие действия с захваченным сигналом.

Обычно третий пункт не затрагивается при обсуждении частоты дискретизации, но на самом деле он может быть важным фактором при выборе оптимального значения частоты дискретизации.

Ширина полосы сигнала определяет наивысшую частоту, которая должна быть оцифрована АЦП. Критерии Найквиста требуют, чтобы частота дискретизации была, как минимум, вдвое больше максимального значения частоты сигнала. Полоса пропускания цифрового сигнала, например, при анализе последовательных данных, может быть оценена, исходя из знания времени нарастания фронта сигнала с помощью уравнения:

BW = k

/Trise, где

• Ширина полосы (BW) в герцах — это отношение коэффициента k к времени нарастания сигнала (Trise) в секундах.
• Значение коэффициента k зависит от полосы пропускания осциллографа. Для осциллографа с полосой пропускания 1 ГГц, k = 0,35. Для осциллографов с полосой пропускания свыше 1 ГГц, k = 0,45.

Например, рассмотрим сигнал CAN, работающий со скоростью 125 кб/с (килобит в секунду) со временем нарастания приблизительно 21 нс. Согласно приведенной выше формуле, полоса пропускания осциллографа, для обработки данного сигнала, должна быть не менее 16,7 МГц. Частота Найквиста — 33,4 МГц. Это минимальная частота дискретизации, необходимая для оцифровки сигнала с полосой пропускания 16,7 МГц. Для обеспечения наиболее точных и достоверных измерений на физическом уровне, рекомендуется увеличить частоту дискретизации осциллографа три или четыре раза по сравнению с частотой Найквиста.

Однако декодирование шины не требует такой высокой частоты дискретизации, как выполнение точных измерений на физическом уровне. Фактически, для более низкоскоростных протоколов частота дискретизации может быть уменьшена до четырех точек дискретизации на бит, при этом будет сохраняться возможность точного декодирования содержимого пакетных данных.

Если все, что вам нужно сделать, это выполнить базовые измерения синхронизации пакетов, проверить правильность переходов, найти ошибки протокола или другие задачи, которые могут быть выполнены путем визуальной оценки трафика шины, вы можете выиграть драгоценное время сбора данных, значительно снизив частоту дискретизации.

На рисунке 1 показан сигнал, захваченный по шине CAN с тактовой частотой 125 кб/с, частота дискретизации осциллографа превышает тактовую частоту сигнала в четыре раза и составляет 500 квыб/с. Увеличенное изображение в середине рисунка ясно показывает четыре точки выборки в каждый тактовый период. Данное значение частоты дискретизации достаточно для декодирования данных, характеристики логических уровней и предварительной визуальной оценке передачи данных.

Рис. 1. Сигнал, захваченный по шине CAN. Корректное выполнение декодирования сигнала и увеличенная длительность сбора данных при частота дискретизации всего четыре точки выборки на тактовый период.

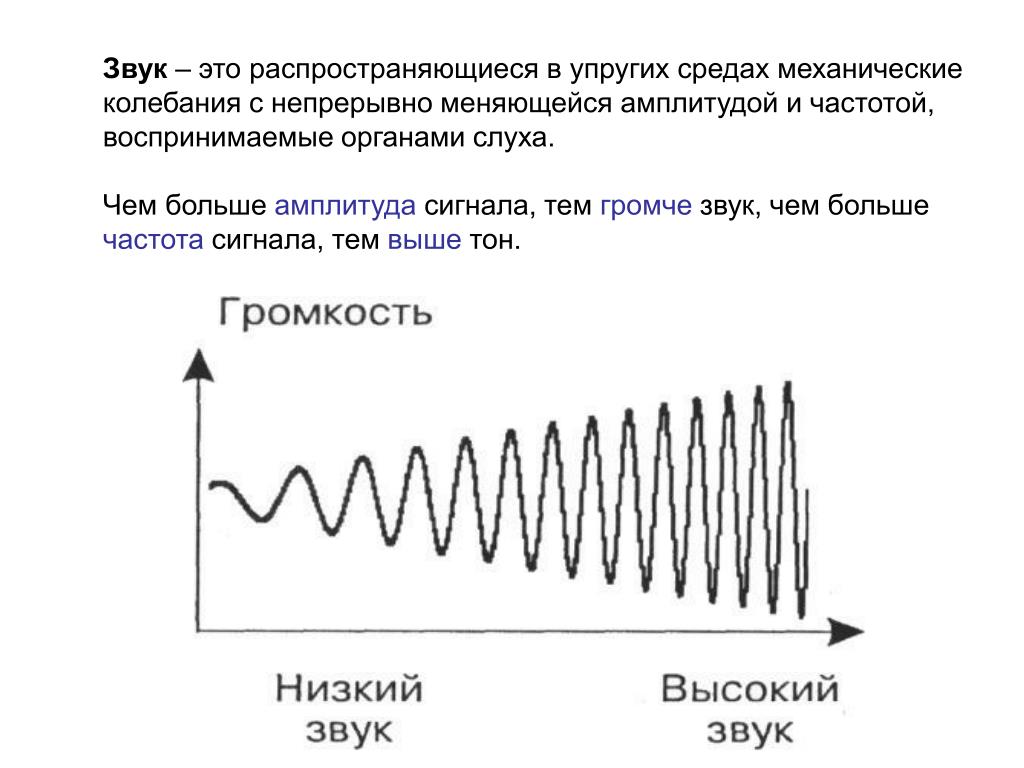
Следующий важный элемент при анализе последовательных данных, это длительность захвата. Длительность зависит от объема памяти осциллографа и выражается следующим уравнением:

T = M/SR, где

• T — продолжительность сбора данных в секундах,
• M — длина памяти осциллографа (выборки)
• SR — частота дискретизации в выборках в секунду (выб/с).

Более длительное время сбора данных может потребоваться для оценки таких характеристик, как уровень загрузки канала шины, процент времени, в течение которого шина активна. В осциллографе, с объемом памяти 250 Мвыб при частоте дискретизации 500 квыб/с, продолжительность сбора данных, согласно приведенной выше формуле, составит 500 секунд или 8,3 минуты. На рисунке 2 показано получение 190 552 пакетов сообщений по CAN шине при данной частоте дискретизации. Это весьма большой объём информации.

Рис. 2. Захват 190 552 пакетов сообщений по шине CAN. Сигнал CAN с тактовой частотой 125 кбит/с, захваченный осциллографом со скоростью выборки 500 квыб/с при длине памяти 250 Мвыб, длительность захвата 500 секунд, 190 552 пакетов сообщений

С другой стороны, более высокая частота дискретизации обеспечивает более точные измерения сигнала на физическом уровне. Если пользователю необходимо измерить электрические характеристики сигнала, то необходимо выполнить сбор данных с максимальной частотой дискретизации, достаточной для длительного захвата, достаточного для достоверных измерений. Стоить помнить, что большинство автоматических измерений в осциллографе выполняется только в видимом окне сбора данных, поэтому необходимо убедится, что на экране прибора отображена вся необходимая для анализа информация.

Как показано на рисунке 3, при соотношении частоты дискретизации к тактовой частоте как 800 к 1 погрешность при измерении времени нарастания может достигать 5% от реального значения.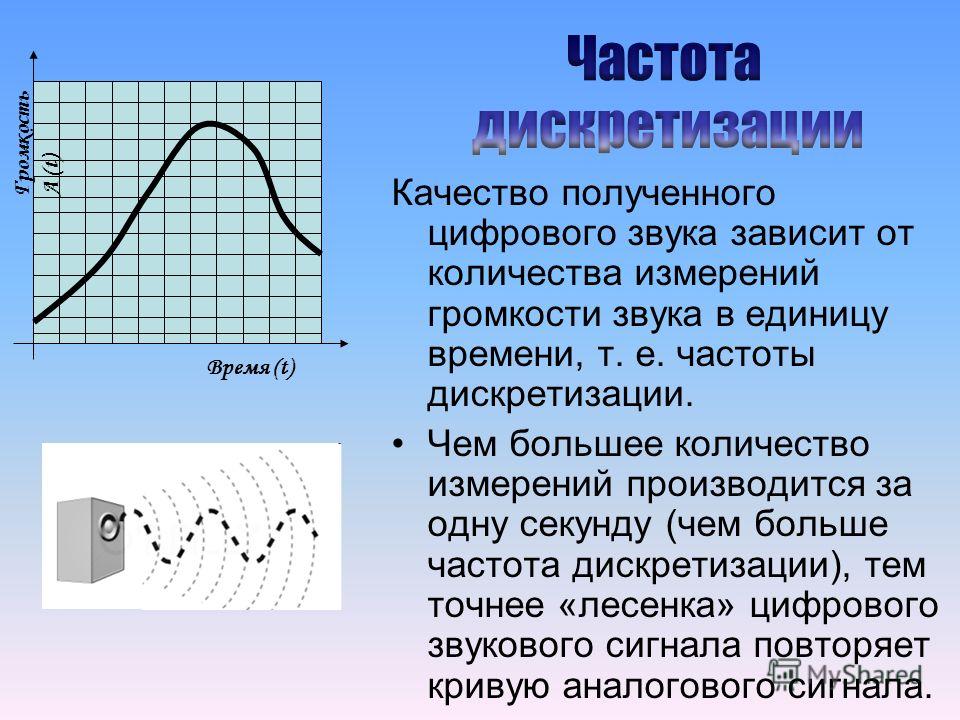 Ниже этой частоты края дискретизируются недостаточно для правильного измерения.

Частота дискретизации 10 ГВыб/с
Дискретизация/Тактовая частота = 80000:1
Измеренное время нарастания = 21,19 нс Частота дискретизации 1 ГВыб/с
Дискретизация/Тактовая частота = 8000:1
Измеренное время нарастания = 21,12 нс Частота дискретизации 100 МВыб/с
Дискретизация/Тактовая частота = 800:1
Измеренное время нарастания = 22,32 нс
Погрешность измерения 5% Частота дискретизации 10 МВыб/с
Дискретизация/Тактовая частота = 80:1
Измеренное время нарастания Погрешность измерения 277% Рис. 3. Влияние частоты дискретизации на измерение времени нарастания сигнала, сигнал CAN с тактовой частотой 125 кбит/с.

В заключении необходимо обобщить основные правила для выбора оптимального значения частоты дискретизации (SR) осциллографа для конкретной задачи при анализе сигналов последовательных шин.

• Декодирование: SR как минимум в четыре раза превышает тактовую частоту сигнала.
• Глазковые диаграммы: SR как минимум в 100 раз превышает тактовую частоту сигнала.
• Измерения сигнала на физическом уровне: SR как минимум в 1000 раз превышает тактовую частоту сигнала.

Автор:  Teledyne LeCroy

Дата публикации:  01.03.2021

У нас представлены товары лучших производителей

ПРИСТ предлагает оптимальные решения измерительных задач.

У нас вы можете купить осциллограф, источник питания, генератор сигналов, анализатор спектра, калибратор, мультиметр, токовые клещи, поверить средства измерения или откалибровать их. Также мы поставляем паяльно-ремонтное оборудование, антистатический инструмент, промышленную мебель. Мы имеем прямые контракты с крупнейшими мировыми производителями измерительного оборудования, благодаря этому можем подобрать то оборудование, которое решит Ваши задачи. Имея большой опыт, мы можем рекомендовать продукцию следующих торговых марок:

АКИП™ (Россия)

В каталоге: 2021

APPA Technology Corporation (Тайвань)

В каталоге: 170

Good Will Instrument Co., Ltd. (Тайвань)

В каталоге: 574

От чего зависит скорость передачи данных в радиоканале

• Главная
• Статьи
• Руководства: нюансы оборудования и технологий
• От чего зависит скорость передачи данных в радиоканале

Версия для печати« к списку статей

Дата: 07.07.2015

Скорость передачи (пользовательских) данных в радиоканале Wi-Fi (и схожих/соседних типах связи) зависит от многих факторов, таких как:

• Используемая ширина канала (Channel Width)
• Используемое число потоков технологии MIMO
• (иногда) Используемая длина защитного интервала (GI) — short/long
• Модуляция (Modulation) (и схема кодирования (MCS)), которой удалось достичь. В свою очередь, для получения высокой модуляции требуются следующие факторы:
  
  • достаточное отношение сигнал/шум (CINR, SINR) и связанный с ним коэффициент ошибок (BER) — https://ru.wikipedia.org/wiki/CINR, http://student.telum.ru/images/2/28/Network_modeling_lecture_03.pdf, https://en.wikipedia.org/wiki/Bit_error_rate 
    • уровень сигнала помех в эфире на частоте радиоканала и соседних частотах (точный диапазон зависит от используемой ширины канала и качественных показателей радиомодуля радиоустройства в задаче фильтрации помех [пример — Ubiquiti airPrism, см. статью Сравнение устройств линейки Rocket ac]). Причиной наличия помех может быть излучение других радиоустройств и излучение исходного источника, отражённое от препятствий. Для минимизации отражений требуется отсутствие препятствий в зоне Френеля (подробнее см. в Калькуляторе радиуса зоны Френеля)
    • программные (протокол) и, в основном, аппаратные (реализация протокола на конкретном радиомодуле и прошивке) параметры зависимости модуляции от отношения сигнал/шум (см. описания радиочасти устройств и результаты тестирования проприетарных протоколов)
  • достаточный уровень принимаемого сигнала (достаточность характеризуется аппаратными параметрами радиомодуля, которые выражаются в зависимости модуляции от чувствительности приёмника), на который влияют:
    • выходная мощность радиомодуля «передающего» устройства
    • усиление антенн «передающего» устройства и «принимающего» устройства
    • чувствительность радиомодуля «принимающего» устройства
    • потери в кабельных сборках (соединение приёмопередающего устройства с антенной) на обоих радиоустройствах
    • затухание сигнала в свободном пространстве (см. Калькулятор запаса энергетики радиоканала)
    • гашение излучения помехами от других устройств, помехами из-за отражённого сигнала исходного источника, препятствиями.
  • возможности радиоустройства (максимальная поддерживаемая модуляция)
• (обычно прямо не упоминается) Скорость кода (Coding rate, Code rate) https://en.wikipedia.org/wiki/Code_rate
• производительность радиоустройства в вопросе обработки передаваемых данных
  
  • «КПД» протокола передачи данных (IEEE 802.11a/b/g/n/ac и проприетарные (airMAX, NV2, iPoll и др.)), т.е. соотношение пользовательских данных («actual») и суммарных передаваемых данных («over the air») (которые дополнительно включают в себя служебные данные). Например, в устройствах, передающих данные непосредственно по протоколам IEEE 802.11a/b/g/n/ac, «КПД» обычно составляет от 40 до 70%, а в airFiber (AF-24) — выше — если использовать за «over the air» значение Capacity (в веб-интерфейсе устройства), то 100% (т.к. все «накладные расходы» уже учтены в этом значении, которое динамически пересчитывается — подробнее см.  сообщение производителя в официальном сообществе).
  • производительность процессора устройства (пакетов в секунду — PPS) (зависит от частоты процессора и особенностей архитектуры). Зачастую производительность при обработке UDP пакетов выше, чем при TCP.
  • аппаратное ускорение установленного шифрования (например, зачастую шифрование WPA2-AES аппаратно ускорено и отнимает меньше ресурсов процессора)

Для качественной работы радиоканала необходимо получать одинаковый уровень сигнала на обоих сторонах радиоканала и по всем поляризациям.

Также при планировании радиоканала стоит учитывать, что в большинстве радиоустройств при высоких скоростях передачи данных повышается и задержка (Latency), что может накладывать отпечаток на максимальную «доступную» скорость передачи данных для конкретной задачи.

Алексей Заворыкин

Вперед
Сравнение устройств линейки Rocket ac / 2016 г.

Все статьи про Ubiquiti

Зависит ли скорость нарастания от частоты входного сигнала?

спросил 7 лет, 4 месяца назад

Изменено 7 лет, 4 месяца назад

Просмотрено 4к раз

\$\начало группы\$

Я только начинаю изучать аналоговый интегральный дизайн.

Допустим, я разработал двухкаскадный операционный усилитель с компенсацией. Скорость нарастания будет равна:

$$\text{SR} = I_{\text{sat}}/C$$

Чтобы синусоидальный сигнал не подвергался ограничению скорости нарастания, скорость нарастания должна быть

$$\text{SR } \geq 2\pi \times f \times V_m$$

1. Не означает ли это, что на разных частотах сигнала скорость нарастания разная?

2. Почему большие сигналы ограничивают полосу пропускания операционных усилителей? Если амплитуда сигнала высока, скорость нарастания также больше. Я прав?

Я также хотел бы знать, почему скорость нарастания называется большой пропускной способностью сигнала.

• скорость нарастания

\$\конечная группа\$

\$\начало группы\$

В операционном усилителе скорость нарастания определяется как скорость изменения выходного напряжения при ступенчатом изменении на входе по времени.

Если вы примените шаг на входе, вы получите линейное изменение на выходе, и выходное напряжение будет изменяться с максимально возможной скоростью для данного конкретного операционного усилителя. Таким образом, скорость нарастания представляет собой максимальный наклон кривой V/T, которую вы можете получить на выходе.

Если вы усиливаете синусоиду, максимальный наклон, с которым вы сталкиваетесь, приходится на пересечение нуля, а его значение равно

$$\text2\pi \times f \times V_m$$

Вы не можете получить синусоиду на выходе если этот наклон больше, чем скорость нарастания операционного усилителя.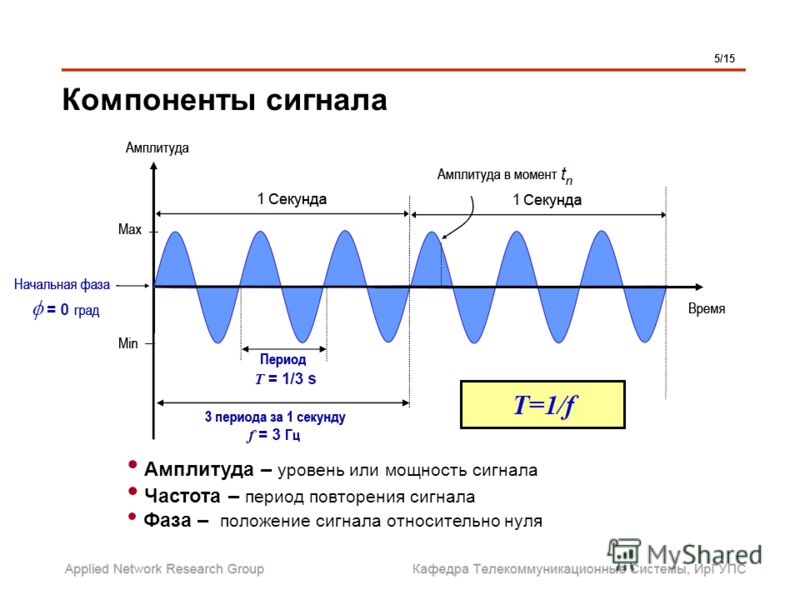

Скорость нарастания является характеристикой не сигнала, а усилителя.

Поскольку наклон синусоиды зависит от частоты И амплитуды, собственная скорость влияет на большие сигналы больше, чем на слабые.

Меньшие сигналы больше подвержены влиянию произведения усиления на полосу пропускания.

\$\конечная группа\$

\$\начало группы\$

Фактическая скорость нарастания на выходе усилителя действительно зависит от входа, при условии, что она не находится в пределе скорости нарастания .

Чем больше сигнал на выходе (и, следовательно, на входе), тем больше требуемый общий размах с точки зрения вольт/времени — вы даже ссылаетесь на него в приведенном выше уравнении.

Скорость нарастания является максимальной, выход может изменить состояние, и для сигнала, который требует скорости нарастания выше доступной, выход не может следовать, и мы теперь находимся на большой территории сигнала; поскольку это максимально быстрое изменение выходного сигнала, это максимальная доступная ширина полосы пропускания сигнала.

Этот документ от TI может быть полезен.

ХТХ

\$\конечная группа\$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Выборка сигнала, зависящего от времени

Выборка сигнала, зависящего от времени
Следующий: Заключение Вверх: номер 6 Предыдущий: Измерение частоты Проблемы, связанные с обработкой более общего сигнал, зависящий от времени, скажем, оцифрованный акустический сигнал. значительно хитрее. Основная проблема состоит в том, как сделать измерения без высокочастотного наложения, искажающего результат. Проблема в том, что если 2 n — частота дискретизации, нет возможности различить сигнал частоты n от сигнала 2n (или любого другого целого числа, кратного n) потому что в обоих случаях мы видим полный цикл в двух образцах. В 2-й случай был весь цикл между наш образцы, которые мы пропустили. Это означает, что если мы делаем выборку в 2 н, есть целый диапазон частот от n вверх, что может исказить наши измерения. Это ложное сворачивание высоких частот к более низким называется алиасингом. Можно несколько уменьшить эту проблему, если производить выборку с высокой частотой. идея в том, что это увеличит частоту, с которой алиасинг начинает происходить, и хочется надеяться, что высших частота вокруг, чтобы беспокоить нас. Проблема в том, что это может не бывает, что на более высокой частоте меньше, а то и хуже это решение использует больше ресурсов ЦП. Лучшее решение — предотвратить попадание высоких частот в ваши сэмплы в первое место. Это делается путем размещения сглаживание фильтр в аналоговой цепи перед аналого-цифровым преобразователем. Ан сглаживающий фильтр — это просто фильтр нижних частот, предназначенный для отбрасывать частоты выше n.

Фильтры сглаживания часто реализуются как простые R-C. фильтры, как на рисунке 1. Этот фильтр не так хорош, как фильтры идут, скорость затухания высоких частот довольно медленный. Доля сигнала, прошедшего через фильтр как функция частоты называется величиной ответ . Кривая отклика величины является важной мерой качества и пригодности фильтра. К сожалению, это часто используется как мера только . Есть еще одна мера, столь же важно учитывать частотно-зависимый эффект фильтр имеет по фазе сигнала. Это фазовая характеристика . Информация о фазовой характеристике наиболее полезна в двух формах: фазовая задержка и групповая задержка . Фазовая задержка — это просто размерная форма фазовой характеристики. дает количество времени задержки сигнала данной частоты по фильтру. Групповая задержка описывает что-то слегка другой. Предположим, что наш сигнал подобен FM-радиосигналу, который модулируется по частоте вокруг основной частоты. Модуляция может рассматриваться как еще один сигнал (огибающая), идущий поверх основная частота (несущая). Фазовая задержка огибающей обычно не совпадает с фазовой задержкой несущей. Групповая задержка дает время задержки огибающей. Итак, чтобы правильно судить о пригодности данного фильтра, нам действительно нужно проверить все три функции: амплитудная характеристика, фазовая задержка и групповая задержка. Как и следовало ожидать, все фильтры теряют производительность. в одной из трех функций, чтобы получить в другой. Лучшее компромисс зависит от вашего приложения.

Все эти характеристики фильтра могут быть получены из фильтров передаточная функция . Это сложная функция (т. содержит комплексные числа) и требует немного математики, чтобы уметь выводить для произвольного фильтра. я дам тебе только результаты здесь для RC-фильтра нижних частот. Если ты заинтересован узнавая больше об этом, Горовиц и Хилл содержат удобочитаемый введение в тему. RC-фильтр нижних частот имеет функция передачи,

здесь я использовал обозначение инженеров для , , а не обозначение ученых, . Термин — это частота в радианах, чтобы получить Герц разделить на . С этим уравнением мы может получить ответ величины,

фазовая характеристика,

Итак, фазовая задержка

и групповая задержка,

Имея фильтр сглаживания, нам все еще нужно решить, правильная частота дискретизации. Возможно, вы помните, что читали в другом месте о чем-нибудь называется теоремой выборки Найквиста. Эта теорема и есть то, что мы хотите, это говорит нам, что частота дискретизации должна быть как минимум в два раза больше ширины полосы сигнала во избежание псевдонимов. Обратите внимание, что я сказал пропускная способность , который представляет собой диапазон от самой низкой до самой высокой частоты (в самый простой случай, когда нет зазоров) в сигнал. Теорема Найквиста часто ошибочно цитируется как утверждение что мы должны пробовать в два раза больше самая высокая частота сигнал. Полоса пропускания и самая высокая частота не совпадают вещь, если мы не имеем дело с сигналом базовой полосы (тот, который имеет контент от нулевой частоты вплоть до самой высокой частота). Различие может быть весьма важным. Учитывать следующий реальный пример. 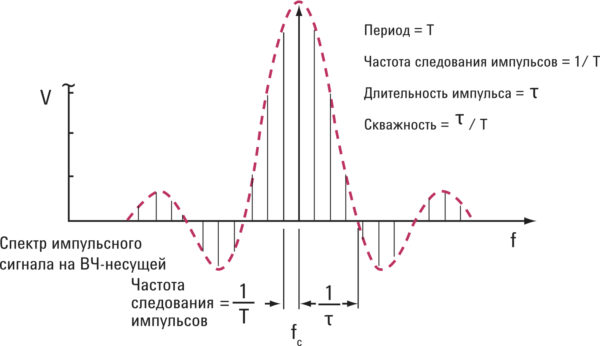В недрах РАФОС океанский дрифтер, которого я помог разработать, мы управляем поплавком прослушивание тона, издаваемого заранее установленным акустическим маяком швартовка. Эти маяки издают длинный тон, меняющийся по частоте. от 258,5 до 261,5 Гц. Полоса пропускания этого тона – это диапазон развертки, 3 Гц. Итак, теорема Найквиста утверждает, что нам нужно частота дискретизации не менее 6 Гц, вместо в два раза больше максимальная частота 261,5 Гц (523 Гц). В результате поплавок РАФОС может комфортно передискретизировать сигнал на частоте 10 Гц, используя скромный 6805 микропроцессор. Ошибочная выборка с частотой 523 Гц потребовала бы более быстрый процессор, который потребовал бы больше электроэнергии что, в свою очередь, сделало бы инструмент непрактичным устройством (дрифтер работает от батарей и имеет время миссии, измеряемое в месяцев, 48 — наш текущий рекорд).

Если мы однородно дискретизируем сигнал с нужной частотой и есть нет наложенный сигнал загрязняет наши измерения, тогда мы можем восстановить значение сигнала в любое время. Для этого нам нужно сделать свертка наших выборок с функцией sinc (это теорема о равномерной выборке),

где время, в которое мы хотим восстановить сигнал, — интервал между выборками, а — индекс выборки. (Я не буду здесь объяснять математику, стоящую за этим. может предоставить материал для нескольких будущих колонок, чтобы объяснить это. Если вы хотите исследовать это самостоятельно, книга Брейсвелла настоятельно рекомендуется). Для практического использования этого уравнения возьмем индекс по количеству выборок данных вместо бесконечности.

Форт-реализация функции sinc такова:

Кстати, если вы посмотрите подобные уравнения в литературе Я могу гарантировать, что у вас будет ужасное время примирения факторов из , 2 и -1 (это обычно известно как метание конкурс. Куда пропал?). В математической литературе эти факторы, как правило, вообще отсутствуют в уравнениях. В инженерной литературе они находятся в разных местах в разные книги. Причина в том, что такие факторы несущественны, поскольку математическая теория всего этого касается, они просто коэффициенты нормализации и размерности. В инженерии контекст, нет единого способа сделать нормализацию и размерность им просто нужно сделать самостоятельно последовательно; поэтому одна версия книги может отличаться от другой.

Теперь, когда мы вооружены теоремой о равномерной выборке, мы можем проведите небольшой эксперимент, чтобы продемонстрировать то, что я сказал о выборке сигнал с ограниченным диапазоном частот. Листинг 2, gensig.fth — программа который будет генерировать тестовый сигнал, который начинается на одной частоте и скользит к другому (чирп). Я настроил все так, чтобы смоделированные колебания сигнала от 10 Гц до 12 Гц за 4,5 секунды. Когда постоянный ВЫБОР? ЛОЖЬ, то выходной сигнал эквивалентен 128 выборкам в секунду.

Подвыборка выходных данных этой программы — это то, что мы будем использовать в качестве данных, график показан на рисунке 2. Этот сигнал имеет полосу пропускания 2 Гц, поэтому частота дискретизации Найквиста составляет 4 Гц. Мы будем передискретизировать и сэмплировать на частоте 6,4 Гц. Теперь мы не можем просто взять каждую 20-ю выборку из данных на рисунке 2. использовать в качестве наших данных измерений; такой сигнал будет содержать серьезное количество алиасинга в нем.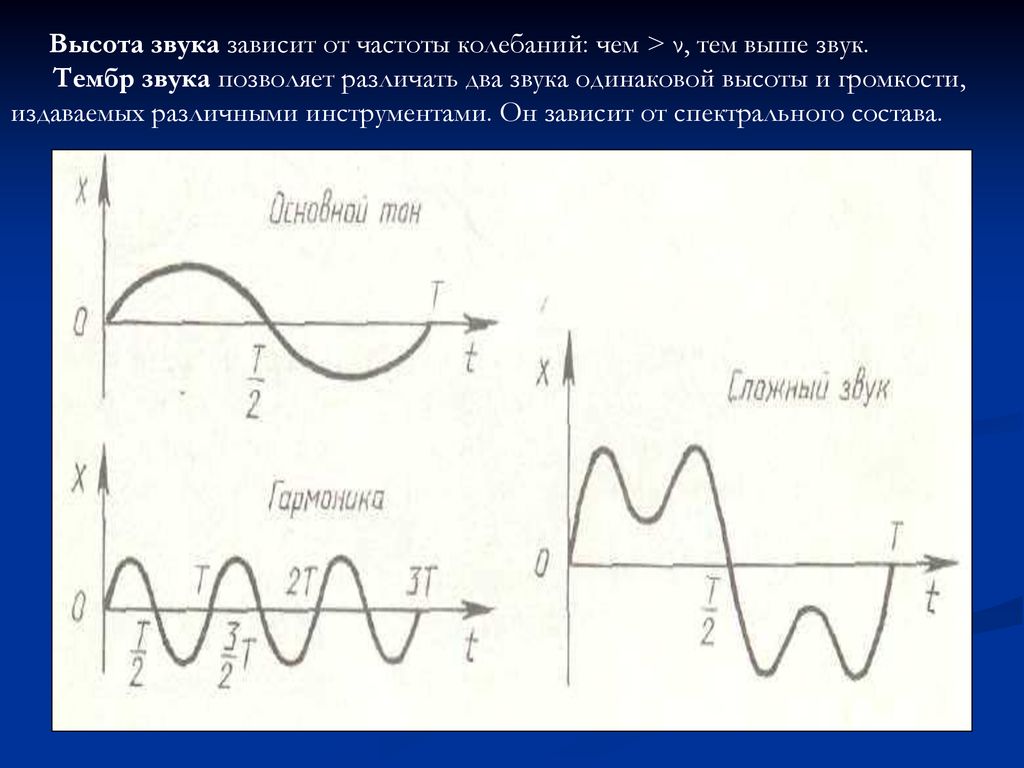 Чтобы сделать сигнал пригодным для использования, мы смешает его с сигналом 11 Гц, а затем применит фильтр нижних частот с отсечкой 5 Гц к результату.

Зачем мы это делаем ? Из элементарной тригонометрии

что означает, что если мы возьмем сигнал одной частоты, и умножаем на другой сигнал частоты , тогда получаем с одним сигналом с частотой , а другим с частотой . Итак, если наш исходный сигнал колеблется от 10 до 12 Гц, и является фиксированным сигналом на частоте 11 Гц, то мы получаем сигнал с центром на 0 Гц, а другой на 22 Гц. Тот, что на 0 Гц, тот мы хотим сохранить, другой на 22 Гц мы будем отфильтровывать. Эта техника для смещения центральной частоты сигнала является сердцем того, что известен как гетеродинный смеситель . Особый случай, когда мы сдвиг к центральной частоте нуля известен как гомодин Смеситель. После микширования и фильтрации исходного сигнала мы можем затем безопасно подвыборки его. Сглаживание Здесь используется фильтр нижних частот Баттерворта первого порядка. Есть лучшие варианты фильтра (например, фильтр Бесселя), но я использую его здесь, потому что он прост и иллюстрирует момент, к которому мы вернемся позже. Все эти операции есть в коде gensig.fth, когда постоянный ВЫБОР? установлено значение ИСТИНА.

Выход для случай выборки — это смоделированные измерения, которые мы хотим использовать теорему о равномерной выборке. Код в regen.fth (листинг 3) считывает данные и применяет к ним теорему. Сравнение вывод регена с его вводом мы видим более плавный результат как и следовало ожидать. Чтобы увидеть, что мы теоретически ожидать, вернуться и запустить gensig с SAMPLING? установлен в FALSE и минимальная и максимальная частоты установлены на -1.0 и 1,0 соответственно. Запуск gensig таким образом генерирует опорный сигнал без несущей 11 Гц.

Сравнение сигнала без несущей с восстановленным сигналом (рис.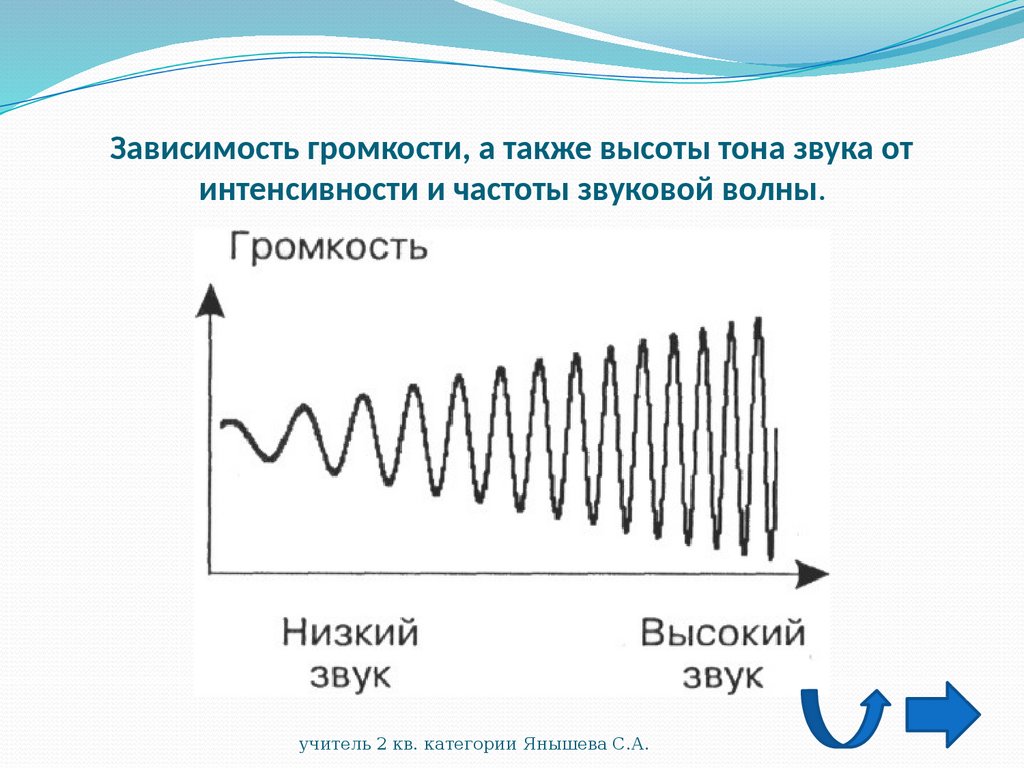 3), мы видим, что в целом мы неплохо справляемся. Есть две проблемы что мы можем увидеть с нашей реконструкцией:

• Конечные точки не очень хорошо совпадают. В этом примере начальный конец выглядит очень хорошо, но это артефакт того, что сигнал начинается с нуля. Проблема конечной точки возникает из-за факт, что теорема, которую мы используем, предполагает, что данные есть по обе стороны нашу точку оценки (а на самом деле их бесконечное количество), но поскольку мы приближаемся к краям, расчет получает большую часть информации от только одна сторона точки. Здесь помогает больше данных, но конечные точки всегда будут проблемы.
• Реконструкция немного запаздывает по фазе. Если вы посмотрите внимательно, вы заметите, что фазовый сдвиг находится в данные измерений и что реконструкция имеет такой же сдвиг. Это связано с тем, что фазовый сдвиг вызван фильтром сглаживания. Групповая задержка фильтра Баттерворта, который используется здесь зависит от частоты. Он начинается с нуля и монотонно увеличивается примерно до 10 Гц; при 2 Гц это около 0,05 секунды.