Переход от поверхностного интеграла ІІ рода к тройному. Формула Остроградского-Гаусса
Формула Остроградського-Гауса применяют для преобразования объемного (тройного) интеграла к интегралу по замкнутой поверхности (двойного), превращения объемного (тройного) интеграла к интегралу по замкнутой поверхности (двойного), и наоборот:
Другое приложение формулы это вычисления потока векторного поля через замкнутую поверхность с помощью интеграла от дивергенции этого поля по объему, что ограничен этой поверхностью.
Дальше будут приведены примеры перехода от двойного к тройному интегралу, расстановки пределов и вычисления объемных интегралов.
Пример 1 Используя формулу Остроградського-Гауса, превратить поверхностный интеграл
если гладкая поверхность S ограничивает конечный объем V и — направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл 2-го рода сводится к тройному интегралу с помощью формулы Остроградського-Гауса:
где P, Q, R выписываем из заданного интеграла
— частичные производные функции.
Далее повторно вычисляем производные, чтобы получить направляющие косинусы в направлении каждой из осей
Можем перейти от двойного интеграла к тройному
здесь обозначили Δu — дельта оператор Лапласа
На этом все объяснения к первому примеру.
Пример 2 Используя формулу Гауса-Остроградського, превратить поверхностный интеграл
по гладкой поверхности S ограничивающей конечный объем V и — направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл второго рода сведем к трехмерному интегралу, используя формулы Гауса-Остроградського:
где P=P(x, y, z)=x3, P=P(x, y, z)=y3, P=P(x, y, z)=z3 берем из условия.
Вычисляем вторые производные по «икс, игрек, зет»
Записываем формулу перехода от двойного интеграла к тройному
На этом примере Вы видите, что сам переход между кратными и тройными интегралами найти не трудно.
Значительное количество ждет при необходимости расставить пределы интегрирования и найти тройной интеграл.
Пример 3 Используя формулу Гауса-Остроградського, превратить поверхностный интеграл
если гладкая поверхность S ограничивает конечный объем V и — направляющие косинусы внешней нормали к поверхности S.
Решение: Поверхностный интеграл второго рода сведем к тройному интегралу, используя формулу Гауса-Остроградського :
где P=P(x, y, z)=yz, Q=Q(x, y, z)=xz, R=R(x, y, z)=xy.
Частичные производные второго порядка от P, Q, R
Поэтому тройной интеграл равен нулю
Пример 4 Используя формулу Гауса-Остроградського, вычислить поверхностный интеграл int[x3dydz+y3dzdx+z3dxdy, S]
где S- внешняя сторона сферы x2+y2+z2=a2.
Решение: Поверхностный интеграл ІІ рода сводим к трехкратному интегралу, используя формулу Гауса-Остроградського:
Выписываем P=P(x, y, z)=x3, Q=Q(x, y, z)=y3, R=R(x, y, z)=z3.
Тогда частичные производные от P, Q, R равны
Область S ограничивает сфера V уравнением:
x2+y2+z2=a2.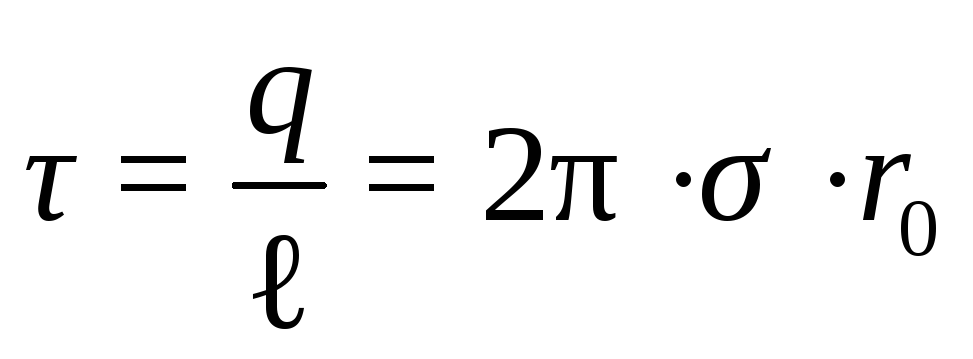
В декартовой системе координат вычислять тройной интеграл когда объем ограничен сферой нецелесообразно, поскольку будем иметь корневые функции в пределах интеграла.
Поэтому всюду перейдем к сферической системе координат:
Находим частичные производные первого порядка по углам от параметризующих координат
Дополнительно необходимо найти якобиан перехода:
Он служит дополнительным множителем в интеграле.
Вычислим подынтегральное выражение в новых координатах:
Дальше используя формулу Остроградського-Гауса находим поверхностный интеграл второго рода:
Внимательно пересмотрите как раскрывали внутренние интегралы в тройном.
Пример 5 Используя формулу Гаусса-Остроградського, превратить поверхностный интеграл
по гладкой поверхности S ограничивающей конечный объем V и — направляющие косинусы внешней нормали к поверхности S.
Решение: Имеем поверхностный интеграл ІІ рода
Сведем к объемному интегралу, используя формулу Гауса-Остроградського:
В соответствии с условием функции P, Q, R принимают значение
Вычисляем частичные производные второго порядка за переменными x, y, z
Подставляем и сводим интегрирование по площади на интегрирование по объему
На сайте размещены сотни развязанных примеров из интегрирования, которые охватывают весь курс из интегралов.
Все что нужно для учебы Вы можете пересмотреть в категории интегрирования!
Математический анализ. Продолжение курса
Математический анализ. Продолжение курса
ОглавлениеПРЕДИСЛОВИЕГлава 1. ЧИСЛОВЫЕ РЯДЫ § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА 2. Критерий Коши сходимости ряда. § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 2. Признаки сравнения. 3. Признаки Даламбера и Коши. 4. Интегральный признак Коши—Маклорена. 5. Признак Раабе. 6. Отсутствие универсального ряда сравнения. § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ 2. О перестановке членов условно сходящегося ряда. § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 2. Связь между сходимостью бесконечных произведений и рядов. 3. Разложение функции sin x в бесконечное произведение. § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ 1. Метод Чезаро (метод средних арифметических). 2. Метод суммирования Пуассона—Абеля. § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ Глава 2.  ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ§ 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ 3. Равномерная сходимость на множестве. 4. Критерий Коши равномерной сходимости последовательности (ряда). § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ 2. Почленное дифференцирование. 3. Сходимость в среднем. § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ § 6. СТЕПЕННЫЕ РЯДЫ 2. Непрерывность суммы степенного ряда. § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ 2. Разложение некоторых элементарных функций в ряд Тейлора. 3. Элементарные представления о функциях кемплексной переменной.  4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами. Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА 2. Условия существования двойного интеграла для прямоугольника. 3. Определение и условия существования двойного интеграла для произвольной области. § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ 2. Случай произвольной области. § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Два признака сходимости несобственных интегралов от неотрицательных функций. 3. Несобственные интегралы от знакопеременных функций. 4. Главное значение кратных несобственных интегралов. Глава 4.  3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора. 4. Инварианты линейного оператора. Дивергенция и ротор. 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе. § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА 2. Дивергенция, ротор и производная по направлению векторного поля. 3. Некоторые другие формулы векторного анализа. 4. Заключительные замечания. § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА 2. Формула Остроградского—Гаусса. 3. Формула Стокса. § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ 2. Билинейные формы. 3. Полилинейные формы. 4. Знакопеременные полилинейные формы. 5. Внешнее произведение знакопеременных форм.  6. Свойства внешнего произведения знакопеременных форм. 7. Базис в пространстве знакопеременных форм. § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 2. Внешний дифференциал. § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ 2. Свойства отображения. § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 2. Дифференцируемые цепи. 4. Примеры. Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ 2. Критерий Коши равномерного стремления функции к предельной. 3. Применения понятия равномерного стремления к предельной функции. § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Случай, когда пределы интегрирования зависят от параметра. § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 2. Несобственные интегралы второго рода, зависящие от параметра. § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ  ИНТЕГРАЛЫ ЭЙЛЕРА ИНТЕГРАЛЫ ЭЙЛЕРА2. В-функция. 3. Связь между эйлеровыми интегралами. 4. Примеры. § 6. ФОРМУЛА СТИРЛИНГА § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ 2. Несобственные кратные интегралы, зависящие от параметра. Глава 8. РЯДЫ ФУРЬЕ § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ 2. Понятие об общем ряде Фурье. § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ 2. Доказательство замкнутости тригонометрической системы. 3. Следствия замкнутости тригонометрической системы. § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье. § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ 2. Выражение для частичной суммы тригонометрического ряда Фурье.  3. Вспомогательные предложения. 4. Принцип локализации. 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера. 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции. 8. Заключительные замечания. § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ 2. Модуль непрерывности и классы Гёльдера для функции N переменных. 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье. Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ 2. Основная теорема. Формула обращения. 3. Примеры. § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ |
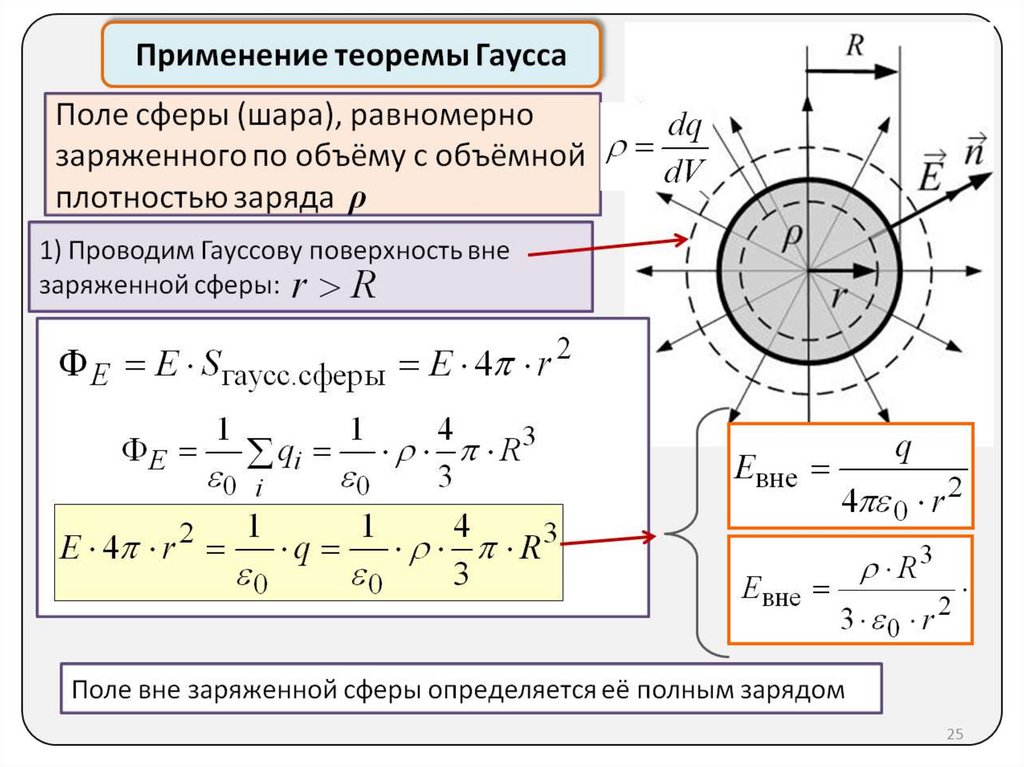
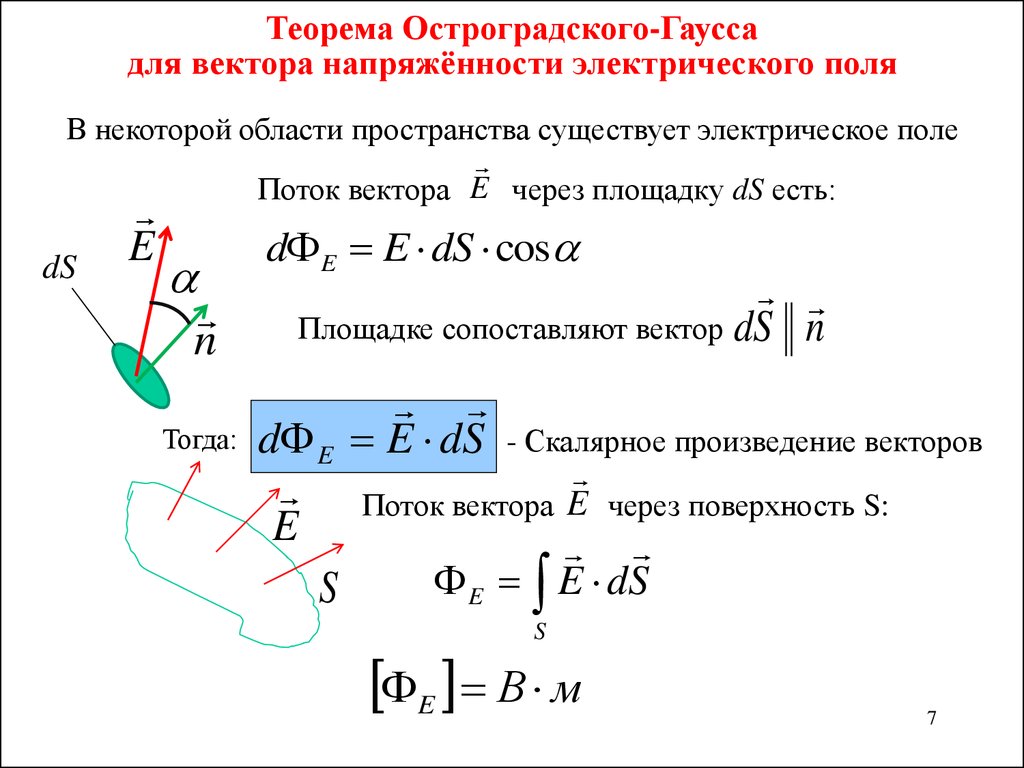
Электр майдон кучи вектор окими. Кичик о’йин майдончаси бо’лсин D S (1.2-расм) йо’налиши нормальный бо’лган электр майдонининг куч чизикларини кесиб о’тинг. п ушбу сайтга бурчак а. Таранглик вектори деб фараз килсак E сайт ичида озгармайди D S , аникланг кучланиш вектор окими сайт оркали D S Кандай DF E = E D S cos a. Maydon Chiziqlarining Zichligi Cuchlanishing Raqamli Qiymatiga Teng Bo’lgani Uchun E , Keyin Maydonni Kesib o’tuvchi kuchciMatglari Sonid S , Son jihatdan oqim qiymatiga lonid. (1.3) ifodaning o’ng tomonini vektorlarning skalyar ko’paytmasi sifatida ifodalaymiz Е ВАД С = n D S , qayerda n sirt birligi normal vektoridirD S . Бошлангич соха учун д С ифода (1.3) шаклни олади дФ Е = Е Г С сайт бойлаб S интенсивлик вектор окими сирт устида интеграл сифатида хисобланади Электр индукционный вектор окими. Электр индуксия векторининг окими электр майдонининг кучланиш векторининг окимига о’хшаш тарзда аникланади. дФ Д = Д Д С Oqimlarning ta’riflarida ba’zi noaniqliklar mavjud, chunki har bir sirt uchun ikkitasini belgilashingiz mumkin. нормальный тескари йо’налишда. Теоремы Гаусса. Ойлаб ко’ринг иджобий нукта электр заряди q , озбошимчалик билан йопик сирт ичида джойлашган S (1.3-расм). Индуксия векторининг сирт элементи оркали окиши д S тэн Компонент d S D = д С cos asirt elementi d S индуксия вектори йо’налыши бойича D радиуси сферик сиртнинг элементи сифатида каралади r , марказида заряд бор q .
Шуни хисобга олиб д С Д / р 2 тэн элментар тана бурчак дв, кайси остида зарьяд кэрда нуктадан q сирт элементи d ко’ринади S , (1.4) ифодани шаклга айлантирамиз d F D = q д ж/4
p, bu erdan zaryadni o’rab turgan butun fazoda, ya’ni 0 dan 4 gacha bo’lgan qattiq burchak ichida integratsiyalashgandan so’ng. F D = q . Электр индуксия векторининг иштиёрий шаклдаги йопик сирт оркали о’тиши ушбу сирт ичида джойлашган зарядга тэн. . Агар озбошимчалик билан йопик сирт бо’лса S мяч зарядини гопламайди кв (1.4-расм), кейин заряд джойлашган нуктада тепаси бо’лган конуснинг абизджитни сирти куриб. S ikki qismga: S 1 va S 2. Вектор окими D yuzasi orqali S biz sirtlardan o’tadigan oqimlarning алгебраик yig’indisi sifatida topamiz S 1 va С 2: . Заряднинг джойлашган джойидан иккала сирт q бир каттик бурчакдан ко’ринади ш. Шундай килиб, окимлар тэн Yopiq sirt orqali oqimni hisoblashda biz foydalanamiz tashqi normal yuzasiga qarab F oqimini ko’rish oson 1D 2D> 0. Электр майдони нуктавий зарядлар тизими томонидан яратилган болса q 1 , q 2 ,¼ , q n , bu yopiq sirt bilan qoplangan S , keyin superpozitsiya printsipiga muvofiq, bu sirt orqali induksiya vektorining oqimi har bir zaryad tomonidan yaratilgan oqimlarning yig’indisi aniqlanadia aniqlanadia. Электр индуксия векторининг иштиёрий шаклдаги йопик сирт оркали о’тиши ушбу сирт qoplagan zaryadlarning алгебраик yig’indisiga teng. : Шуни та’кидлаш керакки, то’ловлар q i нукта бо’лиши шарт эмас, зарурий шарт — зарядланган худуд бутунлай сырт билан копланган бо’лиши керак. Yopiq sirt bilan chegaralangan bo’shliqda bo’lsa S , elektr zaryadi uzluksiz taqsimlanadi, keyin har bir elementar hajm d deb hisoblash kerak V zaryadi bor. (1,6) Ifoda (1.6) eng umumiy formuladir Gauss teoremalari : ixtiyoriy shakldagi yopiq sirt orqali elektr induksiya vektorining oqimi ushbu sirt bilan qoplangan hajmdagi umumiy zaryadga teng va ko’rib chiqilayotgan sirtdan tashqarida joylashgan zaryadlarga bog’liq emas. . Gauss teoremasini elektr maydon kuchi ektorining oqimi uchun ham yozish mumkin: . Elektr maydonining muhim xususiyati Gauss teoremasidan kelib chiqadi: куч чизиклари факат электр зарядларида бошланади йоки тугайди йоки чексизликка боради . Биз яна бир бор та’кидлаймизки, электр майдон кучига карамай E ва электр индукцияси D космосдаги барча зарядларнинг джойлашига, бу векторларнинг икстиёрий йопик сирт оркали о’тишига бог’лик. S Faqat aniqlanadi сирт ичида джойлашган зарядлар S . Теория Гаусса для дифференциальных шакли. Yozib oling интегральные шакли Gauss teoremasi elektr maydonining manbalari (zaryadlari) va hajmdagi elektr maydonining xususiyatlari (kuch yoki induksiya) o’rtasidagi munosabatni tavsiflaydi. V ixtiyoriy, lekin integral munosabatlarni shakllantirish uchun etarli, qiymat. Овозни болиш оркали В кичик хаймлар учун Ви , ифодасини оламиз умумий ва хар бир муддат учун амаль килади. Олинган ифодани куйидагича озгартирамиз: (1,7) ва джингалак кавслар ичига олинган тенгликнинг о’нг томонидаги ифода хаймининг чексиз болиниши билан мойиллик чегарасини ко’риб чикинг. В . Matematikada bu chegara deyiladi farqlanish vektor (buholda, elektr induksiyasi vektori D ): Вектор фарки D Dekart Координатор: Шундай килиб, (1.7) ифода куйидаги шаклга озгартирилади: . Чексиз болиниш билан оксирги ифоданинг чап томонидаги йигинди хайм интегрилига отишини хисобга олсак, биз оламиз Олинган муносабат хар кандай озбошимчалик билан танланган хаджм учун амаль килиши керак V . йоки электростатик майдон кучи вектори учун Bu tengliklar Gauss teoremasini ifodalaydi дифференциальный шакл . Этибор беринг, Гаусс теоремазининг дифференциал шаклига о’тиш джарайонида умумий хусусиятга эга болган муносабат олинади: . Буйфода Гаусса-Остроградского формулы деб аталади ва векторнинг дивергенсиянинг хайм интегралини бу векторнинг хаймни чегараловчи йопик сирт оркали окими билан боглайди. Саволлар 1) Vakuumdagi elektrostatik maydon uchun Gauss teoremasining fizik ma’nosi nimadan iborat 2) Кубнинг маркизида нукта заряди мавджуд q . Векторнинг окими нима E : а) кубнинг то’лик юзаси оркали; б) кубнинг юзларидан бири оркали. Явоблар озгарадими, агар: а) заряд кубнинг марказида эмас, балки унинг ичида ; б) заряд кубдан ташкарида. 3) Чизикли, сирт, хайм заряд зичлиги нима. 4) Hajm va sirt zaryad zichligi o’rtasidagi bog’liqlikni ko’rsating. 5) Карама-карши ва бир хил зарядланган параллель чексиз текисликлар ташкарисидаги майдон нолдан фарк килиши мумкинми? 6) Elektr dipol yopiq sirt ichiga joylashtirilgan. Бу сирт оркали кандай оким бор |
Кхонг Тим Тай Транг Най
Dường như chẳng tìm thấy gì ở đay. Có lẽ nên thử tìm kiem?
Тим Ким Чо:- Гийтиу
| Н | Б | Т | Н | С | Б | С |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 9п | |



 Bunday Holda, toremaning Formulasi quyidagicha bo’ladi: elektr siljish ektorining yopiq sirt orqali oqimi ushbu sirt ichidagi erkin elektr zaryadiga proportsionaldir:
Bunday Holda, toremaning Formulasi quyidagicha bo’ladi: elektr siljish ektorining yopiq sirt orqali oqimi ushbu sirt ichidagi erkin elektr zaryadiga proportsionaldir:
 Ushbu teorema fizikani profil darajasida o’rganishda qo’llanilishi mumkin, chunki u elektr maydonlarini yanada oqilona hisoblash imkonini beradi.
Ushbu teorema fizikani profil darajasida o’rganishda qo’llanilishi mumkin, chunki u elektr maydonlarini yanada oqilona hisoblash imkonini beradi.

 Бундан ташкари, сирт ичидаги зарядларинг джойлашишига боглик эмас. Bu shuni anglatadiki, olingan natija faqat bitta zaryad uchun emas, balki ixtiyoriy joylashgan har qanday miqdordagi zaryadlar uchun ham amal qiladi, agar biz q orqali faqat sirt ichida joylashgan barcha zaryadlarning алгебраик yig’indisini nazarda tutsak.
Бундан ташкари, сирт ичидаги зарядларинг джойлашишига боглик эмас. Bu shuni anglatadiki, olingan natija faqat bitta zaryad uchun emas, balki ixtiyoriy joylashgan har qanday miqdordagi zaryadlar uchun ham amal qiladi, agar biz q orqali faqat sirt ichida joylashgan barcha zaryadlarning алгебраик yig’indisini nazarda tutsak. Интеграция натиджасида хар кандай бир джинсли бо’лмаган электр майдонида С йопик сирт оркали умумий оким куйидагиларга тэн бо’лади: , бу эрда к — йопик сирт билан о’ралган барча зарядларинг алгебраик йиг’индизи С. оксирги тенгламани майдони ) ифодалаймиз: .
Интеграция натиджасида хар кандай бир джинсли бо’лмаган электр майдонида С йопик сирт оркали умумий оким куйидагиларга тэн бо’лади: , бу эрда к — йопик сирт билан о’ралган барча зарядларинг алгебраик йиг’индизи С. оксирги тенгламани майдони ) ифодалаймиз: . Юзаки заряд зичлиги — бу заряднинг у таксимланган сирт майдонига нисбати. . СИДа.
Юзаки заряд зичлиги — бу заряднинг у таксимланган сирт майдонига нисбати. . СИДа. Sfera markazidan uzoqda ajratilgan B nuqtani olaylik . У холда, ручун Е = 0
Sfera markazidan uzoqda ajratilgan B nuqtani olaylik . У холда, ручун Е = 0 Bu oqimlarning ikkalasi ham ijobiy =+; знак равно знак равно ==; Н=2 .
Bu oqimlarning ikkalasi ham ijobiy =+; знак равно знак равно ==; Н=2 . Gauss teoremasiga kelsak, bu sharoitda u o’z ma’nosini butunlay yo’qotadi.
Gauss teoremasiga kelsak, bu sharoitda u o’z ma’nosini butunlay yo’qotadi.
 Вектор чизиклари D таранлик чизикларидан фаркли о’ларок узлюксидир.
Вектор чизиклари D таранлик чизикларидан фаркли о’ларок узлюксидир.  (1.3)
(1.3)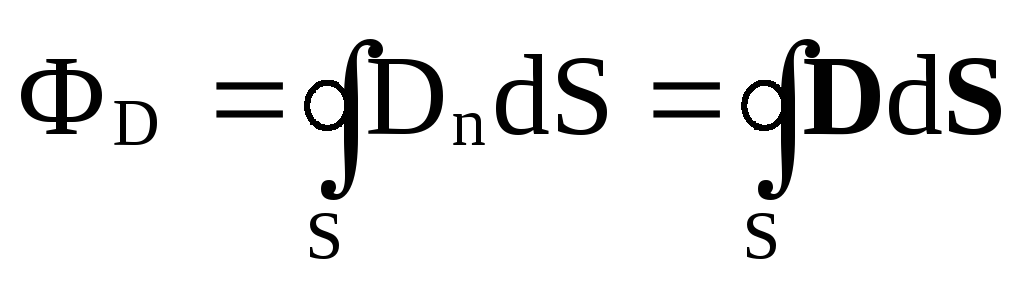 Yopiq sirt uchun tashqi normal ijobiy hisoblanadi.
Yopiq sirt uchun tashqi normal ijobiy hisoblanadi. p, olamiz
p, olamiz Умумий оким F D = 0. Бу шуни англатадики иштиёрий шаклдаги йопик сирт оркали электр индуксия векторининг окими бу сиртдан ташкарида джойлашган зарядларга боглик емас.
Умумий оким F D = 0. Бу шуни англатадики иштиёрий шаклдаги йопик сирт оркали электр индуксия векторининг окими бу сиртдан ташкарида джойлашган зарядларга боглик емас. 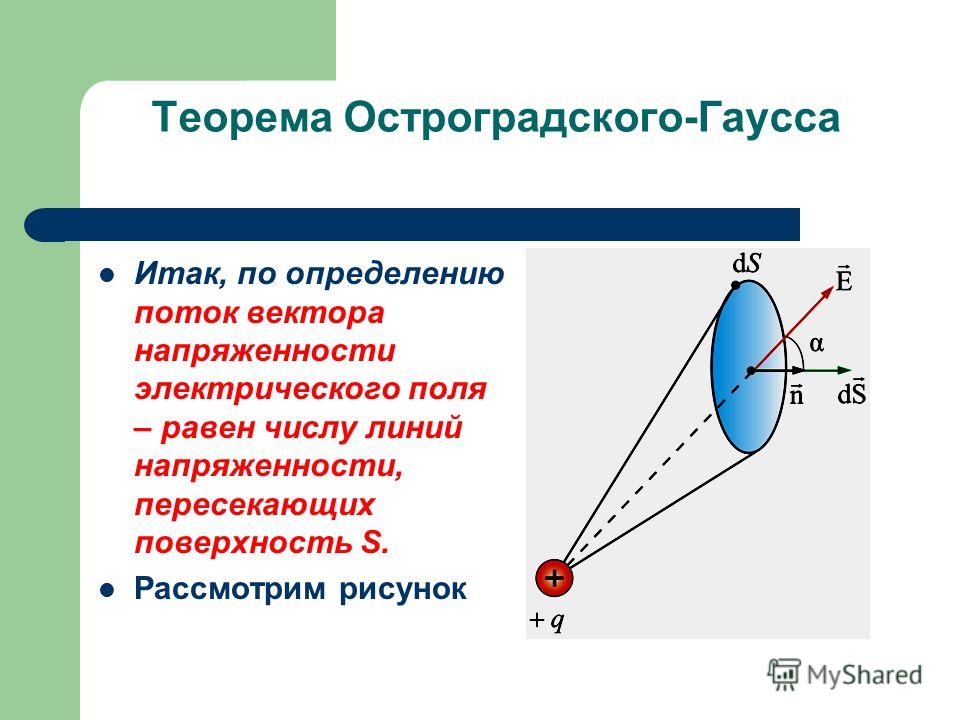 Bunda (1.5) ifodaning o’ng tomonida zaryadlarning алгебраик yig’indisi yopiq sirt ichida yopilgan hajm ustidan integratsiya bilan almashtiriladi. С :
Bunda (1.5) ifodaning o’ng tomonida zaryadlarning алгебраик yig’indisi yopiq sirt ichida yopilgan hajm ustidan integratsiya bilan almashtiriladi. С :
 Bu fazoning har bir nuqtasida integrandlarning qiymatlari bir xil bo’lgandagina mumkin. Шунинг учун векторнинг дивергенцияси Д тенглик билан бир хил нуктадаги заряд зичлиги билан боглик
Bu fazoning har bir nuqtasida integrandlarning qiymatlari bir xil bo’lgandagina mumkin. Шунинг учун векторнинг дивергенцияси Д тенглик билан бир хил нуктадаги заряд зичлиги билан боглик
 Umuman Ольганда, и формула bilan aniqlanadi.
Umuman Ольганда, и формула bilan aniqlanadi. A nuqta orqali radiusi R va uzunligi ℓ bo’lgan xayoliy silindrsimon sirtni chizamiz. Simmetriya tufayli oqim faqat silindrning yon yuzalari orqali chiqadi, chunki r 0 radiusli silindrdagi zaryadlar uning yuzasi bo’ylab bir tekis taqsimlanadi, ya’ni. кучланиш чизиклари иккала цилиндрнинг йон юзаларига перпендикулярно радиальному к’г’ри чизиклар бо’лади. Цилиндрлар асоси оркали оким нолга тэн (кос а = 0) ва цилиндрнинг йон юзаси куч чизикларига перпендикуляр болганлиги сабабли (кос а = 1), у холда
A nuqta orqali radiusi R va uzunligi ℓ bo’lgan xayoliy silindrsimon sirtni chizamiz. Simmetriya tufayli oqim faqat silindrning yon yuzalari orqali chiqadi, chunki r 0 radiusli silindrdagi zaryadlar uning yuzasi bo’ylab bir tekis taqsimlanadi, ya’ni. кучланиш чизиклари иккала цилиндрнинг йон юзаларига перпендикулярно радиальному к’г’ри чизиклар бо’лади. Цилиндрлар асоси оркали оким нолга тэн (кос а = 0) ва цилиндрнинг йон юзаси куч чизикларига перпендикуляр болганлиги сабабли (кос а = 1), у холда Tekislikning sirt zaryadi zichligi s bo’lsin. Yopiq sirt sifatida, o’qi tekislikka perpendikulyar bo’lgan silindrni tanlash qulay va o’ng asosda A nuqtasi mavjud. Самолет цилиндрни ярмига бо’лади. Ko’rinib turibdiki, kuch chiziqlari tekislikka perpendikulary va silindrning yon yuzasiga parallel, shuning uchun barcha oqim faqat silindrning asoslari orqali o’tadi. Иккала асосда майдон кучи бир шил, чунки. A va B nuqtalari tekislikka nisbatan simmetrikdir. Keyin silindrning tagliklari orqali oqim
Tekislikning sirt zaryadi zichligi s bo’lsin. Yopiq sirt sifatida, o’qi tekislikka perpendikulyar bo’lgan silindrni tanlash qulay va o’ng asosda A nuqtasi mavjud. Самолет цилиндрни ярмига бо’лади. Ko’rinib turibdiki, kuch chiziqlari tekislikka perpendikulary va silindrning yon yuzasiga parallel, shuning uchun barcha oqim faqat silindrning asoslari orqali o’tadi. Иккала асосда майдон кучи бир шил, чунки. A va B nuqtalari tekislikka nisbatan simmetrikdir. Keyin silindrning tagliklari orqali oqim Superpozitsiya practsipiga ko’ra, Tekislikdan Tashqaridagi umumiy Maydonning Kuchi Nolga Teng:
Superpozitsiya practsipiga ko’ra, Tekislikdan Tashqaridagi umumiy Maydonning Kuchi Nolga Teng: Ba 2020 (2) Tháng Hai 2020 (2) Tháng Một 2020 (2) Tháng Mười Một 2019(1) Tháng Chín 2019 (1) Tháng Sáu 2019 (2) Tháng Năm 2019 (1) Tháng Tư 2019 (3) Tháng Hai 2019 (1) Tháng Một 2019 (3) Tháng Mười Hai 2018 (2) Tháng Mườt 2018 (2) Tháng Mười 2018 (2) Tháng Chín 2018 (3) Tháng Tám 2018 (1) Tháng Sáu 2018 (1) Tháng Năm 2018 (1) Tháng Tư 2018 (2) Tháng Ba 2018 (1 8 Hái 2) Tháng Tháng Một 2018 (2) Tháng Mười Hai 2017 (1) Tháng Mười Một 2017 (1) Tháng Chín 2017 (1) Tháng Tám 2017 (1) Tháng Sáu 2017 (1) Tháng Năm 2017 (1) Tháng Tư 2017 (1). ) Tháng Ba 2017 (1) Tháng Một 2017 (3) Tháng Mười Hai 2016 (1) Tháng Mười Một 2016 (2) Tháng Mười 2016 (1) Tháng Chín 2016 (1) Tháng Tám 2016 (1) Tháng Bảy 2016 (1) ) Tháng Sáu 2016 (2) Tháng Năm 2016 (1) Tháng Tư 2016 (3) Tháng Ba 2016 (2) Tháng Hai 2016 (2) Tháng Một 2016 (4) Tháng Mười Hai 2015 (1) Tháng Mười MộT 2015 (2 ) Тханг Муи 2015 (3) Тханг Чин 2015 (2) Тханг Там 2015 (2) Тханг Бой 2015 (2) Тханг Сау 2015 (2) Тханг Нам 2015 (3) Тханг Тư 5 (2 Бан 2) 2) Tháng Hai 2015 (1) Tháng Một 2015 (5) Tháng Mười Hai 2014 (1) Tháng Mười Một 2014 (3) Tháng Mười 2014 (3) Tháng Chín 2014 (5) Tháng Tám 2014 (2) Tháng Bảy 2014 (5).
Ba 2020 (2) Tháng Hai 2020 (2) Tháng Một 2020 (2) Tháng Mười Một 2019(1) Tháng Chín 2019 (1) Tháng Sáu 2019 (2) Tháng Năm 2019 (1) Tháng Tư 2019 (3) Tháng Hai 2019 (1) Tháng Một 2019 (3) Tháng Mười Hai 2018 (2) Tháng Mườt 2018 (2) Tháng Mười 2018 (2) Tháng Chín 2018 (3) Tháng Tám 2018 (1) Tháng Sáu 2018 (1) Tháng Năm 2018 (1) Tháng Tư 2018 (2) Tháng Ba 2018 (1 8 Hái 2) Tháng Tháng Một 2018 (2) Tháng Mười Hai 2017 (1) Tháng Mười Một 2017 (1) Tháng Chín 2017 (1) Tháng Tám 2017 (1) Tháng Sáu 2017 (1) Tháng Năm 2017 (1) Tháng Tư 2017 (1). ) Tháng Ba 2017 (1) Tháng Một 2017 (3) Tháng Mười Hai 2016 (1) Tháng Mười Một 2016 (2) Tháng Mười 2016 (1) Tháng Chín 2016 (1) Tháng Tám 2016 (1) Tháng Bảy 2016 (1) ) Tháng Sáu 2016 (2) Tháng Năm 2016 (1) Tháng Tư 2016 (3) Tháng Ba 2016 (2) Tháng Hai 2016 (2) Tháng Một 2016 (4) Tháng Mười Hai 2015 (1) Tháng Mười MộT 2015 (2 ) Тханг Муи 2015 (3) Тханг Чин 2015 (2) Тханг Там 2015 (2) Тханг Бой 2015 (2) Тханг Сау 2015 (2) Тханг Нам 2015 (3) Тханг Тư 5 (2 Бан 2) 2) Tháng Hai 2015 (1) Tháng Một 2015 (5) Tháng Mười Hai 2014 (1) Tháng Mười Một 2014 (3) Tháng Mười 2014 (3) Tháng Chín 2014 (5) Tháng Tám 2014 (2) Tháng Bảy 2014 (5). 3) Tháng Sáu 2014 (8) Tháng Năm 2014 (2) Tháng Tư 2014 (2) Tháng Ba 2014 (4) Tháng Hai 2014 (4) Tháng Một 2014 (3) Tháng Mười Hai 2013 (3) Tháng Mườt Một 2013 ( 2) Тханг Муи 2013 (3) Тханг Чин 2013 (4) Тханг Там 2013 (3) Тханг Бэй 2013 (2) Тханг Сау 2013 (2) Тханг Нам 2013 (2) Тханг Тư 1 (3) 2 Tháng Ba 2013 Tháng Hai 2013 (1) Tháng Một 2013 (2) Tháng Mười Hai 2012 (2) Tháng Mười Một 2012 (1) Tháng Mười 2012 (1) Tháng Chín 2012 (1) Tháng Tám 2012 (5) Tháng Bảy 2012 (3) Tháng Sáu 2012 (5) Tháng Năm 2012 (5) Tháng Tư 2012 (3) Tháng Ba 2012 (4) Tháng Hai 2012 (3) Tháng Một 2012 (2) Tháng Mười Hai 2011 (4) Tháng Mười MộT 2011 (1) Tháng Mười 2011 (2) Tháng Chín 2011 (2) Tháng Tám 2011 (2) Tháng Bảy 2011 (1) Tháng Sáu 2011 (7) Tháng Năm 2011 (3) Tháng Tư 2011 1 0 2 (6) 4) Tháng Hai 2011 (3) Tháng Một 2011 (2) Tháng Mười Hai 2010 (1) Tháng Mười Một 2010 (3) Tháng Mười 2010 (5) Tháng Chín 2010 (6) Tháng Tám 2010 (2) Tháng Bảy 2010 (6). 1) Тханг Сау, 2010 (2) Тханг Нам, 2010 (2) Тханг Тư, 2010 (3) Тханг Ба, 2010 (3) Тханг Хай, 2010 (3) Тханг Мот, 2010 (1) Тханг Муи Хай, 2009 г.
3) Tháng Sáu 2014 (8) Tháng Năm 2014 (2) Tháng Tư 2014 (2) Tháng Ba 2014 (4) Tháng Hai 2014 (4) Tháng Một 2014 (3) Tháng Mười Hai 2013 (3) Tháng Mườt Một 2013 ( 2) Тханг Муи 2013 (3) Тханг Чин 2013 (4) Тханг Там 2013 (3) Тханг Бэй 2013 (2) Тханг Сау 2013 (2) Тханг Нам 2013 (2) Тханг Тư 1 (3) 2 Tháng Ba 2013 Tháng Hai 2013 (1) Tháng Một 2013 (2) Tháng Mười Hai 2012 (2) Tháng Mười Một 2012 (1) Tháng Mười 2012 (1) Tháng Chín 2012 (1) Tháng Tám 2012 (5) Tháng Bảy 2012 (3) Tháng Sáu 2012 (5) Tháng Năm 2012 (5) Tháng Tư 2012 (3) Tháng Ba 2012 (4) Tháng Hai 2012 (3) Tháng Một 2012 (2) Tháng Mười Hai 2011 (4) Tháng Mười MộT 2011 (1) Tháng Mười 2011 (2) Tháng Chín 2011 (2) Tháng Tám 2011 (2) Tháng Bảy 2011 (1) Tháng Sáu 2011 (7) Tháng Năm 2011 (3) Tháng Tư 2011 1 0 2 (6) 4) Tháng Hai 2011 (3) Tháng Một 2011 (2) Tháng Mười Hai 2010 (1) Tháng Mười Một 2010 (3) Tháng Mười 2010 (5) Tháng Chín 2010 (6) Tháng Tám 2010 (2) Tháng Bảy 2010 (6). 1) Тханг Сау, 2010 (2) Тханг Нам, 2010 (2) Тханг Тư, 2010 (3) Тханг Ба, 2010 (3) Тханг Хай, 2010 (3) Тханг Мот, 2010 (1) Тханг Муи Хай, 2009 г.