Основные характеристики:

Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы  действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

.

Также иногда называется силовой характеристикой электрического поля.

Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр).

Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Силовые линии электростатического поля

Свойства:

1. Всегда незамкнуты: начинаются на положительных и заканчиваются на отрицательных зарядах

2. Не пересекаются

3. Густота линий тем больше, чем больше напряженность, то есть напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности

19. Закон Кулона.

    

На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках. Взаимодействие неподвижных электрических зарядов называют 

электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят 

кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

Коэффициент k в системе СИ обычно записывают в виде: 

где  – электрическая постоянная.

19. Электростатическое поле в диэлектрической среде.

Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна ,

где  — поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле , которое направлено против внешнего поля .

,

где  — поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика

.

Поверхностная плотность связанных зарядов  меньше плотности  свободных зарядов, и не все поле E₀ компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее . Таким образом,

,

где  — диэлектрическая проницаемость среды, — химический эквивалент. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума , для диэлектриков .

Теория электромагнитного поля — презентация онлайн

1.

ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ имени С.М. Кирова Кафедра биологической и медицинской физикиЛЕКЦИЯ № 9
по дисциплине «Физика, математика»
на тему: «Основы теории электромагнитного
поля»
для курсантов и студентов I курса по
специальности «Лечебное дело»

2. 1. Электрическое поле. Его основные характеристики. Потенциальное и вихревое электрические поля.

• Все тела в природе способны
электризоваться, то есть приобретать
электрический заряд.
• Наличие электрического заряда
проявляется в том, что заряженное тело
взаимодействует с другими заряженными
телами.
• Опыт показал, что между
наэлектризованными телами имеется либо
притяжение, либо отталкивание.
• Это объясняется тем, что имеется два вида
электрических зарядов, условно
называемых положительными и
отрицательными.
• Одноименные заряды отталкиваются,
разноименные – притягиваются.
• Электрический заряд обозначается буквой
q, единица измерения заряда – кулон (Кл).
• Электрический заряд любой системы тел
состоит из целого числа элементарных
зарядов.
• Элементарный заряд — это наименьший
встречающийся в природе электрический
заряд, равный 1,6·10-19 Кл.
• Наименьшей по массе устойчивой
частицей, имеющей отрицательный
элементарный заряд, является электрон
(m = 9,1·10-31 кг).
• У электрона существует и античастица,
имеющая положительный элементарный
заряд – позитрон.
• Суммарный заряд электрически
изолированной системы не изменяется при
любых процессах, происходящих в этой
системе. Это положение известно под
названием закона сохранения заряда:
q = q1 + q2 + q3 +…+ qn = const
• Силы электростатического взаимодействия
заряженных тел подчиняются закону
Кулона, поэтому их часто называют
кулоновскими силами.
• Закон Кулона. Сила взаимодействия двух
неподвижных точечных зарядов прямо
пропорциональна величине каждого из
зарядов и обратно пропорциональна
квадрату расстояния между ними.
q1q2
1 q1q2
F 12
k 2
2
4 0 r12
r12

12
1
8
,
85
10
Ф
м
где 0
– электрическая
постоянная,
k 9 10 9 Н м 2 Кл 2
– коэффициент
пропорциональности, или константа
Кулона,
• ε – относительная диэлектрическая
проницаемость среды.
• Сила направлена вдоль прямой,
соединяющей заряженные тела.
• Сам по себе закон Кулона не дает
представления о том, каков механизм
взаимодействия зарядов. Физическую
картину взаимодействия электрических
зарядов раскрывает так называемая теория
близкодействия.
• Согласно этой теории вокруг каждого
заряда существует электрическое поле.
• Взаимодействие электрических зарядов q1
и q2 есть результат действия поля заряда q1
на заряд q2 и поля заряда q2 на заряд q1.
• Определение:
Электрическое поле есть особый вид
материи, посредством которого
осуществляются силовые воздействия на
электрические заряды, находящиеся в
этом поле.
• Силовой характеристикой электрического поля
служит вектор напряженности электрического
поля.
• Он численно равен и совпадает по направлению с
силой, действующей на единичный
положительный заряд, помещенный в данную
точку поля:
• Размерность напряженности ЭП: Н/Кл.
• Напряженность поля, создаваемого
точечным зарядом:
,
• где r – расстояние от заряда до
рассматриваемой точки.
• Однородным называют электрическое
поле, векторы напряженности которого
одинаковы во всех точках поля.
• Приблизительно однородным является
электрическое поле между двумя
разноименно заряженными
металлическими пластинами,
расположенными параллельно друг другу.
• Для графического изображения
электростатического поля в пространстве
применяется метод силовых линий, или
линий напряженности.
• Силовыми линиями называются линии,
касательные к которым в каждой точке
совпадают с направлением вектора
напряженности в этой точке.
• Следует помнить, что:
• 1) силовые линии электростатического поля не
пересекаются друг с другом;
• 2) имеют начало на положительном заряде и
конец на отрицательном или уходят на
бесконечность, т.е. являются незамкнутыми;
• 3) густота силовых линий пропорциональна
величине напряженности электростатического
поля.
• Принцип суперпозиции электрических
полей: напряженность электрического
поля системы точечных зарядов равна
векторной сумме напряженностей полей
каждого из зарядов в отдельности:
E E1 E2 … En или
n
Е Еi
i 1
• Помимо силовой характеристики
электрического поля существует и
характеристика его источников электрическое смещение, или вектор
электрической индукции (D) , который
зависит от того, каким образом и в каком
количестве источники ЭП расположены в
пространстве.
D = ε0εE [Кл.м-2]
• Существуют два вида электрических полей:
а) потенциальное ЭП;
б) вихревое ЭП.
• Потенциальное ЭП – это
электростатическое поле, т. е. поле,
созданное системой неподвижных
электрических зарядов.
• Важной характеристикой потенциального
ЭП является потенциал электрического
поля (электрический потенциал).
• Это энергетическая характеристика
потенциального ЭП.
• Потенциал электрического поля –
скалярная физическая величина, численно
равная отношению потенциальной энергии
(+) электрического заряда, помещенного в
данную точку поля, к величине этого
заряда:
• Единица измерения: 1 вольт (В) = 1 Дж/Кл.
• Другими словами, потенциал
электрического поля в данной точке равен
работе сторонних сил по переносу
единичного положительного точечного
заряда от точки, потенциал которой принят
равным нулю (обычно этой точкой является
бесконечность), в данную точку поля.
• Разность потенциалов – величина, равная
работе А1,2 , которую совершают силы
электрического поля при перемещении
единичного положительного заряда q из
точки с потенциалом φ1 в точку с
потенциалом φ2:
• Работа электростатического поля при
перемещении заряда q из точки с
потенциалом 1 в точку с потенциалом 2:
А1,2 = q·( 1 — 2)
• Работа электростатического поля не зависит
от вида траектории перемещения заряда, а
определяется только исходным и
конечным положением перемещенного
заряда.
• Соответственно, при перемещении заряда
по замкнутому контуру полная работа
электростатического поля равна нулю.
• Такое поле называется потенциальным.
• Электростатическое поле – потенциальное
поле.
• Кроме потенциальных ЭП, существуют
также вихревые электрические поля.
• Их силовые линии замкнуты, т.е. не имеют
ни начала, ни конца, а работа по
перемещению заряда по замкнутому
контуру не равна нулю и зависит от
траектории движения заряда.
• Источником вихревых ЭП является
переменное магнитное поле.

33. Связь между разностью потенциалов и напряженностью ЭП

• Между напряженностью ЭП и потенциалом
существует определенная связь. Вектор
напряженности Е численно равен
градиенту потенциала, но направлен в
противоположную сторону, т.е. в сторону
падения потенциала:
или
• Напряженность однородного поля
численно равна разности потенциалов на
единице длины линии напряженности.
• Воображаемую поверхность, все точки
которой имеют одинаковый потенциал,
называют эквипотенциальной
поверхностью.
• Силовые линии и эквипотенциальные
поверхности взаимно перпендикулярны.
• При перемещении заряда по
эквипотенциальной поверхности работа не
совершается.
• Потенциал поля точечного заряда q на
расстоянии r от него:
• Эквипотенциальная поверхность поля
точечного заряда на расстоянии r от
заряда – поверхность сферы радиуса r.
• Принцип суперпозиции электрических
полей – потенциал поля системы точечных
зарядов φ в некоторой точке пространства
равен алгебраической сумме потенциалов,
создаваемых каждым из зарядов в этой
точке:

39. Электрическая емкость

• Электрическая емкость проводника C –
количественная мера его способности
удерживать электрический заряд.
• Электрическая емкость уединенного
проводника равна отношению заряда
проводника q к его потенциалу φ :
[1 Кл/В = 1 Ф]
• Электрическая емкость проводника
определяется его формой,
геометрическими размерами и свойствами
окружающей среды (диэлектрической
проницаемостью ).
• Емкость уединенного шара, погруженного в
однородный безграничный диэлектрик с
проницаемостью ε, равна
C 4 0 R
• Однако уединенные проводники обладают
небольшой емкостью.
• Для накопления большого по величине
заряда применяют конденсаторы.
• Конденсатором называют устройство из
двух проводников (обкладок), разделенных
слоем диэлектрика, толщина которого мала
по сравнению с размерами проводников.
• Плоский конденсатор – система из двух
плоских параллельных металлических
пластин, расположенных на расcтоянии d,
с площадью S каждая, разделенных
диэлектриком с диэлектрической
проницаемостью .
• Электроемкость конденсатора –
отношение заряда одной из его обкладок к
разности потенциалов между обкладками:
,
где φ1 и φ2 – потенциалы пластин,
U – напряжение на конденсаторе.
• Конденсаторы различаются по форме
(плоские, сферические, цилиндрические), а
также по материалу, используемому в
качестве изолирующей прокладки
(парафинированная бумага, полистирол,
слюда, керамика).

45. Формулы для вычисления емкости конденсаторов:

• Плоского: C 0 S
d
• Сферического:
R2 R1
C 4 0
R2 R1
• Цилиндрического:
2 0 l
C
R
ln 2
R1

46. Энергия электрического поля

• Электрическое поле является носителем
энергии.
• В общем случае количественной
характеристикой электрического поля
служит объемная плотность энергии.
• Объемная плотность энергии
электростатического поля ω – физическая
величина, равная отношению энергии
электростатического поля W,
сосредоточенного в некотором объеме V к
этому объему:

48. Энергия плоского конденсатора.

• Исходя из величины работы А,
совершаемой электрическим полем при
разрядке конденсатора:
• получим формулу для энергии
заряженного конденсатора:

49. 2. Магнитное поле и его характеристики

• Магнитные явления были известны
человечеству давно (намагниченные тела,
постоянные магниты, компас и т. д. ).
• Впоследствии выяснилось, что в пространстве
вокруг движущихся заряженных тел,
движущихся заряженных частиц, а также
вокруг проводников, по которым текут
постоянные токи, возникает особого вида
поле, называемое магнитным полем.
• Таким образом, источниками магнитного
поля являются движущиеся электрические
заряды (следовательно, и проводники с
токами).
• Магнитное поле постоянных магнитов
также создается электрическими
микротоками, циркулирующими внутри
молекул вещества (гипотеза Ампера).
• Определение: Магнитное поле есть
особый вид материи, посредством
которого осуществляются силовые
воздействия на движущиеся
электрические заряды, находящиеся в
этом поле, и другие тела, обладающие
магнитным моментом.
• Для описания магнитного поля необходимо
ввести силовую характеристику поля,
аналогичную вектору напряженности
электрического поля. Такой
характеристикой является вектор
магнитной индукции B.
• За положительное направление вектора B
принимается направление от южного
полюса S к северному полюсу N магнитной
стрелки, свободно устанавливающейся в
магнитном поле.
• Таким образом, исследуя магнитное поле,
создаваемое током или постоянным
магнитом, с помощью маленькой
магнитной стрелки, можно в каждой точке
пространства определить направление
вектора B.
• Такое исследование позволяет представить
пространственную структуру магнитного
поля.
• Аналогично силовым линиям в
электростатике можно построить линии
магнитной индукции, в каждой точке
которых вектор B направлен по касательной
к ним.
• Линии магнитной индукции всегда
замкнуты, они нигде не обрываются.
Поэтому магнитное поле является
вихревым силовым полем.
• Для того чтобы количественно описать
магнитное поле, нужно указать способ
определения не только направления
вектора B, но и его модуля.
• Известно, что на заряд, движущийся в
магнитном поле, действует сила Лоренца,
численно равная:
• Здесь
q – величина заряда,
v – его скорость,
В – величина вектора магнитной индукции,
α – угол между векторами v и В.
• Направление силы Лоренца определяют по
правилу левой руки:
• Сила Лоренца (магнитная сила) всегда
перпендикулярна плоскости, в которой
лежат векторы v и В.
• Этим она отличается от электрической
силы, которая направлена так же, как
вектор Е.
• Из формулы Лоренца можно дать
определение магнитной индукции В:
• Вектор магнитной индукции численно
равен силе, действующей на единичный
положительный заряд, двигающийся с
единичной скоростью перпендикулярно
линиям магнитной индукции:
• Единицей магнитной индукции В является
тесла (Тл).
• Для характеристики магнитного поля
источника в любой среде используют
векторную физическую величину –
напряженность магнитного поля :
Н
В
0
• где μ – относительная магнитная
проницаемость среды, а μ0 – магнитная
постоянная, равная 12,57 ·10-7 Гн·м-1.
• Единица напряженности магнитного поля –
1 А·м-1.

65. Действие магнитного поля на проводник с током.

Закон Ампера.• А.М. Ампером было установлено силовое
воздействие магнитного поля на
прямолинейный участок проводника с
током I длиной l , расположенный в
однородном магнитном поле под углом к
магнитной индукции В .
• Сила, действующая в этом случае на
участок проводника со стороны магнитного
поля, вычисляется по формуле:
F IBl sin
• Из курса элементарной физики известно, что
направление действия силы F определяется по
правилу левой руки: если ладонь левой руки
расположить так, чтобы перпендикулярная к
проводнику составляющая вектора В входила в
ладонь, а четыре вытянутых пальца указывали
бы направление тока, то отогнутый на 900
большой палец укажет направление силы,
действующей со стороны поля на проводник с
током.
• Эта сила называется силой Ампера.
• Она достигает максимального по модулю
значения Fmax, когда проводник с током
ориентирован перпендикулярно линиям
магнитной индукции.
• Одним из важных примеров магнитного
взаимодействия является взаимодействие
параллельных токов.
• Закономерности этого явления были
экспериментально установлены Ампером.
• Если по двум параллельным проводникам
электрические токи текут в одну и ту же
сторону, то наблюдается взаимное
притяжение проводников.
• В случае, когда токи текут в противоположных
направлениях, проводники отталкиваются.
• Взаимодействие токов вызывается их
магнитными полями: магнитное поле одного
тока действует силой Ампера на другой ток и
наоборот.
• Опыты показали, что модуль силы,
действующей на отрезок длиной Δl
каждого из проводников, прямо
пропорционален силам тока I1 и I2 в
проводниках, длине отрезка Δl и обратно
пропорционален расстоянию R между
ними:
0 I1 I 2 l
F
2 R

73. Закон Био-Савара-Лапласа

• Позволяет вычислить напряженность
магнитного поля, создаваемого
постоянным током.
• Ж.Б. Био и Ф. Савар (1820 г.) установили
этот закон, экспериментально определяя
действие токов различной формы на
магнитную стрелку.
• П.С. Лаплас проанализировал полученные
данные и нашел, что напряженность
магнитного поля любого тока
складывается из напряженностей полей,
создаваемых его отдельными
элементами.
• Возьмем некоторый проводник с током I,
выделим элемент тока Idl, из которого
проведем радиус-вектор r в точку А.
• В точке А элемент тока создает магнитное
поле, напряженность которого dH
определяется законом Био-Савара-Лапласа:
• k – коэффициент пропорциональности,
зависящий от выбора единиц.
• В системе СИ
• k = 1/(4π), поэтому:
• Интегрируя эту формулу, находим
напряженность поля, создаваемого током
любой формы:
• Так, напряженность магнитного поля в
центре кругового тока:
• Напряженность магнитного поля,
созданного бесконечным прямолинейным
проводником с током в любой точке,
удаленной от проводника на расстояние b:
• Напряженность магнитного поля соленоида
(однородного):
• где N – число витков; l – длина соленоида.

82. Энергия магнитного поля

• Поскольку магнитное поле является
силовым полем, то оно обладает
определенной энергией.
• Объемная плотность энергии магнитного
поля вычисляется по формуле:

Практические задачи: решения для электрического потенциала

Практические задачи: решения для электрического потенциала  

1. (умеренная) Электрон движется вдоль электрического поля. Если начальный K для движения был больше нуля, опишите следующие параметры: ΔK, ΔU, ΔV, W _поле
Поскольку поле будет заставлять электрон двигаться в направлении, противоположном его движению, ΔK уменьшится, ΔU увеличится , ΔV будет уменьшаться (как в случае, когда любых частиц следует за полем), W _поле будет отрицательным.

2. (умеренно) Повторить вопрос №1 с протоном вместо электрона.
Поскольку поле заставит протон двигаться в том же направлении, что и движение, ΔK увеличится, ΔU уменьшится, ΔV уменьшится (как в случае , когда любая частица следует за полем), W _поле будет положительным.

3. (просто) Если 5 Кл заряда перемещаются через разность потенциалов +5 В, определите изменение потенциальной электрической энергии.
ΔV = ΔU/q
5 = ΔU/5
ΔU = 25 Дж

4. (легко) Отрицательно заряженная частица (q = -2 Кл) движется через 2000 v потери электрического потенциала. Будет ли потеря или прирост электрической потенциальной энергии? Будет ли потеря или прирост кинетической энергии? (Примечание: электрическая сила является консервативной силой.)
ΔV = ΔU/q
-2000 = ΔU/-2
ΔU = 4000 Дж
Происходит увеличение (прирост) электрической потенциальной энергии.
Так как сила консервативна:
ΔK = -ΔU = -4000 Дж
Происходит потеря кинетической энергии.

5. (умеренная) Отрицательный заряд движется в электрическом поле так, что замедляется, теряя 100 Дж кинетической энергии. Изменение электрического потенциала, испытываемого зарядом, составляет -10 вольт.
а. Какова величина отрицательного заряда?
ΔV = ΔU/q
-10 = 100/q
q = -10 C (величина 10 C)
b. Если положительный заряд, удвоенный по величине первым зарядом, перемещается между двумя одинаковыми точками поля, определяют изменение электрического потенциала и изменение электрической потенциальной энергии.
Все заряды, перемещающиеся между одними и теми же двумя точками в E-поле, испытывают одинаковое изменение электрического потенциала, которое в данном случае составляет -10 вольт.
ΔV = ΔU/q
-10 = ΔU/20
ΔU = -200 Дж
c. Будет ли положительный заряд в части b ускоряться или замедляться?
Поскольку положительный заряд теряет потенциальную энергию, он должен приобретать кинетическую энергию. Это ускорит.

6. Предположим, что показанный ниже центральный заряд покоится и останется в покое. Оцените сценарий, чтобы ответить на следующие вопросы:
а. В каком направлении будет двигаться пробный заряд?
Испытательный заряд будет двигаться в направлении силы, показанной ниже… к центральному заряду.
б. Тестовый заряд ускорится или замедлится?
Пробный заряд будет ускоряться под действием силы и ускоряться из состояния покоя.
с. Кинетическая энергия частицы увеличится или уменьшится?
Кинетическая энергия увеличится из-за увеличения скорости.
д. Увеличится или уменьшится электрическая потенциальная энергия?
Поскольку сила консервативна, электрическая потенциальная энергия уменьшится.
эл. Электрический потенциал увеличится или уменьшится?
Поскольку ΔU отрицательно, а q _o отрицательно, изменение электрического потенциала (ΔV) положительно, поскольку ΔV = ΔU/q _o.
Электрический потенциал уменьшается, когда заряд «следует за полем», и увеличивается, когда заряд движется «против поля». Эта идея верна как для положительных, так и для отрицательных зарядов.

7. (умеренное) Электрополе существует так, что его компоненты в направлениях x и z равны нулю, но компонент в направлении y равен 6,0 Н/Кл (однородное). Протон движется из начала координат в положение y = 10,0 м. Определите изменение электрического потенциала. Кроме того, найти изменение потенциала, если протон переместился из начала координат на x = 10,0 м.
Для движения по оси y:
ΔV = -Ed
ΔV = -(6,0)(10,0) = -60 v
Для движения по оси x:
ΔV = -Ed
ΔV = -(0)( 10.0) = 0 v

8. (умеренная) Заряженная частица движется прямолинейно в однородном Е-поле (Е = 50 В/м). Поле имеет то же направление, что и смещение. Найдите изменение электрического потенциала, если объект переместится с x = 5,0 м на x = 100,0 м. Зависит ли изменение потенциала от положительного или отрицательного характера заряда?
В случае однородного поля: ΔV = -Ed (где d — расстояние, пройденное вдоль поля)
ΔV = -50((100 — 5) = -4750 вольт
Изменение потенциала не зависит от знака заряда.

9. (умеренная) Заряженная частица (+2,2 пКл) движется вдоль оси x в E-поле (22 Н/м), которое также направлено вдоль оси x. Определить как изменение в электрическом потенциале и изменением электрической потенциальной энергии (в МэВ) для частицы, когда она претерпевает смещение от x = 2 м до x = 20 м. Будет ли эта частица ускоряться или замедляться? 
ΔV = -Ed
ΔV = -22(18) = -396 вольт
ΔU = qΔV
ΔU = 2,2×10 ^-12 (-396) = -8,71×10 ^{-10 909090 Дж (6×10 эВ/1. 19} Дж)= -5,4×10 ⁹ эВ = -5400 МэВ
Потеря U означает увеличение K. Скорость частицы увеличится.

Связь между электрическим полем и электрическим потенциалом: Разница

Сила, действующая на заряженные частицы, измеряется электрическим полем. Каждая заряженная частица имеет свое собственное электрическое поле, которое уменьшается по мере удаления частицы от точки, где измеряется сила. Электрический потенциал, с другой стороны, является измерением электрического поля частицы. С увеличением расстояния уменьшается и электрический потенциал. В этой статье мы обсудим связь между электрическим полем и электрическим потенциалом.

Что такое электрическое поле?

Электрический заряд создает электрическое поле, представляющее собой область пространства вокруг электрически заряженной частицы или объекта, испытывающего силу. Электрическое поле существует везде в пространстве и его можно наблюдать, вводя в него другой заряд. Однако, если заряды достаточно разделены, электрическое поле может быть приближено к нулю для практических целей.

Электрические поля — это векторные величины, которые можно представить в виде стрелок, указывающих на заряды и от них. Линии направлены либо наружу, в сторону от такого положительного заряда, либо радиально внутрь, в сторону отрицательного заряда.

Величина электрического поля определяется по формуле пробный заряд используется для ощущения электрического поля

Электрическое поле непрерывного распределения заряда также может быть рассчитано В этом случае для его расчета используется векторная сумма полей, создаваемых каждым электрическим зарядом Даже в этом случае, поскольку трудно вычислить, предпочтительнее использовать закон Гаусса 9.0005

Силу, которую электрическое поле пытается воздействовать на заряд-свидетель, расположенный в точке P, можно рассчитать, если известен вектор поля:

Что такое электрический потенциал?

Электрический потенциал — это измерение электрического поля, создаваемого при перемещении заряда из одного места в другое. Его также называют энергией или работой, затраченной на перемещение единицы заряда из бесконечности в точку, где ускорение частицы равно нулю. Уравнение для электрического потенциала выглядит следующим образом:

\(\mathrm{V}=\frac{W}{Q}\) или \(\mathrm{V}=\frac{Kq}{r}\)

Где,

В = электрический потенциал

Вт=совершенная работа

Q,q=заряд

r=расстояние

К=постоянная

Из формулы можно вывести единицу электрического потенциала как джоуль на кулон (Дж/Кл). Однако единицей электрического потенциала в системе СИ является вольт (В). Мы действительно могли бы определить электрический потенциал как энергию или работу, совершаемую на единицу заряда, исходя из единиц измерения.

Связь между электрическим полем и электрическим потенциалом

Электрическое поле и электрический потенциал являются важными понятиями электростатики. Электрическое поле или напряженность электрического поля, обозначаемая буквой E, представляет собой силу, испытываемую единичным положительным пробным зарядом. Работа, совершаемая для перемещения единичного заряда против электрического поля, обозначается V. Работа, совершаемая консервативными силами для перемещения единичного положительного заряда, обозначается V. Чтобы найти взаимосвязь между напряженностью электрического поля и электрическим полем, можно использовать простой вывод. потенциал. Мы будем использовать основные электростатические концепции, чтобы установить связь между электрическим полем и электрическим потенциалом.

Вывод

Рассмотрим две эквипотенциальные поверхности, разделенные расстоянием dx, где V представляет потенциал на поверхности 1, а \(\mathrm{V-dV}\) представляет потенциал на поверхности 2. Пусть E — электрическое поле, и пусть его направление перпендикулярно эквипотенциальным поверхностям.

Рассмотрим единичный положительный заряд +1C вблизи точки B; сила, воспринимаемая единичным положительным зарядом, определяется как:

Рассмотрим силу, испытываемую единичным положительным зарядом +1C вблизи точки B:

\(\mathrm{F}= {qE}\)……(1)

Предположим, что q= +1C, уравнение (1) принимает вид \(\mathrm{F} = \mathrm{E}\) ……….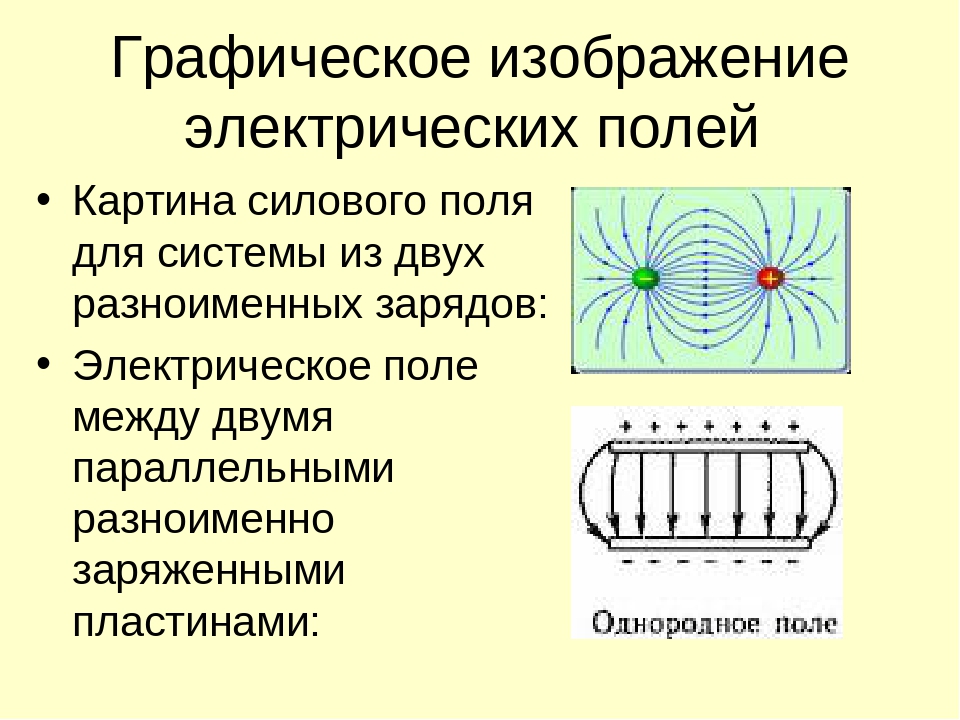 .(2)

Если мы продолжим перемещать заряд из точки B в точку A, работа, выполненная при перемещении заряда, определяется уравнениями ниже

\(\mathrm{W_{BA}} = \ mathrm{F\cdot dx }\)

\(\mathrm{W_{BA}} = \mathrm{F dx Cos\theta}\)…… (3)

Получаем \(\mathrm{W_{BA }} = \mathrm{E dx Cos\theta}\)……. (4) путем замены значения F в уравнении (3) на уравнение (2).

Поскольку сила действует вверх, а смещение направлено вниз, угол между силой и смещением составляет 180°.

В результате работа, выполненная при перемещении точечного заряда из точки B в точку A, определяется как: \(\mathrm{W_{BA}} = \mathrm{-E dx}\)…….(5)

Из определения электрического потенциала мы знаем, что это работа, совершаемая при перемещении точечного заряда из одной точки в другую, W_{BA}=\mathrm{V-(V-dV)}, поэтому мы имеем:

\ (\mathrm{VA-VB}= \mathrm{W_{BA}}\)

\(\mathrm{W_{BA}} =\mathrm{V- (V-dV)}=\mathrm{dV}\)……..(6) путем подстановки соответствующих значений потенциала в точках A и B

Объединение уравнений (5) и (6):

\(\mathrm{dV} = \mathrm{-E dx}\)

\(\mathrm{E}=\mathrm{-dV/dx} \)……. .(7)

В результате связь между полем и потенциалом такова, что электрическое поле, вызванное точечным зарядом, вызывает отрицательный градиент потенциала. Связь электрического поля и потенциала представлена ​​уравнением (7).

Дифференциальная форма зависимости между электрическим полем и разностью потенциалов задается уравнением (7), а интегральная форма задается формулой:

\(\int d V=-\int E \cdot d x\)

\(\Delta V= \mathrm {V_{A}}-\mathrm {V_{B}}= -\int E \cdot d x\)

Приведенное выше уравнение представляет соотношение между электрическим полем и электрическим потенциалом.

Случай 1: Если тестовый заряд положительный, градиент потенциала будет ближе к заряду из-за взаимосвязи между электрическим полем и электрическим потенциалом.

Случай 2: Если тестовый заряд отрицателен, градиент потенциала увеличивается по мере удаления от него.

Случай 3: Поскольку потенциал в каждой точке эквипотенциальной поверхности одинаков, градиент потенциала равен нулю. Линии электрического поля будут перпендикулярны электрическому потенциалу.

Разница между электрическим полем и электрическим потенциалом

Некоторые ключевые различия между электрическим полем и электрическим потенциалом перечислены ниже.

99209 NET0212

Параметры	Электрическое поле	Электрический потенциал
Количество доставленного заряда Определение.	Количество энергии, доставляемой на заряд
Величина	Векторная Количество	Скалярная Количество
UNITS
Измерение	Сила, с которой заряженные частицы действуют на окружающую среду.	Непрерывная мера электрического поля
Непрерывность	Не всегда непрерывна, но никогда не достигает бесконечности.	Непрерывный
Отношение к расстоянию	Уменьшается по мере увеличения расстояния	Уменьшается по мере увеличения квадрата расстояния

Вы можете посмотреть темы по физике. Установите приложение Testbook прямо сейчас, чтобы воспользоваться их исчерпывающими и надежными учебными материалами, а также помощью экспертов Testbook для успешной сдачи желаемого конкурсного экзамена. Воспользуйтесь невероятной экономией прямо сейчас, установив бесплатное приложение Testbook.

Связь между электрическим полем и электрическим потенциалом Часто задаваемые вопросы

Q.1 Какова формула электрического поля?

9{9}\mathrm{N}\).

Q.3 Какова единица измерения электрического поля в системе СИ?

Ответ 3 Единицей измерения электрического поля в СИ является ньютон на кулон (NC)

Q.4 В чем разница между электрическим полем и электрическим потенциалом?

Ответ 4 Основное различие между электрическим полем и электрическим потенциалом можно найти в их определениях.