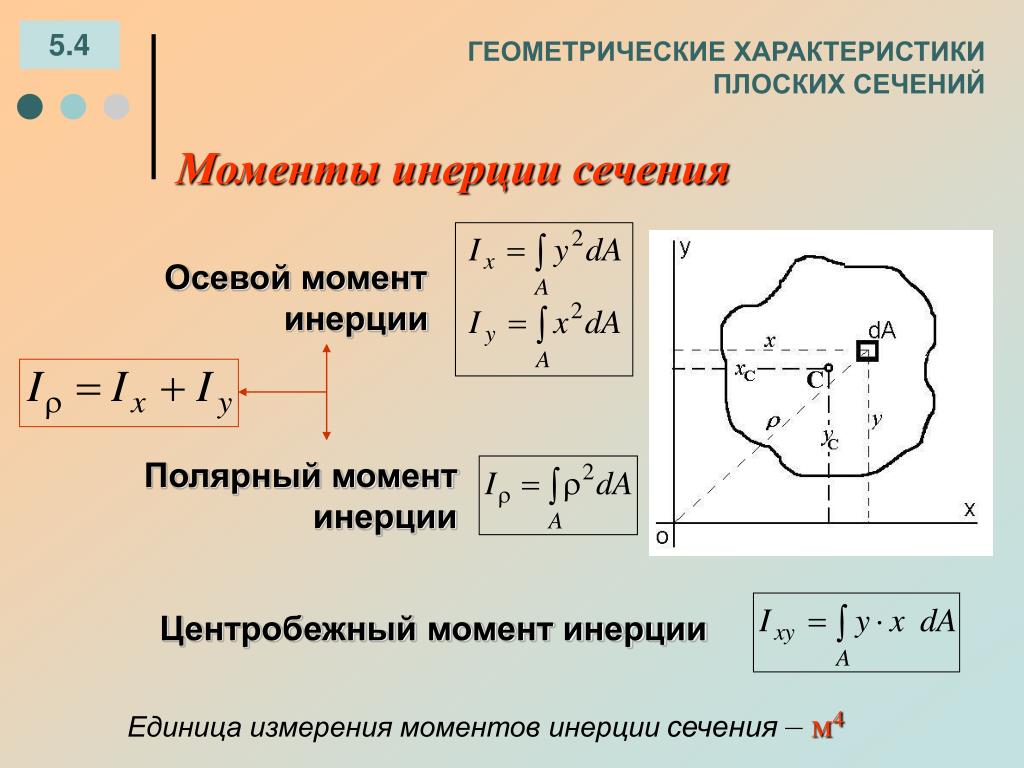
1.2. Осевые моменты инерции Jx ; Jy
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
(7)
(8)
Единица измерения [см4], [мм4].
Знак всегда «+».
Не бывает равным 0.
Свойство:Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.
Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.
Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения Jρ
Рис. 3
(9)
Взаимосвязь полярного и осевого моментов инерции:
(10)
(11)
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство:
при
повороте осей в любую сторону, один из
осевых моментов инерции возрастает, а
другой убывает (и наоборот).
1.4. Центробежный момент инерции сечения Jxy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
(12)
Единица измерения [см4], [мм4].
Знак «+» или «-».
, если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).
Таким образом для симметричных фигур центробежный момент инерции равен 0.
Координатные оси uиv, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называютсяглавными центральными осями инерции сечения.
У
сечений, не обладающих симметрией
относительно осей xилиy, например у
уголка,не будет равен нулю.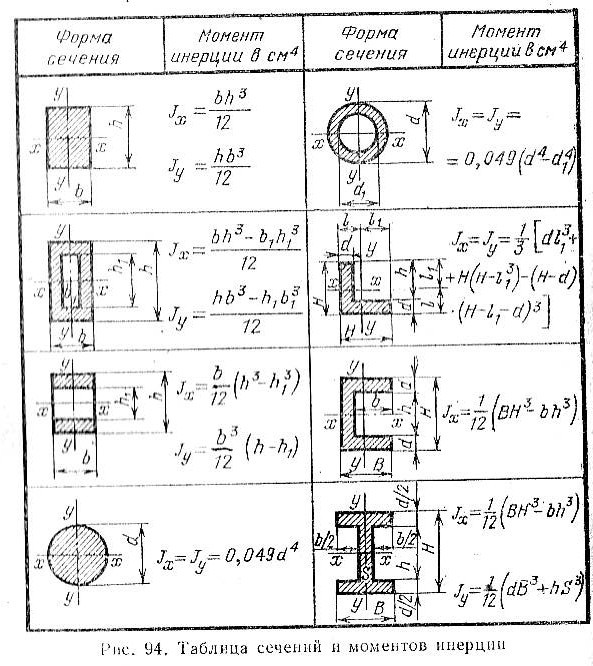 Для этих сечений
определяют положение осейuиvс помощью
вычисления угла поворота осейxиy
Для этих сечений
определяют положение осейuиvс помощью
вычисления угла поворота осейxиy
(13)
Центробежный момент относительно осей uиv—
Формула для определения осевых моментов инерции относительно главных центральных осей
(14)
где — осевые моменты инерции относительно центральных осей,
— центробежный момент инерции относительно центральных осей.
1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
Теорема Штейнера:
Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
(15)
Рис. 4
Доказательство теоремы Штейнера.
Согласно рис. 5 расстояние удо элементарной площадкиdF
Рис. 5
Подставляя значение ув формулу, получим:
 свойство статических
моментов площади сечения относительно
центральных осей).
свойство статических
моментов площади сечения относительно
центральных осей).Для прямоугольника высотой h и шириной b :
Осевой момент инерции:
Момент сопротивления изгибу:
момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
т.к. , то
Для круга:
Полярный момент инерции:
Осевой момент инерции:
Момент сопротивления кручению:
Т.к. , то
Момент сопротивления изгибу:
Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.
Рис. 6
Решение.
Разобьём площадь прямоугольника на
элементарные прямоугольники с размерами b(ширина) иdy(высота). Тогда площадь такого прямоугольника
(на рис. 6 заштрихована) равна dF=bdy. Вычислим значение осевого момента
инерции Jx
Вычислим значение осевого момента
инерции Jx
По аналогии запишем
— осевой момент инерции сечения относительно центральной
оси у
Центробежный момент инерции
, так как оси Сxи Сyявляются осями симметрии.
Пример 3. Определить полярный момент инерции круглого сечения.
Рис. 7
Решение. Разобьём круг на бесконечно тонкие кольца толщиной радиусом, площадь такого кольца. Подставляя значениев выражение для полярного момента инерции интегрируя, получим
Учитывая равенство осевых моментов круглого сечения и
, получаем
Осевые моменты инерции для кольца равны
с – отношение диаметра выреза к наружному диаметру вала.
Лекция №2 «Главные оси иглавные моментыинерции
Рассмотрим, как изменяются моменты
инерции при повороте координатных осей.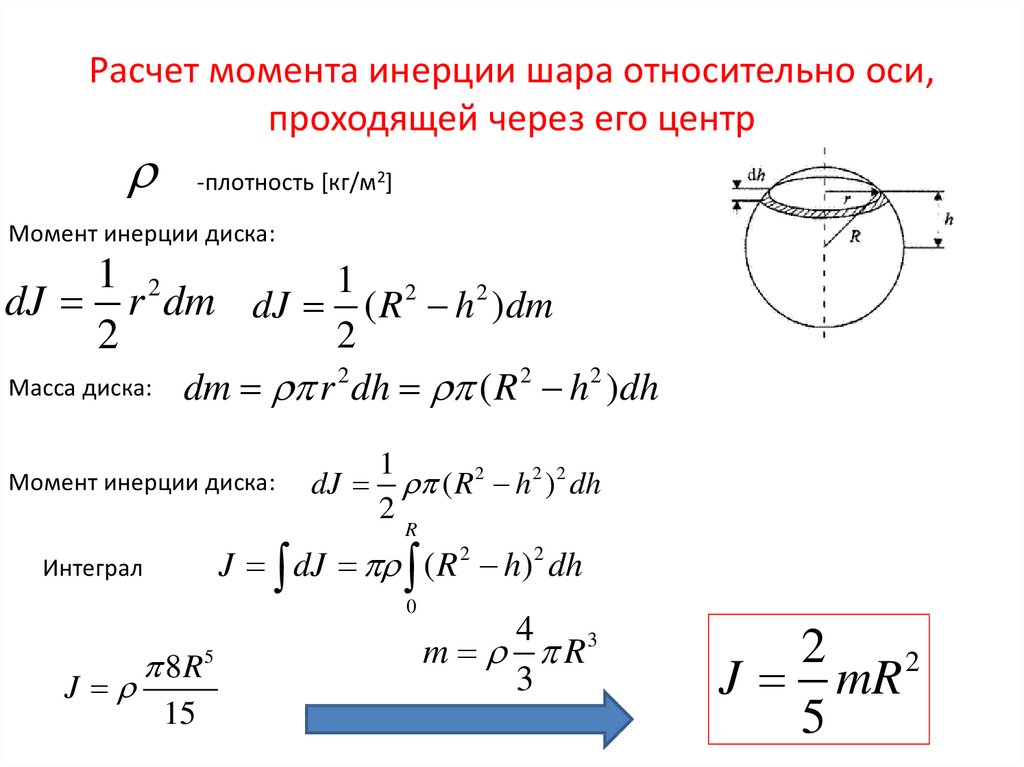 Положим, даны моменты инерции некоторого
сечения относительно осей 0х, 0у(не обязательно центральных)- ,-
осевые моменты инерции сечения. Требуется
определить,-
осевые моменты относительно осейu,v, повёрнутых
относительно первой системы на угол(рис. 8)
Положим, даны моменты инерции некоторого
сечения относительно осей 0х, 0у(не обязательно центральных)- ,-
осевые моменты инерции сечения. Требуется
определить,-
осевые моменты относительно осейu,v, повёрнутых
относительно первой системы на угол(рис. 8)
Рис. 8
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
(15)
Исключим uиvв выражениях моментов инерции:
Тогда
Откуда
(16)
(17)
(18)
Рассмотрим два первых уравнения. Складывая их почленно, получим
Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. Заметим при этом, что
Где — расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом
Где — уже знакомый нам полярный момент инерции:
Определим
осевой момент инерции круга относительно
диаметра.
Так как в силу симметрии но, как известно,
Следовательно, для круга
С изменением угла поворота осей значения моментов именяются, но сумма остается неизменной. Следовательно существует такое значение, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражениепо углуи приравнивая производную к нулю, находим
(19)
При этом значении угла один из осевых моментов будет наибольшим, а другой — наименьшим. Одновременно центробежный момент инерции
Оси,
относительно которых центробежный
момент инерции равен нулю, а осевые
моменты принимают экстремальные
значения, называются главнымиосями.Если они к тому же являются центральными
(точка начала координат совпадает с
центром тяжести сечения), то тогда они
называютсяглавными центральными
осями (u; v).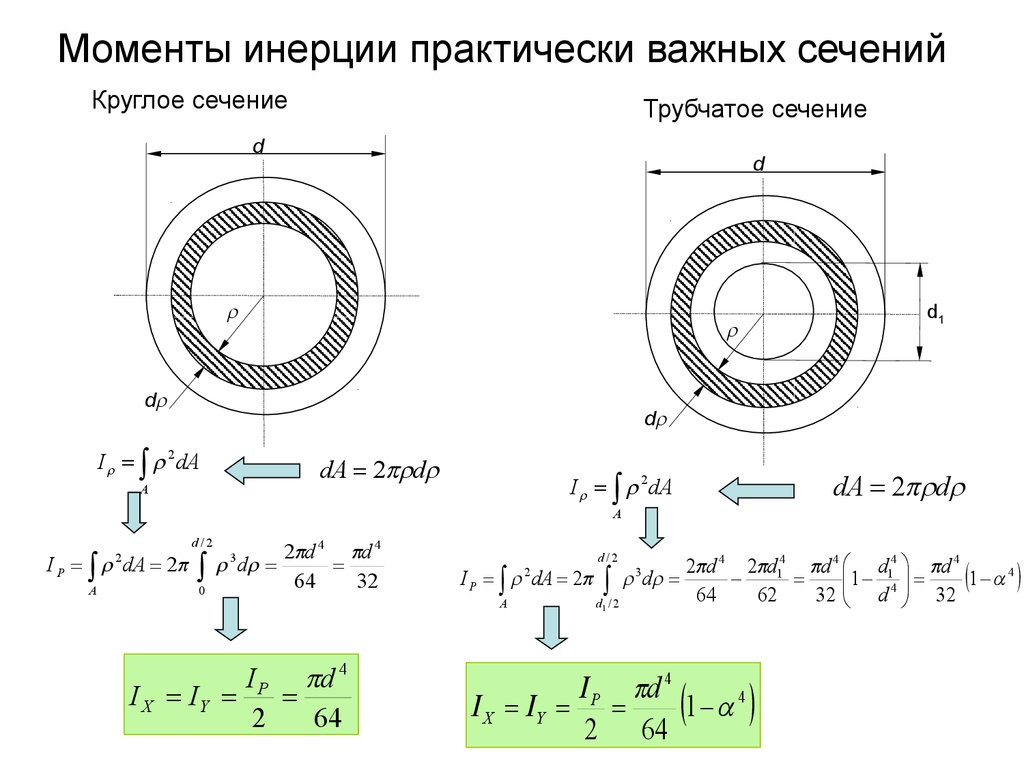 Осевые моменты инерции относительно
главных осей называются
Осевые моменты инерции относительно
главных осей называются
И их значение определяется по следующей формуле:
(20)
Знак плюс соответствует максимальному моменту инерции, знак минус — минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения.Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом инерции сечения относительно некоторой оси, например 0x,называется величина ,определяемая из равенства
(21)
F– площадь поперечного сечения,
— осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0
(22)
Радиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерциии определяются по формулам
(23)
Лекция
3. Кручение стержней круглого поперечного
сечения.
Кручение стержней круглого поперечного
сечения.
Осевой момент — инерция — Большая Энциклопедия Нефти и Газа, статья, страница 2
Cтраница 2
Осевые моменты инерции всегда положительны. [16]
Осевой момент инерции — величина всегда положительная и не равная нулю. [17]
Осевой момент инерции — величина всегда положительная и не равная пулю. [18]
Осевые моменты инерции всегда положительны и не могут быть равны нулю. [19]
Осевой момент инерции тем больше, чем дальше от центра тяжести отстоит ось, относительно которой его вычисляют. [20]
Осевые моменты инерции всегда положительны и отличны от нуля, если площадь сечения отлична от нуля. [21]
| Опыт, демонстрирующий изменение момента инерции тела при неизменной его. [22] |
Осевой момент инерции играет при вращателытом движении ту же роль, что и масса при поступательном ( в том числе и прямолинейном), и таким образом он является мерой инертности ( инерции) тела при вращательном движении. [23]
[23]
Осевые моменты инерции всегда положительны. [24]
Осевой момент инерции сложного сечения относительно некоторой оси равен сумме осевых моментов инерции составляющих его частей относительно этой же оси. [25]
Осевой момент инерции любого элемента сечения, а аначит и всего сечения в целом, есть величина существенно положительная независимо от положения элемента относительно оси, так как координата берется в квадрате. По этой же причине осевой момент инерции не может быть равен нулю. [26]
Осевой момент инерции любого элемента сечения, а значит и всего сечения в целом, есть величина существенно положительная независимо от положения элемента относительно оси, так как координата берется в квадрате. По этой же причине осевой момент инерции не может быть равен нулю. [27]
Осевые моменты инерции наружной рамки карданова подвеса относительно осей Оу, Ох и Ог0 обозначаем через А2, В2 и С2; моменты инерции внутренней рамки относительно осей Ох, Оу и Oz — через А, В, С, а моменты инерции платформы относительно осей О о, Оу и Ozj через А, В и С; моменты инерции гироскопов [ ( ротора и кожуха) относительно осей 0 z, 0& и O z — через Лт, АИ и Am соответственно. Оси наружной xy z внутренней xyz рамок карданова подвеса и оси Ох0у 0 платформы считаем главными осями инерции.
[28]
Оси наружной xy z внутренней xyz рамок карданова подвеса и оси Ох0у 0 платформы считаем главными осями инерции.
[28]
Осевые моменты инерции относительно главных центральных осей называют главными центральными ( или сокращенно главными) моментами инерции. [29]
Осевые моменты инерции относительно главных центральных осей называют главными центральными ( или сокращенно главными) моментами инерции. Относительно одной из главных осей момент инерции максимален, относительно другой — минимален. Конечно, говоря об экстремальности главных моментов инерции, имеется в виду лишь их сравнение с другими моментами инерции, вычисленными относительно осей, проходящих через ту же точку сечения. [30]
Страницы: 1 2 3
Расчет момента инерции площади › Gutekunst Formfedern GmbH
При расчете плоских пружин, фасонных пружин и плоских фасонных пружин помимо напряжения изгиба часто рассчитывается момент инерции площади. Момент инерции площади представляет собой геометрическую величину, используемую в теории прочности. Он используется для расчета деформаций и напряжений при изгибе и скручивании пружин и металлических фасонных деталей. Момент инерции площади получается из поперечного сечения фасонных металлических частей. Момент инерции площади указан в мм4. В зависимости от нагрузки можно выделить два различных типа площади момента инерции.
Момент инерции площади представляет собой геометрическую величину, используемую в теории прочности. Он используется для расчета деформаций и напряжений при изгибе и скручивании пружин и металлических фасонных деталей. Момент инерции площади получается из поперечного сечения фасонных металлических частей. Момент инерции площади указан в мм4. В зависимости от нагрузки можно выделить два различных типа площади момента инерции.
На следующих рисунках показаны симметричные и асимметричные поперечные сечения плоской пружины, фигурной пружины или плоской фигурной пружины, подвергающихся различным нагрузкам. На рисунках показаны зажатая с одной стороны плоская пружина (1 и 2 ) и нагружение фасонной пружины или металлической детали при изгибе (3 ).
Осевой поверхностный момент инерции
Осевой поверхностный момент инерции Ia описывает взаимосвязь между поперечным сечением плоской пружины и кривизной плоской пружины под нагрузкой.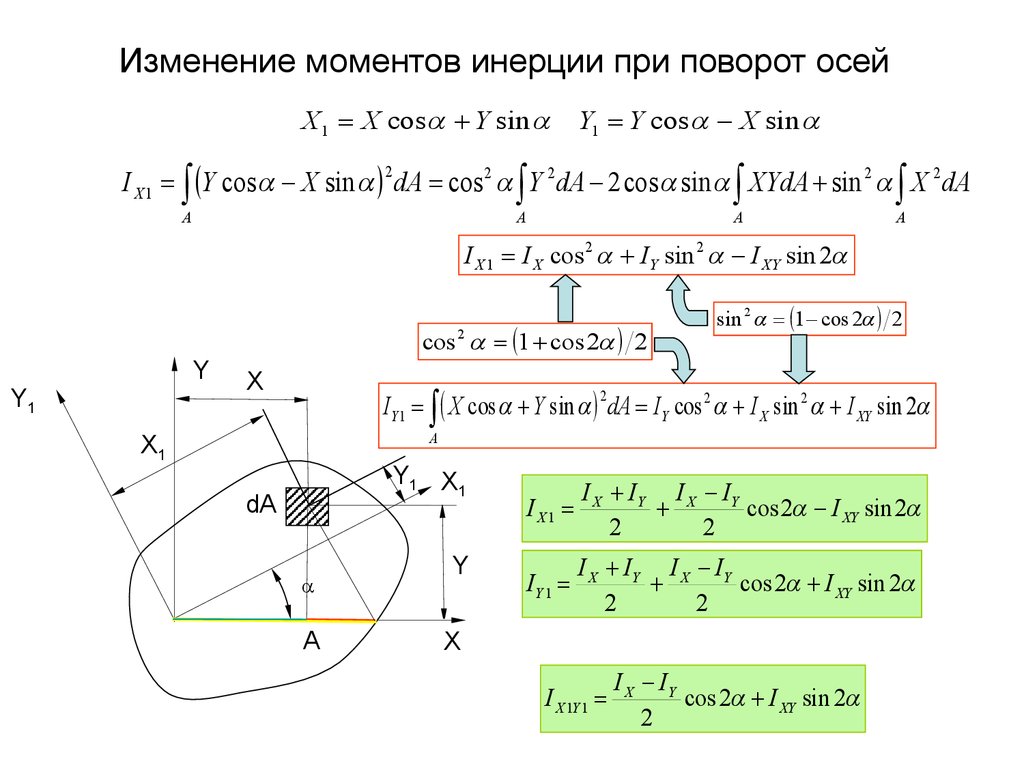 Применяется следующее: Чем больше Ia , тем меньше кривизна и внутренние напряжения, возникающие в поперечном сечении. Здесь важно расширение в направлении атакующих сил. На диаграмме показано, что вертикальная сила меньше изгибает плоскую пружину, когда она зажата на ребре вместо плоской (1 и 2 ). Осевой
Применяется следующее: Чем больше Ia , тем меньше кривизна и внутренние напряжения, возникающие в поперечном сечении. Здесь важно расширение в направлении атакующих сил. На диаграмме показано, что вертикальная сила меньше изгибает плоскую пружину, когда она зажата на ребре вместо плоской (1 и 2 ). Осевой
Момент инерции площади рассчитывается по следующим формулам:
- z = перпендикулярное расстояние оси Y к элементу dA
- y = расстояние перпендикулярно оси Z к элементу dA
Двухосный поверхностный момент инерции
Двухосный поверхностный момент инерции Iyz также называют поверхностным моментом отклонения или поверхностным центробежным моментом. Iyz используется для расчета деформаций и напряжений в нагруженных фасонных пружинах, плоских фасонных пружинах и несимметричных металлических фасонных деталях (3 ).
Эта величина также известна как отклонение или центробежный момент. Он равен нулю, если ось y или ось z является осью симметрии поперечного сечения.
Он равен нулю, если ось y или ось z является осью симметрии поперечного сечения.
Iyz = 0
Производные величиныИз поверхностного момента инерции можно получить различные другие величины, такие как модуль сечения и поверхностный радиус инерции.
Момент сопротивления
Модуль сопротивления используется в теории линейной упругости. Это определяет наибольшее напряжение, возникающее на краю поперечного сечения, механическое напряжение. Эта величина является отношением момента инерции площади к расстоянию от края до нейтрального волокна:
Радиус инерции площади
Для геометрически подобных компонентов, таких как прямоугольники с одинаковым отношением ширины к высоте, радиус инерции поверхности также может быть определен с помощью размерной длины. Это позволяет сравнивать тела, сходные по прогибу и жесткости. Радиус инерции поверхности включен в коэффициент гибкости.
См. здесь дополнительную информацию о расчете плоских, фигурных и плоских пружин. Если вы ищете техническую пружину для своего специального применения, просто отправьте нам необходимые данные пружины с подробным описанием требуемого количества и чертежом или данными САПР с помощью следующей кнопки запроса «Запрос пружины» или по электронной почте info@gutekunst-formfedern .де. Мы подготовим для вас необязывающее предложение в кратчайшие сроки.
здесь дополнительную информацию о расчете плоских, фигурных и плоских пружин. Если вы ищете техническую пружину для своего специального применения, просто отправьте нам необходимые данные пружины с подробным описанием требуемого количества и чертежом или данными САПР с помощью следующей кнопки запроса «Запрос пружины» или по электронной почте info@gutekunst-formfedern .де. Мы подготовим для вас необязывающее предложение в кратчайшие сроки.
Федернанфраге
Для получения дополнительной информации:
- Фасонные, плоские и пластинчатые пружины
- Диаграмма деформации пружинная сталь
- Расчет плоской пружины
- Плоская пружина
- Радиус изгиба при обработке металлов давлением
- Важно при формовании листа из пружинной стали
Расчет момента инерции площади
Tagged on: Момент инерции площади Напряжение изгиба Расчет деформации Плоские рессоры Плоские рессоры Листовые рессоры Нагрузка Момент сопротивления Фасонные пружины Расчет напряжения Напряжение кручения о различии основных направлений
Скачать PDF
- Оригинал
- Открытый доступ
- Опубликовано:
- Владо А. Лубарда 1 и
- Юцзя Лю 1
Архив прикладной механики том 81 , страницы 111–122 (2011 г.)Процитировать эту статью
665 доступов
2 Цитаты
Сведения о показателях
Abstract
Три широко используемых метода для определения главных моментов инерции плоской области и их направлений основаны на: (i) условии стационарности осевого момента инерции, (ii) анализе собственных значений и (iii) Круг Мора. В этой статье мы приводим два новых вывода, которые основаны на: (а) свойствах диагонализации матриц и инвариантных тензоров и (б) свойстве сопряженности векторов моментов инерции. Получено новое общее выражение, задающее главные направления инерции, а также направления максимального и минимального произведения инерции. Дано сравнительное исследование пяти представленных подходов, представляющее интерес как с концептуальной, так и с методологической точек зрения. Дана также связь между девиаторной частью тензора момента инерции и окружностью инерции Ланда. Представленный анализ применим к любому симметричному тензору второго порядка два на два.
В этой статье мы приводим два новых вывода, которые основаны на: (а) свойствах диагонализации матриц и инвариантных тензоров и (б) свойстве сопряженности векторов моментов инерции. Получено новое общее выражение, задающее главные направления инерции, а также направления максимального и минимального произведения инерции. Дано сравнительное исследование пяти представленных подходов, представляющее интерес как с концептуальной, так и с методологической точек зрения. Дана также связь между девиаторной частью тензора момента инерции и окружностью инерции Ланда. Представленный анализ применим к любому симметричному тензору второго порядка два на два.
Скачайте, чтобы прочитать полный текст статьи
Ссылки
Торнтон С.Т., Марион Дж.Б.: Классическая динамика частиц и систем, 5-е изд. Brooks/Cole-Thomson Learning, Belmont (2004)
Google ученый
Барбер Дж.
 Р.: Промежуточная механика материалов. Макгроу-Хилл, Нью-Йорк (2001)
Р.: Промежуточная механика материалов. Макгроу-Хилл, Нью-Йорк (2001)Google ученый
Угурал А.С.: Механика материалов. Джон Уайли, Нью-Йорк (2008)
Google ученый
Хирн Э.Дж.: Механика материалов, 2-е изд. Pergamon Press, Оксфорд (1985)
МАТЕМАТИКА Google ученый
Голуб Г.Х., Ван Лоан К.Ф.: Матричные вычисления, 3-е изд. Издательство Университета Джона Хопкинса, Балтимор (1996)
МАТЕМАТИКА Google ученый
Борези А.П., Шмидт Р.Дж.: Усовершенствованная механика материалов, 6-е изд. Джон-Вили, Нью-Йорк (2003)
Google ученый
Бир Ф.П., Джонстон Э.Р., ДеВольф Дж.Т., Мазурек Д.Ф.: Механика материалов, 5-е изд.
 Макгроу-Хилл, Нью-Йорк (2009)
Макгроу-Хилл, Нью-Йорк (2009)Google ученый
Гир Дж. М., Гудно Б. Дж.: Механика материалов, 7-е изд. Cengage Learning, Торонто (2009 г.))
Google ученый
Крейг Р.Р.: Механика материалов, 2-е изд. Джон Уайли, Нью-Йорк (2000)
Google ученый
Кук Р.Д., Янг В.К.: Передовая механика материалов, 2-е изд. Прентис-холл, река Аппер-Сэдл (1999)
Google ученый
Вейбл М.: Промежуточная механика материалов. Издательство Оксфордского университета, Нью-Йорк (2008)
Google ученый
Леон С.Дж.: Линейная алгебра с приложениями, 6-е изд. Прентис-холл, река Аппер-Сэдл (2002 г.)
Google ученый
Странг Г.
 : Введение в линейную алгебру, 3-е изд. Wellesley-Cambridge Press, Wellesley (2003)
: Введение в линейную алгебру, 3-е изд. Wellesley-Cambridge Press, Wellesley (2003)Google ученый
Малверн Л.Э.: Введение в механику сплошной среды. Прентис-холл, река Аппер-Сэдл (1969)
Google ученый
Друкер Д.К.: Введение в механику деформируемых твердых тел. Макгроу-Хилл, Нью-Йорк (1967)
Google ученый
Теодореску П.П.: Механические системы, классические модели (Том 1, Механика частиц). Спрингер, Берлин (2007)
МАТЕМАТИКА Google ученый
Скачать ссылки
Благодарности
Благодарим за поддержку исследований Черногорской академии наук и искусств.
Открытый доступ
Эта статья распространяется в соответствии с условиями некоммерческой лицензии Creative Commons Attribution, которая разрешает любое некоммерческое использование, распространение и воспроизведение на любом носителе при условии указания автора(ов) и источника.
Информация об авторе
Авторы и организации
Факультет машиностроения и аэрокосмической техники, Калифорнийский университет, Сан-Диего, Ла-Хойя, Калифорния, 92093-0411, США
Владо А. Лубарда и Юджиа Лю
Авторы
- Владо А. Лубарда2 Посмотреть публикацию автора 9000s
Вы также можете искать этого автора в PubMed Google Scholar
- Yujia Liu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
Автор, ответственный за переписку
Владо А. Лубарда.
Права и разрешения
Открытый доступ Это статья в открытом доступе, распространяемая в соответствии с условиями некоммерческой лицензии Creative Commons Attribution (https://creativecommons.org/licenses/by-nc/2.0), которая разрешает любые некоммерческие использование, распространение и воспроизведение на любом носителе при условии указания автора(ов) и источника.


 Р.: Промежуточная механика материалов. Макгроу-Хилл, Нью-Йорк (2001)
Р.: Промежуточная механика материалов. Макгроу-Хилл, Нью-Йорк (2001) Макгроу-Хилл, Нью-Йорк (2009)
Макгроу-Хилл, Нью-Йорк (2009)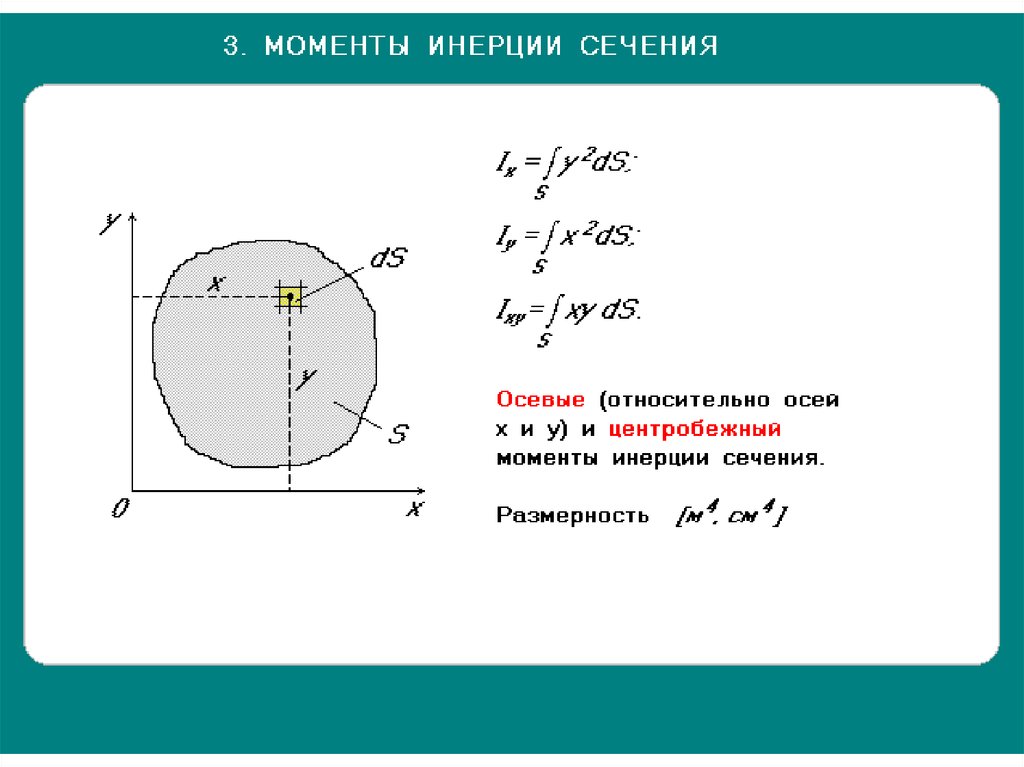 : Введение в линейную алгебру, 3-е изд. Wellesley-Cambridge Press, Wellesley (2003)
: Введение в линейную алгебру, 3-е изд. Wellesley-Cambridge Press, Wellesley (2003)