6.2. Осевой момент инерции сечения
Осевым моментом инерции плоского сечения относительно какой-либо оси, лежащей в той же плоскости, называется сумма произведений элементарных площадок dFна квадраты их расстояний до данной оси.
(6.5)
,
.
6.3. Полярный момент инерции сечения
Полярным моментом инерции плоского сечения относительно какого-либо полюсао (рис. 6.1), лежащего в плоскости сечения, называется сумма произведений элементарных площадокdFна квадраты их расстоянийдо полюса:
,
а так как , то
.
(6.6)
Таким образом, сумма осевых моментов
инерции сечения относительно
двух взаимно перпендикулярных осей
равна полярному моменту инерции
относительно точки пересечения указанных
осей.
6.4. Центробежный момент инерции сечения
(6.7)
Центробежным моментом инерции плоского сечения относительно осейzиyназывается сумма произведений элементарных площадокdFна их координатыzиy.
,
.
Рассмотрим фигуру, симметричную относительно одной или нескольких осей (рис. 6.3).
,
,
,
Рис. 2.3
.
Таким образом, центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.
6.5. Вычисление моментов инерции сечений простой формы
6.5.1. Прямоугольное сечение
1. Осевой момент инерции прямоугольника.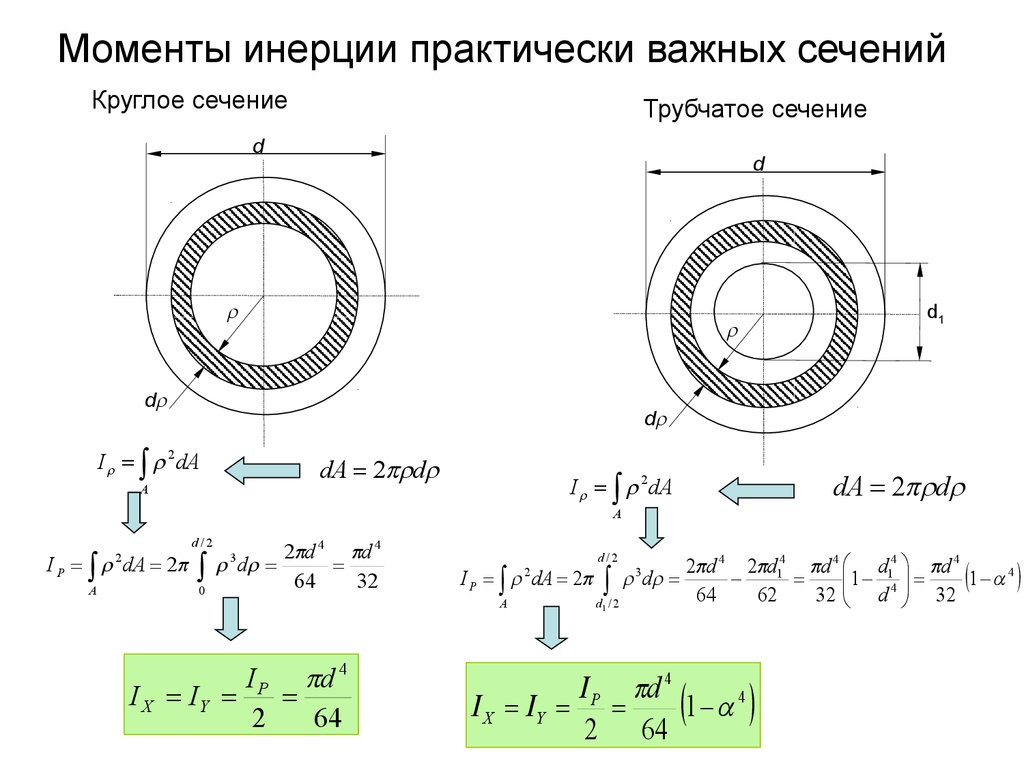
Разбив прямоугольник с основанием bи высотойhна бесконечно узкие горизонтальные полоски, возьмем одну из них на расстоянииyот осиz(рис. 6.4,а). Ширина этой полоскиb, высотаdy. Момент инерции ее относительно оси
.
Момент инерции прямоугольника
,
окончательно
(6.8)
.
Очевидно, что момент инерции прямоугольника относительно оси y
(6.9)
.
Приняв b=h=a, получим формулу для определения момента инерции квадратного сечения со сторонойa:
.
2. Центробежный момент инерции прямоугольника.
Выделим элементарную площадку dF =(рис. 6.4,б).
Вначале вычислим центробежный момент инерции не всего прямоугольника, а лишь вертикальной полоски высотой
(6. 10)
10)
.
а) б)
Рис. 6.4
В выражении (6.10) вынесено за знак интеграла, так как для всех площадок, принадлежащих рассматриваемой вертикальной полоске, оно постоянно.
.
(6.11)
Проинтегрируем в пределах отдо
;
.
(6.12)
Формула (6.12) справедлива для прямоугольника, расположенного в первом или третьем квадрантах, где координатыy иzодного знака. Для прямоугольника, расположенного во втором и четвертом квадрантах, где координатыy иzразного знака:
(6.13)
.
Центробежные моменты инерции
,
так
как оси
ипроходят через центр тяжести сечения.
6.5.2. Треугольное сечение
,,
,.
Рис. 6.5
;
.
(6.14)
6.5.3. Сечение в форме круга
1. Полярный момент инерции круга (рис. 6.6).
;
;
(6.15)
,
где — диаметр круга.
Рис. 6.6
2. Осевой момент инерции круга.
Ввиду симметрии круга относительно
любого диаметра (рис. 6.6) осевые
моменты инерции относительно любых
осей, проходящих через центр круга,
равны между собой. Поэтому
,
а так как,
то величина осевого момента инерции
площади круга относительно любой
оси, проходящей через центр круга, равна
половине полярного момента инерции,
т.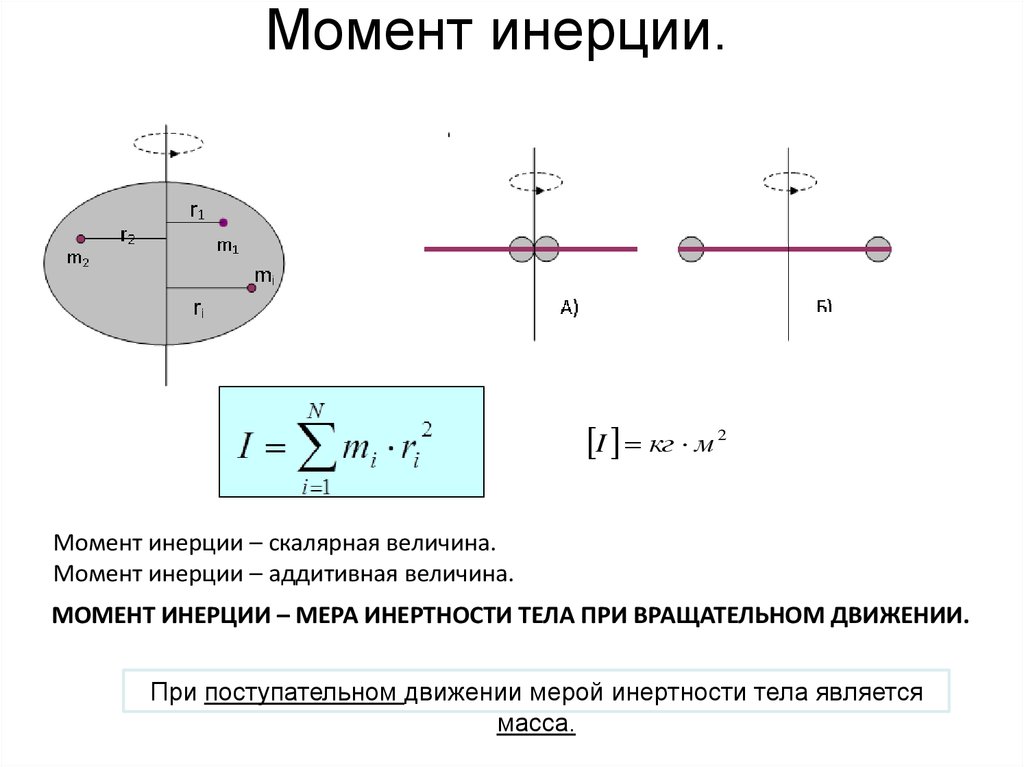
(6.16)
.
3. Осевой момент инерции кругового кольца.
Это разность осевых моментов инерции большого круга диаметром Dи малого круга диаметромd.
;
(6.17)
.
Сопротивление материалов
Сопротивление материалов
ОглавлениеПРЕДИСЛОВИЕГлава 1.  § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.2. ПРОДОЛЬНАЯ СИЛА § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4. 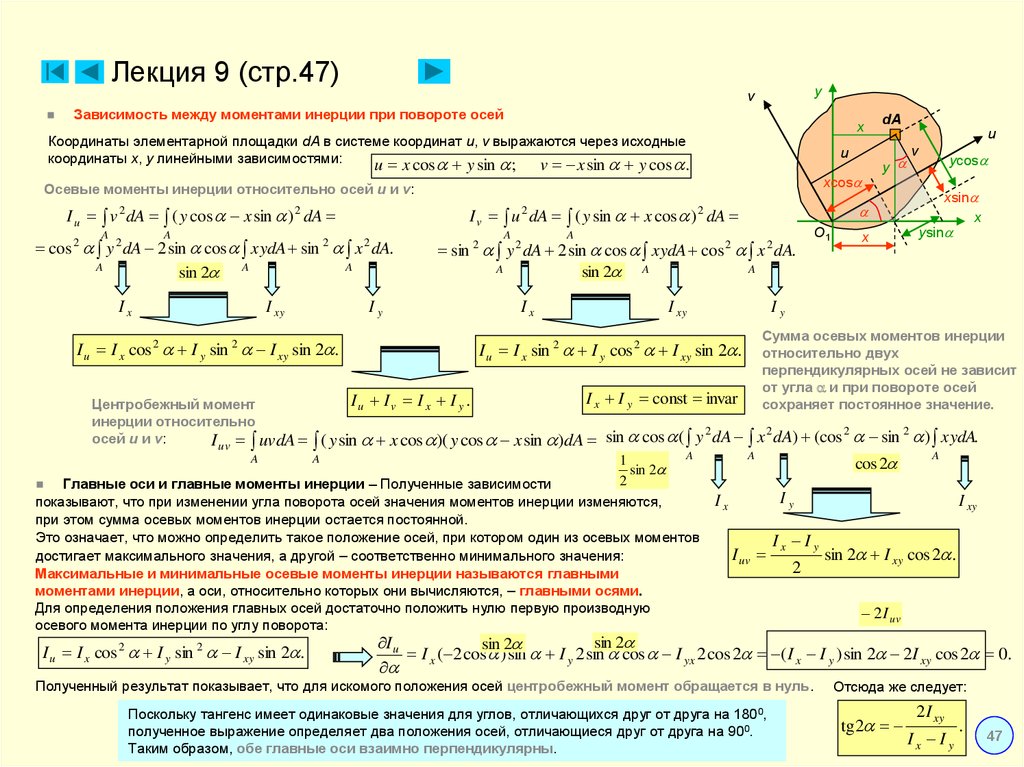 3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ 3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ§ 5.3. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ С ПОМОЩЬЮ КРУГА МОРА § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4. СДВИГ § 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» § 4.4. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НЕКОТОРЫХ ПРОСТЕЙШИХ КОНСТРУКЦИЙ, РАБОТАЮЩИХ НА СДВИГ Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ  5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ 5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ§ 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА § 9.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ СЕЧЕНИЙ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 6. КРУЧЕНИЕ § 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 7.6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.  7. ВНУТРЕННИЕ УСИЛИЯ 7. ВНУТРЕННИЕ УСИЛИЯ§ 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.7. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8.  ТЕОРИИ ПРОЧНОСТИ ТЕОРИИ ПРОЧНОСТИ§ 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 2.8. ТЕОРИЯ ПРОЧНОСТИ МОРА § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.9. ЯДРО СЕЧЕНИЯ § 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11.  ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ§ 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ § 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 2.13. ПРОДОЛЬНЫЙ ИЗГИБ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4. 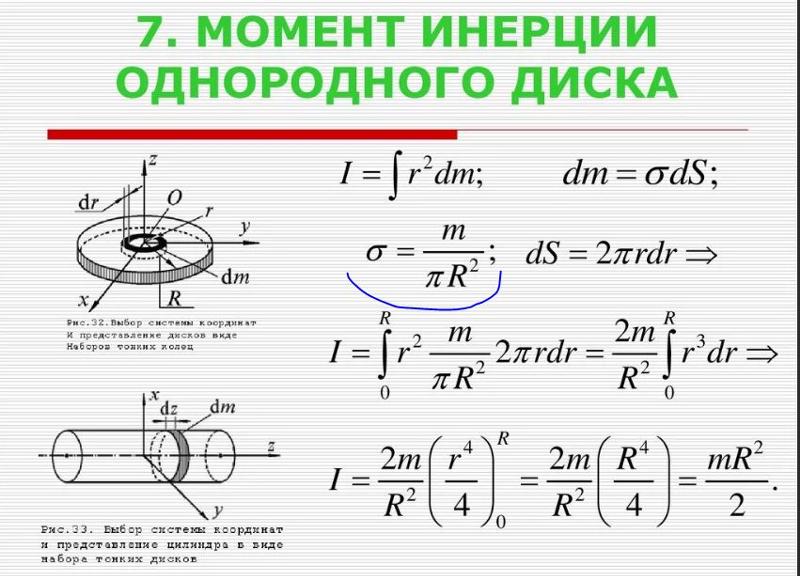 13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ 13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ§ 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15. НАПРЯЖЕНИЯ, ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ § 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2.  16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ 16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВПримеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 3.17. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки ПРИЛОЖЕНИЯ |
ОСЕВОЙ МОМЕНТ ИНЕРЦИИ
Для любого объекта, вращающегося вокруг оси, сумма масс его компонентов, умноженная на квадрат расстояния до оси.
осевой_момент_инерции квадрат расстояние компонент
PSIDДифференциал фунта на квадратный дюйм. фунтов на квадратный дюйм квадрат |
МОМЕНТ ИНЕРЦИИВеличина, полученная путем умножения массы каждой маленькой части тела на квадрат ее расстояния от оси и сложения всех результатов. момент_инерции расстояние масса квадрат |
ВОЗДУХООТВОДУстройство, обеспечивающее движение воздуха между атмосферой и компонентом, в котором оно установлено. воздух_бризер устройство воздух атмосфера компонент движение |
ЧАСОВОЙ УГОЛ ПО ГРИНВИЧУУгловое расстояние к западу от Гринвичского небесного меридиана; дуга небесного экватора или угол на небесном полюсе между верхней ветвью Гринвичского небесного меридиана и часовым кругом точки на небесной сфере, измеренный на запад от Гринвичского небесного меридиана через greenwich_hour_angle расстояние круг угол угловатый угловое_расстояние дуга ветвь небесный небесный_меридиан час_круг запад |
БРЕВНО ДЛЯ ГАРПУНА Бревно, состоящее из поворотного устройства и устройства регистрации расстояния, объединенных в единое целое, которое буксируется по воде. гарпун_журнал устройство расстояние бревно регистрация гаксель taffrail_log |
фунт/кв. дюйм изб.фунта на квадратный дюйм (PSIA — 14,696). фунт/кв. дюйм изб. квадрат |
СКОРОСТЬ СДВИГА Разность скоростей вдоль параллельных граней элемента жидкости, деленная на расстояние между гранями. скорость_сдвига жидкость разница расстояние элемент параллель |
ФИЛЬТР СТРУЖКООБРАЗОВАНИЯФильтр, предназначенный для предотвращения попадания только крупных частиц в компонент, расположенный непосредственно за ним. Также известен как фильтр контроля зернистости, фильтр последнего шанса chip_control_filter grit_control_filter last_chance_filter контроль фильтр частицы компонент вход зернистость |
ВЫСОТА ПРИЛИВА Расстояние по вертикали от точки отсчета карты до поверхности воды на любой стадии прилива. высота_прилива вода поверхность диаграмма уровень воды расстояние уровень датум рост вертикальный chart_sounding_datum высокий высокий уровень воды этап |
ЧАСОВОЙ УГОЛУгловое расстояние к западу от небесного меридиана или часового круга; дуга небесного экватора или угол на небесном полюсе между верхней ветвью небесного меридиана или часового круга и часовым кругом hour_angle расстояние круг угол угловатый угловое_расстояние дуга ветвь небесный небесный_меридиан час_круг меридиан запад |
Вопросы по теме
Полярный момент инерции | Энциклопедия MDPI
Полярный момент (инерции), также известный как второй (полярный) момент площади, представляет собой величину, используемую для описания сопротивления деформациям при кручении (прогибу) в цилиндрических (или нецилиндрических) объектах (или сегментах объект) с неизменным поперечным сечением и без существенного искривления или деформации вне плоскости.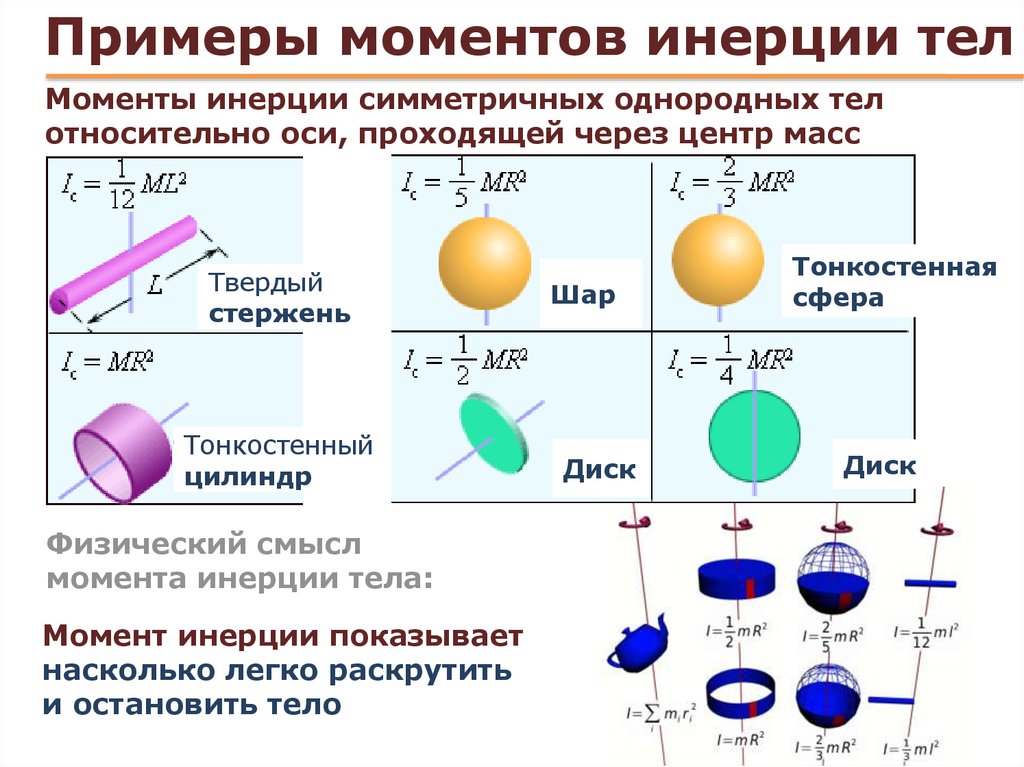 Это составляющая второго момента площади, связанная теоремой о перпендикулярной оси. В то время как плоский второй момент площади описывает сопротивление объекта отклонению (изгибу) при воздействии силы, приложенной к плоскости, параллельной центральной оси, полярный второй момент площади описывает сопротивление объекта отклонению при воздействии момента, приложенного в плоскость, перпендикулярная центральной оси объекта (т.е. параллельная поперечному сечению). Аналогично плоскому секундному моменту вычисления площади ([math]\displaystyle{ I_x }[/math],[math]\displaystyle{ I_y }[/math] и [math]\displaystyle{ I_{xy} }[/math ]), полярный второй момент площади часто обозначается как [math]\displaystyle{ I_z }[/math]. Хотя в некоторых инженерных учебниках и академических публикациях оно также обозначается как [math]\displaystyle{ J }[/math] или [math]\displaystyle{ J_z }[/math], этому обозначению следует уделить особое внимание, чтобы оно не стало путают с константой кручения, [math]\displaystyle{ J_t }[/math], используемой для нецилиндрических объектов.
Это составляющая второго момента площади, связанная теоремой о перпендикулярной оси. В то время как плоский второй момент площади описывает сопротивление объекта отклонению (изгибу) при воздействии силы, приложенной к плоскости, параллельной центральной оси, полярный второй момент площади описывает сопротивление объекта отклонению при воздействии момента, приложенного в плоскость, перпендикулярная центральной оси объекта (т.е. параллельная поперечному сечению). Аналогично плоскому секундному моменту вычисления площади ([math]\displaystyle{ I_x }[/math],[math]\displaystyle{ I_y }[/math] и [math]\displaystyle{ I_{xy} }[/math ]), полярный второй момент площади часто обозначается как [math]\displaystyle{ I_z }[/math]. Хотя в некоторых инженерных учебниках и академических публикациях оно также обозначается как [math]\displaystyle{ J }[/math] или [math]\displaystyle{ J_z }[/math], этому обозначению следует уделить особое внимание, чтобы оно не стало путают с константой кручения, [math]\displaystyle{ J_t }[/math], используемой для нецилиндрических объектов. Проще говоря, полярный момент инерции — это сопротивление вала или балки искажению при кручении в зависимости от их формы. Жесткость исходит только от площади поперечного сечения объекта и не зависит от состава его материала или модуля сдвига. Чем больше величина полярного момента инерции, тем больше сопротивление тела кручению.
Проще говоря, полярный момент инерции — это сопротивление вала или балки искажению при кручении в зависимости от их формы. Жесткость исходит только от площади поперечного сечения объекта и не зависит от состава его материала или модуля сдвига. Чем больше величина полярного момента инерции, тем больше сопротивление тела кручению.
1. Определение
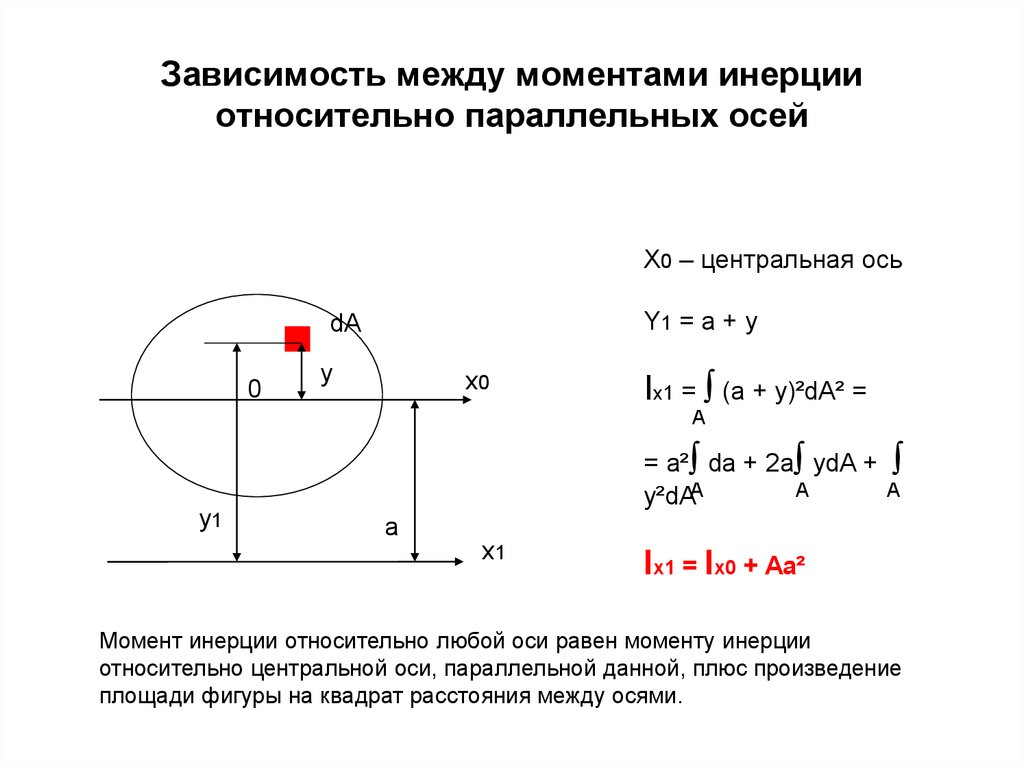
Схема, показывающая, как вычисляется полярный момент инерции для произвольной формы относительно оси [math]\displaystyle{ O }[/math]. Где [math]\displaystyle{ \rho }[/math] — радиальное расстояние до элемента [math]\displaystyle{ dA }[/math].
Примечание: Хотя термин моменты инерции используется для описания полярных и плоских секундных моментов площади, это в первую очередь конструкция инженерных полей. Срок момент инерции , в области физики и математики, является строго вторым моментом массы, используемым для описания сопротивления массивного объекта вращательному движению, а не его сопротивления деформации кручения. В то время как полярные и плоские секундные моменты площади интегрируются по всем бесконечно малым элементам данной площади в некотором двумерном поперечном сечении, полярные и плоские секундные моменты массы (по инерции) интегрируются по всем бесконечно малым элементам массы в трехмерном пространстве, занимаемом объектом. Проще говоря, полярный и плоский секундный моменты площади являются показателем жесткости, а момент инерции (секундный момент массы ) является сопротивлением вращательному движению массивного объекта.
В то время как полярные и плоские секундные моменты площади интегрируются по всем бесконечно малым элементам данной площади в некотором двумерном поперечном сечении, полярные и плоские секундные моменты массы (по инерции) интегрируются по всем бесконечно малым элементам массы в трехмерном пространстве, занимаемом объектом. Проще говоря, полярный и плоский секундный моменты площади являются показателем жесткости, а момент инерции (секундный момент массы ) является сопротивлением вращательному движению массивного объекта.
Уравнение, описывающее полярный момент площади, представляет собой кратный интеграл по площади поперечного сечения [math]\displaystyle{ A }[/math] объекта. 92 dx \, dy }[/math]
Показано, что полярный момент площади может быть описан как сумма [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y } [/math] плоских моментов площади, [math]\displaystyle{ I_x}[/math] и [math]\displaystyle{ I_y}[/math] [math]\displaystyle{ \therefore J = I_z = I_x + I_y }[/math]
Это также показано в теореме о перпендикулярной оси. [1] Для объектов, обладающих вращательной симметрией, [2] , таких как цилиндр или полая труба, уравнение можно упростить до: [math]\displaystyle{ J = 2I_x}[/math] или [math] \displaystyle{ J = 2I_y }[/math] 94}{2} }[/math]
[1] Для объектов, обладающих вращательной симметрией, [2] , таких как цилиндр или полая труба, уравнение можно упростить до: [math]\displaystyle{ J = 2I_x}[/math] или [math] \displaystyle{ J = 2I_y }[/math] 94}{2} }[/math]
2. Единица измерения
Единицей СИ для полярного момента инерции , как и для площади момента инерции , являются метры в четвертой степени ( м 4 ) и дюймов в четвертой степени ( в 4 ) в единицах измерения США и имперских единицах.
3. Ограничения
Полярный момент инерции недостаточен для использования при расчете балок и валов с некруглым поперечным сечением из-за их склонности к короблению при скручивании, вызывая неплоские деформации. В таких случаях следует заменить постоянную кручения, если включена соответствующая постоянная деформации для компенсации эффекта коробления. В рамках этого есть статьи, которые различают полярный момент инерции , [math]\displaystyle{ I_z }[/math] и постоянная кручения , [math]\displaystyle{ J_t }[/math], больше не используется [math]\displaystyle{ J }[/math] для описания полярного момента инерции. [3]
[3]
Для объектов со значительной вариацией поперечного сечения (вдоль оси приложенного крутящего момента), которые невозможно проанализировать по сегментам, возможно, придется использовать более сложный подход. См. 3-D эластичность.
4. Заявка
Хотя полярный момент инерции чаще всего используется для расчета углового смещения объекта, подверженного действию момента (крутящего момента), приложенного параллельно поперечному сечению, предоставленное значение жесткости не имеет никакого отношения к сопротивлению скручиванию, обеспечиваемому объект как функция составляющих его материалов. Жесткость, обеспечиваемая материалом объекта, является характеристикой его модуля сдвига, [math]\displaystyle{ G }[/math]. Объединив эти две функции с длиной вала, [math]\displaystyle{ L }[/math], можно рассчитать угловое отклонение вала, [math]\displaystyle{ \theta }[/math], из-за приложенный крутящий момент, [math]\displaystyle{ T }[/math]: [math]\displaystyle{ \theta = \frac{TL}{JG} }[/math]
Как показано, чем больше модуль сдвига материала и полярный момент площади (т. е. больше площадь поперечного сечения), тем выше сопротивление кручению.
е. больше площадь поперечного сечения), тем выше сопротивление кручению.
Полярный момент площади появляется в формулах, описывающих напряжение кручения и угловое смещение.
Напряжения при кручении: [math]\displaystyle{ \tau = \frac{T \, r}{J_z} }[/math], где [math]\displaystyle{ \tau }[/math] — напряжение сдвига при кручении, [math]\displaystyle{ T }[/math] — приложенный крутящий момент, [math]\displaystyle{ r }[/math] — расстояние от центральной оси, а [math]\displaystyle{ J_z }[/math] — полярный момент площади.
Примечание: В круглом валу напряжение сдвига максимально на поверхности вала.
5. Пример расчета
Ротор современной паровой турбины. https://handwiki.org/wiki/index.php?curid=1484887
Расчет радиуса вала паровой турбины для турбоагрегата:
Допущения:
- Мощность на валу 1000 МВт; это типично для крупной атомной электростанции.
- Предел текучести стали, используемой для изготовления вала ( τ выход ) составляет: 250 × 10 6 Н/м 2 .




 TAFFRAIL LOG аналогичен, за исключением того, что регистрирующее устройство расположено на гаке, а в воде находится только ротатор.
TAFFRAIL LOG аналогичен, за исключением того, что регистрирующее устройство расположено на гаке, а в воде находится только ротатор.
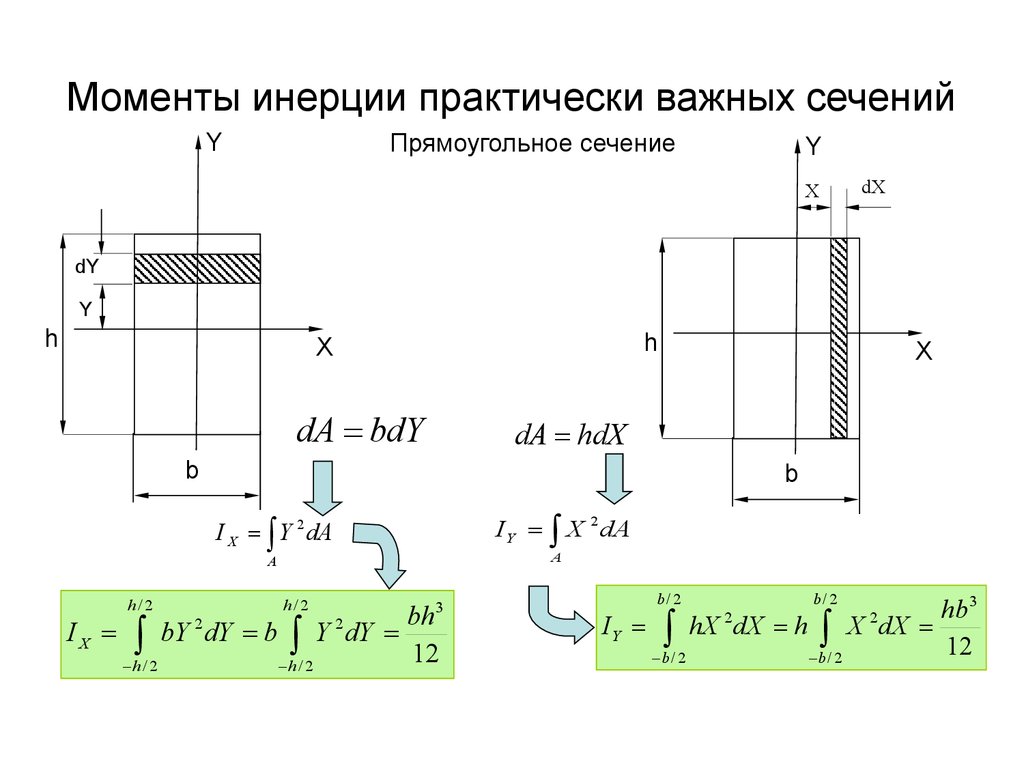 Это положительно, если уровень воды выше, чем точка отсчета карты. Расстояние по вертикали от точки отсчета на карте до отметки прилива называется ПОДЪЕМОМ ПРИЛИВА.
Это положительно, если уровень воды выше, чем точка отсчета карты. Расстояние по вертикали от точки отсчета на карте до отметки прилива называется ПОДЪЕМОМ ПРИЛИВА.