ФИЗИКА с нуля – современный учебник
В настоящее время нет ни одной естественнонаучной или технической области, где в той или иной степени не использовались бы достижения физики. А потому, единственная возможность узнать, как связаны между собой различные области науки и техники, это изучение основ физики. В то же время это и уникальная возможность познакомиться с новыми достижениями физики и их влиянием на другие области науки и техники. Предлагаемый вашему вниманию курс «Физика для чайников» на образовательном ресурсе FIZI4KA.RU удачно преподносит основы физики с нуля, неизменно востребованные все новыми поколениями.


Курс «Физика для чайников» — это не просто учебник, а интерактивный самоучитель по физике для начинающих, который доступен каждому любознательному и трудолюбивому школьнику и тем более студенту. От большинства учебников по физике FIZI4KA выделяется по пяти аспектам:
- Полное и последовательное изложение всего курса физики с нуля.
- Легкий и свободный стиль изложения физики для начинающих.
- Нет сложной математики.
- Продуманный подбор иллюстраций, схем и графиков, способствующих лучшему пониманию основ физики.
- Использование большого числа примеров и решения задач по физике, имеющих реальное практическое значение в повседневной жизни.
Все эти неоспоримые достоинства делают курс «физика для чайников» незаменимым пособием для самообразования или дополнительного чтения.
Во всех случаях, когда это возможно, законы физики выводятся из основных принципов; таким образом, всюду подчеркивается различие между основными принципами и следствиями из них. В курсе прослеживаются взаимосвязи различных областей физики (а также науки и техники). Независимые на первый взгляд разделы воссоединяются друг с другом и образуют единую картину. При введении каждого нового «закона», например закона магнитном силы, действующей на движущийся заряд, или закона равнораспределения энергии, мы стремимся разъяснить, действительно ли это новый закон, или же его можно вывести, используя уже известным материал. В большинстве случаев, проделав простые действия, удается проследить логическую структуру и замечательное единство всего того, что в противном случае выглядело бы просто как энциклопедическое собрание разнообразных явлений и законов.
Некоторых читателей может смутить рассмотрение в этом курсе таких актуальных вопросов современной физики, как нейтронные звезды, черные дыры, энергия Ферми, сохранение четности, кварки, голография, замедление времени, которые слишком сложны для начинающих студентов. Но мы сочли нужным включить их курс «Физика для чайников«, поскольку все эти вопросы захватывают воображение студентов, узнающих о них из средств массовой информации; это означает, что читатели хотели бы ближе познакомиться с этими проблемами в курсе физики, тем более многие из вопросов современном физики легче усваиваются студентами, чем то, что кроется за третьим законом Ньютона.
Стоит также отметить, что в «физике для начинающих» предпринята попытка связать изучение физики с изучением других областей науки, а также обратить внимание на взаимосвязь науки и общества. Например, центральной темой, пронизывающей весь курс, является проблема сокращения мировых ресурсов энергии. Обсуждаются и другие общественные, политические, экономические и философские предпосылки научного знания. Предлагаемый курс основ физики предназначен не только для того, чтобы заложить теоретические основы будущей профессии студентов: он призван также способствовать общему культурному росту человека, который будет занят в сфере науки и техники!
Физика для чайников с нуля, основы химии
4.1 (81.06%) 94 votesПростая физика — EASY-PHYSIC.RU
Приветствую Вас у себя на сайте EASY-PHYSIC.RU!
Меня зовут Денисова Анна Валерьевна.

Закончив кафедру Электротехники и Прецизионных Электро-Механических Систем (ЭТиПЭМС) Университета ИТМО в 1998, я поступила в аспирантуру, защитила диссертацию, став кандидатом наук, и осталась преподавать на кафедре.
Мой сайт называется “Простая физика” – да, физика может быть простой! И математика, и электротехника, и даже электроника!
Этот сайт как раз и был создан мной для того, чтобы студенты не боялись электротехники, а школьники – ЕГЭ.
Уважаемые школьники! Поверьте, ЕГЭ по физике и математике не так уж и страшны! Можно освоить любые задачи, было бы желание и время. Я объясняю доступно и понятно, стараюсь, чтобы на занятиях было интересно. Но от вас самих зависит 80 процентов успеха: большая работа откликается хорошими баллами на экзамене. Когда к экзаменам готовишься заранее, обязательно наступает момент, когда появляется уверенность в себе – а это тоже немаловажный фактор в достижении успеха. Для вас на сайте еженедельно выходят варианты ЕГЭ по физике для подготовки.
Уважаемые студенты! Если вы учитесь в техническом ВУЗе, то электротехника – неотъемлемая часть вашего учебного плана. Опыт показывает, что часов, отведенных нам учебным планом, хватает не всем студентам, чтобы освоить электротехнику. Поэтому не все успешно сдают этот не самый простой предмет. Сайт, я надеюсь, поможет восстановить эти пробелы, какой-то материал повторить, какой-то – освоить самостоятельно (как говорится, раньше студенты учились и подрабатывали, а теперь – работают и подучиваются). Студенты ИТМО найдут здесь полезные видео, статьи, которые помогут им сдать тесты, статьи, помогающие справиться с домашними заданиями, оформить лабораторные работы и т.п. Надеюсь, заглянут и студенты прочих технических вузов, которые также обязательно изучают электротехнику. Я стараюсь наполнить сайт простыми и понятными статьями и видео, чтобы этот нелегкий предмет перестал вызывать у вас сложности. Также вы найдете здесь лекции по электронике и микропроцессорной технике.
Хочется, чтобы на этом сайте вам было удобно, понятно и нескучно! Пишите, если у вас возникнут пожелания: если вам интересна какая-либо тема, а на сайте она еще не раскрыта, я могу сделать статью по вашей просьбе! Также буду благодарна за сообщения об опечатках.
Круг интересов любого человека не может ограничиваться только работой, пусть даже и любимой. Я воспитываю троих детей, увлекаюсь переводами песен с разных языков, сама являюсь автором песен (их пока всего две), играю на гитаре и барабанной установке, пишу картины, очень хорошо знаю и очень люблю собирать грибы, обожаю рыбалку, люблю и умею готовить…
Квантовая физика для чайников / Научный хит
«Если спросят, постоянно ли его положение, нужно сказать „нет“, если спросят, меняется ли оно со временем, нужно сказать „нет“. Если спросят, неподвижен ли он, нужно сказать „нет“, если спросят, движется ли он, нужно сказать „нет“». Законы квантовой механики весьма трудны для восприятия, похожи на мистические откровения, и эти слова Роберта Оппенгеймера о поведении электрона вполне могли быть сказаны Лао Цзы две с половиной тысячи лет назад.Введение. Принципиальная сложность понимания квантовой теории
Сложно представить, как выглядела бы наша цивилизация без классической физики и математики. Понятия об абсолютной «объективной реальности, существующей независимо от нашего сознания», о трехмерном евклидовом пространстве и равномерно текущем времени настолько глубоко укоренились в сознании, что мы не замечаем их. А главное, отказываемся замечать, что применимы они лишь в некоторых рутинных ситуациях и для объяснения устройства Вселенной оказываются попросту неверны.После того как в общих чертах было открыто строение атома и предложена его «планетарная» модель, ученые столкнулись со множеством парадоксов, для объяснения которых появился целый раздел физики — квантовая механика. Она быстро развивалась и далеко продвинулась в объяснении Вселенной. Но объяснения эти настолько сложны для восприятия, что до сих пор мало кто может осознать их хотя бы в общих чертах.
Кроме того, Эйнштейн математически показал, что наши понятия времени и пространства иллюзорны. В действительности пространство и время нераздельны и образуют единый четырехмерный континуум. Представить его вряд ли возможно, ведь мы привыкли иметь дело только с тремя измерениями.
Планетарная теория. Волна или частица
До конца XIX века атомы считались неделимыми «элементами». Открытие радиации позволило Резерфорду проникнуть под «оболочку» атома и сформулировать планетарную теорию его строения: основная масса атома сосредоточена в ядре. Положительный заряд ядра компенсируется отрицательно заряженными электронами, размеры которых настолько малы, что их массой можно пренебречь. Электроны вращаются вокруг ядра по орбитам, подобно вращению планет вокруг Солнца. Теория весьма красивая, но возникает ряд противоречий.Вероятностные электронные облака. Строение ядра и ядерные частицы
Постепенно становилось все более ясно: вращение электронов по орбитам вокруг ядра атома совершенно не похоже на вращение планет вокруг звезды. Обладая волновой природой, электроны описываются в терминах вероятности. Мы не можем сказать об электроне, что он находится в такой-то точке пространства, мы можем только описать примерно, в каких областях он может находиться и с какой вероятностью. Вокруг ядра электроны формируют «облака» таких вероятностей от простейшей шарообразной до весьма причудливых форм, похожих на фотографии привидений.Но тот, кто хочет окончательно понять устройство атома, должен обратиться к его основе, к строению ядра. Составляющие его крупные элементарные частицы — положительно заряженные протоны и нейтральные нейтроны — также обладают квантовой природой, а значит, движутся тем быстрее, чем в меньший объем они заключены. Поскольку размеры ядра чрезвычайно малы даже в сравнении с атомом, эти элементарные частицы носятся со вполне приличными скоростями, близкими к скорости света. Для окончательного объяснения их строения и поведения нам понадобится «скрестить» квантовую теорию с теорией относительности. К сожалению, такая теория до сих пор не создана и нам придется ограничиться несколькими общепринятыми моделями.
Участник вместо наблюдателя
В мире, где понятия пустого пространства, изолированной материи теряют смысл, частица описывается только через ее взаимодействия. Для того чтобы сказать что-то о ней, нам придется «вырвать» ее из первоначальных взаимодействий и, подготовив, подвергнуть другому взаимодействию — измерению. Так что мы меряем в итоге? И насколько правомерны наши измерения вообще, если наше вмешательство меняет взаимодействия, в которых участвует частица, — а значит, меняет и ее саму?В современной физике элементарных частиц все больше нареканий вызывает… сама фигура ученого-наблюдателя. Правомернее было бы называть его «участником».
Наблюдатель-участник необходим не только для измерения свойств субатомной частицы, но и для того, чтобы определить эти самые свойства, ведь и о них можно говорить лишь в контексте взаимодействия с наблюдателем. Стоит ему выбрать способ, каким он будет проводить измерения, и в зависимости от этого реализуются возможные свойства частицы. Стоит сменить наблюдающую систему, и свойства наблюдаемого объекта также изменятся.
Этот важный момент раскрывает глубинное единство всех вещей и явлений. Сами частицы, непрерывно переходя одна в другую и в иные формы энергии, не имеют постоянных или точных характеристик — эти характеристики зависят от способа, каким мы решили их видеть. Если понадобится измерить одно свойство частицы, другое непременно изменится. Такое ограничение не связано с несовершенством приборов или другими вполне исправимыми вещами. Это характеристика действительности. Попробуйте точно измерить положение частицы, и вы ничего не сможете сказать о направлении и скорости ее движения — просто потому, что у нее их не будет. Опишите точно движение частицы — вы не найдете ее в пространстве. Так современная физика ставит перед нами проблемы уже совершенно метафизического свойства.
Принцип неопределенности. Место или импульс, энергия или время
Мы уже говорили, что разговор о субатомных частицах нельзя вести в привычных нам точных терминах, в квантовом мире нам остается лишь вероятность. Это, конечно, не та вероятность, о которой говорят, делая ставки на скачках, а фундаментальное свойство элементарных частиц. Они не то чтобы существуют, но скорее — могут существовать. Они не то чтобы обладают характеристиками, а скорее — могут ими обладать. Научно выражаясь, частица является динамической вероятностной схемой, и все ее свойства находятся в постоянном подвижном равновесии, балансируют, как Инь и Ян на древнем китайском символе тайцзи. Недаром нобелевский лауреат Нильс Бор, возведенный в дворянское звание, для своего герба выбрал именно этот знак и девиз: «Противоположности дополняют друг друга». Математически распределение вероятности представляет собой неравномерные волновые колебания. Чем больше амплитуда волны в определенном месте, тем выше вероятность существования частицы в нем. При этом длина ее непостоянна — расстояния между соседними гребнями неодинаковы, и чем выше амплитуда волны, тем сильнее разница между ними. В то время как амплитуда соответствует положению частицы в пространстве, длина волны связана с импульсом частицы, то есть с направлением и скоростью ее движения. Чем больше амплитуда (чем точнее можно локализовать частицу в пространстве), тем более неопределенной становится длина волны (тем меньше можно сказать об импульсе частицы). Если мы сможем установить положение частицы с предельной точностью, у нее вообще не будет никакого определенного импульса.Это фундаментальное свойство математически выводится из свойств волны и называется принципом неопределенности. Принцип касается и других характеристик элементарных частиц. Еще одна такая взаимосвязанная пара — это энергия и время протекания квантовых процессов. Чем быстрее проходит процесс, тем более неопределенно количество энергии, задействованной в нем, и наоборот — точно охарактеризовать энергию можно только для процесса достаточной продолжительности.
Итак, мы поняли: о частице нельзя сказать ничего определенного. Она движется туда, или не туда, а верней, ни туда и ни сюда. Ее характеристики такие или сякие, а точнее — и не такие, и не сякие. Она находится здесь, но может быть и там, а может и не быть нигде. Так существует ли она вообще?
Роман Фишман
Читать книгу Физика для «чайников». Несерьезное пособие Андрей Ильин : онлайн чтение
Упругость. Если вы понимаете, о чём я.
С силой упругости гораздо проще: не надо представлять себе никакие планеты, чёрные дыры, Вселенные и тому подобные непонятные субстанции. Достаточно взять простую пружину и согнуть её, а потом отпустить. Оба свободных конца заставят руки разжаться. Это и есть сила упругости. Она возникает при деформации тела – проще говоря, при нарушении его естественной формы. Это вносит своеобразный дискомфорт, и тело (пружина) стремится вернуться в первоначальное, «удобное для себя» положение, попутно задевая всё, что находится рядом. Если объяснять, а с чего вообще пружине вдруг распрямляться, – может, ей и так, в согнутом состоянии, хорошо, – придётся забежать немного вперёд, поэтому я к этому вернусь несколько позже (здесь же, в механике).
А пока – простая формула, как эту силу посчитать. Вывел её товарищ по фамилии Гук, отчего решили его именем сие выражение и обозвать.
F = -k.x. F – это сила, k – это жёсткость пружины (того, что деформируют), x – изменение размера (на сколько миллиметров, сантиметров и т. д. – по-прежнему пересчитанных в метры! – сжимаем пружину). Ах да, и минус. Он тут вовсе не по ошибке. Если вспомнить, то сила – это векторная величина. То есть для неё минус означает всего лишь то, что она направлена «в противоположную сторону». Противоположно чему? Тому направлению, в котором идёт деформация. Сжимаешь пружину сверху вниз – а сила идёт снизу вверх. То есть тело как будто сопротивляется сжатию, и чем сильнее сжимаешь, тем сильнее сопротивление.
Самый простой пример, когда используется сила упругости, – простенькие ручные пружинные весы («безмен»). Сила упругости пружины уравновешивает силу тяжести груза, а пружина (естественно, с известной жёсткостью, которую заранее посчитали и померили) удлиняется на несколько миллиметров или сантиметров, в зависимости от массы груза. Зная удлинение и жёсткость, мы знаем силу упругости пружины – значит, знаем силу тяжести груза – значит, знаем массу груза.
Вкратце и поумнее: сила упругости обусловлена возвращением тела в исходное состояние после деформации. Рассчитывается по закону Гука: F = -k.x, k – жёсткость тела, x – изменение размера деформируемого тела. Минус показывает, что сила упругости действует в направлении, противоположном тому, в котором идёт деформация.
Опора реагирует, тело трёт, вес давит
Где-то уже далеко вверху остался перечень из пяти сил…
Так вот, если вернуться к нему, то пункты 3) и 4) (трения и реакция опоры) а также 4) и 5) (реакция опоры и вес) связаны между собой. Сила реакции опоры и вес – это две силы, которые действуют по третьему закону Ньютона между телом и опорой. А именно: вес – это сила, с которой тело давит на опору (или вертикальный подвес, если висит). А сила реакции опоры – это противоположная (по направлению) весу сила, с которой опора действует на то, что на неё давит. То есть: туловище давит на стул, на котором сидит, а стул в ответ давит вверх, на туловище, не давая тому провалиться ещё ниже.
Отсюда можно сделать простой вывод: если нет никаких специально выдуманных условий, то и вес, и реакция опоры (слово «сила» можно опустить) будут равны m.g, только направлены в противоположные стороны. Вес действует на опору и направлен вниз (если задача про тело, а не про опору, то на вес просто забивают), а сила реакции опоры действует на тело и направлена вверх. Разница между силой тяжести и весом в том, что сила тяжести действует на само тело, а вес – на опору, которая под ним. И это не единственное различие: в то время как сила тяжести всегда равна m.g, вес может быть и больше m.g (это называется перегрузкой), и меньше, и даже быть равным нулю (а это уже невесомость). Вообще говоря, вес считается так:
P = m. (g-a). P – это вес, m – масса давящего тела, g – ускорение свободного падения, a – ускорение, с которым движется опора. То есть, если опора неподвижна, то всё хорошо. А вот если она начнёт подниматься или опускаться, вот тогда придётся считать… Самый простой пример – лифт. Если он резко пойдёт вверх, то ускорение будет тоже направлено вверх, то есть противоположно g (которое всегда смотрит вниз). Итого получаем, что минус ускорения на минус в выражении даёт плюс: ускорения надо складывать – получается перегрузка. Если же лифт пойдёт вниз, то ускорение a вычитаем и получаем пониженный вес. Наконец, самый печальный и фантастический случай: если лифт срывается и свободно падает, то ускорение, с которым он падает, равно g. И получается, что несчастный пассажир последние секунды своей жизни проведёт в состоянии невесомости – его вес станет равным нулю. В таком же состоянии будет и свободно падающая пружина с грузиком: если бросить её грузиком вниз, то в падении пружина не будет разжата, а вернётся в «спокойное» состояние, как будто на ней ничего не висит.
Ладно, невесомость оставим научным фантастам. О весе я сказал достаточно, а вот про его вечного противника и союзника – силу реакции опоры – не всё. Эта сила сама по себе мало что значит, но имеет прямое отношение к такой до боли известной вещи, как трение.
Сила трения имеет какое-то сходство с силой реакции опоры. Вообще говоря, трение существует трёх видов. Первое – это когда одно тело скользит по поверхности другого: например, при спуске с горы на санках или при беге на коньках (обычных, которые тоже по льду), оно же трение скольжения. Второе – когда одно тело катится по поверхности другого (любое колесо или шарообразное тело – по земле), оно же трение качения. И третье – трение покоя, когда одно тело (уже неважно, какое именно) находится в таком состоянии, когда оно в принципе может сдвинуться с места, но что-то ему мешает. Это «что-то» и есть трение. То есть, например, если человек стоит на достаточно крутой горке и не двигается, то он не будет падать: мешает сила трения покоя, которая возникает между подошвами ботинок и землёй, не позволяя ногам соскальзывать вниз. Точно так же трение покоя мешает, например, сдвинуть тяжёлый предмет с места: пока сила рук не превысит силу трения покоя шкафа, шкаф не подвинется.
Для всех трений получается одно и то же: сила трения направлена в сторону, противоположную направлению движения (или возможного движения, если это трение покоя), причём направлена вдоль поверхности, по которой тела соприкасаются. В школе, как правило, заморачиваются трением скольжения и трением покоя. Считаются они так:
F = -μ.N. Буква мю – это коэффициент трения, он зависит от поверхностей, которые скользят друг по другу. Для льда этот коэффициент всегда меньше, чем для асфальта или грунта, поэтому на льду лучше отталкиваться и хуже тормозить. Минус напоминает, что сила трения направлена против движения: тело снова как будто сопротивляется. Трение качения в школе обычно не считают, оно несколько сложнее остальных. Про него стоит отметить только одно важное наблюдение: трение качения всегда слабее трения скольжения, если брать одни и те же материалы, трущиеся друг о друга. Собственно, поэтому все на колёсах и ездим.
Вкратце и поумнее: вес – это сила, с которой тело давит на опору или подвес. Считается по формуле P = m. (g-a), где P – вес, m – масса давящего тела, g – ускорение свободного падения, a – ускорение, с которым движется опора. При нулевом ускорении вес равен силе тяжести давящего тела, при противоположно направленном a и g возникает перегрузка, при свободном падении опоры с телом (a = g) имеем невесомость. Вес действует на опору, а не на тело, поэтому при решении задач о телах обычно его не рассматривают. Сила реакции опоры действует на тело со стороны опоры и равна минус силе тяжести (-m.g). Сила трения – это сила, возникающая в результате перемещения одного тела по поверхности другого. Различают силы трения скольжения, качения и покоя. Трение скольжения и трение покоя считаются как F = -μ.N, где μ (мю) – коэффициент трения, N – сила реакции опоры. Направлена сила трения в сторону, противоположную направлению движения (или возможного движения, если это сила трения покоя).
Космос! Долой динамику!
В общем-то, на этом и приближается к концу вся динамика. Остаётся кусочек, который снова заносит в космос. А именно – космические скорости. Сложно сказать, почему их запихнули в динамику. Может быть потому, что каждая из этих скоростей означает рубеж, при котором преодолеваешь силу чьего-нибудь притяжения. А может быть потому, что космос – это тоже такая инерциальная система отсчёта, где космический корабль бороздит просторы Вселенной в гордом одиночестве, никто ему не мешает, он никуда не поворачивает, не тормозит и так далее.
Так вот, первый «рубеж», при котором такое возможно, – это если вывести корабль на орбиту Земли так, чтобы он стал спутником Земли (то бишь так, чтобы он не летел дальше, а «остановился» где-то недалеко от планеты). В итоге сила притяжения Земли вместе с космической «атмосферой» (которой почти нет – значит, ничего не должно мешать движению) заставят его крутиться вокруг нашей планетки. Соответственно, чтобы какой-то предмет смог так летать вокруг, надо ему дать такую скорость, чтобы он преодолел земное притяжение ровно настолько, чтобы оно же «остановило» его ровнёхонько на орбите планеты. Для особо любопытных: я специально пишу «остановиться» в кавычках: оказавшись на орбите, спутник не останавливается, а продолжает лететь. Но летит он с постоянной скоростью всё время в одну и ту же сторону – и с одной стороны, не может улететь дальше (мешает ещё действующее притяжение Земли), а с другой стороны, не может упасть (скорость достаточно большая, чтобы ещё преодолевать это притяжение). А главная её фишка в том, что для всех предметов она одинаковая! Более того, её даже можно посчитать, используя всего лишь второй закон Ньютона, немного кинематики и собственные мозги.
Чтобы понять, как можно посчитать первую космическую скорость, достаточно представить, как будет выглядеть весь запуск: со страшной скоростью подопытное туловище стартует с поверхности. В полёте гравитация и воздух тщетно пытаются его затормозить. Наконец, на орбите он должен «остановиться». Ничего не напоминает? Правильно – это будет замедленное движение. Чтобы совсем не заморачиваться на тему подсчётов – равнозамедленное. Расстояние, на которое летит туловище: радиус Земли. Ускорение, противостоящее нам: g. Расстояние, пройденное при торможении, будет равно: v2.t (как было в кинематике). А нам отсюда нужна скорость. Итого: это будет корень квадратный из произведения g на радиус Земли. Поскольку и то, и другое – числа известные и постоянные, то и скорость будет для всех одинаковая. Если посчитать, то первая космическая скорость получится примерно 7.9 км/с. Вторая космическая скорость – летим ещё дальше, её хватит на то, чтобы вообще преодолеть притяжение Земли и улететь бороздить просторы Солнечной системы. Для Земли она составляет 11.2 км/с. Считается она уже из закона, которым наверняка уже прожужжали все уши, – из закона сохранения энергии. (О нём – ближе к концу механики, сейчас пока не грузимся.) Третья космическая скорость позволяет ухнуть ещё дальше – вылететь вообще за пределы Солнечной системы, то есть преодолеть притяжение Солнца. Она может меняться, потому что космический корабль должен будет уворачиваться от вертящихся планет и тому подобных посторонних предметов, пролетающих мимо в космосе. В среднем она составляет где-то около 42 км/с, но вообще может быть от 16.6 до почти 73 км/с. Наконец, есть ещё четвёртая космическая скорость. Она нужна тогда, когда захочется вышибить наш предмет с Земли настолько сильно, чтобы он преодолел притяжение самой нашей галактики Млечный путь. (Если фантазия разыграется до таких вселенских масштабов…) Её подсчёты ведут уже в какие-то заумные дебри современной физики; говорят, что она непостоянна и зависит от положения тела в галактике. Известно только, что в районе Солнечной системы нужно разогнаться аж до 550 км/с, чтобы иметь хоть какую-то надежду на полный улёт. Улёт в настолько открытый космос, что и представить трудно.
Вкратце и поумнее: космические скорости – это скорости, которые нужно сообщить телу для того, чтобы оно:
1) стало спутником Земли – это 7.9 км/с;
2) преодолело гравитационное притяжение Земли и улетело в пространство Солнечной системы – 11.2 км/с;
3) преодолело гравитационное притяжение Солнца и улетело за пределы Солнечной системы – от 16.6 до 73 км/с, средняя считается около 42 км/с;
4) преодолело гравитационное притяжение галактики «Млечный путь» и улетело чёрт-те куда – приблизительно 550 км/с в районе Солнечной системы.
Статика
Момент равновесия
Наконец, последняя часть из трёх основных составляющих, наименее мучительная. Статика. Которая отвечает на вопрос, при каких условиях тело будет в равновесии. Или в состоянии покоя. Увы и ах, но здесь нельзя использовать всё ту же материальную точку, которая спасала в кинематике и динамике. Потому что наше тело, выходя из равновесия, скорее всего, будет описывать дугу – то бишь вращаться. Грубо говоря, если теряешь равновесие и падаешь, то как бы вращаешься вокруг оси, находящейся прямо под ногами – ну, до тех пор, пока земля не помешает. А материальная точка исключает всякое вращение – как она вокруг себя вращаться-то будет? Нет того, около чего вращаться. Поэтому здесь делают так: просто твёрдое тело каких-то размеров (неважно, каких), его деформациями при внешних воздействиях можно пренебречь. Чтобы не получилось, что оно при малейшем дуновении ветерка разваливается на несколько частей или сплющивается в лепёшку – тогда уже считать будет нечего.
Дальше опять следует куча предположений, которые проще всего себе представить так. Вот у нас есть детские качели, на которых садятся два человека – доска на подставке с двумя сидениями на краях. Подставка намертво закреплена – не отдерёшь, – а к ней прикреплена палка, которая может подниматься-опускаться, как рычаг. Или, по-умному, это получается всё то же вращение. И на сиденьях сидят дети. Ради прикола прикинем, что они идеальные близнецы – полностью одинаковые по массе, силе и т. д. и т. п. Тогда, если всё это перевести в заумные физические понятия, получается так: подставка, она же точка опоры – это ось вращения. Вокруг неё вращается наш «рычаг». Дети – это твёрдые тела. Господа знатоки, внимание, вопрос: так при каких же условиях дети будут находиться в равновесии? За такую формулировку на экзамене по физике могут заколоть заживо. В равновесии должно находиться то, что может вращаться! То есть, в данном случае это наша палка качелей, которая закреплена на подставке. Именно её придётся теребить.
Первое, что идёт прямо из динамики: сумма сил, действующих на тело, должна быть равна нулю. И это действительно так, но это ещё не всё. Здесь есть ещё второе условие, посложнее. Если наших двух одинаковых детей посадить нормально – так, что они будут сидеть каждый на сиденье, – то «палка» действительно будет в равновесии. А если один из них подсядет ближе, качели тут же наклонит в сторону его товарища. Силы-то остались те же! Но поменялись их моменты. Момент силы – это модуль (только значение, без вектора!) силы, умноженный на её плечо (то есть расстояние от оси вращения до линии, по которой действует сила). Притом расстояние выбирается кратчайшее – а как подсказывает заумная геометрия, в таком случае нужно брать длину отрезка, перпендикулярного линии силы. По-русски (и более наглядно) это значит, что надо просто брать длину той части качели, которая идёт от точки опоры до человека. Она всегда будет одна и та же, хоть ты перевернись.
Маленькое замечание к моментам: поскольку крутить он может в две разные стороны – «вверх» и «вниз» (именно в кавычках, потому что строго говоря – это «по часовой стрелке» и «против часовой стрелки»), – то договорились, что момент, крутящий против часовой стрелки, будет больше нуля, а по часовой – меньше. По-чесноку, не знаю, как это лучше запомнить и не перепутать, если только не знать алгебру на уровне синусов-косинусов. (Там тоже углы на единичной окружности отсчитываются таким же образом: против часовой стрелки идёт увеличение (+), по – уменьшение (-).)
Короче говоря, из всех этих страшных слов следует простая вещь: если у тела есть закреплённая ось вращения, и сумма моментов сил, действующих на это тело, равна нулю, то тело будет в равновесии. На этом правиле основана работа весов: если неизвестную массу измеряемого туловища уравновешивают вместе поставленные гирьки, то момент силы тяжести гирек будет равен моменту силы тяжести туловища. Отсюда, поскольку плечи обеих сил равны (а если даже и не равны, то они всё равно известны – хотя так считать было бы гораздо неудобнее), то известны сами силы. А дальше как в ручных весах: сила тяжести гирек равна силе тяжести туловища, откуда при известной массе гирек находим, что масса туловища будет такая же.
Вкратце и поумнее: статика – раздел механики, изучающий условия равновесия взаимодействующих тел (в общем случае). Используется модель твёрдого тела, поскольку при нарушении равновесия оно будет вращаться вокруг некой оси, а материальная точка исключает вращение. Твёрдое тело – модель тела, деформацией которого под действием внешних сил можно пренебречь. Ось вращения – воображаемая прямая, на которой находятся центры всех траекторий точек вращающегося относительно неё твёрдого тела. Плечо силы – расстояние от оси вращения до линии, вдоль которой действует эта сила. Момент силы – произведение модуля силы на её плечо. Единица измерения – ньютон, умноженный на метр. Момент, вращающий тело по часовой стрелке, считается отрицательным, а против часовой стрелки – положительным. Итого условий равновесия твёрдого тела два: тело находится в равновесии, если сумма сил, действующих на это тело, равна нулю, и если сумма моментов сил, действующих на тело относительно произвольно выбранной оси, тоже равна нулю. В том числе отсюда следует правило моментов: тело, имеющее закреплённую ось вращения, будет находиться в равновесии, если сумма моментов сил относительно этой оси будет равна нулю.
Шарики и гора посуды, или Хватит уже этой статики
Кое-как проехали страшную математику статики. Остались только слова. А именно: заумные рассуждения на тему, как лучше держать тело, чтобы оно не упало, и какие вообще могут быть равновесия. Да, у равновесий тоже есть виды, оказывается! Отвлечёмся от качелей и весов, проще всего эти виды равновесия понять так: взять шарик и кинуть его в канаву-кювет U-образной формы. Шарик поболтается туда-сюда, после чего остановится на дне в середине (если смотреть вдоль, по канавке). Попытаешься толкнуть шарик – он снова покатается вправо-влево, но, в конце концов, всё равно вернётся в центр. Это устойчивое равновесие – если вывести шарик из равновесия, он со временем вернётся в него. Считается, что девушки любят парней, находящихся в устойчивом эмоциональном равновесии (то есть если человека «задеть», то он со временем всё равно успокоится и будет, как ни в чём не бывало). Эмоции, конечно, не шарик, расчётам не поддаются. Но суть та же самая – это тоже устойчивое равновесие. Хуже, когда оно неустойчивое: это значит, что невероятными усилиями мы добиваемся равновесия, а потом что-то выводит из него – и всё. Обратно просто так, сам собой, уже не вернёшься. Как таких товарищей называют? Правильно, нытиками. Если не обижать людей и показать на том же шарике – его можно положить, например, на компьютерную мышку (конечно, так, чтоб не двигался). Если его задеть, то он упадёт и, конечно же, обратно не запрыгнет. А вот когда шарик оказался на ровной поверхности стола – он в безразличном равновесии. Тронешь его – он поедет, но потом остановится, как ни в чём не бывало и по-прежнему останется в равновесии. Разница между этими тремя равновесиями – в силе, возникающей при отклонении. Когда равновесие устойчивое, при выведении из него возникает сила, стремящаяся вернуть в положение равновесия (в примере с шариком – сила тяжести). Когда неустойчивое – сила тоже возникает, но она при этом стремится вывести тело из равновесия ещё сильнее (в примере – тоже сила тяжести). Когда безразличное – никакой силы, стремящейся поддержать или подавить равновесие, не возникает. Умники могут возразить: а как же сила трения? Шарик-то трётся о поверхность! На что у меня припрятан туз в рукаве: соль здесь не только в силе, а ещё и в энергии. Об этом – буквально через пару разделов. В двух словах, в чём различие по ней: потенциальная (не пугаться и не смеяться!) энергия тела при выведении из устойчивого равновесия возрастает, при выведении из неустойчивого – уменьшается, а при безразличном – не меняется вообще.
Последнее, о чём разговор здесь, – центр тяжести и центр масс. Если всё хорошо, то эти две точки совпадают и находятся в центре тела – например, центр шара (яблока) или центр параллелепипеда (бруска, какого-нибудь простого бытового предмета вроде губки). Но, вообще говоря, эти две вещи различаются.
Центр масс – это точка, которая как бы является представительством всего тела в целом: если всю массу сосредоточить в этой одной точке, то она будет двигаться ровно так же, как двигается само тело. То есть, если взять центр масс какого-нибудь тела и запихнуть туда всю массу, то получится как раз материальная точка, над которой уже можно законно проводить все расчёты кинематики и динамики. А центр тяжести – это такая точка, в которой просто суммарный момент всех сил тяжести, которые действуют на все места тела, равен нулю. К движению она особо не относится. Разве что если держать тело, грубо говоря, за его центр тяжести, то оно не будет падать – так официант таскает поднос одной рукой, не роняя его. К счастью, в той же статике эти две точки практически всегда совпадают друг с другом, поэтому обычно говорят просто «центр тяжести» и не парятся. Чтобы они не совпадали, нужно, чтобы рассматриваемый предмет находился в неоднородном гравитационном поле (например, если рассматривать его вместе с планетой) – а такими вещами даже физики-шизики заморачиваются достаточно редко.
Вкратце и поумнее: при выведении из устойчивого равновесия возникает сила, стремящаяся вернуть тело в первоначальное положение (равновесия), потенциальная энергия возрастает. При выведении из неустойчивого равновесия возникает сила, стремящаяся ещё сильнее отклонить тело от первоначального положения, потенциальная энергия падает. При выведении из безразличного равновесия никаких «стремящихся» сил не возникает, потенциальная энергия тела неизменна. Центр масс – точка, характеризующая движение тела или системы тел как единого целого. Центр тяжести – точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. На практике оба этих центра практически всегда совпадают, исключение составляют случаи, когда тело находится в неоднородном гравитационном поле.
Квантовая физика для чайников! Лучшие эксперименты
Для новой версии книги «Фаза» (2015 года) нужно было одним абзацем и понятно обывателю выразить те вещи, на понимание которых обычно уходят недели и месяцы. Возможно, вам эти сжатые знания пригодятся. Для упрощения понимания квантовая физика описывается не теорией, а экспериментами.
(Графическая версия статьи)
Первый квантовый эксперимент с двумя щелями
В 1803 году Томас Юнг направил пучок света на непрозрачную ширму с двумя прорезями. Вместо ожидаемых двух полосок света на проекционном экране он увидел несколько полос, как если бы произошла интерференция (наложение) двух волн света из каждой прорези. Фактически именно в этот момент зародилась квантовая физика, вернее вопросы у её основы. В XX и XXI веках было показано, что не только свет, но любая одиночная элементарная частица и даже некоторые молекулы ведут себя как волна, как кванты, будто проходя через обе щели одновременно. Однако если поставить у щелей датчик, который определяет, что именно происходит с частицей в этом месте и через какую именно щель она все-таки проходит, то на проекционном экране появляются только две полосы, словно факт наблюдения (косвенного влияния) рушит волновую функцию и объект ведет себя как материя. (Подробно, видео)
Принципа неопределенности Гейзенберга – фундамент квантовой физики!
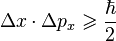
Благодаря открытию 1927 года тысячи ученых и студентов повторяют один и тот же простой эксперимент, пропуская лазерный луч через сужающуюся щель. Логично, видимый след от лазера на проекционном экране становится все уже и уже вслед за уменьшением зазора. Но в определенный момент, когда щель становится достаточно узкой, пятно от лазера вдруг начинает становиться шире и шире, растягиваясь по экрану и тускнея пока щель не исчезнет. Это самое очевидное доказательство квинтэссенции квантовой физики — принципа неопределенности Вернера Гейзенберга, выдающегося физика-теоретика. Суть его в том, что чем точнее мы определяем одну из парных характеристик квантовой системы, тем более неопределенней становится вторая характеристика. В данном случае, чем точнее мы определяем сужающейся щелью координаты фотонов лазера, тем неопределеннее становится импульс этих фотонов. В макромире мы точно также можем измерить либо точное местоположение летящего меча, взяв его в руки, либо его направление, но никак не одновременно, так как это противоречит и мешает друг другу. (Подробно, видео)
Квантовая сверхпроводимость и эффект Мейснера

В 1933 году Вальтер Мейснер обнаружил интересное явление в квантовой физике: в охлажденном до минимальных температур сверхпроводнике магнитное поле вытесняется за его пределы. Это явление получило название эффект Мейснера. Если обычный магнит положить на алюминий (или другой сверхпроводник), а затем его охладить жидким азотом, то магнит взлетит и зависнет в воздухе, так как будет «видеть» вытесненное из охлажденного алюминия свое же магнитное поле той же полярности, а одинаковые стороны магнитов отталкиваются. (Подробно, видео)
Квантовая сверхтекучесть

В 1938 году Петр Капица охладил жидкий гелий до близкой к нулю температуры и обнаружил, что у вещества пропала вязкость. Это явление в квантовой физике получило название сверхтекучесть. Если охлажденный жидкий гелий налить на дно стакана, то он все равно вытечет из него по стенкам. Фактически, пока гелий достаточно охлажденный для него нет пределов, чтобы разлиться, вне зависимости от формы и размера емкости. В конце XX и начале XXI веков сверхтекучесть при определенных условиях была также обнаружена у водорода и различных газов. (Подробно, видео)
Квантовый туннелинг

В 1960 году Айвор Джайевер проводил электрические опыты со сверхпроводниками, разделенными микроскопической пленкой непроводящего ток оксида алюминия. Выяснилось, что вопреки физике и логике часть электронов все равно проходит через изоляцию. Это подтвердило теорию о возможности квантового туннельного эффекта. Он распространяется не только на электричество, но и любые элементарные частицы, они же волны согласно квантовой физике. Они могут проходить препятствия насквозь, если ширина этих препятствий меньше длины волны частицы. Чем препятствие уже, тем чаще частицы проходят сквозь них. (Подробно, видео)
Квантовая запутанность и телепортация

В 1982 году физик Ален Аспэ, будущий лауреат Нобелевской премии, направил два одновременно созданных фотона на разнонаправленные датчики определения их спина (поляризации). Оказалось, что измерение спина одного фотона мгновенно влияет на положение спина второго фотона, который становится противоположным. Так была доказана возможность квантовой запутанности элементарных частиц и квантовая телепортация. В 2008 году ученым удалось измерить состояние квантово-запутанных фотонов на расстоянии 144 километров и взаимодействие между ними все равно оказалось мгновенным, как если бы они были в одном месте или не было пространства. Считается, что если такие квантово-запутанные фотоны окажутся в противоположных участках вселенной, то взаимодействие между ними все равно будет мгновенным, хотя свет это же расстояние преодолевает за десятки миллиардов лет. Любопытно, но согласно Эйнштейну для летящих со скоростью света фотонов времени тоже нет. Совпадение ли это? Так не думают физики будущего! (Подробно, видео)
Квантовый эффект Зенона и остановка времени

В 1989 году группа ученых под руководством Дэвида Вайнленда наблюдала за скоростью перехода ионов бериллия между атомными уровнями. Выяснилось, что сам факт измерения состояния ионов замедлял их переход между состояниями. В начале XXI века в подобном эксперименте с атомами рубидия удалось достичь 30-кратного замедления. Все это является подтверждением квантового эффект Зенона. Его смысл в том, что сам факт измерения состояния нестабильной частицы в квантовой физике замедляет скорость ее распада и в теории может его полностью остановить. (Подробно, видео англ.)
Квантовый ластик с отложенным выбором
В 1999 году группа ученых под руководствам Марлана Скали направляла фотоны через две щели, за которыми стояла призма, конвертирующая каждый выходящий фотон в пару квантово-запутанных фотонов и разделяя их на два направления. Первое отправляло фотоны на основной детектор. Второе направление отправляла фотоны на систему 50%-отражателей и детекторов. Выяснилось, если фотон из второго направления достигал детекторы определяющие щель, из которой он вылетел, то основной детектор фиксировал его парный фотон как частицу. Если же фотон из второго направления достигал детекторы не определяющие щель, из которой он вылетел, то основной детектор фиксировал его парный фотон как волну. Не только измерение одного фотона отражалось на его квантово-запутанной паре, но и это происходило вне расстояния и времени, ведь вторичная система детекторов фиксировала фотоны позже основного, как если бы будущее определяло прошлое. Считается, что это самый невероятный эксперимент не только в истории квантовой физики, но и вполне в истории всей науки, так как он подрывает многие привычные основы мировоззрения. (Подробно англ., видео англ.)
Квантовая суперпозиция и кот Шредингера
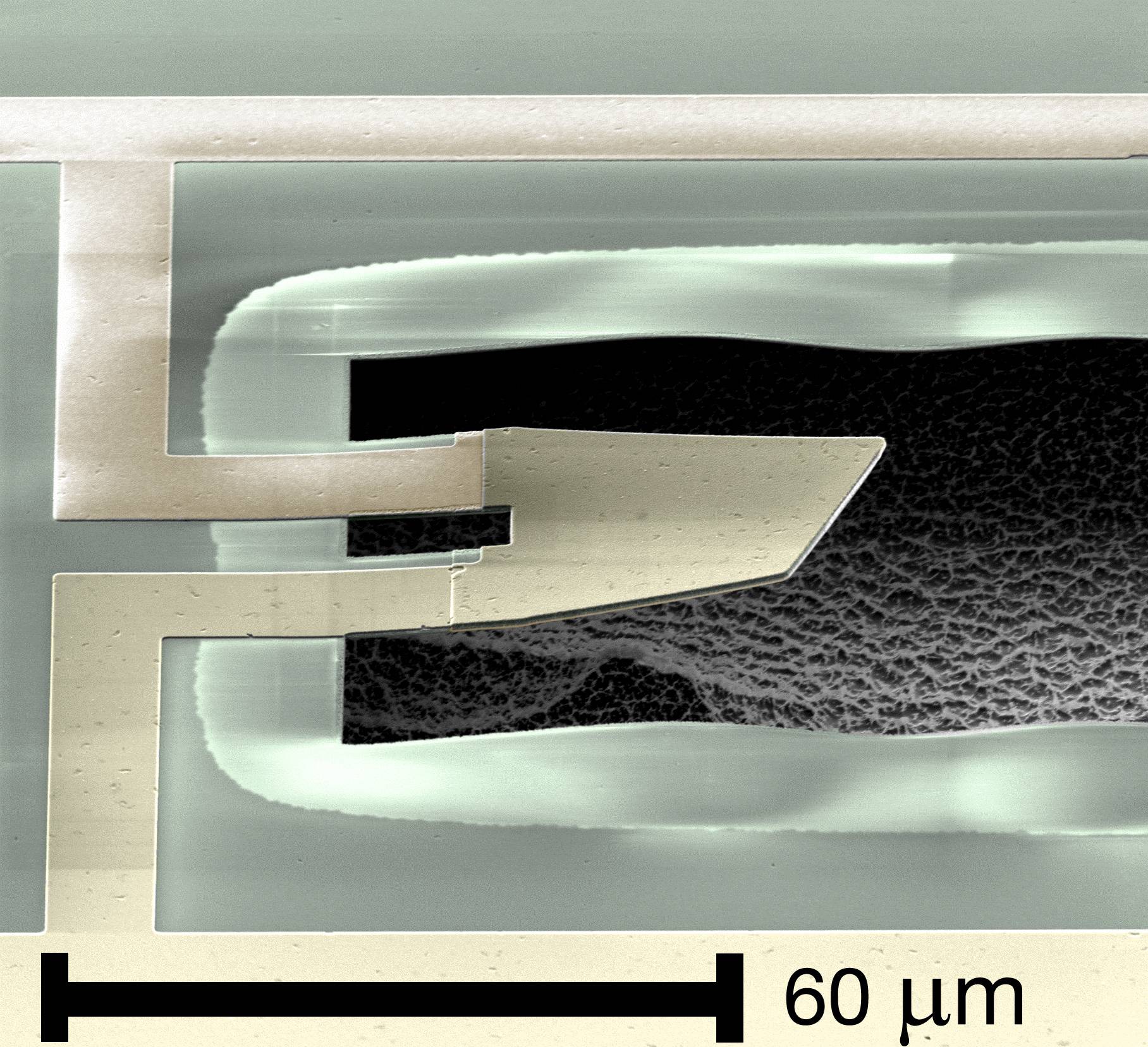
В 2010 году Аарон О’Коннелл поместил небольшую металлическую пластину в непрозрачную вакуумную камеру, которую охладил почти до абсолютного нуля. Затем он придал импульс пластине, чтобы она вибрировала. Однако датчик положения показал, что пластина вибрировала и была спокойна одновременно, что точно соответствовало теоретической квантовой физике. Этим впервые был доказан принцип суперпозиции на макрообъектах. В изолированных условиях, когда не происходит взаимодействия квантовых систем, объект может одновременно находиться в неограниченном количестве любых возможных положений, как если бы он больше не был материальным. (Подробно, видео)
Квантовый Чеширский кот и физика
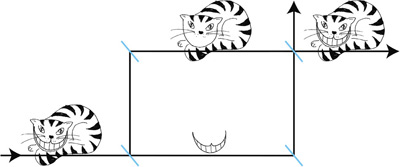
В 2014 году Тобиас Денкмайр и его коллеги разделили поток нейтронов на два пучка и провели серию сложных измерений. Выяснилось, что при определенных обстоятельствах нейтроны могут находиться в одном пучке, а их же магнитный момент в другом пучке. Таким образом был подтвержден квантовый парадокс улыбки Чеширского кота, когда частицы и их свойства могут находиться по нашему восприятию в разных частях пространства, как улыбка отдельно от кота в сказки «Алиса в стране чудес». В очередной раз квантовая физика оказалась загадочней и удивительней любой сказки! (Подробно, видео англ.)
(Графическая версия статьи)
Спасибо за чтение! Теперь вы стали немного умнее и от этого наш мир чуточку посветлел. Поделитесь ссылкой на эту статью с друзьями и мир станет еще лучше!
Автор Михаил Радуга, www.aing.ru
(Книга «Фаза»)
Подписаться на новости:







НУЖНА ПОМОЩЬ: подержите наши исследования!
_______________________
