Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас.

Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.

Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.

В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!

Жду ваших заказов!

С уважением

Пользовательское соглашение

Политика конфиденциальности

Определите сопротивление резистора который необходимо включить в коллекторную цепь усилителя. Бесплатный доступ к решению задач

Зарегистрируйся в два клика и получи неограниченный доступ к материалам, а также промокод на новый заказ в Автор24. Это бесплатно.

Условие

Определите сопротивление резистора, который необходимо включить в коллекторную цепь усилителя (см. рис. 6.44, а), чтобы ток коллектора Iк составлял 3 мА при Uкэ = 7 В, Ек = 16 В.

Решение

Для коллекторной цепи транзистора по второму закону Кирхгофа можно записать Ек = Iк · Rк + Uкэ Отсюда и определим сопротивление резистора: RK=EK-UКЭIK=16-73∙10-3=3 000 (Ом)

Зарегистрируйся, чтобы продолжить изучение работы

и получи доступ ко всей экосистеме Автор24

Больше решений задач по электронике, электротехнике, радиотехнике:

Все Решенные задачи по электронике, электротехнике, радиотехнике

Закажи решение задач

Наш проект является банком работ по всем школьным и студенческим предметам. Если вы не хотите тратить время на написание работ по ненужным предметам или ищете шаблон для своей работы — он есть у нас.

Не нашел ответ на свой вопрос?

Опиши, с чем тебе нужна помощь. Эксперты Автор24 бесплатно ответят тебе в течение часа

Прикрепить файл

Твой вопрос отправлен

Скоро мы пришлем ответ экпертов Автор24 тебе на почту

Помощь эксперта

Нужна помощь по теме или написание схожей работы? Свяжись напрямую с автором и обсуди заказ.

5

Kirchhoff1

Электроника, электротехника, радиотехника 677 заказов

Отправить письмо схожим авторам, которые сейчас на сайте

Регистрация прошла успешно!

Теперь вам доступен полный фрагмент работы, а также открыт доступ ко всем сервисам
экосистемы

Введи почту

Зарегистрируйся через почту и получи неограниченный доступ к материалам. Это бесплатно.

Читать тексты на сайте можно без ограничений. Однако для копирования и использования работ нужно зарегистрироваться в экосистеме Автор24. Это бесплатно.

20.3 Сопротивление и удельное сопротивление – College Physics

Глава 20 Электрический ток, сопротивление и закон Ома

Резюме

• Объясните понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рис. 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра [латекс]{R}[/латекс] прямо пропорционально его длине [латекс]{L}[/латекс], аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле, [латекс]{R}[/латекс] обратно пропорционален площади поперечного сечения цилиндра [латекс]{А}[/латекс].

Рисунок 1.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Мы определяем удельное сопротивление  [латекс]{\rho}[/латекс] вещества, так что сопротивление  [латекс]{R}[/латекс] объекта прямо пропорционально [латекс]{\ро}[/латекс ]. Удельное сопротивление [латекс] {\ rho} [/латекс] — это внутреннее свойство материала, не зависящее от его формы или размера. Сопротивление [латекс]{R}[/латекс] однородного цилиндра длиной [латекс]{L}[/латекс], площадью поперечного сечения [латекс]{А}[/латекс], изготовленного из материала с удельным сопротивлением [латекс]{\rho}[/латекс], составляет

[латекс] {R =} [/латекс] [латекс] {\ гидроразрыва {\ Rho L} {A}} [/латекс] .

В таблице 1 приведены репрезентативные значения [латекс]{\ро}[/латекс]. Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах. 9{11}}[/латекс] Таблица 1. Удельное сопротивление [латекс]{\rho}[/латекс] различных материалов при 20ºC

Пример 1.

Нить накала автомобильной фары изготовлена ​​из вольфрама и имеет морозостойкость [латекс]{0,350 \;\Омега}[/латекс]. Если нить представляет собой цилиндр длиной 4,00 см (можно свернуть в спираль для экономии места), то каков ее диаметр?

Стратегия

Мы можем преобразовать уравнение [латекс]{R = \frac{\rho L}{A}}[/латекс], чтобы найти площадь поперечного сечения [латекс]{А}[/латекс] нити из предоставленной информации. Тогда его диаметр можно найти, предполагая, что он имеет круглое поперечное сечение. 9{-5} \;\text{m}} \end{array}.[/latex]

Обсуждение

Диаметр чуть меньше одной десятой миллиметра. Он заключен в кавычки только с двумя цифрами, потому что [латекс]{\rho}[/латекс] известен только с двумя цифрами.

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.) И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или менее) удельное сопротивление [латекс] {\ rho} [/латекс] зависит от изменения температуры [латекс] {\ Delta T} [/латекс], как выражается в следующем уравнении 9.0005

[латекс]{ \rho = \rho_{0} (1 + \alpha \Delta T)},[/latex]

, где [latex]{\rho_0}[/latex] — исходное удельное сопротивление, а [latex]{\ alpha}[/latex] — температурный коэффициент удельного сопротивления . (См. значения [латекс] {\ альфа} [/латекс] в таблице 2 ниже.) Для больших изменений температуры [латекс] {\ альфа} [/латекс] может варьироваться, или может потребоваться нелинейное уравнение, чтобы найти [ латекс] {\ rho} [/латекс]. Обратите внимание, что [латекс] {\ альфа} [/ латекс] положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет [латекс] {\ альфа} [/латекс] близок к нулю (до трех цифр по шкале в таблице 2), поэтому его удельное сопротивление лишь незначительно зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Обратите внимание, что [латекс]{\альфа}[/латекс] имеет отрицательное значение для полупроводников, перечисленных в таблице 2, а это означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшать [латекс] {\ rho} [/латекс] с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, так как [латекс]{R_0}[/латекс] прямо пропорционален [латекс]{\ро}[/латекс]. Для цилиндра мы знаем [латекс]{R = \rho L/A}[/латекс], и поэтому, если [латекс]{L}[/латекс] и [латекс]{А}[/латекс] не меняются сильно зависит от температуры, [латекс] {R} [/латекс] будет иметь ту же температурную зависимость, что и [латекс] {\ rho} [/латекс]. (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на [латекс]{L}[/латекс] и [латекс]{А}[ /latex] примерно на два порядка меньше, чем на [latex]{\rho}[/latex]. ) Таким образом,

[латекс]{R = R_0(1 + \alpha \Delta T)}[/латекс]

— температурная зависимость сопротивления объекта, где [латекс]{R_0}[/латекс] — исходное сопротивление, а [латекс]{R}[/латекс] — сопротивление после изменения температуры [латекс]{\ Дельта Т}[/латекс]. Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Пример 2: Расчет сопротивления: сопротивление горячей нити

Хотя следует соблюдать осторожность при нанесении [латекса]{ \rho = \rho_0(1 + \alpha \Delta T)}[/latex ] и [латекс]{R = R_0(1 + \alpha \Delta T)}[/латекс] для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо при очень больших изменениях температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температуру повысить с комнатной (20°С) до типичной рабочей температуры 2850°С? 9{\circ}C)]} \\[1em] & {4.8 \;\Omega} \end{array}.[/latex]

Обсуждение

Это значение согласуется с примером сопротивления фары в Примере 1 Глава 20.2 Закон Ома: сопротивление и простые цепи.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

• Сопротивление [латекс]{R}[/латекс] цилиндра длиной [латекс]{L}[/латекс] и площадью поперечного сечения [латекс]{А}[/латекс] равно [латекс]{R = \frac{\rho L}{A}}[/latex], где [latex]{\rho}[/latex] — удельное сопротивление материала.
• Значения [латекс]{\rho}[/латекс] в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры [латекс] {\ Delta T} [/ латекс] удельное сопротивление равно [латекс] {\ rho = \ rho_0 (1 + \ alpha \ Delta T)} [/ латекс], где [латекс] {\ rho_0}[/latex] — исходное удельное сопротивление, а αα — температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения [латекс]{\альфа}[/латекс], температурного коэффициента удельного сопротивления.
• Сопротивление [латекс]{R}[/латекс] объекта также зависит от температуры: [латекс]{R = R_0(1 + \alpha \Delta T)}[/латекс], где [латекс]{R_0} [/latex] — исходное сопротивление, а [latex]{R}[/latex] — сопротивление после изменения температуры.

Задачи и упражнения

1: Чему равно сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?

2: Диаметр медной проволоки 0-го калибра 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.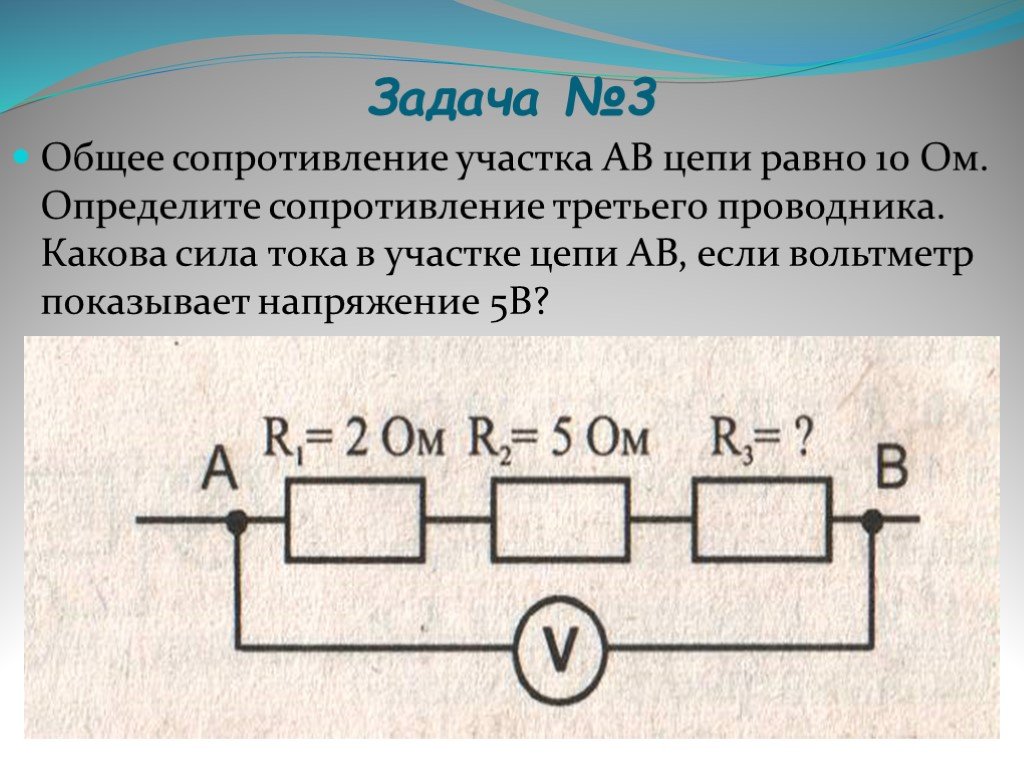

3: Если вольфрамовая нить накаливания диаметром 0,100 мм в лампочке должна иметь сопротивление [латекс]{0,200 \;\Омега}[/латекс] при 20,0ºC, какой длины она должна быть?

4: Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке). 93 \;\text{V}}[/latex] применяется к нему? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц). в габаритах? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7: Резистор из нихромовой проволоки используется в тех случаях, когда его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8: Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9: Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит чисто углеродные резисторы. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10: (a) Из какого материала изготовлен провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление [латекс]{77,7 \;\Омега}[/латекс] при 20,0ºC ? б) Каково его сопротивление при 150°С?

11: При постоянном температурном коэффициенте удельного сопротивления, каково максимальное процентное уменьшение сопротивления константановой проволоки, начиная с 20,0ºC?

12: Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?

13: Медная проволока имеет сопротивление [латекс]{0,500 \;\Омега}[/латекс] при 20,0ºC, а железная проволока имеет сопротивление [латекс]{0,525 \;\Омега}[ /латекс] при той же температуре. При какой температуре их сопротивления равны? 9{\circ} \text{C}}[/latex]), когда он имеет ту же температуру, что и пациент. {\circ} \text{C}}[/латекс]. б) На сколько процентов ваш ответ отличается от ответа в примере?

16: Необоснованные результаты

(a) До какой температуры нужно нагреть резистор, сделанный из константана, чтобы удвоить его сопротивление при постоянном температурном коэффициенте удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?

Сноски

1. 1 Значения сильно зависят от количества и типов примесей
2. 2 Значения при 20°C.

Глоссарий

Удельное сопротивление

внутреннее свойство материала, независимое от его формы или размера, прямо пропорциональное сопротивлению, обозначаемому ρ

температурный коэффициент удельного сопротивления

эмпирическая величина, обозначаемая α , которая описывает изменение сопротивления или удельного сопротивления материала при изменении температуры

Как найти сопротивление чего-либо с помощью моста Уитстона

Найти сопротивление очень просто, все, что вам нужно сделать, это поместить в него резисторы определенного типа.

Каково сопротивление любого данного материала?

Сопротивление — это способность останавливать протекание через них тока.

Какая теория использовалась для поиска сопротивления?

Мост Уитстона используется для определения сопротивления.

Что такое мост Уитстона?

Мост Уитстона — это электрическая цепь, используемая для измерения неизвестного электрического сопротивления путем уравновешивания двух ветвей мостовой схемы, одна из которых включает неизвестный компонент. Его работа аналогична оригинальному потенциометру. Он был изобретен Сэмюэлем Хантером Кристи в 1833 году и улучшен и популяризирован сэром Чарльзом Уитстоном в 1843 году. Одно из первых применений моста Уитстона было для анализа и сравнения почв.

Цель: Узнать сопротивление угольного резистора.

Теория: Соотношение 1 ^st комбинации резисторов равно соотношению 2 ^nd комбинаций резисторов. (Вы поймете это позже, когда увидите приведенную ниже диаграмму.)

Вывод:

Сначала первое правило Кирхгофа используется для нахождения токов в соединениях B и D :

Затем , второе правило Кирхгофа используется для нахождения напряжения в петлях ABD и BCD :

Когда мост сбалансирован, затем I _G = 0, так что второй набор уравнений может быть переверт. Разделен и перегружен, давая:

от первого правила, I ₃ = I _x и I ₁ = I ₂ 2 2 2 2 2 2 2 2 2 2 _{2 1} = 2 ₁ . Искомое значение R _x теперь известен как:

Если известны значения всех четырех резисторов и напряжение питания ( В _S ), а сопротивление гальванометра достаточно велико, чтобы I _G можно пренебречь, напряжение на мосту ( В _G ) можно найти, вычислив напряжение от каждого делителя потенциала и вычитая одно из другого. Уравнение для этого:

, где В _G  является напряжением узла B относительно узла D.

Необходимые материалы:

Шкала, провод железного элемента, комбинация нескольких резисторов, соединительный провод, вольтметр (я использую мультиметр).

 Процедура

Процедура:

1.      Возьмите весы (я использую весы из нержавеющей стали).

2.     Обмотайте его изолентой, чтобы он не проводил ток.

3.      Теперь возьмите железный элемент

4.      Свяжите, как показано на рисунке.

5.     Подсоедините провода и резистор на весах.

6.     Подключите мультиметр в соответствии со схемой, приведенной выше.

7.     Подсоедините провод аккумулятора к проводу весов. Положительный на один конец и отрицательный на второй конец.

8.      Установите мультиметр так, чтобы милливольтаж стал нулевым или почти нулевым.

9.     Измерьте показания весов.

10. Положительный провод должен быть подключен к известному резистору. А минус должен быть с неизвестным резистором. Вы также можете увидеть в цепи.

11. Длина провода между плюсом и проводом мультиметра R1. А длина провода между минусом и проводом гальванометра R2.

12. Теперь осталось сделать последний шаг и найти сопротивление неизвестного сопротивления.

13. Показания моего мультиметра достигают 0,6 В, а затем я читаю, что R1 равно 10, а R2 остальное 20.

14. Теперь посчитайте.

Сопротивление неизвестного резистора 36 Ом.

Преимущества:

          1.      Это самый безопасный метод или, можно сказать, более легкий метод для работы.

          2.      Можно найти очень малое сопротивление, а также можно найти очень высокое сопротивление, изменив значение тока.

          3.      Не требует тяжелых металлов.

          4.      Очень экологичный.

          5.     Отсутствие загрязнения.

Недостатки:

         1.      Это дает вам точное значение, которое вы не можете использовать, поскольку приборы, которые дают, требуют точного количества резистора.

         2.      Если провод нигде не подключен должным образом, вы получите правильное значение.

         3.       Любая ошибка может привести к серьезному вреду для здоровья.

         4.      Всегда надевайте изолятор при работе с высоким напряжением, чтобы определить высокое сопротивление. Если забыли, это может привести к поражению электрическим током. 9.

         Так что работайте усердно, и когда вы привыкнете к этому, вам будет очень легко это делать.

Исходный код проекта

Принципиальные схемы

Рубрики: Electronic Projects
С тегами: сопротивление, мост Уитстона
 

Расчет параллельного сопротивления — Pi My Life Up

В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления.

Параллельное сопротивление является полезной частью электроники, но его может быть трудно рассчитать, когда вы начинаете иметь дело с более чем двумя резисторами.

Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Такое поведение удобно, когда вам нужно определенное сопротивление, но у вас нет резистора, соответствующего требуемому значению.

Уменьшение сопротивления вызвано тем, что у тока больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больший ток через цепь и, следовательно, уменьшает общее сопротивление, с которым сталкивается ваша цепь.

Например, в цепи с двумя параллельными резисторами одинакового номинала сопротивление уменьшится ровно вдвое. Математика немного отличается для разных сопротивлений и если у вас больше резисторов. Мы углубимся в это позже в руководстве.

Если вы хотите увеличить сопротивление цепи, а не уменьшить его, то вместо этого вы можете использовать последовательно соединенные резисторы.

Чтобы рассчитать общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает этот процесс.

Если вас смущают цвета резистора, обязательно ознакомьтесь с руководством по цветовой маркировке резистора, поскольку оно научит вас всему, что вам нужно знать.

Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление. Затем введите значение для каждого резистора.

Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.

Количество резисторов:

Резистор 1:

Резистор 2:

Расчет общего сопротивления при параллельном соединении

Если вы предпочитаете учиться, вы можете рассчитать сопротивление параллельно подключенных резисторов вручную. Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами, включенными параллельно.

Существуют три различных уравнения, которые можно использовать для параллельного расчета общего сопротивления.

Суммарное сопротивление двух одинаковых резисторов

Первое уравнение следует использовать только в том случае, если у вас есть два параллельных резистора с одинаковым сопротивлением.

Если у вас есть два резистора с одинаковым сопротивлением параллельно, то общее сопротивление равно половине одного резистора.

Пример использования уравнения

Для этого примера предположим, что у нас есть два резистора по 200 Ом , включенных параллельно, как показано на схеме ниже.

Зная, что параллельно подключены только два резистора и что они одного номинала, мы можем использовать наше уравнение.

Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).

Чтобы получить общее сопротивление, все, что нам нужно сделать сейчас, это разделить наше значение 200 Ом на 2 .

Ответ очень легко вычислить: 100 .

Теперь у вас должно быть представление о том, как справиться с простейшим сценарием с двумя параллельными резисторами одинакового номинала.

Суммарное сопротивление двух разных резисторов

Второе уравнение представляет собой упрощенную версию основного уравнения, которое мы будем использовать позже. Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.

Есть несколько других процессов, которые необходимо выполнить для расчета сопротивления двух параллельных резисторов, но это не намного сложнее.

Пример использования уравнения

В этом примере предполагается, что у нас есть цепь с двумя параллельными резисторами разных номиналов.

В этой схеме у нас есть резистор 600 Ом и резистор 250 Ом , соединенные параллельно. Теперь мы хотим определить общее сопротивление, обеспечиваемое этими резисторами.

Для начала нам нужно заполнить наше уравнение, где R1 — это резистор 600  Ом, а значение R2 — 9. 0018 250  Ом резистор.

Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение, прежде чем продолжить.

Умножение 600 (R1) на 250 (R2) должно дать вам результат 150,000 . Добавление 600 (R1) к 250 (R2) должно дать вам ответ 850 .

Выработав оба значения, все, что нам нужно сделать, это разделить верхнее число на нижнее число. Сделав это, мы можем определить общее сопротивление двух резисторов, включенных параллельно.

Математика, которую вы должны выполнить в этом примере, равна 150 000 , деленная на 850 . Отсюда вы должны получить результат 176,47 . Будут лишние десятичные знаки, но мы округлим до ближайших двух.

Теперь у вас должно быть представление о том, как рассчитать общее сопротивление двух параллельно соединенных резисторов.

Далее мы покажем вам, как обращаться с тремя или более резисторами. Это уравнение представляет собой немного более сложный процесс, так как оно включает в себя много делений, что приводит к большим десятичным числам.

Общее сопротивление нескольких резисторов

Третье и последнее уравнение, с которым мы будем иметь дело, это то, которое вы будете использовать для трех или более резисторов, включенных параллельно.

Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.

Единственным недостатком этого уравнения является то, что оно занимает больше времени, чем больше резисторов вы добавляете.

Простым решением является использование параллельного калькулятора резисторов, который мы включили выше.

Пример использования уравнения

В этом примере мы покажем, как использовать более сложное уравнение параллельного резистора.

Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1 кОм (R4) .

Для начала нам нужно заполнить уравнение всеми нашими значениями.

Каждый из наших номиналов резисторов будет делителем 1 , и вы можете добавить в это уравнение столько резисторов, сколько вам нужно. В этом примере мы обрабатываем только четыре.

Наш следующий шаг — разделить 1 на значения каждого из наших резисторов . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.

Например, в нашем расчете мы делим 1 на 100 , что дает нам результат 0,01 .

После того, как вы закончили деление каждого набора значений, теперь нам нужно сложить каждое значение вместе.

Для нашего примера схемы это будет означать: 0,01 + 0,004 + 0,005 + 0,001 . К счастью для нас, это довольно плавно складывается и дает нам красивое круглое число 0,02 .

Далее мы должны переместить делитель из левой части уравнения в правую.