Урок 35. Контрольная работа по теме «Мпгнитное поле»

РАЗДЕЛ I. Поурочные разработки по физике к учебнику С. В. Громова

Урок 35. Контрольная работа

 

Вариант 1

1. Самолет летит горизонтально со скоростью 1200 км/ч. Найдите разность потенциалов, возникающую на концах крыльев, если вертикальная составляющая индукции магнитного поля Земли равна 5 · 10^-5 Тл. Размах крыльев равен 40 м.

2. К катушке индуктивностью 0,01 Гн проходит ток силой 20 А. Определите ЭДС самоиндукции, которая возникает в катушке при исчезновении в ней тока за 0,002 с.

3. Катушка сопротивлением 100 Ом, состоящая из 1000 витков, внесена в однородное магнитное поле. Площадь поперечного сечения каждого витка равна 5 см². В течение некоторого времени индукция магнитного поля уменьшилась с 0,8 Тл до 0,3 Тл. Какой заряд индуцирован в проводнике за это время?

4. Какой заряд пройдет через поперечное сечение витка, сопротивлением 0,03 Ом, при уменьшении магнитного потока внутри витка на 12 мВб?

5. Из алюминиевой проволоки, площадь поперечного сечения которой равна 1 мм², сделано кольцо радиусом 10 см. Перпендикулярно плоскости кольца за 0,01 с включают магнитное поле, у которого индукция равна 1 Тл. Найти среднее значение индукционного тока, возникающего за это время в кольце. Удельное сопротивление алюминия равно 2,8 · 10^-8 Ом·м.

6. В однородном магнитном поле, у которого индукция равна 0,1 Тл, проволочный виток расположен так, что его плотность перпендикулярна магнитному полю. Площадь поперечного сечения проволочного витка равна 100 см². Виток замкнут на гальванометр. При повороте витка на угол 90° через гальванометр проходит заряд, равный 1 мКл. Найдите сопротивление витка.      

 

Вариант 2

1. Определите индуктивность катушки, если известно, что сила тока в цепи за 0,02 с возрастает до максимума и равна 4 А, создавая при этом ЭДС самоиндукции 12 В.

2. Катушка, имеющая 100 витков, находится в магнитном поле, индукция которого уменьшилась от 8 Тл до 2 Тл в течение 0,4 с. Определите значение ЭДС индукции, если площадь поперечного сечения катушки равна 50 см², а плоскость витков перпендикулярна силовым линиям поля.

3. Проводник длиной 2 м и сопротивлением 0,02 Ом движется в магнитном поле со скоростью 6 м/с. перпендикулярно силовым линиям поля. Чему равно значение силы тока, возникающего в проводнике, если его замкнуть на коротко? Индукция магнитного поля равно 10 мТл.

4. Катушка сопротивлением 50 Ом и индуктивностью 0,001 Гн находится в магнитном поле. При равномерном изменении магнитного поля, поток магнитной индукции возрос на 0,001 Вб и сила тока в катушке увеличилась на 0,1 А Какой заряд прошел за это время по катушке?

5. Рамка из проволоки сопротивлением 0,01 Ом равномерно вращается в однородном магнитном поле, у которого индукция равна 0,05 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 100 см². Определите, какой заряд пройдет через рамку за время поворота ее на угол 30° (от 0° до 30°)

6. Проволочный виток, имеющий площадь поперечного сечения 100 см², разрезан в некоторой точке, и в разрез включен конденсатор емкостью 40 мкФ. Виток помещен в однородном магнитном поле, линии индукции которого перпендикулярны плоскости витка. Индукция магнитного поля равномерно изменяется на 0,01 Тл за 1 секунду. Найдите заряд конденсатора.

 

Рекомендации к проверке: «3» за задачу 1, 2; «4» за задачу 1, 2, 3 или 2, 4; «5» за задачу 3, 4, 5 или 3, 4, 6.

Ученик сам выбирает задачи.

14.2 Самоиндукция и катушки индуктивности — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

• Соотносить скорость изменения тока с ЭДС индукции, создаваемой этим током в та же схема
• Расчет собственной индуктивности цилиндрического соленоида
• Расчет собственной индуктивности прямоугольного тороида

Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи. Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ — да, и это явление называется самоиндукция .

Катушки индуктивности

На рис. 14.5 показаны некоторые силовые линии магнитного поля, вызванные током в круглой проволочной петле. Если ток постоянен, магнитный поток через контур также постоянен. Однако если бы ток I

менялся со временем, скажем, сразу после замыкания ключа S, то соответственно изменялся бы и магнитный поток ΦmΦm. Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС εε, где

ε=−dΦmdt.ε=−dΦmdt.

14,6

Поскольку магнитное поле, создаваемое проводом с током, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть

Φм∝I.Φм∝I.

14,7

Рисунок 14,5 Магнитное поле создается током I в контуре. Если бы I менялось со временем, магнитный поток через контур также менялся бы и в контуре индуцировалась бы ЭДС.

Это также может быть записано как

Φm=LIΦm=LI

14,8

, где константа пропорциональности L известна как самоиндукция проволочной петли. Если в петле N витков, это уравнение принимает вид

.

НΦм=LI.NΦм=LI.

14,9

По соглашению положительный смысл нормали к контуру связан с током по правилу правой руки, поэтому на рис. 14.5 нормаль направлена ​​вниз. При таком соглашении ΦmΦm положительно в уравнении 14.9, поэтому

L всегда имеет положительное значение .

Для контура с Н витков, ε=-NdΦm/dt,ε=-NdΦm/dt, поэтому ЭДС индукции может быть записана через самоиндукцию как

ε=-LdIdt. ε=-LdIdt.

14.10

При использовании этого уравнения для определения L проще всего игнорировать знаки εanddI/dt, εanddI/dt и вычислить L как

L=|ε||dI/dt|.L=|ε||dI/dt|.

Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией. Например, помимо проволочной петли длинный прямой провод обладает собственной индуктивностью, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно обнаружить при подключении к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.

Элемент цепи, используемый для обеспечения собственной индуктивности, известен как индуктор.

Он представлен символом, показанным на рис. 14.6, который напоминает катушку проволоки, основную форму катушки индуктивности. На рис. 14.7 показаны несколько типов катушек индуктивности, обычно используемых в цепях.

Рисунок 14,6 Символ, используемый для обозначения катушки индуктивности в цепи.

Рисунок 14,7 Различные индукторы. Независимо от того, заключены ли они в капсулу, как показаны три верхние, или намотаны на катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку провода. (кредит: Уинделл Оскей)

В соответствии с законом Ленца отрицательный знак в уравнении 14.10 указывает на то, что ЭДС индукции на катушке индуктивности всегда имеет полярность, которая

противодействует изменению тока. Например, если бы ток, протекающий от А к В на рис. 14.8(а), увеличивался, ЭДС индукции (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8 (б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.

Рисунок 14,8 Индуцированная ЭДС на катушке индуктивности всегда противодействует изменению тока. Это можно представить как воображаемую батарею, заставляющую течь ток, противодействующий изменению в (а) и усиливающий изменение в (б).

Одним из распространенных применений индуктивности является определение сигналов светофора, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом, где остановится ожидающий автомобиль. Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику.

Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рис. 14.9).). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.

Рисунок 14,9 Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но и могут указать их приблизительную высоту над полом. (кредит: Alexbuirds/Wikimedia Commons)

Во вспышках фотокамер обнаружены большие наведенные напряжения. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или генератор для создания больших напряжений. Напомним из книги «Колебания о колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения.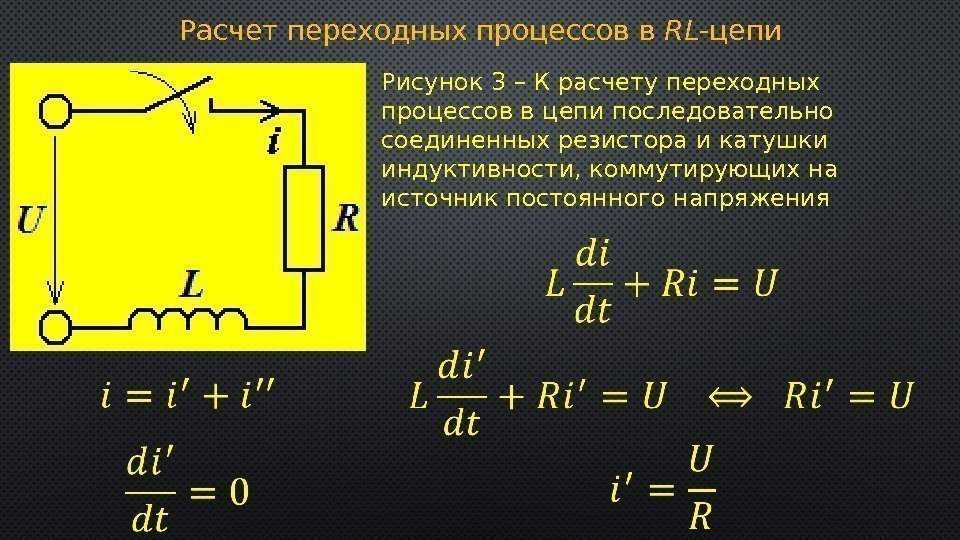

Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.

Пример 14.2

Самоиндукция катушки

ЭДС индукции 20 мВ измеряется на катушке из 50 тесно намотанных витков, при этом ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Чему равна собственная индуктивность катушки? б) Чему равен поток через каждый виток катушки при силе тока 5,0 А?

Стратегия

Обе части этой задачи дают всю информацию, необходимую для определения собственной индуктивности в части (а) или потока через каждый виток катушки в части (б). Необходимые уравнения: уравнение 14.10 для части (а) и уравнение 14.9.для части (б).

Решение

1. Игнорируя отрицательный знак и используя величины, мы имеем из уравнения 14.10,

   L=εdI/dt=20 мВ 5,0 А/0,10 с=4,0×10-4H.L=εdI/dt=20 мВ 5,0 А/0,10 с=4,0×10-4H.
2. Из уравнения 14.9 поток определяется через ток как Φm=LI/NΦm=LI/N, поэтому

   Φm=(4,0×10-4H)(5,0A)50витков=4,0×10-5Wb.Φm=(4,0×10-4H)(5,0A)50витков=4,0×10-5Wb.

Значение

Собственная индуктивность и поток, рассчитанные в частях (а) и (б), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не меняется во времени, поэтому ЭДС не индуцируется.

Проверьте свое понимание 14.2

Ток протекает через катушку индуктивности на рис. 14.8 от B

к A вместо A к B , как показано. Ток увеличивается или уменьшается, чтобы создать ЭДС, указанную на диаграмме (а)? На схеме (б)?

Проверьте свое понимание 14.3

Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?

Хороший подход к расчету собственной индуктивности катушки индуктивности состоит из следующих шагов:

Стратегия решения проблем

Самоиндукция

1. Предположим, что через индуктор протекает ток I .
2. Определите магнитное поле B→B→, создаваемое током. Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
3. Получить магнитный поток, Фм.Фм.
4. Зная магнитный поток, самоиндукцию можно найти по уравнению 14.9., L=NΦm/IL=NΦm/I.

Чтобы продемонстрировать эту процедуру, мы теперь рассчитаем собственные индуктивности двух катушек индуктивности.

Цилиндрический соленоид

Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A и N витков провода. Мы предполагаем, что длина соленоида настолько больше его диаметра, что мы можем принять магнитное поле равным B=µ0nIB=µ0nI во всей внутренней части соленоида, т. е. пренебрегаем концевыми эффектами в соленоиде. С током I течет через катушки, магнитное поле, создаваемое внутри соленоида, равно

B=µ0(Nl)I,B=µ0(Nl)I,

14.11

, поэтому магнитный поток через один виток равен

.

Φm=BA=μ0NAlI.Φm=BA=μ0NAlI.

14.12

Используя уравнение 14.9, мы находим для собственной индуктивности соленоида

Lсоленоид=NΦmI=μ0N2Al.Lсоленоид=NΦmI=μ0N2Al.

14. 13

Если n=N/ln=N/l — число витков на единицу длины соленоида, мы можем записать уравнение 14.13 как

L=μ0(Nl)2Al=μ0n2Al=μ0n2(V),L=μ0(Nl)2Al=μ0n2Al=μ0n2(V),

14,14

, где V=AlV=Al — объем соленоида. Обратите внимание, что собственная индуктивность длинного соленоида зависит только от его физических свойств (таких как число витков провода на единицу длины и объем), а не от магнитного поля или тока. Это справедливо для катушек индуктивности в целом.

Прямоугольный тороид

Тороид с прямоугольным поперечным сечением показан на рис. 14.10. Внутренний и внешний радиусы тороида равны R1 и R2, hR1 и R2, а h — высота тороида. Применяя закон Ампера так же, как мы это делали в примере 13.8 для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также определяется выражением

B=μ0NI2πr, B=μ0NI2πr,

14,15

, где r — расстояние от центральной оси тороида. Поскольку поле изменяется внутри тороида, мы должны вычислить поток путем интегрирования по поперечному сечению тороида. Используя бесконечно малый элемент площади поперечного сечения da=hdrda=hdr, показанный на рис. 14.10, мы получаем

14.16

Рисунок 14.10 Расчет самоиндукции прямоугольного тороида.

Теперь из уравнения 14.16 получаем для собственной индуктивности прямоугольного тороида

L=NΦmI=μ0N2h3πlnR2R1.L=NΦmI=μ0N2h3πlnR2R1.

14.17

Как и ожидалось, собственная индуктивность является константой, определяемой только физическими свойствами тороида.

Проверьте свое понимание 14,4

(a) Рассчитайте собственную индуктивность соленоида, который туго намотан проволокой диаметром 0,10 см и имеет площадь поперечного сечения 0,90 см20,90 см2, длина 40 см. б) Если сила тока через соленоид равномерно уменьшается от 10 до 0 А за 0,10 с, то какая ЭДС индуцируется между концами соленоида?

Проверьте свое понимание 14,5

а) Чему равен магнитный поток через один виток соленоида с собственной индуктивностью 8,0×10−5H8,0×10−5H при протекании через него тока силой 3,0 А? Предположим, что соленоид имеет 1000 витков и намотан из проволоки диаметром 1,0 мм. б) Чему равна площадь поперечного сечения соленоида?

Общая физика II

Q1, Почему ЭДС индукции, возникающая в катушке индуктивности, называемой «счетчиком». или «обратная» ЭДС?

По закону Ленца ожидаем ЭДС индукции to противодействовать изменению — «противостоять» изменению.

Q4, Как можно намотать длинный кусок провода на катушке, чтобы провод имел пренебрежимо малую самоиндукцию?

Если проволока сдвоена, то половина ее закручена в одну сторону, а другая половина закручивается в другую, то магнитное поле, создаваемое одной половиной провода, просто нейтрализует магнитное поле. поле, созданное другой половиной.

Q5, Длинный тонкий провод намотан как соленоид с собственной индуктивностью L. Если он подключен через клеммы батарея, как максимальный ток зависит от L?

Максимальный ток — это установившийся ток и это , а не , на которые влияет самоиндукция.

Q6, Для показанной здесь последовательной цепи RL: может ли противо-ЭДС быть больше, чем ЭДС батареи?

Нет, противо-ЭДС никогда не может быть больше, чем э.д.с. батареи

Q7, Допустим переключатель на схеме выше был закрыт в течение длительного времени и внезапно открывается. Есть ли ток мгновенно упадет до нуля? Почему появляется искра на переключать контакты в момент размыкания переключателя?

Чем быстрее размыкается переключатель, т.е. чем быстрее мы пытаемся остановить ток — тем больше будет скорость при котором магнитное поле схлопывается. как то ставка увеличивается, напряжение увеличивается («противоэдс»), и это может быть здорово достаточно, чтобы вызвать дугу.

Q9, Обсудите сходство между запас энергии в электрическом поле заряженного конденсатора и энергия хранится в магнитном поле катушки с током.

Они очень похожи. Ранее мы говорили о энергия, хранящаяся в конденсаторе, в мельчайших деталях. Мы нашли общее энергия — потенциальная энергия U — равна

U = (1/2) C V ²

В этой главе мы нашли энергию, запасенную в катушке — потенциальная энергия U — должна быть

U = (1/2) L I ²

Q14, В LC-цепи, показанной на рис. 32.12 заряд на конденсаторе иногда равен нулю, хотя там есть ток в цепи. Как это возможно?

Когда заряд конденсатора равен нулю, в конденсаторе не запасается энергия. В это время максимально энергия, запасенная в катушке индуктивности, что означает максимальный ток.

Q16, Как определить, подключена ли цепь RLC? передемпфирован или недодемпфирован?

Если это недостаточно демпфированный , он проходит несколько колебаний.

Если передемпфирован, — , а не колебаться — он просто совершает одно длинное частичное колебание.

Q17 , Какое значение имеет критическое демпфирование в цепи RLC?

Критическое демпфирование описывает наименьшее сопротивление R , которое может иметь цепь и не колеблется . Ток угаснет до нуля быстрее чем при большем R. При большем R — для большего демпфирования — ток вымирает медленнее. Для меньшего R — для меньшего демпфирования — ток колеблется.

32,2, Пружина имеет радиус 4,00 см и индуктивностью 125 мкГн при удлинении до длины 2,00 м. Найдите приблизительное значение общего числа витков пружины?

«Пружина» — это всего лишь соленоид, так что это очень похоже на пример 32.1 на странице 941. Там мы нашли

L = _o N ² A / л

N ² = L л/ _или А

А = г ² = (0,04 м) ² = 0,005 026 м ²

N ² = L l/ _o А = (125 х 10 ^{— 6} )(2,0)/[(4 х 10 ^{— 7} )(0,005)]

N ² = 39,583

N = 199

32,12, Индуктор соленоида 30,0 см длиной и площадью поперечного сечения 4,00 см ² . Когда ток через соленоид уменьшается со скоростью 0,625 А/с, индуцированный ЭДС составляет 200 мкВ. Найдите количество витков на единицу длины соленоид.

На странице 940 у нас есть Уравнение 32.3,

L = [200 x 10 ^{— 6} В]/[0,625 А/с]

L = 0,000 32 H = 0,32 мГн

L = 3,2 x 10 ^{— 4} H

На следующей странице, стр. 941, мы имеем уравнение 32.5, которое дает индуктивность соленоида,

L = _o n ² A l

n ² = L / ( _o A l)

A = 4,0 см ² [м/100 см] ² = 4 x 10 ^{— 4} м ²

Будьте осторожны с преобразованием единиц измерения. Это просто — но все равно будь осторожен ! Хотя это «легче» или «более удобно» говорить о площади в квадратных сантиметрах и длине в сантиметрах, к тому моменту, когда мы делаем расчет, нам нужна площадь в квадратных метрах и длина в метрах. Не думай даже о футах, ярдах, фарлонгах, или миль. Это , как НАСА разбило один из марсианских кораблей. зонды !

n ² = (3,2 х 10 ^{— 4} )/[(4 x 10 ^{— 7} ) (4 x 10 ^{— 4} ) (0,30)]

N ² = 2,12 x 10 ⁶

n = 1,460

32,19, , , , , , , , , , . Цепь RL, в которой L = 2,5 Гн и ток увеличивается до 90% от его конечное значение через 3,0 с.

Мы знаем об экспоненциальном поведении ток, из уравнения 32.7 на стр. 942,

где постоянная времени

R = (2,5/1,3)

R = 1,92

32,22, Индуктивность напряжением 15,0 Гн и сопротивлением 30,0 Ом подключено к сети напряжением 100 В. батарея. Какова скорость увеличения тока

(а) при t = 0 и

(б) при t = 1,50 с?

= (15/30) с = 0,5 с

Мы уже использовали уравнение 32.7 со страницы 9.42,

Для этой схемы мы знаем конечный ток,

I _f = V/R = 100 В/30 = 3,33 А

Это описывает ток , но нам нужна скорость изменения тока,

dI/dt] _{(t = 0,0 с)} = 16,7 А/с

dI/dt] _{(t = 3,0 с)} = 3,73 А/с 5

32.32, Рассчитайте энергию, связанную с магнитным полем 200-виткового соленоида, в котором протекает ток 1,75 А создает поток 3,70 x 10 ^{— 4} Вб в каждый ход.

U = (1/2) L I ²

L = N _B /I

L = (200)(3,70 x 10 ^{— 4} )/1,75

L = 4,23 x 10 ^{— 2} H

U = (1/2) L I ² = (0,5)(4,23 x 10 ^{— 2} )(1,75) 9 ^{2 6,5 x 10 — 2 Дж}

U = 0,065 Дж

32,53, Конденсатор емкостью 1,00 мкФ заряжается от источника питания 40,0 В. Тогда полностью заряженный конденсатор разряжается через катушку индуктивности 10,0 мГн. Найдите максимальную силу тока в результирующие колебания.

Q _макс. = C V = (1 x 10 ^{— 6} F)(40 В)

Q _макс. = 40 x 10 ^{— 6} C

Из уравнения 32.23 или 32.25 мы найти, что

I _max = Q _max

и из уравнения 32.22 мы знаем резонансную частоту

= 1/SQRT[(0,010 H)(1 x 10 ^{— 6} F)]

= 1 х 10 ⁴ Гц

I _макс. = Q _макс. = (1 x 10 ⁴ )(40 x 10 ^{— 6} ) A

I _max = 0,4 A

 

32, 65 Рассмотрим LC-цепь, в которой L = 500 мГн и C = 0,100 мкФ.