Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Решено
Концы U-образной трубки на 26см выше уровня ртути.
После того как левое колено заполнили водой, она образовала столб высотой h. Вычислить h.
Решено
Определить угловое ускорение маховика, частота…
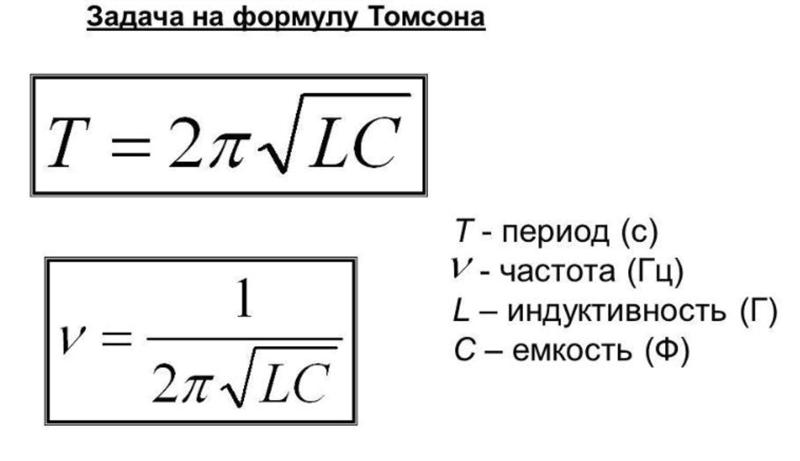
Колебательный контур имеет индуктивность L=1.6 мГн
Решено
Динамик подключен к выходу генератора электрических колебаний с частотой 170 Гц. Определите длину звуковой волны.
Решено
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
06.19
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Рассчитать энергию связи ядра алюминия 27 13 Al .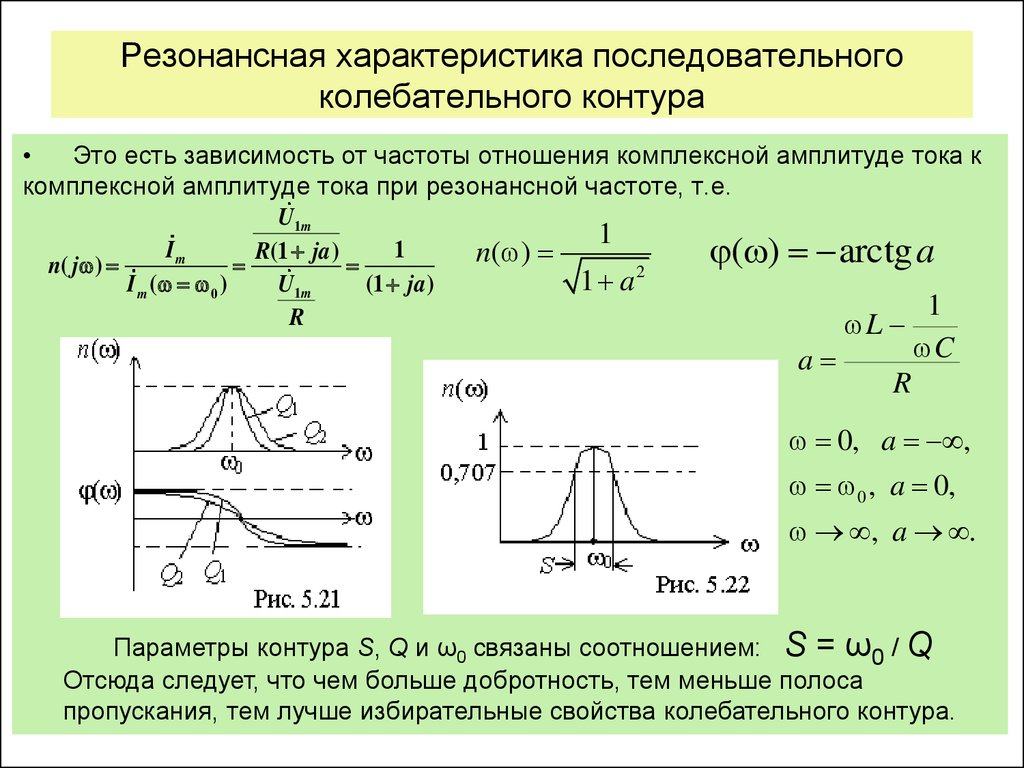
Если масса ядра алюминия 26, 91844 а.е.м
Решено
По проводнику, согнутому в виде прямоугольника со сторонами 8 и 12 см, течет ток силой 50 А. Определить напряженность Н и индукцию В магнитного поля в точке пересечения диагоналей прямоугольника.
Решено
15. Дано уравнение колебательного движения: х = 0,4 sin 5πt. Определить амплитуду, период колебания и смещение при t = 0,1с.
Решено
Определить длину волны красной границы фотоэффекта для серебра. Работа выхода для серебра равна 6,9•10 -19 Дж
К зажимам генератора постоянного тока с ЭДС в 200В и внутренним сопротивлением 0,6 Ом подключен нагреватель сопротивлением 14 Ом. Определите
Пользуйтесь нашим приложением
Что это такое и почему это важно?
Ключевые выводы
● Узнайте, как использовать формулу собственной частоты.
● Получите более полное представление о важности собственной частоты устройства или системы.
● Узнайте, как изменить собственную частоту устройства или системы.
Используя формулу собственной частоты, можно вычислить собственную частоту камертона.
Термины «природа» и «природный» объединены одним определением: «Существующий в природе или инициированный ею; не произведены и не затронуты человечеством». Это определение простое и прямое, но оно также определяет многие явления, которые мы, люди, постоянно черпаем для развития как области электроники, так и науки в целом.
Одним из таких естественных явлений является частота, которая охватывает различные области, включая область электроники. Говоря об электронных устройствах и системах, мы часто говорим о собственной частоте, которую можно рассчитать по формуле собственной частоты.
Что такое собственная частота?
Собственная частота объекта — это частота или скорость, с которой он естественным образом вибрирует, если его потревожить.
Объекты могут иметь более одной собственной частоты, и мы обычно используем гармонические осцилляторы в качестве инструмента для моделирования собственной частоты конкретного объекта.
Мы можем применить к объекту неестественную или принудительную частоту, которая равна собственной частоте объекта. В таких случаях мы фактически создаем резонанс, т. е. колебания на собственной частоте объекта. Если это происходит в определенных конструкциях, амплитуда колебаний будет продолжать увеличиваться, что приведет к разрушению конструкции.
Когда колебания системы эквивалентны ее собственной частоте, она формирует модели движения. Мы называем эти определенные характерные частоты нормальной модой объекта. Более того, собственная частота состоит из различных первичных факторов, а именно:
Мы называем частоту естественной вибрации объекта его собственной частотой.
Мы можем использовать гармонические осцилляторы в качестве инструментов для моделирования собственной частоты объекта.
Собственные частоты возникают естественным образом, когда мы воздействуем на объект физическим образом, в то время как объекты, которые вибрируют в соответствии с приложением определенной частоты, называются вынужденными частотами.
Если мы применим принудительную частоту, эквивалентную собственной частоте объекта, объект столкнется с резонансом.
Формула естественной частоты
Представьте себе пружину с шариком, представляющим массу, прикрепленным к ее концу. Пока шарик и пружина неподвижны, пружина растягивается лишь частично, и наш простой гармонический осциллятор находится в положении равновесия. Следовательно, натяжение пружин равно силе тяжести, которая тянет шарик (массу) вниз.
Как только мы переместим мяч из положения равновесия, возможны два исхода:
Он увеличивает натяжение пружины, т.
е. растягивает ее вниз.Дает гравитации возможность тянуть мяч вниз без напряжения противодействующей пружины, т.е. вы толкаете мяч вверх.
е. растягивает ее вниз.Независимо от того, какое действие вы предпримете, мяч начнет колебаться относительно положения равновесия.
Эта частота колебаний является собственной частотой, и мы измеряем ее в Гц (герцах). Таким образом, это обеспечит колебания в секунду в зависимости от свойств пружины и массы мяча.
Теперь мы будем использовать приведенный выше пример для расчета собственной частоты простого гармонического осциллятора. При расчете собственной частоты мы используем следующую формулу:
f = ω ÷ 2π
Здесь ω — это угловая частота колебаний, которую мы измеряем в радианах или секундах. Определим угловую частоту по следующей формуле:
ω = √(k ÷ m)
Это, в свою очередь, приводит нашу формулу к следующему:
f = √(k ÷ m) ÷ 2π k жесткость пружины m масса мяча Измеряем жесткость пружины в ньютонах на метр. Поскольку мы вычисляем собственную частоту по приведенной выше формуле, мы должны сначала определить жесткость пружины для системы. Обычно мы получаем это значение, проводя тесты. Однако для этого примера мы будем использовать 150 Н/м для представления k и 2 кг для описания нашей массы m . Теперь мы будем использовать эти значения, выполнив шаги расчета: f = √(150 Н/м ÷ 2 кг) ÷ 2π f = √(75 Гц) ÷ 2π 
Пружина с более высокой константой более жесткая и требует дополнительной силы для растяжения.4
f = 8.66 Hz ÷ 2π
f = 8.66 Hz ÷ 2(3.14)
f = 8.66 Hz ÷ 6.28
f = 1.3789 Hz
per
f = 1.38 Гц
Собственная частота составляет 1,38 Гц, что означает, что система колеблется почти полтора раза в секунду.
Важность расчета собственных частот
Мы обычно считаем собственные частоты и формы колебаний единственным наиболее важным свойством практически любой системы. Как вы можете себе представить, чрезмерные вибрации в любой системе приводят к структурным и функциональным проблемам.
Причина этого в том, что собственные частоты могут совпадать с резонансными частотами системы. Например, если вы приложите к системе изменяющуюся во времени силу и выберете частоту, эквивалентную одной из собственных частот, это приведет к вибрациям огромной амплитуды, которые могут подвергнуть вашу систему опасности.
Вот почему при проектировании механической системы важно рассчитать и убедиться, что собственные частоты вибрации намного превышают любую возможную частоту возбуждения, с которой может столкнуться ваша система.
Методы смещения собственных частот
Ниже приведены правила, позволяющие смещать собственные частоты и минимизировать вибрационную реакцию системы:
Чтобы увеличить собственную частоту, добавьте жесткость.
Чтобы уменьшить собственную частоту, добавьте массу.
Увеличение демпфирования снижает пиковый отклик, однако расширяет диапазон отклика.
Уменьшение демпфирования повышает пиковый отклик, однако сужает диапазон отклика.
Уменьшение амплитуд форсирования снижает реакцию на резонансной частоте.
Значение собственной частоты является одним из наиболее важных параметров или свойств любой системы. Необходимость для разработчиков знать точную точку частоты имеет решающее значение для функциональности, производительности и жизненного цикла системы.
Формула собственной частоты позволяет вычислить собственную частоту этого простого гармонического осциллятора.
Ваша компания может наблюдать за поведением цепей своих применимых проектов, используя формулу собственной частоты перед применением окончательного проекта или используя полнофункциональное программное обеспечение для проектирования и анализа печатных плат с полным набором инструментов моделирования.
Allegro PCB Editor интегрируется с инструментами анализа, предоставляя вам полную платформу для проектирования и моделирования. Вы можете изучить электрическое поведение линейных и нелинейных цепей, готовясь к созданию топологии печатной платы.
Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов. Чтобы посмотреть видео по связанным темам или узнать, что нового в нашем наборе инструментов для проектирования и анализа, подпишитесь на наш канал YouTube.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетите вебсайт Больше контента от Cadence PCB Solutions
УЗНАТЬ БОЛЬШЕ Конденсатор— Как рассчитать собственную частоту последовательной LC-цепи?
\$\начало группы\$
Приведенный ниже вопрос просто иллюстрирует то, что я имею в виду, мне не нужна помощь с этим вопросом, а скорее концепции, лежащие в его основе
Из статьи wwikipedia о собственной частоте
я пришел к выводу, что для LC-цепи естественным состоянием будет то, в котором ток встречает незначительное сопротивление. Что будет означать \$X_C=X_L\$
Конденсаторы включены последовательно, как и катушки индуктивности, из чего, используя условие резонанса для последовательной цепи LCR, я получил \$X_C=X_l\$
, что дает \$ \ omega = \frac{1}{ \sqrt{LC}}\$
однако у меня есть некоторые сомнения здесь
а) правильно ли я понимаю собственную частоту? Я просмотрел несколько ответов на этом сайте, но обычно они говорят о полюсах и других вещах, которые на данный момент мне недоступны. о которых я понятия не имею.
b) Если бы конденсаторы были заряжены, с какой частотой колебались бы заряды между конденсатором и катушкой индуктивности (скажем, эквивалентными конденсатором и катушкой индуктивности для простоты)? Если да, то почему?
- конденсатор
- дроссель
- lcr
\$\конечная группа\$
\$\начало группы\$
\$X_L = \omega L\$
\$X_C = \frac{1}{\omega C}\$
Катушки индуктивности последовательно добавляются как резисторы.
Конденсаторы, соединенные последовательно, аналогичны резисторам, соединенным параллельно.
\$C = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2}}\$
а) Да, собственная частота равна \$X_L = X_C\$
Тогда \$\omega = \frac{1}{\sqrt{LC}}\$
b) Да, если предположить, что в начале существует ненулевое условие, энергия будет колебаться между C и Л. Я предлагаю вам поиграть с симулятором, чтобы увидеть его в действии.
\$\конечная группа\$
0
\$\начало группы\$
Величины реактивных сопротивлений одинаковы, но, конечно, импедансы чисто мнимые, а знаки противоположны, поэтому они компенсируются.
имитация этой схемы – Схема создана с помощью CircuitLab
Вот импульсный вход в рассматриваемую схему. Как видите, \$\omega\$ = 1000, как и ожидалось.
«Почему» математически отвечает на решение дифференциального уравнения.
