Составление суммы моментов сил относительно точки

Рассмотрим решение задачи по составлению и определению суммы моментов внешних сил приложенных к заданной системе относительно её точек.

Задача
К составной планке, показанной на рисунке

приложены следующие нагрузки:

1. Внешние сосредоточенные силы F₁=10кН и F₂=50кН расположенная под углом
2. Сосредоточенный момент m=70кНм
3. Равномерно-распределённая нагрузка q интенсивностью 20кН/м

Требуется составить и определить алгебраическую сумму моментов относительно точек A, B и D.

Решение

Обозначим характерные точки системы буквами и покажем систему координат x-y.

Для записи и расчета уравнений суммы моментов надо мысленно закрепить систему в рассматриваемой точке и записать все внешние усилия, которые стремятся повернуть систему.

Момент силы определяется по формуле

где h — расстояние от точки до линии действия силы называемое плечом.

Другие видео

При этом, по правилу знаков, нагрузки, поворачивающие систему против хода часовой стрелки записываются положительными и наоборот.

При записи уравнений суммы моментов:

• Силы умножаются на плечо;
• Равномерно распределенные нагрузки умножаются на длину (получается равнодействующая сила), полученное произведение умножается на плечо, которым служит расстояние от её середины до рассматриваемой точки;
• Сосредоточенный момент в сумме моментов записывается как есть (с учётом знака).

Определим алгебраические суммы моментов сил относительно произвольных точек системы.

Для некоторого упрощения решения задачи, распределенную нагрузку можно заменить её равнодействующей

которая при равномерном распределении приложена посередине:

а сосредоточенную силу F₂ можно разложить на составляющие, спроецировав её на оси x и y.

Получается упрощенная расчетная схема:

Расчет суммы моментов относительно точки, к которой приложена сила

Для точки A:
Силы R_q и F_2X создают момент, вращающий по ходу часовой стрелки, поэтому будут записаны со знаком минус.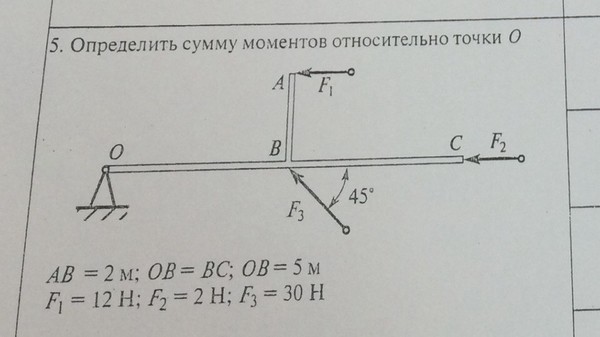
Сила F_2Y относительно точки A имеет обратное направление и создает положительный момент.

Здесь h₁, h₂ и h₃ плечи моментов соответствующих сил и равнодействующей распределенной нагрузки относительно точки A.

Линия действия силы F₁ проходит через саму точку A, следовательно, плечо равно нулю, поэтому момент этой силой в данном случае не создается.

Таким образом, относительно точки A уравнение суммы моментов будет иметь вид:

Здесь сумма моментов относительно точки A отрицательна, поэтому, если данную систему закрепить в этой точке, она будет вращаться по ходу часовой стрелки.

Определение суммы моментов относительно точки, в которой приложен момент

Для точки B надо помнить что момент приложенный в точке, относительно которой записывается сумма, в уравнении участвует.

Поэтому алгебраическая сумма моментов относительно точки B равна:

Знак «-» так же показывает на вращение системы по ХЧС.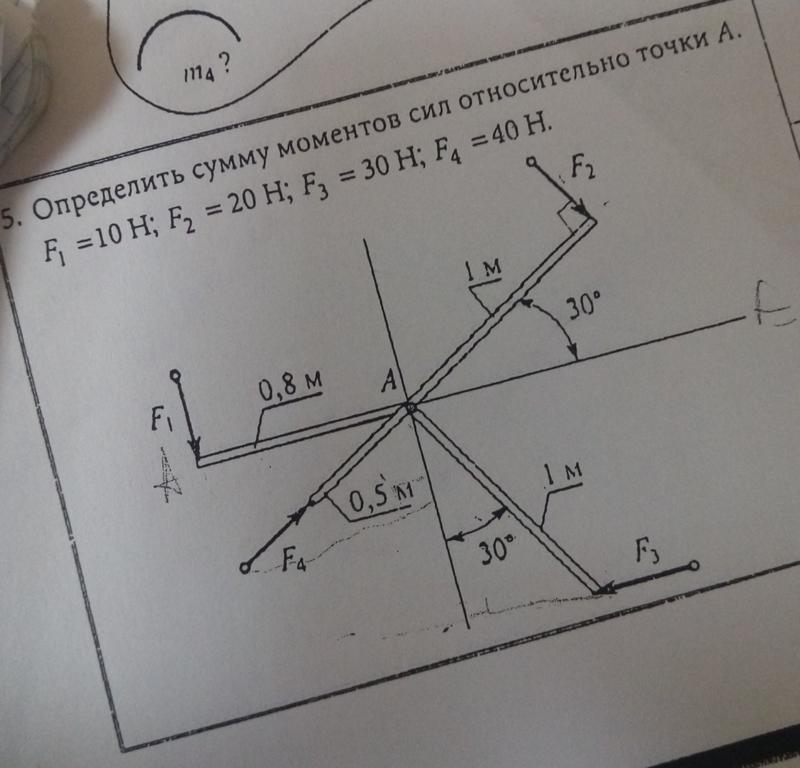

Сумма моментов относительно точки, где действует распределенная нагрузка

Для точки D:
Здесь надо смотреть, как расположена равнодействующая нагрузки по отношению к рассматриваемой точке.
В данном случае она находится справа от точки и направлена вниз, следовательно, создает вращение по ходу часовой стрелки.

Плечом момента нагрузки служит расстояние между равнодействующей и точкой.

Уравнение суммы моментов для точки под распределенной нагрузкой (в точке D) запишется в виде:

Положительный результат показывает вращение системы против ХЧС.

Направления определенных сумм моментов относительно заданных точек

При определении суммы моментов следует помнить, что в отличие от сил и распределенных нагрузок, сосредоточенный момент будет иметь один и тот же знак относительно любой точки системы.

Уравнения суммы моментов можно составить относительно любых других точек системы, в том числе точек, которые лежат вне заданной системы. Но, как правило, при решении задач этого не требуется.

Для статичных, геометрически неизменяемых систем сумма моментов всегда равна нулю.

Другие примеры решения задач статики >

| Типовые задачи по статике 2015

Статика

1.Сколько независимых уравнений равновесия можно составить для пространственной системы параллельных сил? ТРИ

2. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму моментов сил относительно точки А (кНм)? -2

3. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму проекции сил на ось х (кН)? 4

4. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)? 20

5. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму проекций сил на ось у (кН)? 10

6. Что получается в результате приведения силы к заданному центру?

Сила и пара сил

7. Дано: Р1= кН; Р2= 2 кН; Р3 = кН; ОА=АВ=2 м; α=60°

Определить: Сумму проекций сил на ось у (кН)? 0

8. Дано: Р1= кН; Р2= 2 кН; Р3 = кН; ОА=АВ=2 м; α=60°

Определить: Сумму моментов сил относительно точки А (кНм)? -3

9. Сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил? ДВА

10. Дано: Р1= кН; Р2= кН; Р3 = 4 кН; ОА=2 м.

Определить: Сумму проекций сил на ось у (кН)?

11. Сколько неизвестных уравнений равновесия можно составить для произвольной системы сил в пространстве? ШЕСТЬ

12. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 8 кН; ОА= 4 м; sinα = 06; cosα = 0,8.

Определить: Сумму проекций сил на ось х (кН)?— 4

13. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму моментов сил относительно точки А (кНм)? 8

14. Дано Р1= Р3= 10 кН; Р2 = 10 кН; ОА= м; ОВ= 2 м; α=30°

Определить: Сумму проекций сил на ось у (кН)?

15. Дано Р1= Р3= 10 кН; Р2 = 10 кН; ОА= м; ОВ= 2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)? 3

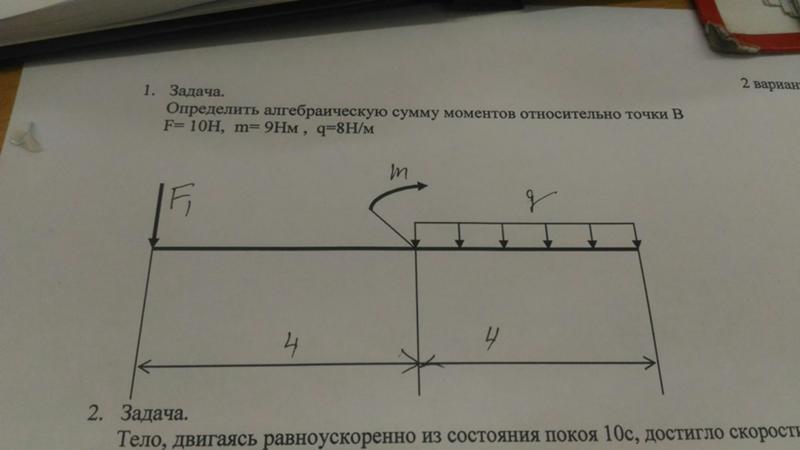
16. Дано Р1= 4 кН; Р2= кН; Р3 = 2кН; α=30°

Определить: Сумму проекции сил на ось х (кН)? -2

17. Дано: Р1= кН; Р2= кН; ОА=2 м; α=30°

Определить: Сумму проекции сил на ось у (кН)? 0

18. Дано: Р1= кН; Р2= 4 кН; Р3 = R=2 м; α=30°; β= 60°

Определить: Сумму проекции сил на ось х (кН)? 1

19. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекции сил на ось х (кН)? 2

20. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекции сил на ось у (кН)? 2

21. Дано: Р1= кН; Р2= 2 кН; Р3 =

Определить: Сумму проекций сил на ось у (кН)? 2

22. Дано: Р1= кН; Р2= 2 кН; Р3 =

Определить: Сумму проекций сил на ось х (кН)? — 2

23. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму проекций сил на ось у (кН)? -2

24. Линия действия Р проходит параллельно оси на расстоянии « а» от оси, момент силы относительно оси равен? НУЛЮ

25.

Дано: Р1= кН; Р2= кН; Р3 = 4

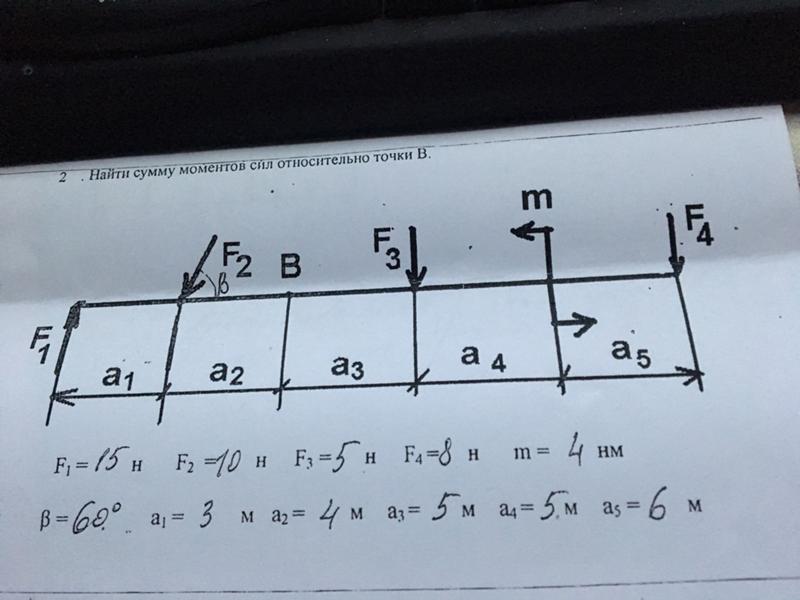
Определить: Сумму моментов сил относительно точки А (кНм)?

26. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекций сил на ось у (кН)? 2

27. Дано: Р1= кН; Р2= кН; ОА=2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)?

28. Сколько условий равновесия можно записать для сходящихся сил?

ОДНО

29. Дано Р1= 2 кН; Р2= кН; Р3 = 3 кН; ОА= 4 м;

Определить: Сумму проекций сил на ось х (кН)?

30. Сколько независимых уравнений равновесия можно составить для плоской системы сил? ТРИ

31. Укажите правильную формулу для центра параллельных сил?

rc =

32. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму проекций сил на ось х (кН)? -10

33. Сколько условий равновесия существует для произвольной системы сил в пространстве? ДВА

34.Можно ли пару сил уравновесить силой ? НЕТ

35.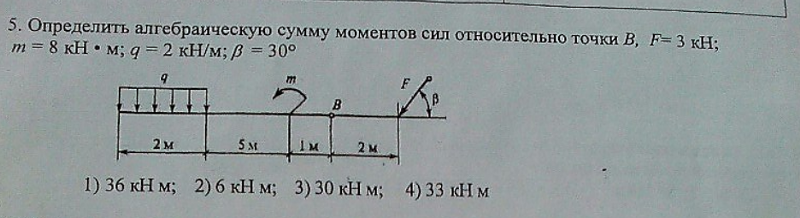 В результате сложения пар сил в пространстве получим пару сил, момент которой равен….? ГЕОМЕТРИЧЕСКОЙ СУММЕ МОМЕНТОВ СОСТАВЛЯЮЩИХ ПАР.

36. Дано: Р1= кН; Р2= кН; Р3 = 4

Определить: Сумму проекций сил на ось

х (кН)? 1

37. Укажите правильную формулу для координаты ХС центра тяжести плоской фигуры? Хс =

38. Сколько условий равновесия можно составить для плоской системы сил? ДВА.

39. Укажите правильную формулу для координаты ХС центра тяжести тел?

Хс =

40.

домашних заданий и упражнений — Как узнать, какую силу использовать при расчете моментов?

Если вы хотите получить сумму моментов, вы должны принять во внимание **все внешние силы**. Сумма моментов не отдает предпочтение определенной силе, позволяя ей быть в уравнении. Все силы находятся в сумме, только их результирующий момент может быть равен нулю. Если мы посмотрим на следующий пример, предполагая, что все интервалы, например. $AB,BC,BE,FC,CD$ равны $l$:

Если мы возьмем сумму моментов вокруг $A$ с положительной по часовой стрелке, мы получим

$$\Sigma M_A=(AA) \cdot R_1 — (AB)\cdot P_1-(AB+BC)\cdot P_2+(AB +BC+CD)\cdot R_2 =0 $$

Как видите, все силы входят в сумму моментов.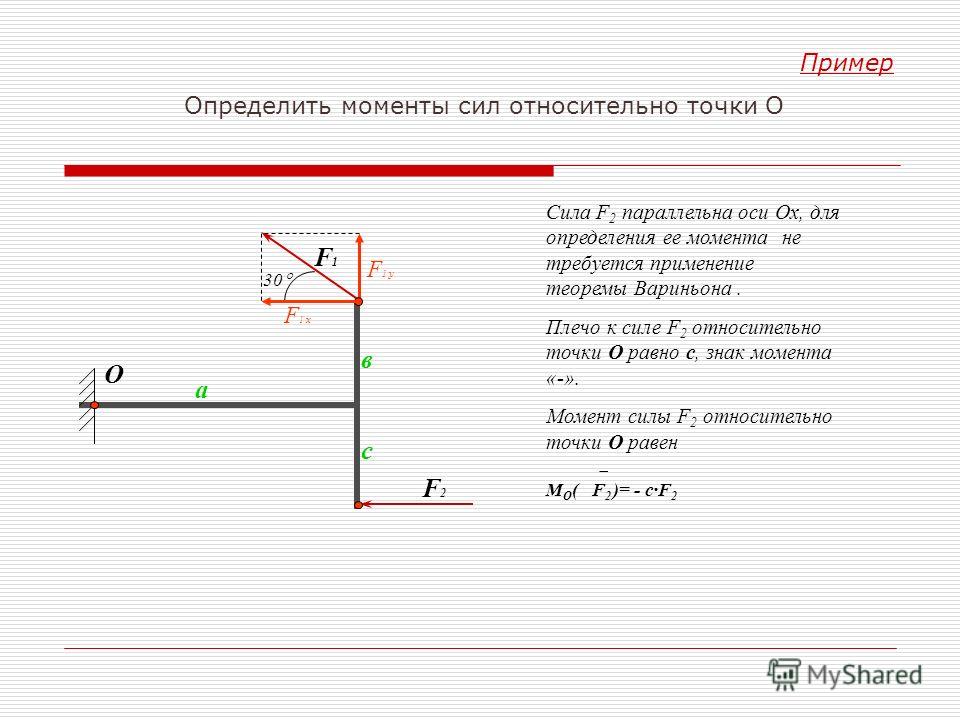 Однако, если мы начнем заполнять соответствующие длины, мы получим:

$$\Sigma M_A=(0l) \cdot R_1 — (l)\cdot P_1-(2l)\cdot P_2+(3l)\cdot R_2 =0$ $

Это связано с тем, что расстояние $AA$ равно нулю, что делает вклад момента равным нулю. На мгновение вам нужно расстояние и сила. Если любой из них равен $0$, момент равен нулю. Можно показать, что каждая сила, проходящая через рассматриваемую точку (в данном случае $A$), имеет моментный вклад, равный нулю. Возьмем, к примеру, $P_1=P_2=F $(вниз), тогда $R_1$ и $R_2$ также равны $F$ (вверх). Если мы затем сделаем разрез вокруг $A$, прямо через середину $AE$ и $AB$, мы получим:

Поскольку все расстояния равны ($AB=AE$), угол равен $45\градусов$. Используя этот угол, мы можем разложить $F_{ae}$ на $F_{ae_x}$ и $F_{ae_y}$ Сумма моментов вокруг $A$ дает: $$\Sigma M_A=(0l) \cdot R_1 + F_{ae_y} \cdot \Delta x_{ae} — F_{ae_x} \cdot \Delta y_{ae} + F_{ab} \cdot \Delta y_{ab }=0$$

Учитывая, что $\Delta y_{ab}=0$, получаем $$\Sigma M_A= F_{ae_y} \cdot \Delta x_{ae} — F_{ae_x} \cdot \Delta y_{ae} =0$$

Если мы перепишем значения $F_{ae_y}$ и $F_{ae_x}$ в пересчете на $F$

$$\Sigma M_A= F_{ae} \sin(45) \cdot \Delta x_{ae} — F_{ae_x} \cos(45) \cdot \Delta y_{ae} =0$$

или

$$\Sigma M_A= F_{ae} \left[ \sin(45) \cdot \Delta x_{ae} — \cos(45) \cdot \Delta y_{ae} \right] =0$$

Если мы посмотрим на эту формулу, мы увидим, что общий вклад момента $F_{ae}$, таким образом, добавленные горизонтальная и вертикальная составляющие составляют $0$. Это означает, что $F_{ae}$ не имеет момента на $A$. Мы можем обобщить этот результат как

Если сила проходит через точку рассмотрения, момент взнос $0$

Как и сказал @Pranav Hosangadi.

Этот пример показывает, что все три силы проходят через точку $A$, поэтому все их вклады равны $0$, что в сумме дает $0$.

Это может быть очень полезным ярлыком. Если, например, у вас есть конструкция, нагруженная 30 силами, из которых 28 проходят через одну и ту же точку, вы можете суммировать моменты вокруг этой точки и пренебречь вкладом моментов 28 сил, что значительно упростит расчет. Вы также можете взять любую другую точку, и результаты будут такими же, это просто больше математики.

Карта механики – анализ равновесия для твердого тела

Для твердого тела в статическом равновесии, т.е. недеформируемого тела, на которое не действуют параллельные силы, сумма действующих сил и моментов на теле должна быть равна нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.

Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси z). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма компонентов силы в направлениях x и y и моментов относительно оси z. Сумма каждого из них будет равна нулю.

Для двумерной задачи мы разобьем наше уравнение одной векторной силы на два уравнения скалярных компонентов.

\[\сумма \vec{F}=0\]
\[\сумма F_x=0\]	\[\сумма F_y=0\]

Векторное уравнение с одним моментом становится скалярным уравнением с одним моментом.

\[\сумма \vec{M}=0\]

\[\сумма M_z=0\]

Если мы рассмотрим трехмерную задачу, то увеличим количество возможных уравнений равновесия до шести. Есть три уравнения равновесия для силы, где сумма компонентов в направлениях x, y и z должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма компонентов момента относительно осей x, y и z также должна быть равна нулю.

Разобьем силы на три составляющие уравнения

\[\сумма \vec{F}=0\]
\[\сумма F_x=0\]	\[\сумма F_y=0\]	\[\сумма F_z=0\]

Моменты разбиваем на три составляющие уравнения

\[\sum \vec{M}=0\]
\[\сумма M_x=0\]	\[\сумма M_y=0\]	\[\сумма M_z=0\]

Как и в случае с частицами, первым шагом в поиске уравнений равновесия является построение диаграммы свободного тела анализируемого тела. На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На диаграмме свободного тела задайте значения для любых известных величин, направлений и точек приложения векторов силы и задайте имена переменных для любых неизвестных (величин, направлений или расстояний).

Далее вам нужно будет выбрать оси x, y, z. Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете координатные оси, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.

После того, как вы выбрали оси, вам нужно разбить все векторы сил на компоненты по направлениям x, y и z (см. страницу векторов в Приложении 1 для более подробной информации об этом процессе). Ваше первое уравнение будет суммой величин компонентов в направлении x, равных нулю, второе уравнение будет суммой величин компонентов в направлении y, равных нулю, а третье (если вы имеют трехмерную задачу) будет равна сумме величин в направлении z, равной нулю.