Статика

Статика

1.Сколько независимых уравнений равновесия можно составить для пространственной системы параллельных сил? ТРИ

2. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму моментов сил относительно точки А (кНм)? -2

3. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму проекции сил на ось х (кН)? 4

4. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)? 20

5. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму проекций сил на ось у (кН)? 10

6. Что получается в результате приведения силы к заданному центру?

Сила и пара сил

7. Дано: Р1= кН; Р2= 2 кН; Р3 = кН; ОА=АВ=2 м; α=60°

Определить: Сумму проекций сил на ось у (кН)? 0

8. Дано: Р1= кН; Р2= 2 кН; Р3 = кН; ОА=АВ=2 м; α=60°

Определить: Сумму моментов сил относительно точки А (кНм)? -3

9. Сколько независимых уравнений равновесия можно составить для плоской системы параллельных сил? ДВА

10. Дано: Р1= кН; Р2= кН; Р3 = 4 кН; ОА=2 м.

Определить: Сумму проекций сил на ось у (кН)?

11. Сколько неизвестных уравнений равновесия можно составить для произвольной системы сил в пространстве? ШЕСТЬ

12. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 8 кН; ОА= 4 м; sinα = 06; cosα = 0,8.

Определить: Сумму проекций сил на ось х (кН)?- 4

13. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму моментов сил относительно точки А (кНм)? 8

14. Дано Р1= Р3= 10 кН; Р2 = 10 кН; ОА= м; ОВ= 2 м; α=30°

Определить: Сумму проекций сил на ось у (кН)?

15. Дано Р1= Р3= 10 кН; Р2 = 10 кН; ОА= м; ОВ= 2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)? 3

16. Дано Р1= 4 кН; Р2= кН; Р3 = 2кН; α=30°

Определить: Сумму проекции сил на ось х (кН)? -2

17. Дано: Р1= кН; Р2= кН; ОА=2 м; α=30°

Определить: Сумму проекции сил на ось у (кН)? 0

18. Дано: Р1= кН; Р2= 4 кН; Р3 = R=2 м; α=30°; β= 60°

Определить: Сумму проекции сил на ось х (кН)? 1

19. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекции сил на ось х (кН)? 2

20. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекции сил на ось у (кН)? 2

21. Дано: Р1= кН; Р2= 2 кН; Р3 =

Определить: Сумму проекций сил на ось у (кН)? 2

22. Дано: Р1= кН; Р2= 2 кН; Р3 =

Определить: Сумму проекций сил на ось х (кН)? — 2

23. Дано Р1= 4 кН; Р2= 1 кН; Р3 = 1 кН; ОА= 2 м; ОВ= 4 м; α=β=30°

Определить: Сумму проекций сил на ось

у (кН)? -2

24. Линия действия Р проходит параллельно оси на расстоянии « а» от оси, момент силы относительно оси равен? НУЛЮ

25. Дано: Р1= кН; Р2= кН; Р3 = 4

Определить: Сумму моментов сил относительно точки А (кНм)?

26. Дано: Р1=4 кН; Р2= кН; Р3 = 8 кН; ОА =

.

Определить: Сумму проекций сил на ось у (кН)? 2

27. Дано: Р1= кН; Р2= кН; ОА=2 м; α=30°

Определить: Сумму моментов сил относительно точки А (кНм)?

28. Сколько условий равновесия можно записать для сходящихся сил?

ОДНО

29. Дано Р1= 2 кН; Р2= кН; Р3 = 3 кН; ОА= 4 м;

Определить: Сумму проекций сил на ось х (кН)?

30. Сколько независимых уравнений равновесия можно составить для плоской системы сил? ТРИ

31. Укажите правильную формулу для центра параллельных сил?

r_c =

32. Дано: Р1=10 кН; Р2= 5 кН; Р3 = 5 кН; ОА= 4 м; АВ= 2 м; α=30°

Определить: Сумму проекций сил на ось х (кН)? -10

33. Сколько условий равновесия существует для произвольной системы сил в пространстве? ДВА

34.Можно ли пару сил уравновесить силой ? НЕТ

35.В результате сложения пар сил в пространстве получим пару сил, момент которой равен….? ГЕОМЕТРИЧЕСКОЙ СУММЕ МОМЕНТОВ СОСТАВЛЯЮЩИХ ПАР.

36. Дано: Р1= кН; Р2= кН; Р3 = 4

Определить: Сумму проекций сил на ось х (кН)? 1

37. Укажите правильную формулу для координаты ХС центра тяжести плоской фигуры? Хс =

38. Сколько условий равновесия можно составить для плоской системы сил? ДВА.

39. Укажите правильную формулу для координаты ХС центра тяжести тел?

Хс =

40.

Алгебраическая сумма — момент — сила

Cтраница 2

Изгибающий момент — алгебраическая сумма моментов сил

, расположенных по одну сторону от рассматриваемого сечения, относительно этого сечения.  [16]

Можно ли определить алгебраическую сумму моментов сил относительно некоторой точки О, если задана только равнодействующая этих сил R я ее плечо а относительно этой точки.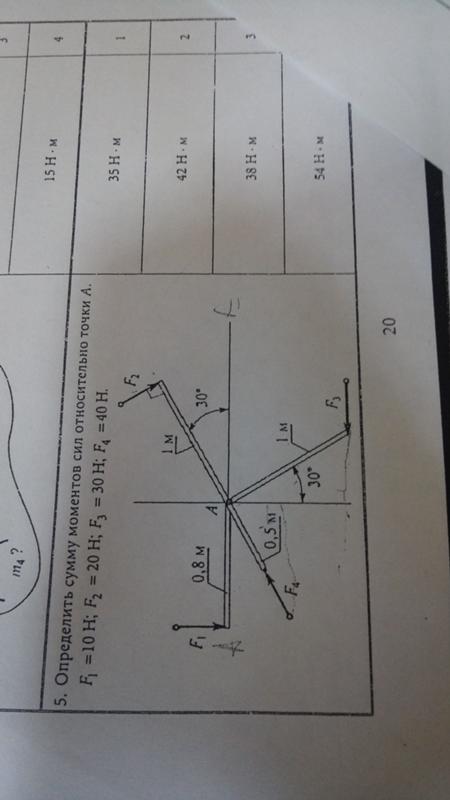  [17]

Перенос пары сил в плоскости.  [18]

Отсюда видно, что алгебраическая сумма моментов сил, составляющих пару, относительно любой оси, перпендикулярной к плоскости действия пары, равна алгебраической величине момента пары сил.  [19]

Величина М0, равная алгебраической сумме моментов сил плоской системы относительно точки О, называется главным моментом системы относительно этой точки.  [20]

Величина М0, равная алгебраической сумме моментов сил плоской системы — относительно точки О, называется главным моментом системы относительно этой точки.  [21]

Второе ( условие моментов): алгебраическая сумма моментов сил относительно любой точки должна равняться нулю. При этом все моменты сил, стремящиеся повернуть тело около выбранной точки в одйу сторону ( например, по часовой стрелке), берутся со знаком плюс, все моменты сил, стремящиеся повернуть тело в другую сторону ( против часовой стрелки), берутся со зна ком минус.

Чтобы записать условие моментов, надо: а) выявить все силы, приложенные к телу; б) выбрать точку, относительно которой предполагается рассматривать моменты сил; в) найти моменты всех сил относительно выбранной точки; г) составить алгебраическую сумму моментов сил и приравнять ее нулю. При использовании условия моментов необходимо учитывать, что, во-первых, приведенная выше формулировка относится к случаю, когда все силы и расстояния в задаче лежат в одной и той же плоскости ( задача не является трехмерной), и во-вторых, равенство нулю алгебраической суммы моментов сил должно выполняться относительно любой точки, взятой как внутри тела, так и вне его.  [22]

Второе ( условие моментов): алгебраическая сумма моментов сил относительно любой точки должна равняться нулю. При этом все моменты сил, стремящиеся повернуть тело около выбранной точки в одну сторону ( например, по часовой стрелке), берутся со знаком плюс, все моменты сил, стремящиеся повернуть тело в другую сторону ( против часовой стрелки), берутся со знаком минус.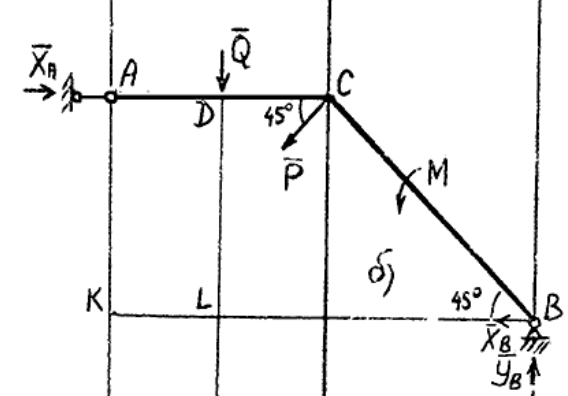

Чтобы записать условие моментов, надо: а) выявить все силы, приложенные к телу; б) выбрать точку, относительно которой предполагается рассматривать моменты сил; в) найти моменты всех сил относительно выбранной точки; г) составить алгебраическую сумму моментов сил и приравнять ее нулю. При использовании условия моментов необходимо учитывать, что, во-первых, приведенная выше формулировка относится к случаю, когда все силы и расстояния в задаче лежат в одной и той же плоскости ( задача не является трехмерной), и во-вторых, равенство нулю алгебраической суммы моментов сил должно выполняться относительно любой точки, взятой как внутри тела, так и вне его. Следует подчеркнуть, что от выбора точки ( относительно которой рассматриваются моменты сил) зависят значения отдельных моментов сил; однако алгебраическая сумма моментов всегда остается равной нулю. Чтобы лучше понять условия равновесия, рассмотрим конкретную задачу.  [23]

Момент равнодействующей силы относительно точки равен алгебраической сумме моментов слагаемых сил относительно той же точки.  [24]

Таким образом, главный момент равен алгебраической сумме моментов сил заданной системы относительно точки приведения.  [25]

Второе условие ( условие моменте): алгебраическая сумма моментов сил относительно любой точки должна равняться нулю.  [26]

Проекция момента пары на какую-либо ось равняется алгебраической сумме моментов сил, составляющих пару, относительно той же оси.  [27]

Докажем следующую теорему о моментах сил пары: алгебраическая сумма моментов сил пары относительно любого центра, лежащего в плоскости ее действия, не зависит от выбора этого центра и равна моменту пары.  [28]

Докажем следующую теорему о моментах сил пары: алгебраическая сумма моментов сил пары относительно любого центра, лежащего в плоскости е действия, не зависит от выбора этого центра и равна моменту пары.  [29]

Поэтому момент равнодействующей относительно произвольной оси будет равен алгебраической сумме моментов слагаемых сил относительно той же оси.  [30]

Страницы:      1    2    3    4

Вопрос Видео: Нахождение величины суммы моментов четырех параллельных сил, действующих на стержень

𝐴𝐵 представляет собой стержень длиной 105 см и незначительным весом. На стержень действуют силы величинами 214 Н, 67 Н, 115 Н и 176 Н, как показано на рисунке. Учитывая, что 𝐶 и 𝐷 — точки трисекции 𝐴𝐵, определить алгебраическую сумму моментов этих сил относительно точки 𝐴.

Стенограмма видео

𝐴𝐵 — стержень длиной 105 сантиметров и ничтожный вес. силы величиной 240 ньютонов, 67 ньютонов, 115 ньютонов и 176 ньютонов действуют на стержень, как показано на рисунке. фигура. Учитывая, что 𝐶 и 𝐷 находятся на трисекции 𝐴𝐵, определить алгебраическую сумму моментов этих сил относительно точка 𝐴.

Нам сказали, что длина стержень 105 сантиметров, а точки 𝐶 и 𝐷 находятся на трисечении. 105 разделить на три равно 35. Следовательно, расстояние между 𝐵 и 𝐷, 𝐷 и 𝐶, и 𝐶 и 𝐴 составляет 35 сантиметров. Момент силы равен сила, умноженная на расстояние от некоторой точки. В этом вопросе нас просят взять моменты о точке 𝐴. Момент силы 𝐴 об этом точка будет равна 214 умноженному на ноль. Это равно нулю.

Момент силы 𝐵 будет равно 176, умноженному на 105, так как оно находится на расстоянии 105 сантиметров от 𝐴. Это равно 18480. Сила в точке 𝐶 равна 67 ньютонов, а это 35 сантиметров от точки 𝐴. 67 умножить на 35 равно 2345. Наконец, сила в точке 𝐷 равна 115. ньютоны. Это в 70 сантиметрах от точка 𝐴. 115 умножить на 70 равно 8050.

Нам говорят, что движущиеся силы в направлении против часовой стрелки вокруг точки 𝐴 положительны, а движущиеся по по часовой стрелке являются отрицательными. Любая сила, движущаяся вертикально вниз будет двигаться против часовой стрелки вокруг точки 𝐴. Следовательно, момент в 𝐵 равен положительный. Поскольку силы в 𝐶 и 𝐷 равны действуя вертикально вверх, они движутся по часовой стрелке. Поэтому момент будет отрицательный.

Сумма моментов относительно точки 𝐴 равны 18480 минус 2345 минус 8050. Это равно 8085. Поскольку силы измеряются в ньютоны и длины в сантиметрах, наши единицы измерения будут ньютоны-сантиметры. Правильный ответ: 8085 ньютонов. сантиметры.

Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.

statics — В чем разница между суммой моментов относительно точки и моментом в точке?

Задавать вопрос

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 326 раз

$\begingroup$

В классе мы изучаем моменты, и я не совсем понимаю, в чем разница между использованием уравнения равновесия для моментов относительно точки (в данном случае C) и фактическим моментом в точке C .

Насколько я понимаю, «сумма» моментов относительно С должна быть равна 0, так как в этой точке С, если «сумма» больше 0, то мы больше не находимся в статическом равновесии, и поэтому дело сдвинется? Итак, чтобы противодействовать этому, нам нужен «внутренний момент», обеспечиваемый балкой в ​​точке C, чтобы противодействовать этому.

Редактировать: Кроме того, не ошибся ли здесь мой профессор в своей схеме направления? Кажется, что он принимает момент, приложенный к C от B, как отрицательный, хотя он установил направление положительного момента по часовой стрелке.

• статика
• моменты

$\endgroup$

0

$\begingroup$

Для меня они означают одно и то же. Хотя я полагаю, что вы могли бы интерпретировать «момент в точке» как конкретный момент из-за конкретной причины, которая составляет часть суммы.