| |||||||||||||||||||||||
| Специальный поиск | |||||||||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||||||||||||||
напряженность электрического поля точке Задача 60007 Электрическое поле создано двумя точечными зарядами: Q1 = 30 нКл и Q2 = –10 нКл. Расстояние d между зарядами равно 20 см, Определить напряженность электрического поля в точке, находящейся на расстоянии r
Задача 60176 Найти напряженность электрического поля в точке, удаленной от первого заряда на r1 и от второго на r2, если поле создано двумя точечными зарядами +q1 и q2, находящимися на расстоянии d друг от друга.
Задача 60289 Точечные заряды +3 мкКл и -2 мкКл находятся в точке А (2,0) и В (6,0). Чему равна напряженность электрического поля в точке С (4,0)?
Задача 60587 Определить полный заряд, который равномерно распределен по тонкому стержню длиной 40 см, если создаваемая им напряженность электрического поля в точке, лежащей на продолжении стержня на расстоянии 20 см от ближайшего конца, равна 60 кВ/м.
Задача 11675 Тонкий стержень длиной l = 12 см заряжен с линейной плотностью τ = 200 нКл/м.
Задача 14790 Даны два точечных заряда –|q| и +4|q|. Как изменятся потенциал и модуль напряженности электрического поля в точке «А», если заряд –|q| убрать?
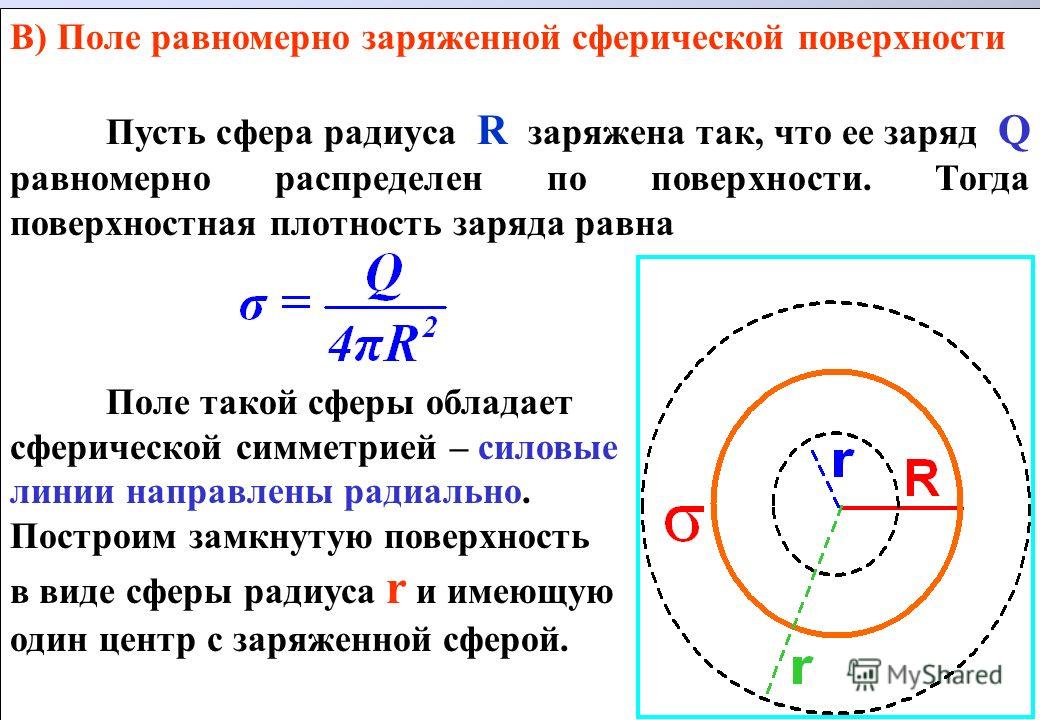
Задача 16319 Шар радиусом R из однородного изотропного диэлектрика с относительной проницаемостью ε равномерно заряжен по объему с плотностью ρ > 0. Найти напряженность электрического поля в точке, находящейся на расстоянии r от центра (r > R).
Задача 16980 Резиновый воздушный шарик несет заряд Q = 10–7 Кл, равномерно распределенный по его поверхности. Радиус шарика равен R1 = 0,02 м. Шарик начинают надувать до радиуса R2 = 0,04 м.
Задача 17088 Два разноименно заряженных с поверхностной плотностью σ1 = σ
Задача 17161 Три точечных заряда 1, 4 и 1 мкКл находятся на трех взаимно перпендикулярных прямых, пересекающихся в точке А. Расстояния от точки А до зарядов соответственно равны 1, 2 и 3 м. Найдите напряженность электрического поля в точке А, а также потенциал в этой точке, если система зарядов находится в вакууме.
Задача 17621 Два точечных заряда q1 и q2 (первый заряд положительный, второй — отрицательный) расположены на расстоянии а = 10 см друг от друга. Величины зарядов q1 = 1 нКл, q2 = –2 нКл. Определить 1) энергию системы зарядов; 2) положение точки, в которой напряженность электрического поля, созданного этими зарядами, равна нулю; 3) потенциал электрического поля в этой точке.
Задача 17781 Тонкий стержень длиной L = 10 см заряжен линейной плотностью τ = 4·10
Задача 17782 Две параллельные нити длиной L1 = L2 = 17,4 см, расположенные на расстоянии 8 см, заряжены линейной плотностью τ1 = τ2 = +10–9 Кл/м.
Задача 17783 Электрическое поле создано тремя нитями, сходящимися к одной точке А под углом 60 градусов друг к другу. Длина нити равна a = b = с = 0,1 м. Нити заряжены одноименными зарядами линейной плотностью τ1 = τ2 = τ3 = 10–7 Кл/м. Рассчитать напряженность электрического поля в точке А.
Задача 17784 Электрическое поле создано заряженными кольцом и нитью, лежащей на оси кольца с одной его стороны. Радиус кольца равен 0,2 м, длина нити равна 0,3 м. Линейные плотности зарядов кольца и нити одинаковые и равны 0,4·10
Задача 17785 По тонкой нити, изогнутой по дуге окружности радиуса R = 10 см, равномерно распределен заряд Q = 20·10–9 Кл. Определить напряженность электрического поля в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
Задача 17722 Точечные заряды q1 = 10–16 Кл, q2 = 2·10–16 Кл и q3 = 4·10–16 Кл расположены в вершинах прямоугольного треугольника со сторонами 3 см, 4 см и 5 см. Найти: 1) напряженность электрического поля в точке, находящейся на середине гипотенузы; 2) энергию системы зарядов; 3) работу по перемещению заряда из вершины прямого угла на середину гипотенузы.
Задача 19278 Тонкое кольцо, радиус которого R = 10 см, заряжено линейной плотностью τ = 8 нКл/м.
Задача 20376 В воде на расстоянии 5 см друг от друга размещено точечные заряды 20 и -10 мкКл. Определить напряженность электрического поля в точке, находящейся на расстоянии 4 см от первого заряда и на расстоянии 3 см от другого. Какая сила действует в этой точке на точечный заряд 1 мкКл?
Задача 21406 Найти напряженность электрического поля в точке, находящейся на расстоянии r1 = 4 см от точечного заряда q1 = 30·10–9 Кл и на расстоянии r2 = 4 см от точечного заряда q2 = –30·10–9 Кл.
Задача 22999 Две параллельные нити равномерно заряжены. Вычислить напряжённость электрического поля в точке, находящейся на расстоянии 20 см от каждой нити. Расстояние между нитями 20 см, линейная плотность заряда равна 10 мкКл/м. Найти силу, действующую на заряд –5·10–8 Кл, помещенный в эту точку.
Задача 23043 Найти напряженность электрического поля E в точке A(4, 2), потенциал которого зависит от координат по закону φ = a(2x–xy), где a = 4 В/м.
Задача 23518 В вершинах равностороннего треугольника находятся точечные заряды q; 2q; 3q; (где величина q = 1 нКл), сторона треугольника а = 0,1 м.
| |||||||||||||||||||||||
Найти напряженность Е электрического поля в точке, находящейся на расстоянии r = 5 см от стержня против его середины.
Рассчитать напряженность электрического поля в точках, отстоящих от центра шара на расстояниях S1 = 0,03 м и S2 = 0,05 м до и после его надувания.
Найти величину и направление напряженности электрического поля в точке пересечения перпендикуляров, проведенных через средние точки нити, на расстоянии S = 10 см от них.
Заряды q1 и q2 расположены на расстоянии r = 5 см друг от друга. Определить силу, с которой поле действует на заряд q = 2·10–9 Кл, помещенный в эту точку поля.
Определить напряженность электрического поля в точке нахождения заряда 3q. Определить энергию системы зарядов.2 Напряженность и потенциал электрического поля
2.1 Нарисовать картину линий напряженности между двумя точечными зарядами +2q и -q. Могут ли линии напряженности электростатического поля быть замкнутыми?
2.2 Иногда говорят, что линии напряженности – это траектории, по которым двигался бы в поле точечный положительный заряд, если его, внеся в это поле, предоставить самому себе. Правильно ли это утверждение?
2.3 В однородном поле напряженностью 40кВ/м находится заряд 27нКл. Найти напряженность результирующего поля на расстоянии 9см от заряда в точках, лежащих: а)на силовой линии однородного поля, проходящей через заряд; б)на прямой, проходящей через заряд и перпендикулярной силовым линиям.
2.4 Точка А находится
на расстоянии r1=2м,
а точка В на расстоянии r2=1м
от точечного заряда q=10-6Кл.
Чему равна разность потенциалов точек
А и В? Как она зависит от угла между
прямыми qA
и qB?
2.5 Построить графики изменения напряженности и потенциала поля вдоль линии, проходящей через два точечных заряда, находящихся на расстоянии 2d друг от друга. Величины зарядов равны: а) +q и -q; б) +q и +q; в) +q и -3q.
2.6 В вершинах равностороннего треугольника со стороной а находятся заряды +q, +q, и -q. Найти напряженность поля в центре треугольника.
2.7 Три одинаковых заряда, q=10-9Кл каждый, расположены в вершинах прямоугольного треугольника с катетами а=40см и b=30см. Найти напряженность электрического поля, создаваемого всеми зарядами в точке пересечения гипотенузы с перпендикуляром, опущенным на нее из вершины прямого угла.
2.8 Два точечных
заряда Q1=4нКл и
Q2=-2нКл находятся
друг от друга на расстоянии 60см. Определите
напряженность Е поля в точке, лежащей
посередине между зарядами.
Чему равна
напряженность, если второй заряд
положительный?
2.9 В вершинах квадрата со стороной 5см находятся одинаковые положительные заряды Q=2нКл. Определите напряженность электростатического поля: а) в центре квадрата; б) в середине одной из сторон квадрата.
2.10 Заряд q>0 равномерно распределен по тонкому кольцу радиусом а. Найти напряженность Е электрического поля на оси кольца как функцию расстояния z от его центра.
2.11 Тонкая прямая нить длиной 2l заряжена равномерно зарядом q. Найти напряженность Е поля в точке, отстоящей на расстоянии х от центра нити и расположенной симметрично относительно ее концов.
2.12 Две бесконечно длинные, равномерно заряженные нити с линейной плотностью зарядов 610-5Кл/м расположены на расстоянии 0,2м друг от друга. Найти напряженность электрического поля, созданного в точке, удаленной на 0,2м от каждой нити.
2.13 Найти напряженность
поля бесконечной плоскости, равномерно
заряженной с поверхностной плотностью
заряда σ.
2.14 Найти напряженность поля двух параллельных плоскостей, заряженных равномерно разноименными зарядами с поверхностными плотностями и -.
2.15 Найти напряженность поля бесконечного круглого цилиндра радиуса а, заряженного равномерно по поверхности так, что на единицу его длины приходится заряд .
2.16 Найти напряженность поля сферической поверхности радиуса а, заряженной равномерно зарядом q.
2.17 Найти напряженность поля шара радиуса а, по объему которого равномерно распределен заряд q.
2.18 Очень тонкий диск равномерно заряжен с поверхностной плотностью >0. Найти напряженность электрического поля на оси этого диска в точке, из которой диск виден под телесным углом .
2.19 Тонкое непроводящее
кольцо радиусом R заряжено
с линейной плотностью =0cos,
где 0–
положительная постоянная,
— азимутальный угол.
Найти напряженность
Е электрического поля в центре кольца.
2.20 Полубесконечная прямая равномерно заряженная нить имеет заряд на единицу длины. Найти модуль и направление напряженности поля в точке, которая отстоит от нити на расстоянии у и находится на перпендикуляре к нити, проходящем через ее конец.
2.21 По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью . Определить напряженность электрического поля, создаваемого таким распределением зарядов в точке, совпадающей с центром кривизны дуги. Длина l нити составляет одну треть длины окружности.
2.22 Шар радиуса R
имеет положительный заряд, объемная
плотность которого зависит только от
расстояния r до его центра как =0(1–r/R),
где 0 –
постоянная. Полагая, что диэлектрическая
проницаемость =1
всюду, найти а) модуль напряженности
электрического поля внутри и вне шара
как функцию r; б) максимальное
значение модуля напряженности Емах и соответственно значение rm.
2.23 Найти потенциал и напряженность электрического поля в центре полусферы радиуса R, заряженной равномерно с поверхностной плотностью .
2.24 Заряд q распределен равномерно по объему шара радиуса R. Полагая, диэлектрическую проницаемость всюду равной единице, найти потенциал: а) в центре шара; б) внутри шара как функцию расстояния r от его центра.
2.25 На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью =0,1нКл/см2 расположена круглая пластинка. Нормаль плоскости пластинки составляет с линиями напряженности угол 30. Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус r=15см.
2.26 Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды Q1=5нКл и Q2=-2нКл.
2.27 Определите
поверхностную плотность заряда,
создающего вблизи поверхности Земли
напряженность Е=200В/м.
2.28 На металлической сфере радиусом 15см находится заряд Q=2нКл. Определите напряженность Е электростатического поля: а) на расстоянии r1=10см от центра сферы; б) на поверхности сферы; в) на расстоянии r2=20см от центра сферы. Постройте график зависимости Е(r).
2.29 Поле создано двумя равномерно заряженными концентрическими сферами радиусами R1=5см и R2=8см. Заряды сфер соответственно равны Q1=2нКл и Q2=-1нКл. Определите напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: а) r1=3см; б) r2=6см; в) r3=10см. Постройте график зависимости Е(r).
2.30 Шар радиусом
R=10см заряжен равномерно
с объемной плотностью =10нКл/м3 Определите напряженность
электростатического поля: а) на расстоянии
r1=5см от центра шара;
б) на расстоянии r2=15см
от центра шара.
Постройте зависимость
Е(r).
2.31 Два металлических шарика радиусом r с зарядами q на каждом расположены на расстоянии а друг от друга и на очень больших равных расстояниях от Земли. Первый шар заземляют и заземляющий проводник убирают. Затем такую же процедуру проделывают и со вторым шариком. После этого снова заземляют первый шар и т.д. Каким будет отношение зарядов шаров после n заземлений второго шара?
2.32 Напряженность электрического поля зависит только от координат х и у как где а – постоянная; и – орты осей Х и Y. Найти заряд внутри сферы радиусом R с центром в начале координат.
2.33 Найти напряженность поля, потенциал которого имеет вид: а) (х,y)=-аху, а–постоянная, б) ( )=- , –постоянный вектор, –радиус-вектор интересующей нас точки поля.
2.34 Потенциал
некоторого электрического поля имеет
вид =(ху–z2).
Найти проекцию вектора
на направление вектора в
точке М(2, 1, -3).
2.35 Потенциал поля внутри заряженного шара зависит только от расстояния r до его центра по закону =аr2+b, где а и b – постоянные. Найти распределение объемного заряда (r) внутри шара.
2.36 Имеются два тонких кольца радиуса R каждое, оси которых совпадают. Заряды Колец равны q и -q. Найти разность потенциалов между центрами колец, отстоящими друг от друга на расстоянии l.
2.37 Кольцо радиусом r=5см из тонкой проволоки несет равномерно распределенный заряд Q=10нКл. Определите потенциал электростатического поля: а) в центре кольца; б) на оси, проходящей через центр кольца, в точке, удаленной на расстояние а=10см от центра кольца.
2.38 Полый шар несет
на себе равномерно распределенный
заряд. Определите радиус шара, если
потенциал в центре шара равен 1=200В,
а в точке, лежащей от его центра на
расстоянии r=50см, 2=40В.
2.39 Электростатическое поле создается положительным точечным зарядом. Определите числовое значение и направление градиента потенциала этого поля, если на расстоянии r=10см от заряда потенциал равен =100В.
2.40 Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью =1нКл/м2. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии х1=20см и х2=50см от плоскости.
2.41 Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом R=10см с общим зарядом Q=15нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии r1=5см и r2=15см от поверхности сферы.
2.42 Электростатическое
поле создается сферой радиусом R=5см,
равномерно заряженной с поверхностной
плотностью =1нКл/м2.
Определите разность потенциалов между
двумя точками поля, лежащими на расстояниях
r1=10см и r2=15см
от центра сферы.
2.43 Электростатическое поле создается шаром радиусом R=10м, равномерно заряженным с объемной плотностью =20нКл/м3. Определите разность потенциалов между двумя точками, лежащими внутри шара на расстояниях r1=2см и r2=8см от его центра.
2.44 Электростатическое поле создается бесконечным цилиндром радиусом 8мм, равномерно заряженным с линейной плотностью =10нКл/м. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r1=2мм и r2=7мм от поверхности этого цилиндра.
2.45 Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью =5нКл/м2. Определите числовое значение и направление градиента потенциала этого поля.
2.46 Электростатическое
поле создается бесконечной прямой
нитью, заряженной равномерно с линейной
плотностью =50пКл/см.
Определите числовое значение и направление
градиента потенциала в точке на расстоянии
r=0,5м от нити.
2.47 Электрон, двигавшийся со скоростью 5106м/с, влетает в параллельное его движению электрическое поле напряженностью 103В/м. Какое расстояние пройдет электрон в этом поле до момента остановки и сколько времени ему для этого потребуется? Какую долю своей первоначальной кинетической энергии потеряет электрон, двигаясь в этом поле, если электрическое поле обрывается на расстоянии 0,8см пути электрона?
2.48 С какой скоростью достигают анода электронной лампы электроны, испускаемые катодом, если напряжение между катодом и анодом равно 200В? Начальной скоростью электронов можно пренебречь.
2.49 Пылинка взвешена в плоском конденсаторе. Ее масса m=10-11г, расстояние между пластинами конденсатора d=0,5см. Пылинка освещается ультрафиолетовым светом и, теряя заряд, выходит из равновесия. Какой заряд потеряла пылинка, если первоначально к конденсатору было приложено напряжение U=154В, а затем чтобы опять вернуть пылинку в равновесие, пришлось прибавить 8В?
2.
50 Между вертикальными
пластинами плоского конденсатора,
находящегося в воздухе, подвешен на
тонкой шелковой нити маленький шарик,
несущий заряд q=3,310-9Кл.
Какой величины заряд надо сообщать
пластинам конденсатора, чтобы нить с
шариком отклонилась на угол =45
от вертикали? Масса шарика m=0,04г,
площадь пластин конденсатора S=314см2.
Массой нити можно пренебречь.
2.51 Между двумя вертикальными пластинами, находящимися на расстоянии d=2см друг от друга, висит заряженный бузиновый шарик массой m=0,1г. После того как на пластины была подана разность потенциалов U=1000B, нить с шариком отклонилась на угол =5. Найти заряд шарика q.
2.52 Электрон вылетает из точки, потенциал которой =600В, со скоростью =12106м/с в направлении линий напряженности поля. Определить потенциал точки, дойдя до которой электрон остановится.
2.53 В плоский
конденсатор длиной l=5см
влетает электрон под углом =15
к пластинам.
Энергия электрона W=1500эВ.
Расстояние между пластинами d=1см.
Определить напряжение U
на конденсаторе, при котором электрон
при выходе из пластин будет двигаться
параллельно им.
2.54 По наклонной плоскости, составляющей угол с горизонтом, соскальзывает с высоты h небольшое тело, заряженное отрицательным зарядом –q. В точке пересечения вертикали, проведенной через начальное положение тела, с основанием находится заряд +q. Определить скорость, с которой тело достигнет основания наклонной плоскости. Проанализируйте зависимость скорости от угла : а)=45; б)<45; в)α>45. Трением пренебречь. Масса тела m. Начальная скорость равна нулю.
2.55 Упругий
металлический шар лежит на изолирующей
горизонтальной упругой подставке. Шар
имеет заряд +q. На какую
высоту поднимется второй такой же шар
после удара о первый, если он падает с
высоты Н (расстояние между центрами
шаров), а его заряд равен: а) –q;
б) +q? Радиус шара r<<H,
его масса m.
[Решено] Напряженность электрического поля и электростатическая напряженность
- 1/r и 1/r 2
- 1/r 2 и 1/r 3 5 0/10
- 1/R 2 и 1/R
04 04 и 3 0 90 90 04 04 R 2
Опция 3: 1/R 3 и 1/R 2
БЕСПЛАТНО
Электрические заряды и закон кулон (базовый)
80,6 тыс. пользователей
10 вопросов
10 баллов
10 минут
КОНЦЕПЦИЯ :
Напряженность электрического поля:
- Напряженность электрического поля в любой точке — это сила электрического поля в этой точке.
- Определяется как сила, испытываемая единичным положительным зарядом в этой точке.
\(\vec E = \frac{{\vec F}}{{{q_o}}}\)
Где F = сила и qo = небольшой пробный заряд
Электрический потенциал (В):
- Разность потенциалов между двумя точками в электрическом поле может быть определена как количество работы, выполненной при перемещении единичного положительного заряда из одной точки в другую против электростатической силы, т.
е.
е.
Электрический диполь:
- Когда два равных и противоположных заряда разделены небольшим расстоянием, эта комбинация зарядов называется электрическим диполем.
- сила электрического диполя измеряется величиной, известной как дипольный момент т.е.
\(\vec P = q \times \overrightarrow {2a} \)
Где q = заряд и 2a = расстояние между двумя заряженными частицами
ОБЪЯСНЕНИЕ :
92}}}\)Поделиться в WhatsApp
Последние обновления Airforce Group X
Последнее обновление: 11 ноября 2022 г.
Дата экзамена Airforce Group X и город. 7 ноября 2022 года ВВС Индии (IAF) выпустили официальное уведомление о группе X IAF (01/2023). Отбор кандидатов будет зависеть от трех этапов: фаза 1 (письменный онлайн-тест), фаза 2 ( DV, тест на физическую подготовку, тест на адаптацию I и II) и этап 3 (медицинское обследование).
Экзамен запланирован с 18 по 24 января 2023 года. Кандидаты, прошедшие все этапы процесса отбора, будут отобраны на должности группы X ВВС и получат зарплату в размере рупий. 30 000. Это одна из самых востребованных вакансий. Кандидаты могут проверить соответствие требованиям Airforce Group X здесь.
Пересмотр концепции поля – Колледж Дугласа, физика 1207
Глава 2 Электрический заряд и электрическое поле
Резюме
- Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
- Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
- Объясните взаимосвязь между электрической силой (F) на испытательном заряде и напряженностью электрического поля (E).
Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют через силы, которые включают кулоновскую силу .
Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.
Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить себе объект, окруженный в пространстве силовое поле . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.
Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю (и все другие массы), представляет собой гравитационную силу, которая могла бы возникнуть, если бы в данной точке поля была помещена другая масса.
Точно так же кулоновское силовое поле, окружающее любой заряд, распространяется по всему пространству.
Используя закон Кулона, F = k q 1 q 2 /r 2 , его величина определяется уравнением имеющий заряд Q ), действующий на пробный заряд q на расстоянии r (см. рисунок ниже). Как величина, так и направление кулоновского силового поля зависят от Q и тестовый заряд q .
Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов q 1 и q 2 , а также заряда Q 90997.Для упрощения мы бы предпочли иметь поле, зависящее только от Q и не на испытательном заряде q . Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле E определяется как отношение кулоновской силы к испытательному заряду:
,
, где F — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд q. Понятно, что E находится в том же направлении, что и
Ф . Также предполагается, что q настолько мало, что не меняет распределения заряда, создающего электрическое поле.
Единицами электрического поля являются ньютоны на кулон (Н/Кл). Если электрическое поле известно, то электростатическая сила на любом заряде q просто получается путем умножения заряда на электрическое поле, или F = q E . Рассмотрим электрическое поле, создаваемое точечным зарядом Q . По закону Кулона сила, действующая на пробный заряд, равна q равно F = k q Q /r 2 . Таким образом, величина электрического поля E для точечного заряда равна
Поскольку тестовый заряд отменяется, мы видим, что
Таким образом видно, что электрическое поле зависит только от заряда Q и расстояния r ; он полностью независим от тестового заряда q.
Пример 1. Расчет электрического поля точечного заряда
Расчет напряженности и направления электрического поля E из-за точечного заряда 2,00 нКл (нанокулоны) на расстоянии 5,00 мм от заряда.
Стратегия
Мы можем найти электрическое поле, создаваемое точечным зарядом, используя уравнение E = kQ/r 2 .
Решение
Здесь Q = 2,00 x 10 -9 C и r = 5,00 x 10 -3 м . Ввод этих значений в приведенное выше уравнение дает
Обсуждение
Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда Q , создающего поле. Он положительный, т. е. направлен в сторону от заряда Q.
Пример 2. Расчет силы, действующей на точечный заряд электрическим полем
Какую силу электрическое поле, найденное в предыдущем примере, действует на точечный заряд -0,250 мкКл ?
Стратегия
Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно рассчитать, используя определение электрического поля E = F/q преобразованное в F = qE .
Решение
Величина силы, действующей на заряд q = -0,250 мкКл действующей на поле напряженностью E = 7,20 x 10 5 N/C отрицательно,
q- Поскольку , сила направлена против направления поля.
- Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.
- Электростатическая сила, действующая точечным зарядом на пробный заряд на расстоянии r , зависит от заряда обоих зарядов, а также от расстояния между ними.
- Электрическое поле E определяется как
, где F – кулоновская или электростатическая сила, действующая на небольшой положительный пробный заряд q . E имеет единицы N/C.
- Величина электрического поля E , создаваемого точечным зарядом В есть
, где r . Электрическое поле E является вектором, а поля из-за множественных зарядов складываются подобными векторами.
Обсуждение
Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом, а здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная небольшая сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.
PhET Explorations: Electric Field of Dreams
Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.
Рисунок 2. Электрическое поле снов. Прямая ссылкаL https://phet.colorado.edu/en/simulation/legacy/efield Аналогичный PhEt, но использующий HTML 5, который будет работать на большинстве компьютеров, можно найти по прямой ссылке: https://phet.
colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_en.html It откроется ниже автоматически, если вы читаете эту книгу онлайн.
