Напряжения в точке.
Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечного малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 3.1.
Совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим какую-либо точку называют напряженным состоянием тела в данной точке
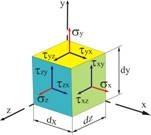
Рис. 3.1
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действуют девять компонентов напряжения. Запишем их в виде следующей квадратной матрицы:
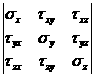
где в первой, второй
и третьей строках расположены составляющие
напряжений соответственно на площадках,
перпендикулярных к осям  ,
, 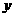 ,
, 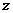 .
Эта совокупность напряжений называется тензором
напряжений.
.
Эта совокупность напряжений называется тензором
напряжений.
Закон парности касательных напряжений. Главные площадки и главные напряжения.
Составим уравнение
моментов всех сил, приложенных к
элементарному параллелепипеду
относительно оси 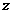
Силы, параллельные
этой оси и пересекающие ее, в уравнение
не войдут. Моменты сил  на двух гранях, перпендикулярных оси
на двух гранях, перпендикулярных оси 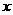 ,
уравновешиваются, равно как и моменты
сил
,
уравновешиваются, равно как и моменты
сил  на верхней и нижней гранях элемента.
Таким образом, получаем:
на верхней и нижней гранях элемента.
Таким образом, получаем:

Отсюда следует,
что 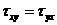 .
.
Аналогично из двух других уравнений находим:
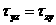
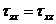
Итак, имеем равенства
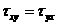
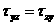

называемые законом парности касательных напряжений
Закон парности касательных напряжений – касательные напряжения на двух любых, но взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения площадок, равны по величине. При этом они стремятся повернуть элемент в разные стороны.
При изменении ориентации граней выделенного элемента меняются также действующие на его гранях напряжения. Можно провести такие площадки, на которых касательные напряжения равны нулю. Площадки, на которых касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения на этих площадках – главными напряжениями
Можно доказать, что в каждой точке напряженного тела существует три главные взаимно перпендикулярные площадки.
Главные напряжения
обозначают 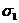 ,
, 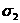 ,
, 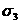 .
При этом индексы следует расставлять
так, чтобы выполнялось неравенство
.
При этом индексы следует расставлять
так, чтобы выполнялось неравенство
 >
>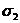 >
>
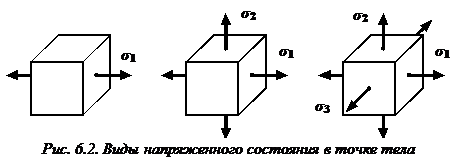
Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным (рис.3.2, а).
Если равно нулю одно из главных напряжения, то напряженное состояние называется двухосным или плоским (рис.3.2, б).
Если равно нулю два главных напряжения, то напряженное состояние называется одноосным или линейным (рис.3.2, в).
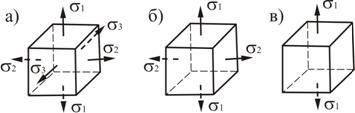
Рис. 3
Плоское напряженное состояние.
При исследовании напряженного состояния элементов конструкций наиболее часто приходится иметь дело с плоским напряженным состоянием. Оно встречается при кручении, изгибе и сложном сопротивлении. Поэтому на нем мы остановимся несколько подробнее.
Рассмотрим элемент, грани которого являются главными площадками.
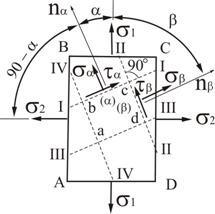
Рис. 3.3
По
ним действуют положительные напряжения 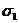 и
и 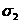
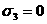 (направление
(направление 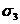 перпендикулярно к плоскости чертежа).
перпендикулярно к плоскости чертежа). Проведем
сечение I
– I,
которое определит площадку (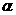 ),
характеризуемую положительным углом
),
характеризуемую положительным углом 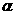 .
Напряжения
.
Напряжения 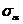
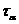 по этой площадке будут определяться по
формулам:
по этой площадке будут определяться по
формулам: 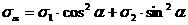 (3.2)
(3.2)
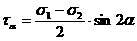 (3.3)
(3.3)
Сжимающие
главные напряжения подставляют в эти
формулы со знаком «минус», а угол 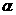 отсчитывают от алгебраически большего
главного напряжения.
отсчитывают от алгебраически большего
главного напряжения.
Проведем
сечение II
– II,
которое определит площадку 
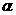 .
Нормаль
.
Нормаль 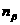 к ней образует с направлением
к ней образует с направлением 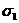 угол
угол 
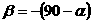 .
.
Подставив
в формулы (3.2) и (3.3) значения угла 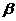
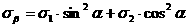 ; (3.4)
; (3.4)
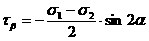 . (3.5)
. (3.5)
Совокупность формул (3.2) — (3.5) дает возможность находить напряжения по любым взаимно перпендикулярным наклонным площадкам, если известны главные напряжения.
Складывая равенства (3.2) и (3.4), обнаруживаем, что
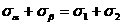 , (3.6)
, (3.6)
т. е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам не зависит от угла наклона этих площадок и равна сумме главных напряжений.
Из
формул (3.3) и (3.5) видим, что касательные
напряжения достигают наибольшей величины
при 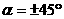 ,
т. е. по площадкам, наклоненным к главным
площадкам под углом
,
т. е. по площадкам, наклоненным к главным
площадкам под углом  ,
причем
,
причем
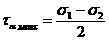 . (3.7)
. (3.7)
Сравнивая формулы (3.3) и (3.5), находим, что
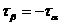 (3.8)
(3.8)
Это равенство выражает закон парности касательных напряжений.
Проведем
теперь еще два сечения (рис. 3.3): Сечение
ІІІ – ІІІ, параллельное І – І,
и сечение ІV
– ІV,
параллельное ІІ – ІІ. Элемент 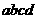 ,
выделенный четырьмя сечениями из
элемента
,
выделенный четырьмя сечениями из
элемента  (рис. 3.4, а), будет иметь вид, показанный
на рис 3.4, б. Оба элемента определяют
одно и то же напряженное состояние, но
элемент
(рис. 3.4, а), будет иметь вид, показанный
на рис 3.4, б. Оба элемента определяют
одно и то же напряженное состояние, но
элемент  представляет его главными напряжениями,
а элемент
представляет его главными напряжениями,
а элемент  — напряжениями на наклонных площадках.
— напряжениями на наклонных площадках.
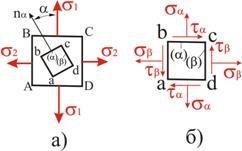
Рис. 3.4
В теории напряженного состояния можно разграничить две основные задачи.
Прямая
задача.
В точке известны положения главных
площадок и соответствующие им главные
напряжения; требуется найти нормальные
и касательные напряжения по площадкам,
наклоненным под заданным углом 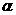 к главным.
к главным.
Обратная задача. В точке известны нормальные и касательные напряжения, действующие в двух взаимно перпендикулярных площадках; требуется найти главные направления и главные напряжения. Обе задачи можно решать как аналитически, так и графически.
Прямая задача в плоском напряженном состоянии. Круг напряжений (круг Мора).
Аналитическое решение прямой задачи дается формулами (3.2) – (3.5).
Проанализируем
напряженное состояние, воспользовавшись
простым графическим построением. Для
этого введем в рассмотрение геометрическую
плоскость и отнесем ее к прямоугольным
координатным осям  и
и  .
Порядок расчета опишем на примере
напряженного состояния, изображенного
на рис. 3.5, а.
.
Порядок расчета опишем на примере
напряженного состояния, изображенного
на рис. 3.5, а.
Выбрав для напряжений некоторый масштаб, откладываем на оси абсцисс (рис 3.5, б) отрезки
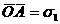
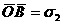
На  как на диаметре строим окружность с
центром в точке
как на диаметре строим окружность с
центром в точке 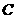 .
Построенный круг носит название круга
напряжений или круга
Мора.
.
Построенный круг носит название круга
напряжений или круга
Мора.
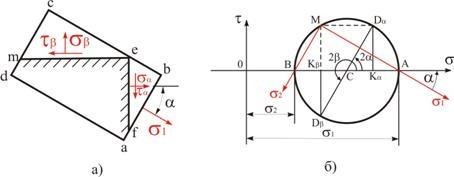
Рис. 3.5
Координаты
точек круга соответствуют нормальным
и касательным напряжениям на различных
площадках. Так, для определения напряжения
на площадке, проведенной под углом 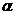 (рис. 3.5, а) из центра круга
(рис. 3.5, а) из центра круга  (рис 3.5, б)
проводим
луч под углом
(рис 3.5, б)
проводим
луч под углом 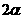 до пересечения с окружностью в точке
до пересечения с окружностью в точке  (положительные углы откладываем против
часовой стрелки). Абсцисса точки (отрезок
(положительные углы откладываем против
часовой стрелки). Абсцисса точки (отрезок 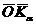 )
равна нормальному напряжению
)
равна нормальному напряжению 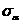 ,
а ордината ее (отрезок
,
а ордината ее (отрезок 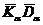 )
– касательному напряжению
)
– касательному напряжению 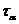 .
.
Напряжение
на площадке, перпендикулярной к
рассмотренной, найдем, проведя луч под
углом 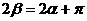 и получив в пересечении с окружностью
точку
и получив в пересечении с окружностью
точку  .
Очевидно, ордината точки
.
Очевидно, ордината точки 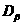 соответствует касательному напряжению
соответствует касательному напряжению 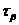 ,
а абсцисса точки
,
а абсцисса точки 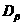 — нормальному напряжению
— нормальному напряжению 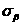 .
.
Проведя
из точки 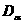 линию, параллельную
линию, параллельную 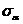 (в нашем случае горизонталь), до пересечения
с кругом, найдем полюс – точку
(в нашем случае горизонталь), до пересечения
с кругом, найдем полюс – точку  .
Линия, соединяющая полюс с любой точкой
круга, параллельна направлению нормального
напряжения на площадке, которой эта
точка соответствует. Так, например,
линия
.
Линия, соединяющая полюс с любой точкой
круга, параллельна направлению нормального
напряжения на площадке, которой эта
точка соответствует. Так, например,
линия 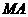 параллельна главному напряжению
параллельна главному напряжению 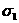 .
Очевидно, что линия
.
Очевидно, что линия 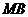 параллельна направлению главного
напряжения
параллельна направлению главного
напряжения 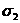 .
.
Обратная задача в плоском напряженном состоянии.
При
практических расчетах обычно определяют
нормальные и касательные напряжения
на некоторых двух взаимно перпендикулярных
площадках. Пусть, например, известны
напряжения 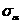 ,
,  ,
, 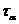 ,
, 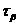 (рис. 3.6, а). По этим данным требуется
определить величины главных напряжений
и положение главных площадок.
(рис. 3.6, а). По этим данным требуется
определить величины главных напряжений
и положение главных площадок.
Сначала
решим эту задачу графически. Примем,
что  >
>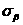 ,
а
,
а  >
> .
.
В
геометрической плоскости в системе
координат  нанесем точку
нанесем точку 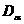 ,
с координатами
,
с координатами 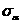 ,
,  и точку
и точку 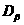 с координатами
с координатами 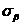 ,
,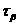 (рис.
3.6, б). Соединив точки
(рис.
3.6, б). Соединив точки  и
и 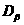 ,
находим центр круга – точку
,
находим центр круга – точку 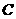 — и радиусом
— и радиусом 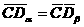 проводим окружность. Абсциссы точек ее
пересечения с осью
проводим окружность. Абсциссы точек ее
пересечения с осью  — отрезки
— отрезки  и
и 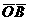 — дадут соответственно величины главных
напряжений
— дадут соответственно величины главных
напряжений  и
и 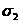 .
.
Для
определения положения главных площадок
найдем полюс и воспользуемся его
свойством. Проведем из точки 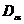 линию параллельно линии действия
напряжения
,
т. е. горизонталь. Точка
линию параллельно линии действия
напряжения
,
т. е. горизонталь. Точка 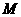 пересечения этой линии с окружностью
и является полюсом. Соединяя полюс
пересечения этой линии с окружностью
и является полюсом. Соединяя полюс  с точками
с точками 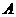 и
и 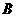 ,
получим направления главных напряжений.
Главные площадки перпендикулярны к
найденным направлениям главных
напряжений.
,
получим направления главных напряжений.
Главные площадки перпендикулярны к
найденным направлениям главных
напряжений.
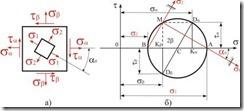
Рис. 3.6
Используем
построенный круг для получения
аналитических выражений главных
напряжений 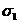 и
и 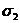 :
:
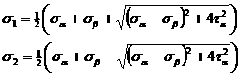 (3.9)
(3.9)
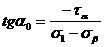 (3.10)
(3.10)
Формула
(3.10) определяет единственное значение
угла 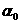 ,
на который нужно повернуть нормаль
,
на который нужно повернуть нормаль 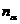 ,
чтобы получить направление алгебраически
большего главного напряжения.
Отрицательному значению
,
чтобы получить направление алгебраически
большего главного напряжения.
Отрицательному значению  соответствует поворот по часовой
стрелке.
соответствует поворот по часовой
стрелке.
Если
одно из главных напряжений окажется
отрицательным, а другое положительным,
то их следует обозначать 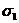 и
и 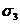 .
Если оба главных напряжения окажутся
отрицательными, то их следует обозначать
.
Если оба главных напряжения окажутся
отрицательными, то их следует обозначать 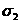 и
и 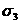 .
.
Лекция 4. Теории прочности. Чистый сдвиг{jcomments on}
Теории прочности.
Важнейшей задачей инженерного расчета является оценка прочности элемента конструкции по известному напряженному состоянию. Для простых видов деформаций, в частности для одноосных напряженных состояний, определение значений опасных напряжений не представляет особых трудностей. Вспомним, что под опасными напряжениями понимают напряжения, соответствующие началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластического состояния материала):
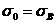 или
или 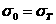
По опасным напряжениям устанавливают допускаемые напряжения, обеспечивающие определенный запас против наступления предельного состояния.
При сложном
напряженном состоянии, как показывают
опыты, опасное состояние может иметь
место при различных значениях главных
напряжений 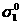 ,
, 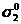 ,
, 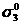 в зависимости от соотношений между
ними. В этом случае вводят гипотезу о
преимущественном влиянии на прочность
материала того или иного фактора.
Предельное значение фактора, определяющего
прочность, находят на основании простых
опытов (на растяжение, сжатие, кручение).
в зависимости от соотношений между
ними. В этом случае вводят гипотезу о
преимущественном влиянии на прочность
материала того или иного фактора.
Предельное значение фактора, определяющего
прочность, находят на основании простых
опытов (на растяжение, сжатие, кручение).
Выбранная указанным образом гипотеза называется механической теорией прочности.
Рассмотрим классические теории прочности.
7. Провода в электрических схемах | 2. Закон Ома | Часть1
7. Провода в электрических схемах
Провода в электрических схемах
До сих пор мы с вами анализировали электрические цепи (состоящие из одной батареи и одного сопротивления) без учета проводов, соединяющих компоненты этих цепей и формирующих полную схему. И вот тут-то, когда мы вспомнили про провода, сразу навязывается вопрос: а как их длина и форма прокладки повлияют на все наши вычисления? Чтобы выяснить это, давайте посмотрим на пару конфигураций электрических схем:
При разработке и анализе электрических схем на бумаге, мы обычно считаем что провода, соединяющие компоненты этих схем, имеют очень незначительное сопротивление, которое не оказывает заметного влияния на общее сопротивление схемы. Поэтому единственное сопротивление, с которым мы считаемся, это сопротивление электронных компонентов (радиодеталей). В приведенных выше схемах сопротивление (величиной 5 Ом) порождается только резисторами, и только это сопротивление мы будем учитывать во всех наших расчетах. В реальности, металлические провода действительно обладают некоторым сопротивлением, но его величина намного меньше сопротивления других компонентов схемы, в связи с чем мы со спокойной совестью можем его игнорировать. Исключение из этого правила составляет силовая электропроводка, где даже небольшое сопротивление провода может создать значительное падение напряжения.
Если сопротивление соединительного провода очень мало или вовсе отсутствует, мы можем рассматривать соединяемые им точки схемы как электрически общие. То есть, точки 1 и 2 в приведенных выше схемах могут быть непосредственно соединены между собой, а могут отстоять друг от друга на расстоянии длины соединяющего их провода, и это не будет влиять на величины напряжения и сопротивления, измеряемых по отношению к этим точкам. То же самое относится и к точкам 3 и 4. Это означает, что вы можете перерисовать любой провод на схеме так, как вам будет удобно, или при необходимости укоротить или удлинить провода в реальной схеме без заметного воздействия на ее функции.
Величина напряжения, измеряемого между наборами «электрически общих» точек, будет одинакова. То есть, напряжение между точками 1 и 4 (на контактах батареи) будет таким же, как и напряжение между точками 2 и 3 (на выводах резистора). Теперь внимательно посмотрите на следующую схему, и попытайтесь определить, какие точки здесь будут электрически общими:
Эта схема, не считая проводов, содержит два компонента: батарею и резистор. Несмотря на то, что провода при формировании облика схемы принимают замысловатый путь, мы можем увидеть две группы электрически общих точек. Общими по отношению друг к другу здесь являются точки 1,2,3, потому что они связаны одним проводом, и точки 4,5,6, которые связаны между собой другим проводом.
Напряжение между точками 1 и 6 составляет 10 В, это напряжение на клеммах батареи. В связи с тем, что точки 4 и 5 являются электрически общими по отношению к точке 6, а точки 2 и 3 — по отношению к точке 1, напряжение между любыми двумя точками этих групп так же будет равно 10 вольтам:
Напряжение между точками 1 и 4 = 10 вольт
Напряжение между точками 2 и 4 = 10 вольт
Напряжение между точками 3 и 4 = 10 вольт (напряжение на резисторе)
Напряжение между точками 1 и 5 = 10 вольт
Напряжение между точками 2 и 5 = 10 вольт
Напряжение между точками 3 и 5 = 10 вольт
Напряжение между точками 1 и 6 = 10 вольт (напряжение батареи)
Напряжение между точками 2 и 6 = 10 вольт
Напряжение между точками 3 и 6 = 10 вольт
Теперь мы рассмотрим электрически общие точки. Так как эти точки связаны между собой одним проводом (имеющим нулевое сопротивление), то между ними не будет никакого напряжения, независимо от величины тока, проходящего по этому проводу от одной его точки до другой. Таким образом, если мы измерим напряжение между этими точками, то оно будет равно нулю:
Напряжение между точками 1 и 2 = 0 вольт Точки 1, 2, и 3 являются
Напряжение между точками 2 и 3 = 0 вольт электрически общими
Напряжение между точками 1 и 3 = 0 вольт
Напряжение между точками 4 и 5 = 0 вольт Точки 4, 5, и 6 являются
Напряжение между точками 5 и 6 = 0 вольт электрически общими
Напряжение между точками 4 и 6 = 0 вольт
Нулевые значения напряжения можно подтвердить математическими расчетами. При напряжении батареи 10 вольт и сопротивлении резистора 5 Ом, сила тока в нашей цепи будет равна 2 амперам. Так как провод имеет нулевое сопротивление, то падение напряжение между двумя любыми его точками по Закону Ома будет равно:
Из этого уравнения видно, что напряжение между двумя точками одного провода, обладающего нулевым сопротивлением, вне зависимости от величины тока равно нулю. (Результатом умножения любого числа на ноль, всегда будет ноль).
В связи с тем, что электрически общие точки при измерениях показывают одинаковые значения напряжения и сопротивления, провода, соединяющие эти точки, очень часто имеют одинаковые обозначения:
В этой схеме точки 1, 2 и 3 являются электрически общими, поэтому провод соединяющий точки 1 и 2 (провод #2) имеет такое же обозначение, как и провод соединяющий точки 2 и 3 (провод #2). В реальной цепи, провод соединяющий точки 1 и 2 может отличаться по цвету и размеру от провода, соединяющего точки 2 и 3, но оба эти повода будут иметь одинаковое обозначение. То же самое касается и проводов, соединяющих точки 6, 5 и 4.
Знание того, что между электрически общими точками напряжение всегда равно нулю, может помочь вам в поиске неисправностей схемы. Если вы уверены, что измеряете напряжение между электрически общими точками, а прибор показывает напряжение отличное от нуля, то между этими точками существует обрыв провода.
Примечание: в подавляющем большинстве практических случаев, мы с вами можем считать, что провода обладают нулевым сопротивлением на всем своем протяжении. В действительности, если провода не являются сверхпроводимыми, то они обладают небольшим сопротивлением. Зная это, мы должны иметь в виду, что принципы электрически общих точек действительны в значительной степени, но не абсолютно. То есть, правило, согласно которому электрически общие точки имеют нулевое напряжение между собой, можно сформулировать поточнее: между электрически общими точками существует очень маленькое напряжение. Такое напряжение практически неизбежно вследствие того, что небольшая величина сопротивления соединительного провода не может не породить небольшое напряжение при прохождении тока по этому проводу. Теперь, когда вы понимаете, что правила основываются на идеальных условиях, вы не будете озадачены, если столкнетесь с некоторыми условиями, кажущимися исключением из правил.
Краткий обзор:
-
Соединительные провода в цепи, как предполагается, имеют нулевое сопротивление, если не указано иное.
-
Провода в схеме можно укоротить или удлинить, и это не повлияет на ее функционирование.
-
Точки цепи, непосредственно связанные между собой проводом с нулевым сопротивлением, называются электрически общими.
-
Напряжение между электрически общими точками, вне зависимости от величины тока, будет равно нулю (в идеале).
-
Напряжение или сопротивление между группами электрически общих точек будет одинаково.
-
Все эти правила описывают идеальные условия, где предполагается, что соединительные провода имеют абсолютно нулевое сопротивление. В реальности дела обстоят не совсем так. Чтобы эти правила выполнялись, провода должны обладать очень маленьким сопротивлением.
1. Введение в электронику
1.1. Ток, напряжение, анергия и мощность в электрической цепи
Электрический ток, как физическое явление, представляет собой упорядоченное движение электрических зарядов. Под термином «ток» также понимают интенсивность или силу тока, измеряемую количеством электрического заряда q, прошедшее через поперечное сечение проводника в единицу времени:i=dq/dt. Следовательно, ток представляет скорость изменения заряда во времени. Ток измеряется в амперах (А). Знак тока зависит от направления движения зарядов одного знака, а именно условно принятого положительного заряда. Выбранное положительное направление тока на схемах обозначается стрелкой.
Прохождение электрического тока в цепи связано с преобразованием или потреблением энергии. Для определения энергии, затрачиваемой на перемещение заряда между двумя рассматриваемыми точками проводника, вводят новую величину — напряжение.
Напряжением называют количество энергии, затрачиваемой на перемещение единицы заряда из одной точки в другую: u = dw / dt, w — энергия. Напряжение измеряется в вольтах (В).
Напряжение величина относительная и всегда определяется между двумя точками. Напряжение между двумя точками на схемеaиbобозначается черезUab. НапряжениеUab– положительное, если точкааимеет более высокий потенциал относительно точкиb, и будет отрицательным, если точкааимеет более низкий потенциал, относительно точкиb. При этом справедливо соотношениеUab= -Uba. Напряжение между двумя точкамиаиbопределяется как разность потенциалов в точкахаиb:
Uab=φа–φb
Потенциал φ – это напряжение в точке относительно общей опорной точки, потенциал, которой условно принимают равный 0. В схемах условным обозначением опорной точки является знак заземления. За опорную точку или узел можно выбрать любую точку схемы, однако на практике, в качестве опорной точки (узла) выбирают точку, к которой подключается наибольшее количество ветвей.
Когда говорят «напряжение в точке», имеют в виду, что напряжение определяется между этой точкой и опорной точкой (землей). Так, если за опорную точку выбран узел b(φb=Ub= 0), то напряжение в точкеаравно
Ua = Uab = φа –φb = Ua – Ub = Ua – 0.
Для однозначного определения знака напряжения между двумя выводами рассматриваемого участка цепи одному из выводов условно приписывают положительную полярность, которую отмечают либо стрелкой, направленной от вывода, либо знаками “+”, “-” . Потенциал вывода со знаком “+”, из которого выходит стрелка, выше потенциала второго вывода.
Перед началом анализа схемы должны быть указаны выбранные положительные полярности напряжений — только при этом условии возможно однозначное определение напряжений. Хотя условно положительную полярность напряжения можно выбирать произвольно, обычно удобно выбирать согласованную с выбранным положительным направлением тока, когда стрелки для тока и напряжения совпадают или знак “+” полярности напряжения находится в хвосте стрелки, обозначающей положительное направление тока.
Из определения напряжения можно получить выражение для энергии, затраченной на перемещение заряда q на участке цепи с напряжением U к моменту времени t:

Дифференцирование этого равенства по времени дает выражение скорости изменения энергии во времени, т.е. мощности, выражаемой в ваттах:

Знак мощности определяется знаками напряжения и тока. При совпадении знаков напряжения и тока мощность положительна, что соответствует потреблению энергии в рассматриваемом участке цепи. При несовпадении знаков напряжения и тока мощность отрицательна, что означает отдачу ее из участка цепи (такой участок является источником энергии).
чему равен общий ток цепи и напряжение на участке при последовательном соединение???
Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3… Ток через все сопротивления протекает один ( I ). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм. I=U/Rсумм Мощность P=U*I или P=I*I*R (так как U=I*R). тогда, P1=I*I*R1 P2=I*I*R2 P3=I*I*R3
исходные данные где?
1) сумма 2)напряжение на участке цепи умножить на ток. При том ток, при последовательном соединении одиноковй в любой точке цепи
Сумма токов в узле равна нулю. Выход равен входу. 1) сложить. 2)сумме мощностей элементов цепи.
При последовательном соединении узлов нет. Ток цепи определяется делением приложенного напряжения в вольтах (V) на сопротивление цепи в омах (R). I=V : R. Падение напряжения на участке будет равнятся сопротивлению участка помноженному на ток. Общее сопротивление равно сумме всех сопротивлений. Мощность участка равняется падению напряжения на участке помноженному на ток. Это Закон Ома. А вообще-то это все в школьном учебнике физики в разделе-Электричество.
Напряжение между двумя точками, находящимися на одной линии
Задача. Напряжение между двумя точками, находящимися на одной линии напряжённости однородного электростатического поля на расстоянии
см друг от друга, В. Определите напряжение между двумя точками, расположенными на этой же линии напряжённости на расстоянии см друг от друга.Дано:
смВ
см
Найти:
Решение
Думаем: связь между напряжением и напряжённостью можно найти используя определение потенциала (1).
(1)Учитывая, что напряжение
, а потенциал начальной точке мы можем принять равным нулю, то: (2)Решаем: т.к. поле и в первом и во втором случае одинаково (
), то запишем (2) для первого и второго случая, описанного в задаче: (3) (4)Поделим (4) на (3) и выделим искомое:
(5)Считаем: для подсчёта можно не переводить расстояния в единицы СИ, т.к. при делении размерности сократятся.
ВОтвет:
В.Ещё задачи на тему «Напряжённость электростатического поля»
Поделиться ссылкой:
- Telegram
Понравилось это:
Нравится Загрузка…
Определить напряжение на сопротивлении R2
Если R1, R2 — последовательно, то U на R2 будет 220 — 180 = 40 (В) . Класс точности вольтметра — это его приведённая погрешность, равная 1% (это Г, гамма) . Вся шкала — 250 В (это П, полное отклонение прибора, или его шкала) . Выражение для приведённой погрешности: Г=DX/П (DX — дельта Х -абсолютная погрешность) . С другой стороны, относительная погрешность dx=DX/xm (xm — измеряемая величина, 40 В) . Тогда, используя выражения относительной и приведённой погрешностей, можно записать: dx=Г*П/xm = 1*250/40 = 6,25 (%) .
Для руских это вопрос не разрешимый — они тупые.
40 вольт падения, это очень много!! ! К тому же не известно внутреннее сопротивление источника тока, и ток проходящий через него, от куда взялось R1? и как они включены? Одни загадки…. Фиг сосчитаешь….
Главные площадки напряжения (сопромат)

Главные площадки – это площадки, проходящие через исследуемую точку, на которых Касательные напряжения отсутствуют.
Главные напряжения – это возникающие на главных площадках нормальные напряжения
В общем случае нагружения (при объемном напряженном состоянии) среди множества площадок, проходящих через некоторую точку тела, всегда можно найти три взаимно перпендикулярные главные площадки. В окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные (главные) напряжения (см. рис. 6.2).
 |
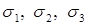 . Индексы расставляются после вычисления главных напряжений. Должно выполняться неравенство:
. Индексы расставляются после вычисления главных напряжений. Должно выполняться неравенство: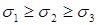
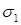 – наибольшее, а
– наибольшее, а 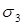 – наименьшее нормальное напряжение в исследуемой точке тела.
– наименьшее нормальное напряжение в исследуемой точке тела.
В частном случае нагружения может получиться так, что все три главных напряжения в исследуемой точке тела равны между собой. Тогда любая площадка, проведенная через эту точку, является главной площадкой.
По значениям главных напряжений дается оценка прочности материала в исследуемой точке деформированного твердого тела.
При плоском напряженном состоянии на грани элементарного параллелепипеда с нормалью х полностью отсутствует не только касательное, но и нормальное напряжение. Площадка тоже является главной площадкой, главное напряжение на которой равно нулю.
Пусть мы нашли для случая плоского напряженного состояния, что экстремальные напряжения в исследуемой точке тела равны 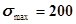 МПа, а
МПа, а  МПа. Индексы главных напряжений:
МПа. Индексы главных напряжений: 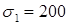 МПа,
МПа,  МПа,
МПа, 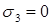 МПа.
МПа.
Если получилось 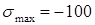 МПа, а
МПа, а 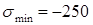 МПа, то тогда
МПа, то тогда 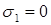 МПа,
МПа, 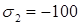 МПа,
МПа, 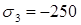 МПа.
МПа.

