Пара сил. Момент пары сил
Парой сил называется система двух равных по величине, противоположных по направлению и не лежащих на одной прямой сил (рисунок 1.19).
Рисунок 1.19
Пара сил не имеет равнодействующей, т.е. не может быть заменена одной силой.
Сумма проекций сил пары на любую ось равна нулю, т.к. их проекции всегда равны и противоположны по знаку (рисунок 1.20).
Рисунок 1.20
Пара сил оказывает вращающее действие, которое может быть оценено моментом пары:
M(F1, F2) = F1h = F2h, (1.11)
где h – плечо пары.
Короткий видеоурок про момент силы с примерами:
Момент силы (видео)
Момент пары считается положительным, если силы пары стремятся повернуть плоскость, в которой они расположены, против хода часовой стрелки (рисунки 1.19, 1.20 – моменты этих пар сил положительны).
Момент пары сил может быть определен как векторная величина:
M(F
т.е. вектор M(F1, F2) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения (рисунок 1.21).
В разделе «Статика» дисциплины «Теоретическая механика» доказывается теорема о том, что сумма моментов сил пары относительно произвольной точки пространства равна моменту этой пары. Следовательно, вектор-момент пары сил может быть приложен (или перенесен) к любой точке твердого тела, на которое действует пара сил.
Рисунок 1.21
Поскольку действие пары сил оценивается величиной и направлением вращающего момента, то на плоскости пару сил изображают в любом месте твердого тела, задавая величину и направление вращающего действия (см. на рисунке 1.22 изображение пар сил
Рисунок 1.22
См. также момент силы
>> Распределенные нагрузки
Пара сил — Википедия
Материал из Википедии — свободной энциклопедии
Па́ра сил — совокупность двух сил, которые приложены к одному абсолютно твёрдому телу и при этом равны по модулю и противоположны по направлению.
Иллюстрация. Синим цветом показано твёрдое тело.Пара сил представляет собой важный частный случай системы сил. Главным вектором для неё служит нулевой вектор, так что действие пары сил на тело полностью характеризуется её главным моментом, который является
В соответствии с этим, момент пары сил не имеет точки приложения (утверждение, иногда называемое «второй теоремой Вариньона»): к каким бы частям твёрдого тела ни прикладывались силы, составляющие пару, при данных модуле и направлении момента пары двигаться оно будет одинаково.
Кратчайшее расстояние между линиями действия сил, образующих пару, называют плечом пары. Модуль момента пары сил равен произведению модуля одной из сил на плечо: M=Cℓ{\displaystyle M=C\ell }. Как и любой механический момент, момент пары сил является псевдовекторной величиной; он направлен перпендикулярно плоскости, задаваемой линиями действия сил: M→=ℓ→×C→{\displaystyle {\vec {M}}={\vec {\ell }}\times {\vec {C}}} (при этом направление вектора плеча ℓ→{\displaystyle {\vec {\ell }}} условно следует задавать в сторону
Пара сил, момент которой отличен от нуля — простейший пример системы сил, не имеющей равнодействующей.
Действие силы, приложенной к твёрдому телу на некотором расстоянии d от центра масс (в точке, в которую из центра масс можно провести вектор d→{\displaystyle {\vec {d}}}), эквивалентно действию такой же силы, приложенной непосредственно к центру масс, комбинированной с некоторой парой сил, такой, что F→×d→=C→×ℓ→{\displaystyle {\vec {F}}\times {\vec {d}}={\vec {C}}\times {\vec {\ell }}}, то есть с моментом, равным моменту силы относительно центра масс (в частности, если F→⊥d→{\displaystyle {\vec {F}}\perp {\vec {d}}}, можем задаться ℓ=2d{\displaystyle \ell =2d}, в таком случае одна из сил будет приложена в той же точке, что и исходная, и составит C→=12F→{\displaystyle {\vec {C}}={\tfrac {1}{2}}{\vec {F}}}).
2. Момент силы, пара сил и их свойства.
Момент силы относительно центра (или точки).
Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом
Рассмотрим
силу 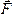 ,
приложенную в точке А твердого
тела (рис. 20). Допустим, что сила
стремится повернуть тело вокруг центра О.
Перпендикуляр h,
опущенный из центра O на
линию действия силы
,
приложенную в точке А твердого
тела (рис. 20). Допустим, что сила
стремится повернуть тело вокруг центра О.
Перпендикуляр h,
опущенный из центра O на
линию действия силы 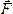 ,
называется плечом силы
,
называется плечом силы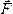
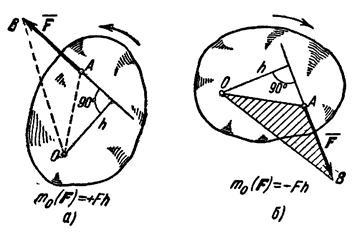
Рис.20
Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.
Тогда
для количественного измерения
вращательного эффекта можно ввести
следующее понятие о моменте силы:
моментом силы 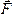 относительно
центраО называется
величина, равная взятому с соответствующим
знаком произведению модуля силы на
длину плеча.
относительно
центраО называется
величина, равная взятому с соответствующим
знаком произведению модуля силы на
длину плеча.
Момент
силы 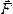 относительно
центраО будем
обозначать символом m0(F).
Следовательно,
относительно
центраО будем
обозначать символом m0(F).
Следовательно,
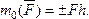
В
дальнейшем условимся считать, что момент
имеет знак плюс, если сила стремится
повернуть тело вокруг центра О против
хода часовой стрелки, и знак минус,
— если по ходу часовой стрелки. Так, для
силы 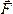 ,
изображенной на рис.20,а,
момент относительно центра О имеет
знак плюс, а для силы, показанной на
рис.20,б,
— знак минус.
,
изображенной на рис.20,а,
момент относительно центра О имеет
знак плюс, а для силы, показанной на
рис.20,б,
— знак минус.
Отметим следующие свойства момента силы:
1) Момент силы не изменяется при переносе точки приложения силы вдоль
2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).
3) Момент силы численно выражается удвоенной площадью треугольника ОАВ (рис. 20,б)
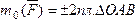
Этот результат следует из того, что
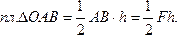
Теорема Вариньона о моменте равнодействующей.
Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
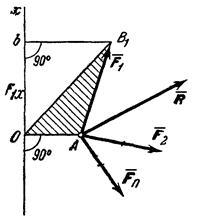
Рис.21
Рассмотрим
систему сил 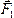 ,
, 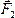 , …,
, …, 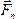 ,
сходящихся в точкеА (рис.21).
Возьмем произвольный центр
,
сходящихся в точкеА (рис.21).
Возьмем произвольный центр
Для
доказательства теоремы найдем
соответствующие выражения моментов m0(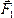 ),m0(
),m0(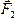 ),
… . По формуле
),
… . По формуле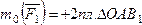 .
Но, как видно из рисунка,
.
Но, как видно из рисунка,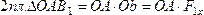
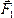 на
осьОх;
следовательно
на
осьОх;
следовательно 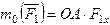 .
.
Аналогично вычисляются моменты всех других сил.
Обозначим
равнодействующую сил 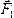 ,
,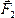 , …,
, …, 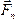 , через
, через 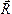 ,
где
,
где 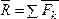 .
Тогда, по теореме о проекции суммы
сил на ось, получим
.
Тогда, по теореме о проекции суммы
сил на ось, получим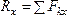 .
Умножая обе части этого равенства наОА,
найдем:
.
Умножая обе части этого равенства наОА,
найдем:
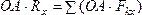
или,
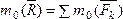 .
.
Пара сил. Момент пары.
Парой
сил (или просто парой) называются две
силы, равные по величине, параллельные
и направленные в противоположные стороны
(рис.22). Очевидно, 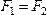 ,
,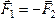 и
и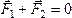 .
.
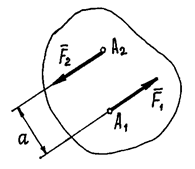
Рис.22
Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:
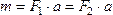 .
.
Расстояние a между линиями действия сил называется плечом пары.
Если пара вращает тело против часовой стрелки, момент её считается положительным (как на рис.22), если по часовой стрелке – отрицательным.
Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.
Вектор
момента пары 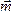 направляется
перпендикулярно плоскости, в которой
расположена пара, в такую сторону, что
если посмотреть оттуда, увидим
вращение тела против часовой стрелки
(рис. 23).
направляется
перпендикулярно плоскости, в которой
расположена пара, в такую сторону, что
если посмотреть оттуда, увидим
вращение тела против часовой стрелки
(рис. 23).
Нетрудно
доказать, что вектор момента пары 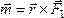 –
есть вектор этого векторного произведения
(рис. 23). И заметим, что он равен вектору
момента силы
–
есть вектор этого векторного произведения
(рис. 23). И заметим, что он равен вектору
момента силы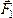 относительно
точкиА,
точки приложения второй силы:
относительно
точкиА,
точки приложения второй силы:
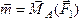 .
.
О
точке приложения вектора 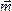 будет
сказано ниже. Пока приложим его к точкеА.
будет
сказано ниже. Пока приложим его к точкеА.
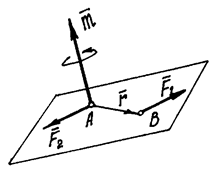
Рис.23
Свойства пар
1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.
2)
Найдём сумму моментов сил 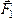 и
и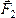 составляющих
пару, относительно какой-либо
точкиО (рис.24).
составляющих
пару, относительно какой-либо
точкиО (рис.24).
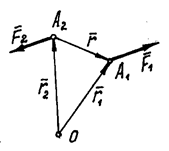
Рис.24
Покажем радиусы-векторы точек А1 и А2 и
вектор 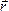 ,
соединяющий эти точки. Тогда момент
пары сил относительно точкиО
,
соединяющий эти точки. Тогда момент
пары сил относительно точкиО
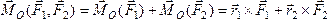 .
.
Но 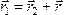 .
Поэтому
.
Поэтому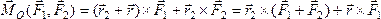 .
.
Но 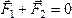 ,
а
,
а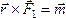 .
.
Значит 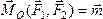 .
.
Момент пары сил относительно любой точки равен моменту этой пары.
Отсюда
следует, что, во-первых, где бы не
находилась точка О и,
во-вторых, где бы не располагалась эта
пара в теле и как бы она не была повёрнута
в своей плоскости, действие её на тело
будет одинаково. Так как момент сил,
составляющих пару, в этих случаях один
и тот же, равный моменту этой пары 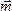 .
.
Поэтому можно сформулировать ещё два свойства.
3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.
4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F1=F2=5 H и плече а = 4 см момент пары m = 20Hсм. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Нсм и действие пары на тело не изменится.
Все
эти свойства можно объединить и, как
следствие, сделать вывод, что пары с
одинаковым вектором момента 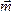 и
неважно где расположенные на теле,
оказывают на него равное действие. То
есть такие пары эквивалентны.
и
неважно где расположенные на теле,
оказывают на него равное действие. То
есть такие пары эквивалентны.
Исходя
из этого, на расчётных схемах пару
изображают в виде дуги со стрелкой,
указывающей направление вращения, и
рядом пишут величину момента m.
Или, если это пространственная конструкция,
показывают только вектор момента
этой пары. И вектор момента пары можно
прикладывать к любой точке тела. Значит
вектор момента пары 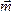 –
свободный вектор.
–
свободный вектор.
И
ещё одно дополнительное замечание. Так
как момент пары равен вектору момента
одной из сил её относительно точки
приложения второй силы, то момент пары
сил относительно какой-либо оси z –
есть проекция вектора момента пары 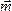 на
эту ось:
на
эту ось:
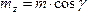 ,
,
где 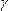 –
угол между вектором
–
угол между вектором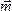 и
осьюz.
и
осьюz.
Сложение пар
Пусть даны две пары с моментами m1 и m2, расположенные в пересекающихся плоскостях (рис.25).
Сделаем
у пар плечи одинаковыми, равными а = АВ.
Тогда модули сил, образующих первую
пару, должны быть равны: 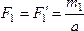 , а
образующих вторую пару:
, а
образующих вторую пару: 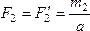 .
.
Эти
пары показаны на рис.25, где 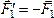 ,
, 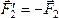 .
И расположены они в своих плоскостях
так, что плечи пар совпадают с прямой АВ на
линии пересечения плоскостей.
.
И расположены они в своих плоскостях
так, что плечи пар совпадают с прямой АВ на
линии пересечения плоскостей.
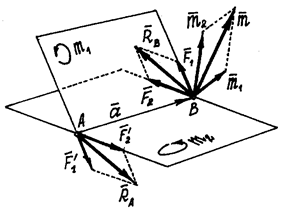
Рис.25
Сложив
силы, приложенные к точкам А и В,
построением параллелограммов, получим
их равнодействующие 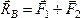 и
и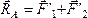 .
Так как
.
Так как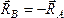 ,
то эти силы
,
то эти силы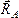 и
и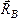 будут
образовывать пару, момент которой
будут
образовывать пару, момент которой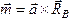 ,
где
,
где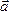 –
радиус-вектор точкиВ,
совпадающий с АВ.
–
радиус-вектор точкиВ,
совпадающий с АВ.
Так
как 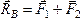 ,
то момент полученной пары
,
то момент полученной пары
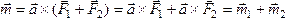 .
.
Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.
При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом
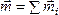 .
.
Конечно,
эта результирующая пара будет располагаться
в плоскости перпендикулярной
вектору 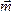 .
.
Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар
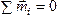 .
.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.
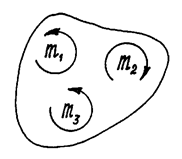
Рис.26
Например, пары, показанные на рис.26, расположены в одной плоскости и моменты их:
m1=2 Hсм , m2=5 Hсм, m3=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:
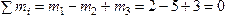 .
.
Пара сил
1. Пара сил — система двух сил, приложенных к телу в двух разных точках:
— равных по модулю
— параллельных
— противоположно направленных
2. Плечо пары сил – кратчайшее расстояние между линиями действия сил пары.
Момент пары сил
Момент пары сил — произведение модуля любой силы на плечо пары (модуль силы х плечо)
Свойства пары сил
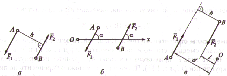
1. Сумма проекций на любую ось сил пары равна нулю
F2cosα – F1cosα = 0
2. Сумма моментов сил пары относительно любой точки плоскости равна моменту пары.
momo(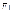 )
= — F1d
= — Fd
)
= — F1d
= — Fd
momo(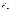 )
= + F2l
= +Fl
)
= + F2l
= +Fl
momo(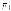 )
+ momo(
)
+ momo(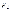 )
= — Fd
+ Fl
= — F(d-l)
= —
Fh
)
= — Fd
+ Fl
= — F(d-l)
= —
Fh
Следовательно, пару сил нельзя заменить равнодействующей.
Самостоятельная работа обучающегося по теме 1.3. (1 час – все)
1. Составить глоссарий основных понятий по теме «Пара сил» — арх, ‘эзс – 1 час
1. Решение задач на определение моментов сил относительно точки: авто – 1час
Тема 1.4. Плоская система произвольно расположенных сил
– (4 час арх, 2час авто, эзс)
Основные понятия
1. Плоская система сил – система сил, линии действия которых лежат в одной плоскости.
2. На плоскости могут быть приложены силы:
А) произвольно расположенные;
Б) пары сил;
В) силы, сходящиеся в одной точке.
3. Плоская система произвольно расположенных сил – все силы или линии их действия не пересекаются в одной точке.
Приведение плоской системы сил к заданному центру
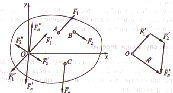
1. Пусть на твёрдое тело действует система сил 
2. Приложим в точке Опо 2 уравновешенные силы:
А) одна равна
и параллельна заданной: 
Б) другая
сила равна заданной, но противоположно
направлена
3. В итоге на тело действует:
А) система
сходящихся сил 
Б) система пар сил с моментами
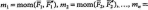

4. Систему сходящихся сил заменяем равнодействующей
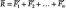
Или
в соответствии с тем, что 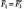 и т.д.
и т.д.
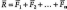
5. В соответствии со вторым свойством пары сил найдём алгебраическую сумму моментов всех пар
Мо =m1+m2+ …+mn
Лемма Пуансо
1. В результате произвольную плоскую систему сил можно заменить:
— одной силой, равной геометрической сумме всех сил, приложенных в произвольно выбранном центре и
— моментом,равным алгебраической сумме моментов присоединенных пар
2. Принятые определения:
А) точка о – центр приведения
Б) главный вектор– векторR, равный геометрической сумме всех сил. Его значение не зависит от выбора центра приведения.
В) главный момент– момент МО, равный алгебраической сумме моментов присоединённых пар. Его значение зависит от выбора центра приведения (величина плеча будет меняться).
Частные случаи приведения
1. R0=0,M0≠0 – система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;
2. R0≠0,M0=0 – система эквивалентна равнодействующей R. Главный вектор в данном случае – является равнодействующей.
3. R0≠0,M0≠0 – система эквивалентна равнодействующей R, приложенной в новом центре приведения, расположенном от прежнего на расстоянии d = Мо\R
4. R=0,M0=0 – плоская система сил находится в равновесии;
Теорема Вариньона (о моменте равнодействующей плоской системы сил)
Момент равнодействующей плоской системы сил относительно произвольного центра О равен алгебраической сумме моментов всех сил системы относительно этого центра.
Аналитические уравнения равновесия плоской системы сил
Условие равновесия выражается тремя уравнениями – основные уравнения равновесия:
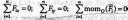
2. Варианты записи уравнений равновесия – в зависимости от расположения сил
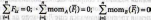
или

Класссификация нагрузок
Сосредоточенная
Распределённая: по линии, по поверхности, по объёму
Изгибающий момент
Балочные системы
1. Объект решения задач статики – балки (или балочные системы)
2. Балка – деталь в виде прямого бруса с опорами в двух (или более) точках.
Виды опор
1. Шарнирно-подвижная: вращение вокруг своей оси (шарнир) + поступательное перемещение (подвижная)
2. Шарнирно-неподвижная: вращение вокруг своей оси (шарнир)
3. Жёсткая заделка(защемление): препятствует любому перемещению.
Решение задач на определение опорных реакций
С помощью трёх уравнений равновесия определяют реакции опор (если число реакций связи не превышает трёх):
1. Показать нагрузки
2. Обозначают нагрузки
3. Освобождаются от опор и заменяют их действие на балку реакциями
4. Составляют уравнение равновесия
5. Решают уравнения равновесия и определяют из них опорные реакции
6. Проверка решения
Определение усилий в стержнях плоских ферм – вырезанием узлов
1. Аналитический способ
2. Графический способ – построением диаграммы Максвелла – Кремоны
Элементы теории трения
ТЕМА 1.5. ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ (авто — 1 час)
Самостоятельная работа обучающегося (авто – 1час)
1. Решение задач по индивидуальным заданиям
1. Понятие о трении
Сила трения возникает при соприкосновении тел и препятствует передвижению одного тела по поверхности другого.
2. Виды сил трения:
А) трение скольжения
Б) трение скольжения
3. Трение скольжения– сопротивление, возникающее при относительном перемещении одного тела по поверхности другого.
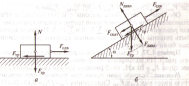
4. Законы трения:
А) Сила трения Fтрнаправлена в сторону, противоположную относительной скорости скольжения
Б) Сила трения не зависит от площади контактирующих поверхностей
В) Модуль силы трения пропорционален нормальному давлению (чем больше нормальное давление, тем больше сила трения).
5. По рисунку:
А) сила тяжести mg– вниз (чем большеmg, тем больше опорная реакцияN(вектор)
Б) тело движется вниз = сила трения направлена вверх по наклонной плоскости
В) гладкая поверхность = опорная реакция N(вектор) направлена перпендикулярна плоскости
Г) по аксиоме 3 строим диагональ параллелограмма R(равнодействующая)
6. Виды сил трения скольжения:
А) сила трения
при покое Fтр foN
foN
Б) сила трения
при движении Fтр fN
fN
N– сила нормального давления
fo– коэффициент трения покоя
f– коэффициент трения скольжения – зависит от скорости скольжения тел.
Оба коэффициента зависят от материала и физического состояния поверхностей
7. Трение качения– сопротивление, возникающее при качении одного тела к другому.

8. Виды связей:
А) идеальные (без трения)
Б) реальные (с трением)
Самостоятельная работа обучающихся – 3час эзс, 4час арх,
1. Решить задачи по определению опорных реакций для однопролётной балки по вариантам
2. Решить задачи на определение усилий в стержнях фермы по вариантам
3. Сравнить способы определения усилий, сделать краткий анализ о преимуществах и недостатках каждого метода — результат оформить в виде таблицы
Авто – 2час
1. Выполнение расчётно-графической работы на определение опорных реакций балочных систем
7. Основные понятия и определения статики. Момент силы. Пара сил.
7. Основные понятия и определения статики. Момент силы. Пара сил.
- Основные понятия и определения статики. Аксиомы статики.
- Связи и их реакции.
- Момент силы относительно центра и оси.
- Пара сил. Векторный и алгебраический момент пары сил (Свойства пар сил на плоскости).
- Условия эквивалентности пар сил.
- Сложение пар сил, лежащих в пересекающихся плоскостях.
- Условия равновесия системы пар сил.
1. Основные понятия и определения статики.
Материальные объекты в статике:
материальная точка,
система материальных точек,
абсолютно твердое тело.
Системой материальных точек, или механической системой, называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения других точек этой системы.
Абсолютно твердое тело – это тело, расстояние между двумя точками которого не изменяется.
Твердое тело может находиться в состоянии покоя или движения определенного характера. Каждое их этих состояний будем называть кинематическим состоянием тела.
|
|
Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила может быть приложена в точке, тогда эта сила – сосредоточенная. Сила может действовать на все точки данного объема или поверхности тела, тогда эта сила – распределенная. |
|
Система сил — совокупность сил, действующих на данное тело. |
|
|
Равнодействующей называется сила, эквивалентная некоторой системе сил. |
|
|
Уравновешивающей силой называется сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону. |
|
|
Системой взаимно уравновешивающихся сил называется система сил, которая будучи приложенной к твердому телу, находящемуся в покое, не выводит его из этого состояния.
|
Внутренние силы – это силы, которые действуют между точками или телами данной системы.
Внешние силы – это силы, которые действуют со стороны точек или тел, не входящих в данную систему.
— преобразование систем сил, действующих на твердое тело в эквивалентные им системы;
— исследование условий равновесия тел под действием приложенных к ним сил.
|
|
1. Аксиома инерции. Под действием взамно-уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.
2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны.
|
|
|
3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно-уравновешивающихся сил. Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление. Сила — скользящий вектор.
|
|
|
|
4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
|
|
5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.
2. Связи и их реакции
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничено связями, называется несвободным.
Все силы, действующие на несвободное твердое тело, можно разделить на:
- задаваемые (активные)
- реакции связей
Задаваемая сила выражает действие на данное тело других тел, способных вызвать изменение его кинематического состояния.
Реакция связи – это сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям.
Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил, действуют реакции связей.
|
|
|
|
|
|
Как определить направление реакции?
Если существует два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление ее реакции противоположно первому направлению.
В общем случае направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.
|
|
Неподвижный шарнир
Подвижный шарнир
|
|
|
3. Момент силы относительно центра
Моментом силы F относительно некоторого неподвижного центра О называется вектор, расположенный перпендикулярно к плоскости, проходящей через вектор силы и центр О, направленный в ту сторону, чтобы смотря с его конца можно было видеть поворот силы F относительно центра О против часовой стрелки.
Свойства момента силы относительно центра:
|
|
1) Модуль момента силы относительно центра может быть выражен удвоенной площадью треугольника ОАВ (1.1)
2) Момент силы относительно центра равен нулю в том случае, если линия действия силы проходит через эту точку, то есть h = 0.
|
|
|
3) Если из точки О в точку приложения силы А провести радиус вектор , то вектор момента силы можно выразить векторным произведением
(1.2) |
|
|
4) При переносе силы по линии ее действия вектор ее момента относительно данной точки не изменяется.
|
|
|
5) Если через центр О провести оси координат Охуz то выражение (4.2) позволяет вычислить момент МО аналитически относительно координатных осей.
(1.3)
|
Если к твердому телу приложено несколько сил, лежащих в одной плоскости, можно вычислить алгебраическую сумму моментов этих сил относительно любой точки этой плоскости
Момент МО, равный алгебраической сумме моментов данной системы относительно какой-либо точки в той же плоскости, называют главным моментом системы сил относительно этой точки.
3. Момент силы относительно оси
Чтобы определить момент силы относительно оси необходимо:
1) провести плоскость, перпендикулярную к оси Z;
2) определить точку О пересечения оси с плоскостью;
3) спроецировать ортогонально силу F на эту плоскость;
4) найти момент проекции силы F относительно точки О пересечения оси с плоскостью.
(1.4)
Правило знаков:
Момент силы относительно оси считается положительным, если, смотря навстречу оси Z, можно видеть проекцию , стремящейся вращать плоскость I вокруг оси Z в сторону, противоположную вращению часовой стрелки.
|
|
Свойства момента силы относительно оси 1) Момент силы относительно оси изображается отрезком, отложенным по оси Z от точки О в положительном направлении, если > 0 и в отрицательном направлении, если < 0. 2) Значение момента силы относительно оси может быть выражено удвоенной площадью Δ (1.5)
3) Момент силы относительно оси равен нулю в двух случаях:
|
4. Пара сил. Векторный и алгебраический момент пары сил
Система двух равных по модулю, параллельных и противоположно направленных сил и , называется парой сил.
Плоскость, в которой находятся линии действия сил и , называется плоскостью действия пары сил.
Кратчайшее расстояние hмежду линиями действия сил, составляющих пару, называется плечом пары сил.
Момент пары сил определяется произведением модуля одной из сил пары на плечо.
(1.6)
|
|
Правило знаков
Вектор момента М пары и направляют перпендикулярно к плоскости действия пары сил в такую сторону, что бы смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки.
- 4. Свойства пар сил на плоскости
Свойство 1. Вектор-момент M пары по модулю и направлению равен векторному произведению радиуса вектора АВ на ту из сил этой пары, к началу которой направлен радиус-вектор АВ, то есть
(1.7)
|
|
Если пары сил лежат в одной плоскости
|
|
Свойство 2. Главный момент сил, составляющих пару относительно произвольной точки на плоскости действия пары, не зависит от положения этой точки и равняется моменту этой пары сил.
|
|
5. Условия эквивалентности пар сил
Теорема об условии эквивалентности пар сил,
лежащих в одной плоскости.
Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты равны численно и одинаковы по знаку.
|
|
следовательно, их можно исключить из этой системы сил. Тогда получим пару с плечом NK=CD=h2, эквивалентную паре с плечом KZ = h1 = AB. Из подобия треугольников
|
Сравнивая (*) и (**) получим, что пару сил, не изменяя ее действия на твердое тело можно переносить в любое место плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять это плечо и модули сил, не изменяя величины ее момента и направления вращения.
Следовательно, основной характеристикой пары является ее момент.
Теорема об условии эквивалентности пар сил в пространстве
Пары сил в пространстве эквивалентны, если их моменты геометрически равны.
|
|
Имеем :
|
|
|
|
Из рассмотренных теорем следует:
- не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а так же изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента.
- вектор момента пары сил определяет все три ее элемента: положение плоскости действия пары, направление вращения и численное значение момента.
Таким образом, вектор момента пары сил можно переносить в любую точку пространства, то есть
момент пары сил является свободным вектором
6. Сложение пар сил, лежащих в пересекающихся плоскостях
Теорема о сложении пар сил, лежащих в пересекающихся плоскостях
Система пар сил, лежащих в пересекающихся плоскостях эквивалентна одной паре с вектором-моментом, равным геометрической сумме векторов –моментов слагаемых пар.
|
|
то есть вектор-момент равнодействующей пары по модулю и направлению изображается диагональю параллелограмма, построенного из векторов-моментов слагаемых пар.
Если на тело действует nпар, лежащих в разных плоскостях, то складывая эти пары в последовательном порядке и применяя каждый раз теорему о сложении двух пар сил, установим, что эта система пар заменится одной равнодействующей парой с вектором-моментом
(1.8)
|
|
|
|
7. Условия равновесия системы пар сил
— векторная форма (1.9)
— в проекциях на оси координат (1.10)
Глава 2 момент силы относительно центра. Пара сил
§6. Момент силы относительно центра (или точки)
При рассмотрении пространственной системы сил применяется понятие момента силы относительно центра (или точки).
Определение.
Моментом силы  относительно центра О называется
приложенный в центре О вектор
относительно центра О называется
приложенный в центре О вектор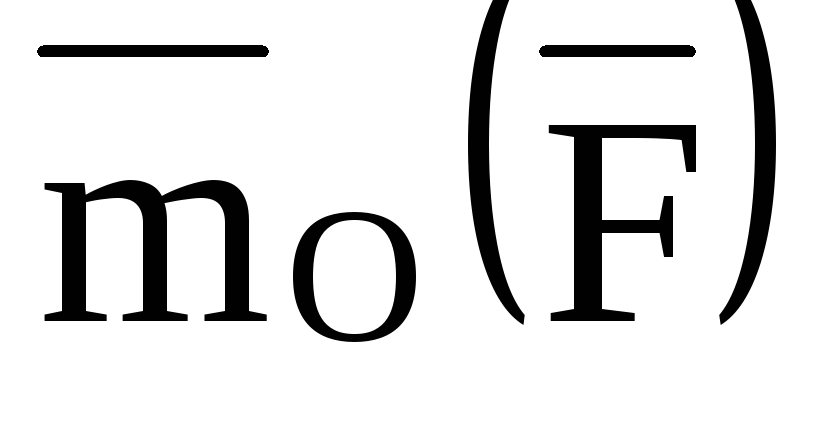 ,
модуль которого равен произведению
модуля F силы на ее плечо h и который
направлен перпендикулярно плоскости,
проходящей через центр О и силу, в ту
сторону, откуда сила видна стремящейся
повернуть тело вокруг центра О против
хода часовой стрелки (рис. 17). Плечом
h силы F относительно центра О называют
длину отрезка перпендикуляра, опущенного
из точки О на линию действия силы.
,
модуль которого равен произведению
модуля F силы на ее плечо h и который
направлен перпендикулярно плоскости,
проходящей через центр О и силу, в ту
сторону, откуда сила видна стремящейся
повернуть тело вокруг центра О против
хода часовой стрелки (рис. 17). Плечом
h силы F относительно центра О называют
длину отрезка перпендикуляра, опущенного
из точки О на линию действия силы.
Согласно этому определению
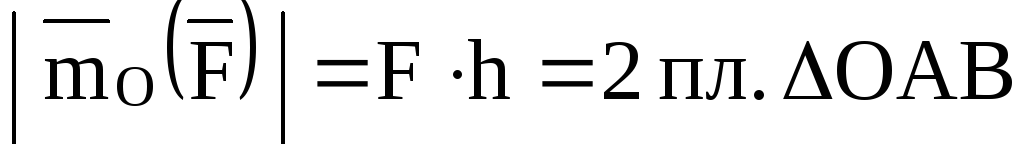 ,
(11)
,
(11)
где 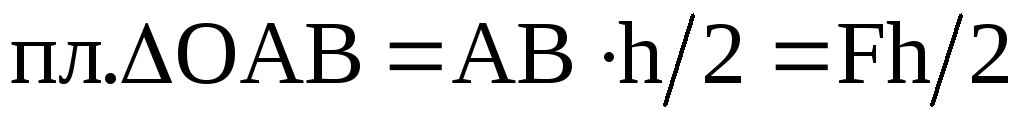 .
.
Измеряется момент силы в ньютон-метрах (Н·м).
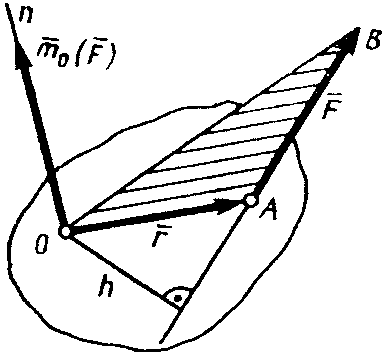
Рис. 17
Для
нахождения формулы, которая выражает
вектор 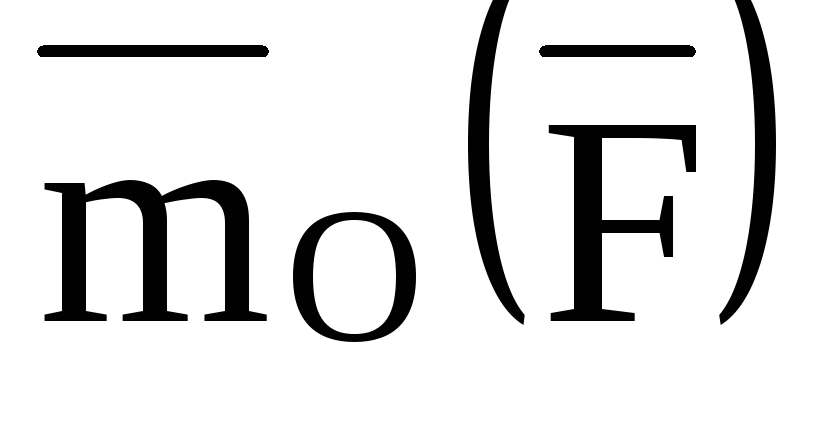 ,
рассмотрим векторное произведение
,
рассмотрим векторное произведение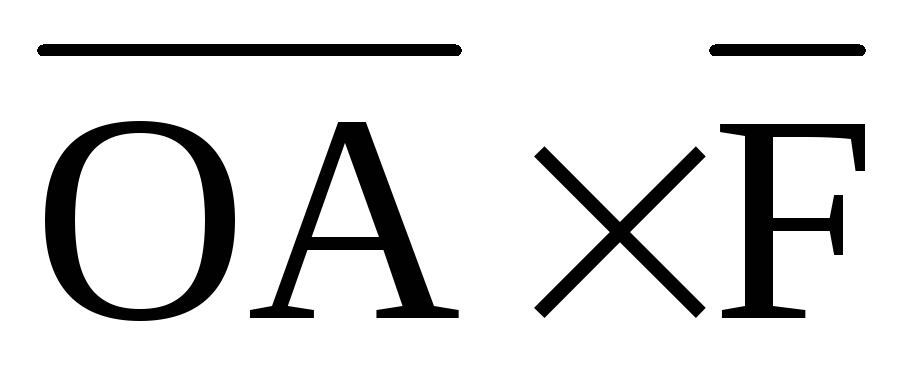 .
По определению
.
По определению
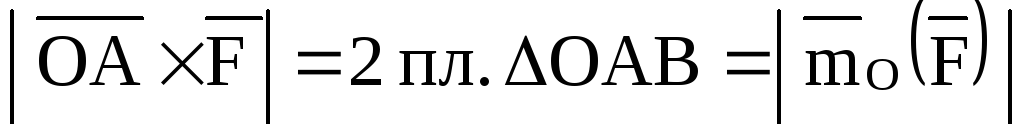
Направлен
вектор 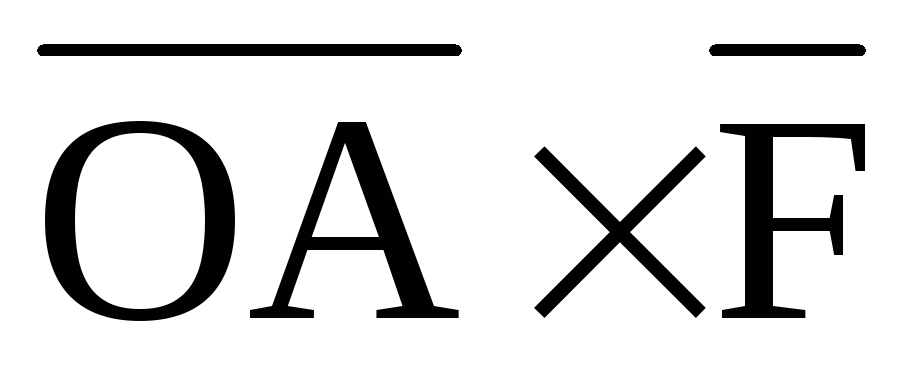 перпендикулярно плоскости OAB в ту
сторону, откуда кратчайшее совмещение
перпендикулярно плоскости OAB в ту
сторону, откуда кратчайшее совмещение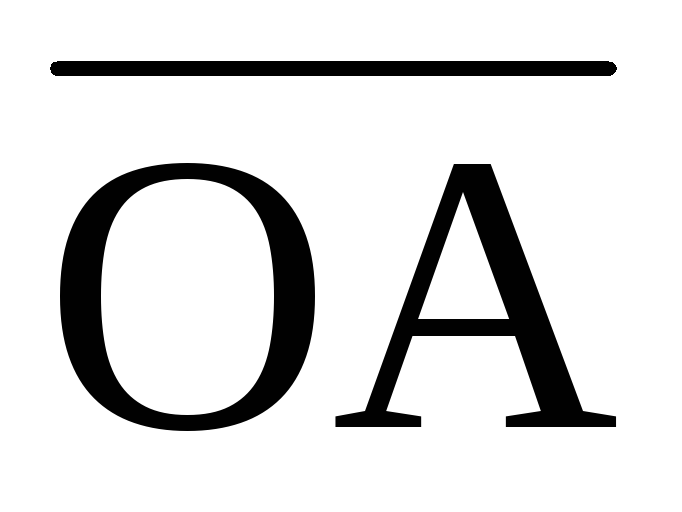 с
с (если их отложить от одной точки) видно
происходящим против хода часовой
стрелки, т.е. так же, как вектор
(если их отложить от одной точки) видно
происходящим против хода часовой
стрелки, т.е. так же, как вектор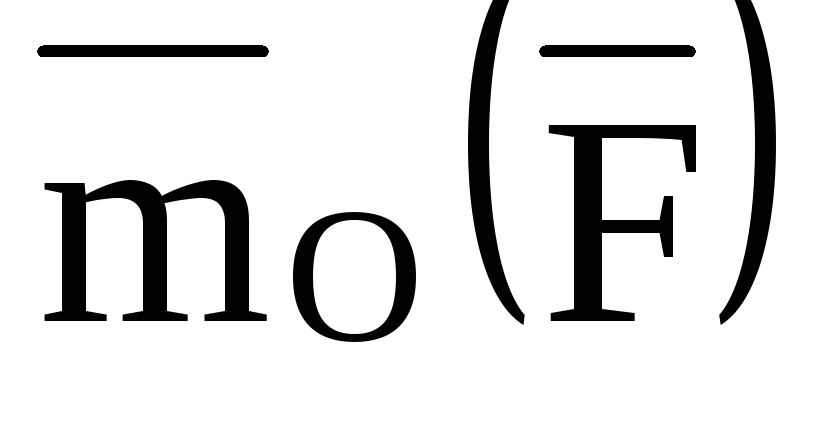 .
Следовательно, векторы
.
Следовательно, векторы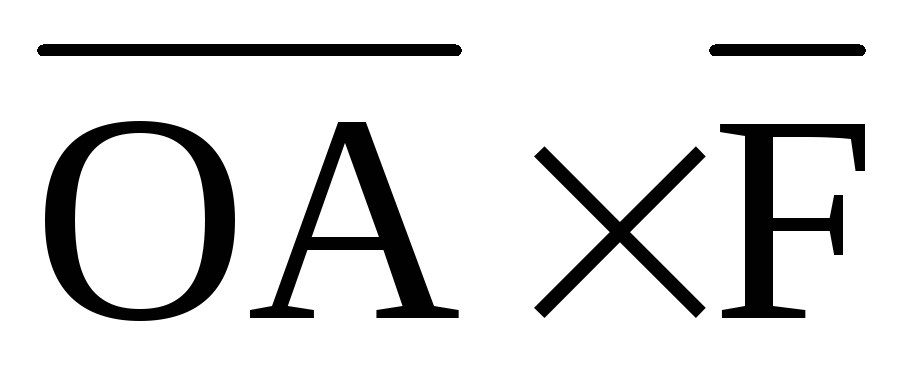 и
и выражают одну и ту же величину. Отсюда
выражают одну и ту же величину. Отсюда
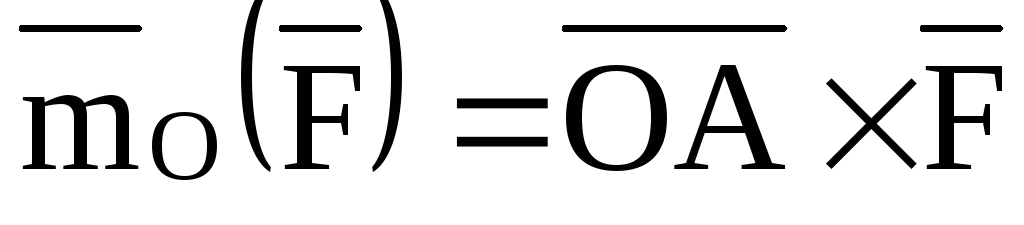 или
или 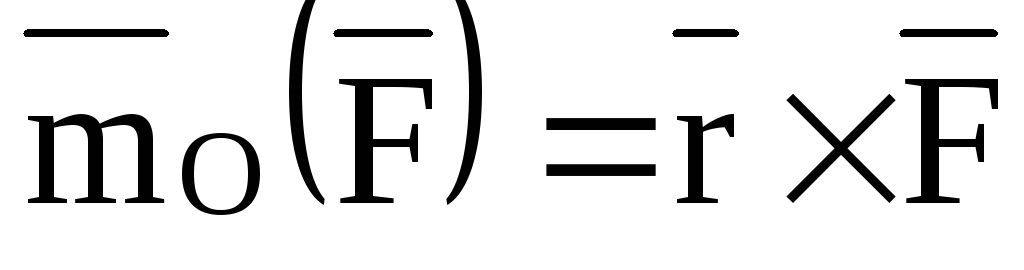 ,
(12)
,
(12)
где 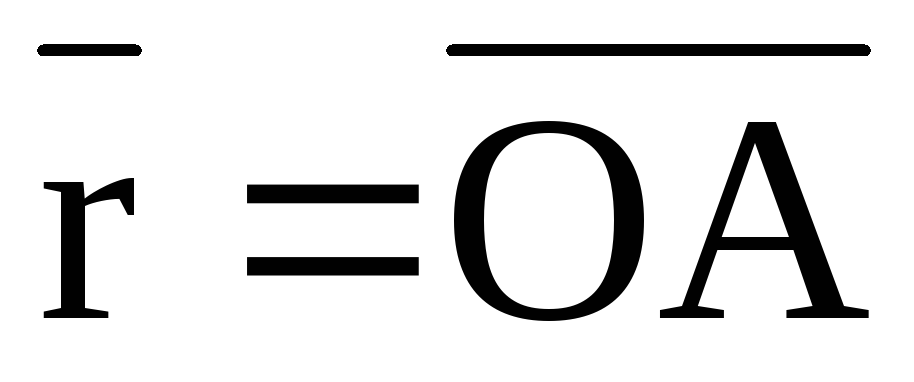 –
радиус-вектор точки А, проведенной из
центра О.
–
радиус-вектор точки А, проведенной из
центра О.
Момент
силы 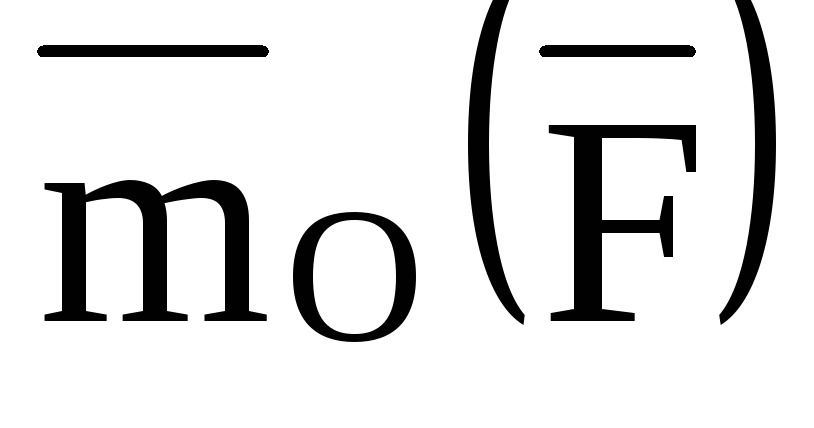 имеет следующие свойства:
имеет следующие свойства:
1) момент силы относительно центра не изменится при переносе точки приложения силы вдоль ее линии действия;
2) момент силы относительно центра О равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр О (плечо равно нулю).
§7. Алгебраический момент силы относительно центра
При
рассмотрении плоской системы сил
используется понятие алгебраического
момента силы относительно центра. Когда
все силы системы лежат в одной плоскости,
их моменты относительно любого центра
О находящегося в той же плоскости,
перпендикулярны этой плоскости, т.е.
направлены вдоль одной и той же прямой.
Тогда, не прибегая к векторной символике
можно направления этих моментов отличить
одно от другого знаком и рассматривать
момент силы  относительно центра О как алгебраическую
величину. Условимся такой момент называть
алгебраическим и обозначать символом
относительно центра О как алгебраическую
величину. Условимся такой момент называть
алгебраическим и обозначать символом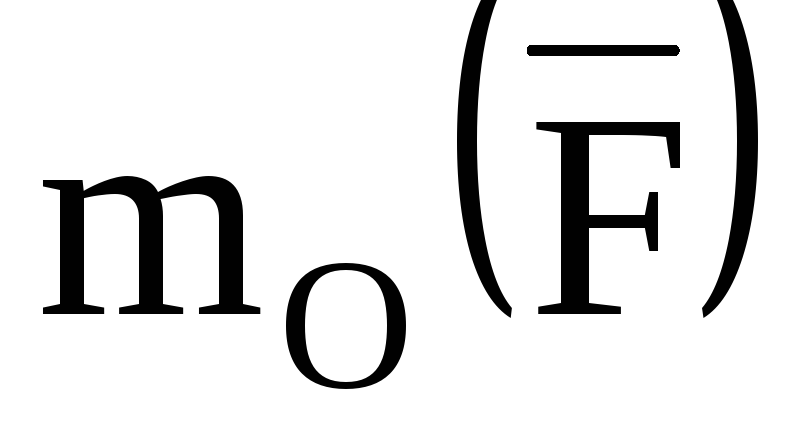 .
Алгебраический момент силы
.
Алгебраический момент силы относительно центра О равенвзятому
с соответствующим знаком произведению
модуля силы на ее плечо, т.е.
относительно центра О равенвзятому
с соответствующим знаком произведению
модуля силы на ее плечо, т.е.
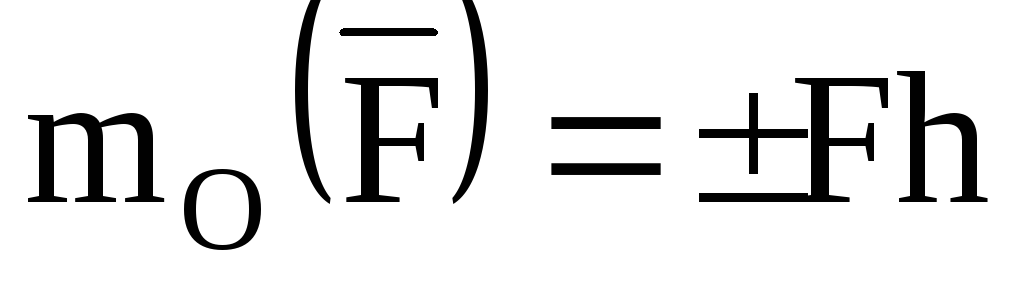 .
(13)
.
(13)
При
этом момент считается положительным,
когда сила стремится повернуть тело
вокруг центра О против хода часовой
стрелки, и отрицательным – когда по
ходу часовой стрелки. Так для сил,
изображенных на рис. 18: 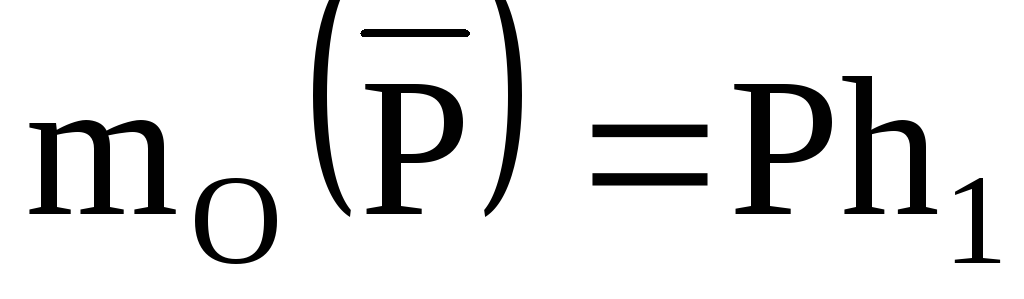 ,
,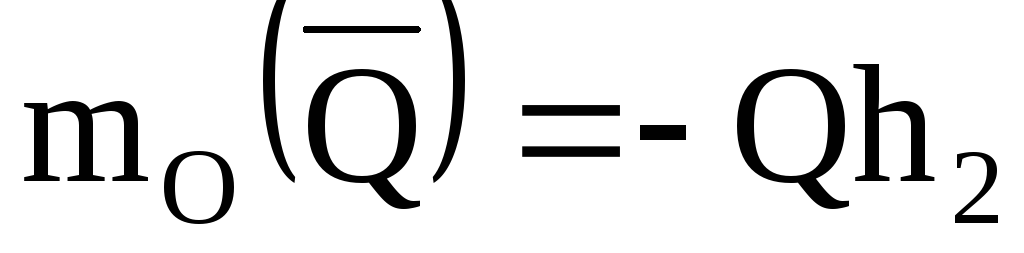 .
.
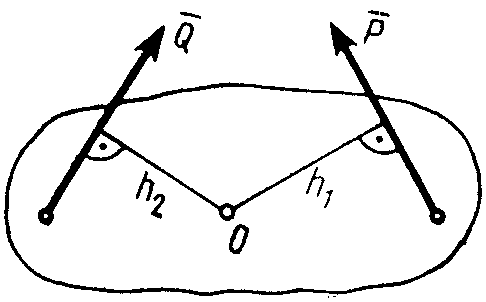
Рис. 18
§8. Пара сил. Момент пары
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 19, а).
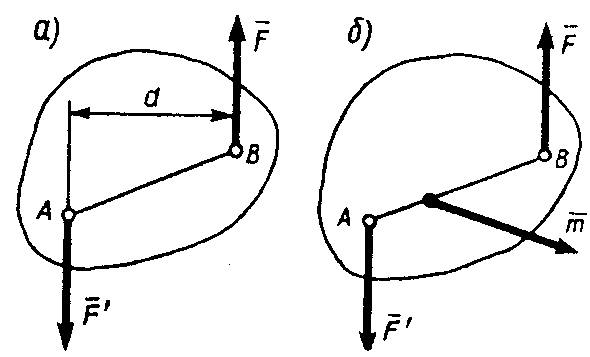
Рис. 19
Система
сил  ,
, ,
образующих пару, не находится в равновесии
(эти силы не направлены вдоль одной
прямой (аксиома 1)). В то же время пара
сил не имеет равнодействующей поскольку
,
образующих пару, не находится в равновесии
(эти силы не направлены вдоль одной
прямой (аксиома 1)). В то же время пара
сил не имеет равнодействующей поскольку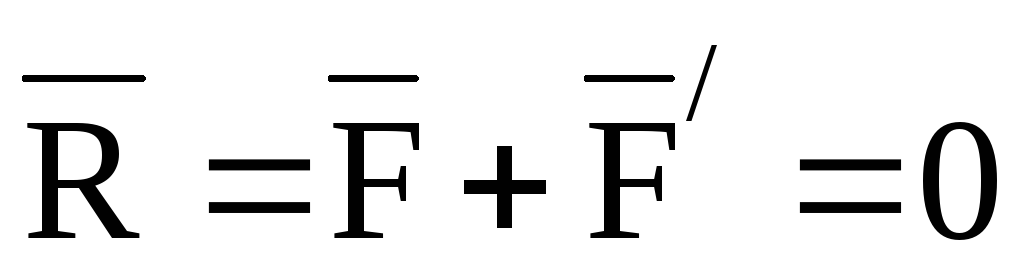 .
Поэтому свойства пары сил, как нового
самостоятельного элемента статики,
должны быть рассмотрены отдельно.
.
Поэтому свойства пары сил, как нового
самостоятельного элемента статики,
должны быть рассмотрены отдельно.
Плоскость, проходящая через линии действия сил пары, называется плоскостью пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к некоторому вращательному моменту пары.
Определение:
моментом пары сил называется вектор 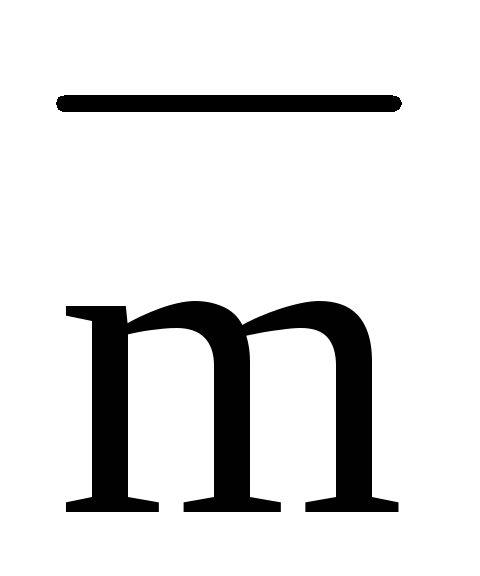 ,
модуль которого равен произведению
модуля одной из сил пары на ее плечо и
который направлен перпендикулярно
плоскости действия пары в ту сторону,
откуда пара видна стремящейся повернуть
тело против хода часовой стрелки
(рис. 19, б), т.е.
,
модуль которого равен произведению
модуля одной из сил пары на ее плечо и
который направлен перпендикулярно
плоскости действия пары в ту сторону,
откуда пара видна стремящейся повернуть
тело против хода часовой стрелки
(рис. 19, б), т.е.
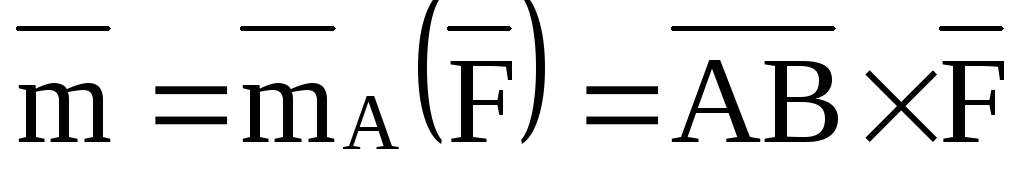 .
.
В отличие от момента силы вектор пары является свободным вектором, т.е. его можно переносить в любую точку тела.
Моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра О сил, образующих пару, т.е.
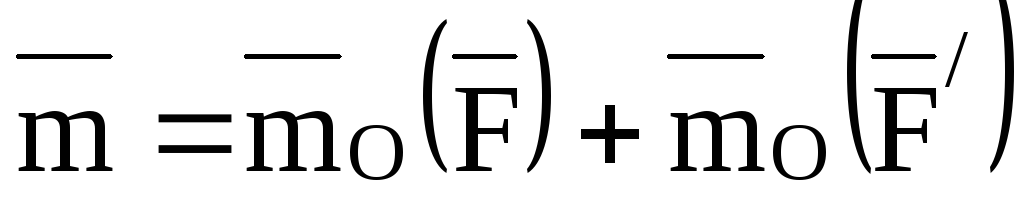 .
(14)
.
(14)
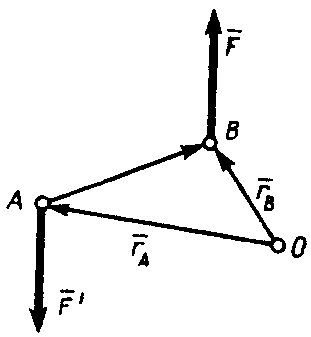
Рис. 20
Для
доказательства проведем из произвольной
точки О (рис. 20) радиусы векторы 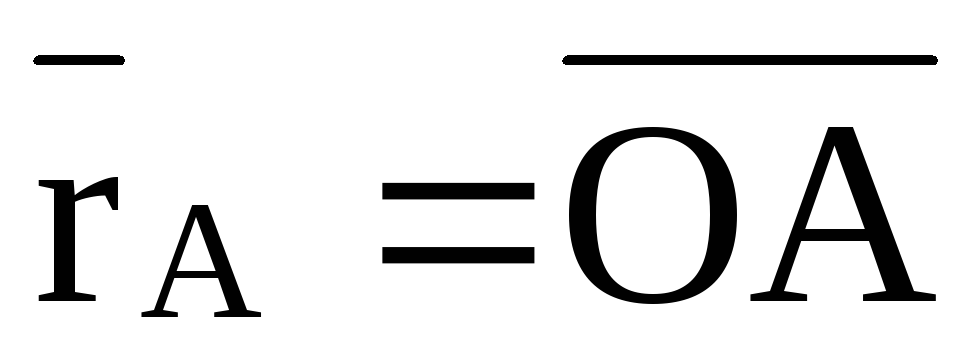 и
и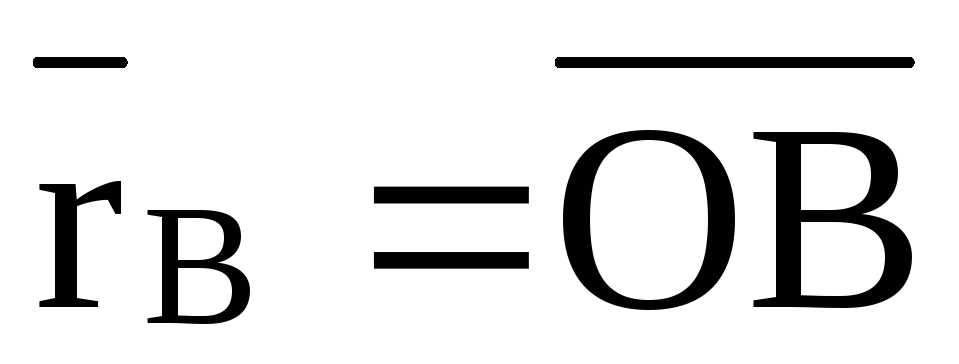 .
Тогда согласно формуле (12), учтя еще, что
.
Тогда согласно формуле (12), учтя еще, что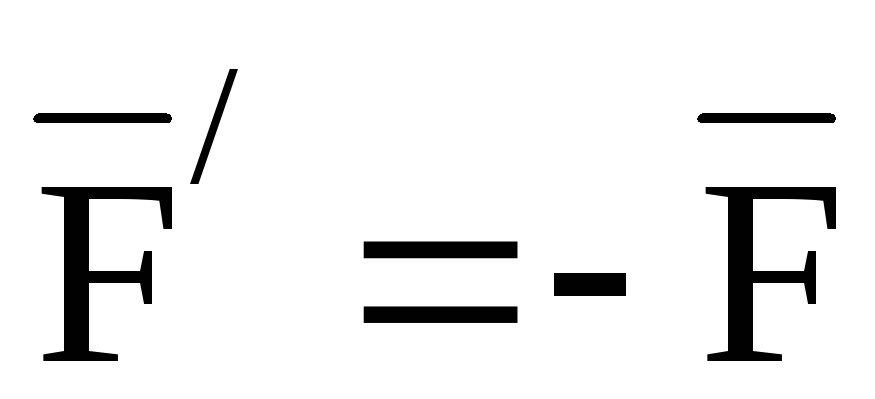 ,
получим
,
получим
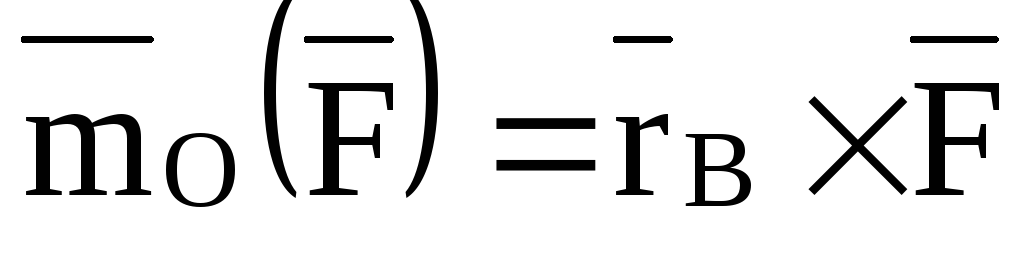 ,
, 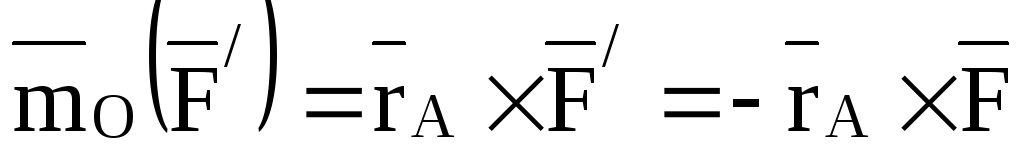 и, следовательно
и, следовательно
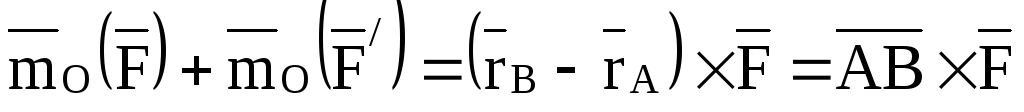 ,
,
где 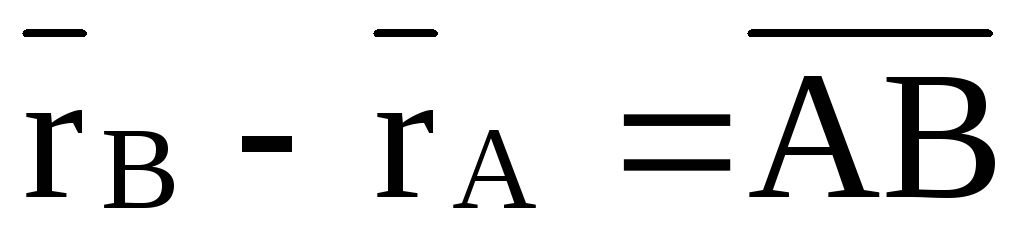 .
.
Так
как 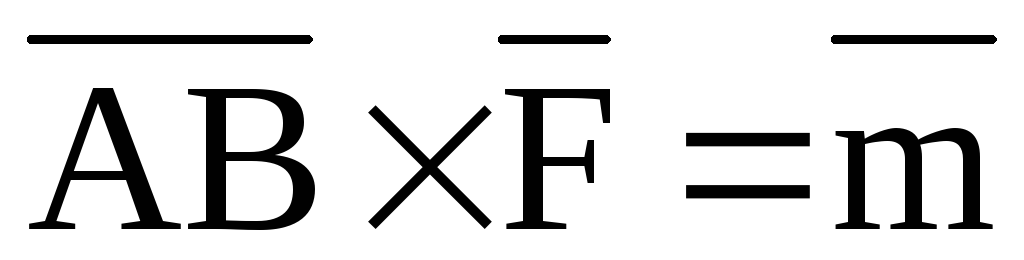 ,
то справедливость равенства (14) доказана.
Отсюда, в частности, следует уже отмеченный
выше результат
,
то справедливость равенства (14) доказана.
Отсюда, в частности, следует уже отмеченный
выше результат
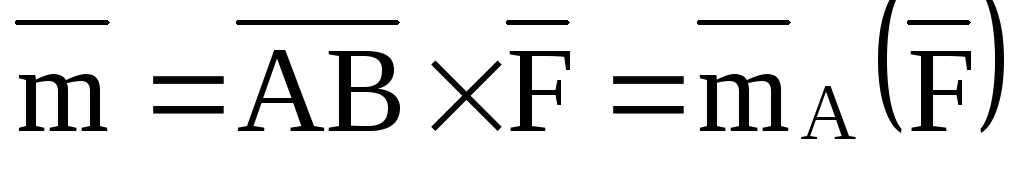 или
или 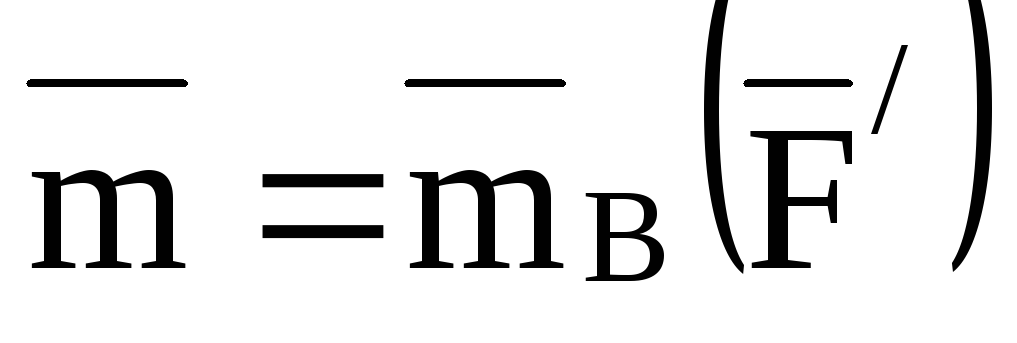 ,
(15)
,
(15)
т.е. момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары
m = Fd . (16)
Из формулы (14) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны.
Из
формулы (14) следует еще, что если на тело
действует несколько пар с моментами 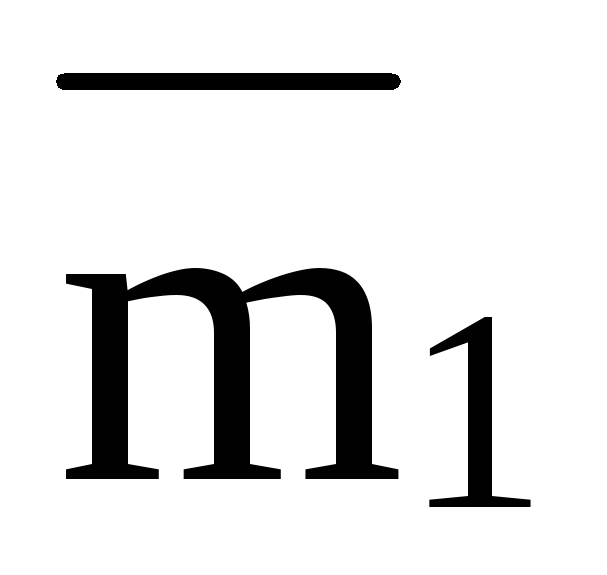 ,
,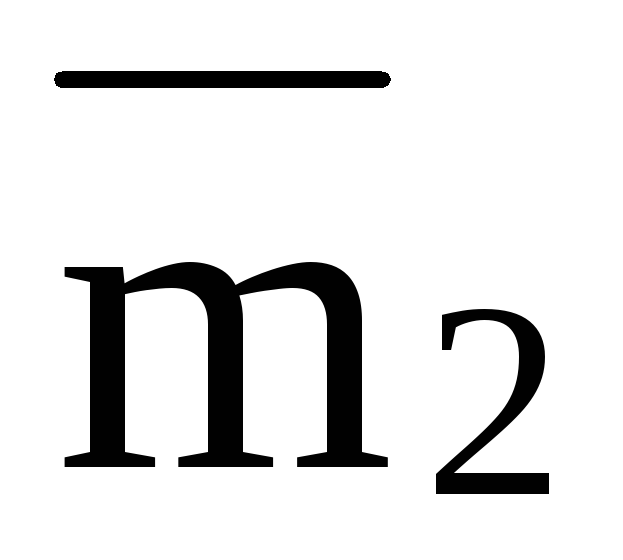 , …,
, …, 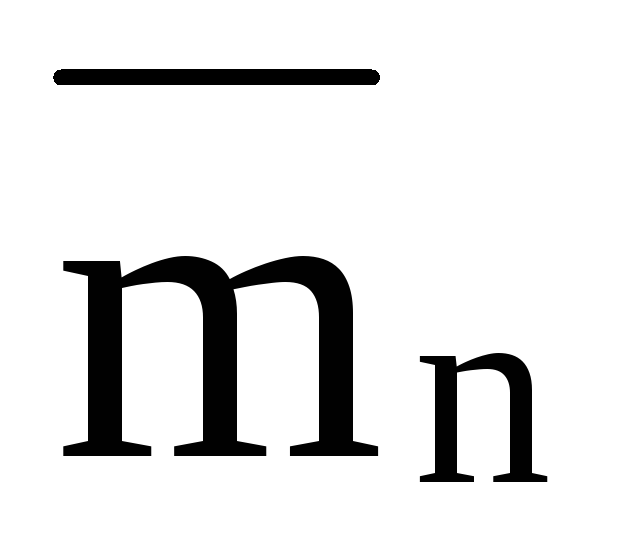 то сумма моментов всех сил, образующих
эти пары, относительно любого центра
будет равна
то сумма моментов всех сил, образующих
эти пары, относительно любого центра
будет равна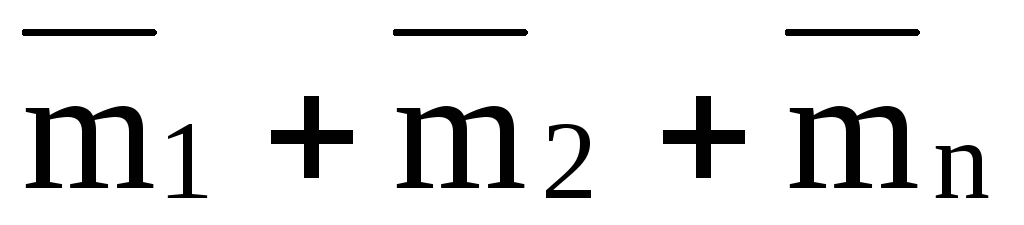 ,
а следовательно, вся совокупность этих
пар эквивалентна одной паре с моментом
,
а следовательно, вся совокупность этих
пар эквивалентна одной паре с моментом
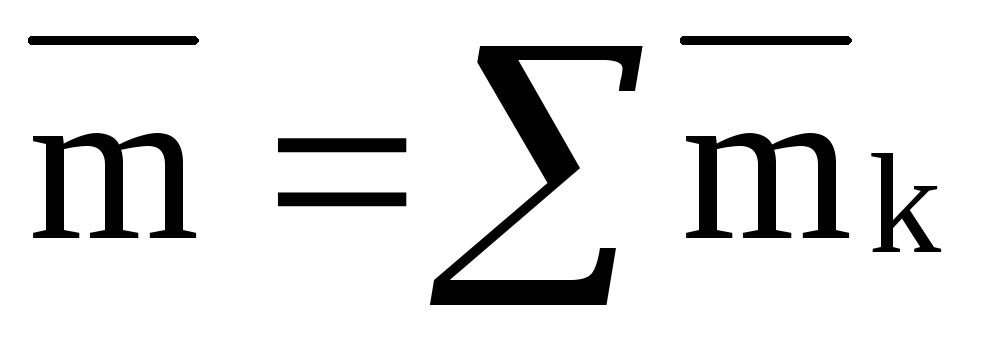 .
(17)
.
(17)
Этот результат выражает теорему о сложении пар.
6. Пара сил. Момент пары сил. Теоремы о парах.
П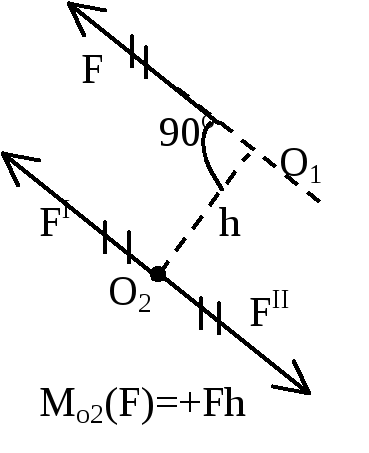 ара
сил – система
двух равных по модулю, параллельных и
направленных в противоположные стороны
сил, действующих на абсолютно твердое
тело. Действие пары сил на твердое тело
сводится к некоторому вращательному
эффекту, который характеризуется
величиной – момент пары. Он определяется:
ара
сил – система
двух равных по модулю, параллельных и
направленных в противоположные стороны
сил, действующих на абсолютно твердое
тело. Действие пары сил на твердое тело
сводится к некоторому вращательному
эффекту, который характеризуется
величиной – момент пары. Он определяется:
Его модулем = F*d. d – расстояние между линиями действия сил пары, называется плечом пары.
Положением в пространстве плоскости действия пары.
Направлением поворота пары в этой плоскости.
Момент пары сил – вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.
Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Для абсолютно твердого тела пара – свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.
Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.
Теоремы
о парах.
1) Две пары, лежащие в одной плоскости,
можно заменить одной парой, лежащей в
той же плоскости, с моментом, равным
сумме моментов данных двух пар. 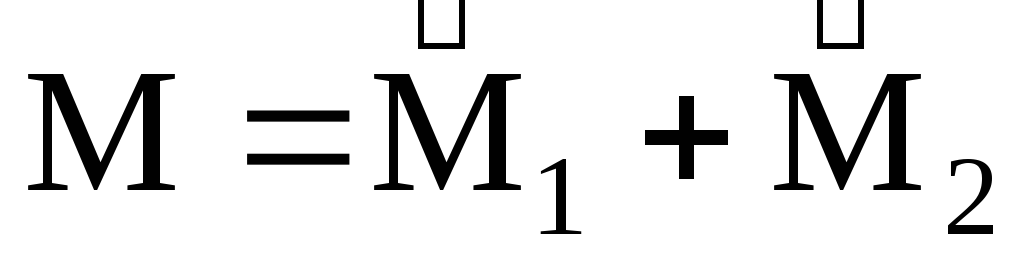 .
2) Две пары, имеющие геометрически равные
моменты, эквиваленты. 3) Не нарушая
состояния твердого тела, пару сил можно
переносить в плоскости ее действия.
Т.е. момент пары сил является свободным
вектором. 4) Система нескольких пар сил
эквивалента одной паре, момент которой
равен векторной сумме моментов данных
пар. Т.е. система пар приводится к одной
паре, момент которой равен сумме моментов
всех пар. Условие равновесия пар сил:
.
2) Две пары, имеющие геометрически равные
моменты, эквиваленты. 3) Не нарушая
состояния твердого тела, пару сил можно
переносить в плоскости ее действия.
Т.е. момент пары сил является свободным
вектором. 4) Система нескольких пар сил
эквивалента одной паре, момент которой
равен векторной сумме моментов данных
пар. Т.е. система пар приводится к одной
паре, момент которой равен сумме моментов
всех пар. Условие равновесия пар сил: 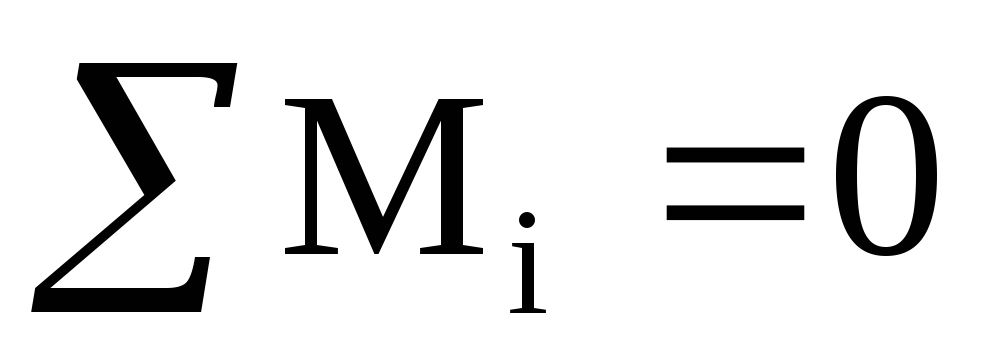 – геометрическая сумма их моментов
равна 0. Пары сил, расположенные в одной
плоскости, взаимно уравновеш-тся, если
алгебраическая сумма их моментовМi=0.
– геометрическая сумма их моментов
равна 0. Пары сил, расположенные в одной
плоскости, взаимно уравновеш-тся, если
алгебраическая сумма их моментовМi=0.
М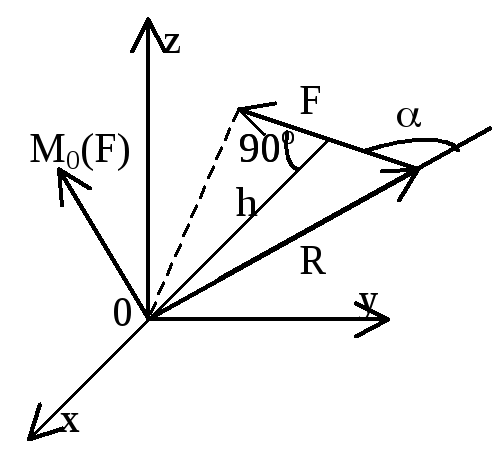 омент
силы относительно точки – вектор,
численно равный произведению модуля
силы на плечо и направленный перпендикулярно
плоскости, содержащей силу и точку, в
такую сторону, чтобы смотря ему навстречу,
видеть силу стремящейся повернуться
против хода час.стрелки. Плечо «h»–
кратчайшее расстояние от точки до линии
действия силы.
омент
силы относительно точки – вектор,
численно равный произведению модуля
силы на плечо и направленный перпендикулярно
плоскости, содержащей силу и точку, в
такую сторону, чтобы смотря ему навстречу,
видеть силу стремящейся повернуться
против хода час.стрелки. Плечо «h»–
кратчайшее расстояние от точки до линии
действия силы. 
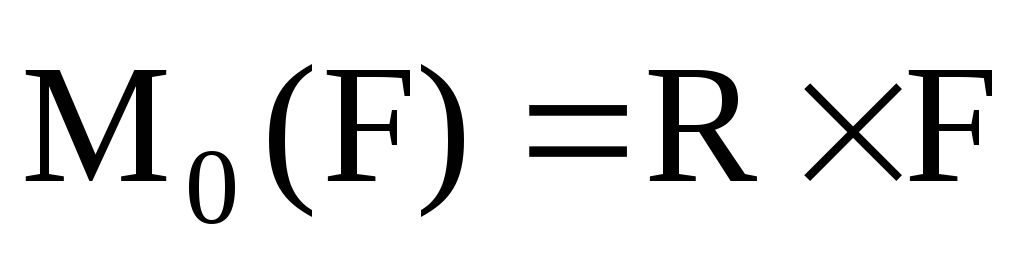 – момент силы равен векторному
произведению вектора
– момент силы равен векторному
произведению вектора  на вектор
на вектор  .
Модуль векторного произведения:
.
Модуль векторного произведения: 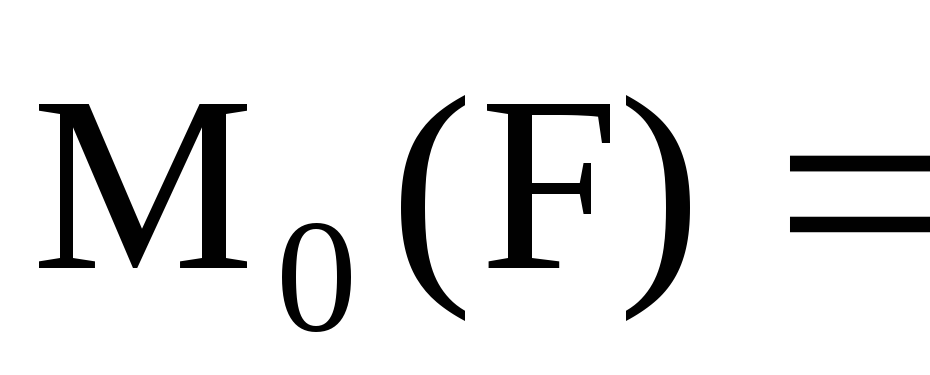 RFsin=
Fh.
Для плоской сист. сил обычно находят не
вектор момента, а только его модуль:
RFsin=
Fh.
Для плоской сист. сил обычно находят не
вектор момента, а только его модуль: 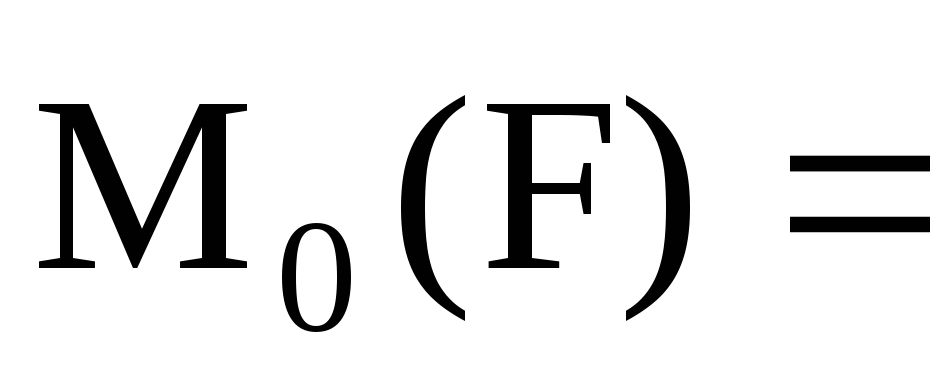 Fh,
>0 – против час.стр.; <0 – по час.стр.
Свойства момента силы: 1) момент силы не
изменяется при переносе точки приложения
силы вдоль ее линии действия; 2) момент
силы относит. точки =0 только тогда, когда
сила =0 или когда линия действия силы
проходит через точку (т.е. плечо =0). Если
x,y,z
– координаты точки приложения силы,
Fx,
Fy,
Fz – проекции силы на оси координат и точка
0 – начало координат, то
Fh,
>0 – против час.стр.; <0 – по час.стр.
Свойства момента силы: 1) момент силы не
изменяется при переносе точки приложения
силы вдоль ее линии действия; 2) момент
силы относит. точки =0 только тогда, когда
сила =0 или когда линия действия силы
проходит через точку (т.е. плечо =0). Если
x,y,z
– координаты точки приложения силы,
Fx,
Fy,
Fz – проекции силы на оси координат и точка
0 – начало координат, то
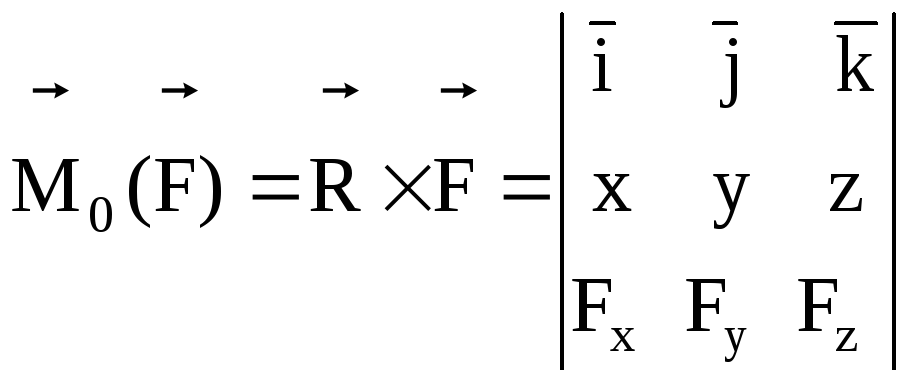 =(yFz – zFy)
=(yFz – zFy)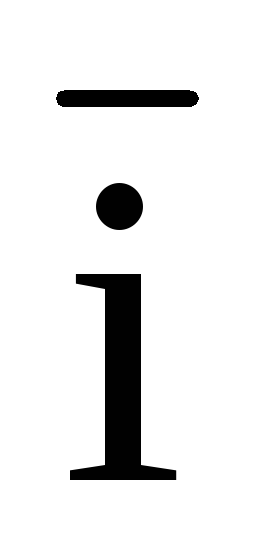 +(zFx – xFz)
+(zFx – xFz)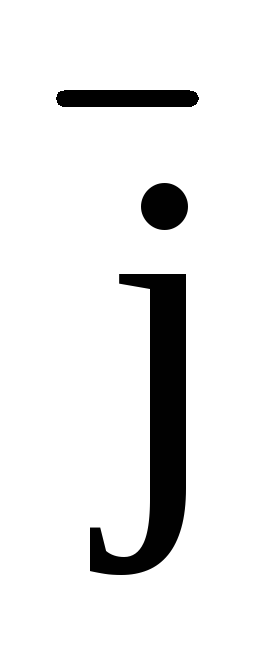 +(xFy – yFx)
+(xFy – yFx) ,
откуда проекции момента силы на оси
коорд.: М0x(
,
откуда проекции момента силы на оси
коорд.: М0x( )=yFz – zFy;
М0y(
)=yFz – zFy;
М0y( )=zFx – xFz;
М0z(
)=zFx – xFz;
М0z( )=xFy – yFx.
)=xFy – yFx.
Г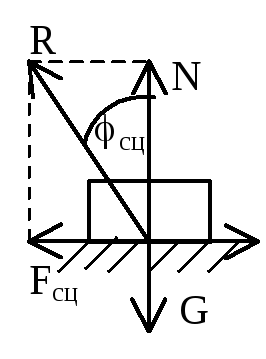 лавный
вектор –
векторная сумма всех сил, приложенных
к телу. Главный
момент относительно центра –векторная сумма
моментов всех сил, приложенных к телу
относительно того же центра.
лавный
вектор –
векторная сумма всех сил, приложенных
к телу. Главный
момент относительно центра –векторная сумма
моментов всех сил, приложенных к телу
относительно того же центра.
Т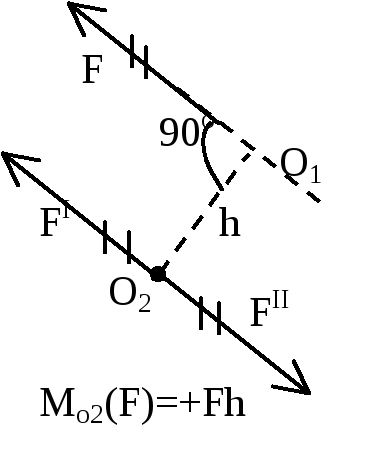 еорема
(лемма) о параллельном переносе силы:
сила приложенная в какой-либо точке
тверд. тела, эквивалента такой же силе,
приложенной в любой др. точке этого
тела, и паре сил, момент которой равен
моменту данной силы относительно новой
точки приложения.
еорема
(лемма) о параллельном переносе силы:
сила приложенная в какой-либо точке
тверд. тела, эквивалента такой же силе,
приложенной в любой др. точке этого
тела, и паре сил, момент которой равен
моменту данной силы относительно новой
точки приложения.

