Сила тяжести и сила всемирного тяготения. Закон всемирного тяготения

Гравитационные силы описываются наиболее простыми количественными закономерностями. Но несмотря на эту простоту проявления сил тяготения могут быть весьма сложны и многообразны.

Гравитационные взаимодействия описываются законом всемирного тяготения, открытым Ньютоном:

Материальные точки притягиваются с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

Гравитационная постоянная. Коэффициент пропорциональности называется гравитациоутой постоянной. Эта величина характеризует интенсивность гравитационного взаимодействия и является одной из основных физических констант. Ее числовое значение зависит от выбора системы единиц и в единицах СИ равно Из формулы видно, что гравитационная постоянная численно равна силе притяжения двух точеных масс по 1 кг, расположенных на расстоянии друг от друга. Значение гравитационной постоянной столь мало, что мы не замечаем притяжения между окружающими нас телами.

Только из-за огромной массы Земли притяжение окружающих тел к Земле решающим образом влияет на все, что происходит вокруг нас.

Рис. 91. Гравитационное взаимодействие

Формула (1) дает только модуль силы взаимного притяжения точечных тел. На самом деле речь в ней идет о двух силах, поскольку сила тяготения действует на каждое из взаимодействующих тел. Эти силы равны по модулю и противоположны по направлению в соответствии с третьим законом Ньютона. Они направлены вдоль прямой, соединяющей материальные точки. Такие силы называются центральными. Векторное выражение, например для силы с которой тело массы действует на тело массы (рис. 91), имеет вид

Хотя радиусы-векторы материальных точек зависят от выбора начала координат, их разность, а значит, и сила зависят только от взаимного расположения притягивающихся тел.

Законы Кеплера. К известной легенде о падающем яблоке, которое якобы навело Ньютона на мысль о тяготении, вряд ли следует относиться серьезно. При установлении закона всемирного тяготения Ньютон исходил из открытых Иоганном Кеплером на основании астрономических наблюдений Тихо Браге законов движения планет Солнечной системы. Три закона Кеплера гласят:

1. Траектории, по которым движутся планеты, представляют собой эллипсы, в одном из фокусов которых находится Солнце.

2. Радиус-вектор планеты, проведенный из Солнца, ометает за равные промежутки времени одинаковые площади.

3. Для всех планет отношение квадрата периода обращения к кубу большой полуоси эллиптической орбиты имеет одно и то же значение.

Орбиты большинства планет мало отличаются от круговых. Для простоты будем считать их точно круговыми. Это не противоречит первому закону Кеплера, так как окружность представляет собой частный случай эллипса, у которого оба фокуса совпадают. Согласно второму закону Кеплера движение планеты по круговой траектории происходит равномерно, т. е. с постоянной по модулю скоростью. При этом третий закон Кеплера говорит о том, что отношение квадрата периода обращения Т к кубу радиуса круговой орбиты одинаково для всех планет:

Движущаяся по окружности с постоянной скоростью планета обладает центростремительным ускорением, равным Воспользуемся этим, чтобы определить силу, которая сообщает планете такое ускорение при выполнении условия (3). Согласно второму закону Ньютона ускорение планеты равно отношению действующей на нее силы к массе планеты:

Отсюда, учитывая третий закон Кеплера (3), легко установить, как сила зависит от массы планеты и от радиуса ее круговой орбиты. Умножая обе части (4) на видим, что в левой части согласно (3) стоит одинаковая для всех планет величина. Значит, и правая часть, равная одинакова для всех планет. Поэтому т. е. сила тяготения обратно пропорциональна квадрату расстояния от Солнца и прямо пропорциональна массе планеты. Но Солнце и планета выступают в их гравитационном

взаимодействии как равноправные партнеры. Они отличаются друг от друга только массами. И поскольку сила притяжения пропорциональна массе планеты то она должна быть пропорциональна и массе Солнца М:

Вводя в эту формулу коэффициент пропорциональности G, который уже не должен зависеть ни от масс взаимодействующих тел, ни от расстояния между ними, приходим к закону всемирного тяготения (1).

Гравитационное поле.

Гравитационное взаимодействие тел можно описывать, используя понятие гравитационного поля. Ньютоновская формулировка закона всемирного тяготения соответствует представлению о непосредственном действии тел друг на друга на расстоянии, так называемом дальнодействии, без какого-либо участия промежуточной среды. В современной физике считается, что передача любых взаимодействий между телами осуществляется посредством создаваемых этими телами полей. Одно из тел непосредственно не действует на другое, оно наделяет окружающее его пространство определенными свойствами — создает гравитационное поле, особую материальную среду, которая и воздействует на другое тело.

Представление о физическом гравитационном поле выполняет как эстетические, так и вполне практические функции. Силы тяготения действуют на расстоянии, они тянут там, где, мы едва ли можем увидеть, что именно тянет. Силовое поле представляет собой некоторую абстракцию, заменяющую нам крюки, веревочки или резинки. Никакой наглядной картины поля дать невозможно, поскольку само понятие физического поля относится к числу основных понятий, которые невозможно определить через другие, более простые понятия.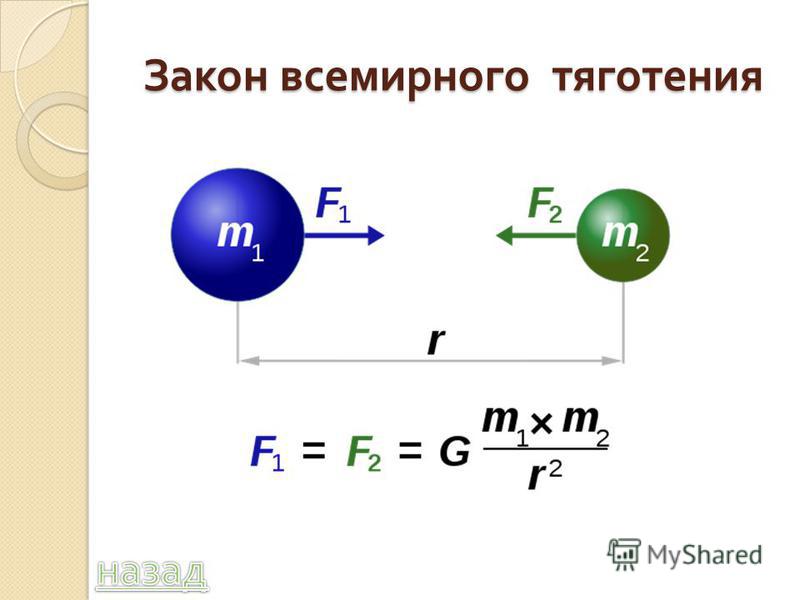 Можно только описать его свойства.

Рассматривая способность гравитационного поля создавать силу, мы считаем, что поле зависит только от того тела, со стороны которого действует сила, и не зависит от того тела, на которое она действует.

Отметим, что в рамках классической механики (механики Ньютона) оба представления — о дальнодействии и взаимодействии через гравитационное поле — приводят к одинаковым результатам и в равной мере допустимы. Выбор одного из этих способов описания определяется исключительно соображениями удобства.

Напряженность поля тяготения. Силовой характеристикой гравитационного поля является его напряженность измеряемая силой, действующей на материальную точку единичной массы, т. е. отношением

Очевидно, что гравитационное поле, создаваемое точечной массой М, обладает сферической симметрией. Это значит, что вектор напряженности в любой его точке направлен к массе М, создающей поле. Модуль напряженности поля как следует из закона всемирного тяготения (1), равен

и зависит только от расстояния до источника поля. Напряженность поля точечной массы убывает с расстоянием по закону обратных квадратов. В таких полях движение тел происходит в соответствии с законами Кеплера.

Принцип суперпозиции. Опыт показывает, что гравитационные поля удовлетворяют принципу суперпозиции. Согласно этому принципу гравитационное поле, создаваемое какой-либо массой, не зависит от наличия других масс. Напряженность поля, создаваемого несколькими телами, равна векторной сумме напряженностей полей, создаваемых этими телами в отдельности.

Принцип суперпозиции позволяет рассчитывать гравитационные поля, создаваемые протяженными телами. Для этого нужно мысленно разбить тело на отдельные элементы, которые можно считать материальными точками, и найти векторную сумму напряженностей полей, создаваемых этими элементами. Пользуясь принципом суперпозиции, можно показать, что гравитационное поле, создаваемое шаром со сферически-симметричным распределением массы (в частности, и однородным шаром), вне этого шара неотличимо от гравитационного поля материальной точки такой же массы, как и шар, помещенной в центр шара.

Это значит, что напряженность гравитационного поля шара дается той же формулой (6). Этот простой результат приводится здесь без доказательства. Оно будет дано для случая электростатического взаимодействия при рассмотрении поля заряженного шара, где сила также убывает обратно пропорционально квадрату расстояния.

Притяжение сферических тел. Используя этот результат и привлекая третий закон Ньютона, можно показать, что два шара со сферически-симметричным распределением масс у каждого притягиваются друг к другу так, как если бы их массы были сосредоточены в их центрах, т. е. просто как точечные массы. Приведем соответствующее доказательство.

Пусть два шара массами притягивают друг друга с силами (рис. 92а). Если заменить первый шар точечной массой (рис. 92б), то создаваемое им гравитационное поле в месте расположения второго шара не изменится и, следовательно, не изменится сила действующая на второй шар. На основании третьего

закона Ньютона отсюда можно сделать вывод, что второй шар действует с одной и той же силой как на первый шар, так и на заменяющую его материальную точку Эту силу легко найти, учитывая, что создаваемое вторым шаром гравитационное поле в том месте, где находится первый шар, неотличимо от поля точечной массы помещенной в его центр (рис.

92в).

Рис. 92. Сферические тела притягиваются друг к другу так, как если бы их массы были сосредоточены в их центрах

Таким образом, сила притяжения шаров совпадает с силой притяжения двух точечных масс ту и расстояние между которыми равно расстоянию между центрами шаров.

Из этого примера наглядно видна практическая ценность концепции гравитационного поля. В самом деле, было бы очень неудобно описывать силу, действующую на один из шаров, как векторную сумму сил, действующих на отдельные его элементы, учитывая при этом, что каждая из этих сил, в свою очередь, представляет собой векторную сумму сил взаимодействия этого элемента со всеми элементами, на которые мы должны мысленно разбить и второй шар. Обратим внимание еще и на то, что в процессе приведенного доказательства мы поочередно рассматривали в качестве источника гравитационного поля то один шар, то другой, в зависимости от того, интересовала ли нас сила, действующая на тот или на другой шар.

Теперь очевидно, что на любое находящееся вблизи поверхности Земли тело массы линейные размеры которого малы по сравнению с радиусом Земли, действует сила тяжести которая в соответствии с (5) может быть записана как Значение модуля напряженности гравитационного поля Земли дается выражением (6), в котором под М следует понимать массу земного шара, а вместо следует подставить радиус Земли

Для применимости формулы (7) необязательно Землю считать однородным шаром, достаточно, чтобы распределение масс было сферически-симметричным.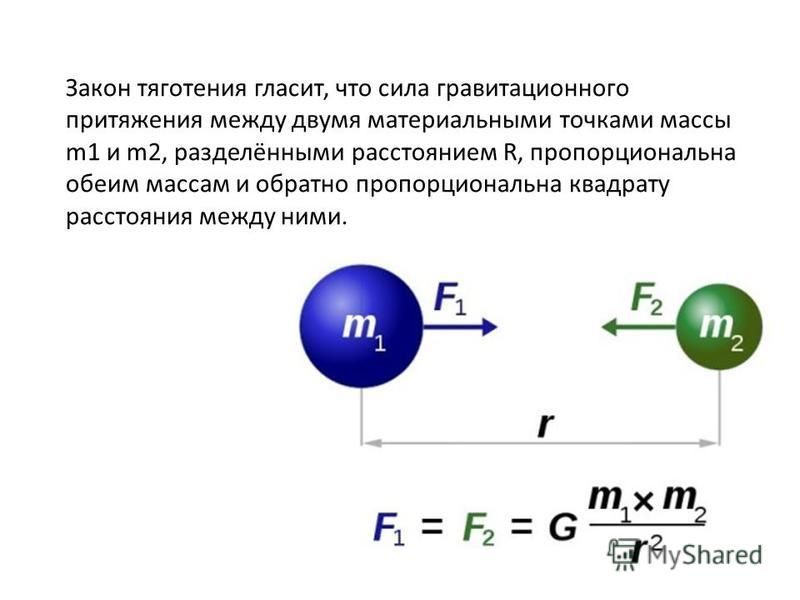

Свободное падение. Если тело вблизи поверхности Земли движется только под действием силы тяжести т. е. свободно падает, то его ускорение согласно второму закону Ньютона равно Видно, что оно направлено к центру Земли и в соответствии с (7) по модулю равно

Но правая часть (8) дает значение напряженности гравитационного поля Земли вблизи ее поверхности. Итак, напряженность гравитационного поля и ускорение свободного падения в этом поле — это одно и то же. Именно поэтому мы сразу обозначили эти величины одной буквой

Взвешивание Земли. Остановимся теперь на вопросе об экспериментальном определении значения гравитационной постоянной Прежде всего отметим, что его нельзя найти из астрономических наблюдений. Действительно, из наблюдений за движением планет можно найти только произведение гравитационной постоянной на массу Солнца. Из наблюдений за движением Луны, искусственных спутников Земли или за свободным падением тел вблизи земной поверхности можно найти только произведение гравитационной постоянной на массу Земли. Для определения необходимо иметь возможность независимо измерить массу источника гравитационного поля. Это можно сделать только в опыте, производимом в лабораторных условиях.

Рис. 93. Схема опыта Кавендиша

Такой опыт был впервые выполнен Генри Кавендишем в с помощью крутильных весов, к концам коромысла которых были прикреплены небольшие свинцовые шары (рис. 93). Вблизи от них закреплялись большие тяжелые шары. Под действием сил притяжения малых шаров к большим коромысло крутильных весов немного поворачивалось, и по закручиванию упругой нити подвеса измерялась сила. Для интерпретации этого опыта важно знать, что шары взаимодействуют так же, как и соответствующие материальные точки такой же массы, ибо здесь в отличие от планет размеры шаров Нельзя считать малыми по сравнению с расстоянием между ними.

В своих опытах Кавендиш получил значение гравитационной постоянной всего на отличающееся от принятого в настоящее время. В современных модификациях опыта Кавендиша производится измерение ускорений, сообщаемых малым шарам на коромысле гравитационным полем тяжелых шаров, что позволяет повысить точность измерений.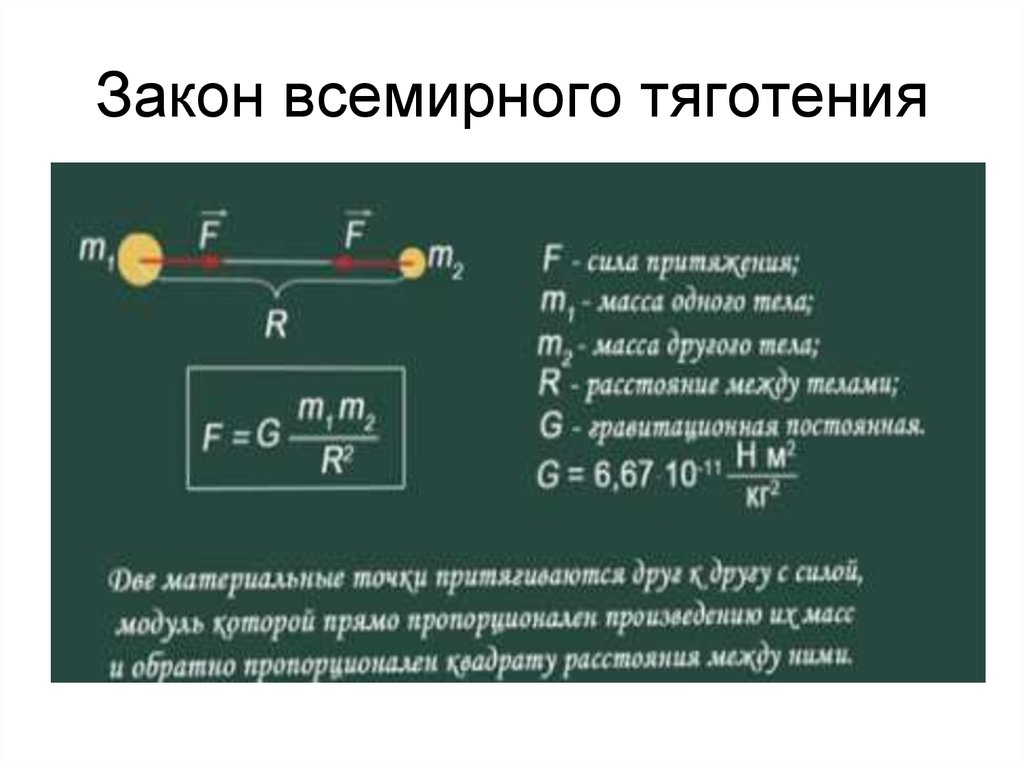 Знание гравитационной постоянной позволяет определить массы Земли, Солнца и других источников тяготения по наблюдениям за движением тел в создаваемых ими гравитационных полях. В этом смысле опыт Кавендиша иногда образно называют взвешиванием Земли.

Всемирное тяготение описывается очень простым законом, который, как мы видели, легко устанавливается на основе законов Кеплера. В чем же величие открытия Ньютона? В нем нашла воплощение идея о том, что падение яблока на Землю и движение Луны вокруг Земли, которое тоже в известном смысле представляет собой падение на Землю, имеют общую причину. В те далекие времена это была удивительная мысль, поскольку общая мудрость гласила, что небесные тела движутся по своим «совершенным» законам, а земные объекты подчиняются «мирским» правилам. Ньютон пришел к мысли о том, что единые законы природы справедливы для всей Вселенной.

Введите такую единицу силы, чтобы в законе всемирного тяготения (1) значение гравитационной постоянной С равнялось единице. Сравните эту единицу силы с ньютоном.

Существуют ли отклонения от законов Кеплера для планет Солнечной системы? Чем они обусловлены?

Как из законов Кеплера установить зависимость силы тяготения от расстояния?

Почему гравитационную постоянную нельзя определить на основе астрономических наблюдений?

Что такое гравитационное поле? Какие преимущества дает описание гравитационного взаимодействия с помощью понятия поля по сравнению с представлением о дальнодействии?

В чем заключается принцип суперпозиции для гравитационного поля? Что можно сказать о гравитационном поле однородного шара?

Как связаны между собой напряженность гравитационного поля и ускорение свободного падения?

Рассчитайте массу Земли М, используя значения гравитационной постоянной радиуса Земли км и ускорения свободного падения

Геометрия и тяготение. С простой формулой закона всемирного тяготения (1) связано несколько тонких моментов, заслуживающих отдельного обсуждения. Из законов Кеплера следует,

что расстояние в знаменатель выражения для силы тяготения входит во второй степени. Вся совокупность астрономических наблюдений приводит к выводу, что значение показателя степени равно двум с очень высокой точностью, а именно Этот факт в высшей степени замечателен: точное равенство показателя степени двум отражает евклидову природу трехмерного физического пространства. Это значит, что положение тел и расстояние между ними в пространстве, сложение перемещений тел и т. д. описывается геометрией Евклида. Точное равенство двум показателя степени подчеркивает то обстоятельство, что в трехмерном евклидовом мире поверхность сферы точно пропорциональна квадрату ее радиуса.

Инертная и гравитационная массы. Из приведенного вывода закона тяготения следует также, что сила гравитационного взаимодействия тел пропорциональна их массам, а точнее — инертным массам, фигурирующим во втором законе Ньютона и описывающим инертные свойства тел. Но инертность и способность к гравитационным взаимодействиям представляют собой совершенно разные свойства материи.

В определении массы на основе инертных свойств используется закон . Измерения массы в соответствии с этим ее определением требуют проведения динамического эксперимента — прикладывается известная сила и измеряется ускорение. Именно так с помощью масс-спектрометров определяются массы заряженных элементарных частиц и ионов (а тем самым и атомов).

В определении массы на основе явления тяготения используется закон Измерение массы в соответствии с таким определением производится с помощью статического эксперимента — взвешиванием. Тела располагают неподвижно в гравитационном поле (обычно это поле Земли) и сравнивают действующие на них силы тяготения. Определенная таким образом масса называется тяжелой или гравитационной.

Будут ли значения инертной и гравитационной масс одинаковыми? Ведь количественные меры этих свойств в принципе могли бы быть различными. Впервые ответ на этот вопрос был дан Галилеем, хотя он, по-видимому, и не подозревал об этом. В своих опытах он намеревался доказать, что неверны господствовавшие тогда утверждения Аристотеля о том, что тяжелые тела падают быстрее легких.

Чтобы лучше проследить за рассуждениями, обозначим инертную массу через а гравитационную — через На поверхности Земли сила тяжести тогда запишется как

где — напряженность гравитационного поля Земли, одинаковая для всех тел. Теперь сравним, что произойдет, если два тела одновременно сбросить с одной высоты. В соответствии со вторым законом Ньютона для каждого из тел можно написать

Но опыт показывает, что ускорения обоих тел одинаковы. Следовательно, одним и тем же будет для них и отношение Итак, для всех тел

Гравитационные массы тел пропорциональны их инертным массам. Надлежащим выбором единиц их можно сделать просто равными.

Совпадение значений инертной и гравитационной масс подтверждалось много раз со все возрастающей точностью в разнообразных опытах ученых разных эпох — Ньютона, Бесселя, Этвеша, Дикке и, наконец, Брагинского и Панова, которые довели относительную погрешность измерений до . Чтобы лучше представить себе чувствительность приборов в таких опытах, отметим, что это эквивалентно возможности обнаружить изменение массы теплохода водоизмещением в тысячу тонн при добавлении к нему одного миллиграмма.

В ньютоновской механике совпадение значений инертной и гравитационной масс не имеет под собой физической причины и в этом смысле является случайным. Это просто экспериментальный факт, установленный с очень высокой точностью. Если бы это было не так, ньютоновская механика ничуть не пострадала бы. В созданной Эйнштейном релятивистской теории тяготения, называемой также общей теорией относительности, равенство инертной и гравитационной масс имеет принципиальное значение и изначально заложено в основу теории. Эйнштейн предположил, что в этом совпадении нет ничего удивительного или случайного, ибо в действительности инертная и гравитационная массы представляют собой одну и ту же физическую величину.

Почему значение показателя степени, в которой расстояние между телами входит в закон всемирного тяготения, связано с евклидовостью трехмерного физического пространства?

Как определяются инертная и гравитационная массы в механике Ньютона? Почему в некоторых книгах даже не упоминается об этих величинах, а фигурирует просто масса тела?

Предположим, что в некотором мире гравитационная масса тел никак не связана с их инертной массой. Что можно было бы наблюдать при одновременном свободном падении разных тел?

Какие явления и опыты свидетельствуют о пропорциональности инертной и гравитационной масс?

Взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным , а само явление всемирного тяготениягравитацией.

Гравитационное взаимодействие осуществляется посредством особого вида материи, называемого гравитационным полем .

Гравитационные силы (силы тяготения) обусловлены взаимным притяжением тел и направлены вдоль линии, соединяющей взаимодействующие точки.

Выражение для силы тяготения в 1666 году получил Ньютон, когда ему было всего 24 года.

Закон всемирного тяготения : два тела притягиваются друг к другу с силами прямопропорциональными произведению масс тел и обратно пропорциональными квадрату расстояния между ними:

Закон справедлив при условии, что размеры тел пренебрежимо малы по сравнению с расстояниями между ними. Также формула может применяться для расчета сил всемирного тяготения, для тел шаровой формы, для двух тел, одно из которых является шаром, другое материальной точкой.

Коэффициент пропорциональности G = 6,68·10 -11 носит название гравитационной постоянной .

Физический смысл гравитационной постоянной заключается в том, что она численно равна силе, с которой притягиваются два тела массой по 1 кг каждая, находящиеся на расстоянии 1 м друг от друга.

Сила тяжести

Сила, с которой Земля притягивает находящиеся вблизи тела, называется силой тяжести , а гравитационное поле Земли – полем тяжести .

Направлена сила тяжести вниз, к центру Земли. В теле же она проходит через точку, которая называется центром тяжести . Центр тяжести однородного тела, имеющего центр симметрии (шар, прямоугольная или круглая пластина, цилиндр и т.д.), находится в этом центре. При этом он может и не совпадать ни с одной из точек данного тела (например, у кольца).

В общем случае, когда требуется найти центр тяжести какого-либо тела неправильной формы, следует исходить из следующей закономерности: если тело подвешивать на нити, прикрепляемой последовательно к разным точкам тела, то отмеченные нитью направления пересекутся в одной точке, которая как раз и является центром тяжести этого тела.

Модуль силы тяжести находиться с помощью закона всемирного тяготения и определяется по формуле:

F т = mg, (2.7)

где g – ускорение свободного падения тела (g=9,8 м/с 2 ≈10м/с 2).

Так как направление ускорения свободного падения g совпадает с направлением силы тяжести F т то можно последнее равенство переписать в виде

Из (2.7) следует, что т. е. отношение силы, действующей на тело массой m в какой-либо точке поля, к массе тела определяет ускорение свободного падения в данной точке поля.

Для точек находящихся на высоте h от поверхности Земли ускорение свободного падения тела равно:

(2.8)

где R З — радиус Земли; М З — масса Земли; h — расстояние от центра тяжести тела до поверхности Земли.

Из этой формулы вытекает, что,

во-первых , ускорение свободного падения не зависит от массы и размеров тела и,

во-вторых , с увеличением высоты над Землёй ускорение свободного падения уменьшается. Например, на высоте 297 км оно оказывается равным не 9,8 м/с 2 , а 9 м/с 2 .

Уменьшение ускорения свободного падения означает, что и сила тяжести по мере увеличения высоты над Землёй также уменьшается. Чем дальше тело находится от Земли, тем слабее она его притягивает.

Из формулы (1.73) видно, что g зависит от радиуса Земли R з.

Но из-за сплюснутости Земли в разных местах имеет разное значение: оно убывает по мере продвижения от экватора к полюсу. На экваторе, например, оно равно 9,780м/с 2 , а на полюсе — 9,832м/с 2 . Кроме того, местные значения g могут отличаться от их средних значений g ср из-за неоднородного строения земной коры и недр, горных массивов и впадин, а также залежей полезных ископаемых. Разность значений g и g ср называют

Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. 2}m = mg \) .

Сила тяжести всегда направлена к центру Земли. В зависимости от высоты \(h \) над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с 2 .

Вес тела

В технике и быту широко используется понятие веса тела.

Вес тела обозначается \(P \) . Единица веса — ньютон (Н ). Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.

При этом предполагается, что тело неподвижно относительно опоры или подвеса.

Вес тела и сила тяжести отличаются по своей природе: вес тела является проявлением действия межмолекулярных сил, а сила тяжести имеет гравитационную природу.

Состояние тела, в котором его вес равен нулю, называют невесомостью . Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, по¬этому в корабле наблюдается состояние невесомости.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Самым главным явлением, постоянно изучаемым физиками, является движение. Электромагнитные явления, законы механики, термодинамические и квантовые процессы – все это широкий спектр изучаемых физикой фрагментов мироздания. И все эти процессы сводятся, так или иначе, к одному – к .

Вконтакте

Все во Вселенной движется. Гравитация – привычное явление для всех людей с самого детства, мы родились в гравитационном поле нашей планеты, это физическое явление воспринимается нами на самом глубоком интуитивном уровне и, казалось бы, даже не требует изучения.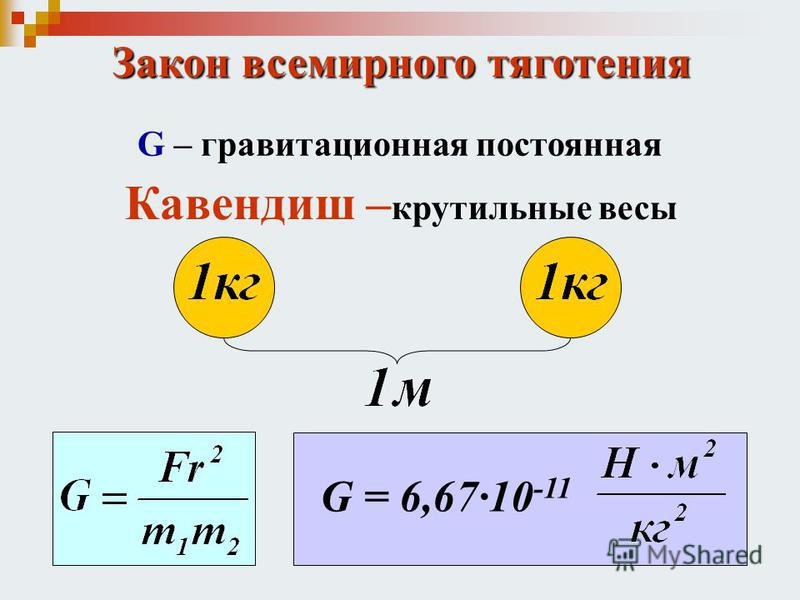

Но, увы, вопрос, почему и каким образом все тела притягиваются друг к другу , остается и на сегодняшний день не до конца раскрытым, хотя и изучен вдоль и поперек.

В этой статье мы рассмотрим, что такое всемирное притяжение по Ньютону – классическую теорию гравитации. Однако прежде чем перейти к формулам и примерам, расскажем о сути проблемы притяжения и дадим ему определение.

Быть может, изучение гравитации стало началом натуральной философии (науки о понимании сути вещей), быть может, натуральная философия породила вопрос о сущности гравитации, но, так или иначе, вопросом тяготения тел заинтересовались еще в Древней Греции .

Движение понималось как суть чувственной характеристики тела, а точнее, тело двигалось, пока наблюдатель это видит. Если мы не можем явление измерить, взвесить, ощутить, значит ли это, что этого явления не существует? Естественно, не значит. И с тех пор, как Аристотель понял это, начались размышления о сути гравитации.

Как оказалось в наши дни, спустя многие десятки веков, гравитация является основой не только земного притяжения и притяжения нашей планеты к , но и основой зарождения Вселенной и почти всех имеющихся элементарных частиц.

Задача движения

Проведем мысленный эксперимент. Возьмем в левую руку небольшой шарик. В правую возьмем такой же. Отпустим правый шарик, и он начнет падать вниз. Левый при этом остается в руке, он по-прежнему недвижим.

Остановим мысленно ход времени. Падающий правый шарик «зависает» в воздухе, левый все также остается в руке. Правый шарик наделен «энергией» движения, левый – нет. Но в чем глубокая, осмысленная разница между ними?

Где, в какой части падающего шарика прописано, что он должен двигаться? У него такая же масса, такой же объем. Он обладает такими же атомами, и они ничем не отличаются от атомов покоящегося шарика. Шарик обладает ? Да, это правильный ответ, но откуда шарику известно, что обладает потенциальной энергией, где это зафиксировано в нем?

Именно эту задачу ставили перед собой Аристотель, Ньютон и Альберт Эйнштейн. И все три гениальных мыслителя отчасти решили для себя эту проблему, но на сегодняшний день существует ряд вопросов, требующих разрешения.

Гравитация Ньютона

В 1666 году величайшим английским физиком и механиком И. Ньютоном открыт закон, способный количественно посчитать силу, благодаря которой вся материя во Вселенной стремится друг к другу. Это явление получило название всемирное тяготение. Когда вас просят: «Сформулируйте закон всемирного тяготения», ваш ответ должен звучать так:

Сила гравитационного взаимодействия, способствующая притяжению двух тел, находится в прямой пропорциональной связи с массами этих тел и в обратной пропорциональной связи с расстоянием между ними.

Важно! В законе притяжения Ньютона используется термин «расстояние». Под этим термином следует понимать не дистанцию между поверхностями тел, а расстояние между их центрами тяжести. К примеру, если два шара радиусами r1 и r2 лежат друг на друге, то дистанция между их поверхностями равна нулю, однако сила притяжения есть. Все дело в том, что расстояние между их центрами r1+r2 отлично от нуля. В космических масштабах это уточнение не суть важно, но для спутника на орбите данная дистанция равна высоте над поверхностью плюс радиус нашей планеты. Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.

Для закона тяготения формула выглядит следующим образом:

,

• F – сила притяжения,
• – массы,
• r – расстояние,
• G – гравитационная постоянная, равная 6,67·10−11 м³/(кг·с²).

Что же представляет собой вес, если только что мы рассмотрели силу притяжения?

Сила является векторной величиной, однако в законе всемирного тяготения она традиционно записана как скаляр. В векторной картине закон будет выглядеть таким образом:

.

Но это не означает, что сила обратно пропорциональна кубу дистанции между центрами. Отношение следует воспринимать как единичный вектор, направленный от одного центра к другому:

.

Закон гравитационного взаимодействия

Вес и гравитация

Рассмотрев закон гравитации, можно понять, что нет ничего удивительного в том, что лично мы ощущаем притяжение Солнца намного слабее, чем земное . Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.

Насколько нам известно, сила тяжести равна:

где m – наша масса, а g – ускорение свободного падения Земли (9,81 м/с 2).

Важно! Не бывает двух, трех, десяти видов сил притяжения. Гравитация – единственная сила, дающая количественную характеристику притяжения. Вес (P = mg) и сила гравитации – одно и то же.

Если m – наша масса, M – масса земного шара, R – его радиус, то гравитационная сила, действующая на нас, равна:

Таким образом, поскольку F = mg:

.

Массы m сокращаются, и остается выражение для ускорения свободного падения:

Как видим, ускорение свободного падения – действительно постоянная величина, поскольку в ее формулу входят величины постоянные — радиус, масса Земли и гравитационная постоянная.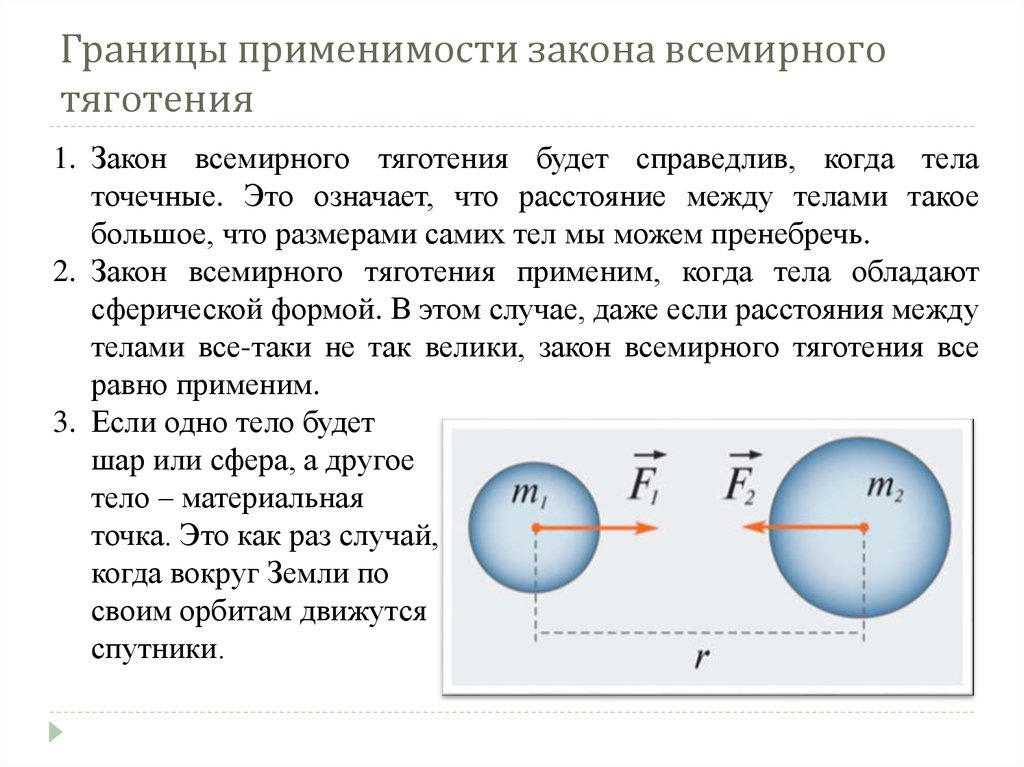 Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с 2 .

На разных широтах радиус планеты несколько отличается, поскольку Земля все-таки не идеальный шар. Из-за этого ускорение свободного падения в отдельных точках земного шара разное.

Вернемся к притяжению Земли и Солнца. Постараемся на примере доказать, что земной шар притягивает нас с вами сильнее, чем Солнце.

Примем для удобства массу человека: m = 100 кг. Тогда:

• Расстояние между человеком и земным шаром равно радиусу планеты: R = 6,4∙10 6 м.
• Масса Земли равна: M ≈ 6∙10 24 кг.
• Масса Солнца равна: Mc ≈ 2∙10 30 кг.
• Дистанция между нашей планетой и Солнцем (между Солнцем и человеком): r=15∙10 10 м.

Гравитационное притяжение между человеком и Землей:

Данный результат довольно очевиден из более простого выражения для веса (P = mg).

Сила гравитационного притяжения между человеком и Солнцем:

Как видим, наша планета притягивает нас почти в 2000 раз сильнее.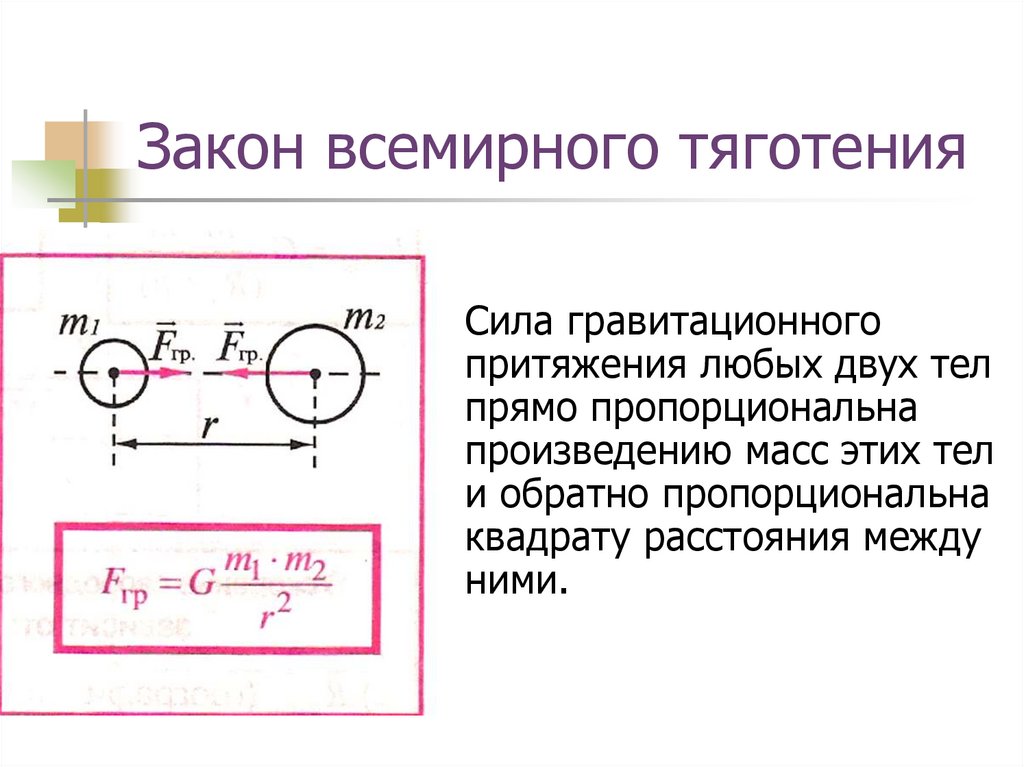

Как найти силу притяжения между Землей и Солнцем? Следующим образом:

Теперь мы видим, что Солнце притягивает нашу планету более чем в миллиард миллиардов раз сильнее, чем планета притягивает нас с вами.

Первая космическая скорость

После того как Исаак Ньютон открыл закон всемирного тяготения, ему стало интересно, с какой скоростью нужно бросить тело, чтобы оно, преодолев гравитационное поле, навсегда покинуло земной шар.

Правда, он представлял себе это несколько иначе, в его понимании была не вертикально стоящая ракета, устремленная в небо, а тело, которое горизонтально совершает прыжок с вершины горы. Это была логичная иллюстрация, поскольку на вершине горы сила притяжения немного меньше .

Так, на вершине Эвереста ускорение свободного падения будет равно не привычные 9,8 м/с 2 , а почти м/с 2 . Именно по этой причине там настолько разряженный , частицы воздуха уже не так привязаны к гравитации, как те, которые «упали» к поверхности.

Постараемся узнать, что такое космическая скорость.

Первая космическая скорость v1 – это такая скорость, при которой тело покинет поверхность Земли (или другой планеты) и перейдет на круговую орбиту.

Постараемся узнать численной значение этой величины для нашей планеты.

Запишем второй закон Ньютона для тела, которое вращается вокруг планеты по круговой орбите:

,

где h — высота тела над поверхностью, R — радиус Земли.

На орбите на тело действует центробежное ускорение , таким образом:

.

Массы сокращаются, получаем:

,

Данная скорость называется первой космической скоростью:

Как можно заметить, космическая скорость абсолютно не зависит от массы тела. Таким образом, любой предмет, разогнанный до скорости 7,9 км/с, покинет нашу планету и перейдет на ее орбиту.

Первая космическая скорость

Вторая космическая скорость

Однако, даже разогнав тело до первой космической скорости, нам не удастся полностью разорвать его гравитационную связь с Землей. Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.

Важно! По ошибке часто считается, что для того чтобы попасть на Луну, космонавтам приходилось достигать второй космической скорости, ведь нужно было сперва «разъединиться» с гравитационным полем планеты. Это не так: пара «Земля — Луна» находятся в гравитационном поле Земли. Их общий центр тяжести находится внутри земного шара.

Для того чтобы найти эту скорость, поставим задачу немного иначе. Допустим, тело летит из бесконечности на планету. Вопрос: какая скорость будет достигнута на поверхности при приземлении (без учета атмосферы, разумеется)? Именно такая скорость и потребуется телу, чтобы покинуть планету .

Вторая космическая скорость

Запишем закон сохранения энергии:

,

где в правой части равенства стоит работа силы тяжести: A = Fs.

Отсюда получаем, что вторая космическая скорость равна:

Таким образом, вторая космическая скорость в раз больше первой:

Закон всемирного тяготения. Физика 9 класс

Закон Всемирного тяготения.

Вывод

Мы с вами узнали, что хотя гравитация является основной силой во Вселенной, многие причины этого явления до сих пор остались загадкой. Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.

«Физика — 10 класс»

Почему Луна движется вокруг Земли?
Что будет, если Луна остановится?
Почему планеты обращаются вокруг Солнца?

В главе 1 подробно говорилось о том, что земной шар сообщает всем телам у поверхности Земли одно и то же ускорение — ускорение свободного падения. Но если земной шар сообщает телу ускорение, то согласно второму закону Ньютона он действует на тело с некоторой силой. Силу, с которой Земля действует на тело, называют силой тяжести . Сначала найдём эту силу, а затем и рассмотрим силу всемирного тяготения.

Ускорение по модулю определяется из второго закона Ньютона:

В общем случае оно зависит от силы, действующей на тело, и его массы. Так как ускорение свободного падения не зависит от массы, то ясно, что сила тяжести должна быть пропорциональна массе:

Физическая величина — ускорение свободного падения, оно постоянно для всех тел.

На основе формулы F = mg можно указать простой и практически удобный метод измерения масс тел путём сравнения массы данного тела с эталоном единицы массы. Отношение масс двух тел равно отношению сил тяжести, действующих на тела:

Это значит, что массы тел одинаковы, если одинаковы действующие на них силы тяжести.

На этом основано определение масс путём взвешивания на пружинных или рычажных весах. Добиваясь того, чтобы сила давления тела на чашку весов, равная силе тяжести, приложенной к телу, была уравновешена силой давления гирь на другую чашку весов, равной силе тяжести, приложенной к гирям, мы тем самым определяем массу тела.

Сила тяжести, действующая на данное тело вблизи Земли, может считаться постоянной лишь на определенной широте у поверхности Земли. Если тело поднять или перенести в место с другой широтой, то ускорение свободного падения, а следовательно, и сила тяжести изменятся.

Сила всемирного тяготения.

Ньютон был первым, кто строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила всемирного тяготения , действующая между любыми телами Вселенной.

Ньютон пришёл к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы (рис. 3.1) с определённой скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался бы вокруг неё подобно тому, как планеты описывают в небесном пространстве свои орбиты.

Ньютон нашёл эту причину и смог точно выразить её в виде одной формулы — закона всемирного тяготения.

Так как сила всемирного тяготения сообщает всем телам одно и то же ускорение независимо от их массы, то она должна быть пропорциональна массе того тела, на которое действует:

«Тяготение существует ко всем телам вообще и пропорционально массе каждого из них… все планеты тяготеют друг к другу.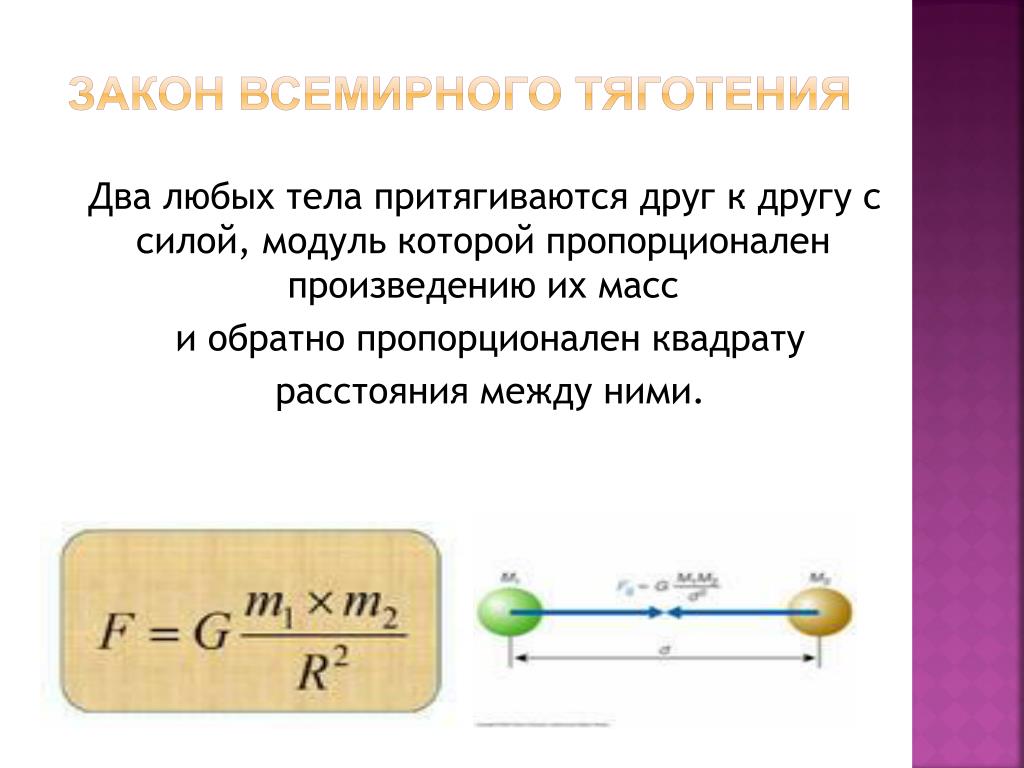 ..» И. Ньютон

Но поскольку, например, Земля действует на Луну с силой, пропорциональной массе Луны, то и Луна по третьему закону Ньютона должна действовать на Землю с той же силой. Причём эта сила должна быть пропорциональна массе Земли. Если сила тяготения является действительно универсальной, то со стороны данного тела на любое другое тело должна действовать сила, пропорциональная массе этого другого тела. Следовательно, сила всемирного тяготения должна быть пропорциональна произведению масс взаимодействующих тел. Отсюда вытекает формулировка закона всемирного тяготения.

Закон всемирного тяготения:

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:

Коэффициент пропорциональности G называется гравитационной постоянной .

Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массой 1 кг каждая, если расстояние между ними равно 1 м. Ведь при массах m 1 = m 2 = 1 кг и расстоянии r = 1 м получаем G = F (численно).

Нужно иметь в виду, что закон всемирного тяготения (3.4) как всеобщий закон справедлив для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 3.2, а).

Можно показать, что однородные тела, имеющие форму шара (даже если их нельзя считать материальными точками, рис. 3.2, б), также взаимодействуют с силой, определяемой формулой (3.4). В этом случае r — расстояние между центрами шаров. Силы взаимного притяжения лежат на прямой, проходящей через центры шаров. Такие силы называются центральными . Тела, падение которых на Землю мы обычно рассматриваем, имеют размеры, много меньшие, чем земной радиус (R ≈ 6400 км).

Такие тела можно, независимо от их формы, рассматривать как материальные точки и определять силу их притяжения к Земле с помощью закона (3.4), имея в виду, что r есть расстояние от данного тела до центра Земли.

Брошенный на Землю камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадёт наконец на Землю.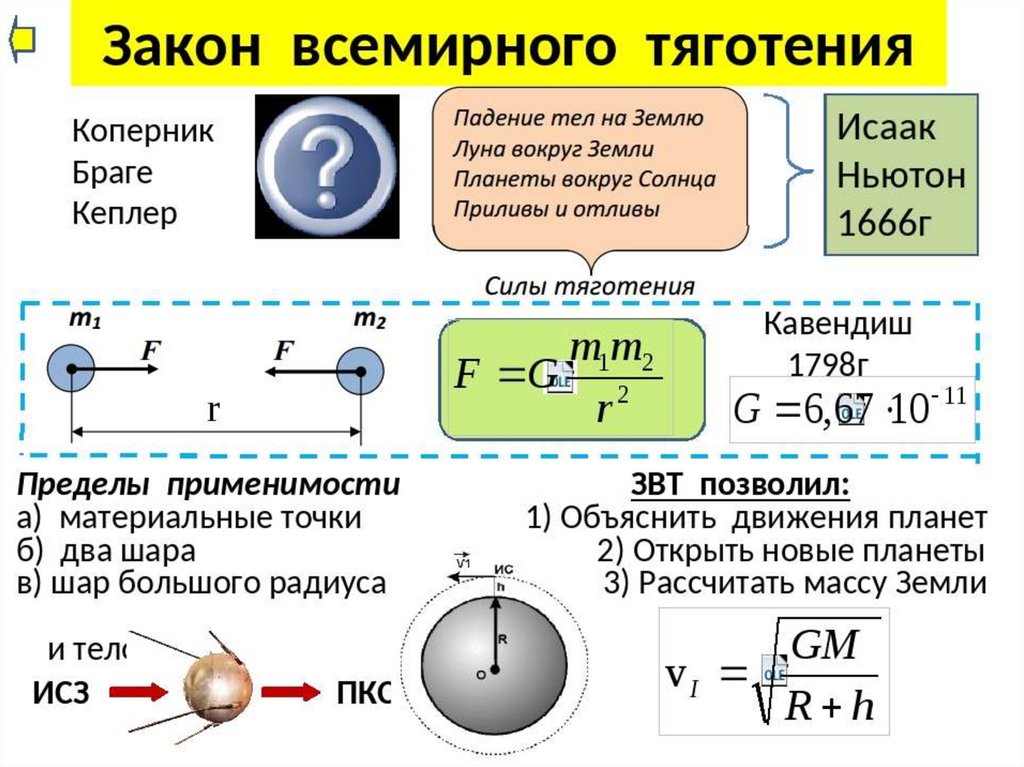 Если его бросить с большей скоростью, то он упадёт дальше». И. Ньютон

Определение гравитационной постоянной.

Теперь выясним, как можно найти гравитационную постоянную. Прежде всего заметим, что G имеет определённое наименование. Это обусловлено тем, что единицы (и соответственно наименования) всех величин, входящих в закон всемирного тяготения, уже были установлены ранее. Закон же тяготения даёт новую связь между известными величинами с определёнными наименованиями единиц. Именно поэтому коэффициент оказывается именованной величиной. Пользуясь формулой закона всемирного тяготения, легко найти наименование единицы гравитационной постоянной в СИ: Н м 2 /кг 2 = м 3 /(кг с 2).

Для количественного определения G нужно независимо определить все величины, входящие в закон всемирного тяготения: обе массы, силу и расстояние между телами.

Трудность состоит в том, что гравитационные силы между телами небольших масс крайне малы. Именно по этой причине мы не замечаем притяжение нашего тела к окружающим предметам и взаимное притяжение предметов друг к другу, хотя гравитационные силы — самые универсальные из всех сил в природе. Два человека массами по 60 кг на расстоянии 1 м друг от друга притягиваются с силой всего лишь порядка 10 -9 Н. Поэтому для измерения гравитационной постоянной нужны достаточно тонкие опыты.

Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1798 г. с помощью прибора, называемого крутильными весами. Схема крутильных весов показана на рисунке 3.3. На тонкой упругой нити подвешено лёгкое коромысло с двумя одинаковыми грузиками на концах. Рядом неподвижно закреплены два тяжёлых шара. Между грузиками и неподвижными шарами действуют силы тяготения. Под влиянием этих сил коромысло поворачивается и закручивает нить до тех пор, пока возникающая сила упругости не станет равна гравитационной силе. По углу закручивания можно определить силу притяжения. Для этого нужно только знать упругие свойства нити. Массы тел известны, а расстояние между центрами взаимодействующих тел можно непосредственно измерить.

Из этих опытов было получено следующее значение для гравитационной постоянной:

G = 6,67 10 -11 Н м 2 /кг 2 .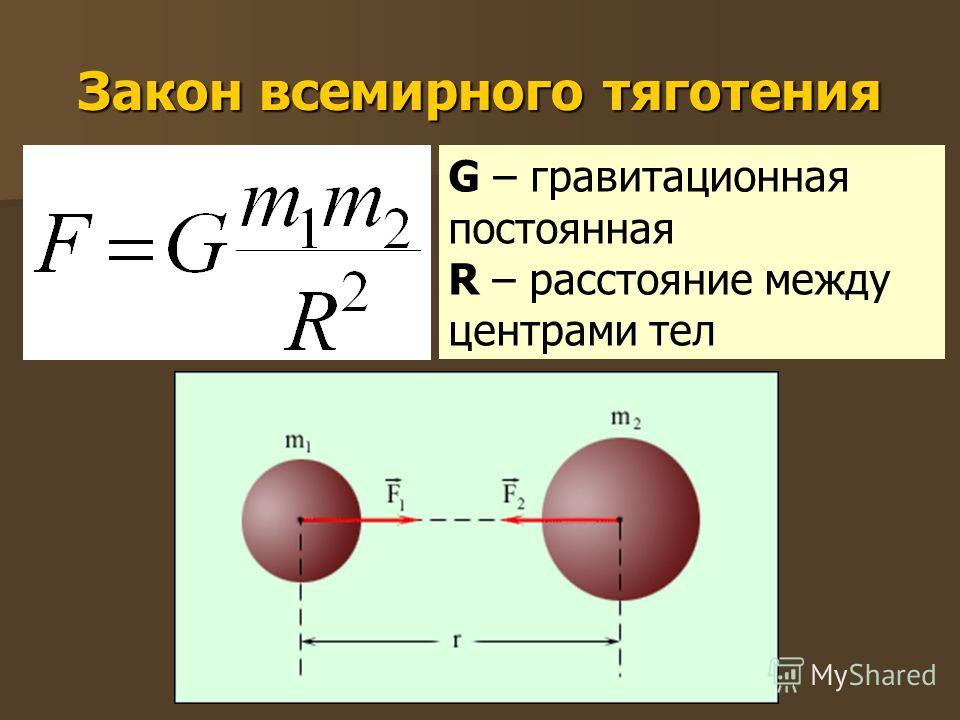

Лишь в том случае, когда взаимодействуют тела огромных масс (или по крайней мере масса одного из тел очень велика), сила тяготения достигает большого значения. Например, Земля и Луна притягиваются друг к другу с силой F ≈ 2 10 20 Н.

Зависимость ускорения свободного падения тел от географической широты.

Одна из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, состоит в том, что земной шар несколько сплюснут у полюсов и расстояние от центра Земли до её поверхности у полюсов меньше, чем на экваторе. Другой причиной является вращение Земли.

Равенство инертной и гравитационной масс.

Самым поразительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их масс, одно и то же ускорение. Что бы вы сказали о футболисте, удар которого одинаково ускорял бы обыкновенный кожаный мяч и двухпудовую гирю? Каждый скажет, что это невозможно. А вот Земля является именно таким «необыкновенным футболистом» с той только разницей, что действие её на тела не носит характера кратковременного удара, а продолжается непрерывно миллиарды лет.

В теории Ньютона масса является источником поля тяготения. Мы находимся в поле тяготения Земли. В то же время мы также являемся источниками поля тяготения, но в силу того, что наша масса существенно меньше массы Земли, наше поле намного слабее и окружающие предметы на него не реагируют.

Необыкновенное свойство гравитационных сил, как мы уже говорили, объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Масса тела, которая входит во второй закон Ньютона, определяет инертные свойства тела, т. е. его способность приобретать определённое ускорение под действием данной силы. Это инертная масса m и.

Казалось бы, какое отношение она может иметь к способности тел притягивать друг друга? Масса, определяющая способность тел притягиваться друг к другу, — гравитационная масса m r .

Из механики Ньютона совсем не следует, что инертная и гравитационная массы одинаковы, т. е. что

m и = m r . (3.5)

Равенство (3.5) является непосредственным следствием из опыта. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.

Определение закона всемирного тяготения, его формула и значение

В физике существует огромное количество законов, терминов, определений и формул, которые объясняют все природные явления на земле и во Вселенной. Одним из основных является закон всемирного тяготения, который открыл великий и всем известный учёный Исаак Ньютон. Определение его выглядит вот так: два любых тела во Вселенной взаимно притягиваются друг к другу с определённой силой. Формула всемирного тяготения, которая и вычисляет эту силу, будет иметь вид: F = G*(m1*m2 / R*R).

…

Оглавление:

• История открытия закона
• Разбор формулы
• Насколько точны вычисления
• Поле тяготения
• Описание взаимодействия и гравитации
• Пример расчётов

История открытия закона

Очень долгое время люди изучали небо. Они хотели знать все его особенности, все законы Ньютона, царящие в недосягаемом космосе. По небу составляли календарь, вычисляли важные даты и даты религиозных праздников. Люди верили, что центром всей Вселенной является Солнце, вокруг которого вращаются все небесные субъекты.

По-настоящему бурный научный интерес к космосу и вообще к астрономии появился в XVI веке. Тихо Браге, великий учёный астроном, во время своих исследований наблюдал за перемещениями планет, записывал и систематизировал наблюдения. К тому моменту, как Исаак Ньютон открыл закон силы всемирного тяготения, в мире уже утвердилась система Коперника, согласно которой все небесные тела вращаются вокруг звёзды по определённым орбитам. Великий учёный Кеплер на основе исследований Браге, открыл кинематические законы, которые характеризуют движение планет.

Это интересно: энтропия — это что такое, где применяется термин?

Основываясь на законах Кеплера, Исаак Ньютон открыл свой и выяснил, что:

• Движения планет указывают на наличие центральной силы. 2)
• m1 и m2 — значение масс тел, между которыми происходит силовое взаимодействие.
• R — значение расстояния между телами. В формуле его необходимо возвести в квадрат.

Насколько точны вычисления

Поскольку закон Исаака Ньютона относится к механике, вычисления не всегда максимально точно отражают реальную силу, с которой тела взаимодействуют. Более того, данная формула может использоваться только в двух случаях:

• Когда два тела, между которыми происходит взаимодействие, являются однородными объектами.
• Когда одно из тел является материальной точкой, а другое — однородным шаром.

Это интересно: система отсчета в физике — определение и ее виды.

Поле тяготения

По третьему закону Ньютона мы пониманием, что силы взаимодействие двух тел одинаковы по значению, но противоположны по её направлению. Направление сил происходит строго вдоль прямой линии, которая соединяет центры масс двух взаимодействующих тел. Взаимодействие притяжения между телами происходит благодаря полю тяготения.

Описание взаимодействия и гравитации

Гравитация обладает полями очень дальнего взаимодействия. Другими словами, её влияние распространяется на очень большие, космических масштабов расстояния. Благодаря гравитации люди и все другие объекты притягиваются к земле, а земля и все планеты Солнечной системы притягиваются к Солнцу. Гравитация — это постоянное воздействие тел друг на друга, это явление, которое обусловливает закон всемирного тяготения. Очень важно понимать одну вещь — чем массивнее тело, тем большей гравитацией оно обладает. Земля имеет огромную массу, поэтому мы притягиваемся к ней, а Солнце весит в несколько миллионов раз больше, чем Земля, поэтому наша планета притягивается к звезде.

Альберт Эйнштейн, один из величайших физиков, утверждал, что тяготение между двумя телами происходит из-за искривления пространства-времени. Учёный был уверен, что пространство, подобно ткани, может продавливаться, и чем массивнее объект, тем сильнее эту ткань он будет продавливать. 24 килограмм.

Закон всемирного тяготения. Движение тел под действием силы тяжести

По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.

Закон всемирного тяготения был открыт Исааком Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей  центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в 1.23.

У однородного шара центр масс совпадает с центром шара.

Рисунок 1.10.1. Гравитационные силы притяжения между телами.

В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом Иоганном Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.

Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R – ее радиус, m – масса данного тела, то сила тяжести равна

где g – ускорение свободного падения у поверхности Земли:

 

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения.

Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с². Зная ускорение свободного падения и радиус Земли (R = 6,38·10⁶ м), можно вычислить массу Земли М:

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт весом 71,5 кг (Гагарин) притягивается к Земле вблизи ее поверхности равна 700 Н.

Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли

Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии r_Л = 3,84·10⁶ м. Это расстояние приблизительно в 60 раз превышает радиус Земли R_З. Следовательно, ускорение свободного падения a_Л, обусловленное земным притяжением, на орбите Луны составляет

 

С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения:

где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.

Собственное гравитационное поле Луны определяет ускорение свободного падения g_Л на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение g_Л определится выражением:

   

 

В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.

Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу R_З. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ₁. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим:

Двигаясь с такой скоростью, спутник облетал бы Землю за время

На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.

Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.

Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия

Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.

Период T обращения такого спутника равен

Здесь T₁ – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 R_З, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 R_З называется геостационарной.

Опубликовано в разделах: Механика, Силы в природе

Что такое закон в науке?

(Изображение предоставлено Shutterstock)

В общем, научный закон — это описание наблюдаемого явления. Это не объясняет, почему явление существует или что его вызывает. Объяснение явления называется научной теорией . Это заблуждение, что теории превращаются в законы при достаточном количестве исследований.

«В науке законы — это отправная точка», — сказал Питер Коппингер, адъюнкт-профессор биологии и биомедицинской инженерии в Технологическом институте Роуз-Халман в Индии. «Отсюда ученые могут задавать вопросы: «Почему и как?»»

Разница между научной теорией и научным законом

Многие люди думают, что если ученые находят доказательства, подтверждающие гипотезу, гипотеза становится теорией, а если оказывается, что теория верна, она становится законом . Однако это не так. Факты, теории и законы — так же как и гипотезы — являются отдельными элементами научного метода . Хотя они могут развиваться, они не обновляются до чего-то другого.

«Гипотезы, теории и законы подобны яблокам, апельсинам и кумкватам: одно не может вырасти в другое, сколько бы удобрений и воды ни предлагалось», согласно Калифорнийский университет, Беркли (открывается в новой вкладке). Гипотеза — это потенциальное объяснение узкого явления; научная теория – это углубленное объяснение, применимое к широкому кругу явлений. Закон — это утверждение о наблюдаемом явлении или объединяющей концепции в соответствии с Государственного университета Кеннесо (открывается в новой вкладке).

«В науке есть четыре основных понятия: факты, гипотезы, законы и теории», — сказал Коппингер Live Science.

Хотя научные законы и теории поддерживаются большим числом эмпирические данные , которые принимаются большинством ученых в этой области научных исследований и помогают унифицировать эту совокупность данных, это не одно и то же.

«Законы — это описания — часто математические описания — природных явлений, например, закон всемирного тяготения Ньютона или закон независимого распределения Менделя. Эти законы просто описывают наблюдение. Не то, как и почему они работают», — сказал Коппингер.

Коппингер указал, что закон гравитации был открыт Исааком Ньютоном в 17 веке. Этот закон математически описывает, как два разных тела во Вселенной взаимодействуют друг с другом. Однако закон Ньютона не объясняет, что такое гравитация и как она работает. Лишь три столетия спустя, когда Альберт Эйнштейн разработал теорию относительности , ученые начали понимать, что такое гравитация и как она работает.

Mendelian Inheritance показан с моделью гороха. (Изображение предоставлено Shutterstock)

«Закон Ньютона полезен для ученых тем, что астрофизики могут использовать этот многовековой закон для посадки роботов на Марс. Но он не объясняет, как работает гравитация или что это такое. Точно так же закон Менделя Закон независимого распределения описывает, как различные черты передаются от родителей к потомству, а не то, как и почему это происходит», — сказал Коппингер. Грегор Мендель обнаружил, что два разных генетических признака проявляются независимо друг от друга у разных потомков. «Однако Мендель ничего не знал о ДНК или хромосомы . Лишь столетие спустя ученые открыли ДНК и хромосомы — биохимическое объяснение законов Менделя. Только тогда ученые, такие как Т. Х. Морган, работая с плодовыми мушками, объяснил закон независимого распределения, используя теорию хромосомной наследственности. До сих пор это общепринятое объяснение (теория) закона Менделя», — сказал Коппингер.

Разницу между научными законами и научными фактами определить немного сложнее, хотя определение важно. наблюдения, которые доказали свою истинность. Согласно НАСА, законы – это обобщенные наблюдения о взаимоотношениях между двумя или более вещами в мире природы, основанные на множестве фактов и эмпирических данных, которые часто оформляются в виде математических утверждений. 

Например, «Яблоки падают с этой яблони» считается фактом, потому что это простое утверждение, которое можно доказать. «Сила гравитации между любыми двумя объектами (например, яблоком и Землей) зависит от масс объектов и расстояния между ними» — это закон, потому что он описывает поведение двух объектов в определенных обстоятельствах. Если обстоятельства изменятся, то последствия закона изменятся. Например, если бы яблоко и Земля уменьшились до субатомных размеров, они бы вели себя по-разному.

Научные законы и математика

(Изображение предоставлено Shutterstock.)

(открывается в новой вкладке)

Многие научные законы можно свести к математическому уравнению. Например, закон всемирного тяготения Ньютона гласит:

F _g = G (m ₁ ∙ m ₂ ) / d ²

Fg — сила тяжести; G — универсальная гравитационная постоянная, которую можно измерить; m1 и m2 — массы двух объектов, а d — расстояние между ними согласно 9.0003 Университет штата Огайо (открывается в новой вкладке).

Научные законы также часто подчиняются математике вероятности. «С большими числами всегда работает вероятность. Дом всегда побеждает», — сказала Сильвия Вассертейл-Смоллер, профессор Медицинского колледжа Альберта Эйнштейна в Нью-Йорке. «Мы можем рассчитать вероятность события, и мы можем определить, насколько мы уверены в нашей оценке, но всегда существует компромисс между точностью и уверенностью. Это известно как доверительный интервал. Например, мы можем быть 9На 5% уверены, что то, что мы пытаемся оценить, находится в определенном диапазоне, или мы можем быть более уверены, скажем, на 99%, что оно находится в более широком диапазоне. Как и в жизни вообще, мы должны признать, что есть компромисс.»

Меняются ли законы?

То, что идея становится законом, не означает, что ее нельзя изменить с помощью научных исследований в Будущее. Использование слова «закон» неспециалистами и учеными различается. Когда большинство людей говорят о законе, они имеют в виду что-то абсолютное. Научный закон гораздо более гибкий. Он может иметь исключения, доказывать свою ошибочность или эволюционировать в течение время, по данным Калифорнийского университета в Беркли.0005

«Хороший ученый — это тот, кто всегда задает вопрос: «Как я могу показать себя неправым?» — сказал Коппингер. «Что касается закона всемирного тяготения или закона независимого распределения, постоянные проверки и наблюдения «подправили» эти законы. Были найдены исключения. Например, закон тяготения Ньютона не работает при рассмотрении на квантовом (субатомном) уровне. Закон независимого ассортимента Менделя нарушается, когда признаки «сцепляются» в одной и той же хромосоме».

Примеры научных законов

• Закон сохранения энергии, который гласит, что полная энергия в изолированной системе остается постоянной. Другими словами, энергия не может быть создана или уничтожена, согласно Britannica .
• Законы термодинамики, которые имеют дело с отношениями между теплом и другими формами энергии новая вкладка)
• Закон космического расширения Хаббла, определяющий взаимосвязь между расстоянием до галактики и скоростью, с которой она удаляется от нас, по словам астрофизика Неты А. Бахколл
• Принцип Архимеда, согласно которому выталкивающая сила действует на объект, жидкости равна весу жидкости, вытесненной этим объектом.

Дополнительные ресурсы

• Этот ресурс Управления по стандартам образования Нового Южного Уэльса (открывается в новой вкладке) содержит подробное объяснение научных теорий и законов.
• Узнайте, почему теория не может превратиться в закон, из этой статьи от Indiana Public Media (откроется в новой вкладке).
• Посмотрите видео о разнице между научным законом и научной теорией от TEDEd. (открывается в новой вкладке)

Библиография

Калифорнийский университет, Беркли, «Заблуждения о науке». https://undsci.berkeley.edu/teaching/misconceptions.php

Образовательный центр NASA IMAGE, «Руководство для учителя: теории, гипотезы, законы, факты и убеждения». https://www.nasa.gov/pdf/371711main_SMII_Problem23.pdf  

Университет штата Огайо, «Лекция 18: Яблоко и Луна: ньютоновская гравитация». https://www.astronomy.ohio-state.edu/pogge.1/Ast161/Unit4/gravity.html  

Британская энциклопедия, «Сохранение энергии». 16 ноября 2021 г. https://www.britannica.com/science/conservation-of-energy  

Университет Виннипега, «Закон тяготения Ньютона». 1997. https://theory.uwinnipeg. ca/physics/circ/node7.html  

Нета А. Бахколл, «Закон Хаббла и расширяющаяся Вселенная», Труды Национальной академии наук, том 112, март 2015 г., https://doi.org/10.1073/pnas.1424299112  

Эшли Хамер — автор статей для Live Science, которая пишет обо всем — от космоса и квантовой физики до здоровья и психологии. Она ведет два подкаста: Curiosity Daily и Taboo Science. Она также писала для каналов YouTube SciShow и «Быть ​​умным — это нормально». Обладая степенью бакалавра и магистра по джазовому саксофону в Университете Северного Техаса, Эшли имеет нетрадиционный опыт, который дает ее научному письму уникальную перспективу и точку зрения со стороны.

Обзор гравитации

Краткий обзор гравитации и силы гравитации

Введение в закон всемирного тяготения Ньютона, пространственную геометрию и квантовую гравитацию.

Гравитация

Слово гравитация имеет множество определений. Как определено словарем.com, гравитация означает «силу притяжения, с которой земные тела имеют тенденцию падать к центру Земли», или «тяжесть или вес», или «серьезный или критический характер», среди других определений ( Dictionary. com, nd). В научных курсах мы в основном используем слово 9.0141 гравитация для описания силы, а не гравитация ситуации, если, конечно, у наших студентов нет проблем с пониманием физических наук!

Материя яблок: закон всемирного тяготения Ньютона

Известному физику сэру Исааку Ньютону обычно приписывают открытие гравитации. В своей основополагающей работе, опубликованной в 1687 г. под названием Philosophiae Naturealis Principia Mathematica (лат. «Математические принципы натуральной философии»), обычно именуемой The Principia (Jones, n.d.), Ньютон изложил свой универсальный закон тяготения, который гласит:

«Каждая частица материи во вселенной притягивает каждую другую частицу с силой, которая прямо пропорциональна произведению масс частиц и обратно пропорциональна квадрату расстояния между ними».

Наблюдая за падением яблок с деревьев и понимая влияние Земли на Луну, Ньютон пришел к выводу, что на яблоки и Луну действует одна и та же сила, которую он назвал gravitas , от латинского слова gravitas , что означает «тяжесть или вес». Он также написал следующее уравнение, которое переводит сформулированный выше закон в символы:

F _G = G x [(m ₁ m ₂₎ / (r ² )]

Где:

2 F _G — сила тяжести (обычно выражается в ньютонах (Н), где 1 Н равен 1 килограмму (кг), умноженному на 1 метр (м), деленному на секунды (с) в квадрате, или, как символы, 1 Н = 1 кг·м·с ^_-2 )

G is the gravitational constant and is equal to 6.674 x 10 ^-11 N×m ² ×kg ^-2

m ₁ and m ₂ are массы двух объектов (в кг)

r — расстояние по прямой между двумя объектами (в м)

Сила (F _G ) в уравнении всегда направлена ​​на другой объект, и согласно согласно третьему закону движения Ньютона сила всегда равна и противоположна. Более легкие объекты с меньшей массой (например, яблоки) падают на Землю (которая намного больше яблока) намного быстрее, чем Земля падает на них, даже при том, что величина силы одинакова. Поскольку сила (F _G ) обратно пропорциональна квадрату расстояния между объектами, большую часть времени расстояние между двумя объектами ограничивает силу гравитации, и только крупные объекты с большими массами имеют значительные гравитационные эффекты. Другими словами, мы придерживаемся Земли и не улетаем в космос, потому что Земля имеет большую массу, которая нас к ней притягивает, а не потому, что мы плотно пообедали.

Эйнштейн: гравитация есть свойство геометрии пространства-времени

В 1915 Альберт Эйнштейн предположил, что гравитация сама по себе является свойством геометрии пространства-времени, а не уникальной силой, как предполагал Ньютон. Ключ к теории Эйнштейна, известной как общая теория относительности, заключается в том, что массы самих объектов заставляют пространство искривляться таким образом, что более мелкие объекты, так сказать, запутываются в искривлении пространства-времени, создаваемом более крупными объектами. Со временем экспериментальные данные, такие как отклонение света от звезд, подтвержденное звездными фотографиями Артура Эддингтона в 1919 ( The Physics of the Universe , 2009) и изменения в записях времени со спутников предоставили доказательства того, что теория заслуживает внимания.

Например, спутники, входящие в состав Глобальной системы позиционирования (GPS), вращаются вокруг Земли на высоте приблизительно 26 600 км (15 960 миль) и движутся со скоростью 14 000 км/ч относительно поверхности Земли. Поскольку искривление пространства-времени тем меньше, чем дальше мы удаляемся от центра Земли (центра ее гравитационной массы), часы на спутниках идут быстрее, чем такие же наземные часы, примерно на 38 микросекунд в день. Другими словами, чем слабее гравитационный потенциал (чем дальше часы от центра масс источника гравитации), тем быстрее течет время. В современном мире инженеры и ученые-физики, разрабатывающие системы GPS, должны учитывать эти релятивистские эффекты, иначе со временем навигационные системы, использующие GPS, не будут правильно работать на поверхности Земли для кораблей, самолетов и т. д.

Квантовая гравитация: сочетание пространства-времени и гравитации

Применение работы Эйнштейна не ограничивается спутниками. Сегодня физики пытаются примирить различия в теориях гравитации, предложенных Ньютоном и Эйнштейном, в области физики, известной как квантовая гравитация (КГ), которая пытается объяснить гравитацию и искривления пространства-времени, используя теории прошлого и квантовую механику. Вопрос о том, может ли единая теория гравитации охватить все нюансы, остается открытым, потому что в настоящее время физики-теоретики испытывают трудности с согласованием различий в трактовке времени в двух теориях (9).0141 Quanta Magazine , nd).

Будем надеяться, что в будущем физики узнают больше о свертывании пространства-времени и гравитации. Поскольку законы физики не препятствуют телепортации больших объектов, возможно, однажды, вместо того, чтобы путешествовать с места на место в машине, самолете или другом транспортном средстве, мы сможем просто телепортироваться в желаемое место отдыха, используя наши знания. гравитации и сворачивания пространства-времени! А пока мы продолжаем изучать физику нашей Вселенной.

Ссылки

Гравитация (н.д.). Словарь.com. Получено 28 февраля и 13 марта 2017 г. с http://www.dictionary.com/browse/gravity?s=t.

Джонс, А.З. (н.д.). Закон всемирного тяготения Ньютона: что вам нужно знать о гравитации.

МысльКо . Получено 28 февраля и 13 марта 2017 г. с https://www.thoughtco.com/newtons-law-of-gracity-2698878.

Мастин, Л. (2009 г.). Важные ученые: Артур Эддингтон (1882—1944).

Физика Вселенной . Получено 28 февраля, 6 марта и 13 марта 2017 г. с http://www.physicsoftheuniverse.com/scientists_eddington.html.

Магазин Quanta (без даты). Проблема времени квантовой гравитации. Получено 28 февраля и 13 марта 2017 г. с https://www.quantamagazine.org/20161201-quantum-gravitys-time-problem/.

Знакомство с комплектом Gravity Kit

Гравитация для детей — Определение гравитации, объяснение и факты для детей

Слово «гравитация» пришло к нам из латыни. Оно означает «вес», и именно так мы называем силу, придающую вес объектам. Это такая физическая сила, благодаря которой люди удерживаются на поверхности Земли, а сама Земля занимает свое место на своей орбите. Хотя люди уже в древности задавались вопросом, почему все предметы падают вниз, у современных ученых все еще есть вопросы о том, как действует гравитационная сила. Так что же это?

Проще говоря, гравитация — это притяжение, существующее между любыми двумя материальными телами. Все, что сделано из материи, к которой можно прикоснуться, имеет собственную гравитацию. Это любые предметы, даже фрукты и овощи (груши, апельсины и т. д.), тела людей и сама наша планета.

Несмотря на термин невесомость, силы гравитации не избежать. У космонавтов на низкой околоземной орбите тоже есть гравитация, но они движутся так быстро, что никогда не приближаются к центру планеты и постоянно находятся в свободном падении.

Существует закономерность, согласно которой степень тяжести тела пропорциональна его массе. Чем больше масса объекта, тем больше у него гравитационная сила. Планета Земля является одновременно самым большим и ближайшим к нам объектом, поэтому все объекты притягиваются ее гравитацией. Вот почему плоды, упавшие с дерева, падают прямо на землю и не привлекаются другими людьми.

Расстояние между объектами также влияет на гравитационное притяжение. Чем дальше объекты друг от друга, тем меньше гравитация между ними. Например, в космосе есть точка, в которой притяжение Марса становится сильнее, чем притяжение Земли.

Ученые обнаружили, что в нашем мире существуют четыре фундаментальные силы. Это гравитация, электромагнитная сила, слабое взаимодействие и сильное взаимодействие. Силы изменяют движение объекта, и эти четыре фундаментальные силы определяют, как взаимодействует все во Вселенной.

Гравитация — самая слабая сила, но ее можно увидеть в природе больше, чем другие, и в больших масштабах она оказывает наибольшее влияние на весь мир. Гравитация является одновременно причиной, по которой люди удерживаются на поверхности Земли, и почему планеты удерживаются на своих орбитах вокруг Солнца, а также Солнечная система в галактике в целом.

---

Вас также может заинтересовать:

Факты о Земле для детей: удивительные факты и много полезной информации, чтобы познакомить вашего ребенка с нашей прекрасной планетой 🌏

---

Гравитация оказывает на наш мир несколько различных эффектов, помимо того факта, что гравитация не только удерживает предметы на земле, но и придает им вес. Предметы весят меньше на планетах с меньшей гравитацией. Гравитация естественного спутника Земли — Луны — обеспечивает морские приливы и отливы на Земле. Гравитация поддерживает движение Земли по своей орбите и сохраняет атмосферу нашей планеты, позволяя существам дышать, а также защищая их от солнечной радиации.

Гравитация также является очень важным явлением в создании Вселенной. Газы, наполняющие нашу Вселенную, притягиваются друг к другу под действием гравитации, образуя скопления, звезды и планеты, а также другие крупные объекты. Некоторые ученые считают, что частицы после Большого Взрыва образовали коллапс во Вселенной, но остановился он именно благодаря гравитации.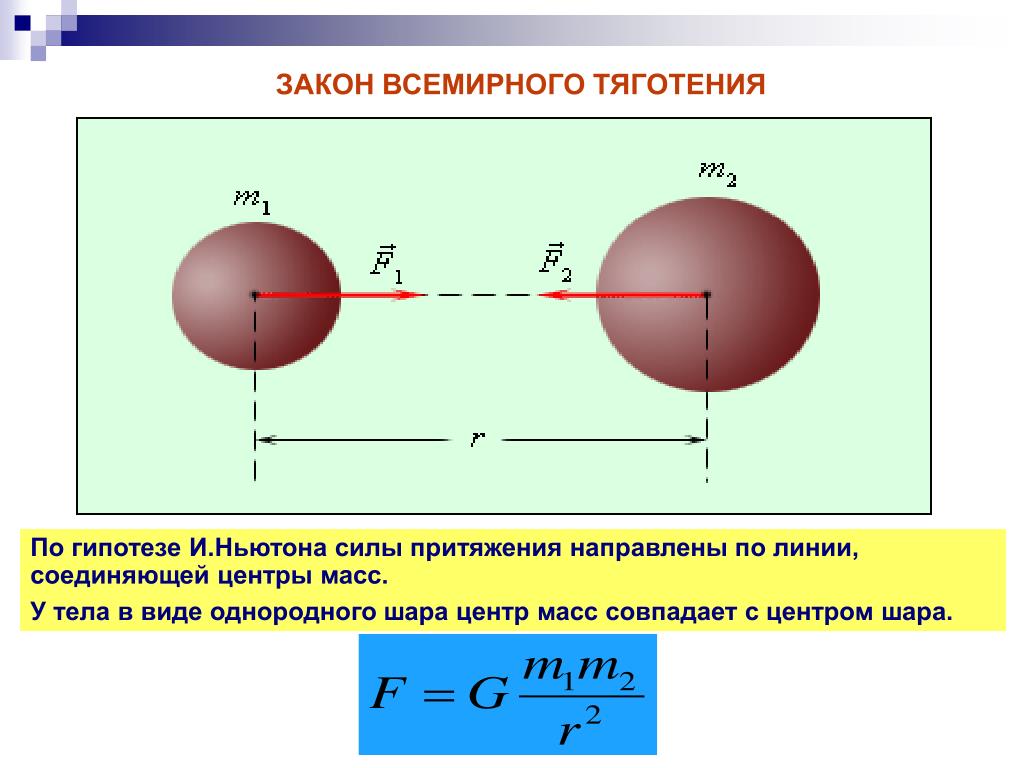 Гравитация сближает звездные системы, поэтому образуются галактики, а это принципиально важно для всей Вселенной.

От чего зависит гравитация?

Очень интересный вопрос.

Исходя из закона всемирного тяготения, гравитационное притяжение между двумя материальными объектами всегда зависит от массы каждого из этих объектов, а также от расстояния между ними.

Вот как звучит формулировка закона всемирного тяготения:

Между любыми двумя материальными объектами существует сила притяжения, действующая по прямой линии, при этом величина этой силы равна прямо пропорционально массе каждого из этих тел и обратно пропорционально квадрату расстояния между ними .

В виде формулы закон всемирного тяготения записывается так:

F = G*M1*M2 / R2 , где

F — сила притяжения между двумя телами,

М1 и М2 – массы частиц,

R – расстояние между ними,

G = 6,6742 · 10–11 м3/(с2 · кг) – гравитационная постоянная.

Кто открыл силу гравитации?

В Древней Греции считалось, что гравитация находится внутри самого объекта, и это позволяет объектам притягиваться к Земле. Тяжелых людей естественно тянет к земле, а легкие языки пламени устремляются к небу. Напротив, индийские ученые, в частности Арьябхата, говорили, что какая-то сила удерживает объекты на Земле. Однако его теория помещает Землю в центр Вселенной.

Около 600 г. н.э. один из математиков по имени Брахмагупта впервые описал гравитацию как силу притяжения. Но и после этого люди не переставали думать о природе гравитационных сил. Так было во времена Ренессанса.

Говорят, что Галилей бросал предметы со стороны падающей Пизанской башни, чтобы посмотреть, что произойдет, когда они упадут. Независимо от того, использовалась ли башня для таких опытов, Галилей установил, что все материальные тела при падении ускоряются с одинаковой скоростью.

Другие ученые также основывали свои аргументы на экспериментах. Гримальди и Риччоли рассчитали значение такого параметра, который впоследствии был назван «гравитационной постоянной». Есть еще одна работа о гравитационных силах, в которой описываются астрономические положения Иоганна Кеплера. Этот ученый рассчитал траектории орбит известных планет на основе своей теории. Но тем не менее в современном мире принято считать, что формулировку классического закона всемирного тяготения предложил ученый по имени Исаак Ньютон.

На закате своих дней Исаак Ньютон рассказал, как это произошло. Он гулял в яблоневом саду в имении своих родителей и вдруг увидел Луну на дневном небе. И тут же, на его глазах, яблоко сорвалось с ветки и упало на землю. В то время Ньютон уже работал над своими знаменитыми законами движения. Он уже знал, что, например, яблоко упадет вертикально вниз к Земле под действием силы тяжести. Он также понял, что Луна находится не только в небе, но и вращается по своей орбите вокруг нашей планеты. Соответственно на Луну действует сила, не позволяющая ей отклониться от своего курса и улететь в космос.

Тут ему пришла в голову мысль, что, скорее всего, это та же самая сила, которая заставляет яблоко падать на поверхность Земли и оставляет Луну на своем месте в космосе. Ньютон предположил, что ряд событий, казалось бы, не имеющих между собой ничего общего, вызываются одной причиной — силами гравитации. Проделав большую работу, этот человек пришел к мысли, что два тела притягиваются друг к другу так, что сила притяжения между ними должна быть прямо пропорциональна массе этих тел и обратно пропорциональна квадрату расстояния между ними. .

Курсы физики для
детей 7-13 лет

Мы воплощаем в жизнь лучшие качества науки — настоящие эксперименты и исследования, безопасные дома и адаптированные для развлечения и развития детей

узнать больше

Важность гравитации в космосе и на Земле

Ньютон знал, что гравитация — это сила, которая притягивает объекты друг к другу. И его законы предсказывали интенсивность этой силы с поразительной точностью. Но как именно работает гравитация? В чем его принципиальное значение? Как Луна притягивается к Земле за сотни тысяч километров?

Но сегодня человек вышел за круг аспектов, в которых формировалась теория Ньютона в XVII веке.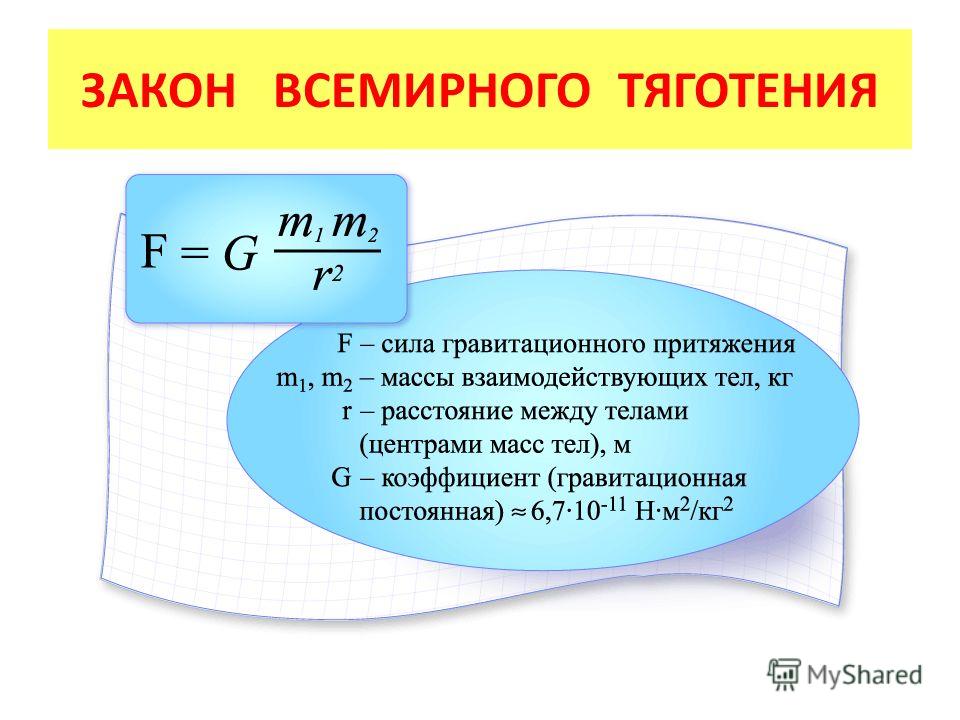 В начале 20 века Альберт Эйнштейн представил новое видение того, как можно рассматривать гравитацию. Он описал эту научную теорию в созданной им «Теории относительности».

Эта теория объясняет гравитационные взаимодействия тел в космическом масштабе искривлением пространства гравитирующими телами. Величина кривизны пропорциональна массе взятых объектов. Но в масштабах земной поверхности и движений на ней нет смысла пользоваться общей теорией относительности, так как ничего нового она дать не может, а если и даст, то лишь мизерными поправками в расчетах можно и вовсе пренебречь.

Тем не менее, эта созданная Эйнштейном теория, описывающая гравитацию как искривление пространства и времени массивными телами пространства, помогает ученым моделировать взаимодействие крупных объектов во Вселенной. Это объясняет многие явления в космосе. Говоря простым языком, космическое пространство представляется как одно большое полотно, натянутое вместе со всей вселенной. На этом полотне располагаются массивные предметы, изгибающие его поверхность. Тем самым близлежащие объекты попадают под влияние этой кривизны. Таким образом, тела притягиваются друг к другу.

А что можно сказать о гравитации на нашей планете?

Если гравитация — это общее понятие, которым обладают все объекты во Вселенной, то гравитация на нашей планете — частный случай проявления этого понятия. Наша планета притягивает все материальные объекты. Благодаря этому люди и все животные могут свободно передвигаться по суше. Водоемы остаются в пределах своих берегов, а воздушная атмосфера удерживается на планете и не улетает в космос.

---

Вам также могут быть интересны другие разделы «Физика для детей»:

• Состояние вещества: твердые, жидкие и газообразные
• Как работает электричество?
• Сила и движение
• Магниты для детей: как работает магнетизм?

---

Что такое вес?

Вес – это сила, с которой любое материальное тело вследствие притяжения Земли воздействует на опору или подвес.

Вес и гравитация имеют разную физическую природу. Сила тяжести возникает от взаимодействия тела и Земли. Вес тела возникает от взаимодействия тела и опоры (подвески). При этом опора (подвеска) деформируется, что приводит к возникновению силы упругости. Из третьего закона Ньютона следует, что вес тела, т. е. сила, с которой тело давит на опору (или растягивает подвес), по величине совпадает с силой, действующей со стороны опоры на данное тело. Сила, с которой опора давит на тело, называется силой реакции опоры.

Массу тела не следует путать с массой тела. Масса тела — скалярная величина, измеряемая в килограммах. Вес предмета, то есть вес материального тела, есть векторная величина, и мы должны измерять ее в единицах, называемых ньютонами.

Интересные факты о гравитации

1. Людям, побывавшим в космосе и вернувшимся на Землю, поначалу достаточно сложно привыкнуть к силе гравитационного воздействия нашей планеты. Иногда это занимает несколько недель.
2. Некоторые исследования показывают, что в условиях невесомости человеческое тело может потерять 1% массы костного мозга в течение одного месяца.
3. Среди планет Марс обладает наименьшей гравитацией в Солнечной системе, а Юпитер — наибольшей.
4. Бактерии, известные человечеству как Salmonella, вызывают кишечные заболевания. Эти бактерии более агрессивно ведут себя в невесомом состоянии и могут нанести более серьезный вред человеку.
5. Из всех известных астрономических объектов во Вселенной наибольшей гравитацией обладают черные дыры. Если взять черную дыру размером с теннисный мяч, она будет иметь такую ​​же гравитацию, как планета Земля.
6. В разных местах нашей планеты сила притяжения тоже будет разной. Например, в районе Гудзонова залива в Канаде она будет ниже, чем в других местах нашей планеты.
7. Гравитация не такая сильная. Какой-то маленький магнит, прицепившийся к металлическому потолку, с легкостью преодолевает его.
8. Чтобы преодолеть гравитацию Земли, ракете необходимо разогнаться до 11,2 километров в секунду.