Скалярное произведение векторов 9 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов

 

Урок: Скалярное произведение векторов

 

1. Тема урока, введение

 

 

Тема урока: «Скалярное произведение векторов». На этом уроке мы рассмотрим скалярное произведение векторов и решим задачи на вычисление скалярного произведения.

 

 

2. Напоминание основных сведений о векторах

 

 

Напомним кратко основные сведения, которые мы знаем о векторах.

 

1.  Определение. Вектор – это направленный отрезок, обозначение 

2.  Операции с векторами.

а)   Сложение векторов.

Правило параллелограмма.

Правило треугольника.

б)   Умножение вектора на число.

3. Угол между векторами.

4. Скалярное произведение векторов.

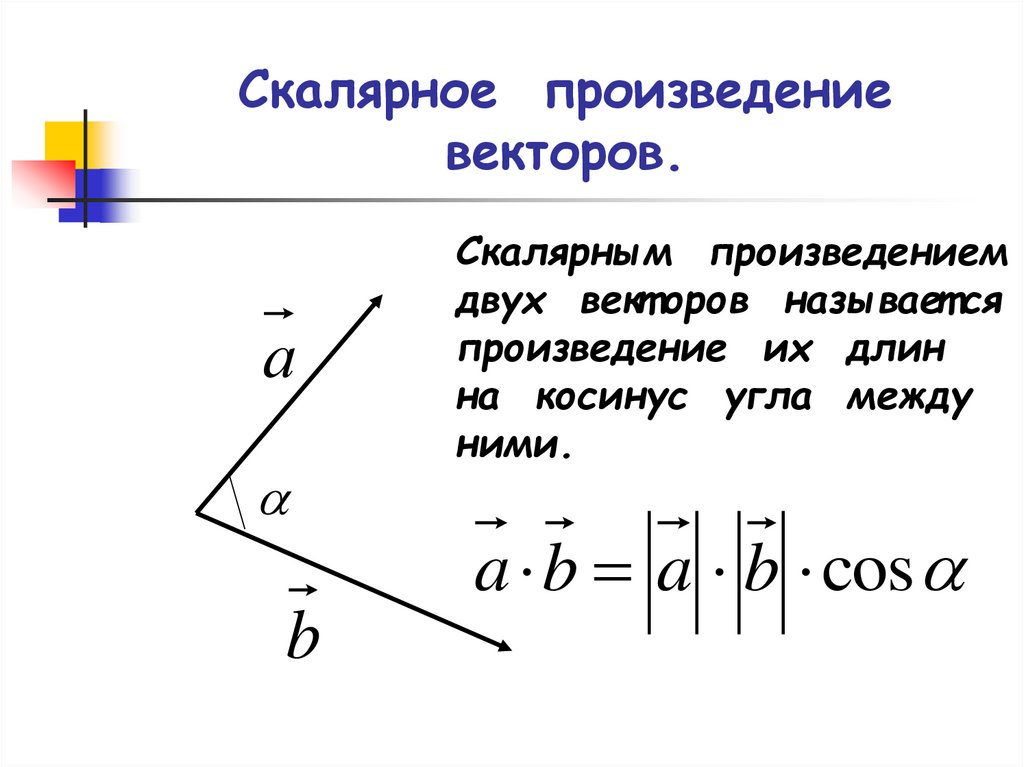
Скалярное произведение векторов – это произведение их длин на косинус угла между ними.

Заметим, что  – это проекция вектора  на направление вектора  . Из определения следует, что скалярное произведение векторов – это число, характеризующее взаимное расположение векторов.

 

 

3. Анализ формулы скалярного произведения векторов

 

 

Рассмотрим некоторые частные случаи взаимного расположения векторов.

 

1.  Перпендикулярные векторы.

Если , то   и  .

Сила в направлении  не совершает никакой работы, скалярное произведение Обратно: если , то   в силу равенства .

Получаем следующий важный вывод: Скалярное произведение векторов равно нулю тогда и только тогда, когда векторы перпендикулярны.

2. Коллинеарные векторы.

Рассмотрим коллинеарные векторы: они могут быть сонаправлены или противоположно направлены.

а) Сонаправленные векторы.

, поэтому Таким образом,

б) Противоположно направленные векторы.

, поэтому  

Таким образом,

3. Равные векторы. Рассмотрим случай, когда

Определение: Скалярное произведение  называется скалярным квадратом вектора и обозначается  ,  . Свойство: Скалярный квадрат вектора равен квадрату его длины,  .

 

4. Решение задач на вычисление скалярного произведения векторов

 

 

Следует научиться вычислять скалярное произведение векторов не только в частных, но и в общих случаях. Рассмотрим следующую задачу.

 

Задача. Вычислить скалярное произведение векторов  и  , если  , угол между ними равен:

а)    

б)   

в)  

 

а) Дано:

Найти: Решение: Ответ:

б)  Дано:

Найти: Решение: или  Ответ: 0.

в) Дано:

Найти:

Решение:Ответ:

 

 

5. Вычисление скалярного произведения векторов в геометрических задачах

 

 

Векторы часто присутствуют и в различных геометрических фигурах. Рассмотрим следующую задачу.

 

Задача. В равностороннем треугольнике ABC со стороной a проведена высота  BD. Вычислить скалярное произведение векторов:

а)                       

б)  

в)  

г)  

Решение:

а)   Ответ:

б) Для определения угла между векторами отложим вектор  от точки

. Ответ: .

в)    Ответ: 0.

г)   Ответ:

 

 

6. Вычисление скалярного произведения векторов в физической задаче

 

 

Задача. К одной и той же точке приложены две силы  и  , действующие под углом  друг к другу, причем . Найти величину равнодействующей силы  .

 

Дано:

Найти: .

Решение:

Ответ:

 

7. Заключение

 

 

Итак, мы рассмотрели разные задачи на вычисление скалярного произведения векторов. На следующем уроке мы рассмотрим скалярное произведение векторов в координатах.

 

 

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science.ru (Источник).
2. Mathematics.ru (Источник). 

 

Домашнее задание

1. Атанасян Л. С. и др. Геометрия 7–9 классы. №№1041, 1042.

 

 

 

Как ⭐ найти скалярное произведение векторов по координатам: теорема и доказательство

Физический смысл скалярного произведения

Распространенное понятие такое, как скалярное произведение обладает физическим смыслом. Его можно объяснить так, что работа А является результатом умножения силы F, которая производится постоянно во время движения тела, вектора а и составляющий с направлением силы F угол ϕ:

A=∣F∣·∣a∣=∣F∣·∣a∣·cosϕ

В качестве презентации введенного понятия рассмотрим рисунок:

Источник: matematicus. ru

На рисунке изображены следующие величины, с которыми можно часто встретиться в классе на уроках алгебры, геометрии и физики при рассмотрении различных теорем и доказательств:

• A является скалярной величиной и обозначением работы;
• a представляет собой вектор перемещения (смещения) материальной точки;
• F определяется, как вектор силы, которая оказывает воздействие на данную точку;
• ϕ является углом силы F, действующим к смещению a.

Пример 1

В качестве примера разберем простую задачу. Предположим, что имеется два вектора а и b с длинами 3 м и 2 м соответственно. Угол между этими векторами составляет 120 градусов. Требуется определить, чему равно скалярное произведение этих векторов.

Решение будет выглядеть следующим образом:

a·b=∣a∣·∣b∣·cos(ϕ)=3·2·cos(120)=−3м2

Основные определения

Определение 1

Системой координат называют метод определения положения и перемещения точки или тела с использованием чисел и других символов.

Определение 2

Координаты представляют собой совокупность чисел, определяющих положение некого объекта относительно прямой, плоскости, поверхности, либо пространства.

Определение 3

Скаляр является величиной, полностью определяемой в какой-либо системе координат с помощью одного числа или функции.

Определение 4

Вектор является направленным отрезком прямой, для которого известны точки начала и конца.

Если вектор начинается в точке А, а заканчивается в точке В, то его обозначают, как AB→. Допускается обозначение вектора с помощью малых латинских букв, над которыми изображены стрелочки или черточки, к примеру, a→.

Определение 5

Скалярное произведение пары векторов a¯ и b¯, отличных от нуля, представляет собой число, равное произведению длин данных векторов на косинус угла между ними:

a¯b¯=a¯·b¯=(a¯,b¯)=|a¯||b¯|cos(a¯,b¯)

Пример 2

Рассмотрим типичный пример. Требуется продемонстрировать, как будет вычисляться скалярное произведение векторов a¯ и b¯. Данные векторы обладают длинами 2 и 3 соответственно, а разделяет их угол в 60°.

Запишем условие задания:

|a¯|=2

|b¯|=3

(a¯,b¯)

В результате:

a¯·b¯=(a¯,b¯)=2·3·cos60°=6·12=3

Примечание 1

Особым случаем является равенство какого-либо из векторов a¯ или b¯ нулевому вектору. Тогда (a¯,b¯)=0.

Скалярное произведение пары векторов характеризуется следующими свойствами:

1. Если вычислить скалярное произведение вектора a¯ самого на себя, то результат в любом случае будет положительным, либо имеет нулевое значение: a¯·a¯=a¯2=a¯, a¯≥0. Выражение a¯·a¯=a¯2=a¯, a¯ является скалярным квадратом вектора a¯.
2. Нулевое значение скалярного произведения вектора самого на себя возможно лишь в том случае, когда рассматривается нулевой вектор: a¯·a¯=0⇔=a¯=0¯.
3. Значение скалярного произведения вектора самого на себя представляет собой квадрат модуля заданного вектора: a¯·a¯=a¯2=a¯2.
4. Действие по поиску скалярного произведения является коммуникативным, то есть: a¯, b¯=b¯, a¯.
5. В том случае, когда скалярное произведение пары ненулевых векторов имеет нулевое значение, данные вектора являются ортогональными, то есть перпендикулярными: a¯, b¯=0, a¯, b¯≠0¯⇔a¯⊥b¯.
6. λa¯, b¯=λ·a¯, b¯
7. Действие по поиску результата скалярного произведения векторов является дистрибутивным, то есть: a¯+b¯, c¯=a¯, c¯+b¯, c¯.
8. Знак скалярного произведения зависит от значения угла между векторами. В том случае, когда угол, разделяющий вектора, является острым, скалярное произведение имеет знак плюс, то есть обладает положительным значением. Это объясняется положительным значением косинуса острого угла. Если вектора составляют тупой угол, то скалярное произведение данных векторов будет иметь знак минус, то есть являться отрицательным. Причиной этому служит отрицательное значение величины косинуса тупого угла. Справедливыми являются и обратные утверждения.
9. Угол между сонаправленными векторами составляет 0°. В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением.

Формулы скалярного произведения векторов заданных координатами

Формула 1

В том случае, когда векторы a¯ и b¯ характеризуются координатами:

a¯=a1;a2;a3,

b¯=b1;b2;b3

Скалярное произведение данных векторов модно определить с помощью следующей формулы:

(a¯,b¯)=a1b1+a2b2+a3b3

Определение 6

Скалярным произведением векторов, которые заданы собственными координатами, называют сумму произведений соответствующих им координат.

Пример 3

Рассмотрим пример. Попробуем определить скалярное произведение двух векторов с координатами:

a¯=(3;-1)

b¯=(-2;7)

Воспользуемся уже знакомой формулой:

a¯b¯=3·(-2)+(-1)·7=-6-7=-13

Формула 2

Определить, какой длиной обладает вектор a¯=a1;a2;a3 с собственными координатами, можно с помощью формулы:

|a¯|=a12+a22+a32

Определение 7

Длина, или модуль вектора с заданными собственными координатами является корнем квадратным из суммы квадратов координат.

Пример 4

Рассмотрим типичный пример. Представим, что требуется найти длину вектора с заданными координатами:

a¯=(-4;3)

Воспользуемся записанной выше формулой и получим:

|a¯|=(-4)2+32=16+9=25=5

Формула 3

Формула для расчета угла, который разделяет два вектора a¯=a1;a2;a3,b¯=b1;b2;b3:

cos(a¯,b¯)=(a¯;b¯)|a¯|·|b¯|=a1b1+a2b2+a3b3a12+a22+a32·b12+b22+b32

Пример 5

Постараемся решить задачу. Требуется вычислить угол, расположенный между двух векторов a¯=(1;3)иb¯=(1;0).

Воспользуемся записанной формулой и выполним вычисления:

cos(a¯,b¯)=1·1+3·012+(3)2·12+02=12

(a¯,b¯)=arccos12=60°

Примеры задач на вычисление скалярного произведения векторов

Задача 1

Даны два вектора с определенными координатами, скалярное произведение которых требуется вычислить:

a¯=(-1;2) и b¯=(2;1)

Решение

Заметим, что для векторов указаны координаты. Применим соответствующую формулу. В процессе выполним умножение соответствующих координат и найдем их сумму:

(a¯,b¯)=-1·2+2·1=-2+2=0

В итоге произведение обладает нулевым значением. Данный результат означает, что векторы расположены перпендикулярно относительно друг друга, или являются ортогональными. Запишем ответ.

Ответ: (a¯,b¯)=0

Задача 2

В пространстве задана пара векторов, которые имеют определенное в нем начало и конец:

A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2)

Необходимо вычислить, чему равно скалярное произведение векторов AB¯ и AC¯.

Решение

В данном случае не получится найти скалярное произведение векторов, так как имеются лишь заданные в условии точки. По этой причине сначала следует определить непосредственно сами векторы AB¯ и AC¯. Для этого вычислим разность конца и начала каждого вектора, то есть найдем разность соответствующих координат данных точек:

AB¯=(-1-1;4-3;1-(-2))=(-2;1;3)

AC¯=(2-1;1-3;-2-(-2))=(1;-2;0)

Далее можно приступать к вычислению скалярного произведения найденных векторов:

(AB¯,AC¯)=-2·1+1·(-2)+3·0=-2-2+0=-4

Ответ: (AB¯,AC¯)=-4

Задача 3

Даны вектора, скалярное произведение которых требуется определить:

a¯=-1; 2; 3, b¯=2; 0; -1.

Решение

Воспользуемся уже знакомой формулой, согласно которой скалярное произведение пары векторов соответствует сумме произведений их координат, которые определены:

a¯, b¯=-1·2+2·0+3·-1=-2+0-3=-5

Ответ: a¯, b¯=-5.

Задача 4

Дана пара векторов:

a¯=x; -1 и b¯=3; 2

Необходимо вычислить такие значения х, при которых записанные векторы являются ортогональными, то есть векторы расположены перпендикулярно по отношению друг к другу.

Решение

Условие задачи, то есть ортогональность заданных векторов, выполняется лишь в том случае, когда скалярное произведение этих векторов обладает нулевым значением. Найдем его по уже известной формуле:

a¯·b¯=x·3+-1·2=3x-2=0⇒3x=2⇒x=23

Ответ: x=23

Задача 5

Дан некий треугольник с равными друг другу сторонами ∆ABC. Длины его сторон составляют 1. Требуется определить, чему равно:

AB→·BC→+BC→·CA→+CA→·AB→

Решение

Ответ: =-32

Задача 6

Имеется пара векторов, которые являются неколлинеарными:

a и b

Нужно определить вектор x, который будет компланарен заданным векторам a и b, а также соответствует следующей системе уравнений:

Решение

Заметим, что в том случае, когда вектора a и b являются неколлинеарными, данные вектора составляют базис относительно плоскости. Какой-либо компланарный вектор для данных векторов допустимо представить в следующем виде:

x=λa+μb

Используя записанное соотношение, изменим вид начальной системы из условий задачи:

Найдем решения записанной системы:

В результате получим нужный вектор:

x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2

Ответ: x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2

Задача 7

Имеется некий параллелограмм OACB. Для этой геометрической фигуры предусмотрены следующие параметры:

длина |OA|=a

длина |OB|=b

угол ∠AOB=α

Необходимо найти, чему равна длина d диагонали OC параллелограмма, а также определить значение косинусов углов, которые расположены между диагональю и сторонами параллелограмма.

Решение

Заметим, что:

OC→=OA→+OB→

В результате длина диагонали составит:

Углы, которые разделяют диагональ и стороны параллелограмма, можно вычислить таким образом:

Ответ: a2+b2+2abcosα,a+bcosαa2+b2+2abcosα,acosα+ba2+b2+2abcosα.

Скалярное произведение векторов

Скалярное произведение векторов

Скалярное произведение и векторное произведение — два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Скалярное произведение двух векторов можно построить, взяв компонент одного вектора в направлении другого и умножив его на величину другого вектора. Это можно выразить в виде: Если векторы выражены через единичные векторы i, j и k вдоль направлений x, y и z, скалярное произведение также может быть выражено в виде: Скалярное произведение также называется «внутренним произведением» или «точечным произведением» в некоторых текстах по математике. Матричный подход к скалярному произведению

Индекс Векторные понятия

Гиперфизика***** Механика R Ступица

Назад

Вы можете ввести значения в любое из полей ниже. Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy. Активная формула: щелкните скалярное произведение или угол, чтобы обновить расчет. Примечание. Приведенные выше числа не будут принудительно согласованы до тех пор, пока вы не щелкнете либо по скалярному произведению, либо по углу в активной формуле выше.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

С геометрической точки зрения скалярное произведение полезно для нахождения направления между произвольными векторами в пространстве. Так как два выражения для произведения: включают компоненты двух векторов, и поскольку величины A и B могут быть рассчитаны из компонентов, используя: , то можно вычислить косинус угла и определить угол. Одним из важных физических применений скалярного произведения является вычисление работы: Скалярное произведение используется для выражения магнитной потенциальной энергии и потенциала электрического диполя.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

Иногда удобно представлять векторы в виде матриц-строк или столбцов, а не в терминах единичных векторов, как это было сделано при рассмотрении скалярного произведения выше. Если мы будем рассматривать обычные пространственные векторы как матрицы-столбцы их компонентов x, y и z, то транспонирование этих векторов будет матрицей-строкой. Тогда мы могли бы написать для векторов A и B: Тогда матричное произведение этих двух матриц даст только одно число, являющееся суммой произведений соответствующих пространственных компонентов двух векторов. Затем это число является скалярным произведением двух векторов. Представленное таким образом скалярное произведение двух векторов иллюстрирует процесс, который используется при умножении матриц, где сумма произведений элементов строки и столбца дает одно число.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

Что такое скалярное произведение?

По

• Роберт Шелдон

Что такое скалярное произведение?

Скалярное произведение, также называемое скалярным произведением, является мерой того, насколько близко два вектора совпадают с точки зрения направлений, которые они указывают.

Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.

Вектор — это величина, которая имеет как направление, так и величину (длину вектора). На рис. 1 показаны два вектора ( a и b ) на двумерной декартовой плоскости. Вектор a имеет величину 8 и расположен под углом 115 градусов к оси x (движется против часовой стрелки). Вектор

b имеет звездную величину 10 и расположен под углом 45 градусов к оси x. Угол между двумя векторами, представленный греческой буквой тета (θ), составляет 70 градусов, что вычисляется путем вычитания 45 градусов из 115 градусов.

Рис. 1. Диаграмма, показывающая два вектора (a и b) на двумерной декартовой плоскости.

Если известна величина двух векторов и угол между ними, легко вычислить скалярное произведение. Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае

a и b , как показано в следующей формуле:

а • б

Полное уравнение для нахождения скалярного произведения несколько сложнее. Это влечет за собой умножение величины вектора a на величину вектора b , а затем умножение произведения на косинус (cos) угла между векторами, как показано в следующем уравнении:0006

а • б = |а| × |б| × cos(θ)

Вертикальные полосы показывают, что эти значения являются модулями вектора. Иногда вместо одинарных стержней используются двойные стержни. Если значения с рисунка 1 подставить в уравнение, можно быстро вычислить скалярное произведение для этих двух векторов, как показано в следующем уравнении:

a • b = 8 × 10 × cos(70 градусов)
a • b = 8 × 10 × 0,342
a • b = 27,36

Косинус угла округлен до трех знаков после запятой, поэтому конечный результат (27,36) является лишь приблизительным, хотя и близким.

Если величина двух векторов и угол между ними неизвестны, используйте следующую формулу для вычисления скалярного произведения:

a • b = (a _x × b _x ) + (a _y × b _y )

Рис. 2. Схема добавления длин векторов, отраженных на каждой оси, к рис. 1.

В этом случае умножьте длины векторов, поскольку они проецируются на оси x и оси y декартовой плоскости. Чтобы лучше понять, как это работает, рассмотрите рис. 2, который был обновлен по сравнению с рис. 1, чтобы включить длины векторов, отраженные на каждой оси.

Vector a измеряет -3,4 по оси x и 7,3 по оси y. (Эти числа были округлены до одного десятичного знака.) Вектор b измеряет 7,1 по оси x и 7,1 по оси y. Для этого вектора измерения одинаковы по каждой оси, потому что вектор находится под углом 45 градусов. Эти суммы можно подставить в следующую новую формулу:

.

a • b = (a _x × b _x ) + (a _y × b _y )
a • b = (-3,4 × 7,1) + (7,3 × 7,1)

а • b = -24,12 + 51,83
а • b = 27,71

Поскольку числа были округлены, окончательная цифра немного отличается от предыдущей (27,36), но они достаточно близки, чтобы продемонстрировать, как можно использовать два разных метода для вычисления скалярного произведения для пары векторов.

Аналогичный подход можно использовать для вычисления скалярного произведения векторов в трехмерном пространстве. Для этого измените формулу следующим образом, чтобы включить третье измерение (представленное осью Z):

a • b = (a _x x b _x ) + (a _y x b _y ) + (a _z x b _z )

Формула теперь включает в свои расчеты ось Z, но исходные компоненты остаются прежними. Чтобы проверить обновленную формулу, предположим, что оба вектора измеряют 5 по оси Z. Расчеты теперь будут выглядеть следующим образом:

a • b = -(3,4 × 7,1) + (7,3 × 7,1) + (5 x 5)
a • b = -24,12 + 51,83 + 25
a • b = 52,71

Неудивительно, что скалярное произведение равно 52,71, что на 25 больше, чем 27,71 в предыдущем вычислении. Число 25 является результатом добавления компонента a _z × b _z (5 x 5) к уравнению для включения трехмерного пространства.

Скалярное произведение используется в таких областях, как физика, математика и другие области, способами, которые имеют практическое применение в реальном мире. Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.

См. также: Математические символы

Последнее обновление: октябрь 2022 г.

Продолжить чтение О точечном произведении (скалярном произведении)

• 11 навыков работы с данными для машинного обучения и искусственного интеллекта

• 18 инструментов обработки данных, которые следует рассмотреть в 2022 году

• 8 лучших приложений для обработки данных и вариантов использования для бизнеса

• Наука о данных, машинное обучение и искусственный интеллект: как они работают вместе

Wi-Fi 6

Wi-Fi 6, также известный как 802. 11ax, — это последнее поколение и стандарт для беспроводных сетей, который заменяет стандарт 802.11ac или Wi-Fi 5.

ПоискСеть

• беспроводная ячеистая сеть (WMN)

  Беспроводная ячеистая сеть (WMN) — это ячеистая сеть, созданная путем соединения узлов беспроводной точки доступа (WAP), установленных в …

• Wi-Fi 7

  Wi-Fi 7 — это ожидаемый стандарт 802.11be, разрабатываемый IEEE.

• сетевая безопасность

  Сетевая безопасность охватывает все шаги, предпринятые для защиты целостности компьютерной сети и данных в ней.

ПоискБезопасность

• Что такое модель безопасности с нулевым доверием?

  Модель безопасности с нулевым доверием — это подход к кибербезопасности, который по умолчанию запрещает доступ к цифровым ресурсам предприятия и …

• RAT (троянец удаленного доступа)

  RAT (троян удаленного доступа) — это вредоносное ПО, которое злоумышленник использует для получения полных административных привилегий и удаленного управления целью . ..

• атака на цепочку поставок

  Атака на цепочку поставок — это тип кибератаки, нацеленной на организации путем сосредоточения внимания на более слабых звеньях в организации …

ПоискCIO

• Пользовательский опыт

  Дизайн взаимодействия с пользователем (UX) — это процесс и практика, используемые для разработки и внедрения продукта, который будет обеспечивать положительные и …

• соблюдение конфиденциальности

  Соблюдение конфиденциальности — это соблюдение компанией установленных правил защиты личной информации, спецификаций или …

• контингент рабочей силы

  Временная рабочая сила — это трудовой резерв, члены которого нанимаются организацией по требованию.

SearchHRSoftware

• Поиск талантов

  Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса . ..

• удержание сотрудников

  Удержание сотрудников — организационная цель, состоящая в сохранении продуктивных и талантливых работников и сокращении текучести кадров за счет поощрения …

• гибридная рабочая модель

  Гибридная модель работы — это структура рабочей силы, включающая сотрудников, работающих удаленно, и тех, кто работает на месте, в офисе компании…

ПоискКлиентОпыт

• CRM (управление взаимоотношениями с клиентами) аналитика

  Аналитика CRM (управление взаимоотношениями с клиентами) включает в себя все программные средства, которые анализируют данные о клиентах и ​​представляют…

• разговорный маркетинг

  Диалоговый маркетинг — это маркетинг, который вовлекает клиентов посредством диалога.

• цифровой маркетинг

  Цифровой маркетинг — это общий термин для любых усилий компании по установлению связи с клиентами с помощью электронных технологий.