2}{3}$ Момент инерции

Статья от экспертов

Рассматривается поведение диска с учётом гироскопического момента, появляющегося при заглаживании свежеотформованных железобетонных изделий. Кроме того, изучается его движение при колебаниях самого диска относительно одной из осей, перпендикулярных к оси динамической симметрии тела. Приводятся формулы, определяющие как величину гироскопического момента, так и силу, с которой прижимается заглаживающий диск к свежеотформованной бетонной смеси.

Научный журнал

Creative Commons

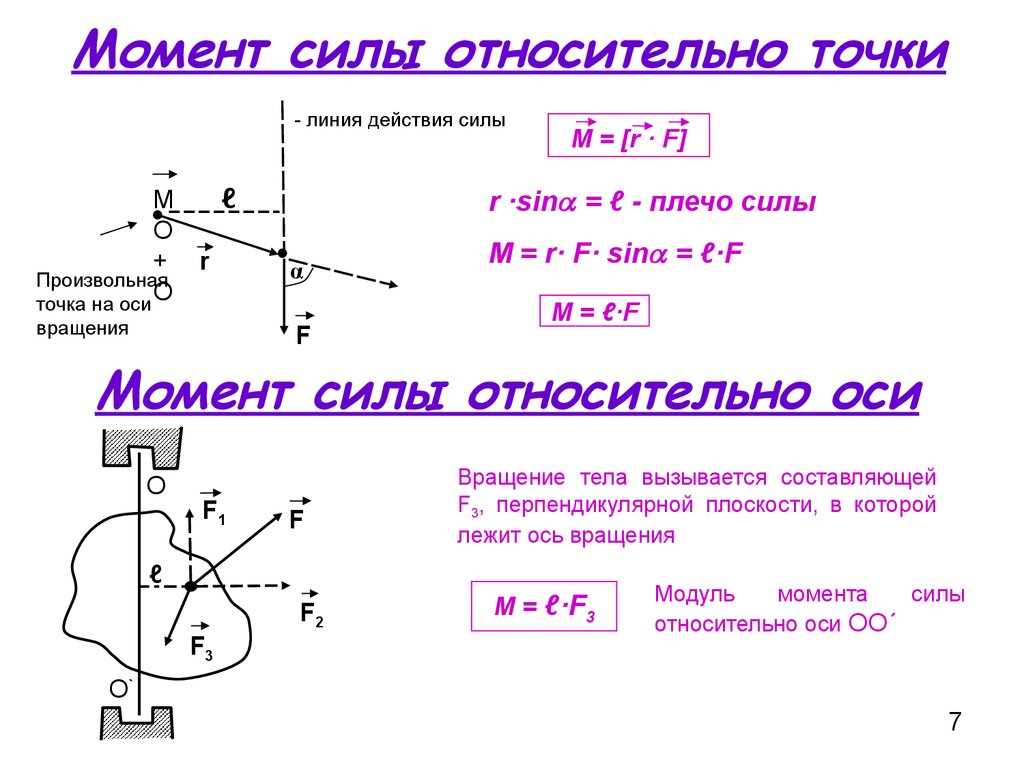
Момент силы относительно оси Замечание 1 Моментом силы относительно оси будет считаться момент…
силы относительно оси нужно: провести перпендикулярно

оси $z$ плоскость и спроецировать на нее силу. ..
Нулевое значение момент силы относительно оси обретает в том случае, когда $F_xy=0$ (при параллельности…
на оси $X$, $Y$: $\sum{F_kx}=0$ $\sum{F_ky}=0$ Момент силы относительно точки Абсолютное значение момента…
Момент силы относительно точки будет выражать следующая формула: $M_0(\vec{F})=hF$.

Статья от экспертов

В работе рассмотрены силы и моменты сил, действующие в фокусе сферической волны с круговой поляризацией на эллипсоидальную диэлектрическую частицу. Расчёты проведены на основе поля дифракции, полученного методом FDTD, расчёт силы и момента силы проводился с помощью тензора напряжений Максвелла. Показано, что в фокусе сферической волны с круговой поляризацией на эллипсоид относительно его центра действует момент силы, который будет стремиться вращать его вокруг оптической оси. При этом эллипсо.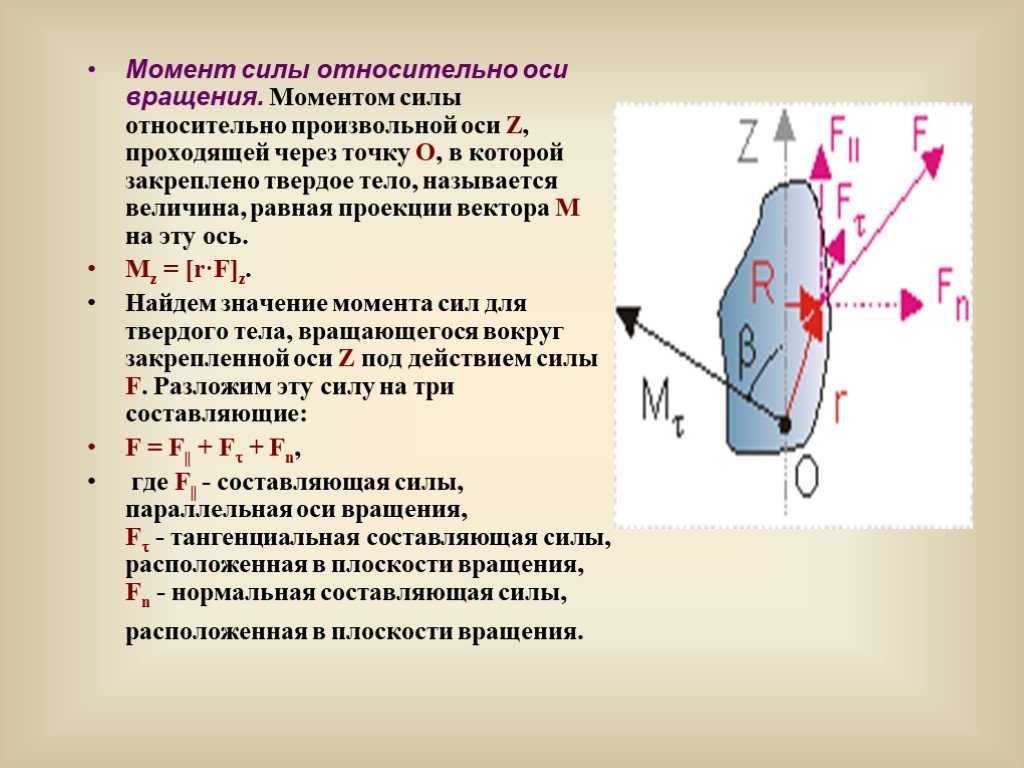

..

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Селицкий Ф.И. Программа(Mathcad). Тренажёр по расчёту момента силы относительно оси

• формат pdf
• размер 96.19 КБ
• добавлен 18 июня 2010 г.

Цель программы — приобрести навыки расчёта момента силы относительно оси, используя разложение силы на cоставляющие, параллельные координатным осям.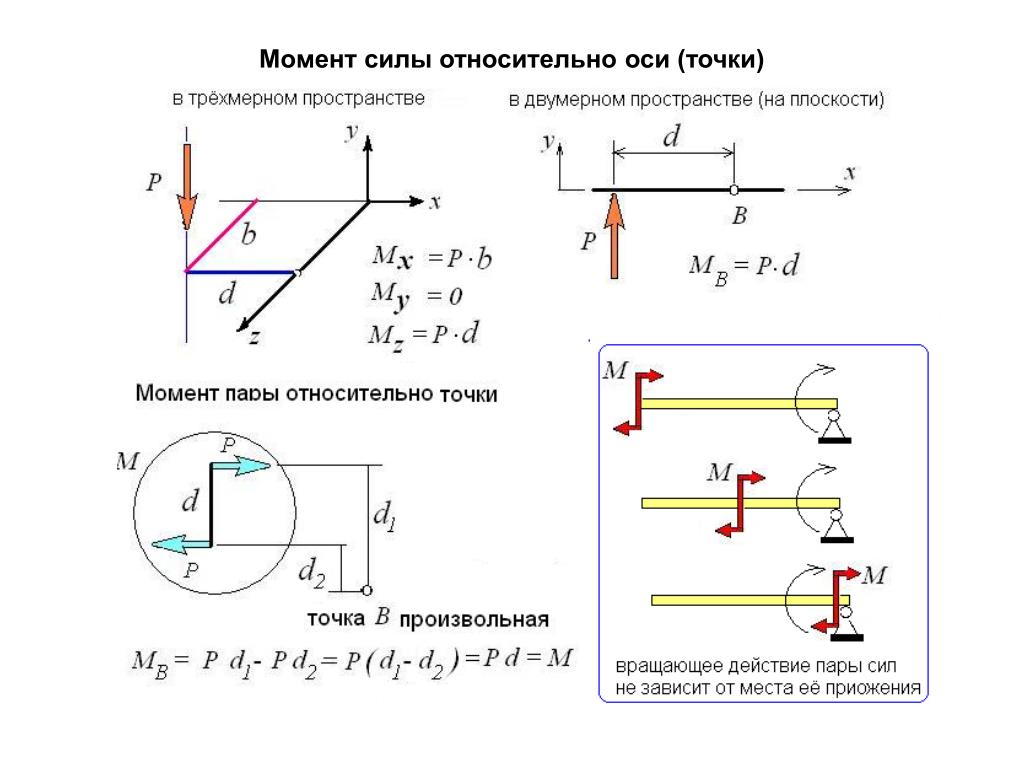

Сила действует в одной из граней параллелепипеда и приложена к одной из его вершин. Требуется найти её момент относительно оси, параллельной одной из координатных осей. При каждом нажатии на клавишу «Новая задача» положение силы и оси меняются. Пользователь должен разложить силу на составляющие и найти сумму их моментов относительно оси. Программа сравнивает ответ пользователя с правильным. В случае неверного ответа указывается характер ошибки (составляющая, плечо, знак момента)

Смотрите также

• формат pdf
• размер 24.15 МБ
• добавлен 14 октября 2009 г.

Пособие, 2005. — 752 с. Рассматривается решение большого количества разнообразных задач курса с помощью Mathcad. Приводятся тексты рабочих документов Mathcad. Изложены основы работы в Mathcad. (Три в одном! )

• формат ppt
• размер 939.32 КБ
• добавлен 26 января 2010 г.

Введение. Основные понятия. Аксиомы статики. Связи и реакции связей. Система сходящихся сил. Теорема о трех силах. Аналитическое определение равнодействующей сходящихся сил. Уравнения равновесия. Произвольная плоская система сил. Момент силы относительно точки. Пара сил. Теоремы о парах. Метод Пуансо. Главный вектор и главный момент. Уравнения равновесия. Три формы уравнений равновесия. Теорема Вариньона. Плоские фермы. Методы расчета. Метод выр…

• формат pdf
• размер 2.23 МБ
• добавлен 21 ноября 2010 г.

Учебное пособие соответствует дисциплине «Теоретическая механика» по ГОС ВПО направления подготовки дипломированных специалистов 190300 «Подвижной состав железных дорог» специальностей 190301 «Локомотивы», 190302 «Вагоны», 190303 «Электрический транспорт железных дорог», направления 270200 «Транспортное строительство» специальности 270204 «Строительство железных дорог, путь и путевое хозяйство», направления 190700 «Организация перевозок и управле.

..

• формат doc
• размер 4.18 МБ
• добавлен 01 февраля 2012 г.

Учебно-методическое пособие для студентов заочной и дистанционной форм обучения при подготовке дипломированного специалиста по направлению 653500 Строительство. – Омск: Изд-во СибАДИ, 2008. – 372 с. Курс теоретической механики разбит на две самостоятельные части, что в основном соответствует распределению материала по семестрам и содержит необходимый минимум для сдачи экзамена. Наглядность и удачно подобранные примеры позволяют в кратчайшие срок…

• формат doc
• размер 8.84 МБ
• добавлен 03 февраля 2012 г.

Учебно-методическое пособие для студентов заочной и дистанционной форм обучения при подготовке дипломированного специалиста по направлению 653500 Строительство.

– Омск: Изд-во СибАДИ, 2007. – 380 с. Курс теоретической механики разбит на две самостоятельные части, что в основном соответствует распределению материала по семестрам и содержит необходимый минимум для сдачи экзамена. Наглядность и удачно подобранные примеры позволяют в кратчайшие срок…

• формат pdf
• размер 130.99 КБ
• добавлен 27 июня 2010 г.

Плоская рама, закрепленная с помощью неподвижного шарнира и невесомого стержня, нагружена силой F и моментом M. Имеется горизонтальная X и вертикальная Y составляющие реакции шарнира и реакция R стержня. Пользователь задает положение стержня, положение силы и направление (знак) момента, которые вместе с реакциями отображаются на экране. Программа составляет уравнения равновесия и находит значения реакций. Программу можно использовать для приобре…

• формат pdf
• размер 134. 02 КБ
• добавлен 17 июня 2010 г.

Цель программы-приобрести навыки расчёта момента силы. В качестве расчётной схемы используется рама, нагруженная силой F и заделанная в точке A. При каждом нажатии на клавишу «Новая задача» конструкция рамы и положение силы меняются. Пользователь должен разложить силу на составляющие по осям координат и найти сумму моментов, составляющих относительно точки A. Программа сравнивает ответ пользователя с правильным. В случае неверного ответа указывае…

• формат djvu
• размер 1.31 МБ
• добавлен 08 декабря 2009 г.

Учебное пособие. Екатеринбург ГОУ ВПО УГТУ-УПИ, 2006. Содержание соответствует программам обучения и требованиям государственных образовательных стандартов. Учебное пособие включает те разделы статики, кинематики и динамики, которые в первую очередь необходимы для последующего изучения основ конструирования. По всем разделам приведены задачи с анализом решения. Содержание. Введение. Статика твердого тела. Основные понятия статики. Аксиомы стати…

• формат pdf
• размер 477.37 КБ
• добавлен 15 июня 2011 г.

Издание НАУ «Харьковский авиационный институт», 2007 г., Харьков, 44 с. Методическое пособие предназначено для студентов, изучающих курс «Теоретическая механика» В методическом пособии хорошо рассмотрены такие вопросы: Понятия и аксиомы статики. Проекция силы на ось и плоскость. Равнодействующая. Момент силы относительно точки Равновесие плоской системы сил, приложенных к твердому телу. Статически определимые и неопределимые задачи Равновесие…

• формат pdf
• размер 582.27 КБ
• добавлен 08 июня 2010 г.

Конспект лекций. — М.: ЭКСМО, 2008. — 160 с. СОДЕРЖАНИЕ Основные понятия и аксиомы статики Сходящиеся силы на плоскости Равнодействующая сходящихся сил на плоскости Леммы о нулевых стержнях Теория пар сил, лежащих в одной плоскости Момент силы относительно точки на плоскости Система сил, произвольно расположенных на плоскости Условия равновесия сил, приложенных к рычагу Сцепление и трение скольжения Графическая статика Диаграмма Максвелла-Кремон…

Момент силы на указанной оси — вопросы и ответы по инженерной механике

Этот набор вопросов и ответов с множественным выбором (MCQ) по инженерной механике посвящен «Моменту силы на указанной оси».

1. Определите модуль момента, создаваемого силой, как показано на диаграмме, которая стремится повернуть стержень ORQP вдоль QP.

a) 80,49 Н·м
b) 72,12 Н·м
c) -36,67 Н·м
d) 36,67 Н·м
Посмотреть ответ

Ответ: a
Объяснение: Использование формулы A.(rxF) дает ответ. В котором A равно 0,89i + 0,447j m.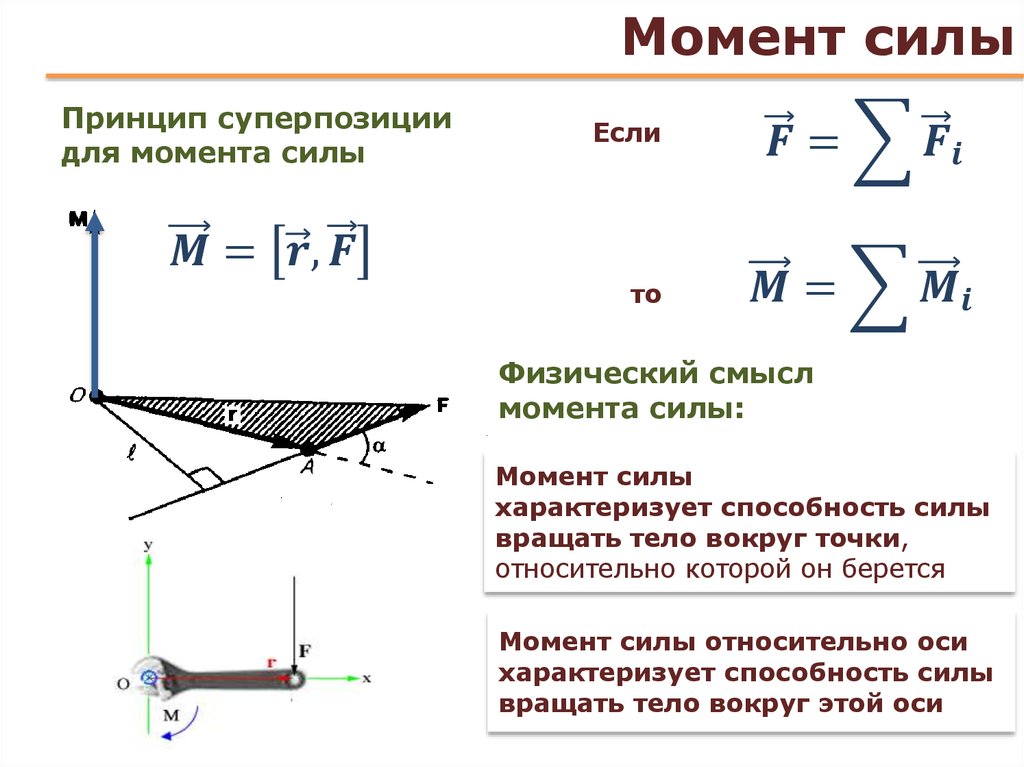 И сила 300 Н, которая приложена к концу стержня. Таким образом, найдя уравнение оси и затем подставив его в уравнение, показанное выше, мы получим ответ. Собственно, основная задача — знать уравнение оси в векторной форме. Тогда получите величину момента.

объявление

объявление

2. Вычисление момента относительно оси и момента относительно любой точки силой, приложенной к телу, отличаются друг от друга.
a) Верно
b) Неверно
Просмотреть ответ

Ответ: a
Объяснение: Вычисление момента относительно оси и момента относительно любой точки силой, приложенной к телу, отличаются друг от друга. Это потому, что оба расчета требуют разных формул. И обе формулы имеют разные входные данные, что, очевидно, отличается.

3. При расчете момента силы относительно оси таблица векторного произведения, т. е. матрица 3X3, созданная для выполнения векторного произведения, имеет 3 строки и содержит три элемента. Какие они сверху вниз?
a) Координаты оси, координаты точки и координаты силы
b) Координаты точки, координаты оси и координаты силы
c) Координаты оси, координаты силы и координаты точки
d) Координаты силы, координаты точки и координаты силы координаты оси
View Answer

Ответ: a
Объяснение: Создаваемая матрица 3X3 имеет координаты осей, координаты точек и координаты силы. Они располагаются сверху вниз. Порядок не может быть изменен. Или, если изменилось, нужно соответствующим образом применить отрицательный знак. Отрицательный, потому что направления меняются местами.

4. Что из следующего верно? (Для A, представляющего векторное представление оси вращения, r радиус-вектор и F вектор силы)
a) A.(rxF)
b) Ax(rxF)
c) A.(r.F)
d) Fx (r.F)
Посмотреть ответ

Ответ: a
Объяснение: Правильная форма уравнения задается как A.(rxF). Где A представляет векторное представление оси вращения, r радиус-вектор и F вектор силы. Обычно это делается для определения момента силы относительно оси. Это если тело под действием силы вращается вокруг оси.

5. Чему равен вектор r в уравнении A.(rxF)?
а) Величина оси, т.е. длина оси
б) Длина вектора силы
в) Длина радиуса
г) Радиус-вектор
Посмотреть Ответ

Ответ: d
Пояснение: r в уравнении A.(rxF) — радиус-вектор. То есть это вектор, который имеет начальную точку на оси и конечную точку в точке действия силы на тело.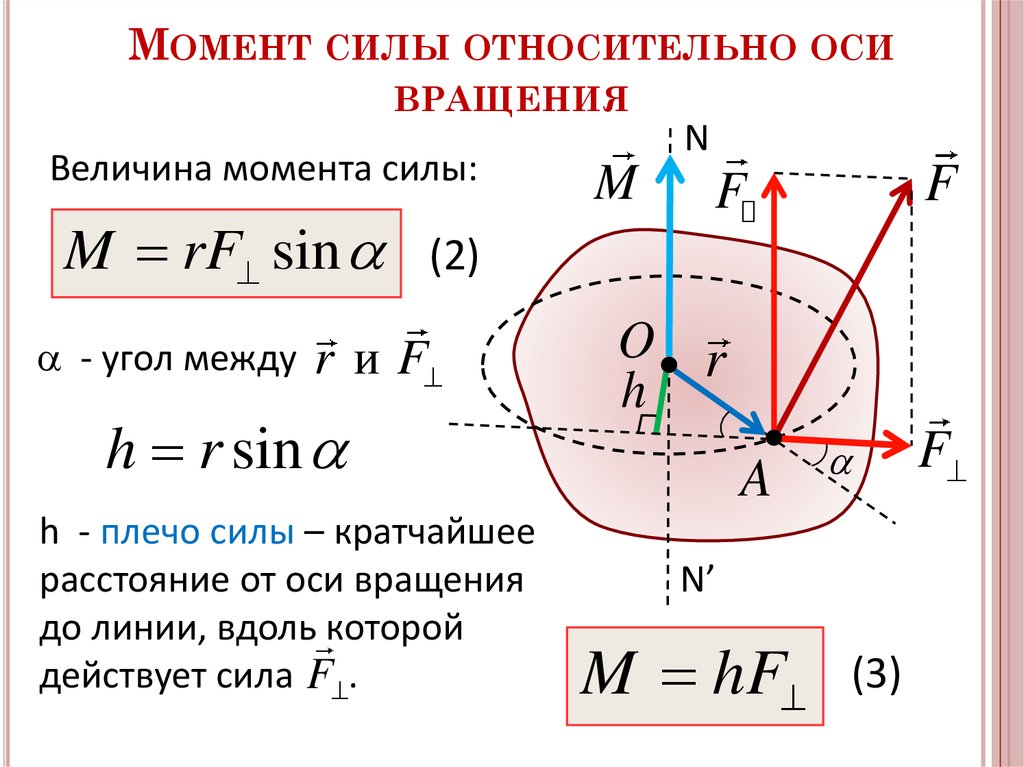 Этот вектор пересекается вектором силы, за которым следует скалярное произведение с вектором оси.

объявление

6. Вектором оси при расчете момента вдоль оси вращения является ось, которая коллинеарна вектору силы.
a) Верно
b) Неверно
Просмотреть ответ

Ответ: b
Объяснение: Ось вращения не может быть коллинеарна вектору силы. Если это так, то вращение тела невозможно. То есть момент силы равен нулю. Это означает, что сила не дает вращения вдоль оси вращения тела.

7. Что из следующего верно?
а) Мы не можем представить момент, вызванный силой вдоль любой оси, в векторной форме
б) Мы можем представить момент, вызванный силой вдоль любой оси, в скалярной форме
в) Мы не можем представить момент, вызванный силой вдоль любая точка в векторной форме
d) Мы можем представить момент, вызванный силой вдоль любой оси, в векторной форме
Просмотреть Ответ

Ответ: d
Объяснение: Поскольку момент является вектором, мы можем легко представить его в векторной форме.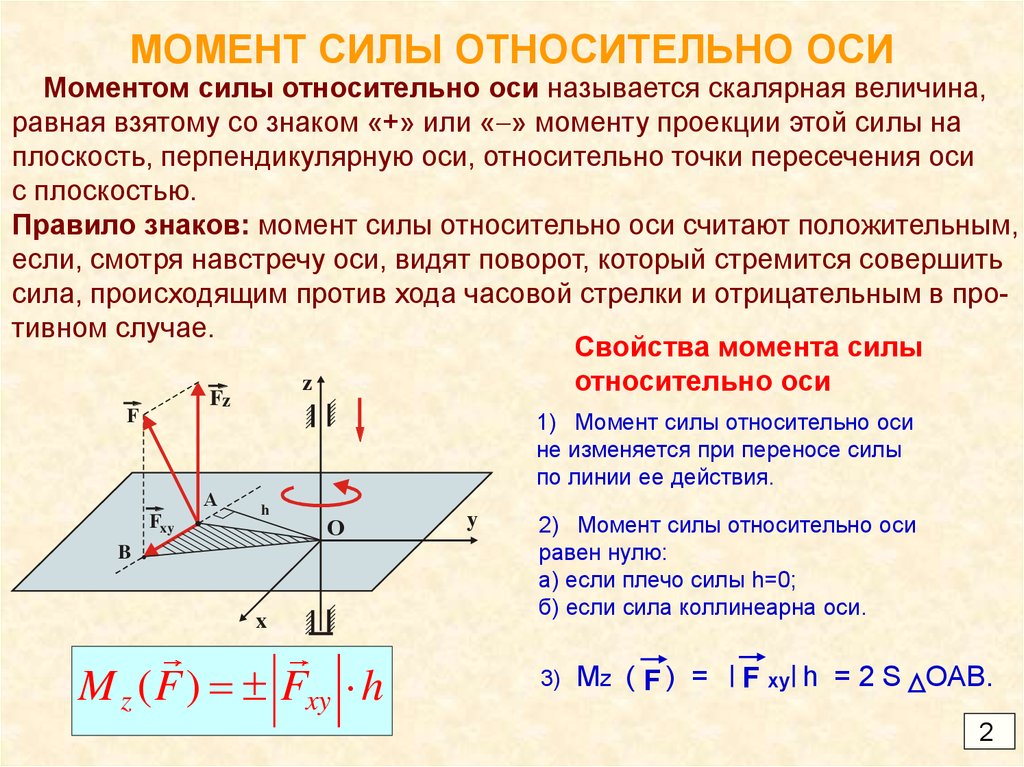 Будь то момент силы, действующей на тело относительно оси, или относительно точки. Мы также можем преобразовать то же самое в декартову форму. Единственное, что нам нужно сделать, это перекрестное произведение радиус-вектора и вектора силы.

реклама

8. Что делать, если перпендикулярное расстояние от оси равно бесконечности?
а) Вращение невозможно
б) Вращение возможно, но создаваемый момент очень мал
в) Приложенная сила будет очень большой даже при небольшом вращении
г) Вращение невозможно, если контакт не нарушен
View Answer

Ответ: c
Объяснение: Большое расстояние означает огромную силу, которую нужно приложить. Поскольку увеличение расстояния также увеличит инерцию сопротивления, что, очевидно, увеличит силу, необходимую для вращения. Хотя мы знаем, что чем больше расстояние, тем меньше сила, приложенная для вращения. Но инерцию иногда приходится принимать в расчет.

9. В уравнении A.(rxF) r направлен от ______________ и заканчивается _____________
a) Ось вращения, вектор силы
b) Ось вращения, точка действия вектора силы на тело
c) Сила вектор, Ось вращения
г) Точка действия вектора силы на тело, Ось вращения
Посмотреть Ответ

Ответ: b
Объяснение: Это радиус-вектор. Радиус-вектор всегда направлен от оси вращения к точке действия силы на тело. Это означает, что радиус-вектор не находится ни в одной точке вектора силы. Скорее он заканчивается в точке на векторе силы, где он находится в контакте с телом.

10. Что делать, если момент силы, вычисленной относительно оси, отрицателен?
а) Это означает, что сила приложена в направлении, противоположном воображаемому
б) Это означает, что направление движения противоположно воображаемому направлению
в) Это означает, что радиус-вектор имеет направление, противоположное воображаемому
d) Такое вычисление означает, что вычисления сделаны неправильно
View Answer

Ответ: b
Объяснение: Это означает, что направление движения противоположно предполагаемому. Мы не можем сказать о направлении силы или направлении радиус-вектора. Но да, мы можем сказать о направлении вращения, поскольку это то, что будет вычисляться. Остальные все детали закреплены. Их нельзя изменить.

11. Определить момент MQP в векторной форме, создаваемой силой, как показано на схеме, которая стремится повернуть стержень ORQP вдоль QP.

а) 72i + 36j Нм
б) 72i – 36j Нм
в) -72i – 36j Нм
г) -72i + 36j Нм
Посмотреть ответ

Ответ: a
Пояснение к формуле .(rxF) дает ответ. В котором A равно 0,89i + 0,447j m. И сила 300 Н, которая приложена к концу стержня. Таким образом, найдя уравнение оси и затем подставив его в уравнение, показанное выше, мы получим ответ. Собственно, основная задача — знать уравнение оси в векторной форме.

12. Определить момент силы F на отрезке QP узла трубы, изображенного на рисунке.

a) 110 Нм
b) 100 Нм
c) 500 Нм
d) 510 Нм
Посмотреть ответ

Ответ: b
Объяснение: Использование формулы A.(rxF) дает ответ. В котором A равно 0,6i + 0,8j m, а r равно 0,5i + 0,5k. И сила 300 Н, которая приложена к концу стержня. Таким образом, найдя уравнение оси и затем подставив его в уравнение, показанное выше, мы получим ответ. Собственно, основная задача — знать уравнение оси в векторной форме. Тогда получите величину момента.

13. Определить модуль момента силы относительно оси PQ.

a) -72Nm
b) 82Nm
c) 90Nm
d) 50Nm
View Answer

Ответ: a
Объяснение: Использование формулы A.(rxF) дает ответ. В котором A равно 0,6i + 0,8j м, а r равно -0,2k, и сила, приложенная к концу стержня. Таким образом, найдя уравнение оси и затем подставив его в уравнение, показанное выше, мы получим ответ. Собственно, основная задача — знать уравнение оси в векторной форме. Тогда получите величину момента.

14. Определить модуль момента силы относительно оси у.

a) -72Nm
b) 82Nm
c) 210Nm
d) 50Nm
View Answer

Ответ: c
Объяснение: Использование формулы A.(rxF) дает ответ. В котором A равно 1j m, r равно -3i + 4j + 2k, а сила приложена к концу стержня. Таким образом, найдя уравнение оси и затем подставив его в уравнение, показанное выше, мы получим ответ. Собственно, основная задача — знать уравнение оси в векторной форме. Тогда получите величину момента.

15. Силы ___________ не вызывают вращения, если вращение рассматривается вокруг оси тела или центральной оси тела.
a) Непараллельные
b) Параллельные
c) Параллельные
d) Непараллельные
Просмотреть ответ

Ответ: b
Объяснение: Совпадающие силы касаются оси вращения. Если какая-либо сила касается этой оси, эта сила не считается или недостаточна, чтобы вызвать вращение. Если сила параллельна, то перпендикулярное расстояние силы от линии оси равно нулю, поэтому вращение отсутствует. Как мы знаем, вращение вызывается моментом.

Sanfoundry Global Education & Learning Series – Инженерная механика.

Чтобы практиковать все области инженерной механики, здесь полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .

Следующие шаги:

• Получите бесплатный диплом инженера-механика
• Участие в конкурсе на получение сертификата инженерной механики
• Стать лучшим специалистом в области инженерной механики
• Пройдите тесты по инженерной механике
• Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
• Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

момент относительно оси — Googlesuche

AlleVideosBilderNewsMapsShoppingBücher

suchoptionen

Вычисление момента относительно оси с помощью скалярного произведения 2: Момент силы относительно оси равен точечному произведению →u и векторному произведению →r и →F. Единичный вектор →u имеет модуль, равный единице, и будет указывать в направлении интересующей нас оси.

_{15. Jan. 2022}

3.5: Момент силы относительно оси — Engineering LibreTexts

eng.libretexts.org › … › 3: Статическое равновесие в системах с твердым телом

20hncheppets

Hervorgehobene Fragen

Что означает момент относительно оси?

Чему равен момент силы относительно данной оси?

Чему равен момент пары относительно оси?

Момент силы относительно оси — Механика Карта

mechanicsmap.psu.edu › 3_равновесие_жесткое_тело

Чтобы найти момент силы относительно определенной оси, мы находим момент, когда сила действует на некоторую точку на этой оси, а затем находим составляющую …

Момент относительно указанной оси | Механика Статика — YouTube

www.youtube.com › смотреть

13.01.2021 · Научитесь находить момент относительно конкретной оси вместо особой точки. Мы говорим о…
Дауэр: 6:51
Прислан: 13.01.2021

Статика: Урок 25 — Момент о заданной оси — YouTube

www.youtube.com › смотреть

13.06.2020 · How to Ace Statics with Jeff Hanson: https://amzn .to/3apfegwtop 15 пунктов Каждая инженерия …
Дауэр: 10:14
Gepostet: 13.06.2020

Bilder

Alle Anzeigen

Alle Anzeigen

[PDF] Момент силы. .ce.cet.ac.in › загрузок

Эффективность силы в отношении ее стремления вызвать вращение тела вокруг оси или точки называется моментом силы. • Измеряется …

Момент силы

www.ae.msstate.edu › vlsm › момент › оси

— плечо момента силы относительно оси x. В этом случае ось момента указывает в положительном направлении x, как показано.

[PDF] Ахмед Абдель-Рахим Урок #10: Момент про линию/Пары…

www.webpages.uidaho.edu › …

Урок № 10: Момент про линию/Пары. Страница 1 из 2. Сегодняшние задачи: 1.